A Reproducible Benchmark for Gas Sensor Array Classification: From FE-ELM to ROCKET and TS2I-CNNs
Abstract
1. Introduction
- (1)
- (2)
- (3)
- systematically compare and analyze the effectiveness of single image representations, RGB fusion combining multiple representations, and late fusion strategies [24];
- (4)
- provide a comprehensive benchmark from traditional classifiers to the latest deep learning models to offer insights for practical model selection in this field.
2. Methods
2.1. Datasets and Experimental Design
2.2. Time-Series to Image Transformation for Feature Extraction
2.2.1. Recurrence Plot
2.2.2. Gramian Angular Field
2.2.3. Markov Transition Field
2.3. Model Architectures and Learning Strategies
2.3.1. Traditional Vector-Based Classifiers
- Flattening: The 3D time-series data (samples, sensors, time points) was transformed into a 2D matrix (samples, features).
- Standardization: Each feature was standardized to have a zero mean and unit variance (z-score normalization) using StandardScaler.
- Dimensionality Reduction: Principal Component Analysis (PCA) was employed to reduce the dimensionality of the feature space.
- Random Vector Functional Link (RVFL)Model Description: A type of single-hidden-layer neural network that combines the input features with non-linear features generated by a random projection of the input. This augmented feature vector is then trained with a linear classifier.Implementation Details: Implemented in the RVFL class, the feature combination is performed using Numpy’s concatenate function. A linear Ridge Regression model serves as the final classifier.Key Hyperparameters: The model’s complexity is governed by the number of hidden neurons (hidden) and the choice of activation function (act), which determines the non-linearity.
- Bagging ELM (BAGELM)Model Description: An ensemble of ELM trained on bootstrap-resampled subsets of the training data. Each base ELM uses a single hidden layer with randomly initialized hidden weights/biases (kept fixed) to produce a non-linear feature map, and fits output weights via ridge-regularized least squares. Final predictions are obtained by probability averaging (or majority voting) across members, which reduces the variance of a single ELM.Implementation Details: Implemented as an ensemble wrapper around an ELM base learner. For each member, a stratified bootstrap sample is drawn; hidden weights/biases are re-initialized; the output layer is solved with ridge regression. At inference, member class probabilities are averaged to yield calibrated predictions; ties fall back to argmax of the averaged scores.Key Hyperparameters: M number of ELM members in the ensemble (e.g., 50–200). hidden (L) number of hidden neurons in each ELM (controls feature capacity). hidden-layer activation (e.g., sigmoid/tanh/ReLU). Lambda (λ) ridge regularization strength for the output weights.
- Feature Ensemble ELMModel Description: A unique ensemble model that takes 3D time-series as direct input, decomposing the temporal axis into multiple ‘phases’ to generate a diverse set of features. Each feature set is processed by an independent ELM, and the final prediction is determined by a majority vote.Implementation Details: This was implemented as the FE-ELM class. The core logic of phase decomposition is handled by the _make_phase_features method.Key Hyperparameters: The model’s structure is primarily defined by the number of phases (tau), which controls the ensemble size and the granularity of feature extraction, and the number of hidden neurons in each ELM (hidden).
2.3.2. Modern Time-Series Classifiers
- ROCKET/MiniROCKETModel Description: These models use 1D convolutions to extract robust features from time-series with exceptional speed. ROCKET generates thousands of random kernels, while MiniROCKET combines a fixed kernel with random parameters.Implementation Details: Implemented as the RocketLite and MiniRocketLite classes, respectively. Both generate feature vectors via their transform methods, which are ultimately classified by Scikit-learn’s linear_model.RidgeClassifierCV.Key Hyperparameters: The dimensionality of the transformed feature space is determined by the number of kernels (n_kernels) for ROCKET, and the number of features to generate (n_features) for MiniROCKET.
- Temporal Convolutional Network (TCN)Model Description: A deep learning architecture for learning long-term dependencies in time-series. It uses dilated causal convolutions to efficiently process wide temporal ranges and employs residual connections for stable training of deep networks.Implementation Details: Implemented as a TCN class inheriting from torch.nn.Module within the PyTorch 1.12.1 framework. Its core module, TemporalBlock, is composed of layers such as nn.Conv1d and nn.BatchNorm1d.Key Hyperparameters: The network architecture is defined by the number of TemporalBlocks (tcn_levels) and hidden channels (tcn_hidden). The training process is controlled by parameters such as the learning rate (lr), batch_size, maximum epochs, and early stopping patience.
2.3.3. Image-Based CNNs
- Implementation Strategies
- 1.
- Single Representation (Sensor Stack)
- 2.
- RGB Fusion
- 3.
- Late Fusion
- Detailed Implementation of Sensor Stack
- Model Architecture and Transfer Learning
2.3.4. Hyperparameter Optimization and Evaluation Protocol
3. Results
3.1. Overall Model Performance
3.2. Analysis of Time-Series-to-Image and Fusion Strategies
3.3. Efficacy of Transfer Learning
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Family | Method | Accuracy (Mean ± Std) | 95% CI | Macro-F1 |
|---|---|---|---|---|
| Time-Series Classifiers | ROCKET | 0.9721 ± 0.0480 | [0.9627, 0.9815] | 0.9757 |
| FE-ELM | 0.9639 ± 0.0578 | [0.9524, 0.9753] | 0.9679 | |
| TCN | 0.9455 ± 0.0745 | [0.9309, 0.9601] | 0.9503 | |
| LR | 0.9030 ± 0.0928 | [0.8846, 0.9214] | 0.9184 | |
| MiniROCKET | 0.8927 ± 0.0885 | [0.8754, 0.9100] | 0.8997 | |
| SVM-LIN | 0.8911 ± 0.0826 | [0.8747, 0.9075] | 0.9015 | |
| RF | 0.8536 ± 0.0953 | [0.8346, 0.8725] | 0.8777 | |
| SVM-RBF | 0.8414 ± 0.1045 | [0.8207, 0.8622] | 0.8656 | |
| AdaBoost | 0.7616 ± 0.1162 | [0.7385, 0.7846] | 0.7981 | |
| ELM | 0.7100 ± 0.1730 | [0.6757, 0.7443] | 0.7424 | |
| KNN | 0.7058 ± 0.1228 | [0.6814, 0.7301] | 0.7425 | |
| BAGELM | 0.6421 ± 0.1477 | [0.6132, 0.6710] | 0.6599 | |
| RVFL | 0.5952 ± 0.1494 | [0.5659, 0.6245] | 0.615 | |
| MLP | 0.5840 ± 0.1684 | [0.5506, 0.6174] | 0.599 | |
| Image CNN (Time-Series → RP/GAF/MTF) | RP | 0.9482 ± 0.0619 | [0.9239, 0.9724] | 0.9529 |
| GASF | 0.9394 ± 0.0853 | [0.9059, 0.9728] | 0.9416 | |
| RGB (GADF, GASF, RP) | 0.9079 ± 0.0778 | [0.8774, 0.9384] | 0.9024 | |
| GADF | 0.8591 ± 0.1172 | [0.8131, 0.9050] | 0.8511 | |
| RGB (GADF, GASF, MTF) | 0.8118 ± 0.1003 | [0.7725, 0.8511] | 0.7858 | |
| MTF | 0.6979 ± 0.2059 | [0.6172, 0.7786] | 0.6766 | |
| Fusion | RP + GADF | 0.9309 ± 0.0795 | [0.8981, 0.9637] | 0.9343 |
| Family | Method | Accuracy (mean ± std) | 95% CI | Macro-F1 |
|---|---|---|---|---|
| Time-Series Classifiers | ROCKET | 0.9578 ± 0.0433 | [0.9493, 0.9663] | 0.9555 |
| FE-ELM | 0.9406 ± 0.0531 | [0.9300, 0.9511] | 0.9407 | |
| MiniROCKET | 0.9356 ± 0.0524 | [0.9253, 0.9459] | 0.9329 | |
| TCN | 0.9111 ± 0.0556 | [0.9002, 0.9220] | 0.9079 | |
| SVM-RBF | 0.8978 ± 0.0655 | [0.8848, 0.9108] | 0.8984 | |
| SVM-LIN | 0.8833 ± 0.0629 | [0.8708, 0.8958] | 0.8829 | |
| LR | 0.8778 ± 0.0675 | [0.8644, 0.8912] | 0.8776 | |
| BAGELM | 0.8711 ± 0.0859 | [0.8543, 0.8879] | 0.8671 | |
| RVFL | 0.8644 ± 0.0865 | [0.8474, 0.8814] | 0.8602 | |
| KNN | 0.8522 ± 0.0733 | [0.8377, 0.8668] | 0.8528 | |
| RF | 0.8444 ± 0.0786 | [0.8289, 0.8600] | 0.8456 | |
| AdaBoost | 0.7928 ± 0.1071 | [0.7715, 0.8140] | 0.7928 | |
| MLP | 0.7056 ± 0.1364 | [0.6785, 0.7326] | 0.7021 | |
| ELM | 0.6394 ± 0.1087 | [0.6179, 0.6610] | 0.6392 | |
| Image CNN (Time-Series → RP/GAF/MTF) | RGB (GADF, GASF, MTF) | 0.9022 ± 0.0627 | [0.8776, 0.9268] | 0.8973 |
| RP | 0.8933 ± 0.0698 | [0.8660, 0.9207] | 0.8899 | |
| GADF | 0.8889 ± 0.0642 | [0.8637, 0.9140] | 0.8835 | |
| RGB (GADF, GASF, RP) | 0.8867 ± 0.0777 | [0.8562, 0.9171] | 0.8793 | |
| GASF | 0.7733 ± 0.0847 | [0.7401, 0.8066] | 0.7529 | |
| MTF | 0.7556 ± 0.0769 | [0.7254, 0.7857] | 0.7344 | |
| Fusion | RP + GADF | 0.9089 ± 0.0733 | [0.8786, 0.9391] | 0.9048 |
References
- Zhao, L.; Wang, L.; Wang, X.; Liu, S.; Zhang, S.; Zhang, H. Feature Ensemble Learning for Sensor Array Data Classification Under Low-Concentration Gas. IEEE Trans. Instrum. Meas. 2023, 72, 2507809. [Google Scholar] [CrossRef]
- Persaud, K.; Dodd, G. Analysis of discrimination mechanisms in the mammalian olfactory system using a model nose. Nature 1982, 299, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Gardner, J.W.; Bartlett, P.N. A brief history of electronic noses. Sens. Actuators B Chem. 1994, 18, 210–211. [Google Scholar] [CrossRef]
- Vergara, A.; Vembu, S.; Ayhan, T.; Ryan, M.A.; Homer, M.L.; Huerta, R. Chemical gas sensor drift compensation using classifier ensembles. Sens. Actuators B Chem. 2012, 166, 320–329. [Google Scholar] [CrossRef]
- Gutierrez-Osuna, R. Pattern analysis for machine olfaction: A review. IEEE Sens. J. 2002, 2, 189–202. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Pao, Y.-H.; Park, G.-H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Eckmann, J.-P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. In Turbulence, Strange Attractors and Chaos; Springer: Berlin/Heidelberg, Germany, 1995; pp. 441–445. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Encoding time series as images for visual inspection and classification using tiled convolutional neural networks. In Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence; AAAI: Palo Alto, CA, USA, 2015; Volume 1. [Google Scholar]
- Wang, Z.; Oates, T. Imaging time-series to improve classification and imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar] [CrossRef]
- Campanharo, A.S.L.O.; Sirer, M.I.; Malmgren, R.D.; Ramos, F.M.; Amaral, L.A.N. Duality between time series and networks. PLoS ONE 2011, 6, e23378. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1094–1096. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; Volume 4, Available online: https://link.springer.com/9780387310732 (accessed on 17 August 2006).
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning; PMLR: Lille, France, 2015; pp. 448–456. Available online: https://proceedings.mlr.press/v37/ioffe15.html (accessed on 1 June 2015).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 14, pp. 1137–1143. [Google Scholar]
- Nadeau, C.; Bengio, Y. Inference for the Generalization Error. In Advances in Neural Information Processing Systems 12; Solla, S.A., Leen, T.K., Müller, K.-R., Eds.; MIT Press: Cambridge, MA, USA, 1999; pp. 307–313. [Google Scholar]
- Dietterich, T.G. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
- Fengchun, T.; Zhao, L.; Deng, S. Gas Sensor Array Low-Concentration [Dataset]. Available online: https://archive.ics.uci.edu/dataset/1081/gas+sensor+array+low-concentration (accessed on 16 November 2024).
- Ziyatdinov, A.; Fonollosa, J. Gas Sensor Array Under Flow Modulation [Dataset]. Available online: https://archive.ics.uci.edu/dataset/308/gas+sensor+array+under+flow+modulation (accessed on 9 September 2014).
- Ziyatdinov, A.; Fonollosa, J.; Fernandez, L.; Pomares, A.; Huerta, R.; Marco, S. Bioinspired early detection through gas flow modulation in chemo-sensory systems. Sens. Actuators B Chem. 2015, 206, 538–547. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 2006; pp. 366–381. [Google Scholar] [CrossRef]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of time-series images using deep convolutional neural networks. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017; SPIE: Bellingham, WI, USA, 2018; Volume 10696. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?”: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]


| Model | Parameter | Default Value |
| FE-ELM | tau (phases) | 64 |
| hidden (hidden neurons) | 200 | |
| RVFL | hidden (hidden neurons) | 200 |
| act (activation function) | relu’ | |
| BAGELM | n_estimators (M members) | 20 |
| base_hidden (L neurons) | 200 | |
| ridge (Lambda λ) | 1 × 10−6 | |
| ROCKET | n_kernels | 10,000 |
| MiniROCKET | n_features | 10,000 |
| TCN | levels (TemporalBlocks) | 3 |
| hidden (hidden channels) | 64 | |
| epochs (max epochs) | 20 | |
| patience (early stopping) | 10 | |
| batch_size | 8 | |
| lr (learning rate) | 1 × 10−3 | |
| Model | Parameter | Search Space |
| SVM-RBF | pca_var | [0.90, 0.95, 0.99] |
| C (regularization) | 1 × 10([−4...4]) | |
| gamma (kernel coefficient) | 1 × 10([−4...4]) | |
| SVM-LIN | pca_var | [0.90, 0.95, 0.99] |
| C (regularization) | 1 × 10([−4...4]) | |
| Random Forest | pca_var | [0.90, 0.95, 0.99] |
| n_estimators | [100, 200, 400, 800, 1600, 3200] | |
| KNN | pca_var | [0.90, 0.95, 0.99] |
| k (neighbors) | [1, 3, 5, 7] | |
| AdaBoost | pca_var | [0.90, 0.95, 0.99] |
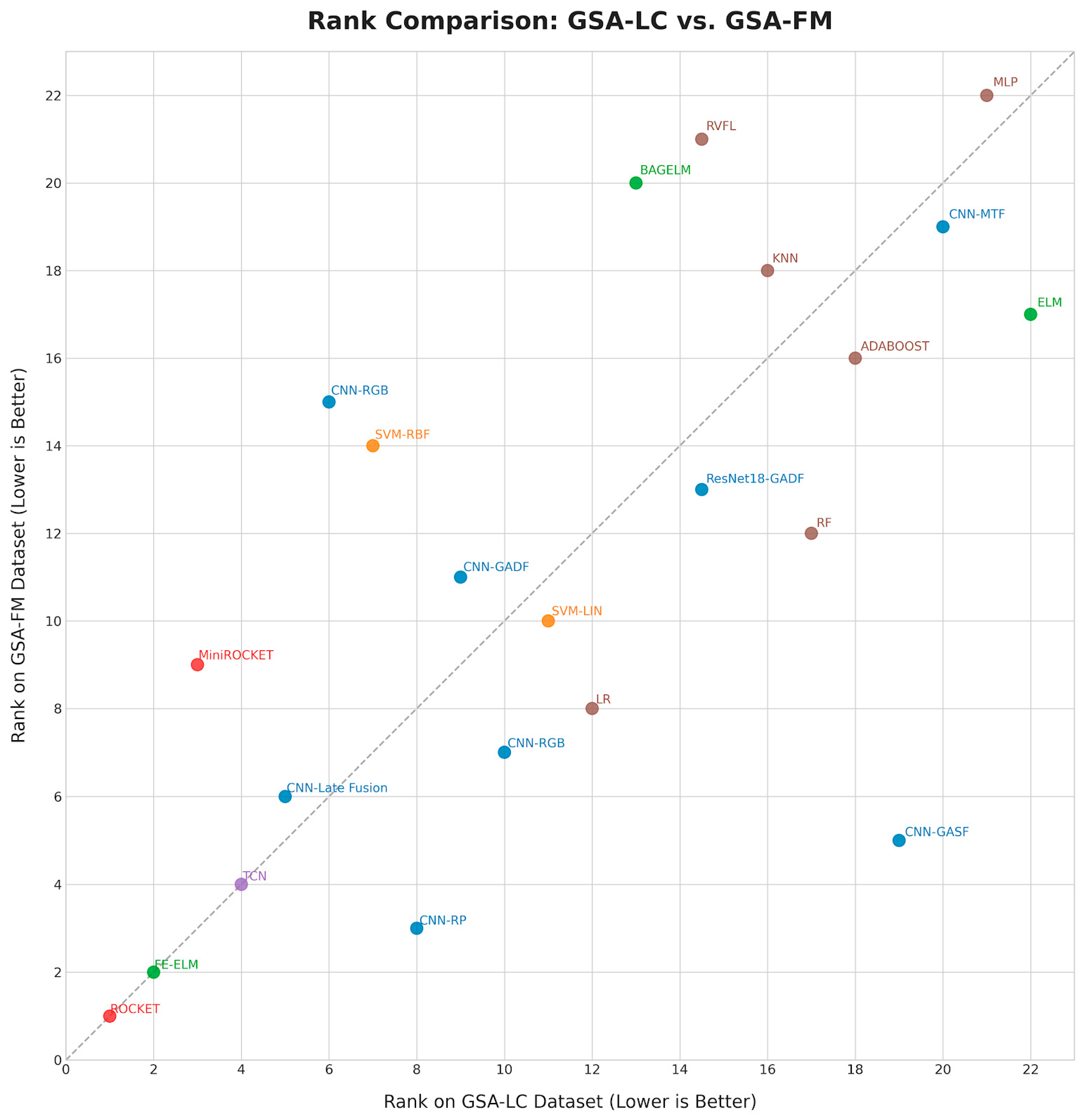
| Family | Method | Rank (FM) | Macro-F1 (FM) | Rank (LC) | Macro-F1 (LC) |
|---|---|---|---|---|---|
| Time-Series Classifiers | ROCKET | 1 | 0.9757 | 1 | 0.9555 |
| FE-ELM | 2 | 0.9679 | 2 | 0.9407 | |
| TCN | 4 | 0.9503 | 4 | 0.9079 | |
| LR | 7 | 0.9184 | 12 | 0.8776 | |
| SVM-LIN | 9 | 0.9015 | 10 | 0.8829 | |
| MiniROCKET | 10 | 0.8997 | 3 | 0.9329 | |
| RF | 11 | 0.8777 | 16 | 0.8456 | |
| SVM-RBF | 12 | 0.8656 | 6 | 0.8984 | |
| AdaBoost | 14 | 0.7981 | 17 | 0.7928 | |
| KNN | 16 | 0.7425 | 15 | 0.8528 | |
| ELM | 17 | 0.7424 | 21 | 0.6392 | |
| BAGELM | 19 | 0.6599 | 13 | 0.8671 | |
| RVFL | 20 | 0.615 | 14 | 0.8602 | |
| MLP | 21 | 0.599 | 20 | 0.7021 | |
| Image CNN | RP | 3 | 0.9529 | 8 | 0.8899 |
| GASF | 5 | 0.9416 | 18 | 0.7529 | |
| RGB (GADF, GASF, RP) | 8 | 0.9024 | 11 | 0.8793 | |
| GADF | 13 | 0.8511 | 9 | 0.8835 | |
| RGB (GADF, GASF, MTF) | 15 | 0.7858 | 7 | 0.8973 | |
| MTF | 18 | 0.6766 | 19 | 0.7344 | |
| Fusion | RP + GADF | 6 | 0.9343 | 5 | 0.9048 |
| A | B | (Acc) | 95% CI | t | p | p_Holm | Holm adj. p < 0.05 | |
|---|---|---|---|---|---|---|---|---|
| RP | GASF | 0.12 | [0.1059, 0.1341] | 16.86 | <1 × 10−15 | 9.80 × 10−8 | 1.686 | ✓ |
| ROCKET | TCN | 0.0467 | [0.0341, 0.0593] | 7.34 | 6.04 × 10−11 | 0.00836 | 0.734 | ✓ |
| ROCKET | MiniROCKET | 0.0222 | [0.0103, 0.0341] | 3.70 | 3.54 × 10−4 | 0.3821 | 0.370 | |
| ROCKET | FE-ELM | 0.02 | [0.0078, 0.0322] | 3.24 | 0.00163 | 0.4076 | 0.324 | |
| RP | GADF | 0.0044 | [−0.0107, 0.0195] | 0.60 | 0.7698 | 1 | 0.060 | |
| FE-ELM | MiniROCKET | 0.0022 | [−0.0057, 0.0101] | 0.2 | 0.550 | 1 | 0.040 |
| A | B | (Acc) | 95% CI | t | p | p_Holm | Holm adj. p < 0.05 | |
|---|---|---|---|---|---|---|---|---|
| ROCKET | TCN | 0.0518 | [0.0312, 0.0724] | 5 | 2.48 × 10−6 | 0.0984 | 0.5 | |
| ROCKET | MiniROCKET | 0.0794 | [0.0612, 0.0976] | 8.66 | 9.08 × 10−14 | 0.00229 | 0.866 | ✓ |
| ROCKET | FE-ELM | 0.0067 | [−0.0054, 0.0188] | 1.1 | 0.274 | 1 | 0.11 | |
| CNN-RP | CNN-GADF | 0.0891 | [0.0619, 0.1163] | 7.72 | 9.50 × 10−12 | 0.00598 | 0.772 | ✓ |
| RGB (GADF, GASF, RP) | RGB (GADF, GASF, MTF) | 0.0961 | [0.0698, 0.1224] | 7.24 | 9.79 × 10−11 | <1 × 10−10 | 0.724 | ✓ |
| TCN | MiniROCKET | 0.0527 | [0.0195, 0.0859] | 3.26 | 0.00332 | 0.01993 | 0.326 | ✓ |
| CNN-RP | CNN-GASF | 0.0088 | [−0.0113, 0.0289] | 0.88 | 0.381 | 1 | 0.088 |
| Dataset | A | B | (Acc) | 95% CI | t | p | p_Holm | Holm adj. p < 0.05 | |
|---|---|---|---|---|---|---|---|---|---|
| GSA-FM | CNN-RP | CNN-GADF | 0.089 | [0.0619, 0.1163] | 7.72 | 9.50 × 10−12 | 0.00598 | 0.772 | ✓ |
| GSA-FM | CNN-RP | CNN-GASF | 0.009 | [−0.0113, 0.0289] | 0.88 | 0.381 | 1 | 0.088 | |
| GSA-FM | RGB (GADF, GASF, RP) | RGB (GADF, GASF, MTF) | 0.096 | [0.0698, 0.1224] | 7.24 | 9.79 × 10−11 | <1 × 10−10 | 0.724 | ✓ |
| GSA-LC | CNN-RP | CNN-GASF | 0.12 | [0.1059, 0.1341] | 16.86 | <1 × 10−15 | 2.5 × 10−8 | 1.686 | ✓ |
| GSA-LC | CNN-RP | CNN-GADF | 0.004 | [−0.0107, 0.0195] | 0.6 | 0.55 | 1 | 0.06 |
| Dataset | Model | ∆ (Mean) | p-Value |
|---|---|---|---|
| FM | CNN-RP | −0.0173 | 0.2838 |
| FM | CNN-GASF | −0.0261 | 0.1743 |
| FM | CNN-RGB (GADF, GASF, MTF) | −0.1536 | 4.6 × 10−7 |
| FM | CNN-RGB (GADF, GASF, RP) | −0.0576 | 0.005 |
| LC | CNN-RP | −0.0333 | 0.0699 |
| LC | CNN-GASF | −0.1533 | 9.0 × 10−8 |
| LC | CNN-RGB (GADF, GASF, MTF) | −0.0244 | 0.156 |
| LC | CNN-RGB (GADF, GASF, RP) | −0.04 | 0.0648 |
| Dataset | Transform | A | B | ∆(Acc) | 95% CI | t | p | pHolm | Holm adj. p < 0.05 | |
|---|---|---|---|---|---|---|---|---|---|---|
| GSA-FM | RP | ResNet18 | CNN | −0.013 | [−0.0238, −0.0022] | −2.38 | 0.0192 | 0.0385 | −0.238 | ✓ |
| GSA-FM | GADF | ResNet18 | CNN | −0.0118 | [−0.0368, 0.0132] | −1 | 0.3197 | 0.6204 | −0.1 | |
| GSA-LC | GADF | ResNet18 | CNN | −0.0244 | [−0.0386, −0.0102] | −3.40 | 9.73 × 10−4 | 0.1019 | −0.34 | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.-H.; Choi, S.-H.; Choi, S.; Lee, S. A Reproducible Benchmark for Gas Sensor Array Classification: From FE-ELM to ROCKET and TS2I-CNNs. Sensors 2025, 25, 6270. https://doi.org/10.3390/s25206270
Kim C-H, Choi S-H, Choi S, Lee S. A Reproducible Benchmark for Gas Sensor Array Classification: From FE-ELM to ROCKET and TS2I-CNNs. Sensors. 2025; 25(20):6270. https://doi.org/10.3390/s25206270
Chicago/Turabian StyleKim, Chang-Hyun, Seung-Hwan Choi, Sanghun Choi, and Suwoong Lee. 2025. "A Reproducible Benchmark for Gas Sensor Array Classification: From FE-ELM to ROCKET and TS2I-CNNs" Sensors 25, no. 20: 6270. https://doi.org/10.3390/s25206270
APA StyleKim, C.-H., Choi, S.-H., Choi, S., & Lee, S. (2025). A Reproducible Benchmark for Gas Sensor Array Classification: From FE-ELM to ROCKET and TS2I-CNNs. Sensors, 25(20), 6270. https://doi.org/10.3390/s25206270






