Spatio-Temporal Joint Trajectory Planning for Autonomous Vehicles Based on Improved Constrained Iterative LQR
Abstract
1. Introduction
2. Proposed Method
2.1. ILQR Method
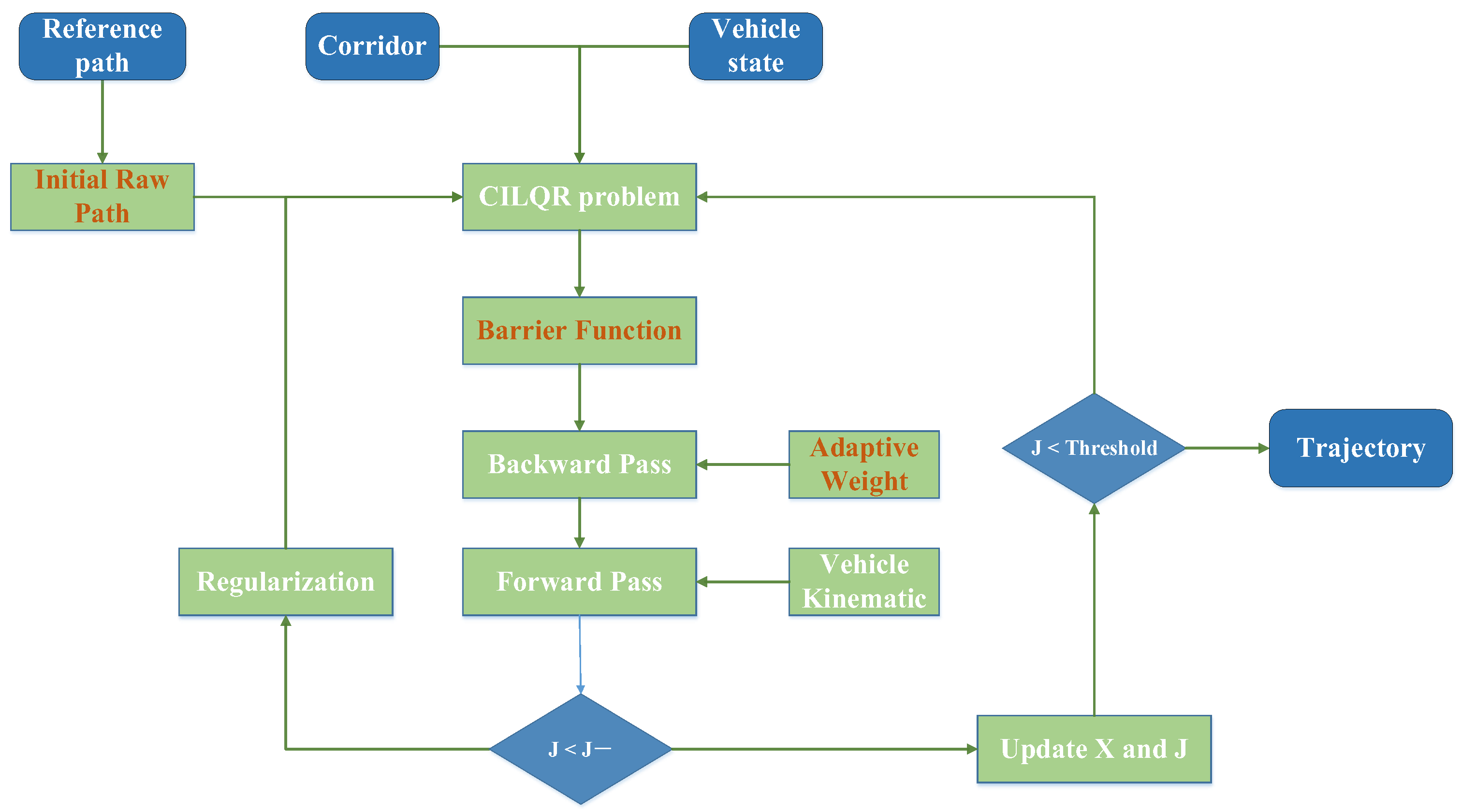
2.2. Improved CILQR Method
| Algorithm 1. Improved CILQR Algorithm |
|
2.3. Problem Formulation
- (1)
- Cost function-distance to the reference line
- (2)
- Cost function-lateral motion
- (3)
- Cost function-longitudinal motion
- (4)
- Cost function-trajectory curvature
3. Experiment Validation
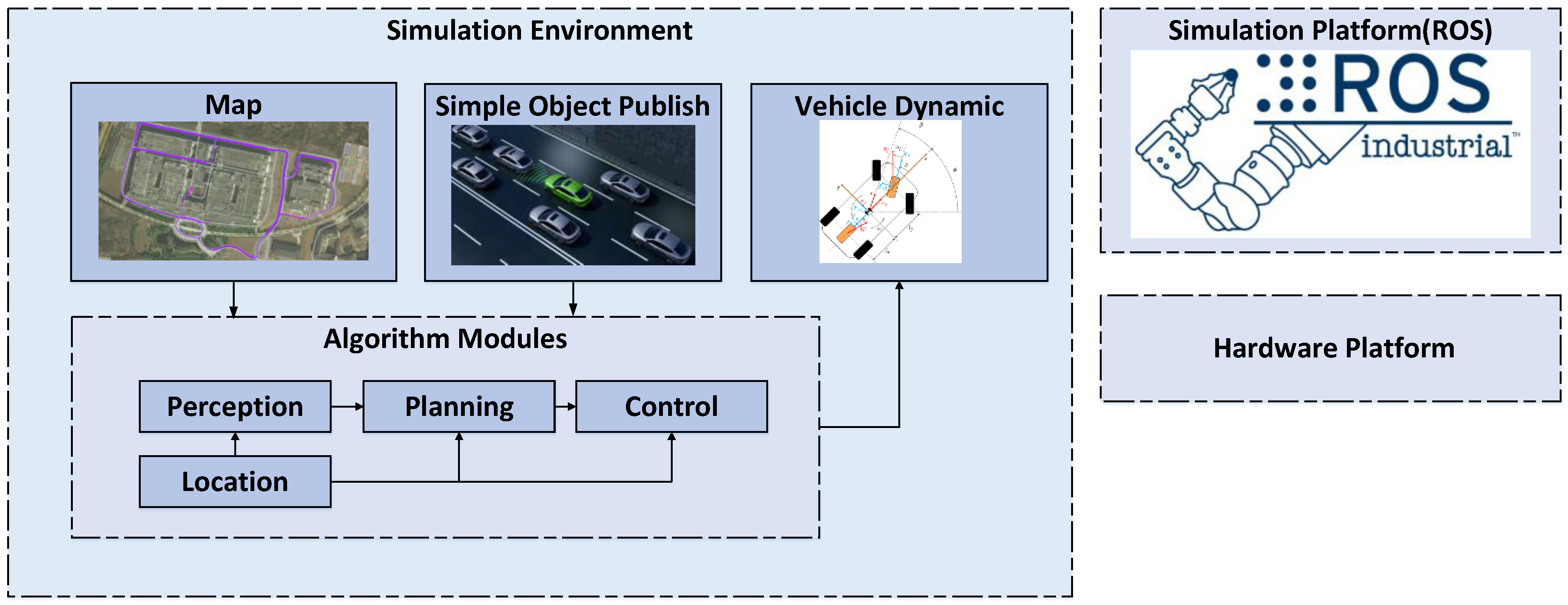
3.1. Simulation Experiment
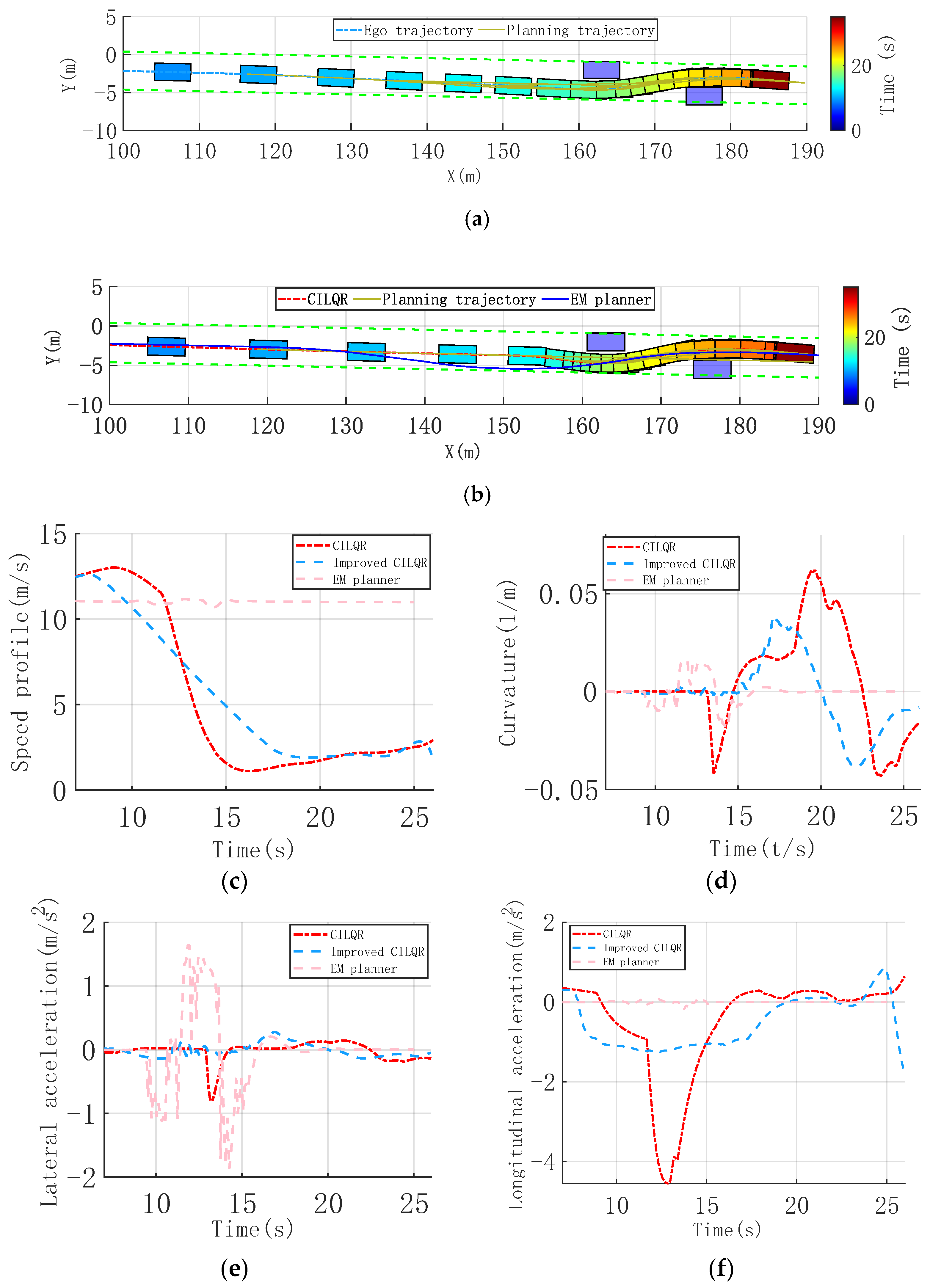
3.1.1. Continuous Nudge Static Obstacle Scenario
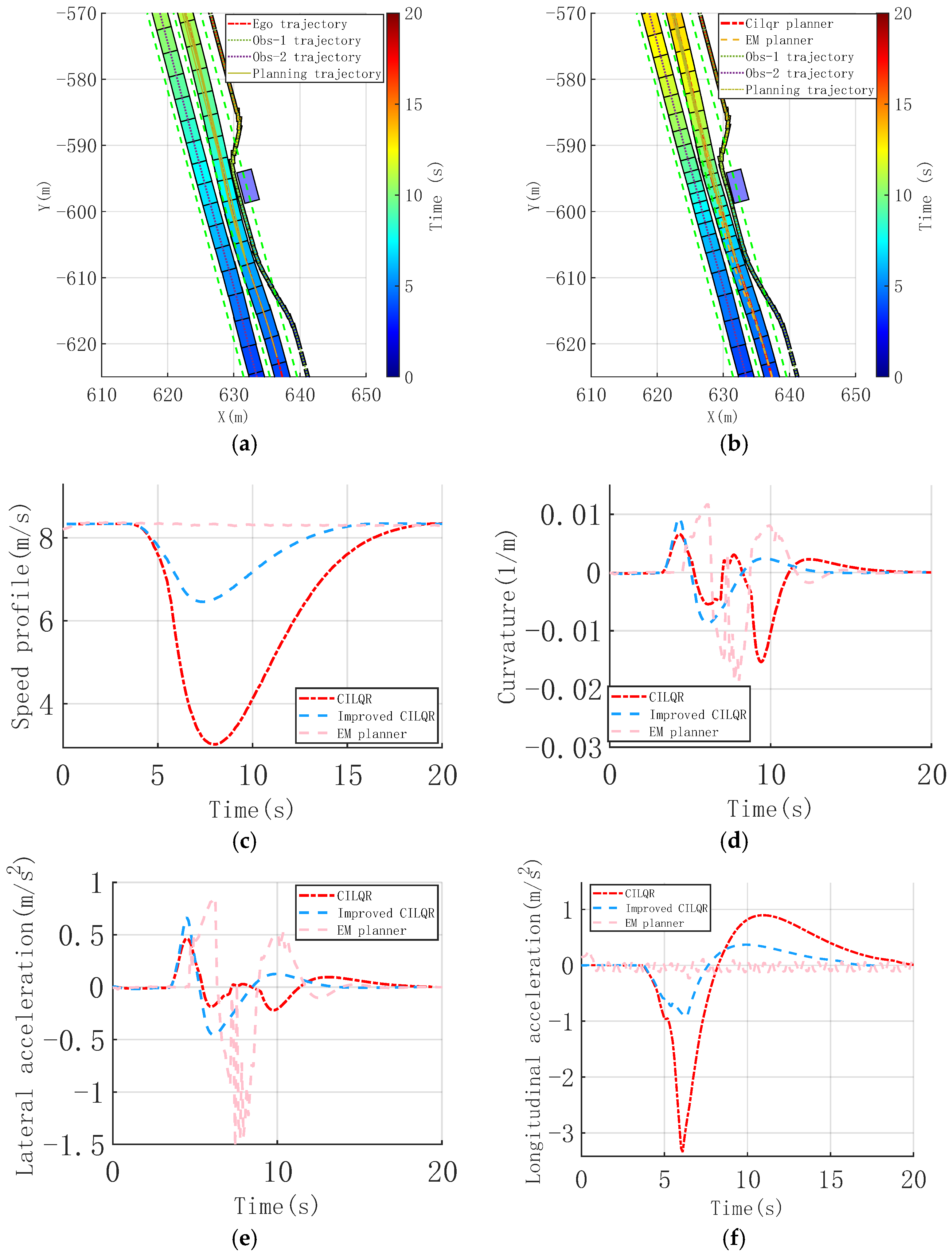
3.1.2. Dynamic Cut-In with Narrow Corridor Scenario
3.2. Real-Vehicle Experiment
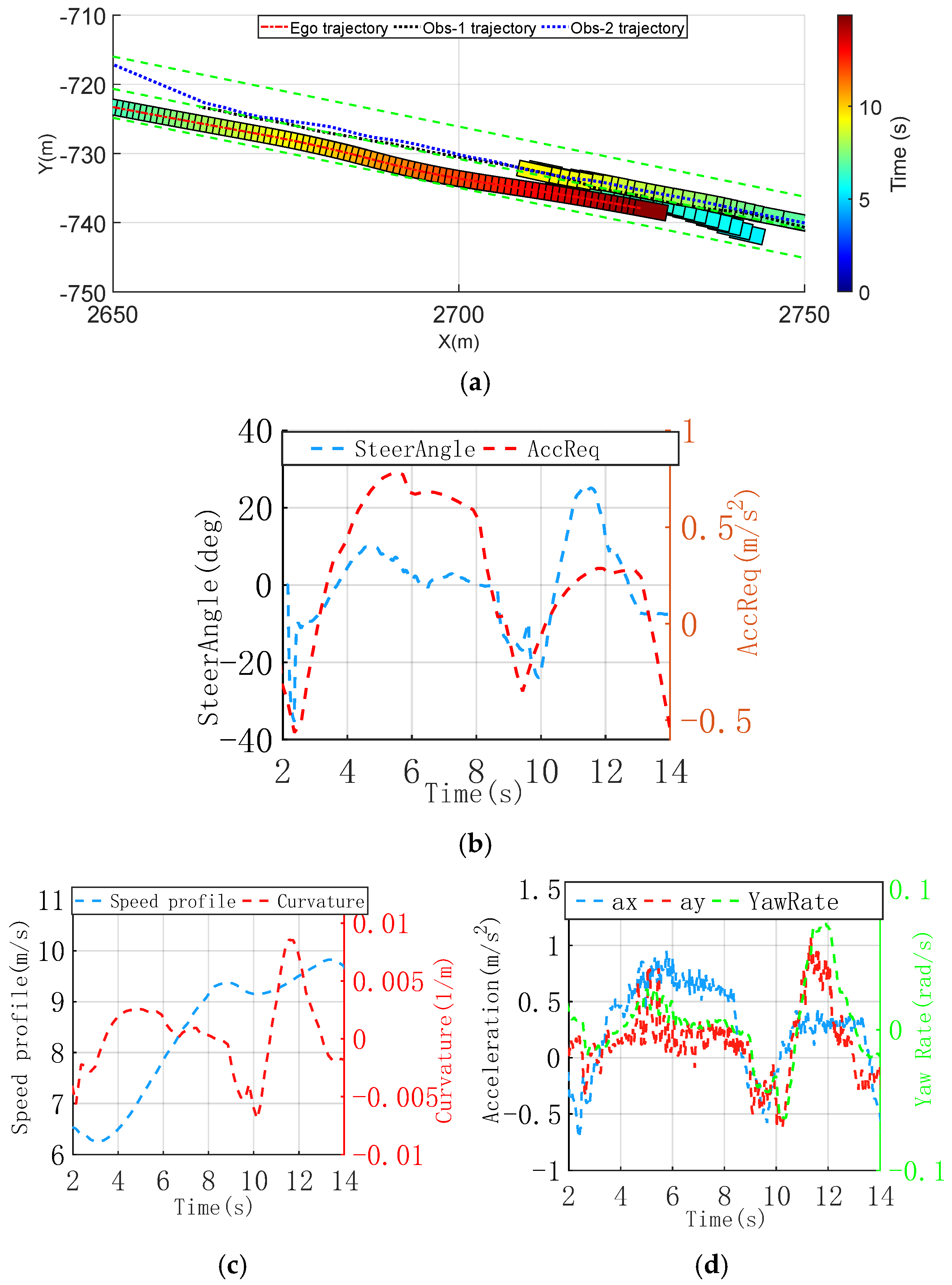
3.2.1. Dynamic Overtaking of Oncoming Obstacles Scenario
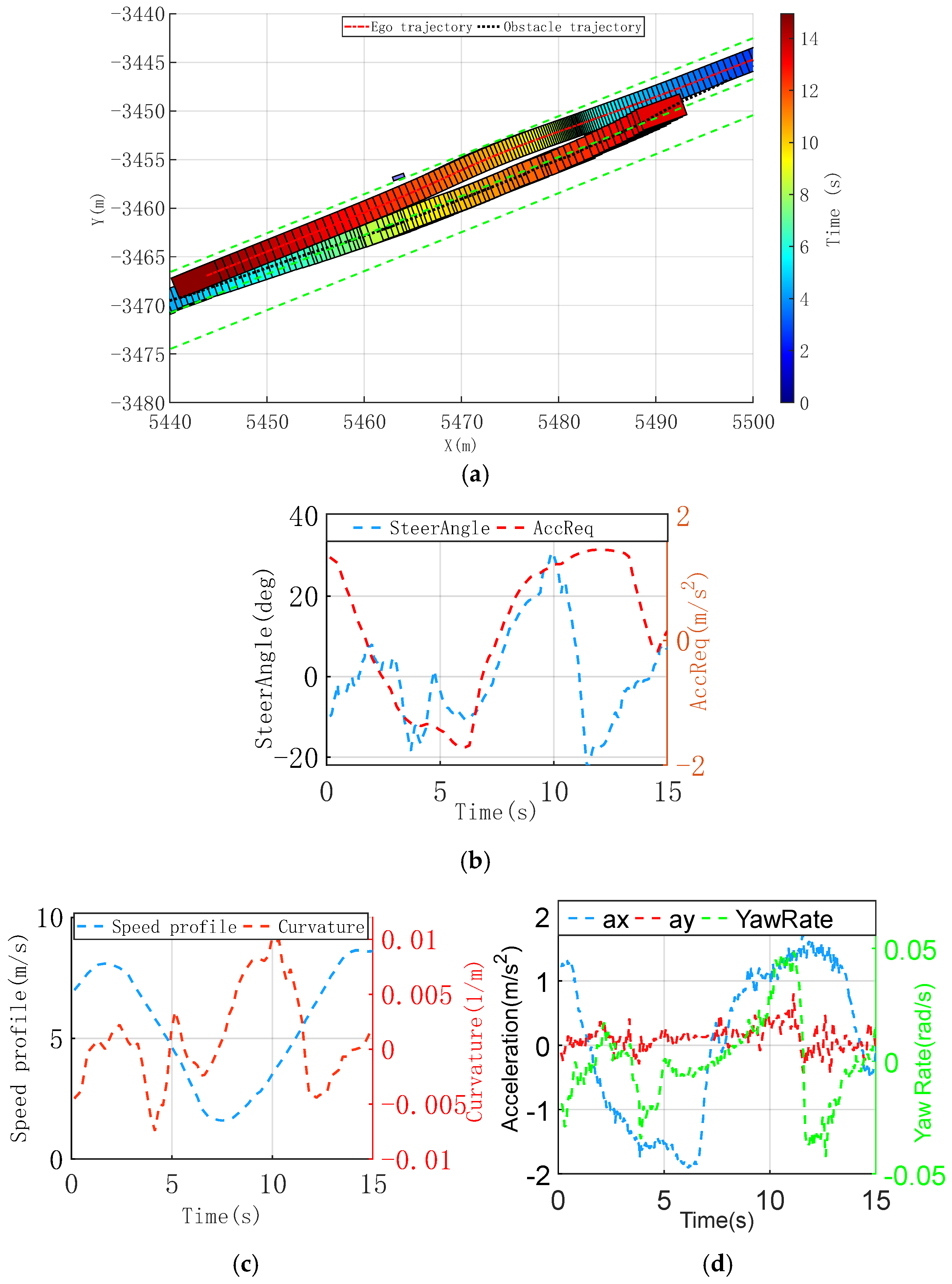
3.2.2. Collision Avoidance with Dynamic and Static Obstacles Scenario
3.3. Analysis of Results
4. Conclusions
- (1)
- First, by optimizing the barrier function, the CILQR method achieves more efficient constraint handling. This enhancement allows for better trajectory adaptation while maintaining safety and comfort, leading to improved numerical stability and a 12.65% average increase in traffic efficiency in complex scenarios.
- (2)
- Second, the adaptive weight adjustment strategy enhances the CILQR method’s adaptability across different scenarios, improving lateral and longitudinal control coordination and increasing the human-like driving indicator by 16.35%.
- (3)
- Integrating the hybrid A* method for initial trajectory preprocessing improves solution efficiency, reducing computation time by 39.29%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Y.; He, H.; Wang, Y.; Mao, Z.; Wang, H. Multi-Modality 3D Object Detection in Autonomous Driving: A Review. Neurocomputing 2023, 553, 126587. [Google Scholar] [CrossRef]
- Xia, T.; Chen, H. A Survey of Autonomous Vehicle Behaviors: Trajectory Planning Algorithms, Sensed Collision Risks, and User Expectations. Sensors 2024, 24, 4808. [Google Scholar] [CrossRef] [PubMed]
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Ai, Y.; Yang, D.; Li, L.; Zhe, X.; Zhu, F.; et al. Motion Planning for Autonomous Driving: The State of the Art and Future Perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Li, Q.; Ou, B.; Liang, Y.; Wang, Y.; Yang, X.; Li, L. TCN-SA: A Social Attention Network Based on Temporal Convolutional Network for Vehicle Trajectory Prediction. J. Adv. Transp. 2023, 2023, 1286977. [Google Scholar] [CrossRef]
- Lin, P.; Tsukada, M. Model Predictive Path-Planning Controller with Potential Function for Emergency Collision Avoidance on Highway Driving. IEEE Robot. Autom. Lett. 2022, 7, 4662–4669. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Gammell, J.D.; Barfoot, T.D.; Srinivasa, S.S. Informed Sampling for Asymptotically Optimal Path Planning. IEEE Trans. Robot. 2018, 34, 966–984. [Google Scholar] [CrossRef]
- Strub, M.P.; Gammell, J.D. Adaptively Informed Trees (AIT*) and Effort Informed Trees (EIT*): Asymmetric Bidirectional Sampling-Based Path Planning. Int. J. Robot. Res. 2022, 41, 390–417. [Google Scholar] [CrossRef]
- Maw, A.A.; Tyan, M.; Lee, J.W. iADA*: Improved Anytime Path Planning and Replanning Algorithm for Autonomous Vehicle. J. Intell. Robot. Syst. 2020, 100, 1005–1013. [Google Scholar] [CrossRef]
- Abdulsaheb, J.A.; Kadhim, D.J. Classical and Heuristic Approaches for Mobile Robot Path Planning: A Survey. Robotics 2023, 12, 93. [Google Scholar] [CrossRef]
- Zhou, Q.; Gao, S.; Qu, B.; Gao, X.; Zhong, Y. Crossover Recombination-Based Global-Best Brain Storm Optimization Algorithm for UAV Path Planning. Proc. Rom. Acad. Ser. A-Math. Phys. Tech. Sci. Inf. Sci. 2022, 23, 207–216. [Google Scholar]
- Aradi, S. Survey of Deep Reinforcement Learning for Motion Planning of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 740–759. [Google Scholar] [CrossRef]
- Zhong, Y.; Shirinzadeh, B.; Yuan, X. Optimal Robot Path Planning with Cellular Neural Network. Int. J. Intell. Mechatron. Robot. 2011, 1, 20–39. [Google Scholar] [CrossRef]
- Hills, J.; Zhong, Y. Cellular Neural Network-Based Thermal Modelling for Real-Time Robotic Path Planning. Int. J. Agil. Syst. Manag. 2014, 7, 261. [Google Scholar] [CrossRef]
- Sun, L.; Peng, C.; Zhan, W.; Tomizuka, M. A Fast Integrated Planning and Control Framework for Autonomous Driving via Imitation Learning. arXiv 2017, arXiv:1707.02515. [Google Scholar]
- Li, J.; Sun, L.; Chen, J.; Tomizuka, M.; Zhan, W. A Safe Hierarchical Planning Framework for Complex Driving Scenarios Based on Reinforcement Learning. arXiv 2021, arXiv:2101.06778. [Google Scholar]
- Perot, E.; Jaritz, M.; Toromanoff, M.; Charette, R.D. End-to-End Driving in a Realistic Racing Game with Deep Reinforcement Learning. In Proceedings of the Computer Vision & Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wu, Z.; Sun, L.; Zhan, W.; Yang, C.; Tomizuka, M. Efficient Sampling-Based Maximum Entropy Inverse Reinforcement Learning with Application to Autonomous Driving. arXiv 2020, arXiv:2006.13704. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, H.; Wu, Y.; Peng, J. Hybrid Electric Vehicle Energy Management with Computer Vision and Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2021, 17, 3857–3868. [Google Scholar] [CrossRef]
- Han, Z.; Wu, Y.; Li, T.; Zhang, L.; Pei, L.; Xu, L.; Li, C.; Ma, C.; Xu, C.; Shen, S.; et al. An Efficient Spatial-Temporal Trajectory Planner for Autonomous Vehicles in Unstructured Environments. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1797–1814. [Google Scholar] [CrossRef]
- Ramezani, M.; Habibi, H.; Sanchez-Lopez, J.L.; Voos, H. UAV Path Planning Employing MPC-Reinforcement Learning Method Considering Collision Avoidance. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6 June 2023; IEEE: Piscataway, NJ, USA; pp. 507–514. [Google Scholar]
- Pfrommer, S.; Gautam, T.; Zhou, A.; Sojoudi, S. Safe Reinforcement Learning with Chance-Constrained Model Predictive Control. In Proceedings of the Learning for Dynamics and Control Conference, Stanford, CA, USA, 23–24 June 2022; pp. 291–303. [Google Scholar]
- Wang, Y.; Wu, Y.; Tang, Y.; Li, Q.; He, H. Cooperative Energy Management and Eco-Driving of Plug-in Hybrid Electric Vehicle via Multi-Agent Reinforcement Learning. Appl. Energy 2023, 332, 120563. [Google Scholar] [CrossRef]
- Wang, Y.; He, H.; Wu, Y.; Wang, P.; Wang, H.; Lian, R.; Wu, J.; Li, Q.; Meng, X.; Tang, Y.; et al. LearningEMS: A Unified Framework and Open-Source Benchmark for Learning-Based Energy Management of Electric Vehicles. Engineering 2024, S2095809924007136. [Google Scholar] [CrossRef]
- Zuo, Z.; Yang, X.; Li, Z.; Wang, Y.; Han, Q.; Wang, L.; Luo, X. MPC-Based Cooperative Control Strategy of Path Planning and Trajectory Tracking for Intelligent Vehicles. IEEE Trans. Intell. Veh. 2021, 6, 513–522. [Google Scholar] [CrossRef]
- Svensson, L.; Bujarbaruah, M.; Kapania, N.; Törngren, M. Adaptive Trajectory Planning and Optimization at Limits of Handling. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019. [Google Scholar]
- Su, J.; Gao, R.; Xu, Z.; Zhang, W. VS-DDP: Variable Splitting Based Differential Dynamic Programming Algorithm for Autonomous Trajectory Planning. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 4382–4387. [Google Scholar]
- Ma, J.; Cheng, Z.; Zhang, X.; Lin, Z.; Lewis, F.L.; Lee, T.H. Local Learning Enabled Iterative Linear Quadratic Regulator for Constrained Trajectory Planning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5354–5365. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, W.; Tomizuka, M. Constrained Iterative LQR for On-Road Autonomous Driving Motion Planning. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Chen, J.; Zhan, W.; Tomizuka, M. Autonomous Driving Motion Planning with Constrained Iterative LQR. IEEE Trans. Intell. Veh. 2019, 4, 244–254. [Google Scholar] [CrossRef]
- Pan, Y.; Lin, Q.; Shah, H.; Dolan, J.M. Safe Planning for Self-Driving Via Adaptive Constrained ILQR. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2377–2383. [Google Scholar]
- Li, H.; Zhang, J.; Zhu, S.; Tang, D.; Xu, D. Integrating Higher-Order Dynamics and Roadway-Compliance into Constrained ILQR-Based Trajectory Planning for Autonomous Vehicles. arXiv 2023, arXiv:2309.14566. [Google Scholar]
- Guo, J.; Xie, Z.; Liu, M.; Hu, J.; Dai, Z.; Guo, J. Data-Driven Enhancements for MPC-Based Path Tracking Controller in Autonomous Vehicles. Sensors 2024, 24, 7657. [Google Scholar] [CrossRef]
- Ye, X.; Lian, J.; Zhao, G.; Zhang, D. A Novel Closed-Loop Structure for Drag-Free Control Systems with ESKF and LQR. Sensors 2023, 23, 6766. [Google Scholar] [CrossRef]
- Wang, Y.; Lian, R.; He, H.; Betz, J.; Wei, H. Auto-Tuning Dynamics Parameters of Intelligent Electric Vehicles via Bayesian Optimization. IEEE Trans. Transp. Electrif. 2024, 10, 6915–6927. [Google Scholar] [CrossRef]
- Fan, H.; Zhu, F.; Liu, C.; Zhang, L.; Zhuang, L.; Li, D.; Zhu, W.; Hu, J.; Li, H.; Kong, Q. Baidu Apollo Em Motion Planner. arXiv 2018, arXiv:1807.08048. [Google Scholar]
- Yamakado, M.; Abe, M. An Experimentally Confirmed Driver Longitudinal Acceleration Control Model Combined with Vehicle Lateral Motion. Veh. Syst. Dyn. 2008, 46, 129–149. [Google Scholar] [CrossRef]

| Parameter | Description | Value | Unit |
|---|---|---|---|
| Vehicle mass | 2063.4 | ||
| Front axle distance | 1351.8 | ||
| Rear axle distance | 1548.2 | ||
| Equivalent front axle cornering stiffness | 100,640 | N/rad | |
| Equivalent rear axle cornering stiffness | 100,640 | N/rad | |
| Equivalent tire rolling radius | 366 | mm | |
| Yaw moment of inertia about the Z-axis | 3347.8 | ||
| Vehicle length | 4766 | mm | |
| Vehicle width | 2267 | mm | |
| Vehicle height | 1684 | mm | |
| Longitudinal distance from the center of mass to the rear axle | 1549 | mm | |
| Lateral position of the center of mass | 5 | mm | |
| Vertical position of the center of mass | 596 | mm | |
| Distance from the front bumper to the rear axle center | 3829 | mm | |
| Distance from the rear bumper to the rear axle center | 937 | mm | |
| Steering ratio between front wheels and steering wheel | 16.7 | / |
| Adaptive Weighting Parameters | Value | Cost Function Weighting | Value |
|---|---|---|---|
| 1.2 | 2.5 | ||
| 0.1 | 12 | ||
| 20 | 18 | ||
| 120 | 5 | ||
| 0.12 | 25 | ||
| 600 | 3 | ||
| 0.05 | |||
| 300 |
| Scenarios | Comfortable Indicator | Human-Like Indicator | Computation Cost | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulation 1 | CILQR | 6.2 × 10−2 | 4.8 × 10−2 | −4.55 | −0.81 | −0.14 | 0.63 | 48.34 | 55 |
| Improved CILQR | −3.8 × 10−2 | 2.3 × 10−2 | −1.77 | 0.28 | 0.09 | 0.57 | 24.10 | 25 | |
| Simulation 2 | CILQR | −1.5 × 10−2 | −1.2 × 10−2 | −3.34 | 0.47 | −0.06 | 0.82 | 44.71 | 49 |
| Improved CILQR | 9.4 × 10−3 | −2.0 × 10−3 | −0.92 | 0.67 | 0.08 | 0.63 | 29.34 | 29 | |
| Vehicle Test 1 | 8.5 × 10−3 | −3.3 × 10−3 | −1.31 | 1.27 | 0.22 | 0.51 | 30.15 | 28 | |
| Vehicle Test 2 | 1.0 × 10−2 | 4.7 × 10−3 | −1.91 | 0.80 | 0.05 | 0.68 | 33.88 | 31 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; He, H.; Hu, M.; Wang, Y. Spatio-Temporal Joint Trajectory Planning for Autonomous Vehicles Based on Improved Constrained Iterative LQR. Sensors 2025, 25, 512. https://doi.org/10.3390/s25020512
Li Q, He H, Hu M, Wang Y. Spatio-Temporal Joint Trajectory Planning for Autonomous Vehicles Based on Improved Constrained Iterative LQR. Sensors. 2025; 25(2):512. https://doi.org/10.3390/s25020512
Chicago/Turabian StyleLi, Qin, Hongwen He, Manjiang Hu, and Yong Wang. 2025. "Spatio-Temporal Joint Trajectory Planning for Autonomous Vehicles Based on Improved Constrained Iterative LQR" Sensors 25, no. 2: 512. https://doi.org/10.3390/s25020512
APA StyleLi, Q., He, H., Hu, M., & Wang, Y. (2025). Spatio-Temporal Joint Trajectory Planning for Autonomous Vehicles Based on Improved Constrained Iterative LQR. Sensors, 25(2), 512. https://doi.org/10.3390/s25020512







