Range Extension of Borehole Strainmeters Using MOSFET-Based Multi-Switch Automatic Zero Setting
Abstract
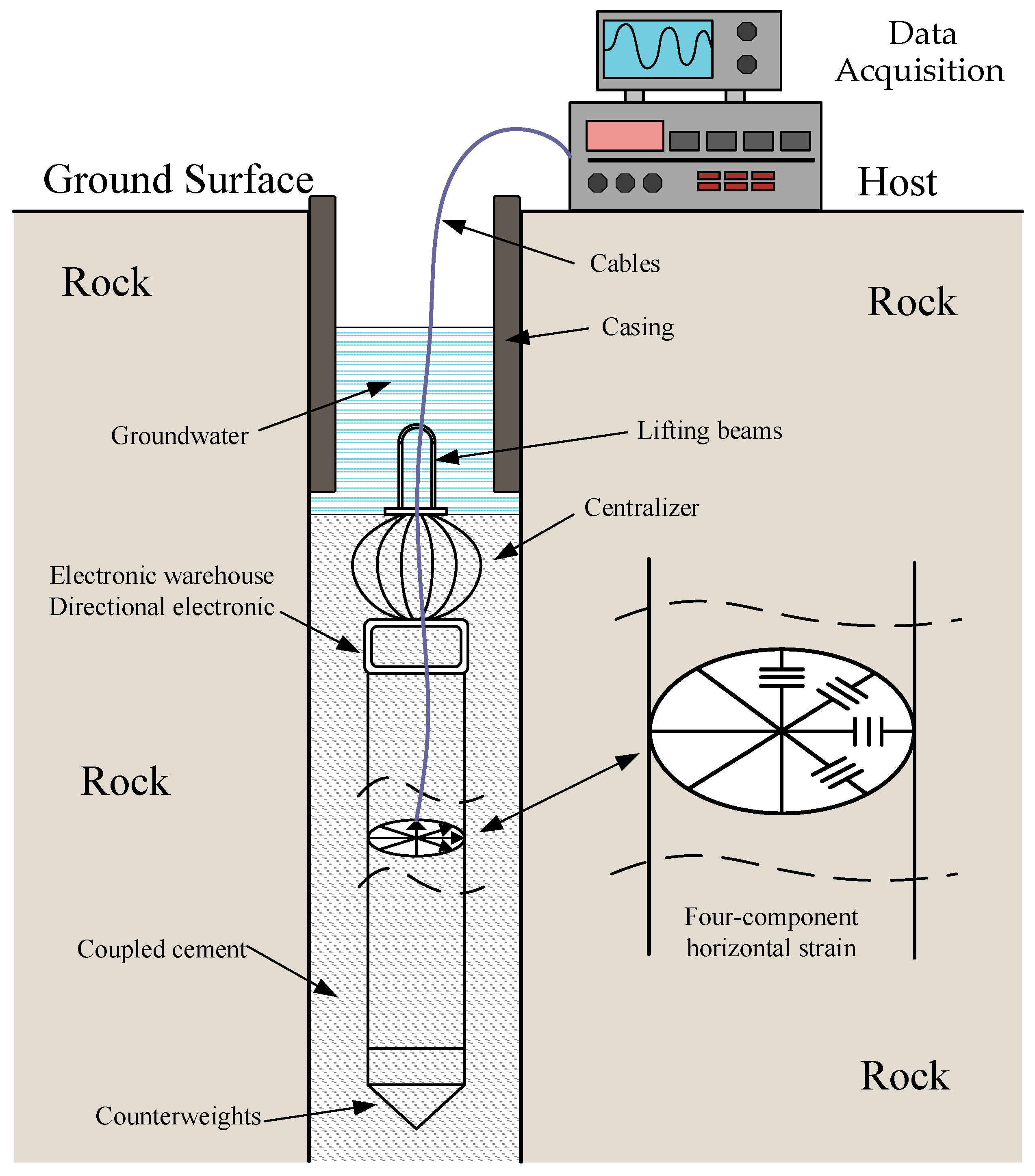
1. Instruction
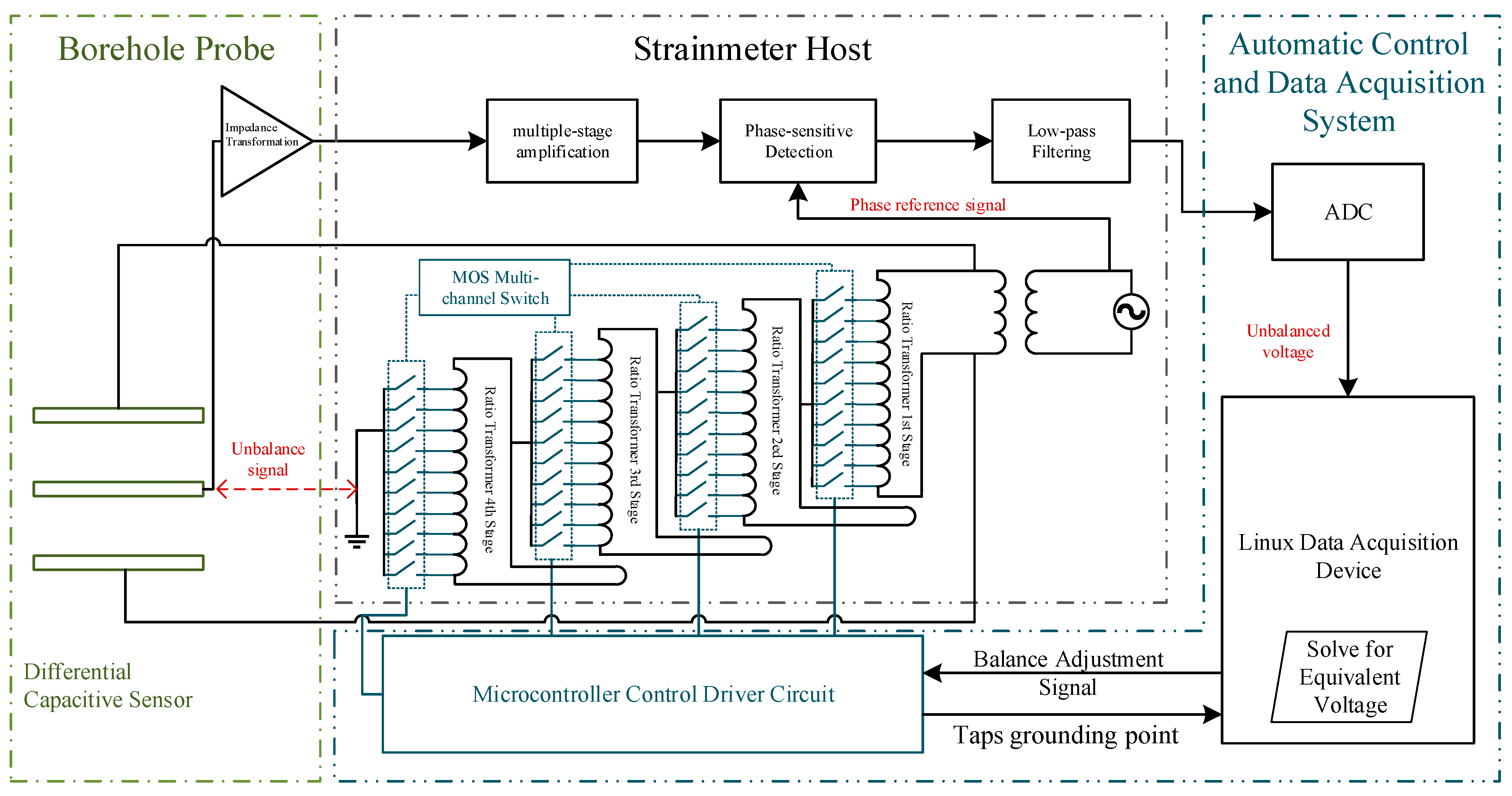
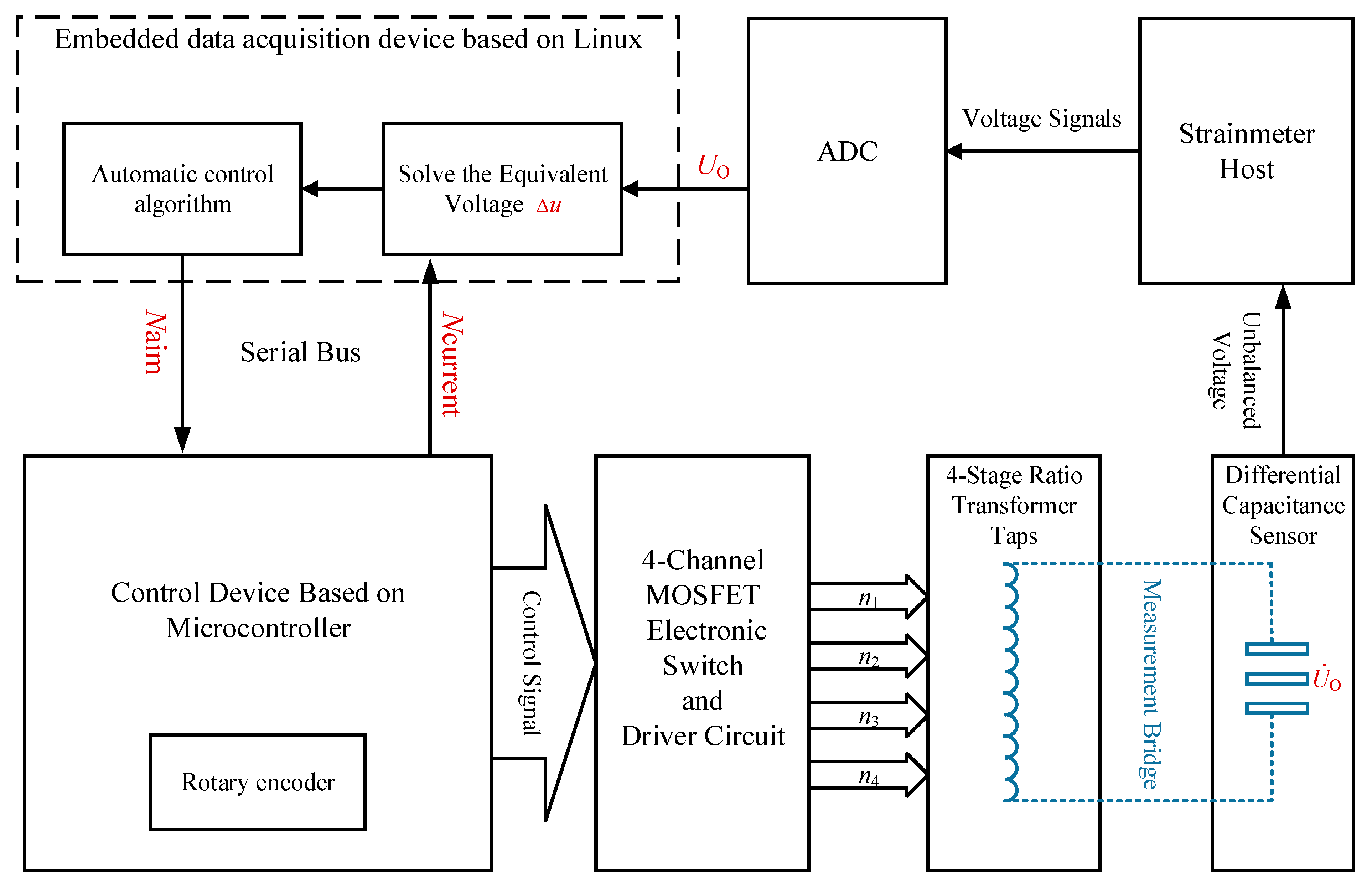
2. Automatic Zero-Setting Measurement System Design
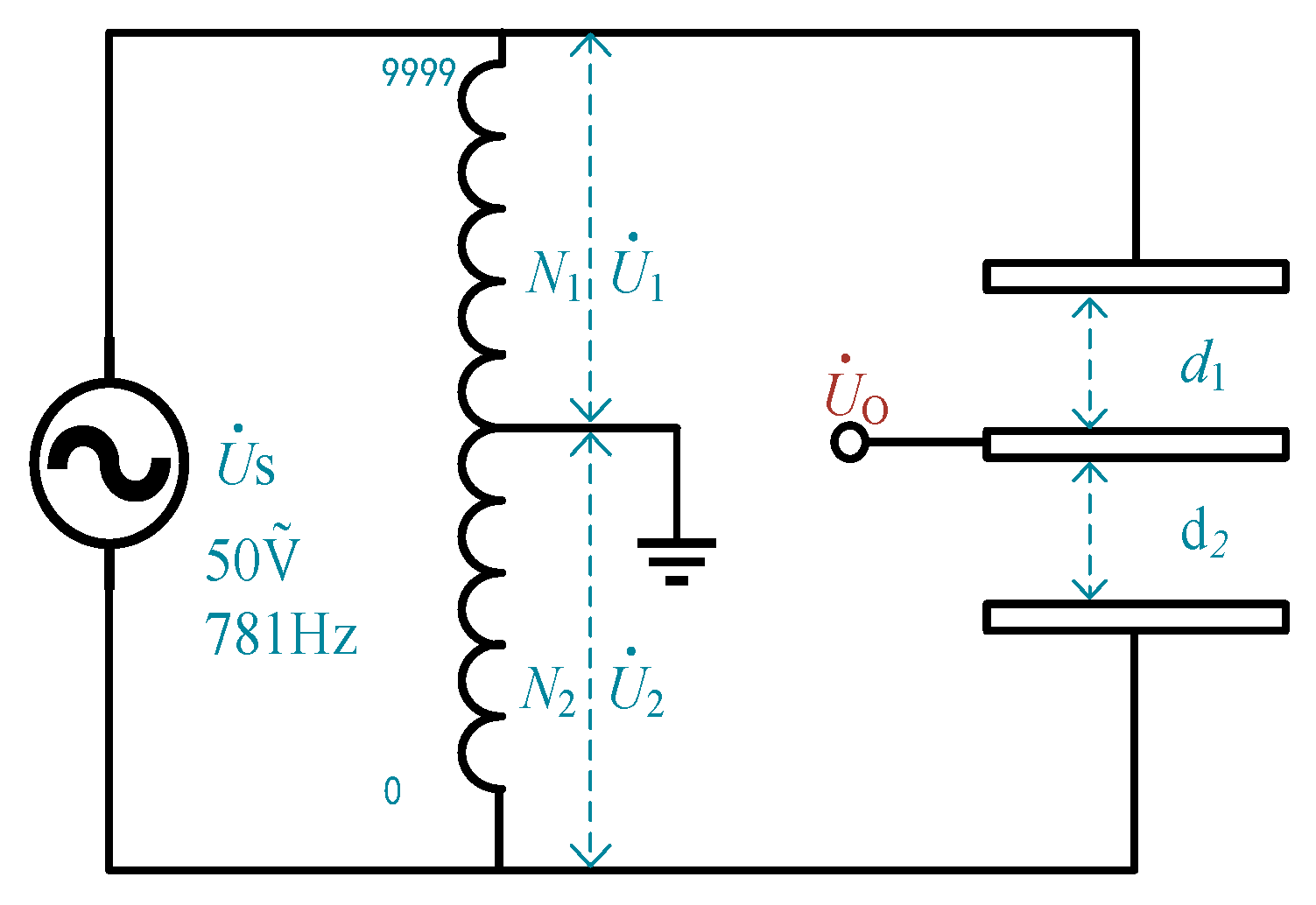
2.1. Principle of Range Extension
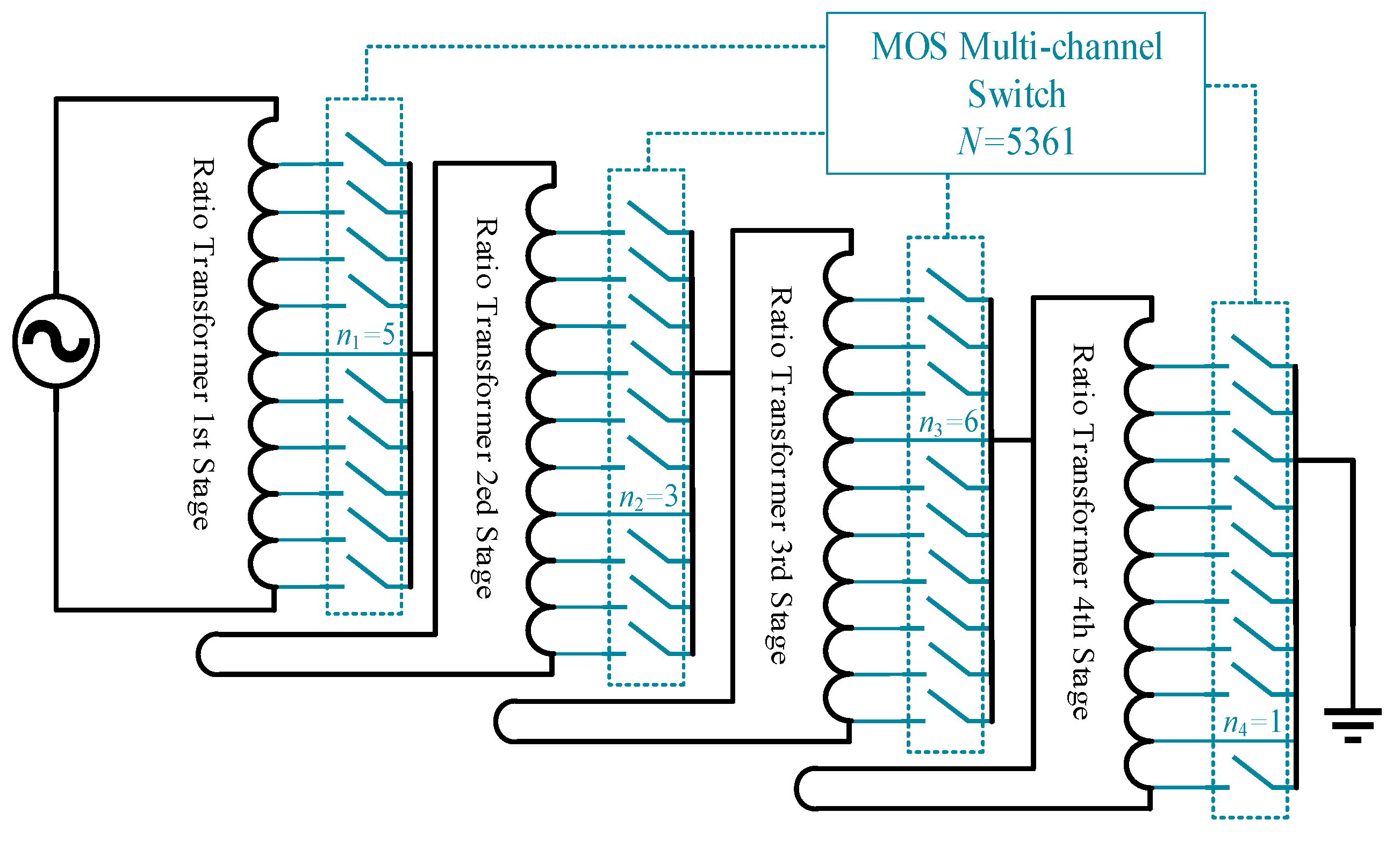
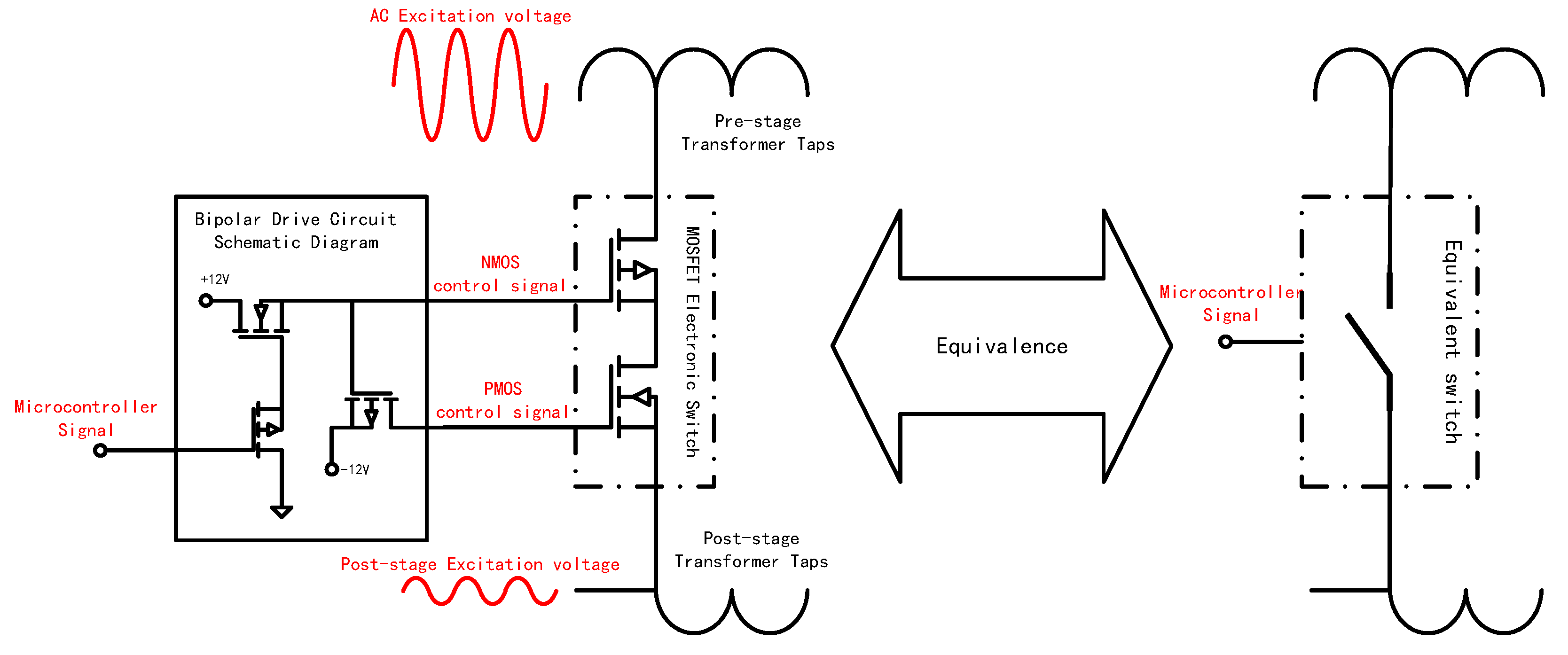
2.2. Design of the MOSFET Multi-Channel Switch
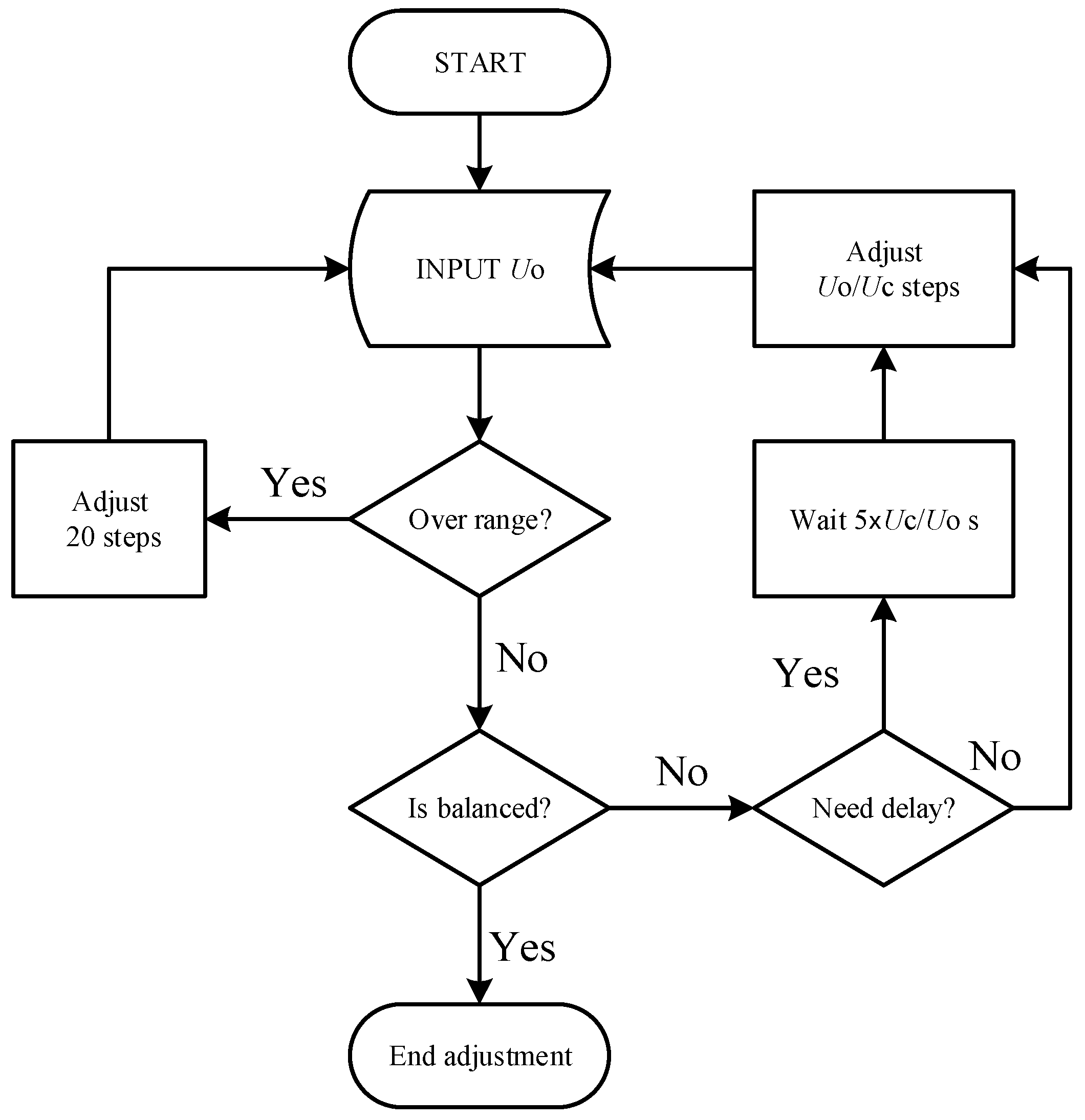
2.3. Design of the Automatic Zero-Setting Control System
3. Experiments and Testing
3.1. Experimental Platform Introduction
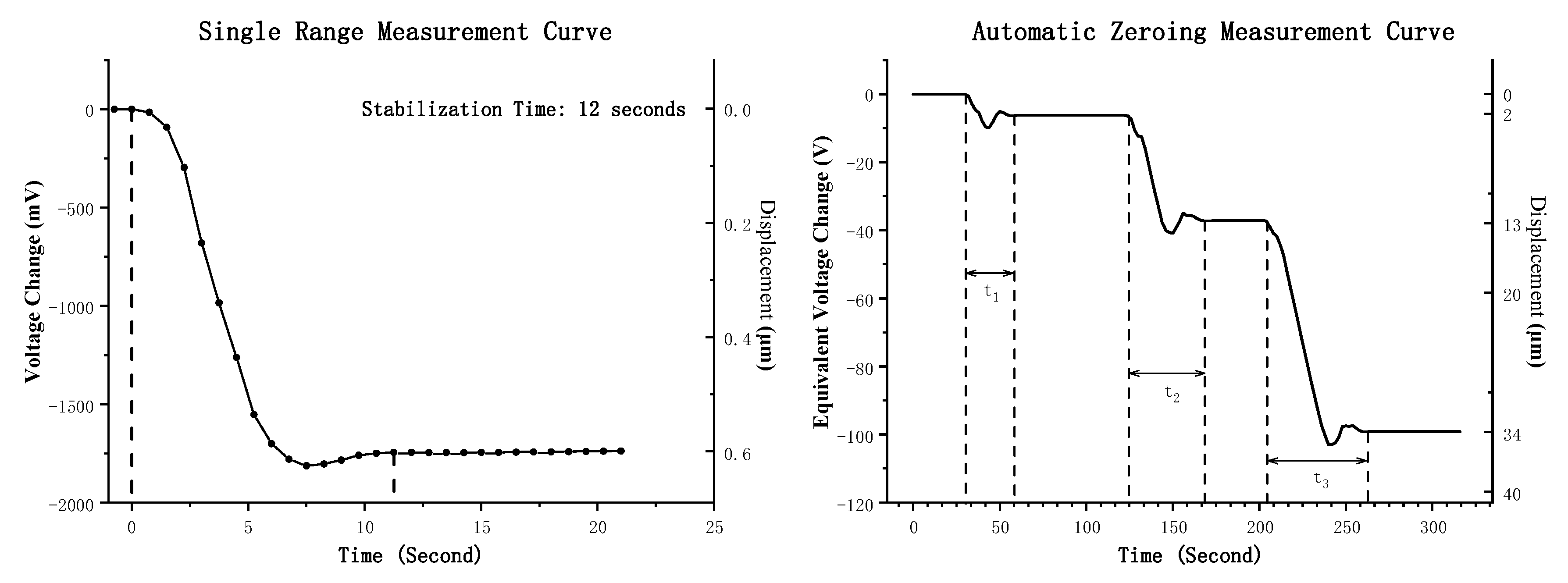
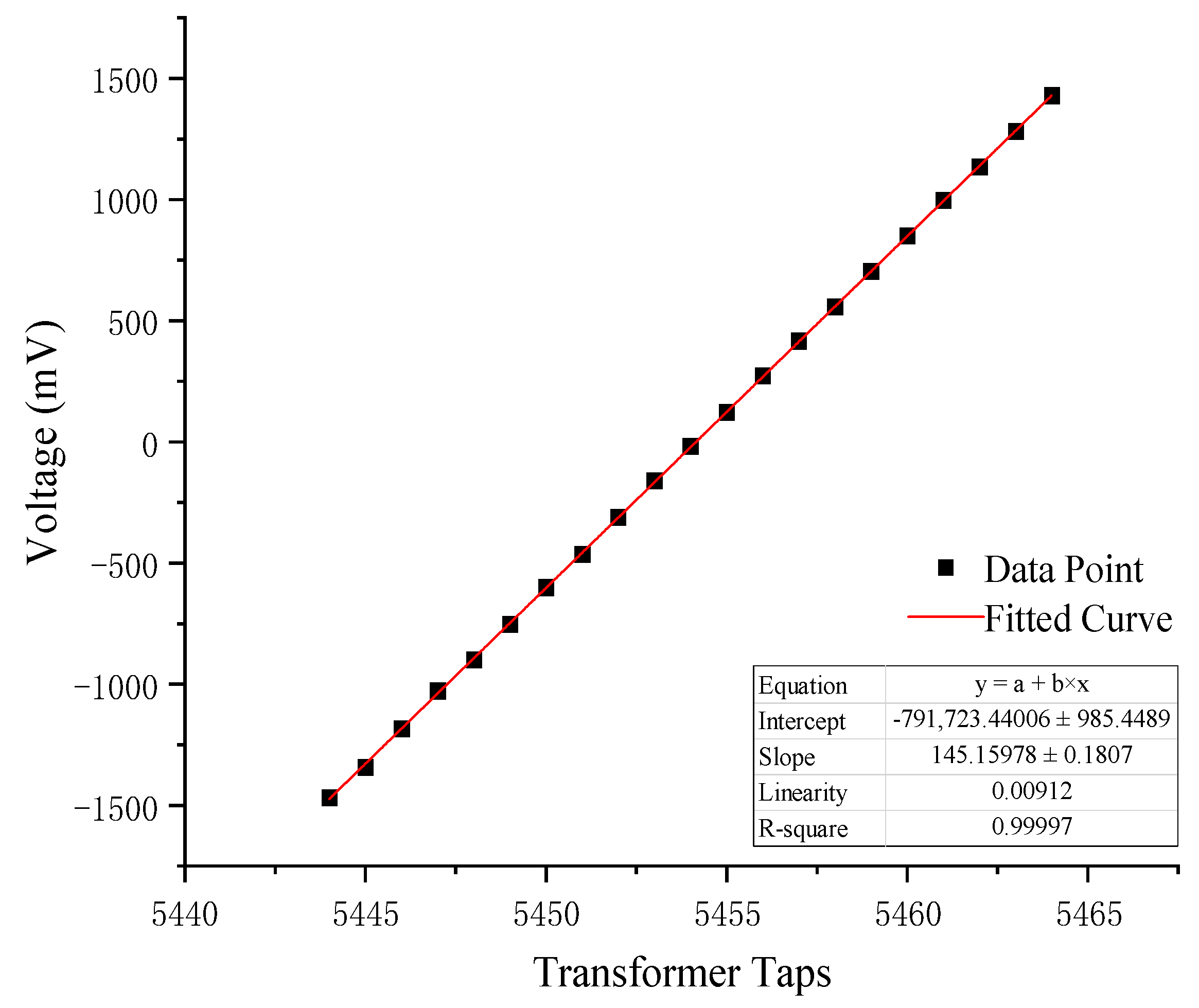
3.2. Quantitative Calibration of the Zero-Setting Experiment
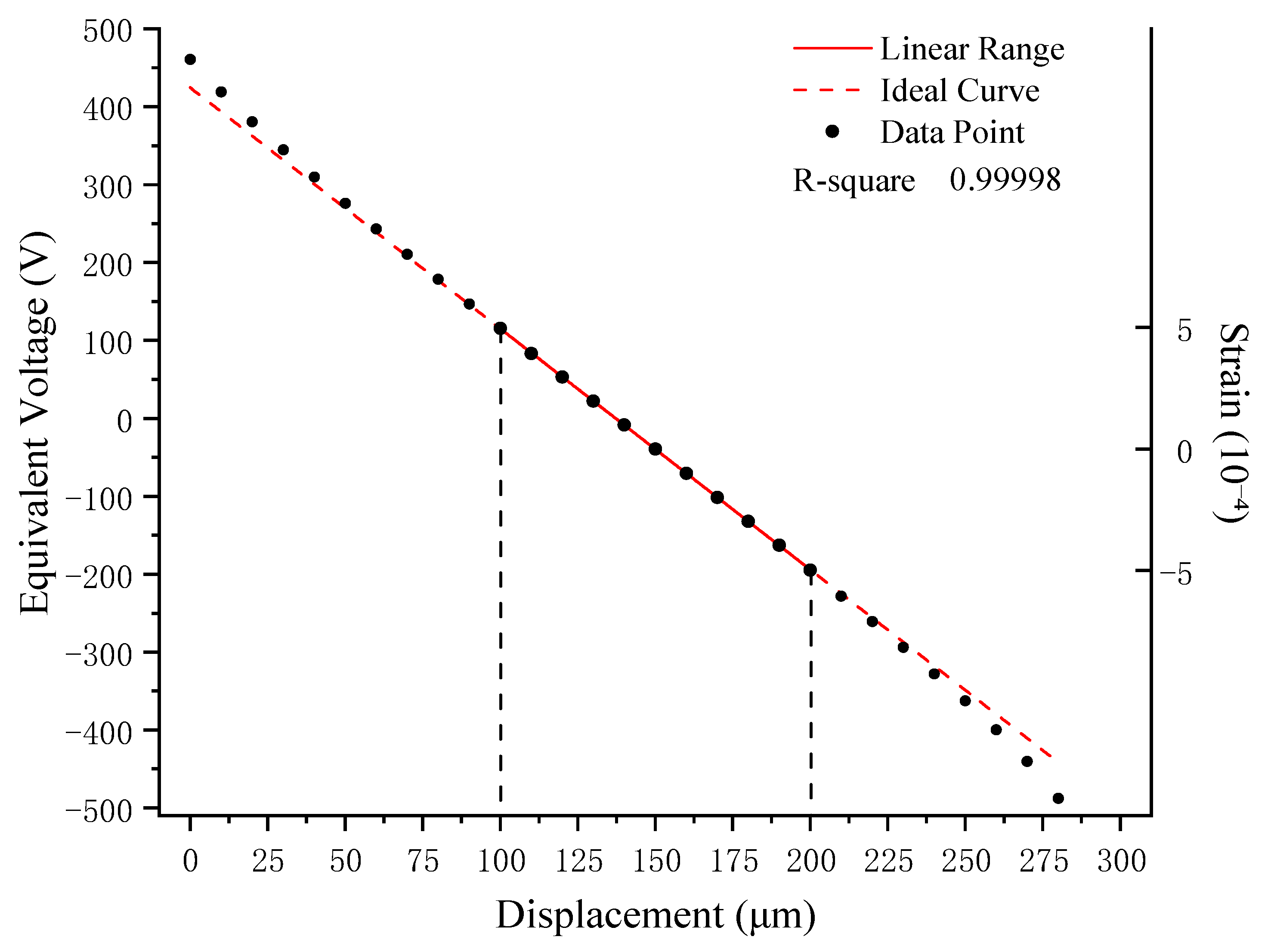
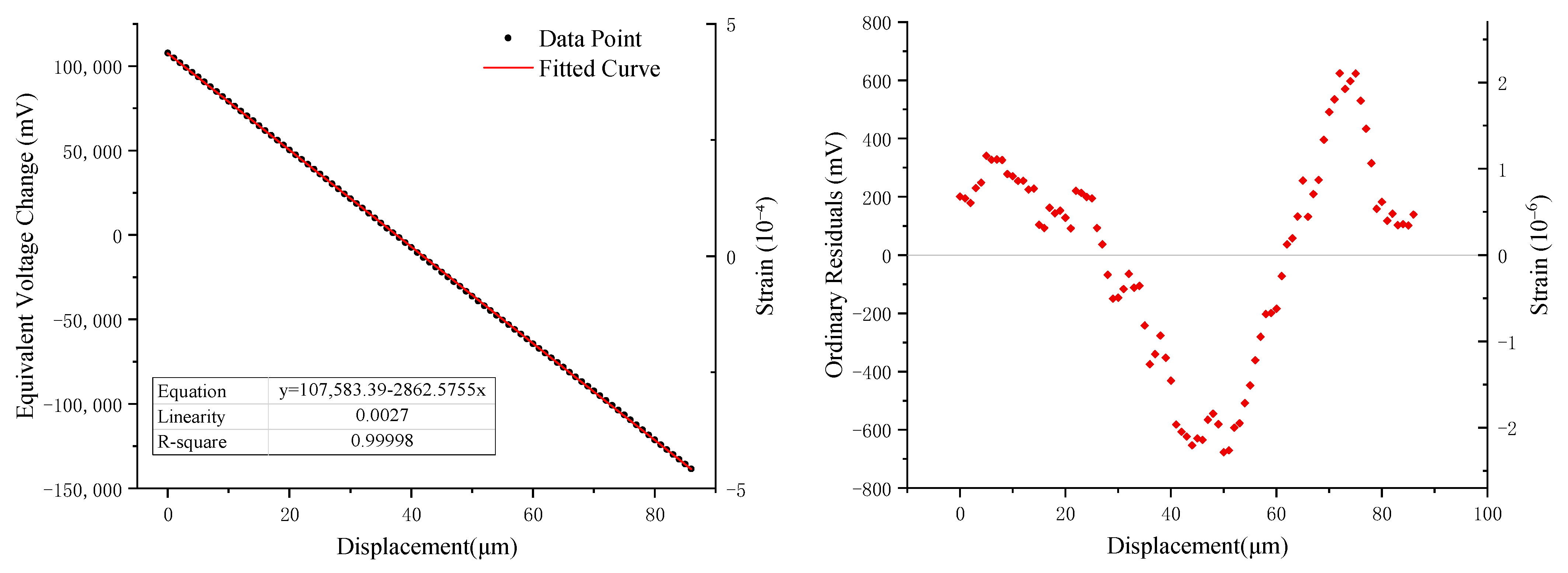
3.3. Linearity Calibration Experiment
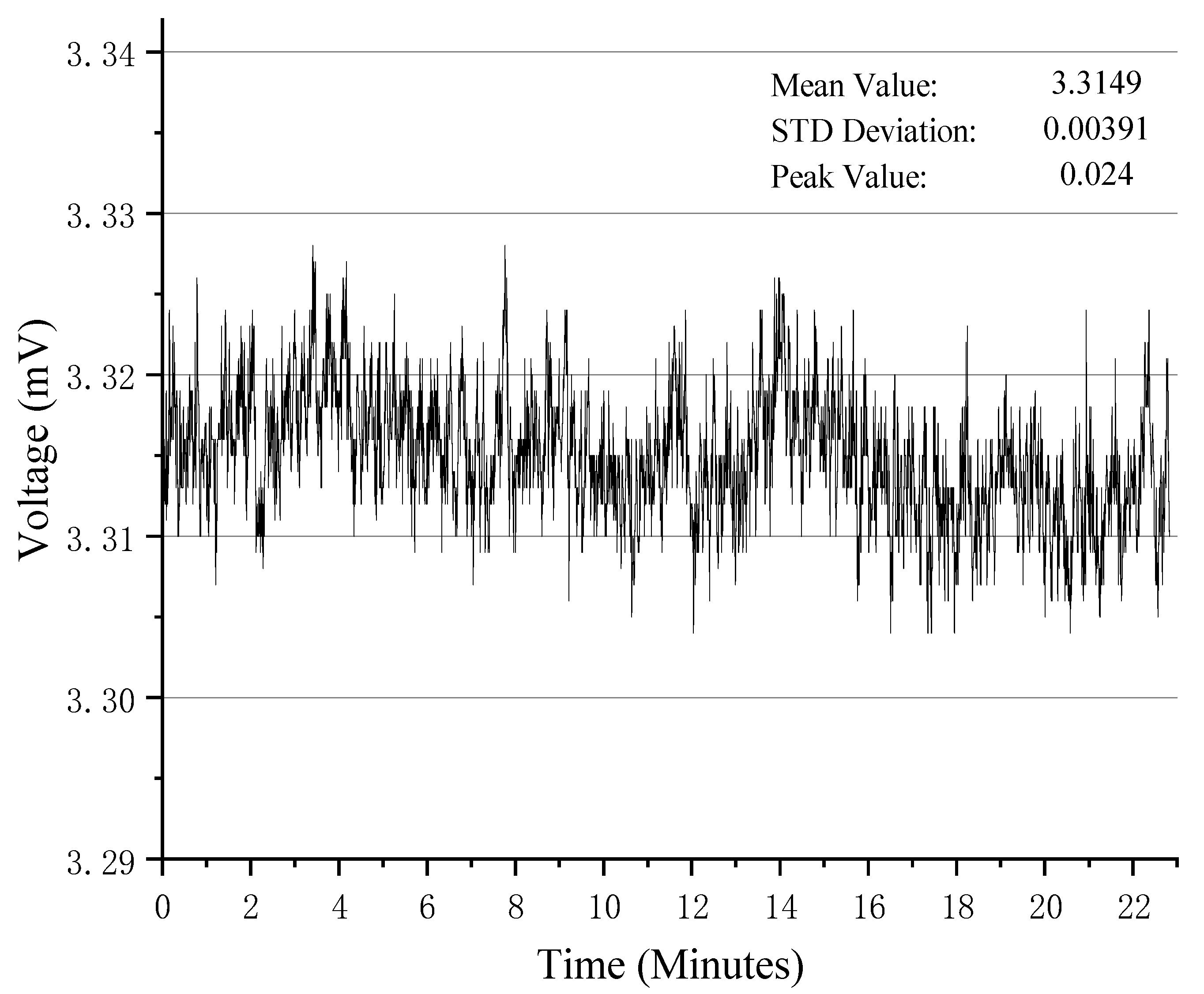
3.4. Noise Testing and Resolution Testing
4. Conclusions
- (1)
- The system successfully implements automatic zero-setting and full-range measurement, reducing data loss risks associated with traditional manual zero-setting methods. Its fully electronic design enhances its integration and stability.
- (2)
- Laboratory testing showed an electronic noise level below 0.024 mV and a theoretical minimum resolution of 0.00136 nm. Zero-setting quantification calibration achieved a linearity error of 0.91% and large-range linearity calibration with a differential capacitive sensor yielded a nonlinearity error of 0.27%. The system can zero large step changes of up to 20 μm within 1 min and record the full measurement curve.
- (3)
- The system design incorporates modularity and compatibility, facilitating ease of human–machine interaction and ensuring compatibility with legacy equipment. It can serve as a solution for automated full-range measurements or as an upgrade to traditional manual dial systems, particularly in applications involving crustal stress and strain measurements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, Z.H.; Xie, F.R.; Su, K.Z.; Ouyang, Z. New era of borehole strain observation. Recent Dev. World Seismol. 2004, 1, 7–14. [Google Scholar]
- Tang, L.; Fan, J.; Liu, G.; Qiu, Z. The Reliability Analysis of Strain Seismic Waves Recorded by High Sampling Four-component Borehole Strainmeter. Earthq. Res. China 2023, 39, 78–87. [Google Scholar]
- Wang, L.; Li, P.; Zhang, C.; Zhu, X.Q.; Gao, X.; Wang, B.P. Comparison and Analysis of Component Borehole Strain (YRY,RZB) Data in Yingkou Seismic Station. J. Disaster Prev. Reduct. 2018, 34, 46–56. [Google Scholar]
- Tang, L.; Qiu, Z.H.; Li, Y.J.; Li, Y.; Fan, J.Y. Determination and analysis of near-surface stress-strain state of 4-component borehole strainmeter. Geomat. Inf. Sci. Wuhan Univ. 2025, 50, 63–73. [Google Scholar] [CrossRef]
- Tang, L.; Qiu, Z.H.; Fan, J.Y.; Luo, Z.H. Characteristic analysis of coseismic variation of 4-component borehole strain observation with different sampling rates. J. Geod. Geodyn. 2022, 42, 1196–1201. [Google Scholar]
- Li, X.D.; Deng, W.P.; Jia, H.F.; He, A.H. Upgrading of Mainframe of RZB-Type Capacitor Borehole Strainmenters. J. Geod. Geodyn. 2016, 36, 1020–1024. [Google Scholar] [CrossRef]
- Liu, G.; Dong, S.W.; Chen, X.H. EarthScope-the latest advances of the United State’s deep exploration program. Acta Geol. Sin. 2010, 84, 909–926. (In Chinese) [Google Scholar]
- Buehler, J.S.; Shearer, P.M. Pn tomography of the western United States using USArray. J. Geophys. Res. Solid Earth 2010, 115, B09315. [Google Scholar] [CrossRef]
- Williams, M.L.; Fischer, K.M.; Freymueller, J.T.; Tikoff, B.; Tréhu, A.M. Unlocking the Secrets of the North American Continent: An EarthScope Science Plan for 2010–2020; EarthScope: Washington, DC, USA, 2010; 78p. [Google Scholar]
- Qiu, Z.H.; Shi, Y.L. Developments of borehole strain observation outside China. Acta Seismol. Sin. 2004, 17, 172–178. [Google Scholar] [CrossRef]
- Gladwin, M.T. High-precision multicomponent borehole deformation monitoring. Rev. Sci. Instrum. 1984, 55, 2011–2016. [Google Scholar] [CrossRef]
- Su, K.Z. Forty years of four-component borehole strain gauge in China. Seismol. Geomagn. Obs. Res. 2020, 41, 172–180. (In Chinese) [Google Scholar]
- Li, H.L.; Li, H. Status and developments of borehole strain observations in China. Acta Geol. Sin. 2010, 84, 895–900. [Google Scholar]
- Wu, S.G. The key technology analysis of borehole strain meter design. Seismol. Geomagn. Obs. Res. 2014. (In Chinese) [Google Scholar]
- Chen, Z.; Li, H.; Dong, Y.; Wang, W.; Wu, L.; Zhan, W. Research on the RZB-Type Three-Dimensional Drilling Strain Measurement System. Sensors 2024, 24, 3954. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.H.; Shi, Y.L.; Ouyang, Z.X. Relative in-situ calibration of 4-component borehole strain observation. J. Geod. Geodyn. 2005, 25, 118–122. [Google Scholar]
- Ouyang, Z.X.; Zhang, Z.R.; He, C.P. A High-Precision Displacement Measurement System Based on Inductive Coupling Ratio Arm. Appl. Electron. Technol. 2004, 30, 41–43. (In Chinese) [Google Scholar] [CrossRef]
- Wu, L.H.; Li, H.; Chen, Z.; Wang, W.B.; Dong, Y.K. Research on the Stability of RZB Borehole Strainmeter Sensor with Range Extension and In-Situ Calibration. J. Geod. Geodyn. 2022, 42, 318–320. [Google Scholar] [CrossRef]
- Wu, L.H.; Xiong, Y.Z.; Li Tao Chen, Z. Study of the Range Expansion of the RZB Borehole Strain Meter. J. Geod. Geodyn. 2015, 35, 4. [Google Scholar] [CrossRef]
- DB/T 31.2-2008; Technical Requirements of Instruments in Network for Earthquake Monitoring. The Instrument for Crustal Deformation Observation. Part 2: Strainmeter. China Earthquake Administration: Beijing, China, 2008. (In Chinese)

| N | Voltage (mv) | N | Voltage (mv) |
|---|---|---|---|
| 5444 | −1469 | 5455 | 122 |
| 5445 | −1343 | 5456 | 273 |
| 5446 | −1183 | 5457 | 416 |
| 5447 | −1028 | 5458 | 556 |
| 5448 | −900 | 5459 | 704 |
| 5449 | −752 | 5460 | 850 |
| 5450 | −601 | 5461 | 997 |
| 5451 | −463 | 5462 | 1136 |
| 5452 | −312 | 5463 | 1281 |
| 5453 | −160 | 5464 | 1429 |
| 5454 | −18 | 5455 | 122 |
| 5444 | −1469 |
| Δd (μm) | ΔV (mv) | Err (mv) | Δd (μm) | ΔV (mv) | Err (mv) | Δd (μm) | ΔV (mv) | Err (mv) | Δd (μm) | ΔV (mv) | Err (mv) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 107,784.111 | 200.724 | 22 | 44,827.505 | 220.779 | 44 | −19,023.257 | −653.322 | 66 | −81,215.114 | 131.482 |
| 1 | 104,915.231 | 194.419 | 23 | 41,957.199 | 213.049 | 45 | −21,862.209 | −629.698 | 67 | −83,999.909 | 209.263 |
| 2 | 102,037.514 | 179.278 | 24 | 39,081.193 | 199.618 | 46 | −24,729.664 | −634.578 | 68 | −86,813.207 | 258.540 |
| 3 | 99,225.926 | 230.265 | 25 | 36,213.737 | 194.738 | 47 | −27,523.011 | −565.349 | 69 | −89,538.145 | 396.178 |
| 4 | 96,381.843 | 248.758 | 26 | 33,249.370 | 92.946 | 48 | −30,364.813 | −544.575 | 70 | −92,305.838 | 491.060 |
| 5 | 93,611.300 | 340.790 | 27 | 30,330.608 | 36.760 | 49 | −33,263.622 | −580.809 | 71 | −95,124.837 | 534.636 |
| 6 | 90,735.293 | 327.360 | 28 | 27,363.391 | −67.882 | 50 | −36,222.288 | −676.900 | 72 | −97,898.231 | 623.818 |
| 7 | 87,873.539 | 328.181 | 29 | 24,418.976 | −149.721 | 51 | −39,078.342 | −670.379 | 73 | −100,814.142 | 570.482 |
| 8 | 85,008.934 | 326.151 | 30 | 21,560.072 | −146.050 | 52 | −41,863.137 | −592.598 | 74 | −103,650.244 | 596.956 |
| 9 | 82,098.723 | 278.516 | 31 | 18,726.821 | −116.726 | 53 | −44,710.640 | −577.526 | 75 | −106,486.345 | 623.430 |
| 10 | 79,228.418 | 270.786 | 32 | 15,916.372 | −64.599 | 54 | −47,503.986 | −508.296 | 76 | −109,442.161 | 530.190 |
| 11 | 76,349.561 | 254.505 | 33 | 13,006.162 | −112.234 | 55 | −50,305.884 | −447.618 | 77 | −112,400.828 | 434.099 |
| 12 | 73,487.806 | 255.325 | 34 | 10,150.108 | −105.712 | 56 | −53,082.128 | −361.286 | 78 | −115,382.298 | 315.205 |
| 13 | 70,594.698 | 224.792 | 35 | 7151.536 | −241.708 | 57 | −55,864.072 | −280.656 | 79 | −118,400.822 | 159.256 |
| 14 | 67,735.793 | 228.464 | 36 | 4155.815 | −374.854 | 58 | −58,648.867 | −202.875 | 80 | −121,239.773 | 182.880 |
| 15 | 64,748.623 | 103.869 | 37 | 1328.265 | −339.829 | 59 | −61,507.772 | −199.204 | 81 | −124,167.086 | 118.143 |
| 16 | 61,875.467 | 93.288 | 38 | −1470.782 | −276.300 | 60 | −64,355.275 | −184.131 | 82 | −127,006.038 | 141.766 |
| 17 | 59,082.121 | 162.518 | 39 | −4409.496 | −352.439 | 61 | −67,105.865 | −72.147 | 83 | −129,907.697 | 102.682 |
| 18 | 56,200.414 | 143.386 | 40 | −7351.061 | −431.428 | 62 | −69,859.307 | 36.988 | 84 | −132,766.602 | 106.353 |
| 19 | 53,347.210 | 152.758 | 41 | −10,363.884 | −581.676 | 63 | −72,701.109 | 57.761 | 85 | −135,634.057 | 101.474 |
| 20 | 50,459.803 | 127.926 | 42 | −13,251.292 | −606.508 | 64 | −75,488.754 | 132.691 | 86 | −138,458.757 | 139.349 |
| 21 | 47,560.994 | 91.692 | 43 | −16,130.149 | −622.789 | 65 | −78,227.944 | 256.077 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Chen, Z.; Li, H.; Wang, W.; Zhan, W.; Wu, L.; Dong, Y.; Chen, J. Range Extension of Borehole Strainmeters Using MOSFET-Based Multi-Switch Automatic Zero Setting. Sensors 2025, 25, 476. https://doi.org/10.3390/s25020476
Yang C, Chen Z, Li H, Wang W, Zhan W, Wu L, Dong Y, Chen J. Range Extension of Borehole Strainmeters Using MOSFET-Based Multi-Switch Automatic Zero Setting. Sensors. 2025; 25(2):476. https://doi.org/10.3390/s25020476
Chicago/Turabian StyleYang, Chen, Zheng Chen, Hong Li, Wenbo Wang, Weiwei Zhan, Liheng Wu, Yunkai Dong, and Jiaxin Chen. 2025. "Range Extension of Borehole Strainmeters Using MOSFET-Based Multi-Switch Automatic Zero Setting" Sensors 25, no. 2: 476. https://doi.org/10.3390/s25020476
APA StyleYang, C., Chen, Z., Li, H., Wang, W., Zhan, W., Wu, L., Dong, Y., & Chen, J. (2025). Range Extension of Borehole Strainmeters Using MOSFET-Based Multi-Switch Automatic Zero Setting. Sensors, 25(2), 476. https://doi.org/10.3390/s25020476






