TARREAN: A Novel Transformer with a Gate Recurrent Unit for Stylized Music Generation
Abstract
1. Introduction
- (1)
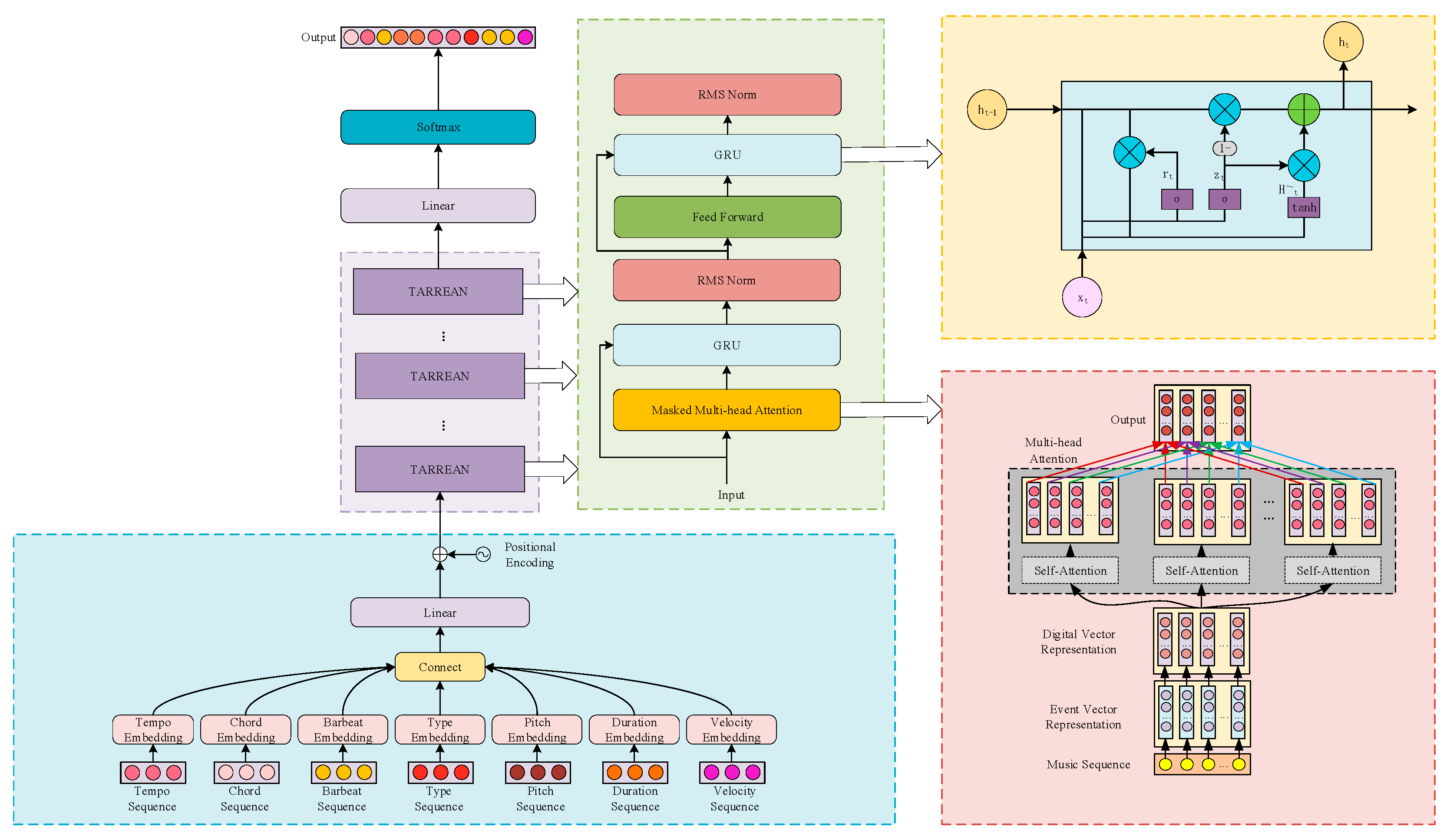
- A TARREAN model for music generation is proposed, which replaces residual connection modules with GRU modules. It utilizes an update gate to control the iteration of old music sequence feature information and a reset gate to determine the degree of influence of old feature information on the training process in order to adapt to the current music characteristics. This improvement allows the TARREAN model to exhibit better performance in modeling long sequences and capturing dependencies in music.
- (2)
- Replacing layer norm with RMS norm can smooth gradients while reducing model training time. By propagating more gradient signals to early layers during network training, it helps the network to better learn the statistical characteristics of music sequences.
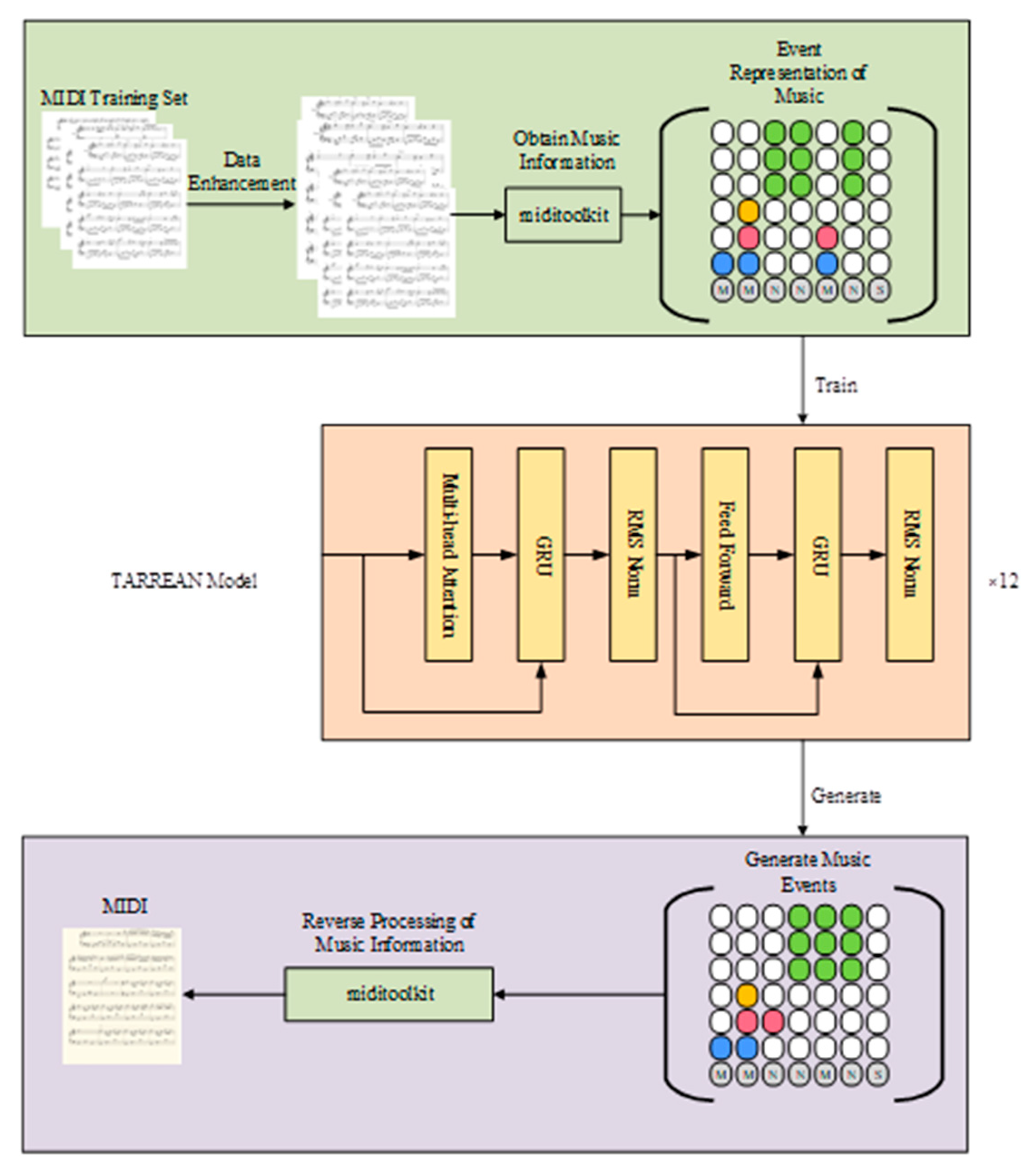
2. Data Pre-Processing and Data Representation
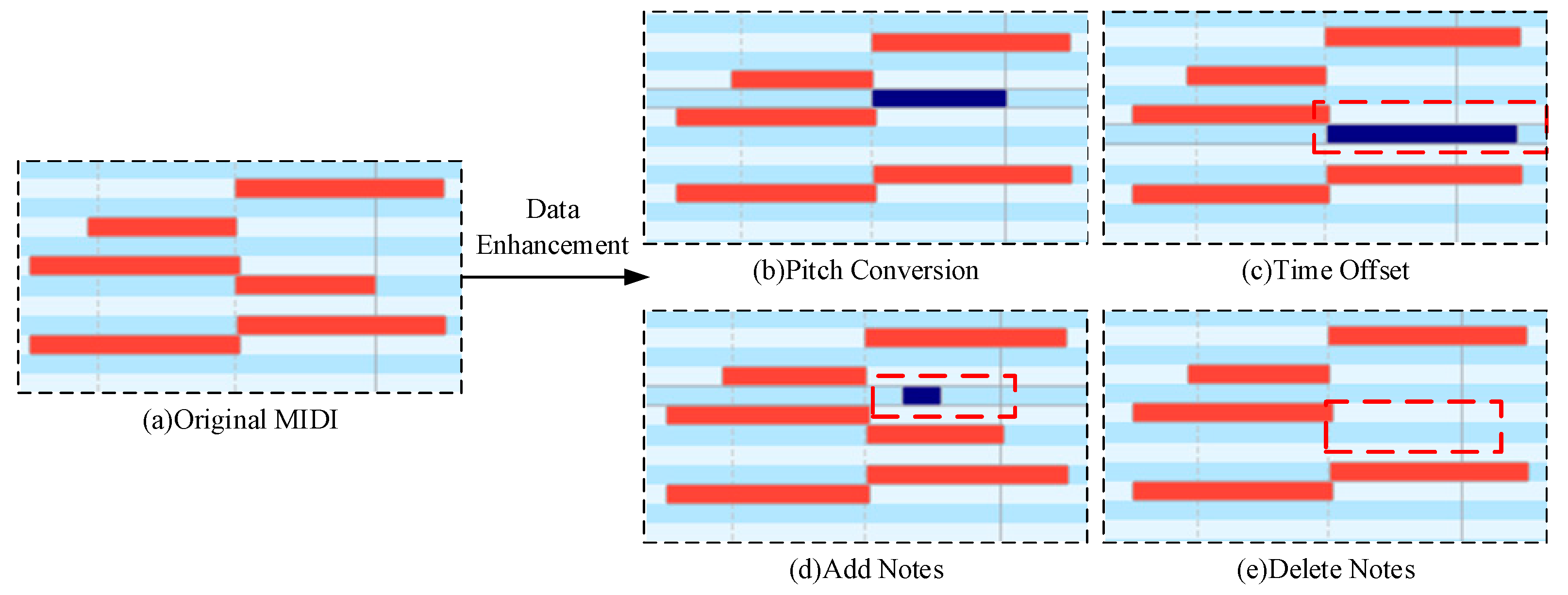
2.1. Musical Data Enhancement
- (1)
- Pitch conversion: Create a new melody by converting the notes in the MIDI data through moving the pitch of each note up or down. For example, moving all notes up by a half tone or all notes down by a quarter to create a different yet still somewhat similar melody as to the original one, shown in Figure 2b.
- (2)
- Time offset: Make the length of the notes become longer or shorter by changing the MIDI duration value of the notes. Change the rhythm and performance of the music by adjusting the timestamps of the MIDI events. Random time offsets generate a random time offset for each MIDI event, which can control the range and distribution of random offsets. By introducing randomness, more variation and expressiveness can be added to the music, as shown in Figure 2c).
- (3)
- Add notes: Add additional notes to the existing MIDI data to increase the complexity and hierarchy of the music; this can extend the melody or harmony, as shown in Figure 2d.
- (4)
- Delete notes: Delete specific notes in MIDI data to reduce certain elements in music; this can make the music concise or change its structure, as shown in Figure 2e.
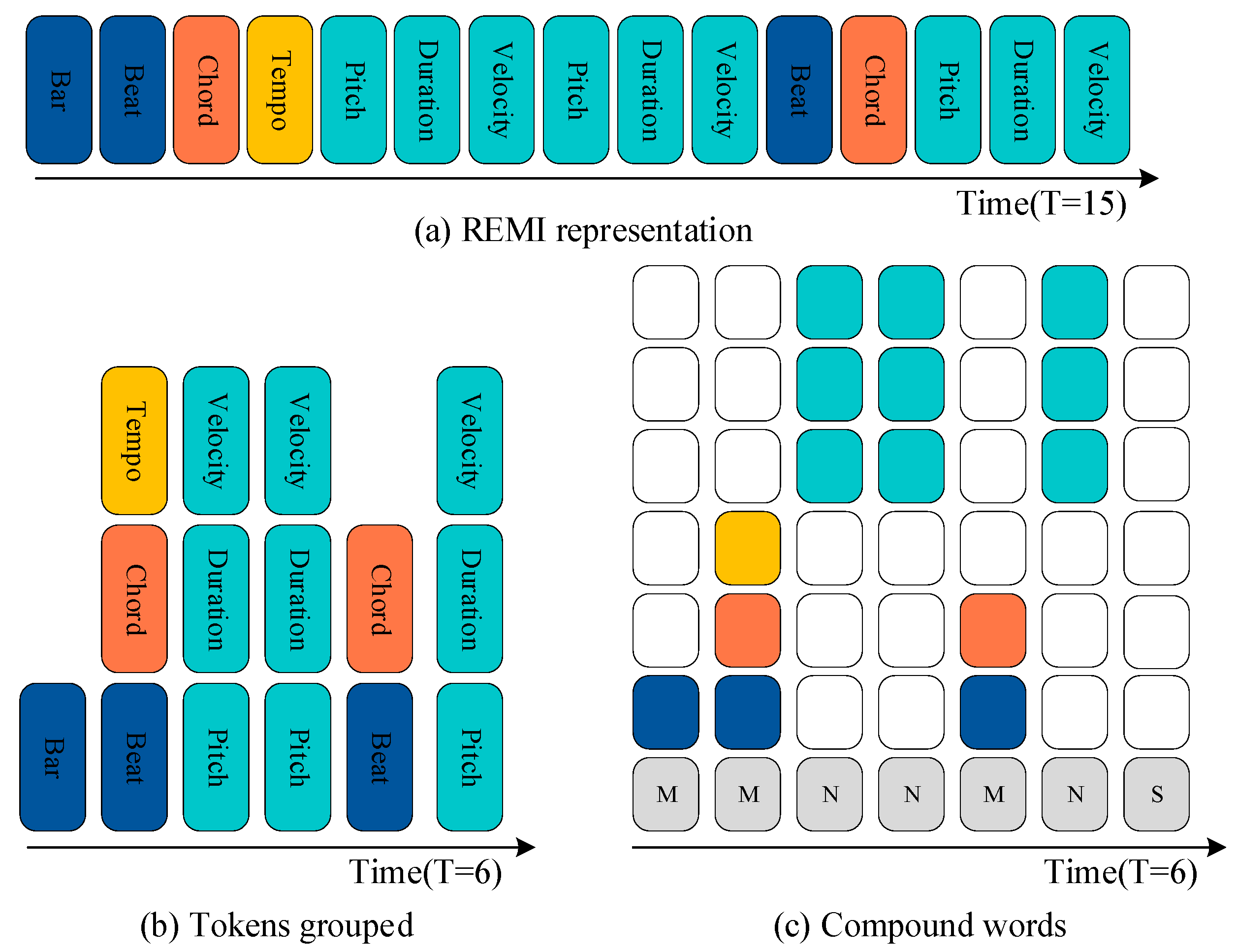
2.2. Data Representation of Music Event
3. Model Structure
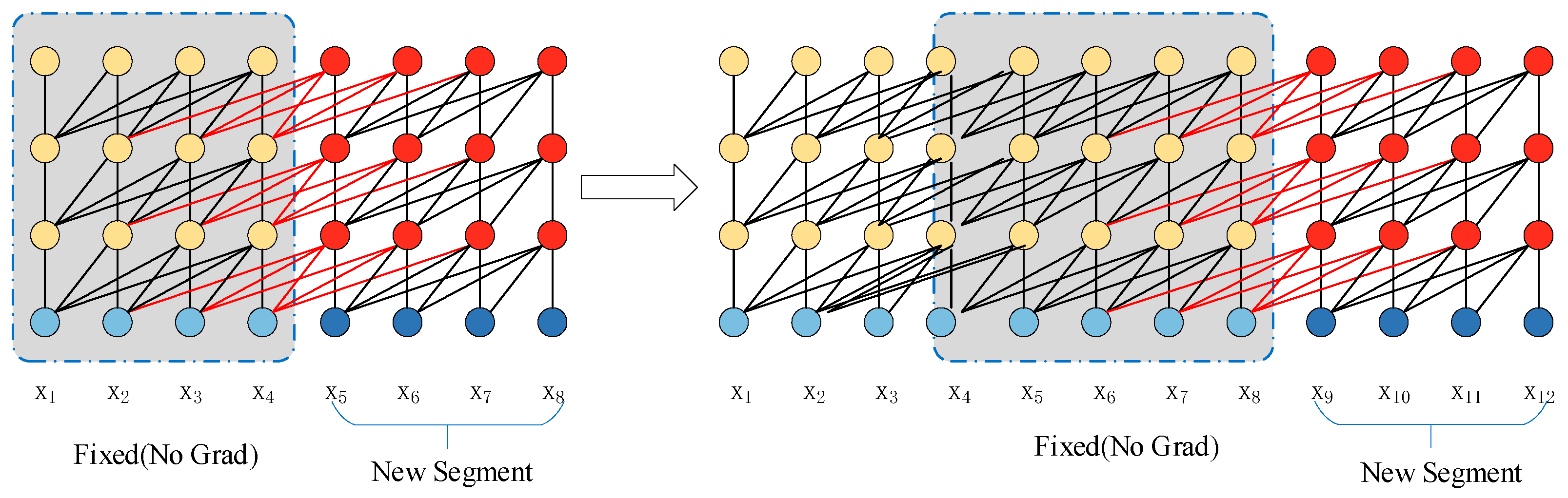
3.1. The TARREAN Network Structure
3.2. Multi-Head Attention Unit with Mask
3.3. GRU
3.4. RMS Norm Unit
4. Experiments and Results Analysis
4.1. Dataset and Experimental Setup
4.2. Model Performance Comparison
4.3. Objective Evaluation Experiments and Results
4.3.1. Objective Evaluation Index
- (1)
- Index related to pitch
- (2)
- Index related to rhythm
- (3)
- Structural indicators
4.3.2. Experimental Results and Analysis
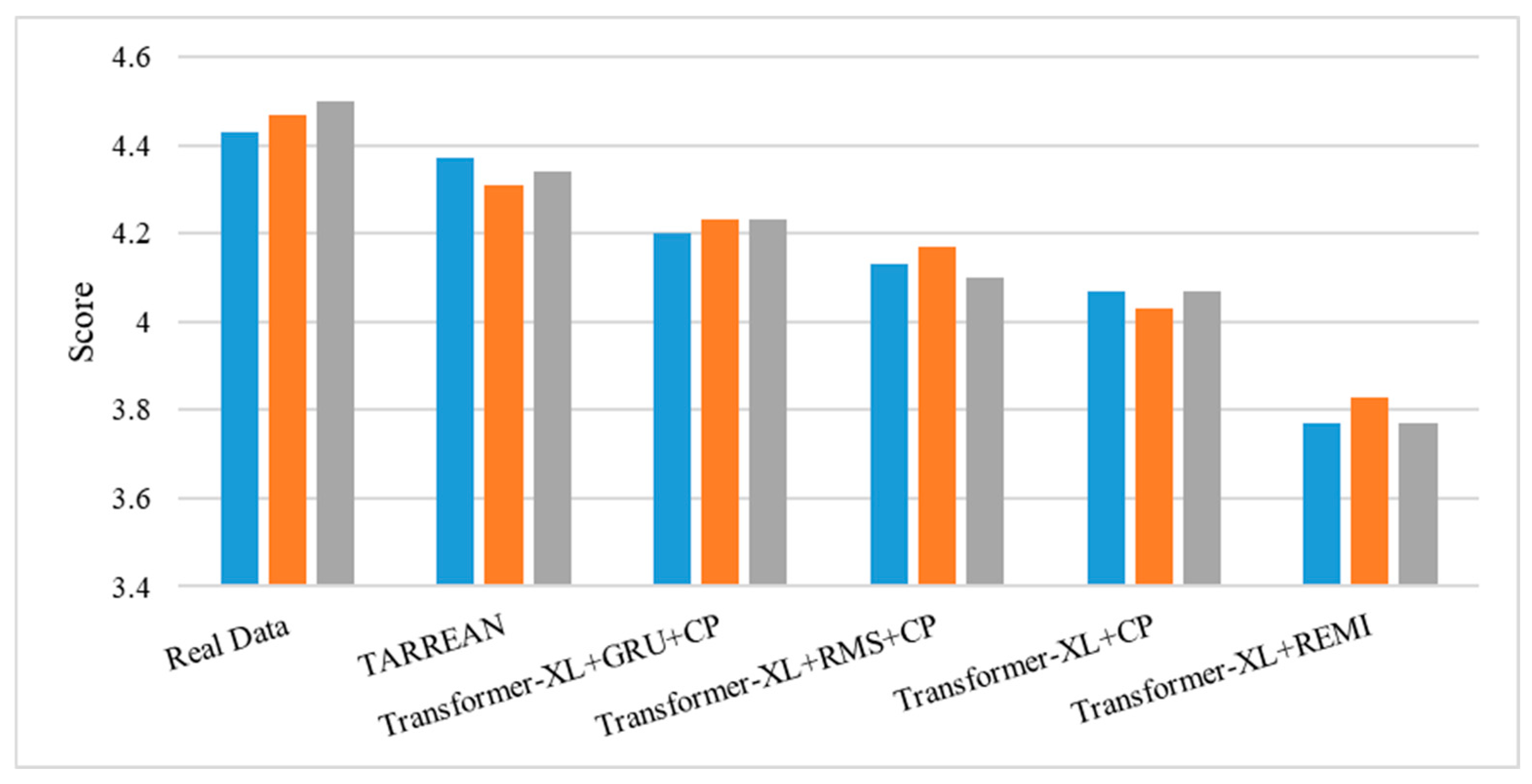
4.4. Subjective Evaluation Experiment and Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalingeri, V.; Grandhe, S. Music generation with deep learning. Comput. Sci. 2016, 18, 126–134. [Google Scholar]
- Briot, J.P.; Pachet, F. Deep learning for music generation: Challenges and directions. Neural Comput. Appl. 2020, 32, 215–228. [Google Scholar] [CrossRef]
- Hsiao, W.Y.; Liu, J.Y.; Yeh, Y.C.; Yang, Y.H. Compound Word Transformer: Learning to compose full-song music over dynamic directed hypergraphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021. [Google Scholar]
- Verbeurgt, K.A.; Dinolfo, M.; Fayer, M. Extracting patterns in music for composition via Markov chains. In Proceedings of the International Conference on Innovations in Applied Artificial Intelligence, Ottawa, ON, Canada, 17–20 May 2004; pp. 734–758. [Google Scholar]
- Todd, P.M. A connectionist approach to algorithmic composition. Comput. Music. J. 1989, 13, 27–43. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhube, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Eck, D.; Schmidhuber, J. A first look at music composition using lstm recurrent neural networks. Ist. Dalle Molle Di Studi Sull Intell. Artif. 2002, 103, 48–59. [Google Scholar]
- Li, S.; Sung, Y. INCO-GAN: Variable-length music generation method based on inception model-based conditional GAN. Mathematics 2021, 9, 102–110. [Google Scholar] [CrossRef]
- Dong, H.W.; Hsiao, W.Y.; Yang, L.C.; Yang, Y.H. Musegan: Multi-track sequential generative adversarial networks for symbolic music generation and accompaniment. In Proceedings of the the Association for the Advance of Artificial Intelligence Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 1124–1136. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 123–130. [Google Scholar]
- Yang, L.; Chou, S.; Yang, Y. MidiNet: A convolutional generative adversarial network for symbolic-domain music generation. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Suzhou, China, 23–27 October 2017; pp. 324–331. [Google Scholar]
- Huang, C.; Vaswani, A.; Uszkoreit, J.; Shazeer, N.; Simon, I.; Hawthorne, C.; Dai, A.M.; Hoffman, M.D.; Dinculescu, M.; Eck, D. Music Transformer: Generating music with long-term structure. Learn. Represent. 2019, 34, 86–99. [Google Scholar]
- Deng, X.; Chen, S.; Chen, Y.; Xu, J. Multi-level convolutional transformer with adaptive ranking for semi-supervised crowd counting. In Proceedings of the Conference Proceedings of 2021 4th International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 22–24 December 2021; pp. 28–34. [Google Scholar]
- Huang, Y.S.; Yang, Y.H. Pop music transformer: Beat-based modeling and generation of expressive pop piano compositions. In Proceedings of the ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1180–1188. [Google Scholar]
- Choi, K.; Hawthorne, C.; Simon, I.; Dinculescu, M.; Engel, J. Encoding musical style with transformer autoencoders. Mach. Learn. 2020, 15, 178–190. [Google Scholar]
- Wu, S.; Yang, Y. The Jazz Transformer on the front line: Exploring the shortcomings of AI-composed music through quantitative measures. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Milan, Italy, 5–9 November 2020; pp. 134–156. [Google Scholar]
- Donahue, C.; Mao Li, Y.E.; Cottrell, G.W.; McAuley, J. LakhNES: Improving multi-instrumental music generation with cross-domain pre-training. In Proceedings of the Music Information Retrieval Conference, Delft, The Netherlands, 4–8 November 2019; pp. 685–692. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive language models beyond a fixed-length context. In Proceedings of the Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 2978–2988. [Google Scholar]
- Xiong, R.; Yang, Y.; He, D.; Zheng, K.; Zheng, S.; Xing, C.; Zhang, H.; Lan, Y.; Wang, L.; Liu, T. On layer normalization in the Transformer architecture. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 10524–10533. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN Encoder-Decoder for statistical machine translation. Comput. Sci. 2014, 14, 1154–1179. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- Zhang, B.; Sennrich, R. Root mean square layer normalization. NeurIPS 2019, 13, 12360–12371. [Google Scholar]
- Tang, Z. Melody generation algorithm based on LSTM network. Inf. Comput. 2021, 32, 62–64. [Google Scholar]
- Ma, N.; Zhang, X.; Liu, M.; Sun, J. Activate or not: Learning customized activation. Comput. Vis. Pattern Recognit. 2020, 21, 145–157. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. Comput. Sci. 2014, 46, 122–127. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Foote, J. Visualizing music and audio using self-similarity. In Proceedings of the Acm International Conference on Multimedia, Orlando, FL, USA, 30 October–5 November 1999; pp. 77–80. [Google Scholar]
- Müller, M.; Grosche, P.; Jiang, N. A Segment-based fitness measure for capturing repetitive structures of music recordings. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Miami, FL, USA, 24–28 October 2011; pp. 615–620. [Google Scholar]
| Method | Strengths | Limitations |
|---|---|---|
| Music Transformer | Long-range dependency modeling | Lacks temporal coherence in ultra-long sequences; high computational cost |
| Pop Music Transformer | Beat-based modeling; expressive output | Limited scalability; requires extensive data |
| Transformer + GRU Hybrid | Improved coherence; contextual learning | Limited applications in music generation |
| Model | Training Duration (Days) |
|---|---|
| Transformer-XL + CP | 2.27 |
| Transformer-XL + RMS + CP | 2.25 |
| Transformer-XL + GRU + CP | 3.07 |
| TARREAN | 2.37 |
| Model | Pitch-Related | Rhythm-Related | SI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PR | PSR | PE | PH | SC | EBR | GS | SI_short | SI_mid | SI_long | |
| Real Data | 16.31 | 0.8724 | 2.7804 | 2.3313 | 0.9991 | 0.0574 | 0.9353 | 0.7077 | 0.6891 | 0.6705 |
| Transformer-XL + REMI | 30.10 | 0.8857 | 4.0688 | 3.1572 | 0.8773 | 0.2568 | 0.8674 | 0.6405 | 0.6086 | 0.6027 |
| Transformer-XL + CP | 29.42 | 0.8871 | 4.0254 | 3.1427 | 0.8877 | 0.2187 | 0.8678 | 0.6399 | 0.6161 | 0.6044 |
| Transformer-XL + RMS + CP | 30.94 | 0.8810 | 3.9987 | 3.1453 | 0.8816 | 0.2525 | 0.8674 | 0.6360 | 0.6118 | 0.6108 |
| Transformer-XL + GRU + CP | 31.06 | 0.8934 | 4.0038 | 3.1234 | 0.8936 | 0.2542 | 0.8651 | 0.6344 | 0.6158 | 0.6130 |
| TARREAN | 29.10 | 0.8674 | 3.9357 | 3.1764 | 0.8694 | 0.2580 | 0.8714 | 0.6462 | 0.6289 | 0.6169 |
| Model | Pitch-Related | Rhythm-Related | SI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PR | PSR | PE | PH | SC | EBR | GS | SI_short | SI_mid | SI_long | |
| Transformer-XL + REMI | 13.79 | 0.0133 | 1.2884 | 0.8259 | 0.1218 | 0.1994 | 0.0679 | 0.0672 | 0.0805 | 0.0678 |
| Transformer-XL + CP | 13.11 | 0.0147 | 1.2450 | 0.8114 | 0.1114 | 0.1613 | 0.0675 | 0.0678 | 0.0730 | 0.0661 |
| Transformer-XL + RMS + CP | 14.63 | 0.0086 | 1.2183 | 0.8140 | 0.1175 | 0.1951 | 0.0679 | 0.0717 | 0.0773 | 0.0597 |
| Transformer-XL + GRU + CP | 14.75 | 0.0210 | 1.2234 | 0.7921 | 0.1055 | 0.1968 | 0.0702 | 0.0733 | 0.0733 | 0.0575 |
| TARREAN | 12.79 | 0.0050 | 1.1553 | 0.8451 | 0.1297 | 0.2006 | 0.0639 | 0.0615 | 0.0602 | 0.0536 |
| Average Scores | Real Data | Transformer-XL + REMI | Transformer-XL + CP | Transformer-XL + RMS + CP | Transformer-XL + GRU + CP | TARREAN |
|---|---|---|---|---|---|---|
| Professionals | 4.43 | 3.60 | 4.03 | 4.07 | 4.20 | 4.28 |
| Non-professionals | 4.48 | 3.88 | 4.07 | 4.17 | 4.23 | 4.37 |
| All participants | 4.47 | 3.79 | 4.06 | 4.13 | 4.22 | 4.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, Y.; Lv, X.; Li, J.; Lu, H.; Su, Y.; Yang, H. TARREAN: A Novel Transformer with a Gate Recurrent Unit for Stylized Music Generation. Sensors 2025, 25, 386. https://doi.org/10.3390/s25020386
Zhang Y, Zhou Y, Lv X, Li J, Lu H, Su Y, Yang H. TARREAN: A Novel Transformer with a Gate Recurrent Unit for Stylized Music Generation. Sensors. 2025; 25(2):386. https://doi.org/10.3390/s25020386
Chicago/Turabian StyleZhang, Yumei, Yulin Zhou, Xiaojiao Lv, Jinshan Li, Heng Lu, Yuping Su, and Honghong Yang. 2025. "TARREAN: A Novel Transformer with a Gate Recurrent Unit for Stylized Music Generation" Sensors 25, no. 2: 386. https://doi.org/10.3390/s25020386
APA StyleZhang, Y., Zhou, Y., Lv, X., Li, J., Lu, H., Su, Y., & Yang, H. (2025). TARREAN: A Novel Transformer with a Gate Recurrent Unit for Stylized Music Generation. Sensors, 25(2), 386. https://doi.org/10.3390/s25020386






