Validation and Analysis of Recreational Runners’ Kinematics Obtained from a Sacral IMU
Abstract
1. Introduction
2. Materials and Methods
2.1. Validation Study
2.1.1. Data Collection
2.1.2. Data Analysis
2.2. Movement Pattern Study
2.2.1. Data Collection
2.2.2. Data Analysis
3. Results
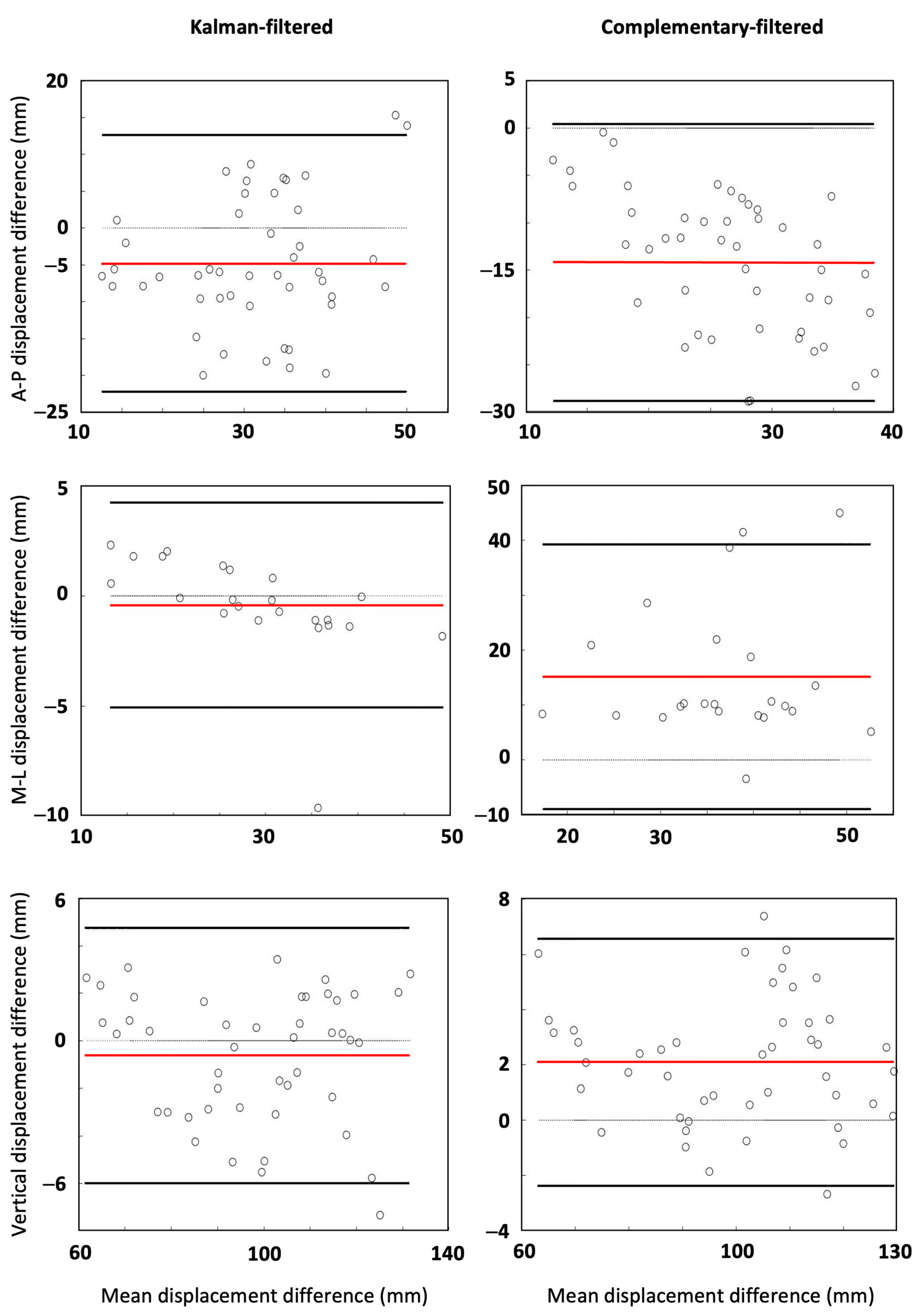
3.1. Validation Study
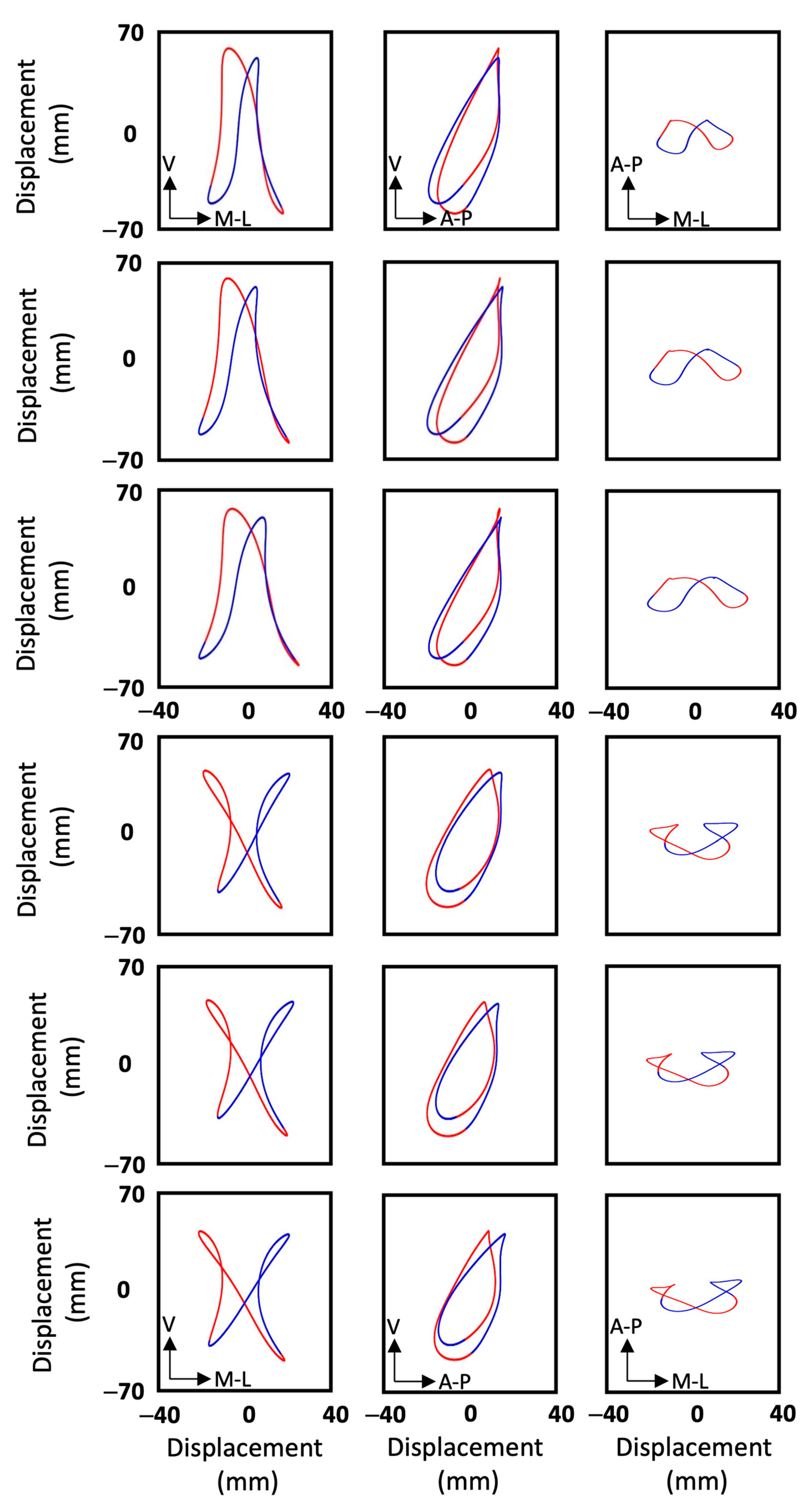
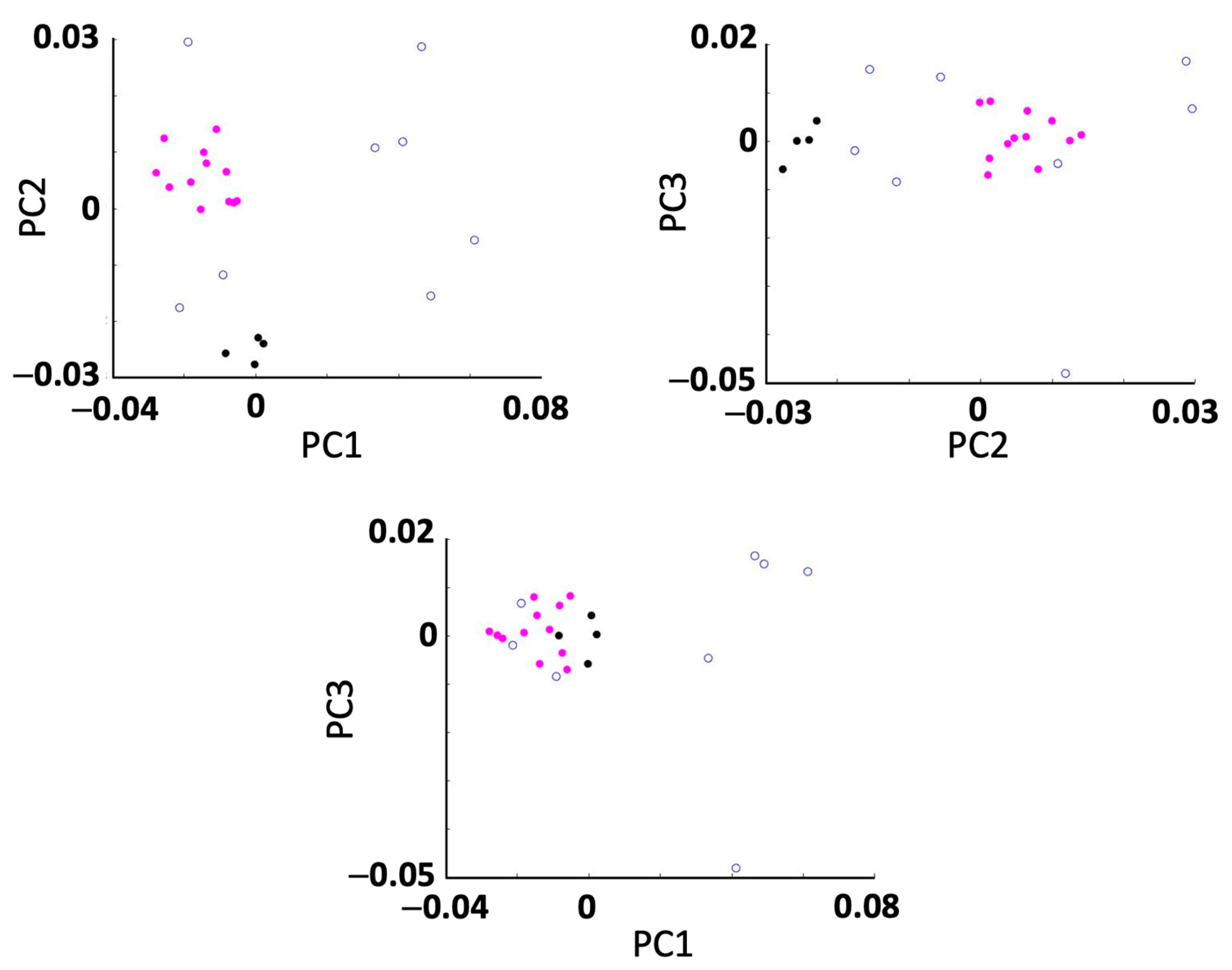
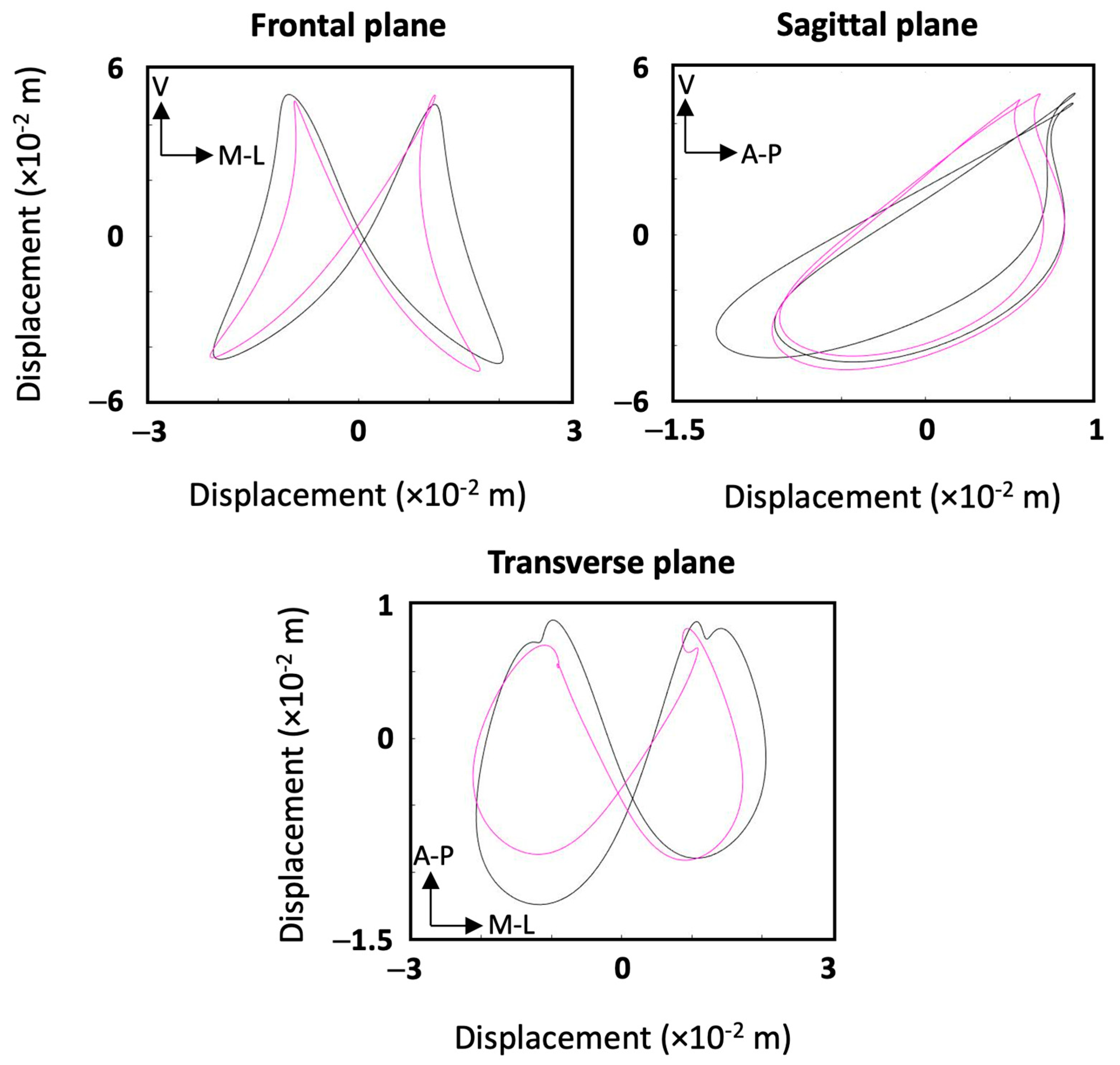
3.2. Movement Pattern Study
4. Discussion
4.1. Validation Study
4.2. Movement Pattern Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Folland, J.P.; Allen, S.J.; Black, M.I.; Handsaker, J.C.; Forrester, S.E. Running Technique is an Important Component of Running Economy and Performance. Med. Sci. Sports Exerc. 2017, 49, 1412–1423. [Google Scholar] [CrossRef] [PubMed]
- Abt, J.P.; Sell, T.C.; Chu, Y.; Lovalekar, M.; Burdett, R.G.; Lephart, S.M. Running Kinematics and Shock Absorption Do Not Change After Brief Exhaustive Running. J. Strength Cond. Res. 2011, 25, 1479–1485. [Google Scholar] [CrossRef] [PubMed]
- Daoud, A.I.; Geissler, G.J.; Wang, F.; Saretsky, J.; Daoud, Y.A.; Lieberman, D.E. Foot Strike and Injury Rates in Endurance Runners: A Retrospective Study. Med. Sci. Sports Exerc. 2012, 44, 1325–1334. [Google Scholar] [CrossRef]
- Milner, C.E.; Hamill, J.; Davis, I.S. Distinct Hip and Rearfoot Kinematics in Female Runners With a History of Tibial Stress Fracture. J. Orthop. Sports Phys. Ther. 2010, 40, 59–66. [Google Scholar] [CrossRef]
- Williams, K.R. Biomechanical Factors Contributing to Marathon Race Success. Sports Med. 2007, 37, 420–423. [Google Scholar] [CrossRef] [PubMed]
- Daly, C.; Persson, U.M.; Twycross-Lewis, R.; Woledge, R.C.; Morrissey, D. The biomechanics of running in athletes with previous hamstring injury: A case-control study: Running biomechanics after hamstring injury. Scand. J. Med. Sci. Sports 2016, 26, 413–420. [Google Scholar] [CrossRef]
- Bartlett, R.; Wheat, J.; Robins, M. Is movement variability important for sports biomechanists? Sports Biomech. 2007, 6, 224–243. [Google Scholar] [CrossRef] [PubMed]
- Phinyomark, A.; Osis, S.; Hettinga, B.A.; Ferber, R. Kinematic gait patterns in healthy runners: A hierarchical cluster analysis. J. Biomech. 2015, 48, 3897–3904. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, H.; Allard, P.; Prince, F.; Labelle, H. Symmetry and limb dominance in able-bodied gait: A review. Gait Posture 2000, 12, 34–45. [Google Scholar] [CrossRef]
- Mezghani, N.; Fuentes, A.; Gaudreault, N.; Mitiche, A.; Aissaoui, R.; Hagmeister, N.; De Guise, J.A. Identification of knee frontal plane kinematic patterns in normal gait by principal component analysis. J. Mech. Med. Biol. 2013, 13, 1350026. [Google Scholar] [CrossRef]
- Williams, K.R.; Cavanagh, P.R. Relationship between distance running mechanics, running economy, and performance. J. Appl. Physiol. 1987, 63, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P. 25 years of lower limb joint kinematics by using inertial and magnetic sensors: A review of methodological approaches. Gait Posture 2017, 51, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Kobsar, D.; Charlton, J.M.; Tse, C.T.F.; Esculier, J.; Graffos, A.; Krowchuk, N.M.; Thatcher, D.; Hunt, M.A. Validity and reliability of wearable inertial sensors in healthy adult walking: A systematic review and meta-analysis. J. Neuroeng. Rehabil. 2020, 17, 62. [Google Scholar] [CrossRef] [PubMed]
- Benson, L.C.; Räisänen, A.M.; Clermont, C.A.; Ferber, R. Is This the Real Life, or Is This Just Laboratory? A Scoping Review of IMU-Based Running Gait Analysis. Sensors 2022, 22, 1722. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Y.; Li, Z.; Yuan, S.; Zhu, S. IMU/UWB Fusion Method Using a Complementary Filter and a Kalman Filter for Hybrid Upper Limb Motion Estimation. Sensors 2023, 23, 6700. [Google Scholar] [CrossRef] [PubMed]
- Gullstrand, L.; Halvorsen, K.; Tinmark, F.; Eriksson, M.; Nilsson, J. Measurements of vertical displacement in running, a methodological comparison. Gait Posture 2009, 30, 71–75. [Google Scholar] [CrossRef]
- Napier, C.; Jiang, X.; MacLean, C.L.; Menon, C.; Hunt, M.A. The use of a single sacral marker method to approximate the centre of mass trajectory during treadmill running. J. Biomech. 2020, 108, 109886. [Google Scholar] [CrossRef]
- Baker, R. Pelvic angles: A mathematically rigorous definition which is consistent with a conventional clinical understanding of the terms. Gait Posture 2001, 13, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Pedley, M. Tilt Sensing Using a Three-Axis Accelerometer. Free. Semicond. Appl. Note 2013, 1, 2012–2013. [Google Scholar]
- Chang, R.H.; Mu, X.D.; Shen, X.W. Attitude Estimation with Complementary Filter. Appl. Mech. Mater. 2011, 44, 3781–3784. [Google Scholar] [CrossRef]
- Wundersitz, D.W.T.; Netto, K.J.; Aisbett, B.; Gastin, P.B. Validity of an upper-body-mounted accelerometer to measure peak vertical and resultant force during running and change-of-direction tasks. Sports Biomech. 2013, 12, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Little, C.; Lee, J.B.; James, D.A.; Davison, K. An evaluation of inertial sensor technology in the discrimination of human gait. J. Sports Sci. 2013, 31, 1312–1318. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Rivadulla, A.R.; Chen, X.; Cazzola, D.; Trewartha, G.; Preatoni, E. Data should be made as simple as possible but not simpler: The method chosen for dimensionality reduction and its parameters can affect the clustering of runners based on their kinematics. J. Biomech. 2024, 177, 112433. [Google Scholar] [CrossRef] [PubMed]
- Bolink, S.A.A.N.; NAisas, H.; Senden, R.; Essers, H.; Heyligers, I.C.; Meijer, K.; Grimm, B. Validity of an inertial measurement unit to assess pelvic orientation angles during gait, sit–stand transfers and step-up transfers: Comparison with an optoelectronic motion capture system. Med. Eng. Phys. 2016, 38, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Cuesta-Vargas, A.I.; Galán-Mercant, A.; Williams, J.M. The use of inertial sensors system for human motion analysis. Phys. Ther. Rev. 2010, 15, 462–473. [Google Scholar] [CrossRef] [PubMed]



| Participant Numbers | Age | Height (m) | Weight (kg) | Speed Range (km/h) | Mean Running Score | Running Score Range | |
|---|---|---|---|---|---|---|---|
| Validation study | |||||||
| Male | 5 | 23 ± 1.6 | 1.74 ± 0.04 | 70.6 ± 3.7 | 9.0–18.4 | 52.5 ± 4.3 | 46.9 ± 58.6 |
| Female | 1 | 23 | 1.64 | 49.0 | 9.4–13.7 | ||
| Movement pattern study | |||||||
| Male | 14 | 28.2 ± 8.8 | 1.77 ± 0.07 | 73.59 ± 8.58 | 8.8–15.8 | 54.4 ± 11.3 | 45.2–72.5 |
| Female | 10 | 24.2 ± 3.1 | 1.69 ± 0.06 | 62.73 ± 8.34 | 7.6–17.1 | 58.2 ± 9.1 | 42.3–84.7 |
| Kalman Filter | |||||
|---|---|---|---|---|---|
| Mean Difference | LOA | RMSE (Instantaneous) | RMSE (Mean Stride) | ||
| AP acc (m/s2) | 1.94 | −1.72 to 5.61 | 1.97 | 1.86 | |
| ML acc (m/s2) | 0.20 | −1.30 to 1.69 | 0.45 | 0.38 | |
| V acc (m/s2) | 0.27 | −1.47 to 2.02 | 0.72 | 0.67 | |
| AP vel (m/s) | −0.058 | −0.330 to 0.215 | 0.074 | 0.065 | |
| Sacrum | ML vel (m/s) | 0.009 | −0.038 to 0.056 | 0.023 | 0.014 |
| V vel (m/s) | 0.006 | −0.009 to 0.110 | 0.050 | 0.031 | |
| AP dis (mm) | −4.8 | −22.0 to 12.0 | 5.2 | 3.7 | |
| ML dis (mm) | −0.4 | −5.0 to 4.0 | 3.1 | 0.8 | |
| V dis (mm) | −0.6 | −6.0 to 4.0 | 5.8 | 1.8 | |
| Obliquity (deg) | −0.50 | −2.95 to 1.95 | 0.85 | 0.77 | |
| Pelvis | Tilt (deg) | −0.10 | −0.89 to 0.69 | 1.06 | 0.69 |
| Rotation (deg) | −0.49 | −2.56 to 1.58 | 1.54 | 1.22 | |
| Complementary filter | |||||
| Mean Difference | LOA | RMSE (instantaneous) | RMSE (mean stride) | ||
| AP acc (m/s2) | −0.24 | −5.61 to 5.14 | 2.46 | 2.36 | |
| ML acc (m/s2) | 1.91 | −3.08 to 6.90 | 0.81 | 1.11 | |
| V acc (m/s2) | 0.41 | −0.94 to 1.75 | 0.95 | 0.82 | |
| AP vel (m/s) | −0.232 | −0.462 to 0 | 0.124 | 0.121 | |
| Sacrum | ML vel (m/s) | 0.121 | 0.024 to 0.21 | 0.042 | 0.072 |
| V vel (m/s) | 0.055 | −0.034 to 0.145 | 0.055 | 0.036 | |
| AP dis (mm) | −14.2 | −28.8 to 0.4 | 7.9 | 7.2 | |
| ML dis (mm) | 15.2 | −8.0 to 39.0 | 4.3 | 7.5 | |
| V dis (mm) | 2.11 | −2.0 to 6.0 | 5.6 | 2.2 | |
| Obliquity (deg) | 4.68 | −11.34 to 20.70 | 4.46 | 4.32 | |
| Pelvis | Tilt (deg) | −0.58 | −1.78 to 0.61 | 5.25 | 4.58 |
| Rotation (deg) | −5.03 | −22.91 to 12.86 | 5.93 | 5.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asgari, H.; Heller, B. Validation and Analysis of Recreational Runners’ Kinematics Obtained from a Sacral IMU. Sensors 2025, 25, 315. https://doi.org/10.3390/s25020315
Asgari H, Heller B. Validation and Analysis of Recreational Runners’ Kinematics Obtained from a Sacral IMU. Sensors. 2025; 25(2):315. https://doi.org/10.3390/s25020315
Chicago/Turabian StyleAsgari, Hossein, and Ben Heller. 2025. "Validation and Analysis of Recreational Runners’ Kinematics Obtained from a Sacral IMU" Sensors 25, no. 2: 315. https://doi.org/10.3390/s25020315
APA StyleAsgari, H., & Heller, B. (2025). Validation and Analysis of Recreational Runners’ Kinematics Obtained from a Sacral IMU. Sensors, 25(2), 315. https://doi.org/10.3390/s25020315






