Data Reduction Methodology for Dynamic Characteristic Extraction in Photoplethysmogram
Abstract
1. Introduction
| Topic of Case Study | Time Series Length Used |
|---|---|
| Distinction between normal blood pressure and hypertension [37] | 2.1 s |
| Estimation model of systolic and diastolic blood pressure [35] | 2~3 s |
| Subject authentication method [36] | 7 s |
| Love at first sight impulse detection [43] | 10 s |
| Analgesia depth during anesthesia [44] | 10 s |
| Blood Pressure Estimation [15] | 20 s |
| Mental health assessment [19] | 30 s |
| Correlation with fear/anxiety [45] | 30 s |
| Automatic sleep staging [46] | 30 s |
| Blood sugar estimation [47] | 60 s |
| Early detection of cardiovascular disease [16] | 60 s |
| Automatic Emotion Recognition [48] | 60 s |
| Effects of Mental Stress [22] | 100 s |
| Fatigue Detection [49] | 120 s |
| Estimation of cardiovascular age [17] | 120 s |
| Automatic detection of hypertension [18] | 120 s |
| PPG time series length criteria [41] | 120 s |
| Early detection of depression [21] | 180 s |
| Estimation of blood glucose level [50] | 180 s |
| Effects of changes in gestational age [51] | 180 s |
| Effects of mental illness [20] | 180 s |
| The rPPG dynamics investigation [25] | 300 s |
| The rPPG and gPPG dynamics investigation [11] | 300 s |
| Estimation of blood pressure [38] | 300 s |
| Early hypertension detection [52] | 300 s |
| Effects of tractor noise on the cardiovascular system [53] | 300 s |
| Variation of fatigue during driving [54] | 300 s |
| Comparison between surgical patients and healthy subjects [55] | 300 s |
| Detection of sleep apnea syndrome [56] | 300 s |
2. Data
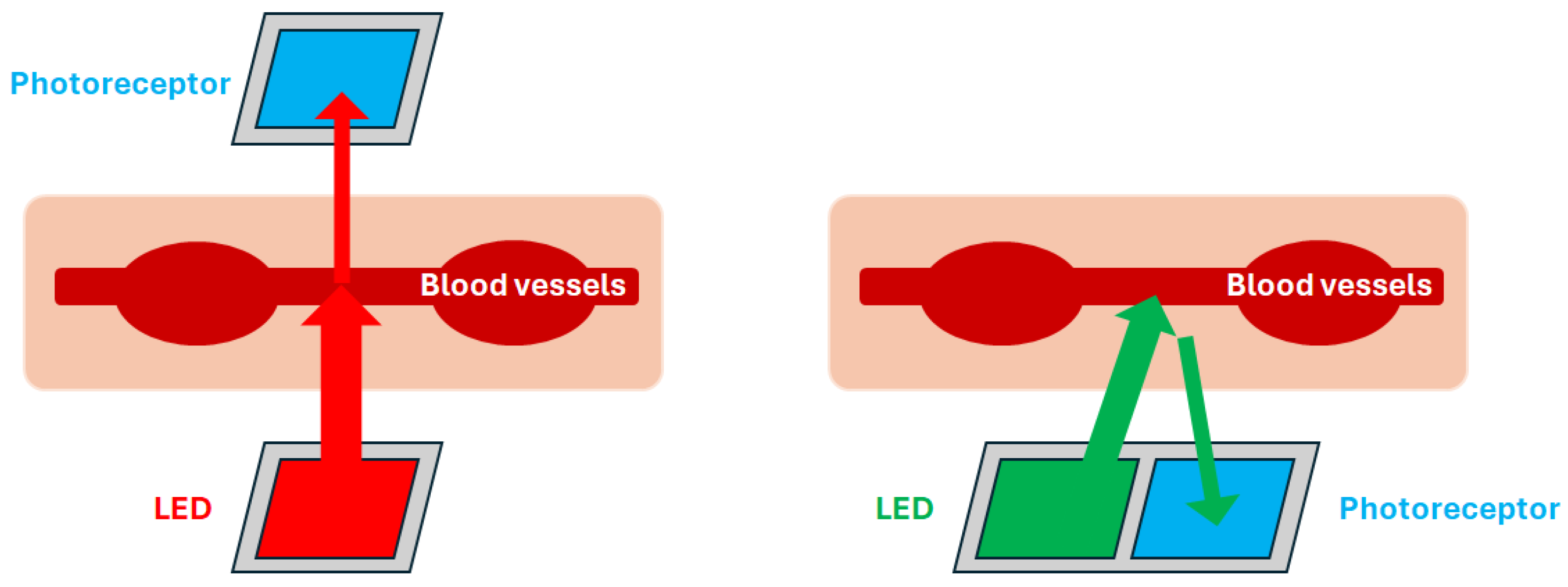
2.1. Photoplethysmogram Signal
2.2. Data Collection Experiment
2.3. Data Preprocessing
2.4. Data Selection
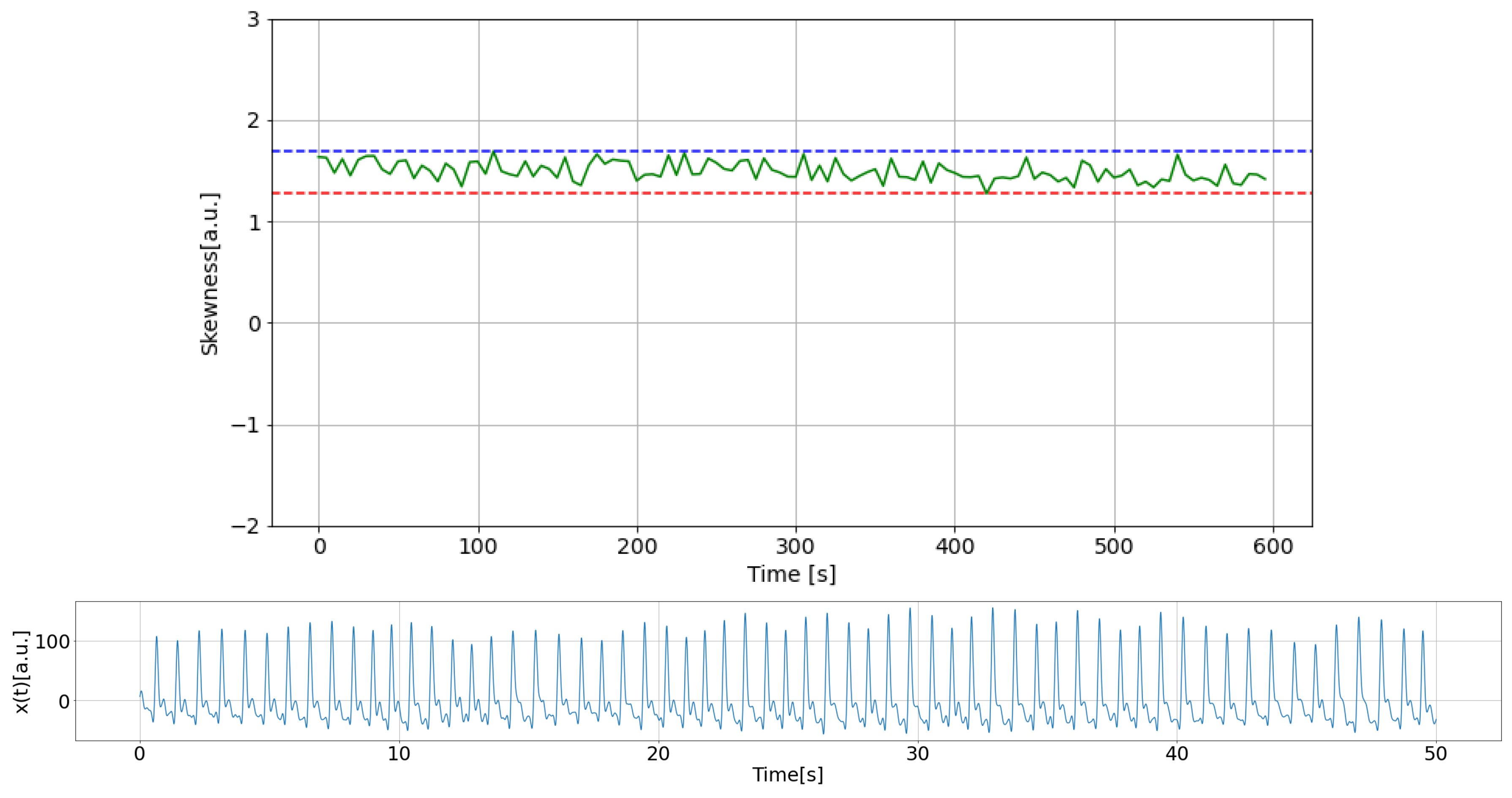
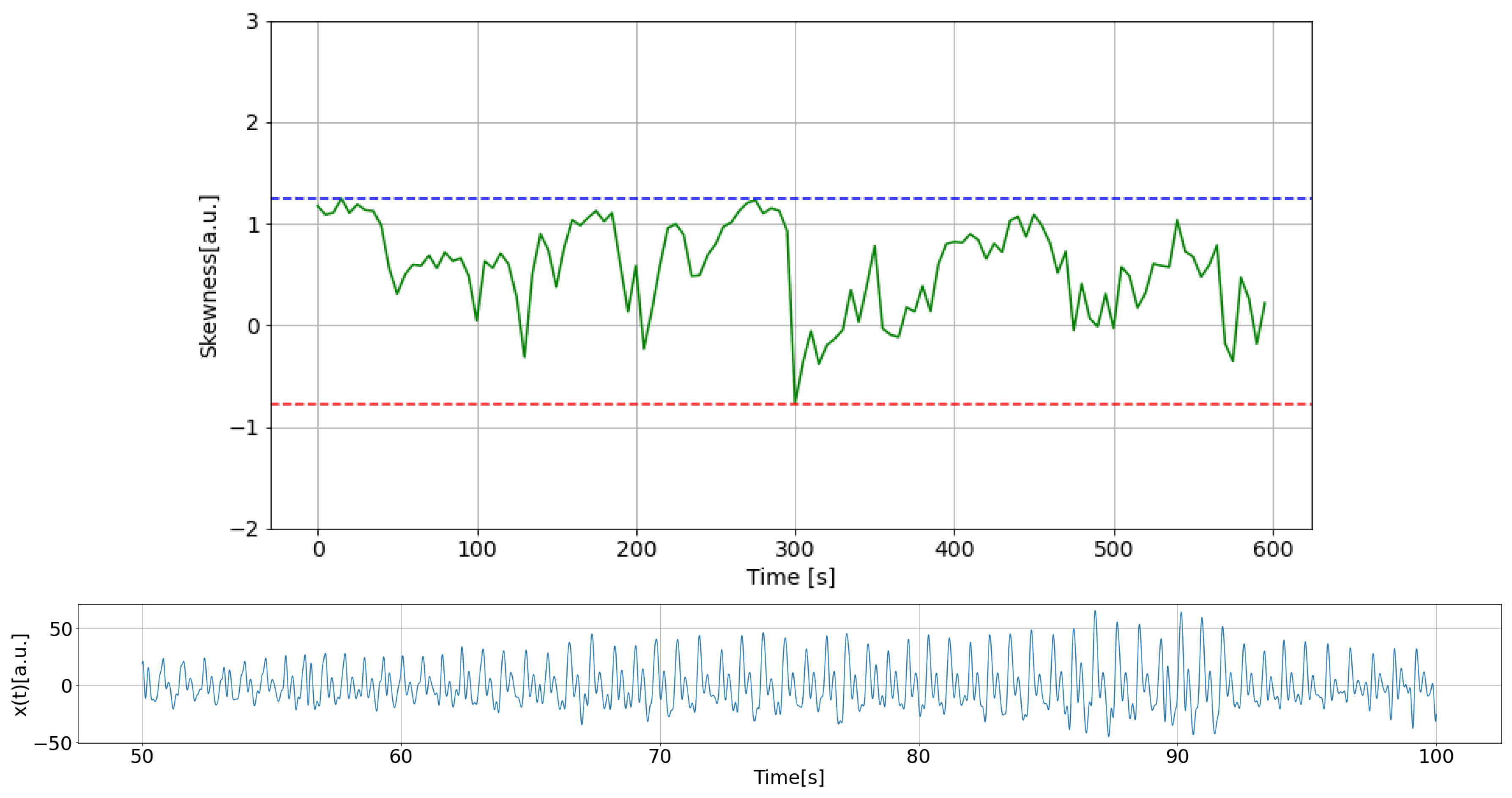
2.4.1. Quality of PPG Data
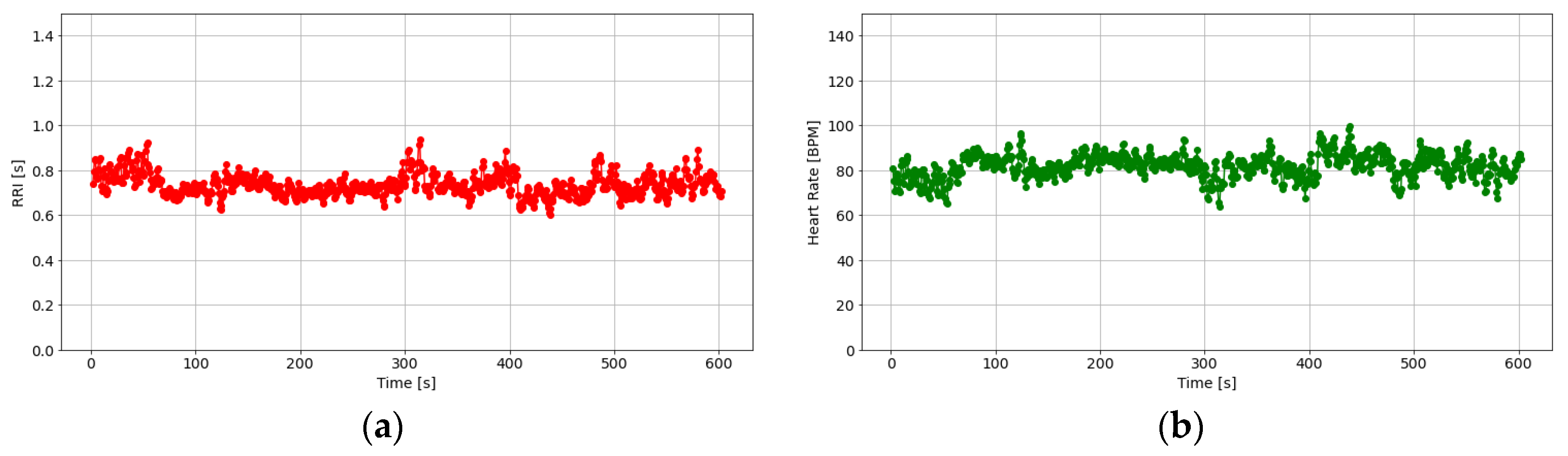
2.4.2. Estimation of Stationarity Through Heart Rate
2.4.3. HRV Analysis
2.4.4. Results of PPG Data Selection
3. Analysis Methods
3.1. Reconstruction into a Delay Coordinate System
3.2. Recurrence Plot (RP)
3.3. Recurrence Quantification Analysis (RQA)
3.4. Error
4. Results
4.1. PPG Time Series Subsets
4.2. Parameter Settings
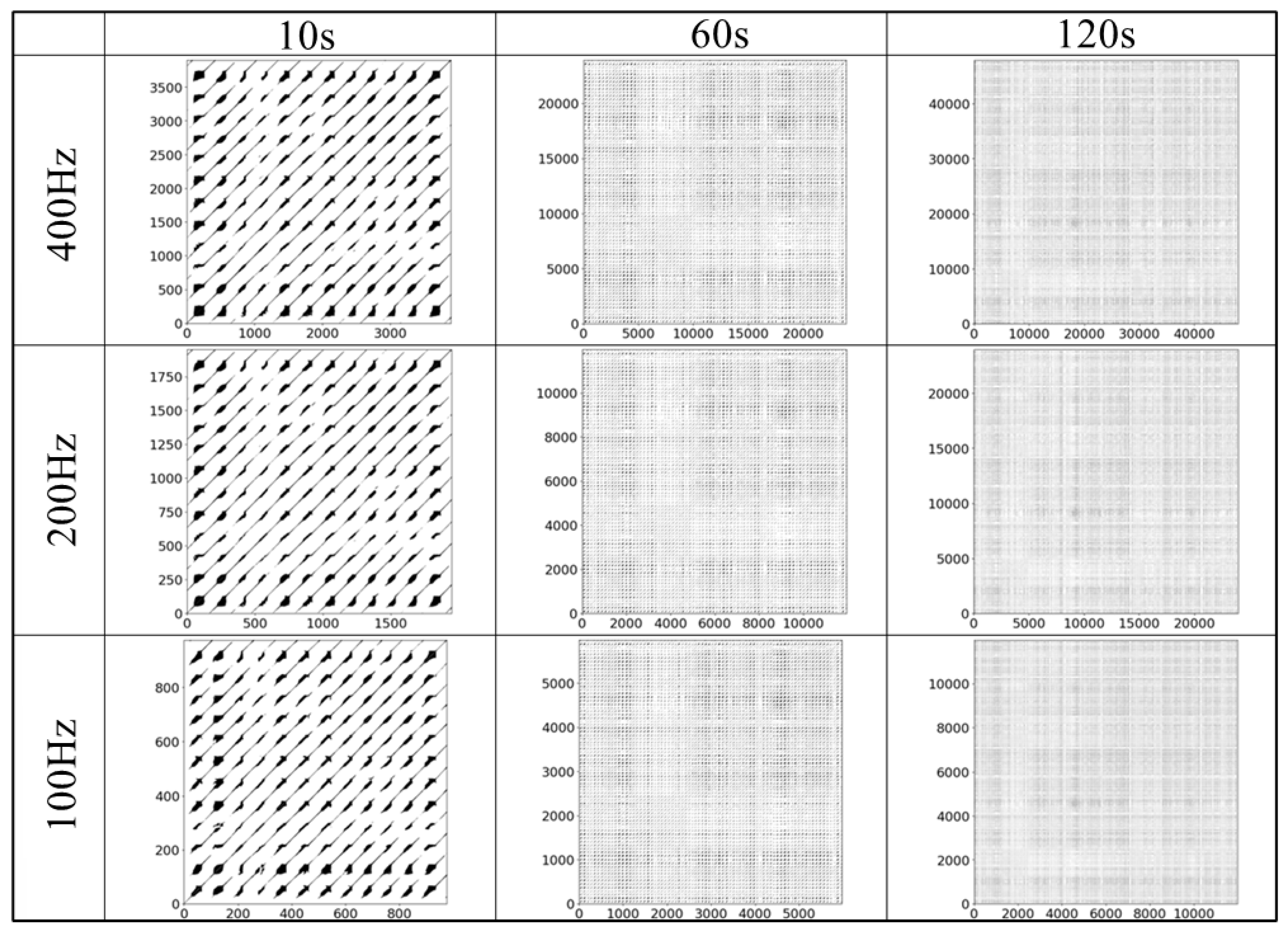
4.3. Reconstructed Attractor and Recurrence Plot
4.4. Recurrence Quantification Analysis
4.5. Effects of Down-Sampling
4.6. Difference Between gPPG and rPPG by Recurrence Quantification Analysis
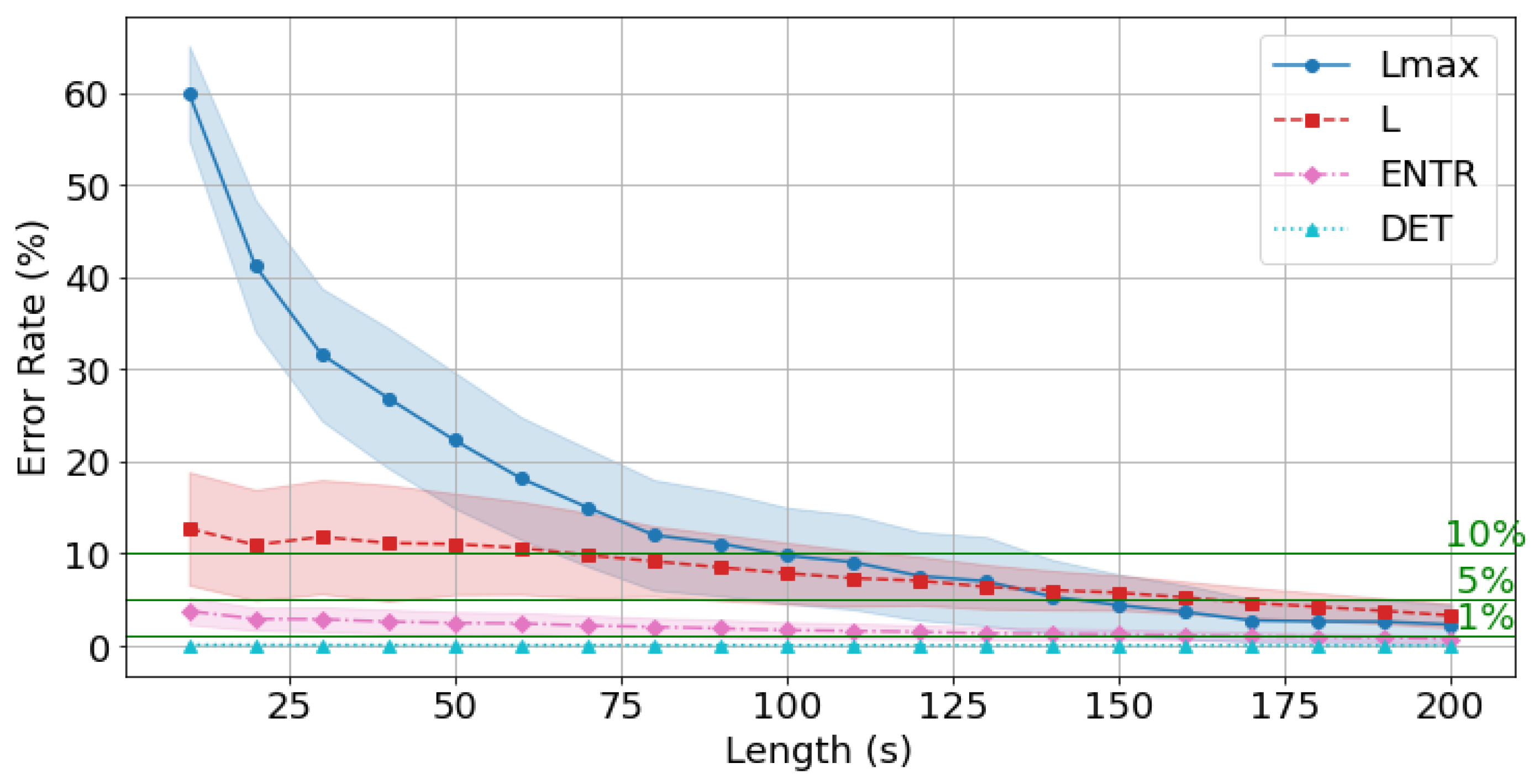
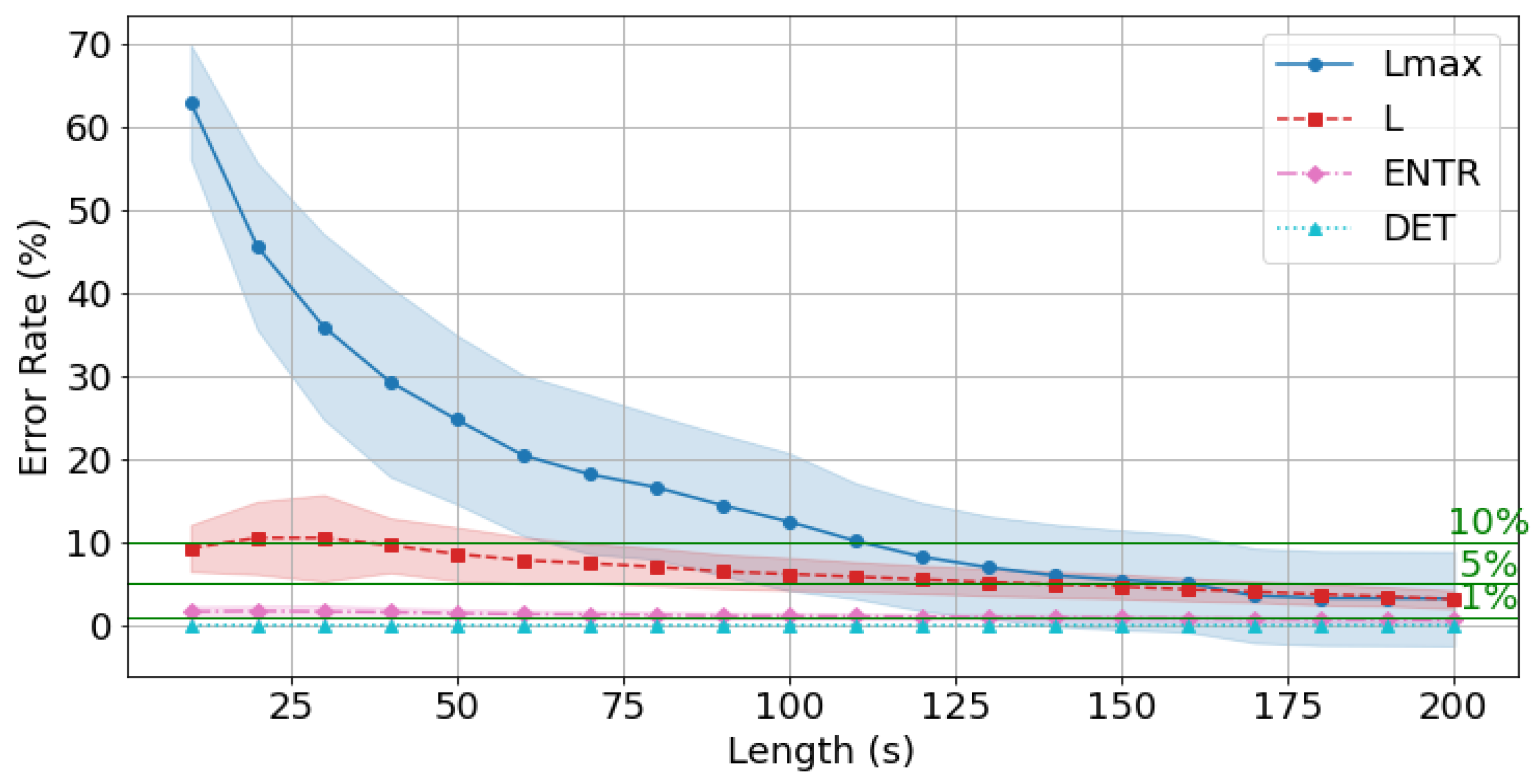
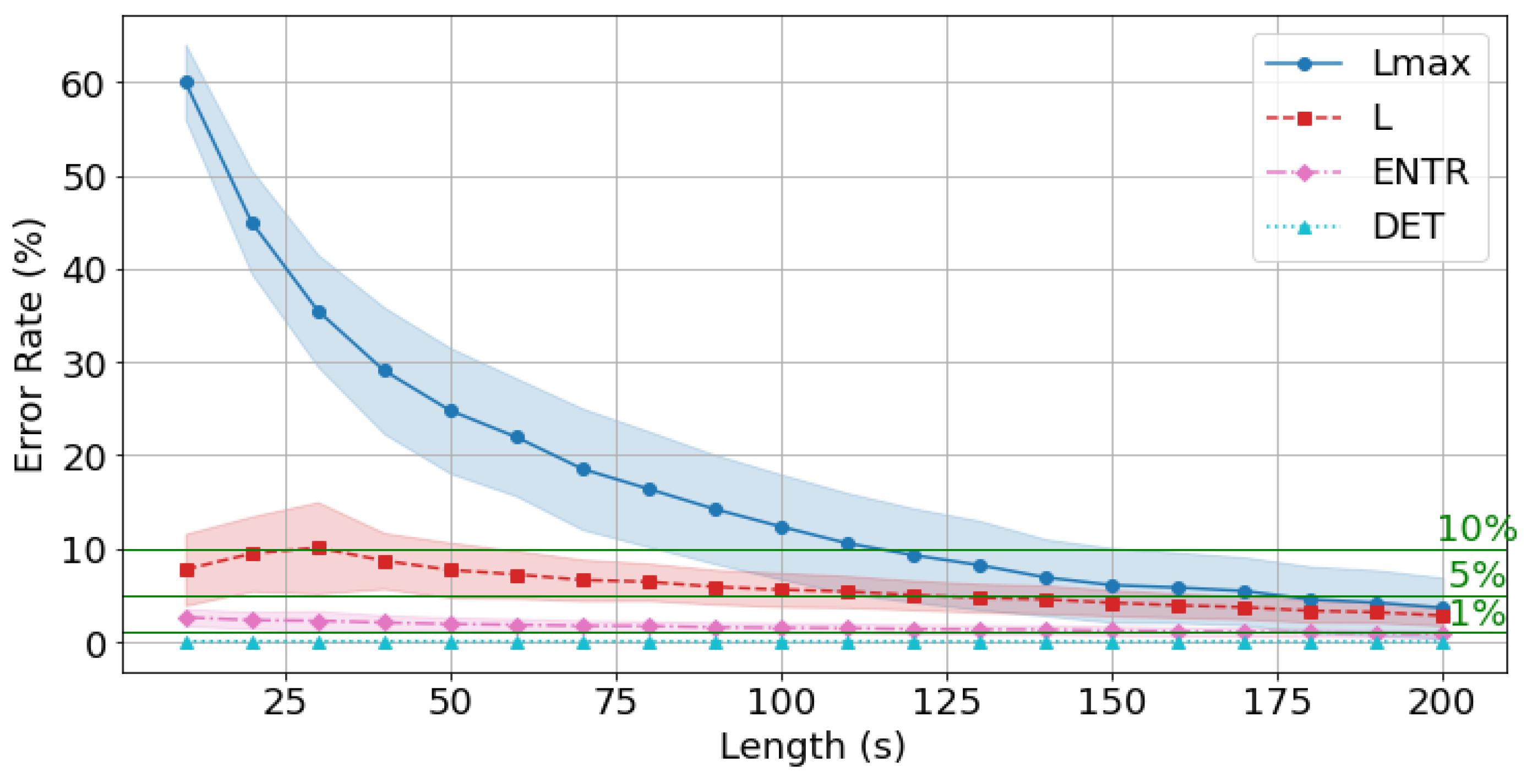
4.7. Effects of Time Series Length
4.8. Error for gPPG with the Standard Reference Value (300 s)
4.9. Error for rPPG with the Standard Reference Value (300 s)
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PPG | Photoplethysmogram |
| rPPG | Photoplethysmogram recorded with red light |
| gPPG | Photoplethysmogram recorded with green light |
| HRV | Heart Rate Variability |
| RP | Recurrence Plot |
| RQA | Recurrence Quantification Analysis |
References
- Park, J.; Seok, H.S.; Kim, S.-S.; Shin, H. Photoplethysmogram Analysis and Applications: An Integrative Review. Front. Physiol. 2022, 12, 808451. [Google Scholar] [CrossRef]
- Kim, K.B.; Baek, H.J. Photoplethysmography in Wearable Devices: A Comprehensive Review of Technological Advances, Current Challenges, and Future Directions. Electronics 2023, 12, 2923. [Google Scholar] [CrossRef]
- Namvari, M.; Lipoth, J.; Knight, S.; Jamali, A.A.; Hedayati, M.; Spiteri, R.J.; Syed-Abdul, S. Photoplethysmography Enabled Wearable Devices and Stress Detection: A Scoping Review. J. Pers. Med. 2022, 12, 1792. [Google Scholar] [CrossRef] [PubMed]
- Kyriacou, P.A.; Allen, J. (Eds.) Photoplethysmography, 1st ed.; Academic Press: New Delhi, India, 2021; ISBN 978-0-12-823374-0. [Google Scholar]
- Allen, J. Photoplethysmography and Its Application in Clinical Physiological Measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Sekine, M.; Tamura, T.; Moriya, A.; Suzuki, T.; Kameyama, K. Comparison of Reflected Green Light and Infrared Photoplethysmography. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; Volume 2008, pp. 2270–2272. [Google Scholar] [CrossRef]
- Tamura, T. Current Progress of Photoplethysmography and SPO2 for Health Monitoring. Biomed. Eng. Lett. 2019, 9, 21–36. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Shin, H.; Hahm, C. Effective PPG Sensor Placement for Reflected Red and Green Light, and Infrared Wristband-Type Photoplethysmography. In Proceedings of the 2016 18th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 31 January–3 February 2016; pp. 556–558. [Google Scholar] [CrossRef]
- Maeda, Y.; Sekine, M.; Tamura, T. The Advantages of Wearable Green Reflected Photoplethysmography. J. Med. Syst. 2011, 35, 829–834. [Google Scholar] [CrossRef]
- Tamura, T.; Maeda, Y.; Sekine, M.; Yoshida, M. Wearable Photoplethysmographic Sensors—Past and Present. Electronics 2014, 3, 282–302. [Google Scholar] [CrossRef]
- Sviridova, N.; Zhao, T.; Aihara, K.; Nakamura, K.; Nakano, A. Photoplethysmogram at Green Light: Where Does Chaos Arise From? Chaos Solitons Fractals 2018, 116, 157–165. [Google Scholar] [CrossRef]
- de Sá Ferreira, A.; Filho, J.B.; Cordovil, I.; de Souza, M.N. Three-Section Transmission-Line Arterial Model for Noninvasive Assessment of Vascular Remodeling in Primary Hypertension. Biomed. Signal Process. Control 2009, 4, 2–6. [Google Scholar] [CrossRef]
- Chuang, C.-C.; Ye, J.-J.; Lin, W.-C.; Lee, K.-T.; Tai, Y.-T. Photoplethysmography Variability as an Alternative Approach to Obtain Heart Rate Variability Information in Chronic Pain Patient. J. Clin. Monit. Comput. 2015, 29, 801–806. [Google Scholar] [CrossRef]
- Gil, E.; Orini, M.; Bailón, R.; Vergara, J.M.; Mainardi, L.; Laguna, P. Photoplethysmography Pulse Rate Variability as a Surrogate Measurement of Heart Rate Variability during Non-Stationary Conditions. Physiol. Meas. 2010, 31, 1271–1290. [Google Scholar] [CrossRef]
- Fujita, D.; Suzuki, A.; Ryu, K. PPG-Based Systolic Blood Pressure Estimation Method Using PLS and Level-Crossing Feature. Appl. Sci. 2019, 9, 304. [Google Scholar] [CrossRef]
- Rubins, U.; Grabovskis, A.; Grube, J.; Kukulis, I. Photoplethysmography Analysis of Artery Properties in Patients with Cardiovascular Diseases. In Proceedings of the 14th Nordic-Baltic Conference on Biomedical Engineering and Medical Physics, Riga, Latvia, 16–20 June 2008; pp. 319–322. [Google Scholar] [CrossRef]
- Wright, G.; Caceres, J.L.H. Extracting Clinically Relevant Information from Pulse Oximetry Traces. J. Health Inform. Afr. 2017, 4. [Google Scholar] [CrossRef]
- Sharma, M.; Rajput, J.S.; Tan, R.S.; Acharya, U.R. Automated Detection of Hypertension Using Physiological Signals: A Review. Int. J. Environ. Res. Public Health 2021, 18, 5838. [Google Scholar] [CrossRef] [PubMed]
- Nakagome, K.; Makinodan, M.; Uratani, M.; Kato, M.; Ozaki, N.; Miyata, S.; Iwamoto, K.; Hashimoto, N.; Toyomaki, A.; Mishima, K.; et al. Feasibility of a Wrist-Worn Wearable Device for Estimating Mental Health Status in Patients with Mental Illness. Front. Psychiatry 2023, 14, 1189765. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.-H.; Wu, Y.-C. A Novel Rapid Assessment of Mental Stress by Using PPG Signals Based on Deep Learning. IEEE Sens. J. 2022, 22, 21232–21239. [Google Scholar] [CrossRef]
- Hu, Y.; Miyoshi, E. Technology development and the prospect of chaos analysis through pulse waves: The potential for the applied development of the correspondence method to mental illness in China. Bull. Grad. Sch. Hum. Sci. Osaka Univ. 2014, 40, 27–46. (In Japanese) [Google Scholar] [CrossRef]
- Khaleghi, A.; Shahi, K.; Saidi, M.; Babaee, N.; Kaveh, R.; Mohammadian, A. Linear and Nonlinear Analysis of Multimodal Physiological Data for Affective Arousal Recognition. Cogn. Neurodyn. 2024, 18, 2277–2288. [Google Scholar] [CrossRef]
- Small, M.; Judd, K.; Lowe, M.; Stick, S. Is Breathing in Infants Chaotic? Dimension Estimates for Respiratory Patterns during Quiet Sleep. J. Appl. Physiol. 1999, 86, 359–376. [Google Scholar] [CrossRef]
- Poon, C.-S.; Merrill, C.K. Decrease of Cardiac Chaos in Congestive Heart Failure. Nature 1997, 389, 492–495. [Google Scholar] [CrossRef]
- Sviridova, N.; Sakai, K. Human Photoplethysmogram: New Insight into Chaotic Characteristics. Chaos Solitons Fractals 2015, 77, 53–63. [Google Scholar] [CrossRef]
- Tsuda, I.; Tahara, T.; Iwanaga, H. Chaotic Pulsation in Human Capillary Vessels and Its Dependence on the Mental and Physical Conditions. Proc. Annu. Meet. Biomed. Fuzzy Syst. Assoc. BMFSA 1992, 4, 1–40. [Google Scholar] [CrossRef]
- Sumida, T.; Arimitu, Y.; Tahara, T.; Iwanaga, H. Mental Conditions Reflected by the Chaos of Pulsation in Capillary Vessels. Int. J. Bifurc. Chaos 2000, 10, 2245–2255. [Google Scholar] [CrossRef]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Shelhamer, M. Nonlinear Dynamics in Physiology: A State-Space Approach; WORLD SCIENTIFIC: Singapore, 2006; ISBN 978-981-270-029-2. [Google Scholar]
- Sviridova, N. Towards Understanding of Photoplethysmogram Dynamics through Nonlinear Time Series Analysis. Seisan Kenkyu 2019, 71, 141–145. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Webber, C.L.; Zbilut, J.P. Dynamical Assessment of Physiological Systems and States Using Recurrence Plot Strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef]
- Recurrence Quantification Analysis: Theory and Best Practices; Understanding Complex Systems; Webber, C.L., Marwan, N., Eds.; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-07154-1. [Google Scholar]
- Skazkina, V.V.; Mureeva, E.N.; Ishbulatov, Y.M.; Prokhorov, M.D.; Karavaev, A.S.; Hramkov, A.N.; Ezhov, D.M.; Kurbako, A.V.; Panina, O.S.; Chernenkov, Y.V.; et al. Cross-Recurrence Quantification Of Cardiovascular Signals In Newborns Is A Sensitive Marker Of Health Status. Russ. Open Med J. 2024, 13, e0203. [Google Scholar] [CrossRef]
- Hamedani, N.E.; Sadredini, S.Z.; Khodabakhshi, M.B. A CNN Model for Cuffless Blood Pressure Estimation from Nonlinear Characteristics of PPG Signals. In Proceedings of the 2021 28th National and 6th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 25–26 November 2021; pp. 228–235. [Google Scholar] [CrossRef]
- Alotaiby, T.N.; Alshebeili, S.A.; Alotibi, G.; Alotaibi, G.N. Recurrence Quantification Analysis for PPG/ECG-Based Subject Authentication|IEEE Conference Publication|IEEE Xplore. In Proceedings of the 2022 4th International Conference on Data Intelligence and Security (ICDIS), Shenzhen, China, 24–26 August 2022; pp. 288–291. [Google Scholar] [CrossRef]
- Sviridova, N.; Ikeguchi, T. Application of Recurrence Quantification Analysis to Hypertension Photoplethysmograms. IEICE Proc. Ser. 2020, 74, 56–58. [Google Scholar]
- Mejía-Mejía, E.; May, J.M.; Elgendi, M.; Kyriacou, P.A. Classification of Blood Pressure in Critically Ill Patients Using Photoplethysmography and Machine Learning. Comput. Methods Programs Biomed. 2021, 208, 106222. [Google Scholar] [CrossRef]
- Ohtomo, N.; Terachi, S.; Tanaka, Y. Nonlinear Time Series Analysis: 1. A New Method of Analysis and the Theoretical Background. Bull. Fac. Eng. Hokkaido Univ. 1992, 158, 43–55. [Google Scholar]
- Marwan, N. HOW TO AVOID POTENTIAL PITFALLS IN RECURRENCE PLOT BASED DATA ANALYSIS. Int. J. Bifurc. Chaos 2011, 21, 1003–1017. [Google Scholar] [CrossRef]
- Sviridova, N.; Zhao, T.; Nakano, A.; Ikeguchi, T. Photoplethysmogram Recording Length: Defining Minimal Length Requirement from Dynamical Characteristics. Sensors 2022, 22, 5154. [Google Scholar] [CrossRef] [PubMed]
- Baghaee Ivriq, S.; Laursen, K.; Jørgensen, A.M.; Mondal, T.; Zamani, M.; Rezaeiyan, Y.; Corbett, B.; Iversen, B.B.; Moradi, F. A System-Level Feasibility Study of a Lead-Free Ultrasonically Powered Light Delivery Implant for Optogenetics. Adv. Intell. Syst. 2024, 6, 2300527. [Google Scholar] [CrossRef]
- Lu, H.; Yuan, G.; Zhang, J.; Liu, G. Recognition of Impulse of Love at First Sight Based On Photoplethysmography Signal. Sensors 2020, 20, 6572. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, F.; Chen, X.; Feng, Y.; Miao, J.; Chen, S.; Jiao, C.; Chen, H. Photoplethysmography-Derived Approximate Entropy and Sample Entropy as Measures of Analgesia Depth during Propofol–Remifentanil Anesthesia. J. Clin. Monit. Comput. 2021, 35, 297–305. [Google Scholar] [CrossRef]
- Imanishi, A.; Oyama-Higa, M. On the Largest Lyapunov Exponents of Finger Plethysmogram and Heart Rate under Anxiety, Fear, and Relief States. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 3119–3123. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, G. A Multi-Class Automatic Sleep Staging Method Based on Photoplethysmography Signals. Entropy 2021, 23, 116. [Google Scholar] [CrossRef]
- Hina, A.; Saadeh, W. A 186μW Photoplethysmography-Based Noninvasive Glucose Sensing SoC. IEEE Sens. J. 2022, 22, 14185–14195. [Google Scholar] [CrossRef]
- Goshvarpour, A.; Goshvarpour, A. Poincaré’s Section Analysis for PPG-Based Automatic Emotion Recognition. Chaos Solitons Fractals 2018, 114, 400–407. [Google Scholar] [CrossRef]
- Shi, P.; Xu, Y.; Guo, M.; Yu, H. Heart Rate Variability for Assessment of Fatigue of Central Motor Control in a Rhythmical Finger Tapping Task. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Habbu, S.; Dale, M.; Ghongade, R. Estimation of Blood Glucose by Non-Invasive Method Using Photoplethysmography. Sādhanā 2019, 44, 135. [Google Scholar] [CrossRef]
- Li, N.; Yu, J.; Mao, X.; Zhao, Y.; Huang, L. The Nonlinearity Properties of Pulse Signal of Pregnancy in the Three Trimesters. Biomed. Signal Process. Control 2023, 79, 104158. [Google Scholar] [CrossRef]
- Vraka, A.; Hornero, F.; Fácila, L.; Ravelli, F.; Alcaraz, R.; Rieta, J.J. Harnessing Photoplethysmography and Deep Learning in Continuous Blood Pressure Monitoring for Early Hypertension Detection. In Advances in Digital Health and Medical Bioengineering; Springer: Berlin/Heidelberg, Germany, 2024; pp. 213–220. [Google Scholar] [CrossRef]
- Sviridova, N.; Sakai, K. Application of Photoplethysmogram for Detecting Physiological Effects of Tractor Noise. Eng. Agric. Environ. Food 2015, 8, 313–317. [Google Scholar] [CrossRef]
- Miao, T.; Ogura, Y.; Fujita, E.; Oyama-Higa, M. Fluctuation Analysis of Finger Plethysmograms Related to Various Conditions. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 3332–3337. [Google Scholar] [CrossRef]
- Xing, X.; Dong, W.-F.; Xiao, R.; Song, M.; Jiang, C. Analysis of the Chaotic Component of Photoplethysmography and Its Association with Hemodynamic Parameters. Entropy 2023, 25, 1582. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Chen, M.; Wei, K.; Liu, G. Sleep Apnea Screening Based on Photoplethysmography Data from Wearable Bracelets Using an Information-Based Similarity Approach. Comput. Methods Programs Biomed. 2021, 211, 106442. [Google Scholar] [CrossRef] [PubMed]
- Pulse Sensor|Electronics Basics|ROHM. Available online: https://www.rohm.com/electronics-basics/sensors/sensor_what3 (accessed on 1 August 2025).
- Gitman, Y.; Murphy, J. Heartbeat Sensor Projects with PulseSensor: Prototyping Devices with Biofeedback; Apress: Berkeley, CA, USA, 2023; ISBN 978-1-4842-9324-9. [Google Scholar]
- Carey, R.M.; Whelton, P.K.; for the 2017 ACC/AHA Hypertension Guideline Writing Committee. Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults: Synopsis of the 2017 American College of Cardiology/American Heart Association Hypertension Guideline. Ann. Intern. Med. 2018, 168, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Béres, S.; Hejjel, L. The Minimal Sampling Frequency of the Photoplethysmogram for Accurate Pulse Rate Variability Parameters in Healthy Volunteers. Biomed. Signal Process. Control 2021, 68, 102589. [Google Scholar] [CrossRef]
- Scipy.Signal.Butter—SciPy v1.7.1 Manual. Available online: https://docs.scipy.org/doc//scipy-1.7.1/reference/reference/generated/scipy.signal.butter.html (accessed on 10 December 2024).
- Liang, Y.; Elgendi, M.; Chen, Z.; Ward, R. An Optimal Filter for Short Photoplethysmogram Signals. Sci. Data 2018, 5, 180076. [Google Scholar] [CrossRef]
- Krishnan, R.; Natarajan, B.; Warren, S. Two-Stage Approach for Detection and Reduction of Motion Artifacts in Photoplethysmographic Data. IEEE Trans. Biomed. Eng. 2010, 57, 1867–1876. [Google Scholar] [CrossRef]
- Elgendi, M. Optimal Signal Quality Index for Photoplethysmogram Signals. Bioengineering 2016, 3, 21. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Mori, N.; Mitajiri, R.; Jiang, Z. Study of Mental Stress Evaluation based on analysis of Heart Rate Variability. J. Life Support Eng. 2010, 22, 105–111. [Google Scholar] [CrossRef]
- Rubenstein, D.A.; Yin, W.; Frame, M.D. Biofluid Mechanics. An Introduction to Fluid Mechanics, Macrocirculation, and Microcirculation; Biomedical Engineering; Academic Press: Cambridge, MA, USA, 2021; ISBN 978-0-12-818034-1. [Google Scholar]
- Ni, Z.; Sun, F.; Li, Y. Heart Rate Variability-Based Subjective Physical Fatigue Assessment. Sensors 2022, 22, 3199. [Google Scholar] [CrossRef]
- Kuratsune, H.; Tajima, S.; Koizumi, J.; Nishizawa, Y.; Watanabe, Y.; Kataoka, Y. Fatigue Level Determination Processing System (疲労度の判定処理システム)|特許情報|J-GLOBAL 科学技術総合リンクセンター 2010. Japan Patent 2010-201113, 16 September 2010. (In Japanese). [Google Scholar]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys 1991, 65, 579–616. [Google Scholar] [CrossRef]















| L | ENTR | DET | ||
|---|---|---|---|---|
| gPPG | ||||
| 400 Hz vs. 200 Hz | 0.78 | 0.98 | 0.98 | 0.98 |
| 400 Hz vs. 100 Hz | 0.78 | 0.95 | 0.93 | 0.88 |
| 200 Hz vs. 100 Hz | 0.94 | 0.95 | 0.91 | 0.89 |
| rPPG | ||||
| 400 Hz vs. 200 Hz | 0.60 | 0.98 | 0.96 | 0.98 |
| 400 Hz vs. 100 Hz | 0.50 | 0.96 | 0.92 | 0.96 |
| 200 Hz vs. 100 Hz | 0.94 | 0.97 | 0.94 | 0.96 |
| L | ENTR | DET | ||
|---|---|---|---|---|
| 400 Hz | ||||
| 200 Hz | ||||
| 100 Hz |
| Time | 400 Hz | 200 Hz | 100 Hz | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lmax | L | ENTR | DET | Lmax | L | ENTR | DET | Lmax | L | ENTR | DET | |
| 10 s | 64.557 | 14.577 | 2.881 | 0.002 | 59.423 | 13.777 | 3.202 | 0.015 | 59.970 | 12.723 | 3.773 | 0.108 |
| 20 s | 49.232 | 13.567 | 2.256 | 0.002 | 42.189 | 12.545 | 2.508 | 0.014 | 41.224 | 10.939 | 2.911 | 0.101 |
| 30 s | 41.739 | 13.067 | 2.109 | 0.001 | 33.824 | 12.212 | 2.460 | 0.013 | 31.595 | 11.823 | 2.884 | 0.096 |
| 40 s | 37.282 | 12.756 | 2.039 | 0.001 | 29.463 | 12.012 | 2.347 | 0.012 | 26.874 | 11.144 | 2.618 | 0.089 |
| 50 s | 34.412 | 12.358 | 1.878 | 0.001 | 24.410 | 11.690 | 2.142 | 0.011 | 22.293 | 11.040 | 2.478 | 0.086 |
| 60 s | 32.731 | 11.671 | 1.769 | 0.001 | 21.657 | 11.238 | 2.065 | 0.011 | 18.165 | 10.616 | 2.426 | 0.084 |
| 70 s | 30.191 | 10.897 | 1.680 | 0.001 | 18.543 | 10.497 | 1.950 | 0.010 | 15.014 | 9.827 | 2.188 | 0.080 |
| 80 s | 26.836 | 10.309 | 1.572 | 0.001 | 15.044 | 9.795 | 1.787 | 0.010 | 12.017 | 9.180 | 2.047 | 0.076 |
| 90 s | 23.885 | 9.525 | 1.445 | 0.001 | 14.085 | 9.130 | 1.645 | 0.009 | 11.092 | 8.500 | 1.890 | 0.073 |
| 100 s | 20.458 | 8.685 | 1.300 | 0.001 | 11.797 | 8.247 | 1.476 | 0.009 | 9.790 | 7.878 | 1.698 | 0.069 |
| 110 s | 19.406 | 8.226 | 1.230 | 0.001 | 10.167 | 7.792 | 1.381 | 0.008 | 9.072 | 7.330 | 1.614 | 0.066 |
| 120 s | 16.807 | 7.829 | 1.144 | 0.001 | 9.258 | 7.466 | 1.278 | 0.008 | 7.574 | 7.059 | 1.514 | 0.062 |
| 130 s | 13.878 | 7.099 | 1.032 | 0.001 | 7.220 | 6.801 | 1.174 | 0.007 | 7.002 | 6.398 | 1.362 | 0.058 |
| 140 s | 12.753 | 6.673 | 0.976 | 0.001 | 5.735 | 6.415 | 1.111 | 0.007 | 5.322 | 6.033 | 1.308 | 0.054 |
| 150 s | 12.162 | 6.375 | 0.923 | 0.001 | 5.221 | 6.098 | 1.039 | 0.006 | 4.410 | 5.763 | 1.250 | 0.051 |
| 160 s | 10.919 | 5.710 | 0.835 | 0.001 | 4.185 | 5.497 | 0.953 | 0.006 | 3.664 | 5.233 | 1.144 | 0.048 |
| 170 s | 10.231 | 5.181 | 0.767 | 0.001 | 3.055 | 4.989 | 0.859 | 0.005 | 2.747 | 4.658 | 1.044 | 0.044 |
| 180 s | 9.616 | 4.690 | 0.705 | 0.001 | 2.322 | 4.512 | 0.790 | 0.005 | 2.649 | 4.233 | 0.959 | 0.041 |
| 190 s | 8.279 | 4.132 | 0.634 | 0.001 | 2.085 | 3.996 | 0.712 | 0.004 | 2.616 | 3.781 | 0.868 | 0.037 |
| 200 s | 7.350 | 3.629 | 0.541 | 0.001 | 1.613 | 3.529 | 0.615 | 0.004 | 2.304 | 3.293 | 0.743 | 0.033 |
| Time | 400 Hz | 200 Hz | 100 Hz | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lmax | L | ENTR | DET | Lmax | L | ENTR | DET | Lmax | L | ENTR | DET | |
| 10 s | 62.898 | 9.272 | 1.638 | 0.002 | 59.245 | 8.432 | 1.950 | 0.009 | 59.447 | 7.916 | 2.651 | 0.062 |
| 20 s | 45.576 | 10.500 | 1.698 | 0.001 | 44.217 | 10.231 | 2.009 | 0.007 | 44.910 | 9.541 | 2.380 | 0.049 |
| 30 s | 35.891 | 10.498 | 1.640 | 0.001 | 35.843 | 10.497 | 2.001 | 0.007 | 35.216 | 10.084 | 2.319 | 0.053 |
| 40 s | 29.250 | 9.613 | 1.571 | 0.001 | 27.330 | 9.433 | 1.860 | 0.007 | 28.858 | 8.717 | 2.115 | 0.052 |
| 50 s | 24.730 | 8.569 | 1.438 | 0.001 | 23.973 | 8.475 | 1.688 | 0.006 | 24.623 | 7.822 | 1.984 | 0.047 |
| 60 s | 20.420 | 7.817 | 1.329 | 0.001 | 21.131 | 7.783 | 1.607 | 0.006 | 22.021 | 7.318 | 1.890 | 0.044 |
| 70 s | 18.147 | 7.454 | 1.297 | 0.001 | 17.512 | 7.355 | 1.538 | 0.006 | 18.259 | 6.709 | 1.775 | 0.043 |
| 80 s | 16.584 | 7.015 | 1.225 | 0.001 | 15.899 | 6.958 | 1.467 | 0.005 | 15.986 | 6.567 | 1.761 | 0.041 |
| 90 s | 14.427 | 6.470 | 1.137 | 0.001 | 13.932 | 6.526 | 1.382 | 0.005 | 14.020 | 6.053 | 1.626 | 0.039 |
| 100 s | 12.437 | 6.158 | 1.125 | 0.001 | 11.744 | 6.258 | 1.368 | 0.005 | 11.855 | 5.791 | 1.584 | 0.038 |
| 110 s | 10.135 | 5.842 | 1.079 | 0.001 | 10.421 | 5.926 | 1.309 | 0.005 | 10.236 | 5.624 | 1.555 | 0.035 |
| 120 s | 8.228 | 5.511 | 1.009 | 0.000 | 9.748 | 5.662 | 1.242 | 0.004 | 9.083 | 5.265 | 1.460 | 0.033 |
| 130 s | 6.952 | 5.186 | 0.975 | 0.000 | 8.094 | 5.323 | 1.205 | 0.004 | 8.046 | 4.943 | 1.399 | 0.032 |
| 140 s | 5.982 | 4.914 | 0.942 | 0.000 | 6.549 | 5.003 | 1.157 | 0.004 | 6.850 | 4.740 | 1.367 | 0.030 |
| 150 s | 5.434 | 4.658 | 0.873 | 0.000 | 5.888 | 4.765 | 1.074 | 0.003 | 6.099 | 4.361 | 1.252 | 0.027 |
| 160 s | 5.024 | 4.308 | 0.817 | 0.000 | 5.238 | 4.399 | 1.012 | 0.003 | 5.803 | 4.082 | 1.178 | 0.026 |
| 170 s | 3.562 | 4.033 | 0.772 | 0.000 | 4.138 | 4.129 | 0.963 | 0.003 | 5.468 | 3.858 | 1.137 | 0.024 |
| 180 s | 3.257 | 3.707 | 0.714 | 0.000 | 3.931 | 3.862 | 0.900 | 0.003 | 4.644 | 3.494 | 1.035 | 0.022 |
| 190 s | 3.233 | 3.455 | 0.668 | 0.000 | 3.544 | 3.554 | 0.825 | 0.002 | 3.975 | 3.290 | 0.950 | 0.020 |
| 200 s | 3.203 | 3.111 | 0.609 | 0.000 | 2.454 | 3.170 | 0.754 | 0.002 | 3.433 | 2.912 | 0.858 | 0.019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sviridova, N.; Okazaki, S. Data Reduction Methodology for Dynamic Characteristic Extraction in Photoplethysmogram. Sensors 2025, 25, 6232. https://doi.org/10.3390/s25196232
Sviridova N, Okazaki S. Data Reduction Methodology for Dynamic Characteristic Extraction in Photoplethysmogram. Sensors. 2025; 25(19):6232. https://doi.org/10.3390/s25196232
Chicago/Turabian StyleSviridova, Nina, and Sora Okazaki. 2025. "Data Reduction Methodology for Dynamic Characteristic Extraction in Photoplethysmogram" Sensors 25, no. 19: 6232. https://doi.org/10.3390/s25196232
APA StyleSviridova, N., & Okazaki, S. (2025). Data Reduction Methodology for Dynamic Characteristic Extraction in Photoplethysmogram. Sensors, 25(19), 6232. https://doi.org/10.3390/s25196232






