High-Precision Alignment Method for Electro-Optic Modulators via Combined Twyman-Green and Conoscopic Interferometry
Abstract
Highlights
- A combined Twyman-Green and conoscopic interferometry method is proposed to achieve high-precision alignment of electro-optic modulators (EOMs), simultaneously addressing optical axis, transmission axis, and crystal azimuthal alignment.
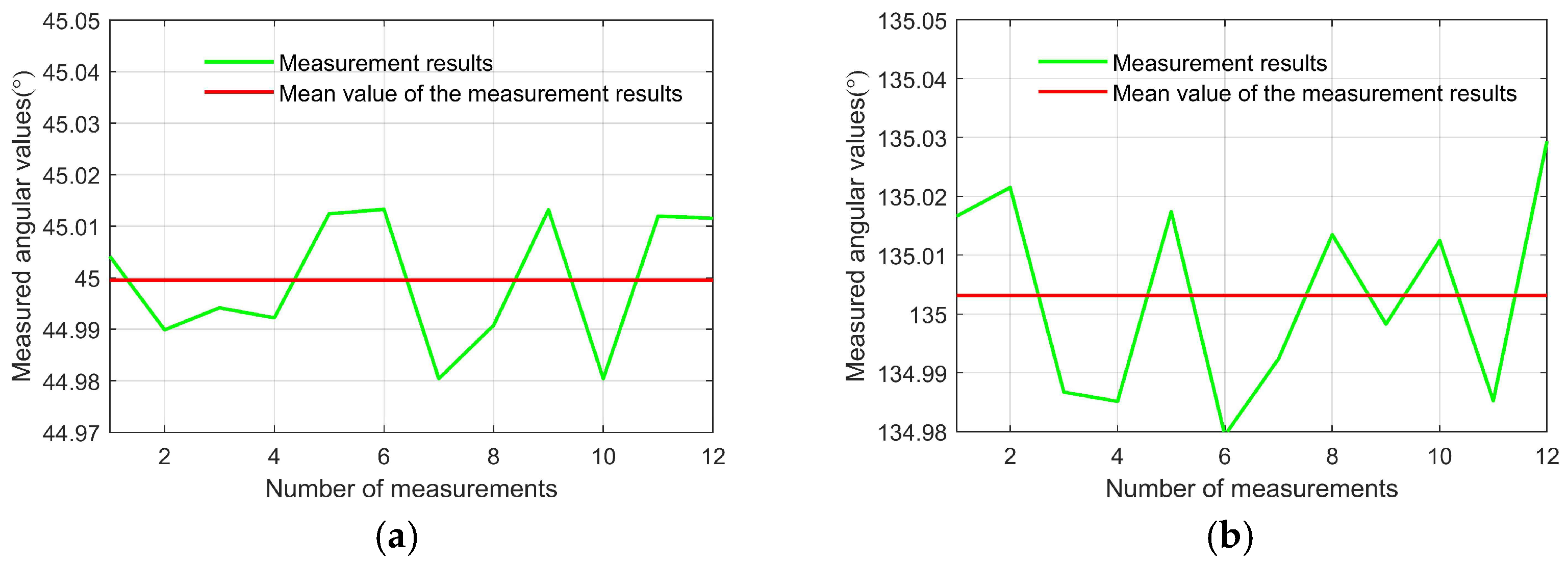
- The experimental results demonstrate alignment errors below 0.2862 mrad for alignment of polarizer/analyzer transmission axes and 0.3229 mrad for azimuth alignment of the electro-optic crystal, with sub-arcsecond repeatability validated via Bessel’s method.
- This method enables ultra-precise EOM alignment essential for emerging applications in quantum communication, lidar, and high-resolution imaging, where conventional techniques fall short.
- The proposed system offers a reproducible approach to alignment, potentially improving the performance and stability of advanced optical systems relying on EOMs.
Abstract
1. Introduction
2. Methods
2.1. Alignment Errors
- (1)
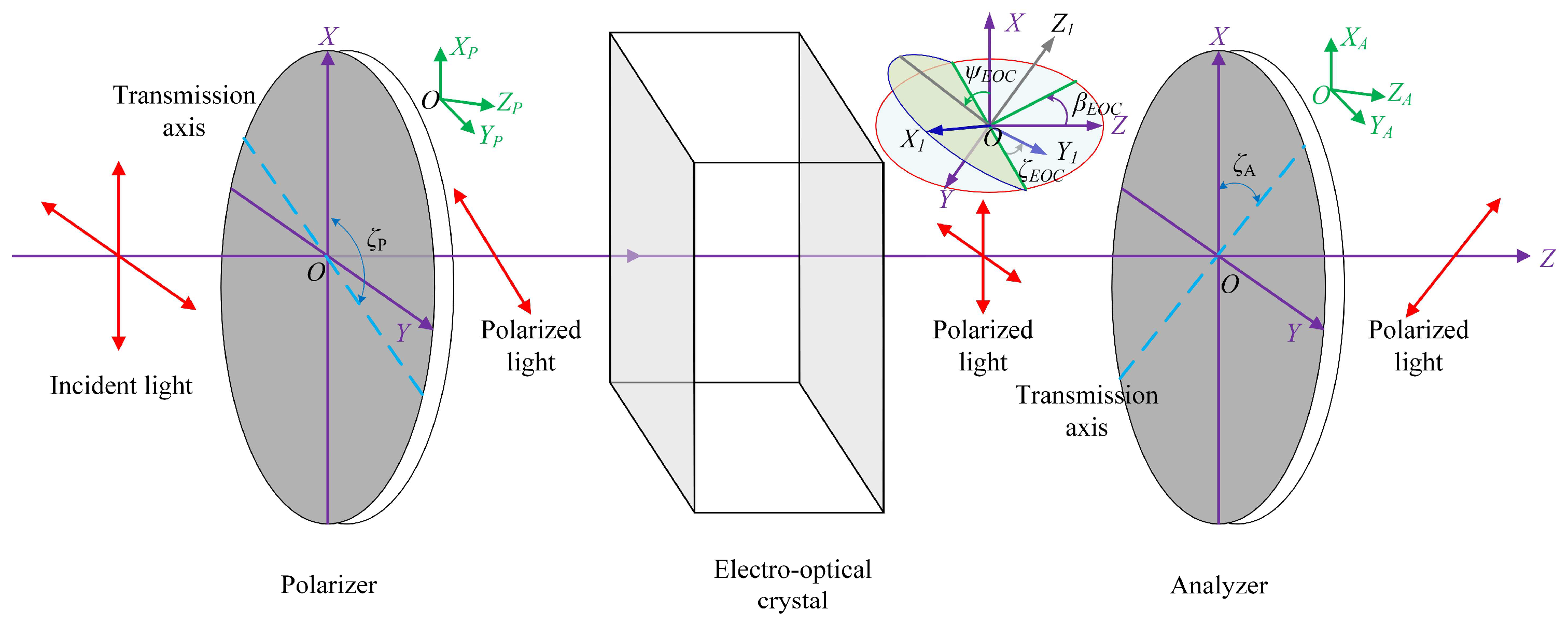
- Optical axis alignment: The electro-optic crystal, polarizer, and analyzer are adjusted to ensure their surface normal directions (OZ1-axis, OZP-axis, and OZA-axis) coincide with the optical axis direction (OZ-axis) of the optical system. Specifically, the horizontal alignment angles are adjusted as βEOC = βP = βA = 0°, and the vertical alignment angles as ψEOC = ψP = ψA = 0°. In practical applications, the polarizer and analyzer exhibit low sensitivity to the incident light direction, where the reflection co-point method suffices for alignment requirements. However, the electro-optic crystal demonstrates remarkable sensitivity to the incident light direction. Consequently, significant effort is required to achieve precise optical axis alignment, ensuring that the optical axis of the electro-optic crystal coincides with that of the optical system. Specifically, the horizontal alignment angle of the electro-optic crystal is βEOC = 0°, and its vertical alignment angle is ψEOC = 0°.
- (2)
- Transmission axis alignment: The transmission axes of the polarizer (OXP-axis) and analyzer (OXA-axis) are precisely aligned to be parallel with the OX-axis and OY-axis of the optical system, respectively. Specifically, the rotation alignment angle of the polarizer is ζP = 0°, and that of the analyzer is ζA = 90°.
- (3)
- Azimuthal alignment of the electro-optic crystal: The principal dielectric axes OX1 and OY1 of the electro-optic crystal under zero-voltage conditions are precisely aligned with the OX-axis and OY-axis of the optical system, achieving a rotation alignment angle of ζEOC = 0°.
2.2. Alignment Principle and System
2.2.1. Alignment Principle
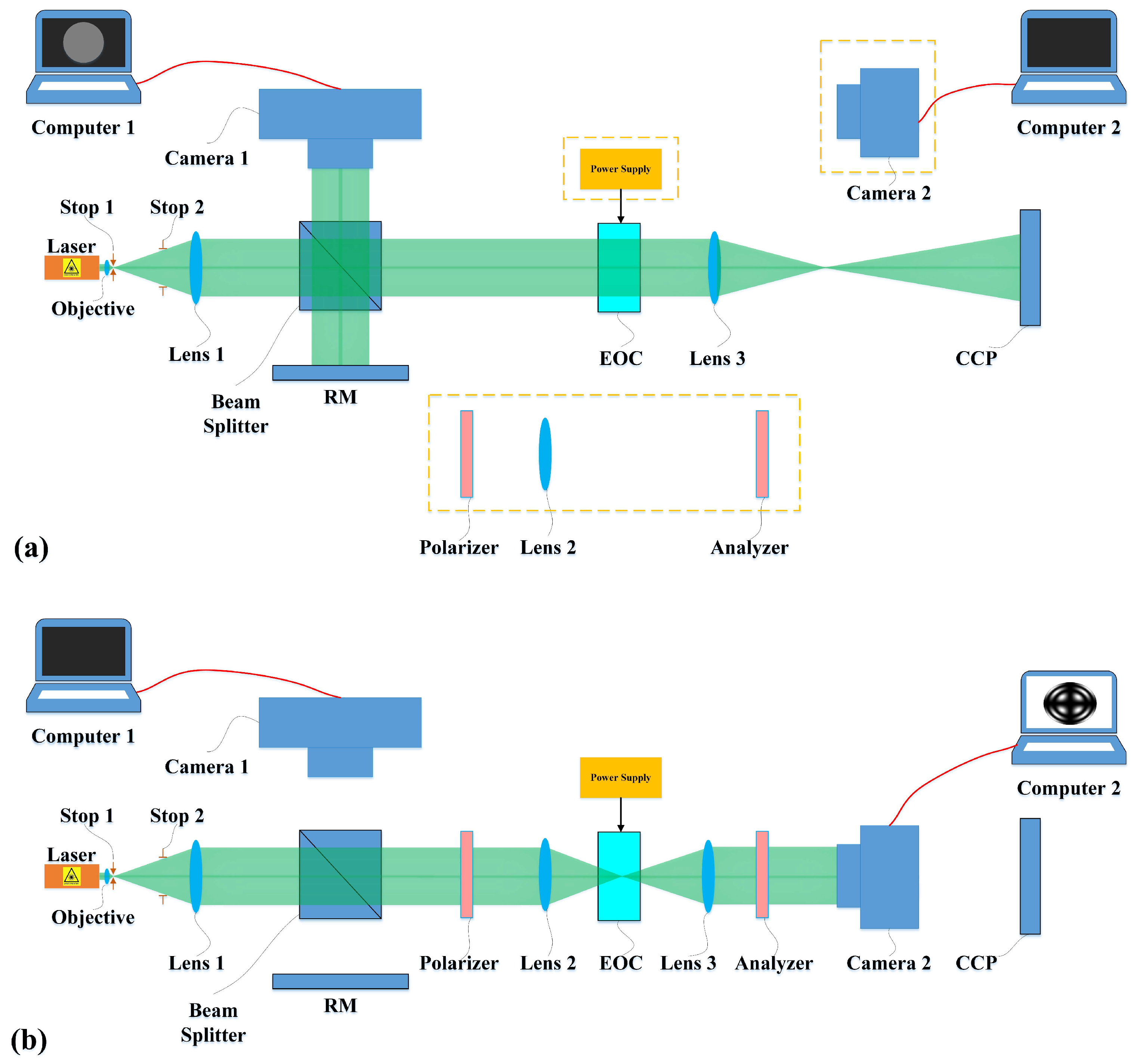
2.2.2. Alignment System
3. Experiments and Results
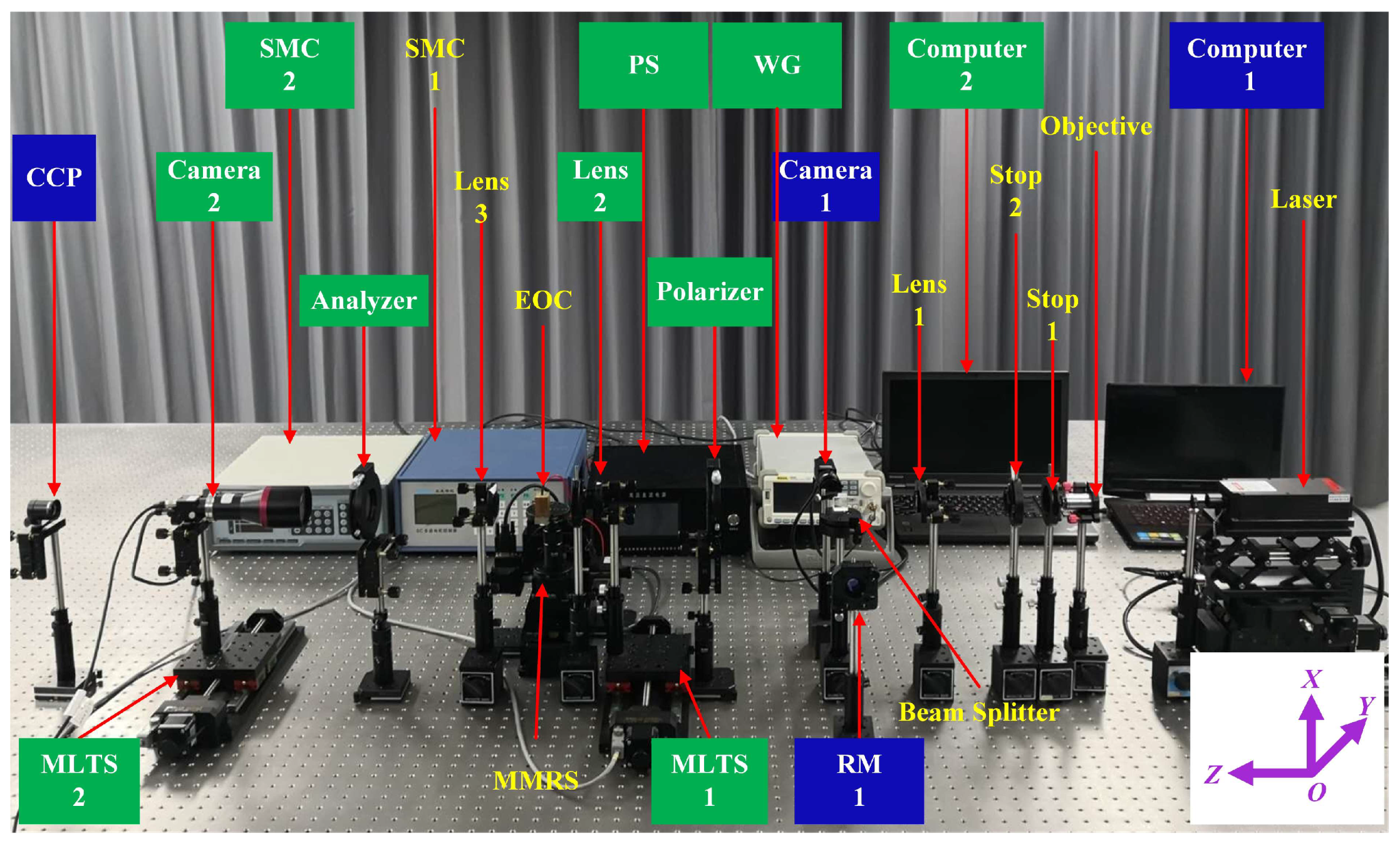
3.1. Experimental Alignment System
3.2. Alignment Procedure
3.2.1. Optical Axis Alignment
- (1)
- SMC 2 is employed to actuate MLTS 1 and MLTS 2, thereby removing lens 2 and camera 2 from the optical path along the negative Y-axis direction. This configuration ensures that the reflected light from both the reference mirror and the corner cube prism can be received by camera 1.
- (2)
- The electro-optic crystal is mounted on a high-precision MMRS. First, the aperture of stop 2 is adjusted to its minimum size. The reflected spot of the laser is observed on the electro-optic crystal. Then, SMC 2 is used to control the MMRS for rotation around the X-axis, and slow adjustments are performed to make the reflected spot pass through the small aperture of stop 2 along the negative Z-axis direction, thereby achieving the preliminary alignment of the optical axis of the electro-optic crystal. Following this preliminary adjustment, fine-tuning is implemented through SMC 1 to drive the MMRS. Under MMRS control, the electro-optic crystal rotates around the X and Y axes. Throughout the alignment process, real-time monitoring of crystal orientation can be achieved by observing the optical images captured by camera 1.
- (3)
- The output images from camera 1 are monitored on computer 1 to verify the presence of well-defined interference fringes. Optical axis alignment is achieved when the computer-monitored interference fringes progressively widen until they completely disappear.
3.2.2. Transmission Axes Alignment
- (1)
- SMC 2 is activated to coordinate the motion of MLTS 1 and MLTS 2 along the +Y-axis direction. This mechanical adjustment positions lens 2 and camera 2 in the optical path, effectively transitioning the measurement configuration from Twyman-Green interferometry to conoscopic interferometry.
- (2)
- The analyzer is positioned in front of the polarizer, with a high-precision laser power meter detecting the emergent beam from the analyzer. By rotating the analyzer around the Z axis, we minimize the detected optical power through angular adjustment. This alignment procedure establishes the perpendicular relationship between the transmission axes of the polarizer and analyzer, as confirmed by the power meter reaching its minimum reading.
- (3)
- The adjusted analyzer is repositioned behind the electro-optic crystal. The transmission axes of the polarizer and analyzer are synchronously rotated around the Z axis with identical angular increments. With no voltage applied to the crystal, the conoscopic interference pattern generated by camera 2 is recorded using computer 2.
- (4)
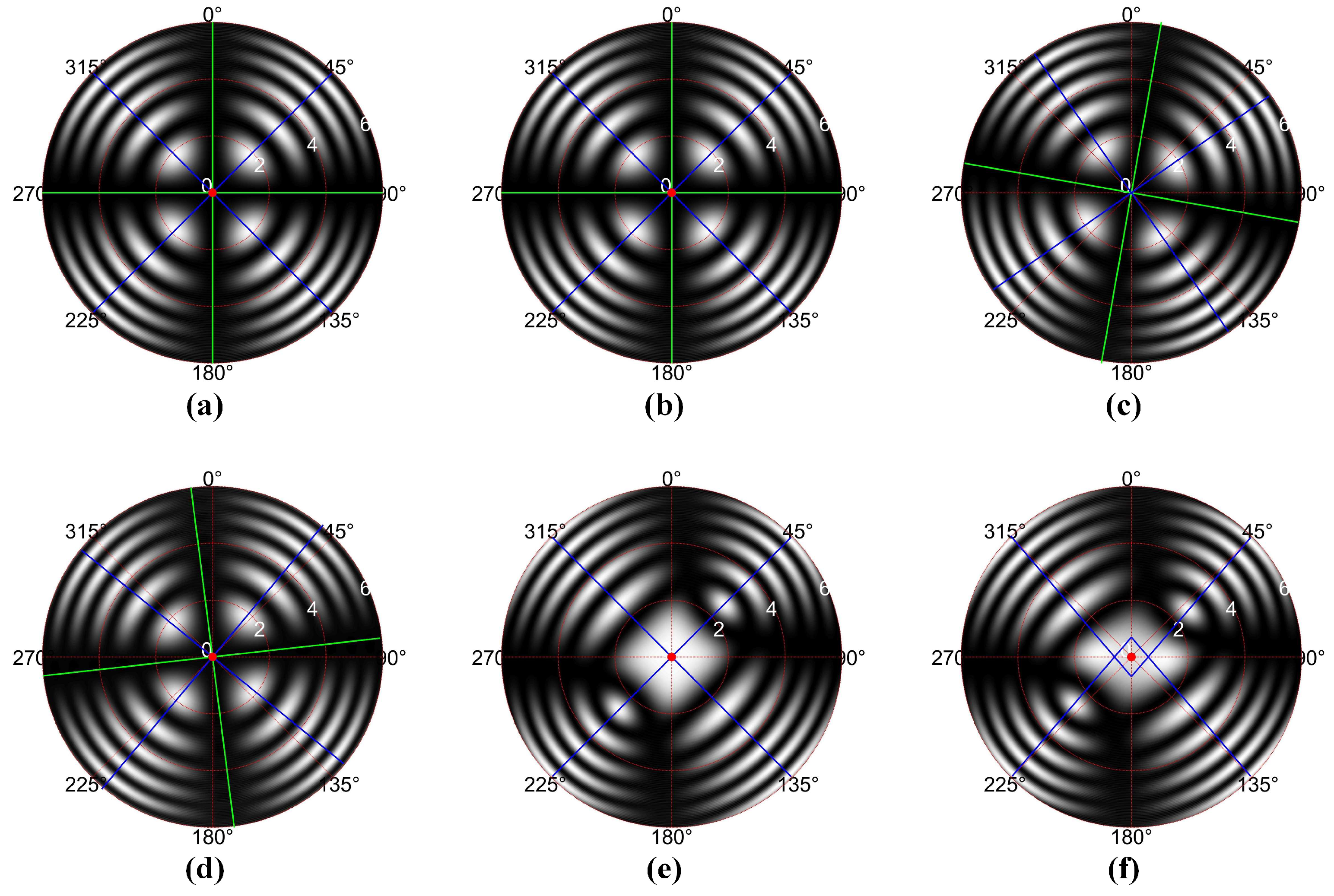
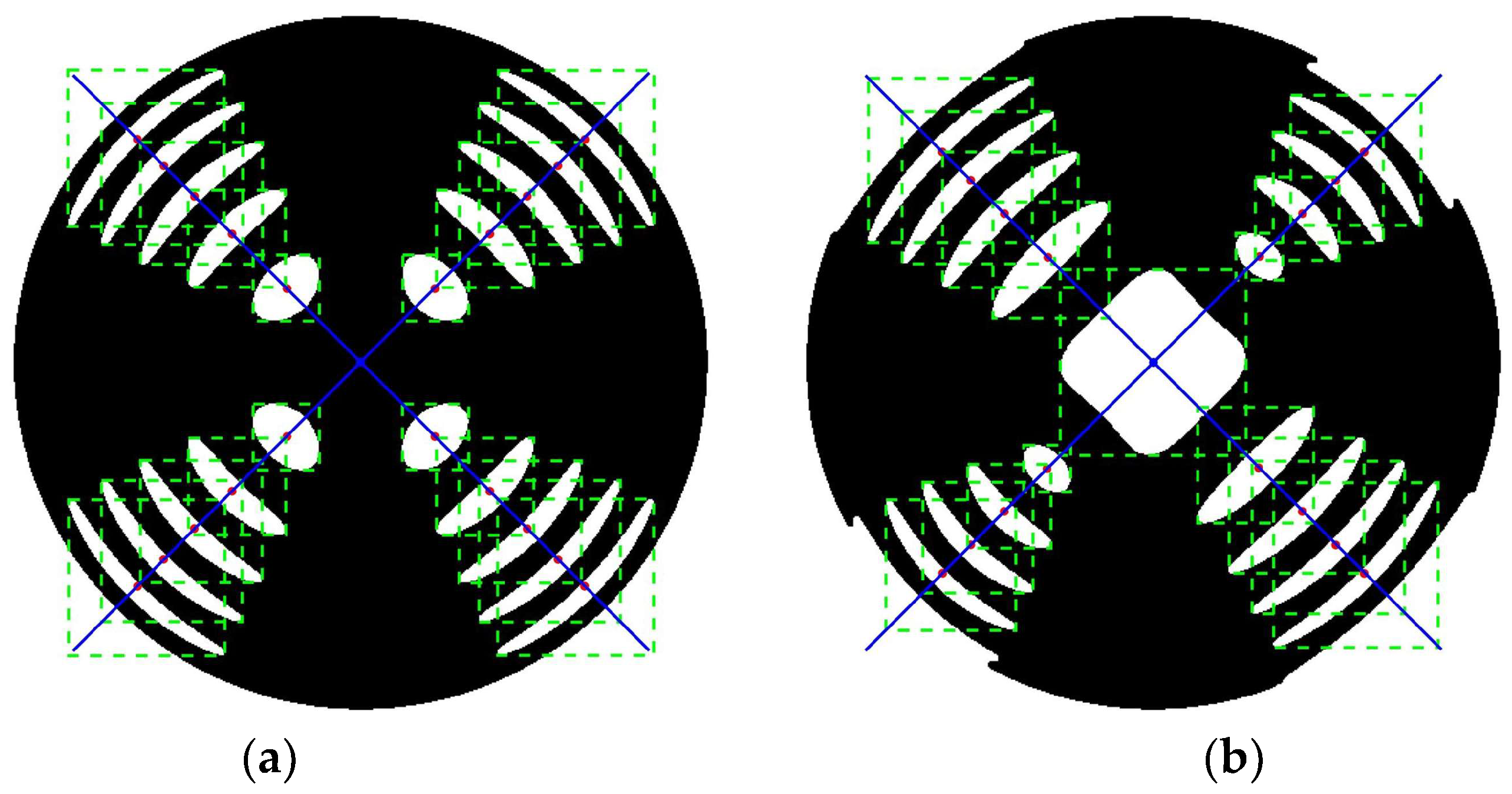
- The conoscopic interference patterns under zero-voltage conditions should be processed to analyze whether the centroids of the white area distribute on the two lines oriented at 45° and 135°. When misalignment occurs, iterative adjustments should be made to the transmission axes of both the polarizer and analyzer.
3.2.3. Azimuthal Alignment of the Electro-Optic Crystal
- (1)
- The applied voltage on the electro-optic crystal is set to half-wave voltage, and the crystal should be precisely rotated by the multi-axis motorized rotation stage around the Z axis.
- (2)
- The conoscopic interference patterns generated by camera 2 are digitally recorded by computer 2.
- (3)
- The conoscopic interference patterns under half-wave voltage conditions should be processed to analyze whether the centroids of the white area distribute on the two lines oriented at 45° and 135°. When misalignment occurs, iterative adjustments should be made to the azimuthal orientation of the electro-optic crystal.
3.3. Experimental Results
3.3.1. Twyman-Green Interferometry Experimental Results
3.3.2. The Processed Conoscopic Interference Patterns
3.3.3. Verification of Electro-Optic Modulator Alignment
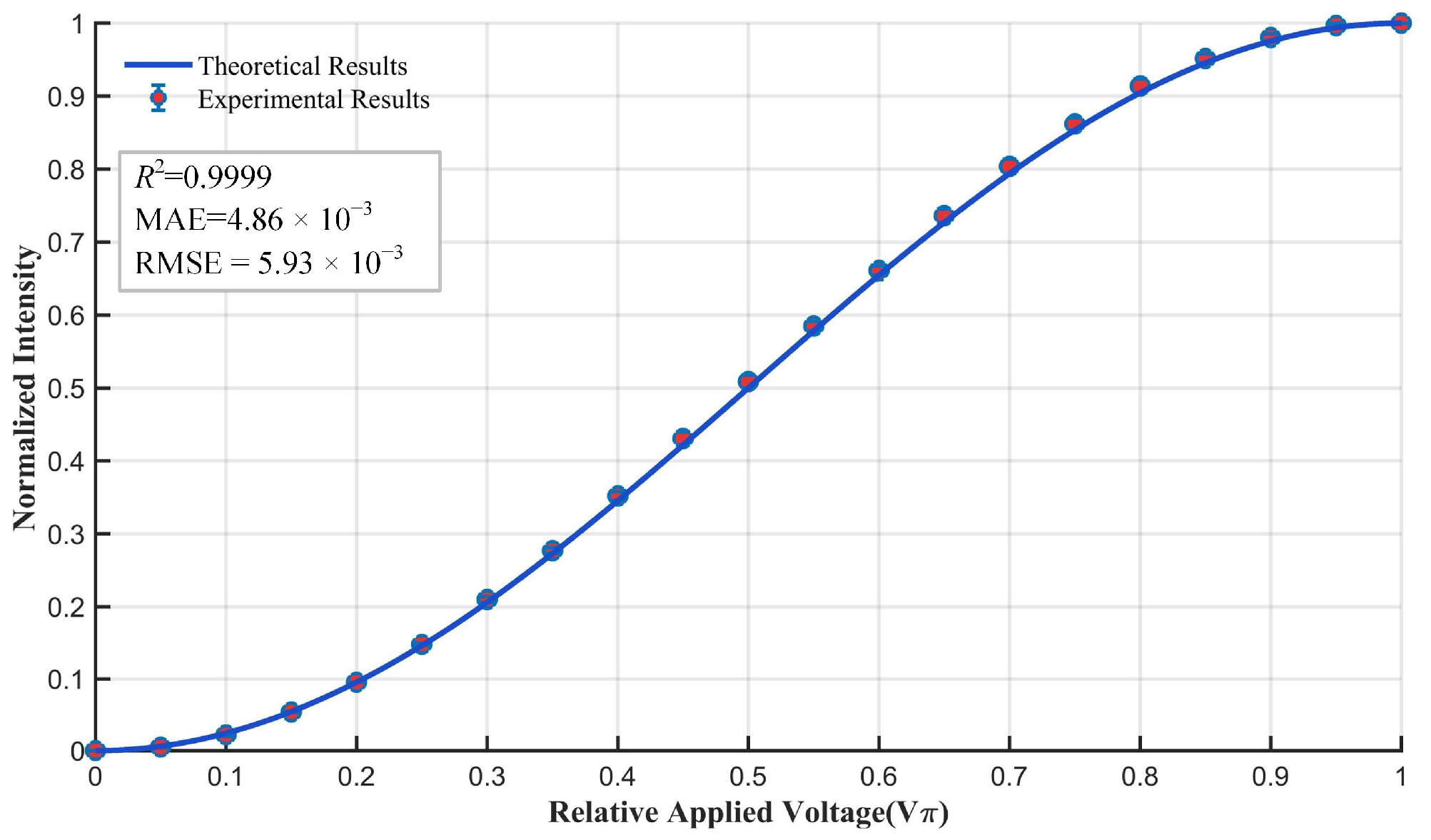
3.3.4. Experimental Results for the Transmission Axes Alignment
3.3.5. Experimental Results for Azimuthal Alignment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EOMs | Electro-optic modulators |
| RM | Reference Mirror |
| SMC | Stepping Motor Controller |
| MMRS | Multi-axis Motorized Rotation Stage |
| WG | Waveform Generator |
| EOC | Electro-optic Crystal |
| PS | Power Supply |
| MLTS | Motorized Linear Translation Stage |
| CCP | Corner Cube Prism |
References
- Ivankovski, Y.; Mendlovic, D. High-rate–long-distance fiber-optic communication based on advanced modulation techniques. Appl. Opt. 1999, 38, 5533–5540. [Google Scholar] [CrossRef] [PubMed]
- Wooten, E.L.; Kissa, K.M.; Yi-Yan, A.; Murphy, E.J.; Lafaw, D.A.; Hallemeier, P.F.; Maack, D.; Attanasio, D.V.; Fritz, D.J.; McBrien, G.J.; et al. A review of lithium niobate modulators for fiber-optic communications systems. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 69–82. [Google Scholar] [CrossRef]
- Jeffrey, D.B.; Nicolas, A.F.J.; Hiroshi, K.; Mark, F.; Adam, R.; Pejman, G. In 40-GHz electro-optic polarization modulator for fiber optic communications systems. Proc. SPIE 2004, 5577, 133–143. [Google Scholar]
- Wang, Y.; Zheng, Y.; Fang, C.; Shi, H.; Pan, W. Light-injection attack against practical continuous-variable measurement-device-independent quantum key distribution systems. Opt. Express 2024, 32, 33656–33676. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, Y.-H.; Xie, H.-B.; Li, Z.-P.; Jiang, X.; Cai, W.-Q.; Ren, J.-G.; Yin, J.; Liao, S.-K.; Peng, C.-Z. High-speed robust polarization modulation for quantum key distribution. Opt. Lett. 2019, 44, 5262–5265. [Google Scholar] [CrossRef] [PubMed]
- Sangeetha, R.G.; Hemanth, C.; Jaiswal, I. Performance of different modulation scheme in free space optical transmission—A review. Optik 2022, 254, 168675. [Google Scholar] [CrossRef]
- Bowman, A.J.; Klopfer, B.B.; Juffmann, T.; Kasevich, M.A. Electro-optic imaging enables efficient wide-field fluorescence lifetime microscopy. Nat. Commun. 2019, 10, 4561. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Du, X.; Zhao, J.; Song, Y.; Chen, H. High resolution flash three-dimensional LIDAR systems based on polarization modulation. Appl. Opt. 2017, 56, 3889–3894. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zhao, J.; Wang, B.; Wang, X.; Liu, B.; Lv, X.; Zhang, J. Potassium tantalate niobate (KTN) crystal-based polarization-modulated 3D ladar with a large field of view. Opt. Lett. 2020, 45, 5319–5322. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Ho, C.P.; Xue, J.; Lim, L.W.; Chen, G.; Fu, Y.H.; Lee, L.Y.T. A Progress Review on Solid-State LiDAR and Nanophotonics-Based LiDAR Sensors. Laser Photonics Rev. 2022, 16, 2100511. [Google Scholar] [CrossRef]
- Kumagai, T.; Hibino, K.; Tomita, K.; Wasaki, K. Inertia alignment of phase-shifting algorithms for high-numerical-aperture spherical testing in Fizeau interferometry. Appl. Opt. 2022, 61, 8926–8935. [Google Scholar] [CrossRef] [PubMed]
- Stangner, T.; Dahlberg, T.; Svenmarker, P.; Zakrisson, J.; Wiklund, K.; Oddershede, L.B.; Andersson, M. Cooke-Triplet tweezers: More compact, robust, and efficient optical tweezers. Opt. Lett. 2018, 43, 1990–1993. [Google Scholar] [CrossRef] [PubMed]
- Sommargren, G.; Phillion, D.; Johnson, M.; Nguyen, N.; Barty, A.; Snell, F.; Dillon, D.; Bradsher, L. 100-picometer interferometry for EUVL. SPIE 2002, 4688, 316–328. [Google Scholar]
- Otaki, K.; Ota, K.; Nishiyama, I.; Yamamoto, T.; Fukuda, Y.; Okazaki, S. Development of the point diffraction interferometer for extreme ultraviolet lithography: Design, fabrication, and evaluation. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2002, 20, 2449–2458. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, B.; Kang, X.; Chen, L.; Wei, X. Precision optical path alignment system for point diffraction interferometer based on image information. Appl. Opt. 2019, 58, 3703–3711. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.G.; Sun, L.D.; Flores-Camacho, J.M.; Hohage, M.; Liu, C.Y.; Hu, X.T.; Zeppenfeld, P. A rotating-compensator based reflectance difference spectrometer for fast spectroscopic measurements. Rev. Sci. Instrum. 2010, 81, 043108. [Google Scholar] [CrossRef] [PubMed]
- Cui, G.; Liu, T.; Li, G.; Chen, Y.; Guo, X. Calibration of the MgF2 Biplate Compensator Using a Straight-Through Ellipsometer. In Proceedings of the 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, Shenyang, China, 21–23 September 2013; pp. 731–735. [Google Scholar]
- Han, Z.; Xu, Z.; Chen, L. A three-spectrum method for accurate calibration of bi-plate zero-order retarder. Chin. Opt. Lett. 2014, 12, 031202. [Google Scholar]
- Gu, H.; Liu, S.; Chen, X.; Zhang, C. Calibration of misalignment errors in composite waveplates using Mueller matrix ellipsometry. Appl. Opt. 2015, 54, 684–693. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Du, X.; Song, Y. Modeling and Analysis of the Electro-Optic Modulator with Alignment Errors. IEEE Access 2020, 8, 2023–2031. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Ordinary refractive index no in the absence of an external electric field | 2.2797 |
| Length L in the direction of light propagation | 18.8 mm |
| Thickness d in the direction of the external electric field | 9 mm |
| Electro-optic coefficient () | 6.74 × 10−12 m/V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Lu, Q. High-Precision Alignment Method for Electro-Optic Modulators via Combined Twyman-Green and Conoscopic Interferometry. Sensors 2025, 25, 6231. https://doi.org/10.3390/s25196231
Zhang P, Lu Q. High-Precision Alignment Method for Electro-Optic Modulators via Combined Twyman-Green and Conoscopic Interferometry. Sensors. 2025; 25(19):6231. https://doi.org/10.3390/s25196231
Chicago/Turabian StyleZhang, Peng, and Qi Lu. 2025. "High-Precision Alignment Method for Electro-Optic Modulators via Combined Twyman-Green and Conoscopic Interferometry" Sensors 25, no. 19: 6231. https://doi.org/10.3390/s25196231
APA StyleZhang, P., & Lu, Q. (2025). High-Precision Alignment Method for Electro-Optic Modulators via Combined Twyman-Green and Conoscopic Interferometry. Sensors, 25(19), 6231. https://doi.org/10.3390/s25196231





