Fault Ride-Through Optimization Scheme for Hybrid AC/DC Transmission Systems on the Same Tower
Abstract
1. Introduction
2. Limitations of the Phase-Shift FRT in SM-LCC-HVDC Systems and Corresponding Improvements
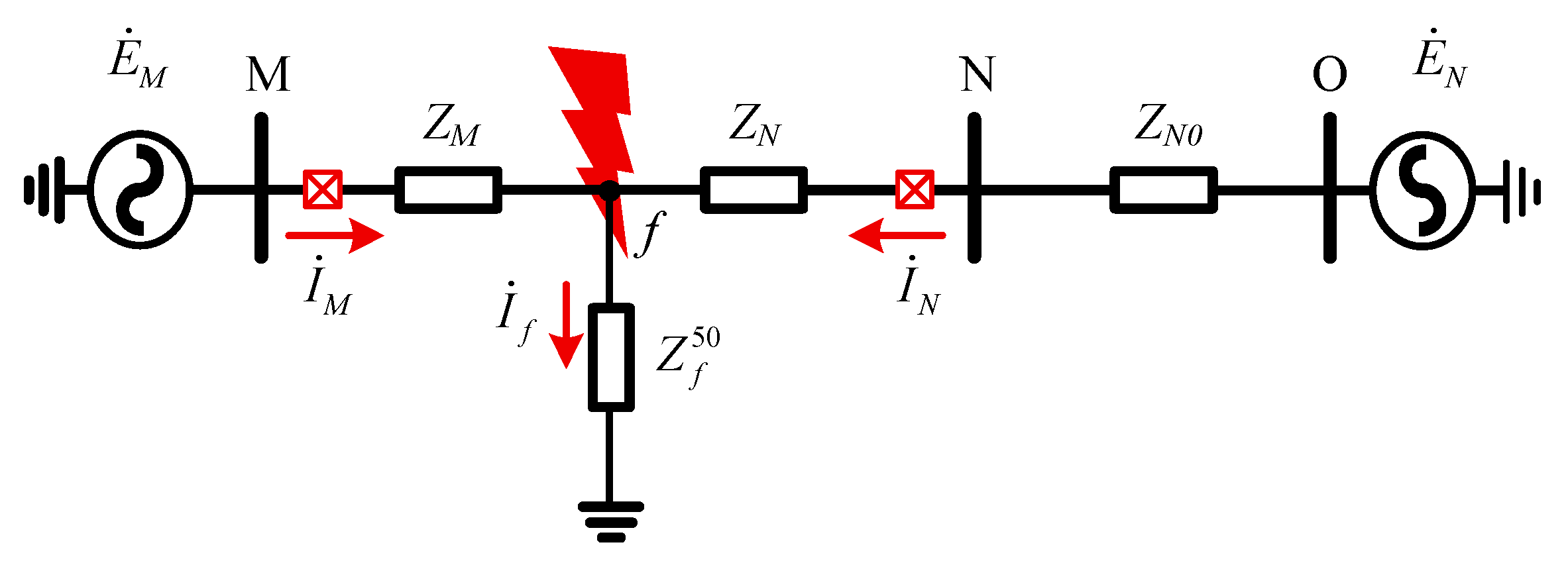
2.1. Fault Types of Hybrid AC/DC Transmission Systems
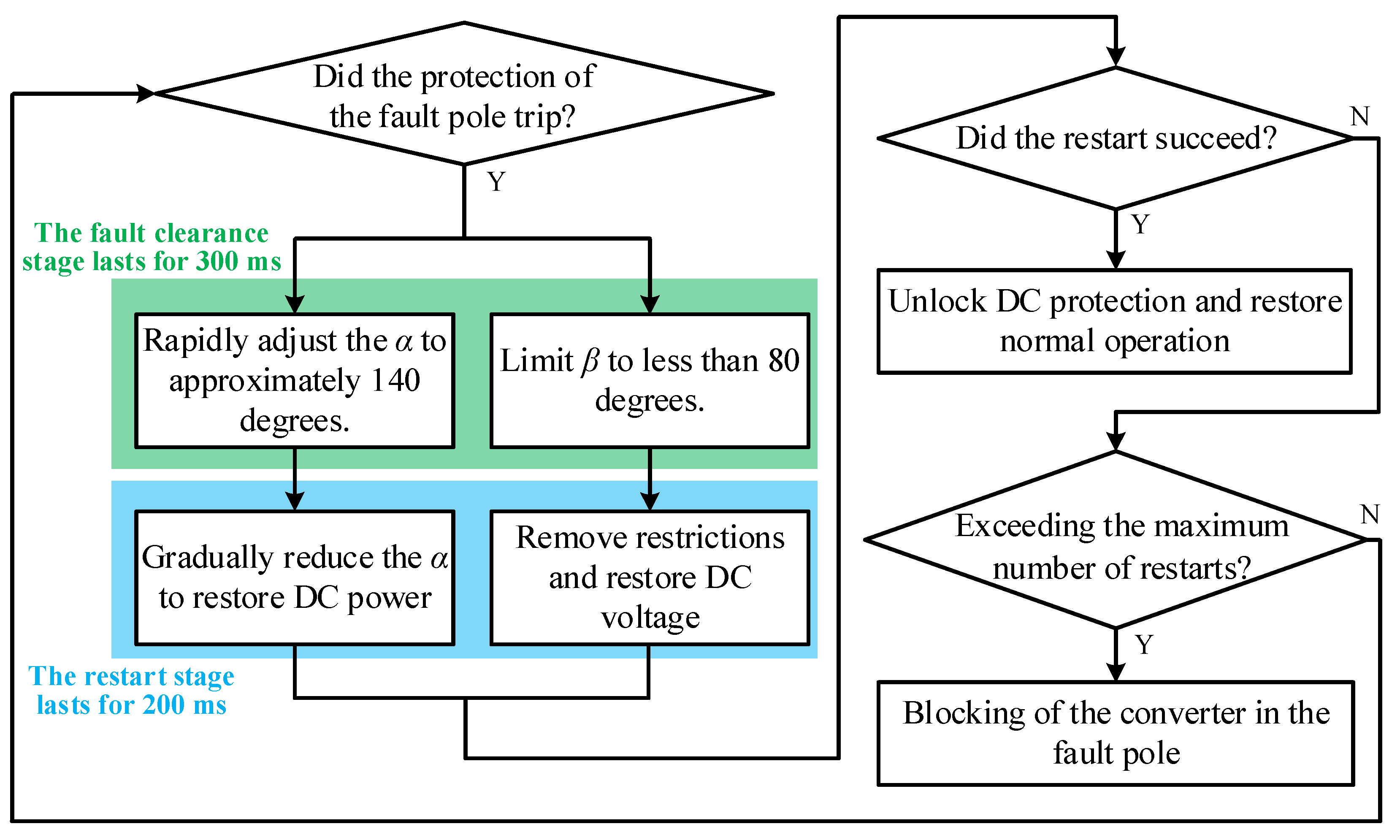
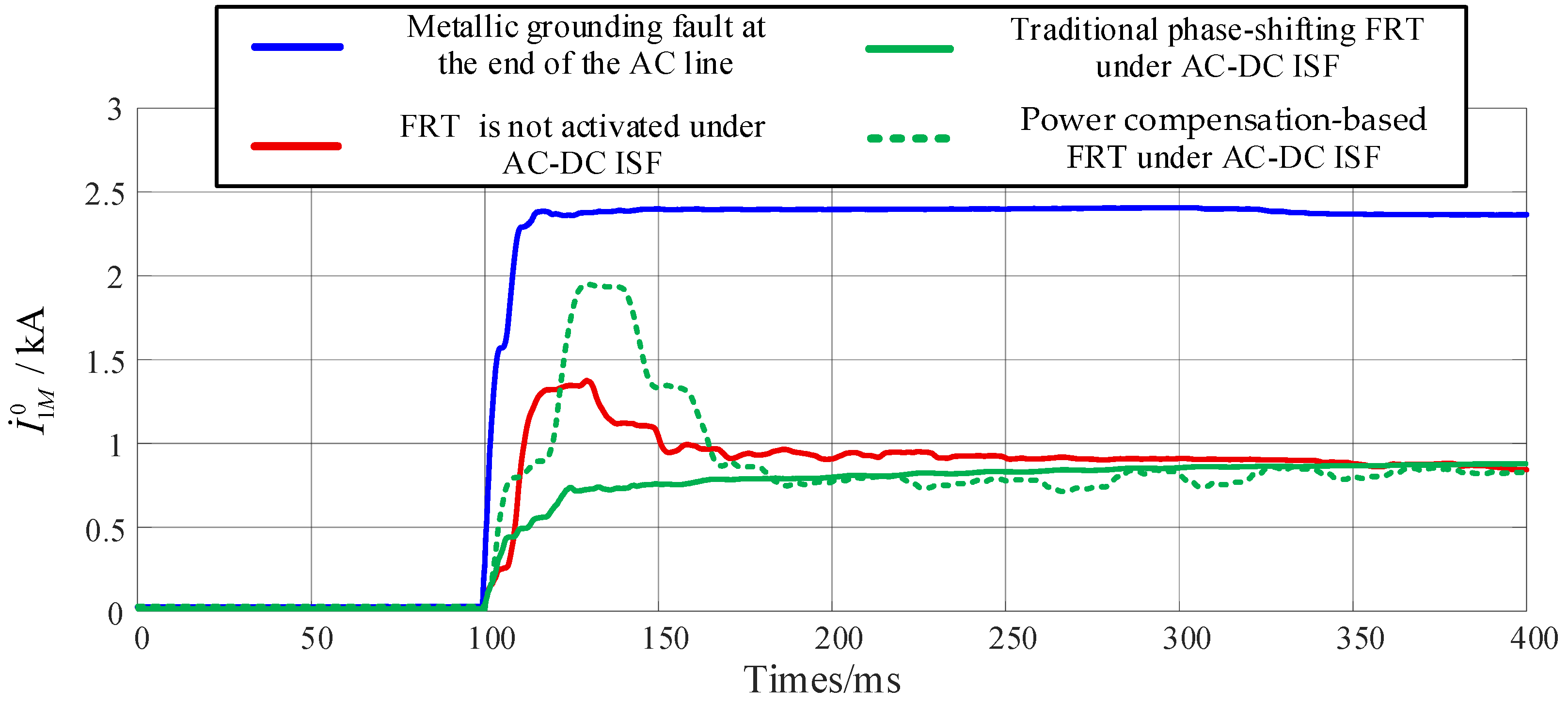
2.2. Adaptability Analysis of Phase-Shifting FRT Applied to SM-LCC-HVDC Systems
2.3. Power Compensation-Based FRT Strategy
3. Adaptive Analysis of FRT Strategy Under ISF
3.1. Core Requirements for FRT Under ISF
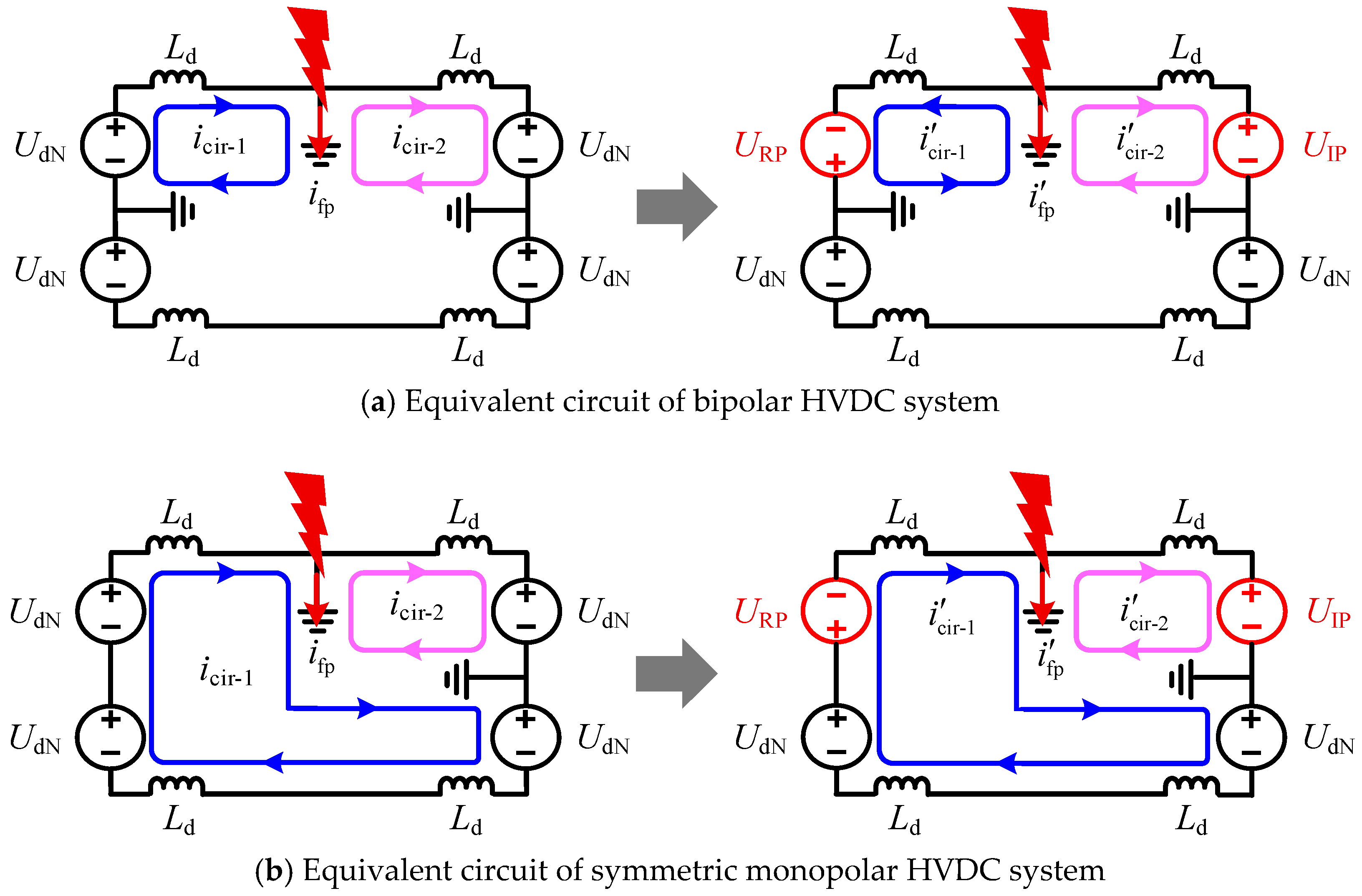
3.2. Performance of Primary AC Protection Under AC-DC ISF
3.3. Performance of AC Backup Protection Under AC-DC ISF
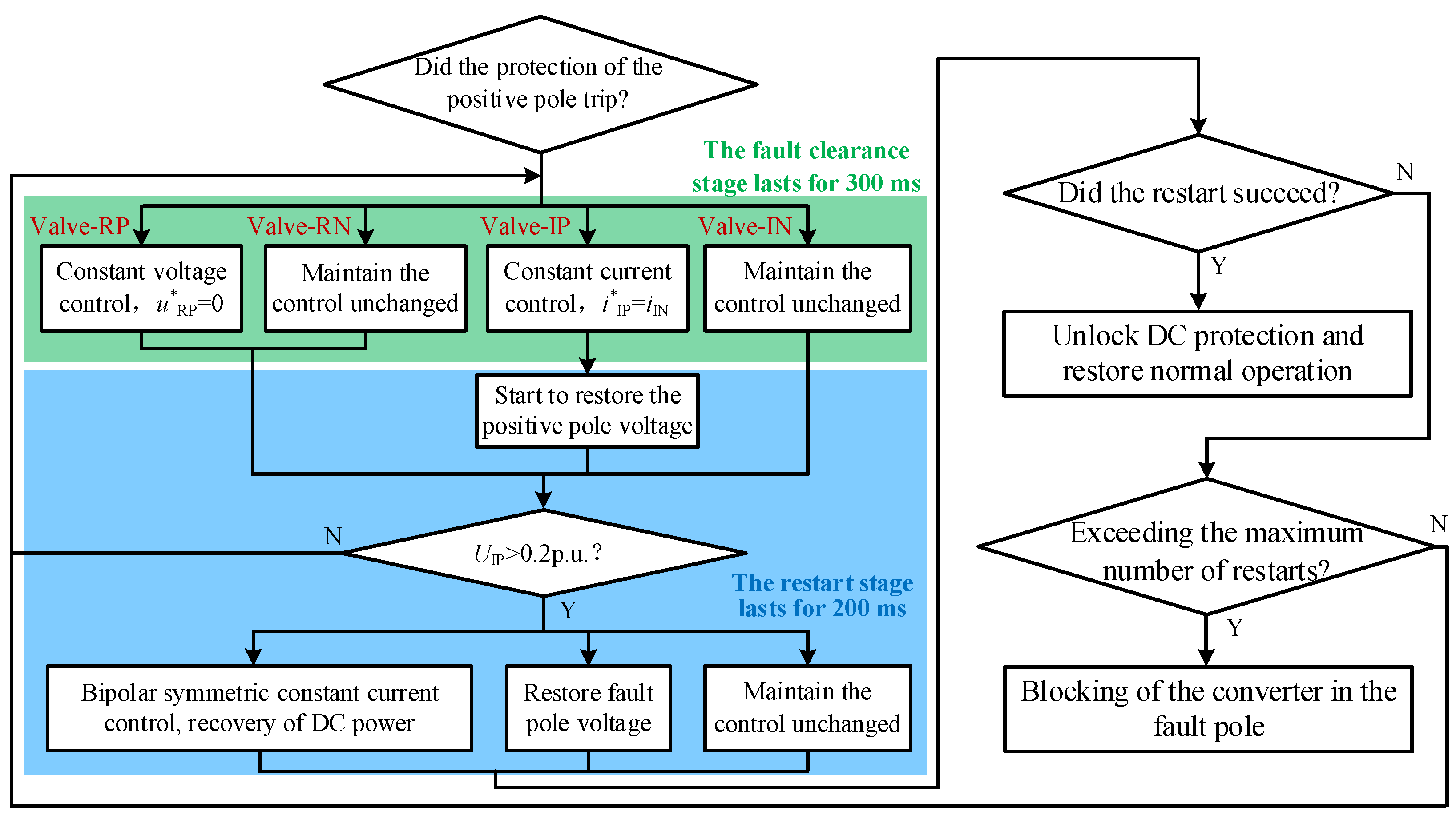
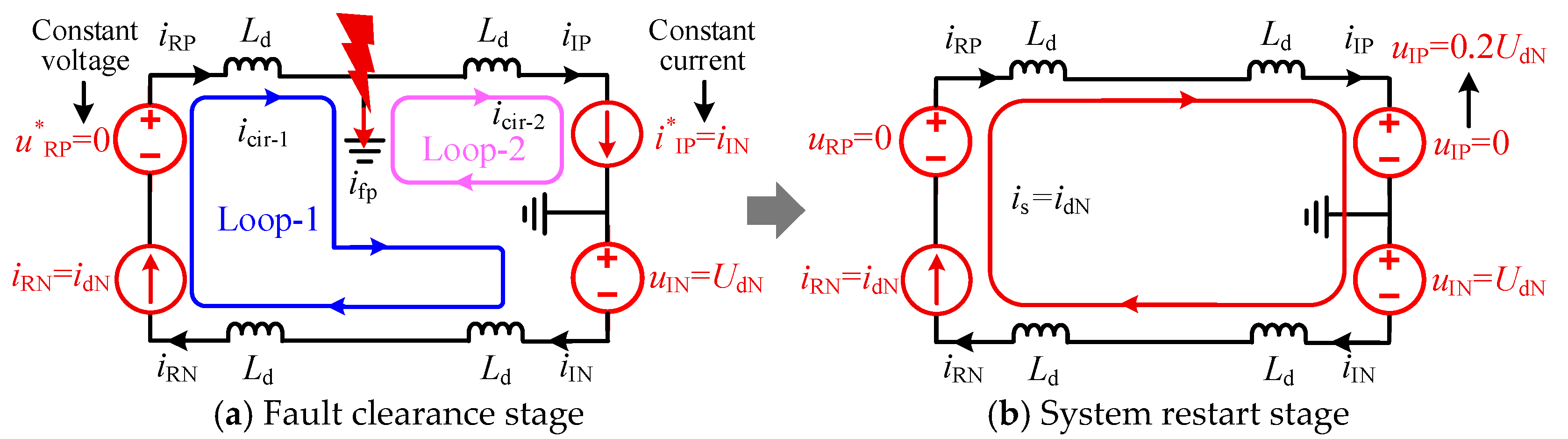
4. Protection-Control Cooperation FRT Strategy for AC-DC ISF
4.1. Implementation Method
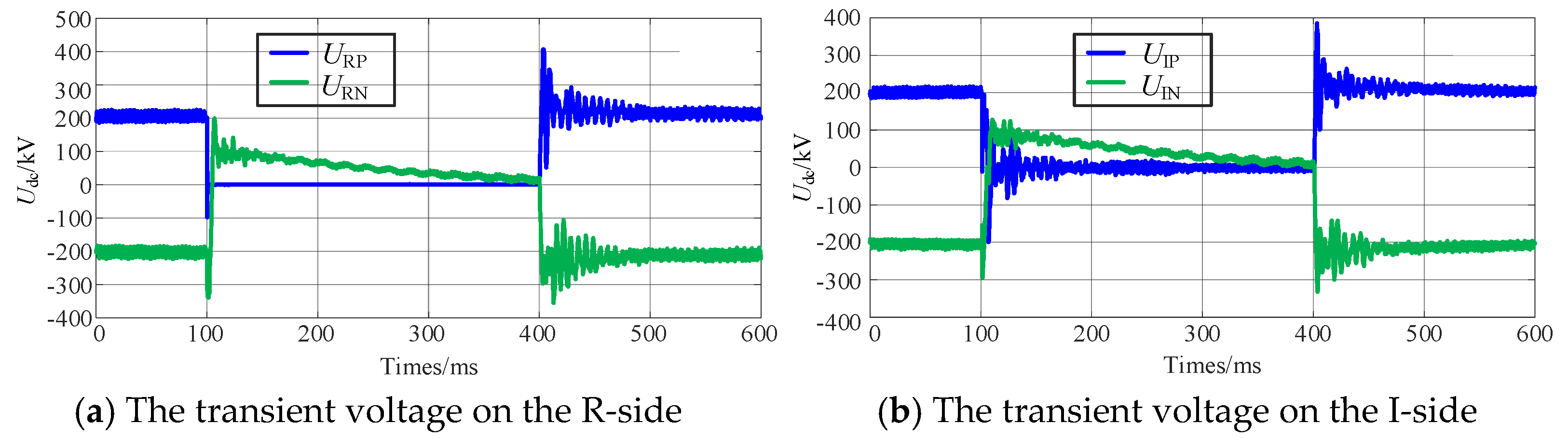
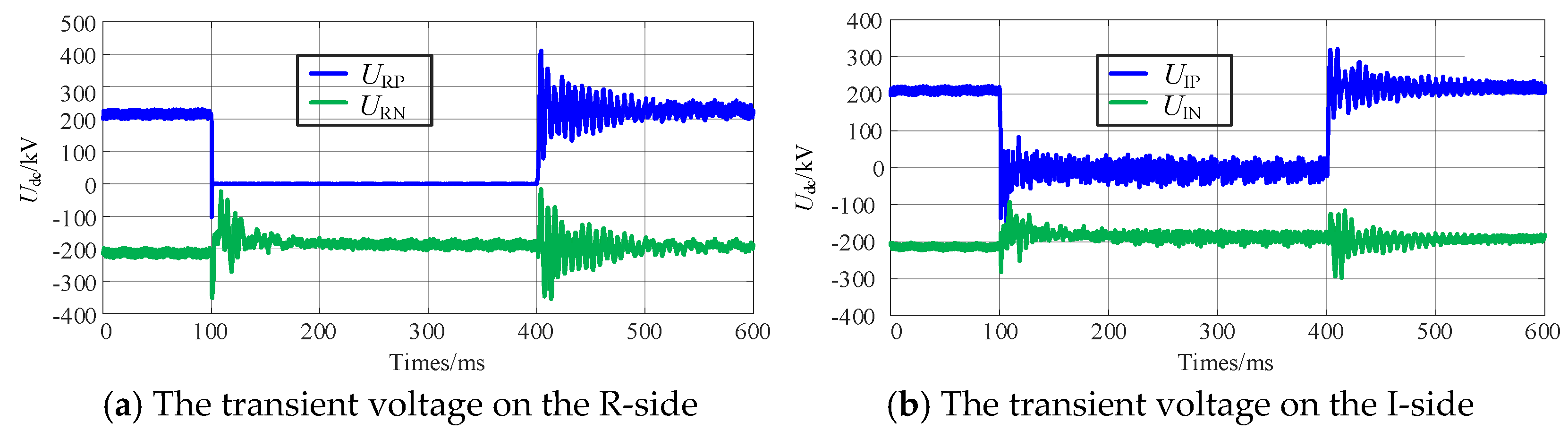
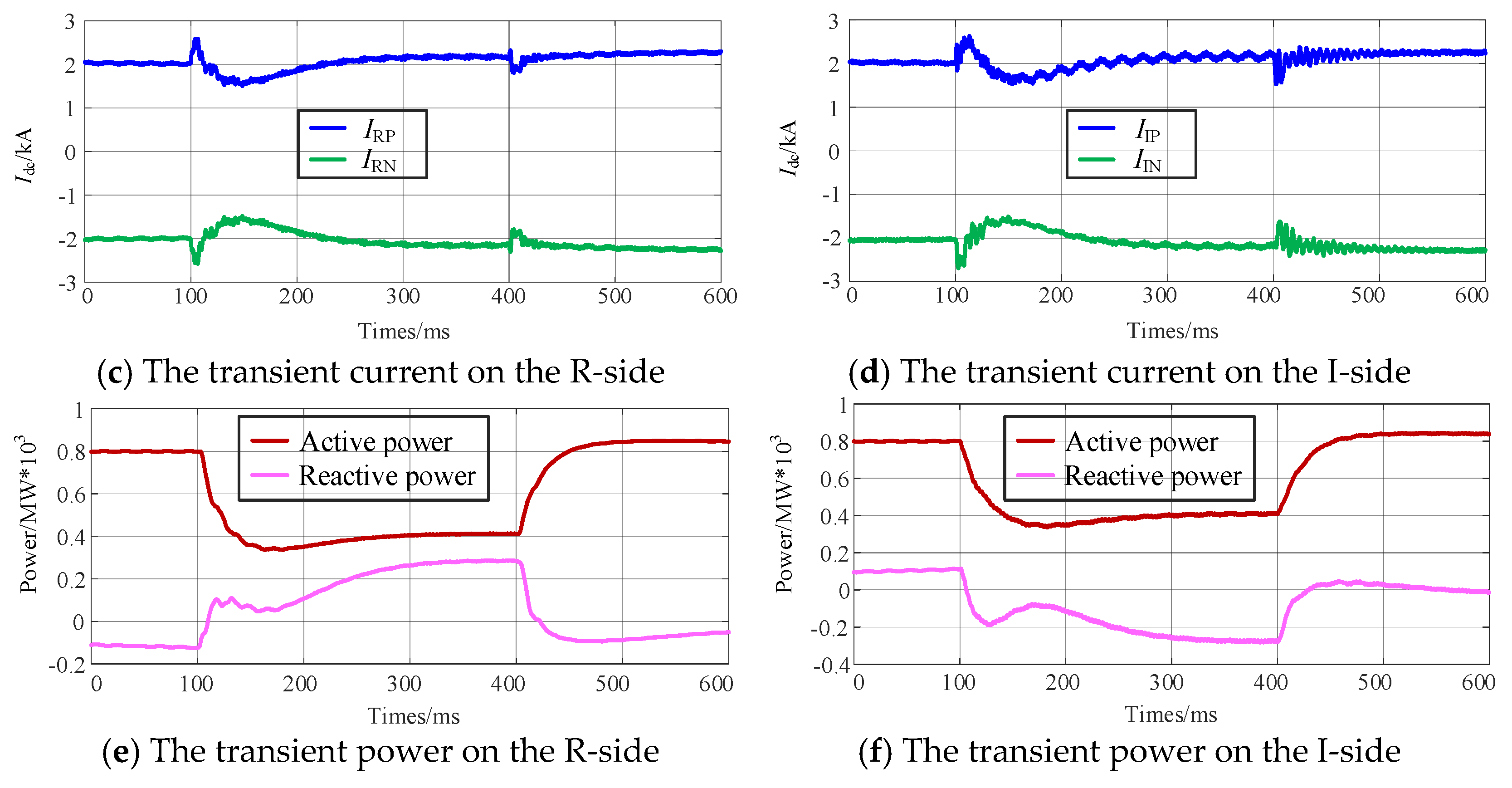
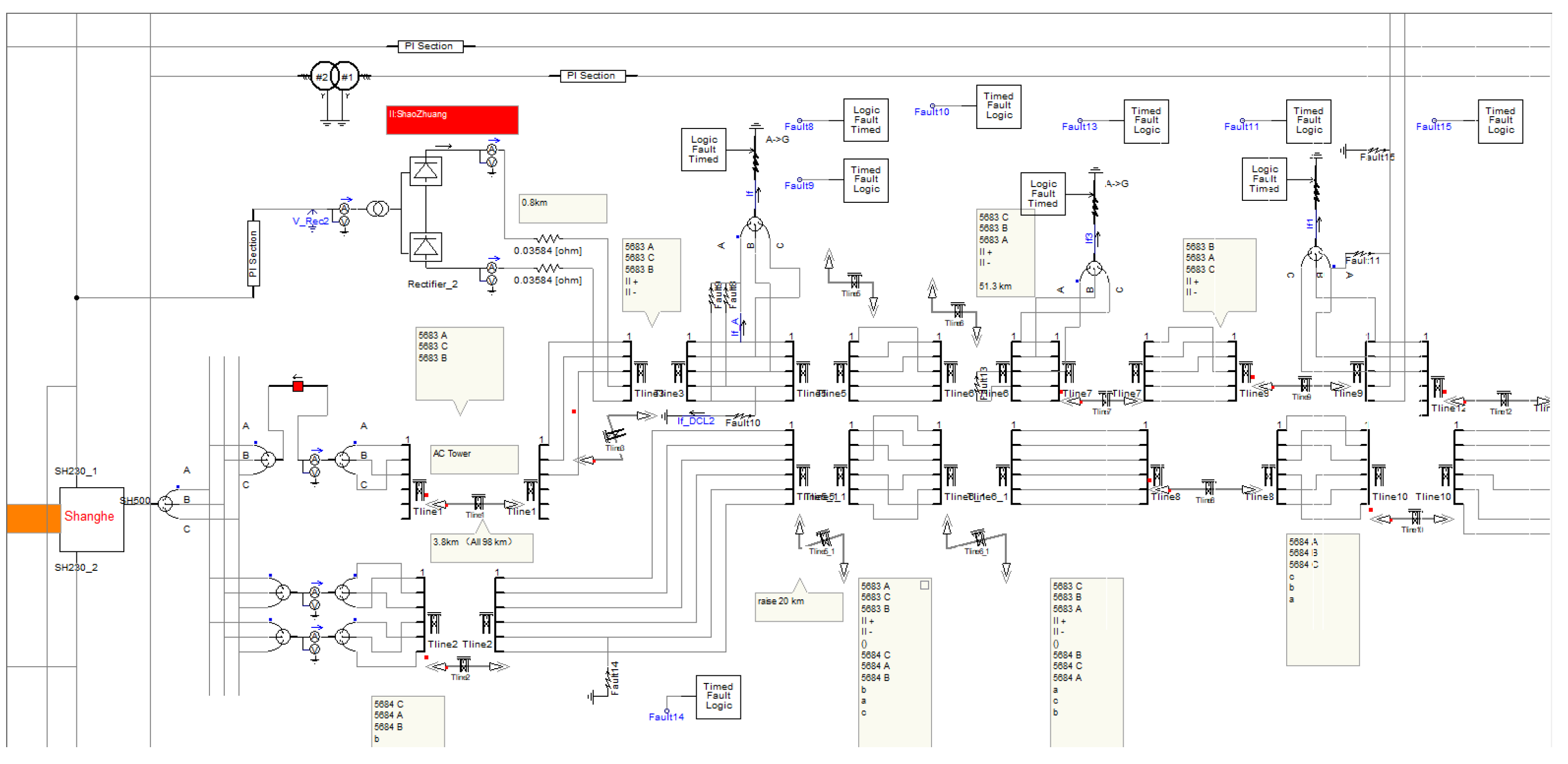
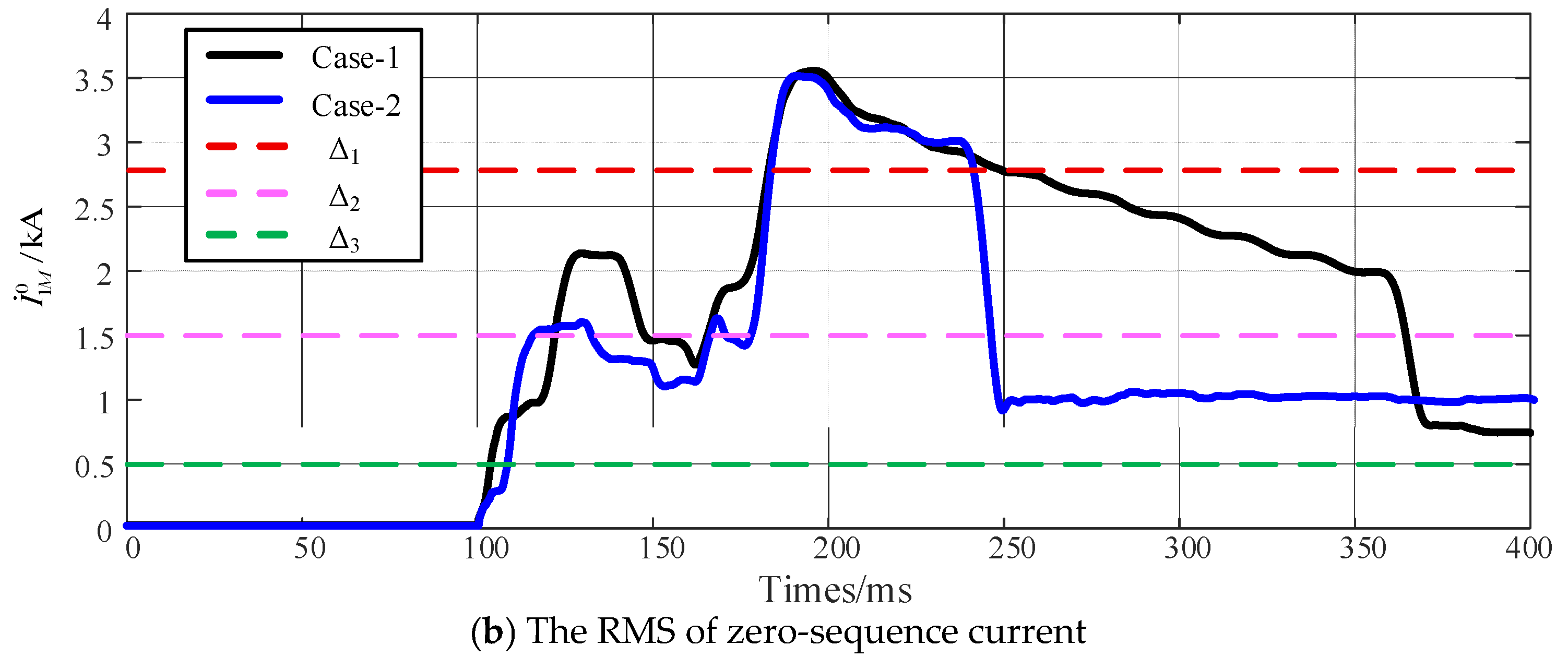
4.2. Simulation Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alassi, A.; Banales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC Transmission: Technology Review, Market Trends and Future Outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Bianchi, F.D.; José Luis Domínguez-García Gomis-Bellmunt, O. Control of multi-terminal HVDC networks towards wind power integration: A review. Renew. Sustain. Energy Rev. 2016, 55, 1055–1068. [Google Scholar] [CrossRef]
- Bloom, A.; Novacheck, J.; Brinkman, G.; McCalley, J.; Figueroa-Acevedo, A.; Jahanbani-Ardakani, A.; Nosair, H.; Venkatraman, A.; Caspary, J.; Osborn, D.; et al. The Value of Increased HVDC Capacity Between Eastern and Western U. S. Grids: The Interconnections Seam Study. Power Systems. IEEE Trans. Power Syst. 2022, 37, 1760–1769. [Google Scholar]
- Silva, F.F.D.; Irnawan, R.; Mochamad, R.F.; Zhang, Z.; Zhang, Q. Power-flow for archipelago-based multi-terminal HVDC grids. Electr. Power Syst. Res. 2024, 231, 110274. [Google Scholar] [CrossRef]
- Rodriguez, P.; Rouzbehi, K. Multi-terminal DC grids: Challenges and prospects. J. Mod. Power Syst. Clean Energy 2017, 5, 515–523. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T. Fault location for overhead and cable hybrid DC line based on the energy transmission characteristics. Electr. Power Syst. Res. 2023, 221, 109414. [Google Scholar] [CrossRef]
- Mirsaeidi, S.; Dong, X. An Integrated Control and Protection Scheme to Inhibit Blackouts Caused by Cascading Fault in Large-Scale Hybrid AC/DC Power Grids. IEEE Trans. Power Electron. 2018, 34, 7278–7291. [Google Scholar] [CrossRef]
- Jiang, S.; Xu, Y.; Li, G.; Xin, Y.; Wang, L. Coordinated Control Strategy of Receiving-End Fault Ride-Through for DC Grid Connected Large-Scale Wind Power. Power Delivery. IEEE Trans. Power Deliv. 2022, 37, 2673–2683. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, Y.; Yang, G.; Wang, Z. A Dissipation Energy Based Method for the Optimization of Fault Transient Characteristics of AC/DC Hybrid System. Power Systems. IEEE Trans. Power Syst. 2023, 38, 514–527. [Google Scholar] [CrossRef]
- Hao, X.; Lei, X.; Liu, H.; Liang, W.; Li, H. Researches on Two Kinds of Fault Restart Logic of Qishao ± 800 kV UHVDC Project. Power Syst. Prot. Control 2018, 46, 143–150. [Google Scholar]
- Hussain, K.S.T.; Song, G.; Wang, T.; Hou, J.; Masood, B. Adaptive fault recovery strategy of LCC-MMC based hybrid HVDC. IET Gener. Transm. Distrib. 2021, 15, 2396–2409. [Google Scholar] [CrossRef]
- Ma, J.; Wang, R.; Liu, C.; Zhang, J.; Phadke, A. An adaptive DC line fault recovery strategy for LCC-HVDC system based on voltage gradient. Int. J. Electr. Power Energy Syst. 2022, 135, 107558. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Hussain, K.S.T. Adaptive Single-Pole Auto-Reclosing Scheme for Hybrid MMC-HVDC Systems. IEEE Trans. Power Deliv. 2019, 34, 2194–2203. [Google Scholar] [CrossRef]
- Jiang, S.; Xin, Y.; Li, G.; Wang, L. A Novel DC Fault Ride-Through Method for Wind Farms Connected to the Grid Through Bipolar MMC-HVDC Transmission. IEEE Trans. Power Deliv. 2020, 35, 2937–2950. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, X.; Wang, X.; Liu, S. Upgrading Transmission Capacity by Altering HVAC Into Fractional Frequency Transmission System. Power Delivery. IEEE Trans. Power Deliv. 2022, 37, 3855–3862. [Google Scholar] [CrossRef]
- Hu, C.; Wu, X.; Cai, H. Overload Control of the Embedded HVDC for Hybrid AC/DC Power System Security Enhancement. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4586–4590. [Google Scholar] [CrossRef]
- Larruskain, D.M.; Zamora, I.; Abarrategui, O.; Aginako, Z. Conversion of AC distribution lines into DC lines to upgrade transmission capacity. Electr. Power Syst. Res. 2011, 81, 1341–1348. [Google Scholar] [CrossRef]
- Mircea, A.; Philip, M. HVDC Submarine Power Cables in the World: State-of-the-Art Knowledge; Report. EUR-27527-EN; European Commission: Brussels, Belgium, 2015. [Google Scholar]
- Staudt, V.; Steimel, A.; Kohlmann, M.; Jager, M.K.; Heising, C.; Meyer, D.; Vennemann, K.; Grebe, E.; Kleinekorte, K. Control concept including validation strategy for an AC/DC hybrid link. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Pittsburgh, PA, USA, 14–18 September 2014; pp. 750–757. [Google Scholar]
- Wang, Z.W.; Huang, J.; Cheng, L.; Hu, W.; Cai, H.; Han, X. Planning and application of embedded DC transmission technology in the provincial transmission power grid. Electr. Power Eng. Tech. 2022, 41, 65–74. [Google Scholar]
- Liu, Q.; Chu, X.; Fu, L.; Yu, S.; Wang, W. Integrated protection scheme for hybrid AC/DC transmission grids. Int. J. Electr. Power Energy Syst. 2025, 169, 110806. [Google Scholar] [CrossRef]
- Prommetta, J.; Schindler, J.; Jaeger, J.; Keil, T.; Butterer, C.; Ebner, G. Protection Coordination of AC/DC Intersystem Faults in Hybrid Transmission Grids. IEEE Trans. Power Deliv. 2020, 35, 2896–2904. [Google Scholar] [CrossRef]
- Zhou, H.; Ge, S.; Qin, L. Coordinate Fault Ride-Through Strategy for Connection of Offshore Wind Farms Using Voltage Source-Converter-Based High-Voltage Direct-Current Transmission under Single Polar Fault. Sensors 2023, 23, 5760. [Google Scholar] [CrossRef]
- Saeed, S.; Asghar, R.; Mehmood, F.; Saleem, H.; Azeem, B.; Ullah, Z. Evaluating a Hybrid Circuit Topology for Fault-Ride through in DFIG-Based Wind Turbines. Sensors 2022, 22, 9314. [Google Scholar] [CrossRef]
- Zheng, T.; Yu, S.; Wu, J. Adaptability Analysis of AC/DC Line-touching Protection Based on Piecewised and Linearized Model of Converter. Power Syst. Technol. 2021, 45, 3478–3488. [Google Scholar]
- Wang, H.M. DC/AC Cross Line Fault Analysis; North China Electric Power University: Beijing, China, 2016. [Google Scholar]
- Fayazi, M.; Saffarian, A.; Joorabian, M.; Monadi, M. Analysis of induced components in hybrid HVAC/HVDC transmission lines on the same tower for various fault conditions. Electr. Power Syst. Res. 2020, 226, 109884. [Google Scholar] [CrossRef]
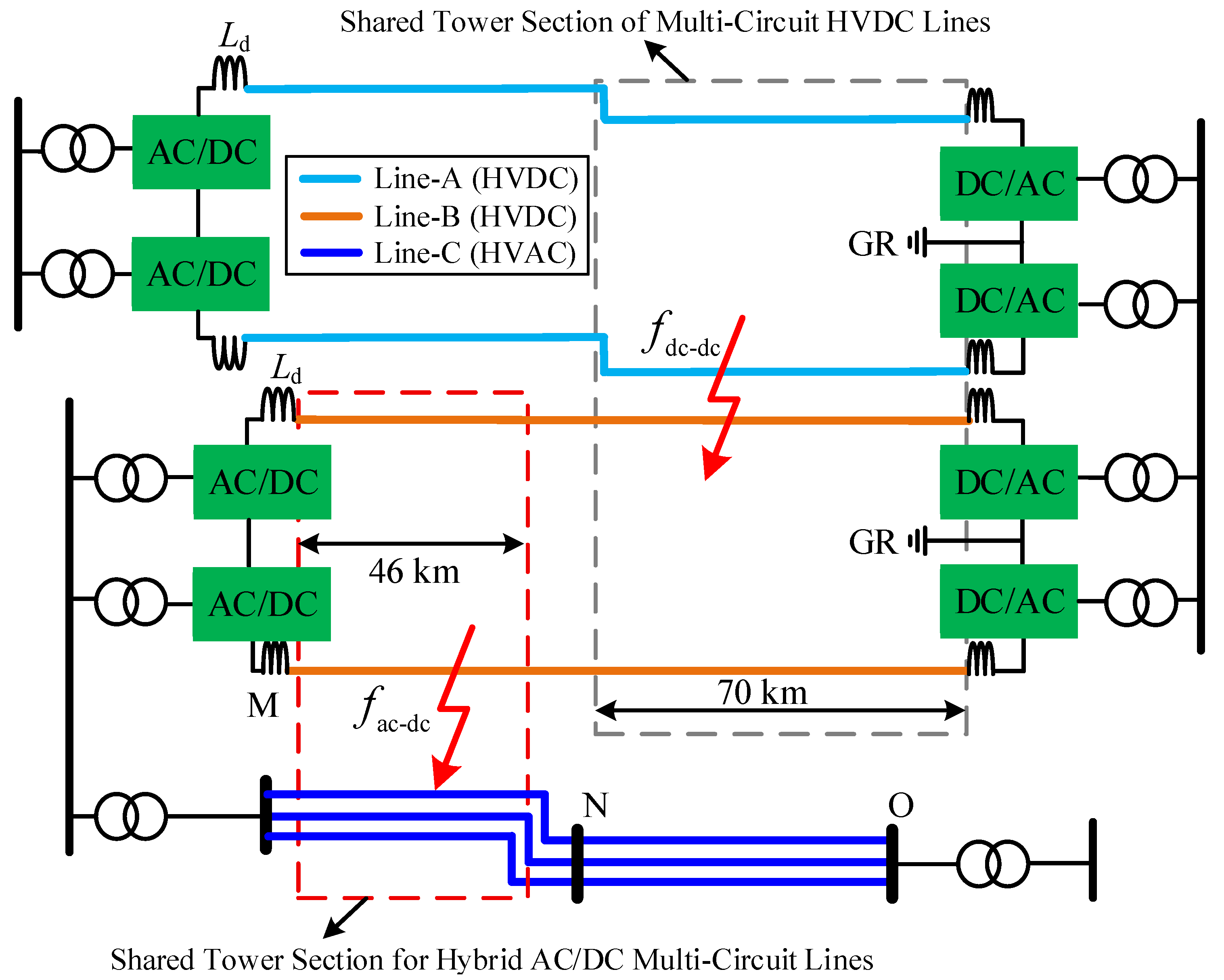







| AC System | DC System A | DC System B |
|---|---|---|
| UN = 500 kV (50 Hz) | UNA = ±200 kV | UNB = ±200 kV |
| ZTh(1) = 2.03 Ω | IDC = 2.5 kA | IDC = 1.9 kA |
| X/R = 9.23 | Ld = 150 mH | Ld = 150 mH |
| Solidly grounded | PDC = 500 MW | PDC = 380 MW |
| Length = 98 km | Length = 201 km | Length = 142 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, X.; Liu, Q.; Fu, L.; Yu, S.; Wang, W. Fault Ride-Through Optimization Scheme for Hybrid AC/DC Transmission Systems on the Same Tower. Sensors 2025, 25, 6216. https://doi.org/10.3390/s25196216
Chu X, Liu Q, Fu L, Yu S, Wang W. Fault Ride-Through Optimization Scheme for Hybrid AC/DC Transmission Systems on the Same Tower. Sensors. 2025; 25(19):6216. https://doi.org/10.3390/s25196216
Chicago/Turabian StyleChu, Xu, Qi Liu, Letian Fu, Shaoshuai Yu, and Weidong Wang. 2025. "Fault Ride-Through Optimization Scheme for Hybrid AC/DC Transmission Systems on the Same Tower" Sensors 25, no. 19: 6216. https://doi.org/10.3390/s25196216
APA StyleChu, X., Liu, Q., Fu, L., Yu, S., & Wang, W. (2025). Fault Ride-Through Optimization Scheme for Hybrid AC/DC Transmission Systems on the Same Tower. Sensors, 25(19), 6216. https://doi.org/10.3390/s25196216





