Error Correction in Bluetooth Low Energy via Neural Network with Reject Option
Abstract
1. Introduction
2. Preliminaries
2.1. Channel Fading and Equalization
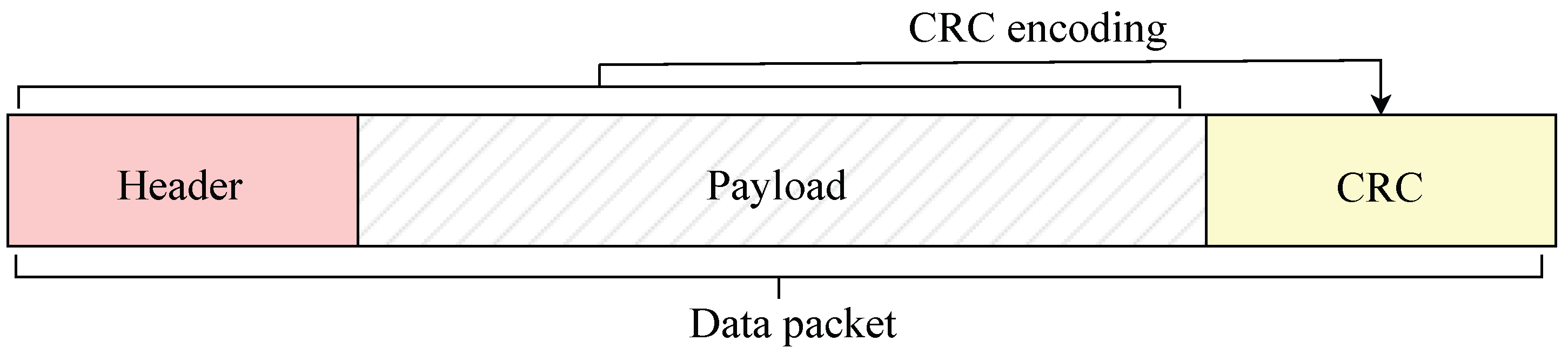
2.2. Cyclic Redundancy Check
2.3. Classification with Reject Option
2.4. Neural Networks
3. Proposed Method
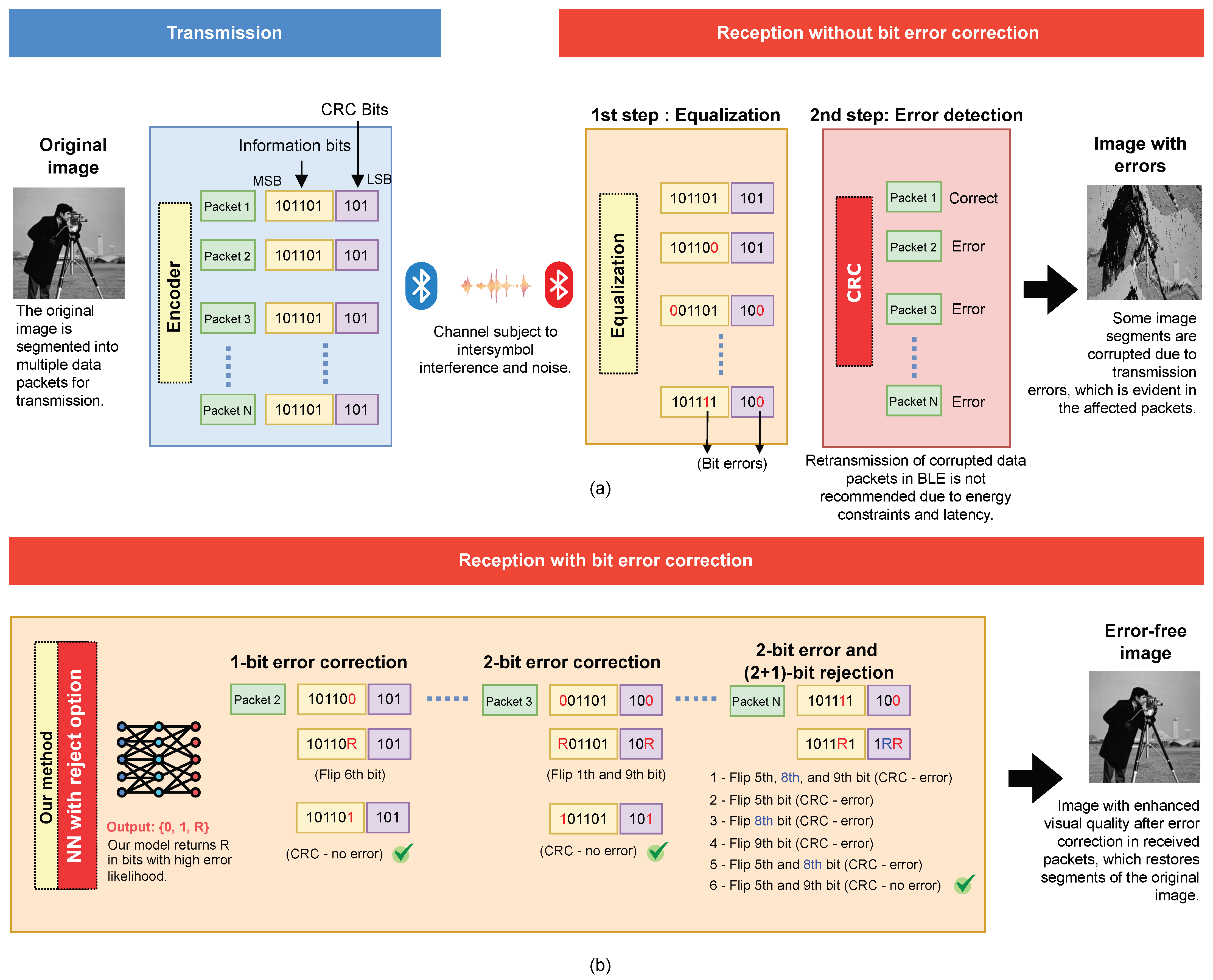
3.1. Data Modeling
3.2. Training a Neural Network with Reject Option
3.3. Prediction in a Neural Network with Reject Option
- I.
- , if the pattern is most likely to belong to class ;
- II.
- , if the pattern is most likely to belong to class ;
- III.
- , if neither class receives a sufficiently confident estimate to justify classification.
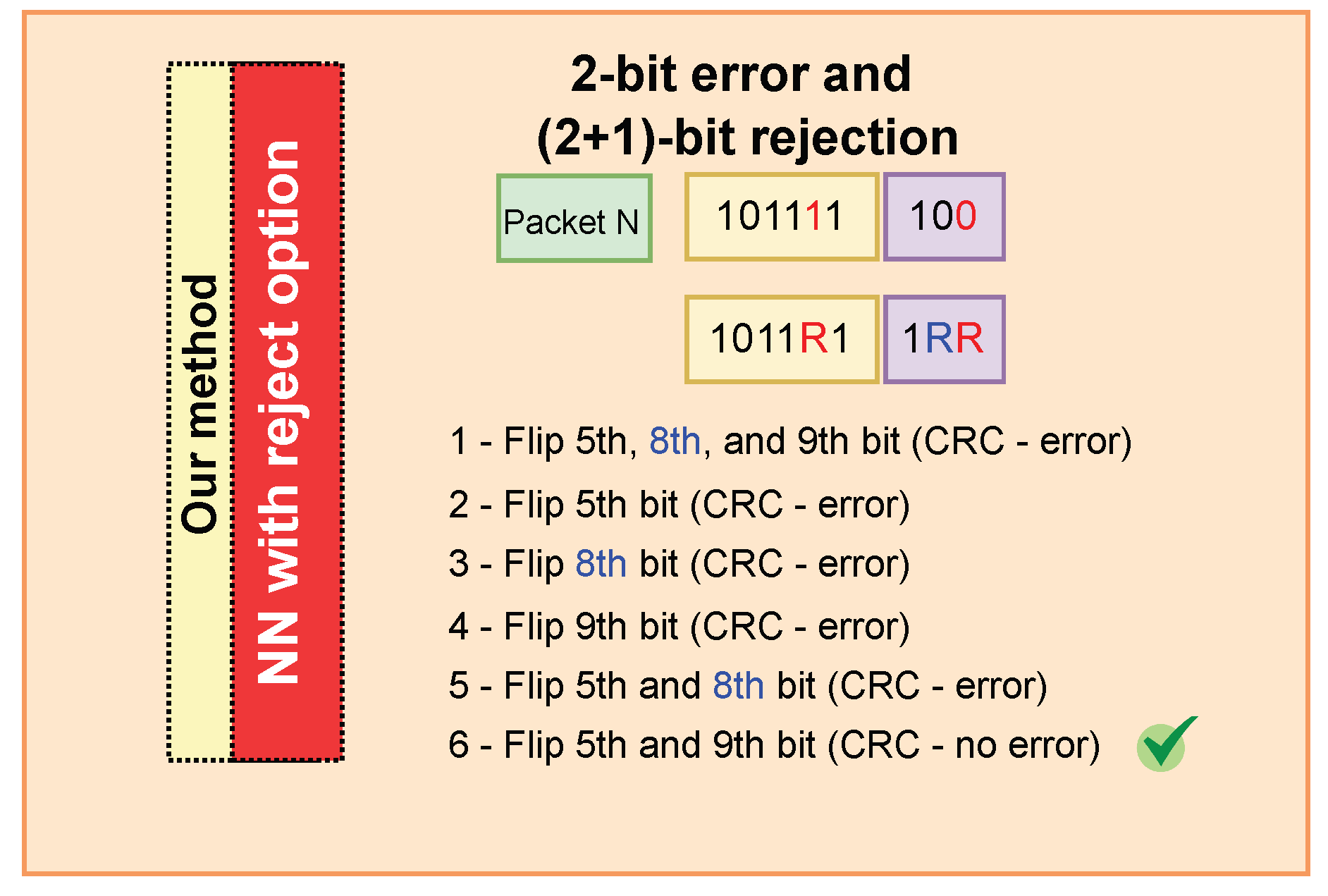
3.4. Error Detection and Correction Process
| Algorithm 1 Correcting bit errors in data packets with our approach. |
| Input: Packet bit sequence seq, rejected positions rejected_pos |
| Output: Correct error positions corrected_errors |
|
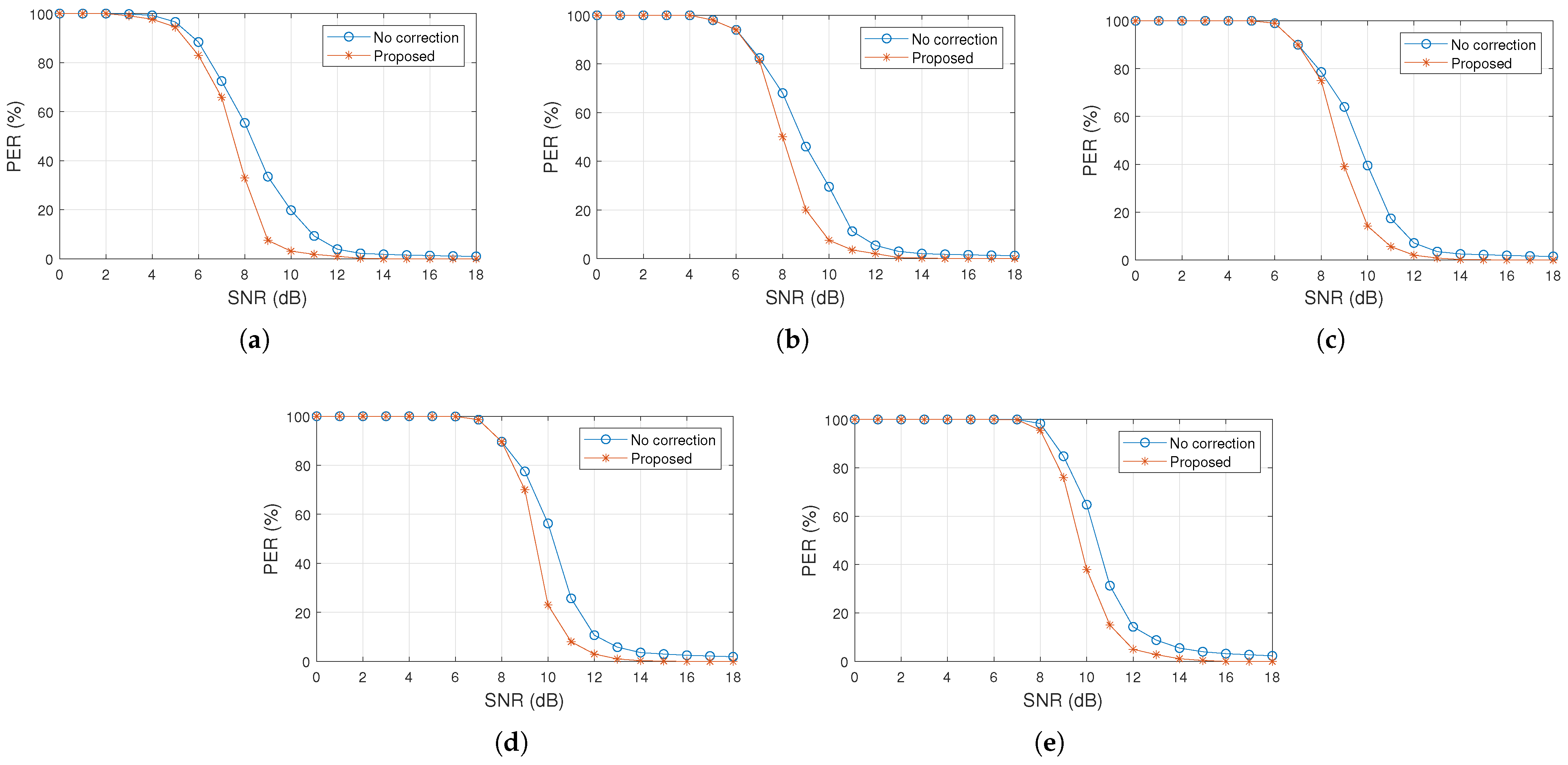
4. Experiments and Results
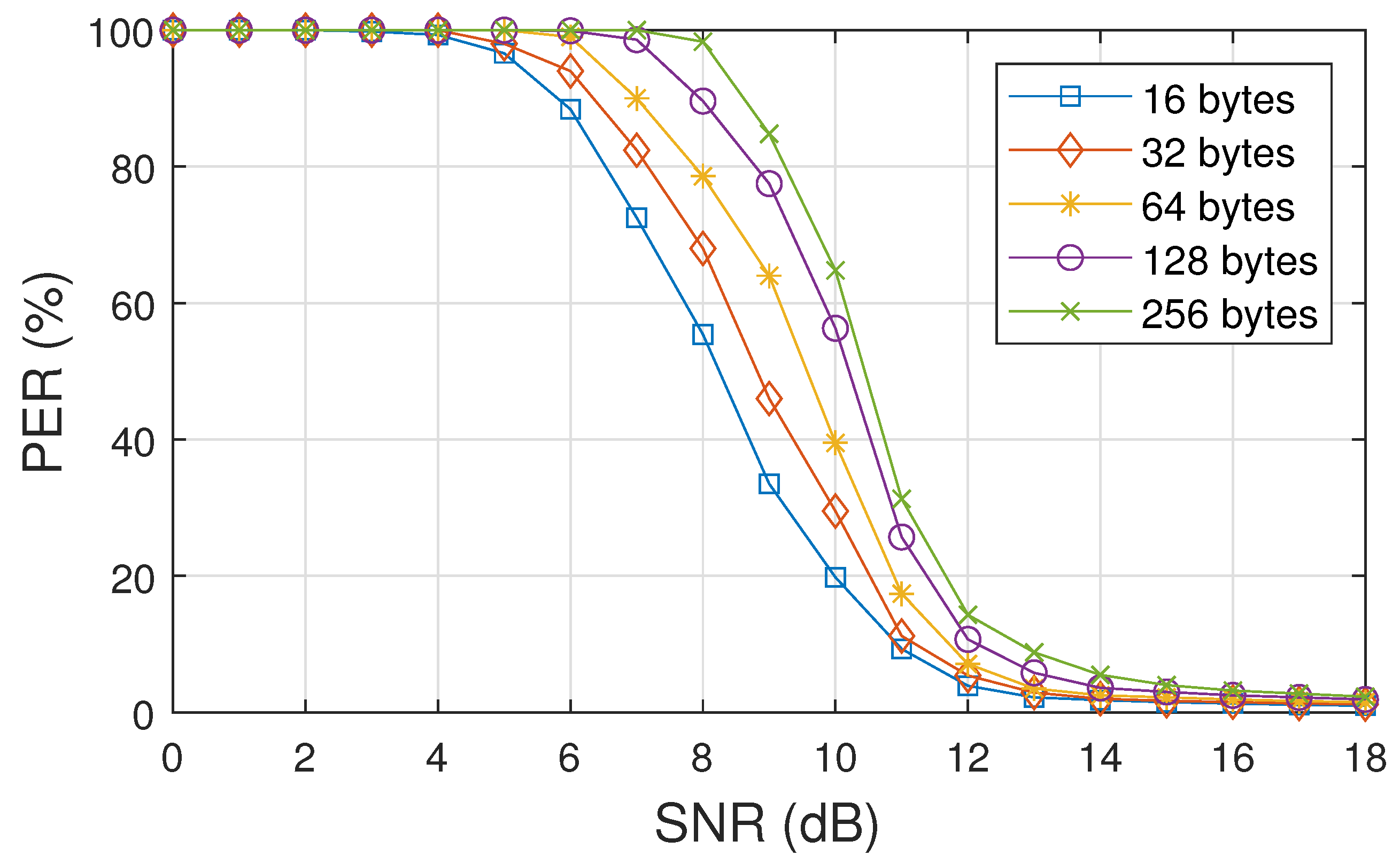
4.1. Error Correction in Data Packets
4.2. Image Bit Error Correction
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ye, H.; Li, G.Y. Initial Results on Deep Learning for Joint Channel Equalization and Decoding. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Tai, Y.; Guilloud, F.; Laot, C.; Le Bidan, R.; Wang, H. Joint Equalization and Decoding Scheme Using Modified Spinal Codes for Underwater Communications. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–6. [Google Scholar]
- Su, T.J.; Cheng, J.C.; Yu, C.J. An Adaptive Channel Equalizer Using Self-Adaptation Bacterial Foraging Optimization. Opt. Commun. 2010, 283, 3911–3916. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.L. Machine Learning for Joint Channel Equalization and Signal Detection. In Machine Learning for Future Wireless Communications; Wiley: Hoboken, NJ, USA, 2020; pp. 213–241. [Google Scholar]
- Alencar, A.S.C.; Neto, A.R.R.; Gomes, J.P.P. A New Pruning Method for Extreme Learning Machines via Genetic Algorithms. Appl. Soft Comput. 2016, 44, 101–107. [Google Scholar] [CrossRef]
- Alabady, S.A.; Salleh, M.F.M.; Al-Turjman, F. LCPC Error Correction Code for IoT Applications. Sustain. Cities Soc. 2018, 42, 663–673. [Google Scholar] [CrossRef]
- Carrasco, R.A.; Johnston, M. Non-Binary Error Control Coding for Wireless Communication and Data Storage; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Leiner, B.M.J. LDPC Codes—A Brief Tutorial. 2005. Available online: https://bernh.net/media/download/papers/ldpc.pdf (accessed on 5 September 2025).
- Ray, J.; Koopman, P. Efficient High Hamming Distance CRCs for Embedded Networks. In Proceedings of the International Conference on Dependable Systems and Networks (DSN’06), Philadelphia, PA, USA, 25–28 June 2006; pp. 3–12. [Google Scholar]
- Tsimbalo, E.; Fafoutis, X.; Piechocki, R.J. CRC Error Correction for Energy-Constrained Transmission. In Proceedings of the 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 430–434. [Google Scholar]
- Liu, X.; Wu, S.; Wang, Y.; Zhang, N.; Jiao, J.; Zhang, Q. Exploiting error-correction-CRC for polar SCL decoding: A deep learning-based approach. IEEE Trans. Cogn. Commun. Netw. 2019, 6, 817–828. [Google Scholar] [CrossRef]
- Gamelas Sousa, R.; Rocha Neto, A.R.; Cardoso, J.S.; Barreto, G.A. Robust Classification with Reject Option Using the Self-Organizing Map. Neural Comput. Appl. 2015, 26, 1603–1619. [Google Scholar] [CrossRef]
- Chow, C. On Optimum Recognition Error and Reject Tradeoff. IEEE Trans. Inf. Theory 1970, 16, 41–46. [Google Scholar] [CrossRef]
- Kompa, B.; Snoek, J.; Beam, A.L. Second Opinion Needed: Communicating Uncertainty in Medical Machine Learning. NPJ Digit. Med. 2021, 4, 4. [Google Scholar] [CrossRef]
- Condessa, F.; Bioucas-Dias, J.; Castro, C.A.; Ozolek, J.A.; Kovačević, J. Classification with Reject Option Using Contextual Information. In Proceedings of the 2013 IEEE 10th International Symposium on Biomedical Imaging, San Francisco, CA, USA, 7–11 April 2013; pp. 1340–1343. [Google Scholar] [CrossRef]
- da Rocha Neto, A.R.; Sousa, R.; Barreto, G.A.; Cardoso, J.S. Diagnostic of Pathology on the Vertebral Column with Embedded Reject Option. In Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis, Las Palmas de Gran Canaria, Spain, 8–10 June 2011; pp. 588–595. [Google Scholar] [CrossRef]
- Marinho, L.B.; Almeida, J.S.; Souza, J.W.M.; Albuquerque, V.H.C.; Rebouças Filho, P.P. A Novel Mobile Robot Localization Approach Based on Topological Maps Using Classification with Reject Option in Omnidirectional Images. Expert Syst. Appl. 2017, 72, 1–17. [Google Scholar] [CrossRef]
- Mesquita, D.P.P.; Rocha, L.S.; Gomes, J.P.P.; Neto, A.R.R. Classification with Reject Option for Software Defect Prediction. Appl. Soft Comput. 2016, 49, 1085–1093. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, R.; Han, F.; Wang, Z. Image Error Concealment Based on Deep Neural Network. Algorithms 2019, 12, 82. [Google Scholar] [CrossRef]
- Han, Y.-H.; Leou, J.-J. Detection and Correction of Transmission Errors in JPEG Images. IEEE Trans. Circuits Syst. Video Technol. 1998, 8, 221–231. [Google Scholar] [CrossRef]
- Boussard, V.; Coulombe, S.; Coudoux, F.X.; Corlay, P. Enhanced CRC-Based Correction of Multiple Errors with Candidate Validation. Signal Process. Image Commun. 2021, 99, 116475. [Google Scholar] [CrossRef]
- Tsimbalo, E.; Fafoutis, X.; Piechocki, R. Fix It, Don’t Bin It!—CRC Error Correction in Bluetooth Low Energy. In Proceedings of the 2015 IEEE 2nd World Forum on Internet of Things (WF-IoT), Milan, Italy, 14–16 December 2015; pp. 286–290. [Google Scholar]
- Tsimbalo, E.; Fafoutis, X.; Mellios, E.; Haghighi, M.; Tan, B.; Hilton, G.; Piechocki, R.; Craddock, I. Mitigating Packet Loss in Connectionless Bluetooth Low Energy. In Proceedings of the 2015 IEEE 2nd World Forum on Internet of Things (WF-IoT), Milan, Italy, 14–16 December 2015; pp. 291–296. [Google Scholar]
- Tsimbalo, E.; Fafoutis, X.; Piechocki, R.J. CRC Error Correction in IoT Applications. IEEE Trans. Ind. Inform. 2016, 13, 361–369. [Google Scholar] [CrossRef]
- Boussard, V.; Coulombe, S.; Coudoux, F.X.; Corlay, P. CRC-Based Correction of Multiple Errors Using an Optimized Lookup Table. IEEE Access 2022, 10, 23931–23947. [Google Scholar] [CrossRef]
- Boussard, V.; Coulombe, S.; Coudoux, F.X.; Corlay, P. Table-Free Multiple Bit-Error Correction Using the CRC Syndrome. IEEE Access 2020, 8, 102357–102372. [Google Scholar] [CrossRef]
- Shukla, S.; Bergmann, N.W. Single bit error correction implementation in CRC-16 on FPGA. In Proceedings of the 2004 IEEE International Conference on Field-Programmable Technology (IEEE Cat. No. 04EX921), Brisbane, Australia, 6–8 December 2004; pp. 319–322. [Google Scholar]
- Babaie, S.; Zadeh, A.K.; Es-hagi, S.H.; Navimipour, N.J. Double bits error correction using CRC method. In Proceedings of the 2009 Fifth International Conference on Semantics, Knowledge and Grid, Zhuhai, China, 12–14 October 2009; pp. 254–257. [Google Scholar]
- Zhang, G.; Heusdens, R.; Kleijn, W.B. Large scale LP decoding with low complexity. IEEE Commun. Lett. 2013, 17, 2152–2155. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Vasic, B. Iterative decoding of linear block codes: A parity-check orthogonalization approach. IEEE Trans. Inf. Theory 2005, 51, 3347–3353. [Google Scholar] [CrossRef]
- Malik, G.; Sappal, A.S. Adaptive Equalization Algorithms: An Overview. Int. J. Adv. Comput. Sci. Appl. 2011, 2, 3. [Google Scholar] [CrossRef]
- Huo, Y.; Li, X.; Wang, W.; Liu, D. High Performance Table-Based Architecture for Parallel CRC Calculation. In Proceedings of the 21st IEEE International Workshop on Local and Metropolitan Area Networks, Beijing, China, 22–24 April 2015; pp. 1–6. [Google Scholar]
- Hanczar, B.; Dougherty, E.R. Classification with reject option in gene expression data. Bioinformatics 2008, 24, 1889–1895. [Google Scholar] [CrossRef]
- Chow, C. An Optimum Character Recognition System Using Decision Functions. IRE Trans. Electron. Comput. 1957, 4, 247–254. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tran, V.-D. Computer vision based asphalt pavement segregation detection using image texture analysis integrated with extreme gradient boosting machine and deep convolutional neural networks. Measurement 2022, 196, 111207. [Google Scholar] [CrossRef]
- Reza, S.; Ferreira, M.C.; Machado, J.J.M.; Tavares, J.M.R.S. A customized residual neural network and bi-directional gated recurrent unit-based automatic speech recognition model. Expert Syst. Appl. 2023, 215, 119293. [Google Scholar] [CrossRef]
- Chen, T.-L.; Chen, J.C.; Chang, W.-H.; Tsai, W.; Shih, M.-C.; Nabila, A.W. Imbalanced prediction of emergency department admission using natural language processing and deep neural network. J. Biomed. Inform. 2022, 133, 104171. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Wu, K.; Zheng, G. Fixed-time neural network trajectory tracking control for the rigid-flexible coupled robotic mechanisms with large beam-deflections. Appl. Math. Model. 2023, 118, 665–691. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- MathWorks. End-to-End Bluetooth LE PHY Simulation with Multipath Fading Channel, RF Impairments, and Corrections. Available online: https://www.mathworks.com/help/bluetooth/ug/end-to-end-bluetooth-le-phy-simulation-with-multipath-fading-channel-rf-impairments-and-corrections.html (accessed on 5 May 2024).
- Soyjaudah, K.M.S.; Catherine, P.C.; Coonjah, I. Evaluation of UDP tunnel for data replication in data centers and cloud environment. In Proceedings of the 2016 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 29–30 April 2016; pp. 1217–1221. [Google Scholar]




| CRC | Value |
|---|---|
| CRC-4-ITU (4 bits) | |
| CRC-8-CCITT (8 bits) | |
| CRC-16-CCITT (16 bits) | |
| CRC-24-BLE (24 bits) |
| Technique | Description | Values |
|---|---|---|
| ELM | Number of neurons per hidden layer Activation function Number of patterns Executions Cross validation using the k-fold | 20:20:200 Sigmoid bits per dB 20 5 |
| Reject option | Rejection cost Decision threshold Maximum number of rejections | 0.04:0.04:0.48 0.00:0.01:0.50 6, 8, 10 |
| Packet Size (Bytes) | |||||
|---|---|---|---|---|---|
| Errors | 16 | 32 | 64 | 128 | 256 |
| 1 error | 98.1 | 96.9 | 95.8 | 94.1 | 93.6 |
| 2 errors | 68.7 | 64.9 | 61.7 | 55.1 | 54.3 |
| 3 errors | 29.7 | 28.5 | 27.2 | 25.8 | 25.1 |
| >3 errors | 1.9 | 1.3 | 0.9 | 0.2 | 0.2 |
| SNR Value | |||
|---|---|---|---|
| Errors | 11 dB | 10 dB | 9 dB |
| 1 error | 85.1 | 76.5 | 53.3 |
| 2 errors | 12.2 | 13.5 | 27.4 |
| 3 errors | 2.1 | 4.8 | 13.0 |
| >3 errors | 0.6 | 5.2 | 6.3 |
| Images | PS | SNR = 11 dB (n = 6) | SNR = 10 dB (n = 8) | SNR = 9 dB (n = 10) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ➀ | ➁ | ➂ | ➃ | ➀ | ➁ | ➂ | ➃ | ➀ | ➁ | ➂ | ➃ | ||
| Baboon | 8 Bytes | 0.1261 | 0.3102 | 0.8882 | 0.9990 | 0.0832 | 0.3538 | 0.5962 | 0.8401 | 0.0614 | 0.0601 | 0.0656 | 0.4762 |
| 21 Bytes | 0.1507 | 0.5326 | 0.2742 | 0.8220 | 0.0797 | 0.1870 | 0.2562 | 0.2805 | 0.0653 | 0.0648 | 0.0604 | 0.1184 | |
| 39 Bytes | 0.1352 | 0.1470 | 0.5465 | 0.4663 | 0.0856 | 0.1138 | 0.1388 | 0.1650 | 0.0725 | 0.0617 | 0.0760 | 0.0650 | |
| Barbara | 8 Bytes | 0.2084 | 0.8190 | 0.7520 | 0.9999 | 0.1383 | 0.6199 | 0.7092 | 0.9181 | 0.0714 | 0.0765 | 0.0729 | 0.4809 |
| 21 Bytes | 0.2193 | 0.6801 | 0.4486 | 0.7187 | 0.1254 | 0.3436 | 0.3132 | 0.6541 | 0.0650 | 0.0698 | 0.0767 | 0.2236 | |
| 39 Bytes | 0.2342 | 0.4137 | 0.4380 | 0.4585 | 0.1263 | 0.2304 | 0.2075 | 0.2850 | 0.0773 | 0.0748 | 0.0766 | 0.1081 | |
| Boat | 8 Bytes | 0.1964 | 0.3981 | 0.3880 | 0.8500 | 0.0780 | 0.2663 | 0.3634 | 0.5719 | 0.0421 | 0.0542 | 0.0384 | 0.4725 |
| 21 Bytes | 0.1925 | 0.3721 | 0.3241 | 0.6590 | 0.0718 | 0.3268 | 0.1600 | 0.3288 | 0.0495 | 0.0522 | 0.0483 | 0.1506 | |
| 39 Bytes | 0.1317 | 0.2326 | 0.3860 | 0.4725 | 0.0861 | 0.1615 | 0.1506 | 0.1486 | 0.0421 | 0.0448 | 0.0492 | 0.0718 | |
| Butterfly | 8 Bytes | 0.0862 | 0.4202 | 0.7263 | 0.9936 | 0.0560 | 0.2749 | 0.3315 | 0.3964 | 0.0326 | 0.0275 | 0.0233 | 0.4419 |
| 21 Bytes | 0.1104 | 0.5374 | 0.2425 | 0.6248 | 0.0412 | 0.1378 | 0.2483 | 0.1144 | 0.0326 | 0.0232 | 0.0272 | 0.0681 | |
| 39 Bytes | 0.0871 | 0.1265 | 0.1136 | 0.4715 | 0.0482 | 0.1082 | 0.0874 | 0.1039 | 0.0181 | 0.0218 | 0.0312 | 0.0373 | |
| Columbia | 8 Bytes | 0.2317 | 0.5526 | 0.5367 | 0.8234 | 0.1377 | 0.6539 | 0.7468 | 0.9250 | 0.0748 | 0.0852 | 0.0668 | 0.4919 |
| 21 Bytes | 0.2762 | 0.5798 | 0.6307 | 0.6459 | 0.1524 | 0.3216 | 0.5130 | 0.5023 | 0.0788 | 0.0758 | 0.0807 | 0.2893 | |
| 39 Bytes | 0.2623 | 0.4521 | 0.5452 | 0.6507 | 0.1628 | 0.2694 | 0.2114 | 0.2575 | 0.0716 | 0.0839 | 0.0933 | 0.0953 | |
| Cornfield | 8 Bytes | 0.2565 | 0.5752 | 0.6089 | 0.8798 | 0.1641 | 0.5057 | 0.5941 | 0.6282 | 0.0830 | 0.0839 | 0.0757 | 0.4674 |
| 21 Bytes | 0.2326 | 0.6290 | 0.5660 | 0.5081 | 0.1459 | 0.3947 | 0.3902 | 0.3813 | 0.0796 | 0.0786 | 0.0803 | 0.2411 | |
| 39 Bytes | 0.2868 | 0.4050 | 0.4005 | 0.5636 | 0.1507 | 0.2357 | 0.2467 | 0.3043 | 0.0727 | 0.0874 | 0.0873 | 0.1016 | |
| Couple | 8 Bytes | 0.2661 | 0.6622 | 0.5181 | 0.8359 | 0.1559 | 0.6995 | 0.5834 | 0.4792 | 0.0886 | 0.1002 | 0.0751 | 0.4261 |
| 21 Bytes | 0.2924 | 0.4469 | 0.4152 | 0.5649 | 0.1796 | 0.4617 | 0.3780 | 0.4520 | 0.0761 | 0.0837 | 0.0826 | 0.2641 | |
| 39 Bytes | 0.3097 | 0.3608 | 0.4628 | 0.4155 | 0.1484 | 0.2729 | 0.2603 | 0.3494 | 0.0855 | 0.0819 | 0.0818 | 0.1165 | |
| Goldhill | 8 Bytes | 0.1770 | 0.3577 | 0.7885 | 0.9975 | 0.1320 | 0.4677 | 0.8129 | 0.7406 | 0.0688 | 0.0645 | 0.0632 | 0.4471 |
| 21 Bytes | 0.2087 | 0.4692 | 0.4653 | 0.6051 | 0.1161 | 0.2384 | 0.2247 | 0.4066 | 0.0516 | 0.0644 | 0.0519 | 0.1199 | |
| 39 Bytes | 0.2113 | 0.5291 | 0.4699 | 0.4838 | 0.1003 | 0.2627 | 0.1787 | 0.2603 | 0.0556 | 0.0723 | 0.0707 | 0.0905 | |
| Hat | 8 Bytes | 0.3534 | 0.5973 | 0.7636 | 0.9320 | 0.1669 | 0.6700 | 0.6065 | 0.5173 | 0.0853 | 0.0817 | 0.0909 | 0.4524 |
| 21 Bytes | 0.2739 | 0.5454 | 0.6903 | 0.7629 | 0.1543 | 0.4427 | 0.4034 | 0.5824 | 0.0871 | 0.0892 | 0.1033 | 0.2449 | |
| 39 Bytes | 0.2649 | 0.4663 | 0.5504 | 0.6013 | 0.1660 | 0.2473 | 0.2616 | 0.3455 | 0.0883 | 0.0778 | 0.0904 | 0.1279 | |
| Man | 8 Bytes | 0.1000 | 0.3324 | 0.6541 | 0.5659 | 0.0475 | 0.5917 | 0.3545 | 0.5219 | 0.0275 | 0.0304 | 0.0459 | 0.2790 |
| 21 Bytes | 0.0768 | 0.4078 | 0.5683 | 0.6442 | 0.0498 | 0.3352 | 0.1799 | 0.1657 | 0.0394 | 0.0346 | 0.0316 | 0.0783 | |
| 39 Bytes | 0.1091 | 0.1971 | 0.3029 | 0.2199 | 0.0505 | 0.0908 | 0.0633 | 0.1875 | 0.0417 | 0.0438 | 0.0385 | 0.0505 | |
| Peppers | 8 Bytes | 0.2850 | 0.5240 | 0.6449 | 0.9992 | 0.1354 | 0.7675 | 0.6455 | 0.6607 | 0.0420 | 0.0391 | 0.0426 | 0.4860 |
| 21 Bytes | 0.2786 | 0.5673 | 0.6397 | 0.6319 | 0.1394 | 0.4656 | 0.3313 | 0.3946 | 0.0540 | 0.0386 | 0.0391 | 0.1070 | |
| 39 Bytes | 0.2586 | 0.4172 | 0.4331 | 0.4764 | 0.0851 | 0.3198 | 0.1803 | 0.3434 | 0.0364 | 0.0440 | 0.0352 | 0.0585 | |
| Cameraman | 8 Bytes | 0.2867 | 0.6703 | 0.7991 | 0.7793 | 0.1434 | 0.6366 | 0.5447 | 0.6796 | 0.0592 | 0.0677 | 0.0680 | 0.5758 |
| 21 Bytes | 0.2915 | 0.6985 | 0.5789 | 0.6327 | 0.1565 | 0.4042 | 0.3984 | 0.5724 | 0.0641 | 0.0605 | 0.0676 | 0.2150 | |
| 39 Bytes | 0.3024 | 0.5407 | 0.5041 | 0.4910 | 0.1246 | 0.2387 | 0.2744 | 0.3620 | 0.0605 | 0.0567 | 0.0542 | 0.0988 | |
| Tower | 8 Bytes | 0.2554 | 0.4919 | 0.7859 | 0.7422 | 0.1331 | 0.5699 | 0.8024 | 0.7233 | 0.0617 | 0.0741 | 0.0672 | 0.5150 |
| 21 Bytes | 0.2752 | 0.7309 | 0.4984 | 0.6642 | 0.1651 | 0.4337 | 0.4135 | 0.5124 | 0.0602 | 0.0617 | 0.0717 | 0.2083 | |
| 39 Bytes | 0.2496 | 0.4767 | 0.4930 | 0.5897 | 0.1273 | 0.2484 | 0.2739 | 0.3358 | 0.0665 | 0.0672 | 0.0653 | 0.1035 | |
| Average | 8 Bytes | 0.2176 | 0.5162 | 0.6811 | 0.8767 | 0.1208 | 0.5445 | 0.5916 | 0.6617 | 0.0615 | 0.0650 | 0.0613 | 0.4624 |
| 21 Bytes | 0.2214 | 0.5536 | 0.4879 | 0.6526 | 0.1213 | 0.3456 | 0.3239 | 0.4113 | 0.0618 | 0.0613 | 0.0632 | 0.1792 | |
| 39 Bytes | 0.2187 | 0.3665 | 0.4343 | 0.4892 | 0.1125 | 0.2154 | 0.1949 | 0.2652 | 0.0607 | 0.0629 | 0.0654 | 0.0865 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, W.D.; Marinho, F.P.; de Almeida, A.L.F.; Rocha Neto, A.R. Error Correction in Bluetooth Low Energy via Neural Network with Reject Option. Sensors 2025, 25, 6191. https://doi.org/10.3390/s25196191
Almeida WD, Marinho FP, de Almeida ALF, Rocha Neto AR. Error Correction in Bluetooth Low Energy via Neural Network with Reject Option. Sensors. 2025; 25(19):6191. https://doi.org/10.3390/s25196191
Chicago/Turabian StyleAlmeida, Wellington D., Felipe P. Marinho, André L. F. de Almeida, and Ajalmar R. Rocha Neto. 2025. "Error Correction in Bluetooth Low Energy via Neural Network with Reject Option" Sensors 25, no. 19: 6191. https://doi.org/10.3390/s25196191
APA StyleAlmeida, W. D., Marinho, F. P., de Almeida, A. L. F., & Rocha Neto, A. R. (2025). Error Correction in Bluetooth Low Energy via Neural Network with Reject Option. Sensors, 25(19), 6191. https://doi.org/10.3390/s25196191






