Research on Ultrasonic Focusing Stacked Transducers for Composite
Abstract
1. Introduction
1.1. Purpose and Significance
1.2. Resonance Frequency
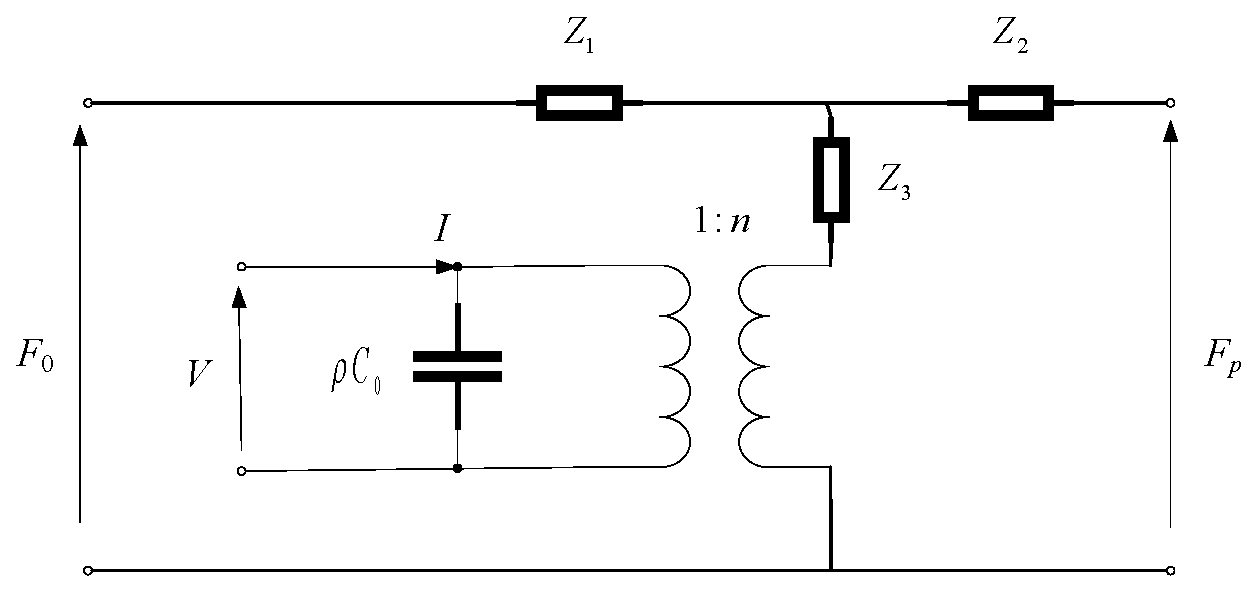
2. Design of Ultrasonic Focusing Transducer Scheme Based on Laminated Structure
2.1. The Structural Design of the Transducer
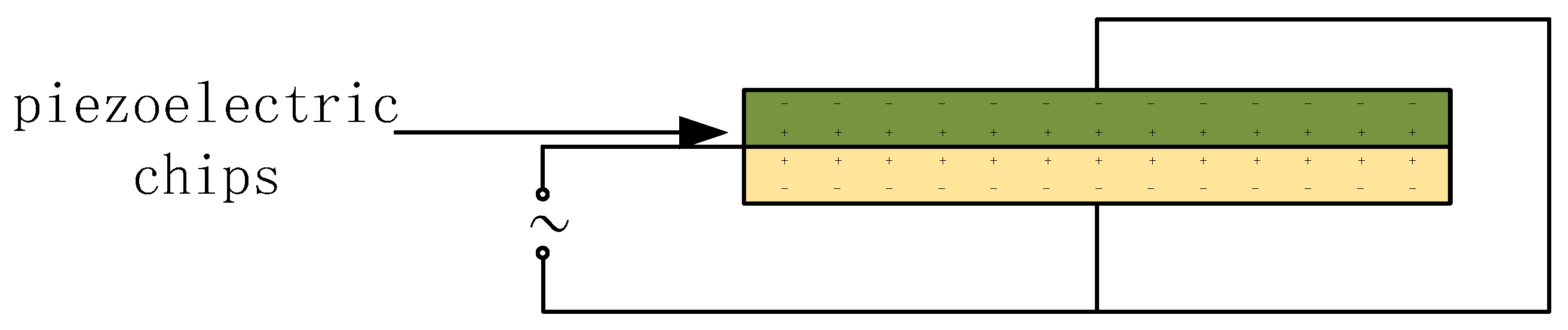
2.2. The Material of the Transducer
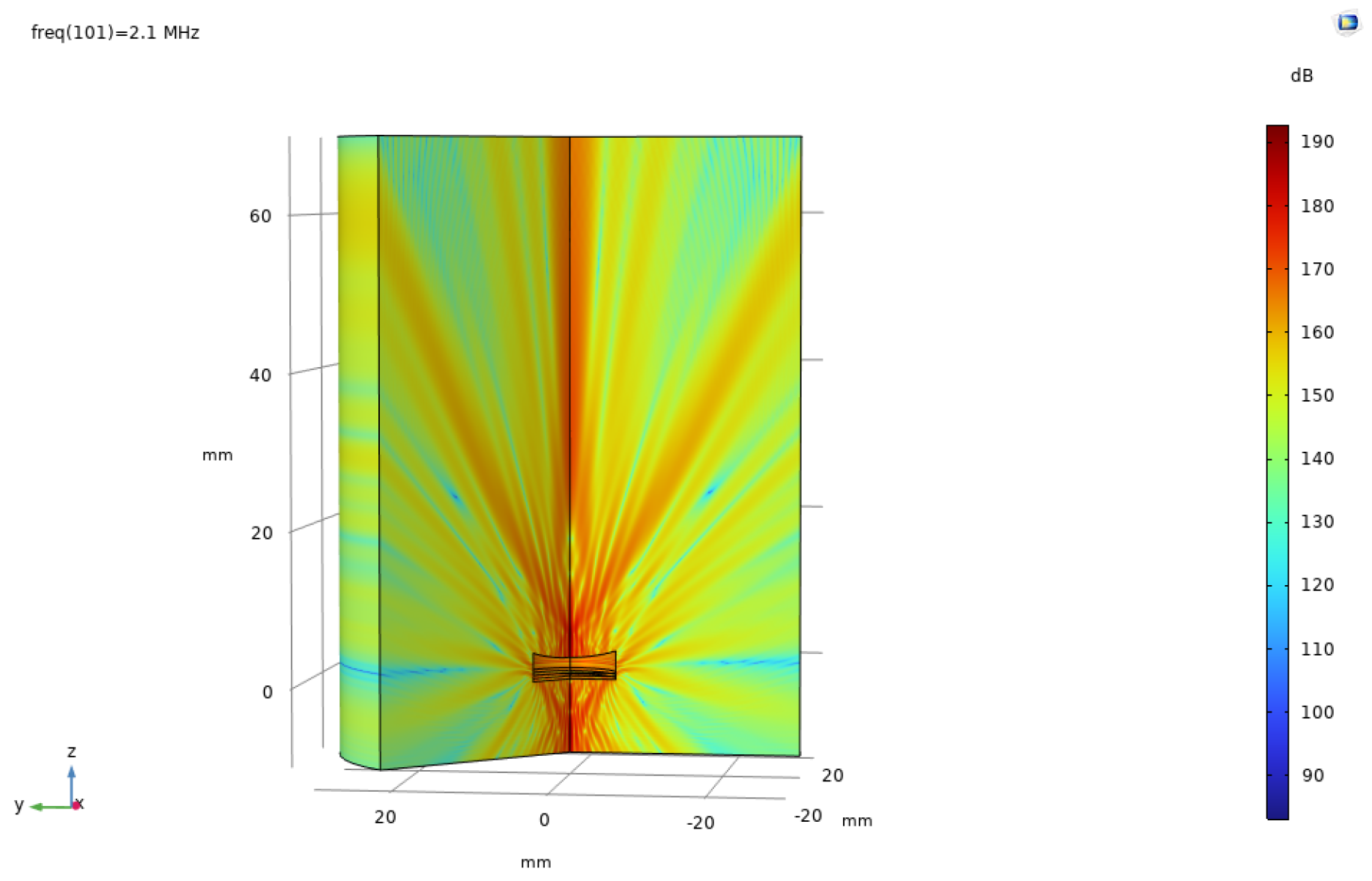
3. Simulation Analysis of Focused Laminated Transducers
4. Preparation and Performance Testing of Sensors
4.1. Electrode Wire Connection
4.2. Preparation of the Matching Layer
4.3. Preparation of Backing Layer
4.4. Acrylic Lens
4.5. Carbon Fiber Test Block
4.6. Testing Equipment
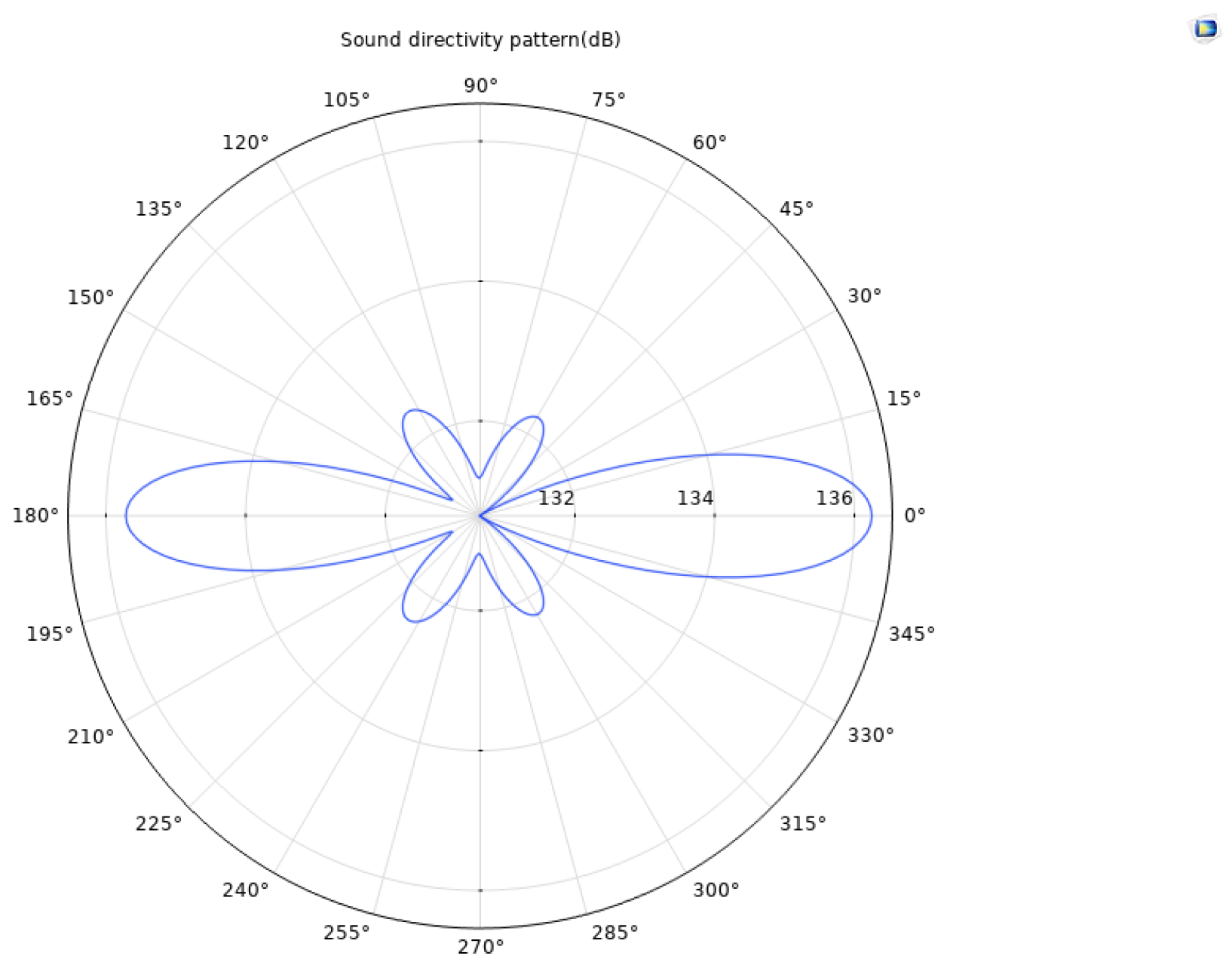
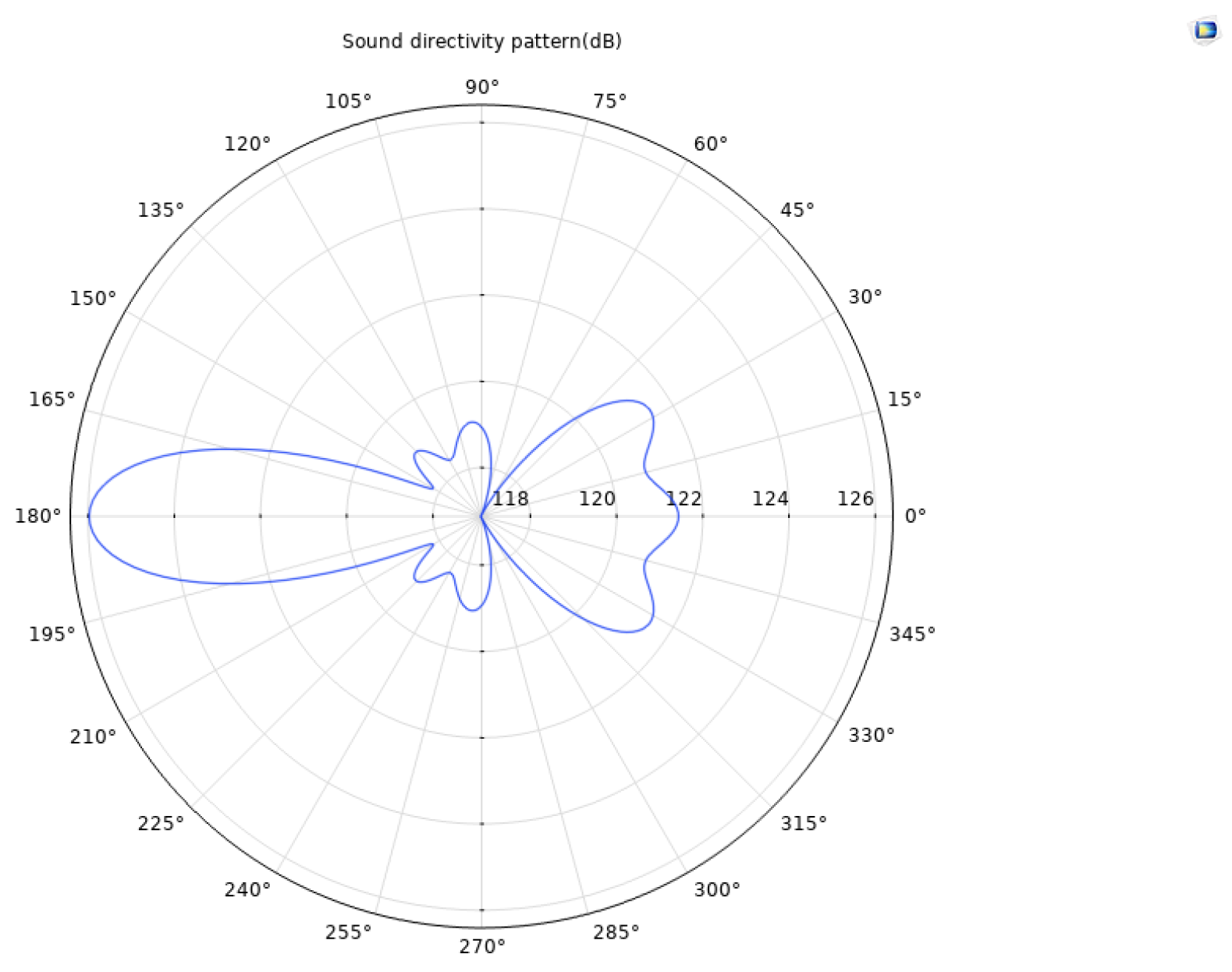
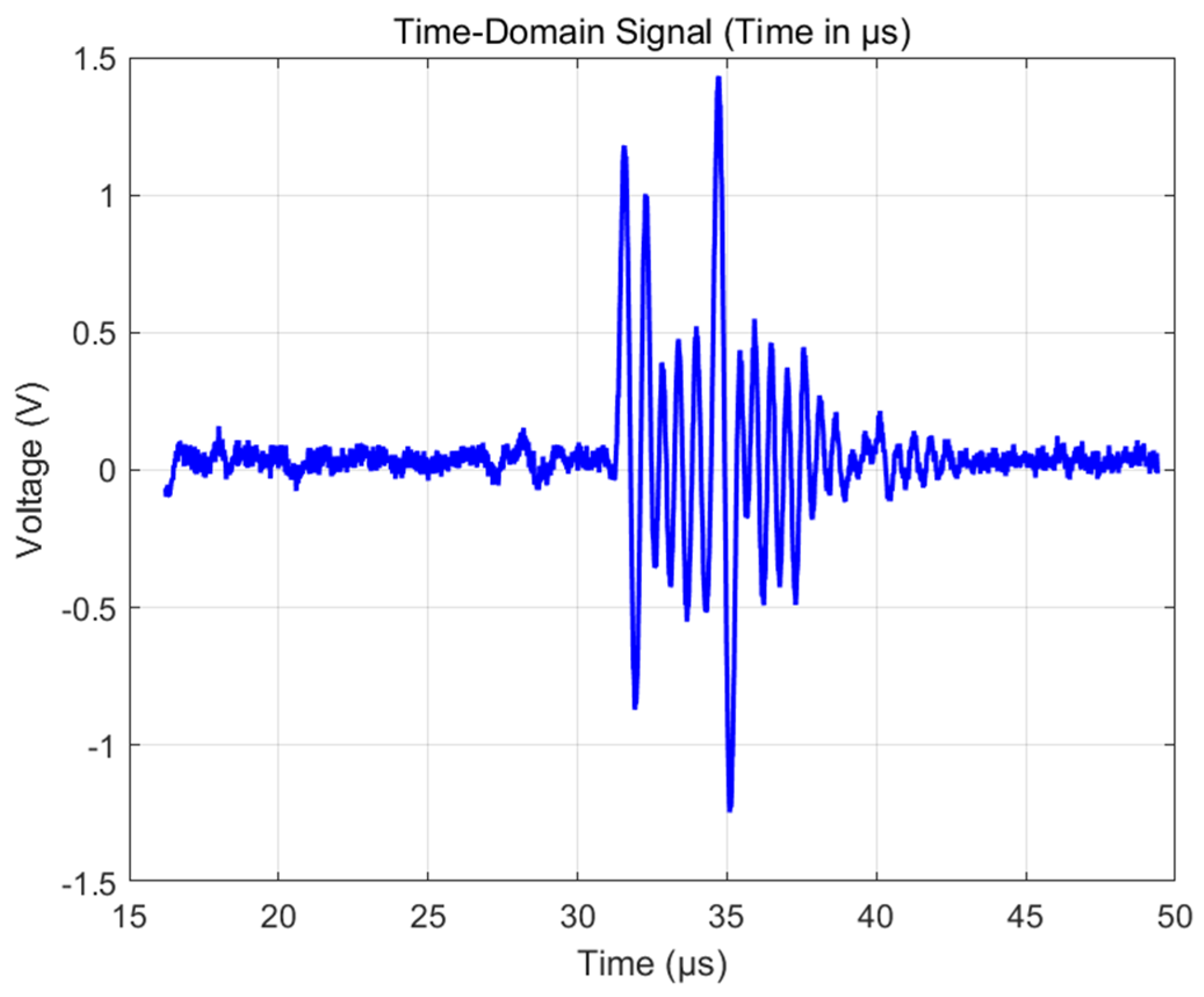
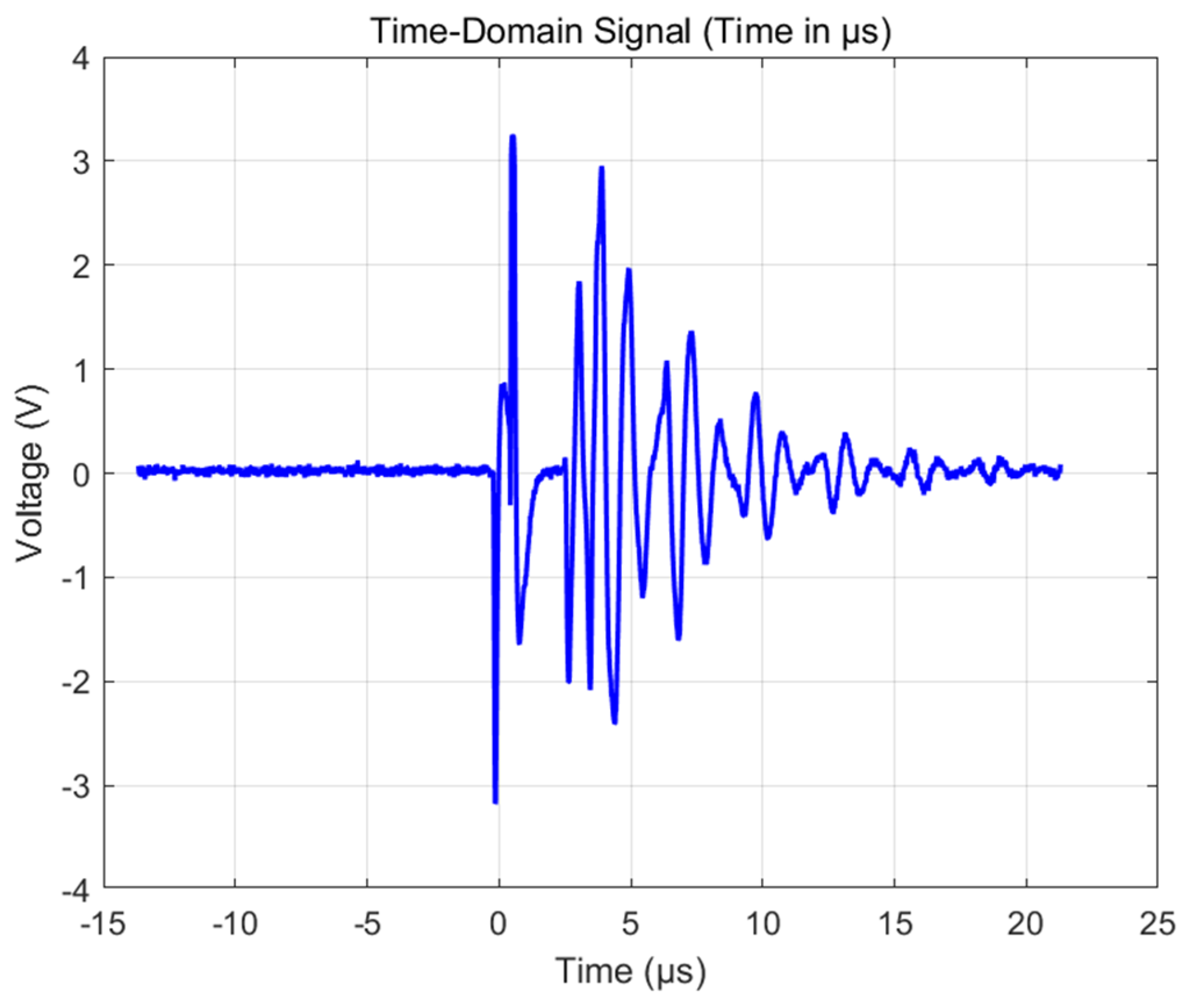
4.7. Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jung, S.; Ghim, H.D.; Lee, D.Y.; Yoo, S.H. Synergetic effect of cross-linking and interfacial interaction in carbon fiber reinforced thermoplastic to enhance its tensile strength by electron-beam irradiation. Carbon Lett. 2020, 30, 165–175. [Google Scholar] [CrossRef]
- Firmo, J.P.; Correia, J.R.; França, P. Fire behaviour of reinforced concrete beams strengthened with CFRP laminates: Protection systems with insulation of the anchorage zones. Compos. Part B Eng. 2012, 43, 1545–1556. [Google Scholar] [CrossRef]
- Hegde, S.; Shenoy, B.S.; Chethan, K.N. Review on carbon fiber-reinforced polymer (CFRP) and their mechanical performance. Mater. Today Proc. 2019, 19, 658–662. [Google Scholar] [CrossRef]
- Kishi, H.; Nakao, N.; Kuwashiro, S.; Matsuda, S. Carbon fiber-reinforced thermoplastic composites from acrylic polymer matrices: Interfacial adhesion and physical properties. Express Polym. Lett. 2017, 11, 334–342. [Google Scholar] [CrossRef]
- Li, F.; Hua, Y.; Qu, C.B.; Ji, J.H.; Li, Y.Q.; Hu, N.; Fu, S.Y. Effectively enhanced mechanical properties of injection molded short carbon fiber-reinforced polyethersulfone composites by phenol-formaldehyde resin sizing. Compos. Part B Eng. 2018, 139, 216–226. [Google Scholar] [CrossRef]
- Pathak, A.K.; Borah, M.; Gupta, A.; Yokozeki, T.; Dhakate, S.R. Improved mechanical properties of carbon fiber/graphene oxide-epoxy hybrid composites. Compos. Sci. Technol. 2016, 135, 28–38. [Google Scholar] [CrossRef]
- Kwon, D.J.; Park, S.M.; Kwon, I.J.; Park, J.M.; Jeong, E. Improvement of interlaminar properties of carbon fiber-reinforced epoxy composites using aluminum trihydroxide. Carbon Lett. 2019, 29, 183–191. [Google Scholar] [CrossRef]
- Torokhov, V.G.; Chukov, D.I.; Tcherdyntsev, V.V.; Sherif, G.; Zadorozhnyy, M.Y.; Stepashkin, A.A.; Larin, I.I.; Medvedeva, E.V. Mechanical and Thermophysical Properties of Carbon Fiber-Reinforced Polyethersulfone. Polymers 2022, 14, 2956. [Google Scholar] [CrossRef]
- Gao, Z.Q.; Liu, B.; Bai, Y.P. Processing and Molding Technology of Carbon Fiber Reinforced Composites. Plast. Addit. 2025, 77–81. [Google Scholar] [CrossRef]
- Sayam, A.; Rahman, A.N.M.M.; Rahman, M.S.; Smriti, S.A.; Ahmed, F.; Rabbi, M.F.; Hossain, M.; Faruque, O. A review on carbon fiber-reinforced hierarchical composites: Mechanical performance, manufacturing process, structural applications and allied challenges. Carbon Lett. 2022, 32, 1173–1205. [Google Scholar] [CrossRef]
- Ciecieląg, K.; Kęcik, K.; Skoczylas, A.; Matuszak, J.; Korzec, I.; Zaleski, R. Non-Destructive Detection of Real Defects in Polymer Composites by Ultrasonic Testing and Recurrence Analysis. Materials 2022, 15, 7335. [Google Scholar] [CrossRef]
- Gholizadeh, S. A Review of Non-Destructive Testing Methods of Composite Materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Rojek, M.; Stabik, J.; Wróbel, G. Ultrasonic Methods in Diagnostics of Epoxy-Glass Composites. J. Mater. Process. Technol. 2005, 162–163, 121–126. [Google Scholar] [CrossRef]
- Kersemans, M.; De Baere, I.; Degrieck, J.; Van Den Abeele, K.; Pyl, L.; Zastavnik, F.; Sol, H.; Van Paepegem, W. Nondestructive Damage Assessment in Fiber Reinforced Composites with the Pulsed Ultrasonic Polar Scan. Polym. Test. 2014, 34, 85–96. [Google Scholar] [CrossRef]
- Miao, X.L.; Zhang, X.Y. Overview of non-destructive testing of composite materials. In Proceedings of the 2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; pp. 166–169. [Google Scholar] [CrossRef]
- Yuan, Y. Research on Internal Defect Detection Methods of Carbon Fiber Composites. Master’s Thesis, Shaoxing University, Shaoxing, China, 2021. [Google Scholar] [CrossRef]
- Han, H.S.; Fu, T.H.; Wang, W.G.; Bai, J.P. Application and Development of Nondestructive Testing Technology for Advanced Aeronautical Composites. In Proceedings of the 7th China Aeronautical Science and Technology Conference, Xiamen, China, 24–26 October 2025; pp. 1095–1107. [Google Scholar] [CrossRef]
- Guo, W.; Xie, S.; Du, Y.; Chen, H.E.; Chen, Z.; Takagi, T.; Uchimoto, T. A Numerical Simulation Method for High-Frequency Eddy Current Testing Considering Displacement Current Effect. IEEE Trans. Magn. 2024, 60, 1–4. [Google Scholar] [CrossRef]
- Huang, M.; Wang, J.; Zhou, W.; Zhang, P.F.; Zhao, R.Y.; Liu, R. Eddy Current Testing and Finite Element Simulation Research on Surface Defects of Unidirectional CFRP. Electron. Meas. Technol. 2023, 46, 182–187. [Google Scholar] [CrossRef]
- Sun, Y.; Quan, Y.; Fei, C.; Xue, X.; Zhang, J.; Wang, Y.; Sun, X.; Li, Z.; Zhao, T.; Xing, G.; et al. Ultrasonic Flexible Array for Non-Destructive Testing of Complex Curved Surfaces. Ceram. Int. 2024, 50, 51979–51986. [Google Scholar] [CrossRef]
- Harzallah, S.; Benhadda, N. New Approach for Determining the Fracture Parameters by Electromagnetic-Mechanical Coupling. Theor. Appl. Fract. Mech. 2024, 131, 104381. [Google Scholar] [CrossRef]
- Mouritz, A.P. Ultrasonic and Interlaminar Properties of Highly Porous Composites. J. Compos. Mater. 2000, 34, 218–239. [Google Scholar] [CrossRef]
- Kim, H.J.; Hong, C.S. Buckling and Postbuckling Behavior of Composite Laminates with a Delamination. Compos. Sci. Technol. 1997, 57, 557–564. [Google Scholar] [CrossRef]
- Meng, X.D.; Lin, S.Y. Analysis of a Cascaded Piezoelectric Ultrasonic Transducer with Three Sets of Piezoelectric Ceramic Stacks. Sensors 2019, 19, 580. [Google Scholar] [CrossRef]
- Wu, S.R.; Xie, Y.H.; Bai, F.S.; Duo, T. Optimal design and experimental study on a novel relaxor ferroelectric single crystal transducer based on face shear vibration mode. Ultrasonics 2025, 156, 107763. [Google Scholar] [CrossRef] [PubMed]
- Zang, X.L.; Xu, Z.D.; Lu, H.F. Stacked piezoelectric transducer with time-delay layer for unidirectional SH0 guided wave excitation and reception. Sens. Actuators A Phys. 2025, 394, 116898. [Google Scholar] [CrossRef]
- Wen, S.H.; Xu, L.; Gong, T.; Zhang, H.D.; Liang, Z.F.; Yao, L. Longitudinal-flexural composite axe-shaped sandwich piezoelectric ultrasonic transducer designed based on the principle of acoustic black hole. Appl. Acoust. 2025, 239, 110826. [Google Scholar] [CrossRef]
- Luan, G.D.; Zhang, J.Z.; Wang, R.Q. Piezoelectric Transducer and Transducer Array; Peking University Press: Beijing, China, 2005; pp. 146–156. [Google Scholar]
- Yang, S.; Song, W.; Chen, Y.; Yang, L.; Wang, M.; Lian, Y.; Liu, K. An Ultrasonic Laminated Transducer for Viscoelastic Media Detection. Sensors 2021, 21, 7188. [Google Scholar] [CrossRef]
- GB/T 27664.2-2011; Non-destructive testing—Characterization and verification of ultrasonic test equipment—Part 2: Probes. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Standardization Administration of China: Beijing, China, 30 December 2011.







| Parameter | PT |
|---|---|
| d33 (×10−12C/N) | 352 |
| g33 (×10−3m2/C) | 18.7 |
| Kt (×10−2) | 53 |
| Y33E (×1010N/m2) | 5.9 |
| Tc (°C) | 260 |
| ρ (g/cm3) | 7.45 |
| σ | 0.32 |
| Qm | 65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bo, Y.; Li, J.; Yang, S.; Zhou, C.; Tian, Y. Research on Ultrasonic Focusing Stacked Transducers for Composite. Sensors 2025, 25, 6179. https://doi.org/10.3390/s25196179
Bo Y, Li J, Yang S, Zhou C, Tian Y. Research on Ultrasonic Focusing Stacked Transducers for Composite. Sensors. 2025; 25(19):6179. https://doi.org/10.3390/s25196179
Chicago/Turabian StyleBo, Yi, Jie Li, Shunmin Yang, Chenju Zhou, and Yutao Tian. 2025. "Research on Ultrasonic Focusing Stacked Transducers for Composite" Sensors 25, no. 19: 6179. https://doi.org/10.3390/s25196179
APA StyleBo, Y., Li, J., Yang, S., Zhou, C., & Tian, Y. (2025). Research on Ultrasonic Focusing Stacked Transducers for Composite. Sensors, 25(19), 6179. https://doi.org/10.3390/s25196179






