Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review
Abstract
1. Introduction
2. Overview of Machine Learning
2.1. Terminology and Definitions
2.2. Models and Algorithms
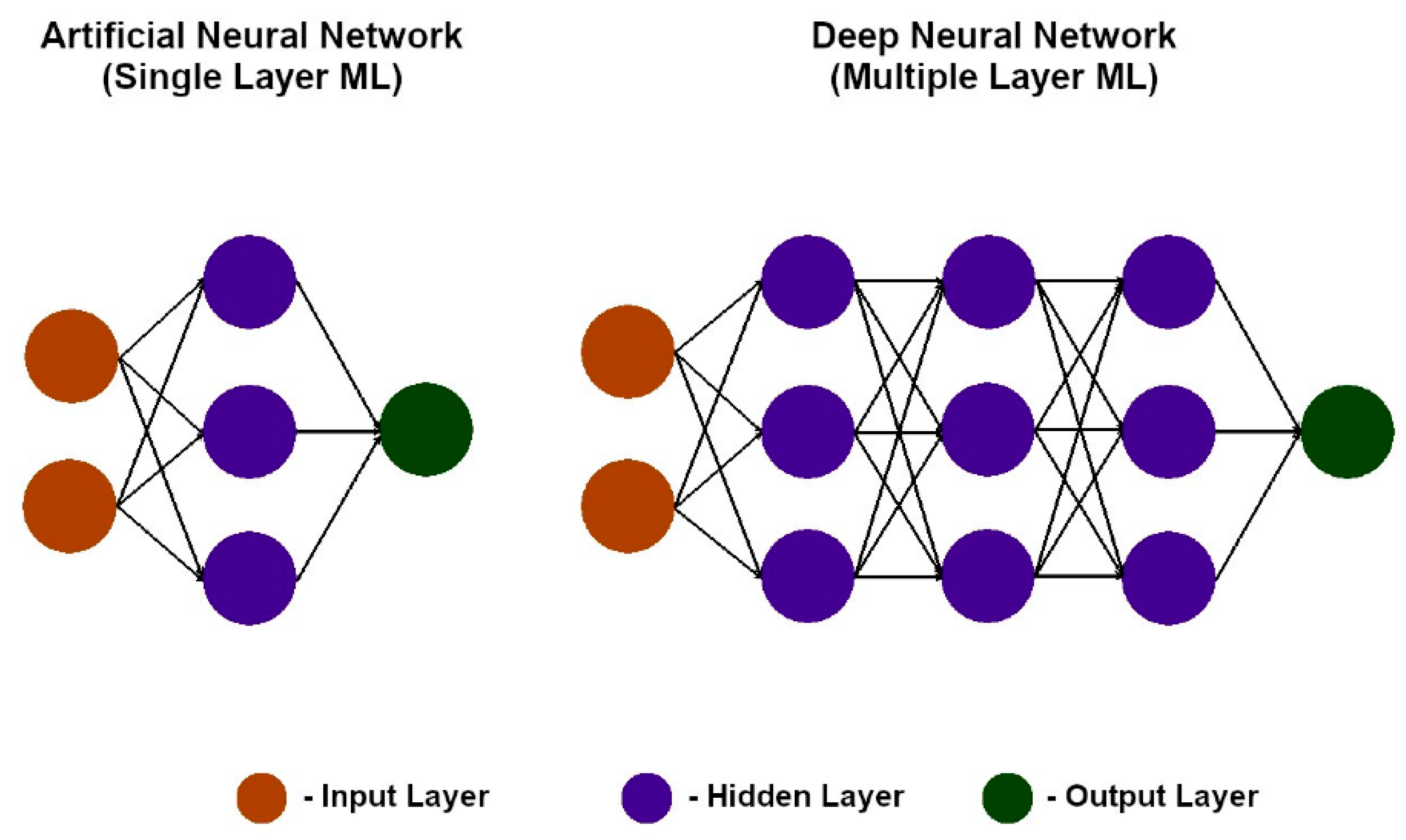


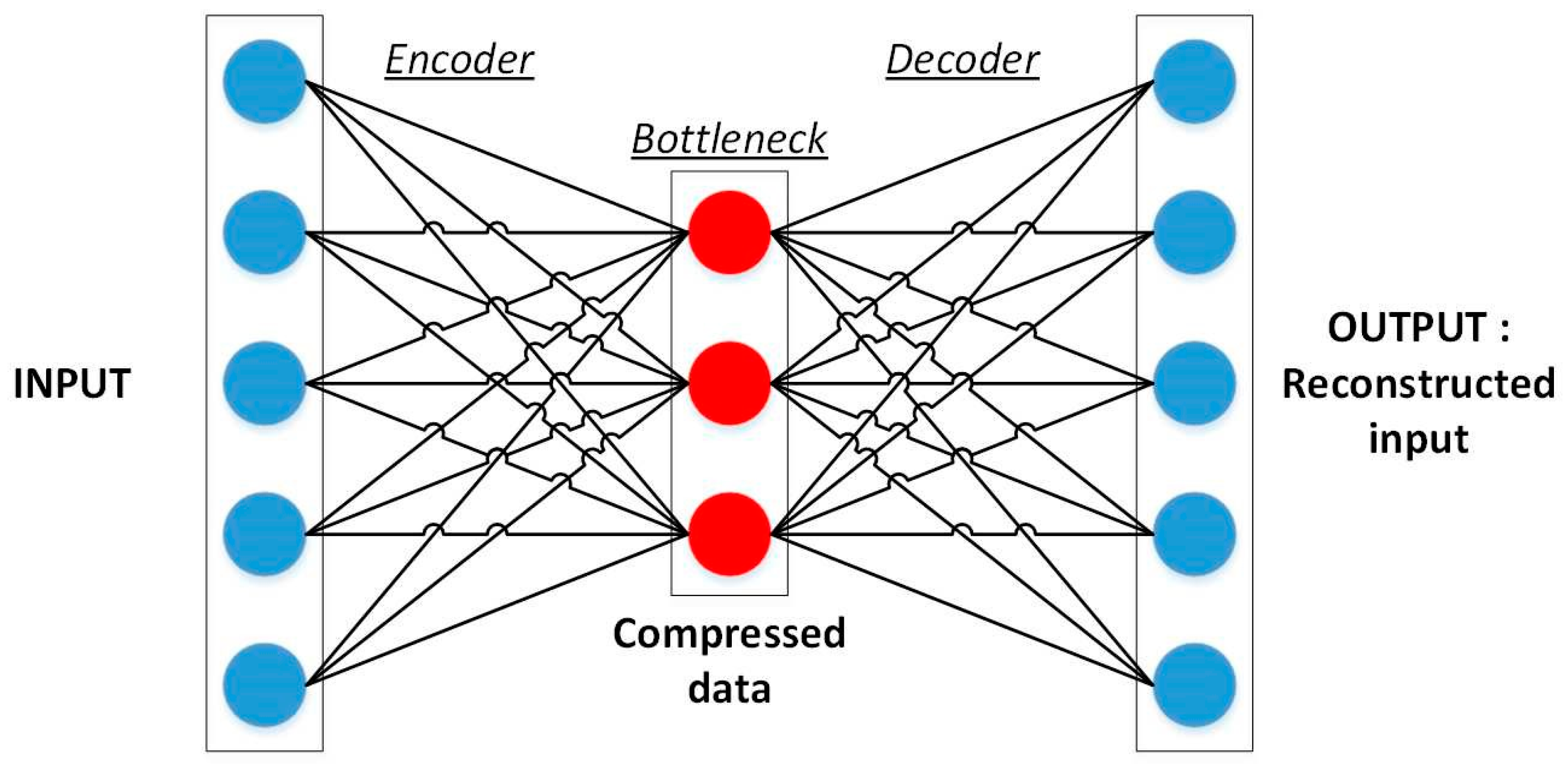
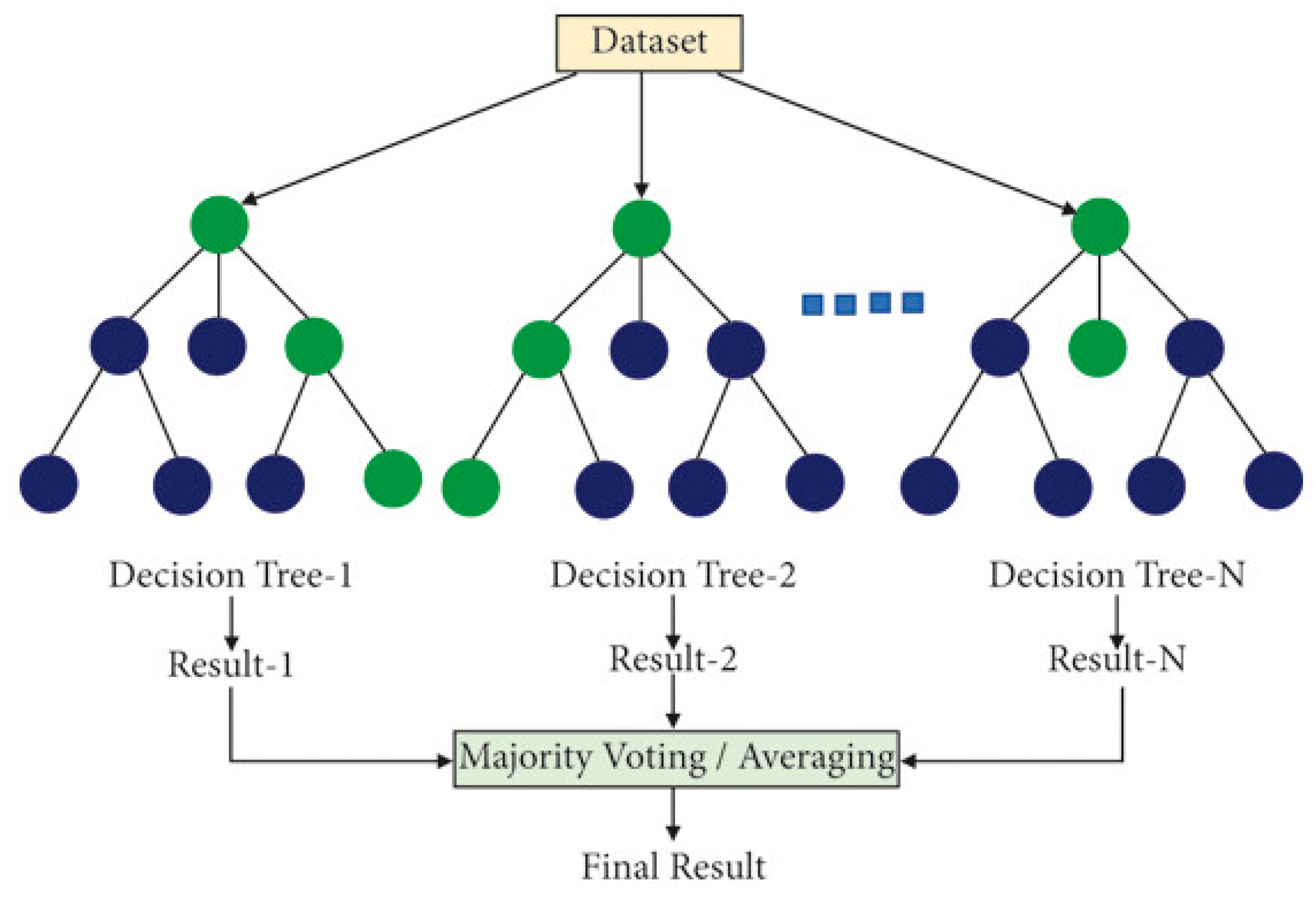
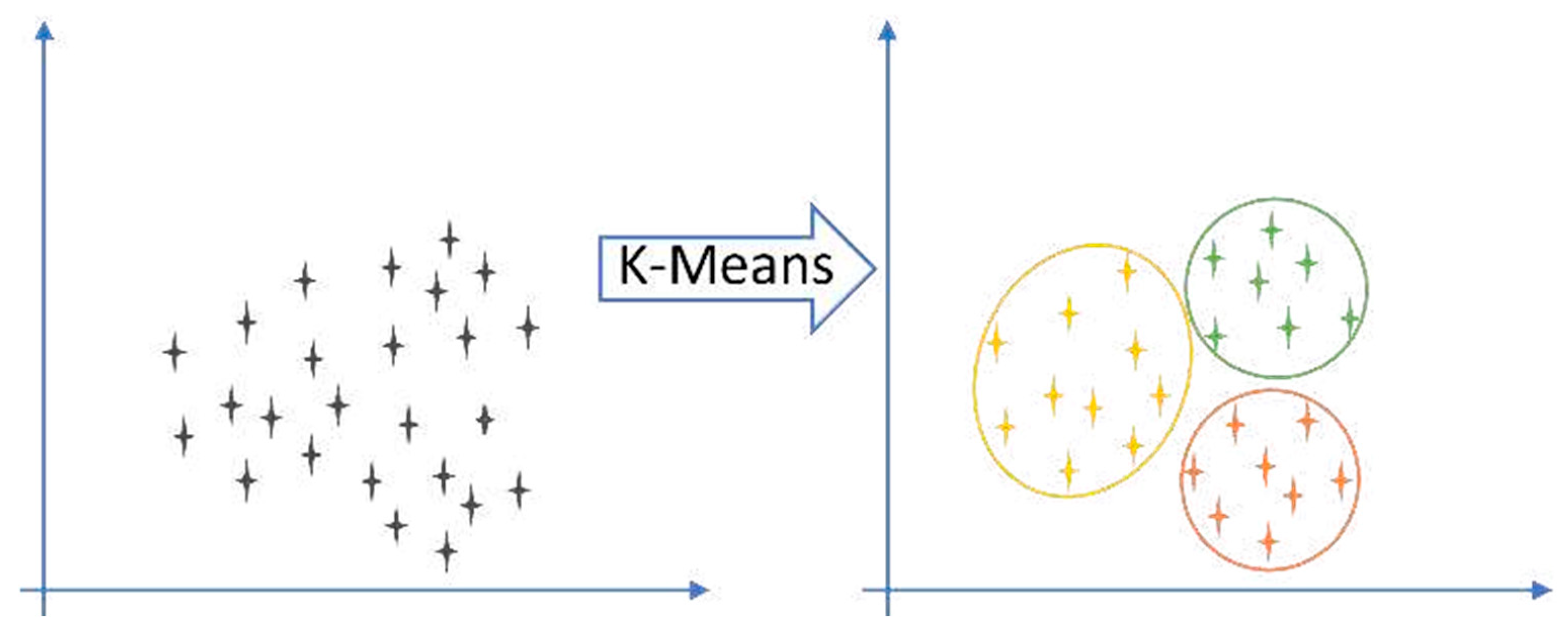
2.3. Matching Aerospace Structural Problems with Machine Learning Algorithms: Principles and Trade-Offs
3. Overview of Structural Health Monitoring (SHM) for Aerospace Structures
- model-based;
- data-driven;
- hybrid.
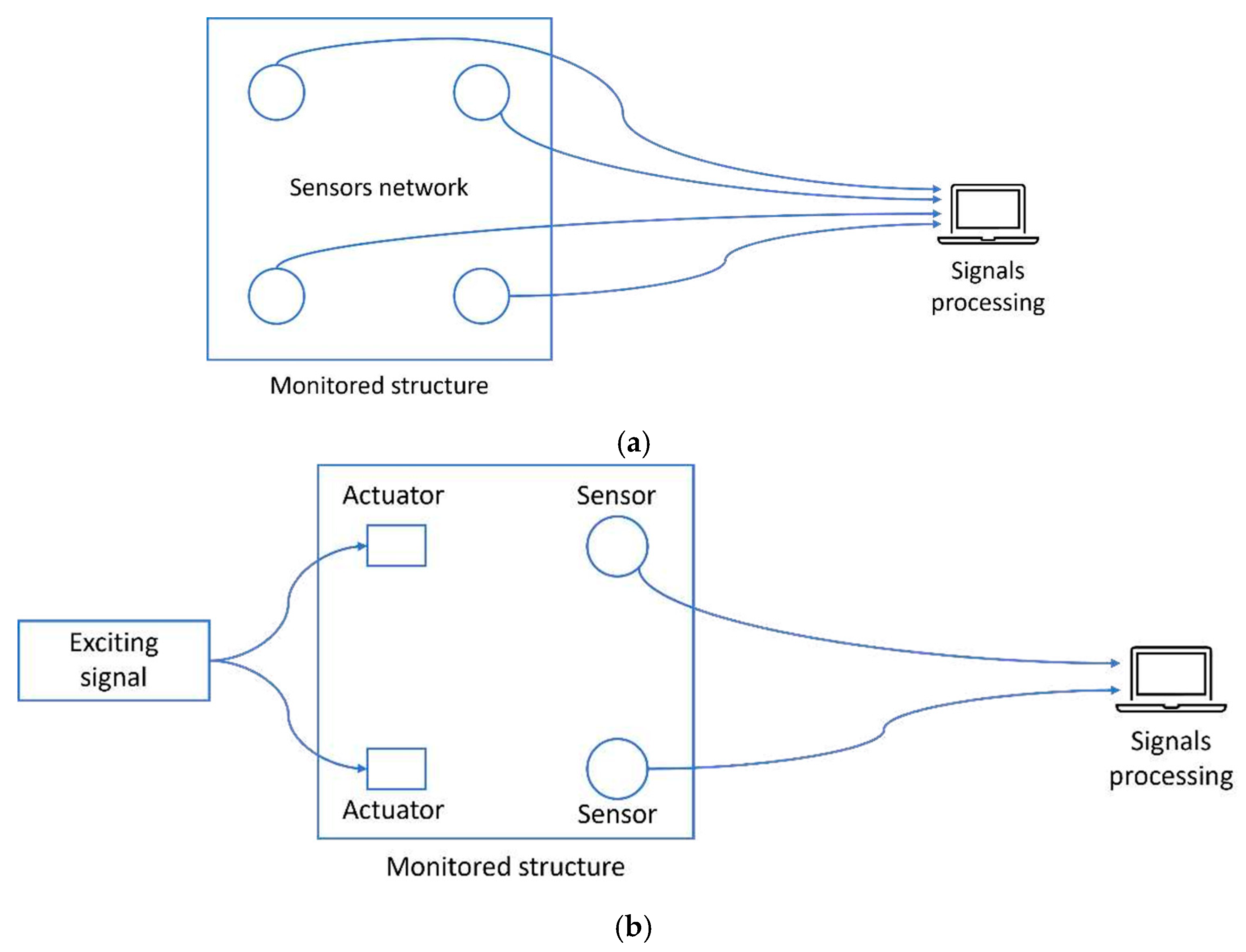
3.1. Sensors
- In passive SHM, sensors are used to detect any change in the physical properties of the structure under examination, “listening” to the structural dynamical behavior (Figure 10a);
- In active SHM, the structure is triggered via actuator sensors, and its response is detected via receiving ones (Figure 10b).
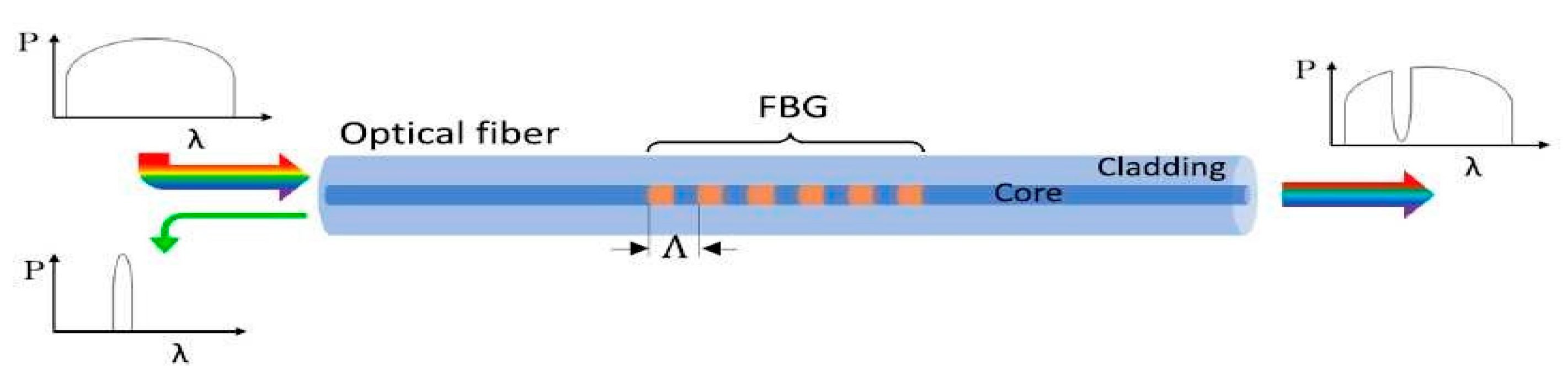
- fiber optic sensors, used to monitor the health of structures, as they can detect changes in strain (e.g., fiber Bragg gratings (FBGs));
- piezoelectric sensors, used to detect damage, both globally and locally (e.g., piezoelectric lead zirconated titanate (Pb[ZrxTi1−x]O3 (0 ≤ x ≤ 1), PZT)).
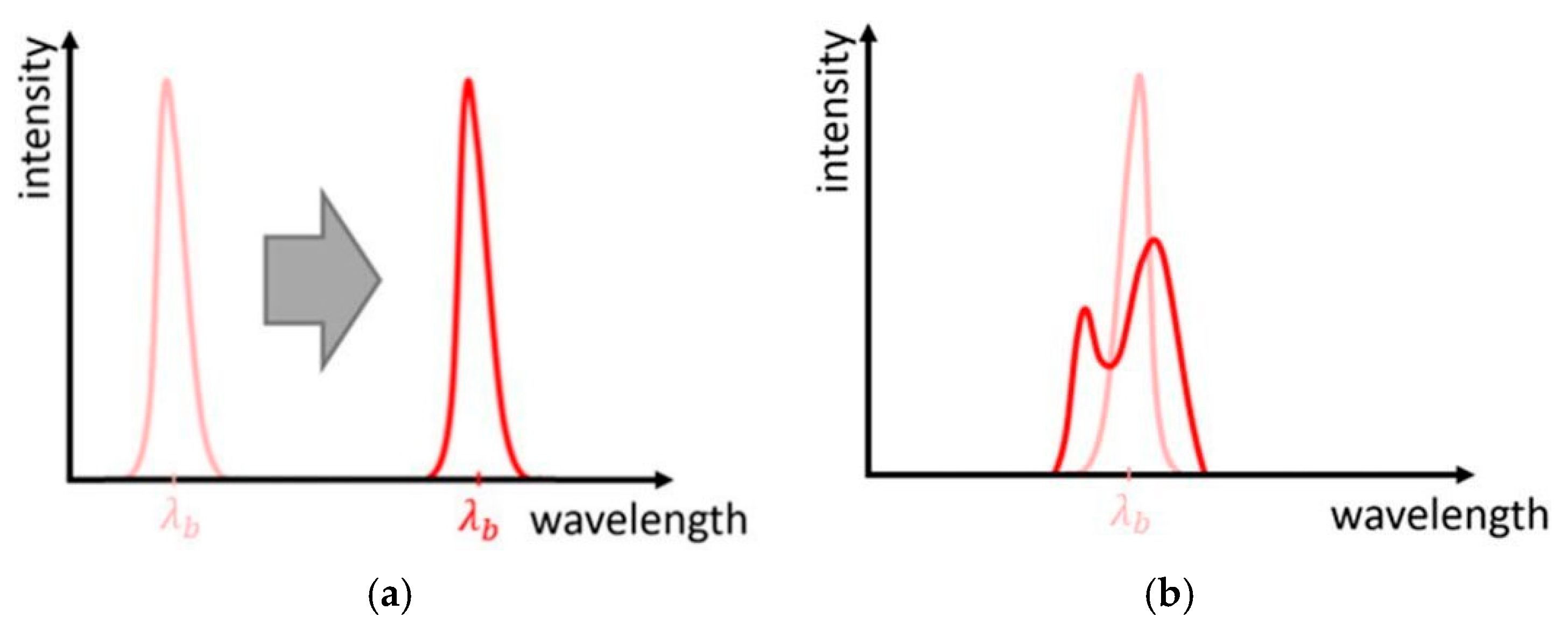
3.1.1. Fiber Optic Sensors
3.1.2. Piezoelectric Sensors
- Inorganic materials, which are subdivided into piezoelectric single crystals, piezoelectric ceramics, and piezoelectric films. Among these, PZT is the one with the best performance.
- Organic materials, mainly piezoelectric polymer, which are employed in flexible sensors.
- Composite materials, developed to improve the piezoelectric properties of organic materials by blending them with inorganic materials.
- Guided-wave and ultrasonic propagation (active);
- Electro mechanical impedance (EMI) (active);
- Acoustic emission (passive).
3.1.3. Smart Structures
- Sphere of influence monitoring is primarily local;
- Signal interference with external factors leads to measurement uncertainty;
- Wiring is required, which can deteriorate, limiting large-scale use, causing electromagnetic interference and adding weight.
- Low weight and compact dimensions;
- Continuous operational working;
- High sensitivity.
- Incorrect installation could lead to their own breakage;
- Composite fiber orientation influences the spectral FOS response;
- Optical fiber interleaving between composite fibers implies a defect that leads to the matrix breaking and structure delamination.
3.2. Data Collection
3.2.1. Deployment
3.2.2. Data Acquisition
3.2.3. Preprocessing and Signal Conditioning
3.2.4. Feature Extraction and Representation
3.2.5. Analysis and Model Training
3.2.6. Challenges
4. ML Applications for SHM on Aerospace Structures
4.1. SHM Methods
4.1.1. Guided Waves and Ultrasonic Propagation
- Pitch-catch, in which there are two sensors, one acting as an actuator to propagate the ultrasonic wave that passes through the structures and reaches the other sensors. The time-of-light (TOF) varies in the presence of a defect.
- Pulse-echo, in which there is only one sensor, which sends the guided wave and receives the reflected one in the presence of a defect.
- Thickness mode, in which the sensor excites the structure in the thickness direction. Changes in thickness, due to corrosion and/or damage, are detected.
- Impact/AE detection, in which the sensor receives a guide acoustic wave during an impact.
4.1.2. EMI Acoustic Emissions
4.1.3. Vibration-Based
4.1.4. Strain-Based
| Monitoring Method | Sensors | Research Articles |
|---|---|---|
| Guided-wave/ultrasonic propagation | Piezoelectric | [124,125,126] |
| EMI | Piezoelectric | [127,128] |
| Acoustic emissions | Piezoelectric | [129,130,131] |
| Vibration-based | Piezoelectric/accelerometers | [132,133] |
| Strain-based | Fiber optic/strain gauges | [134,135,136] |
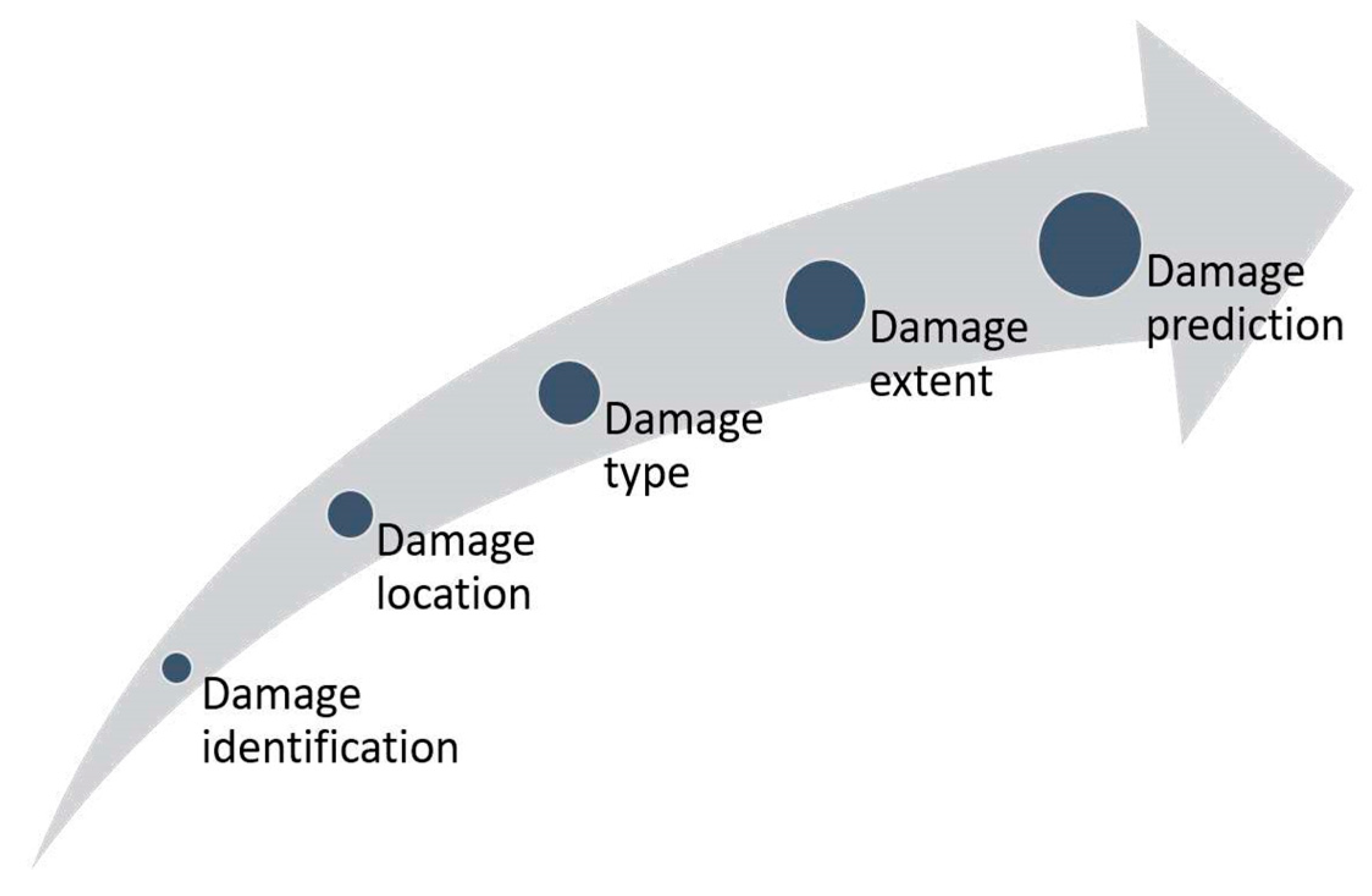
4.2. Damage Diagnosis
4.2.1. Detection
4.2.2. Localization
4.2.3. Classification and Quantification
4.3. Fatigue
4.4. Impacts
4.5. Others
5. Critical Synthesis and Adoption Challenges of ML for Aerospace SHM
- Most mature approaches (TRL 5–6) are supervised learning- and hybrid model-based methods for detection and localization under controlled conditions. These are close to operational readiness but require more flight validation.
- Emerging but less mature (TRL 2–4) are digital twin integration, federated learning, and physics-informed deep learning. While promising for operational robustness and adaptability, they remain at early experimental stages.
- Common barriers across methods include dataset scarcity and lack of standardized benchmarks, sensitivity to environmental variability (temperature, humidity, vibration), interpretability and certification challenges for “black-box” models, and real-time processing constraints for onboard SHM.
- Enabling technologies for advancing TRL include synthetic data generation (GANs, physics-based simulators), transfer learning to leverage cross-platform knowledge, adaptive algorithms capable of recalibration under changing conditions, and multi-sensor fusion for complementary damage indicators.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A 2007, 365, 303–315. [Google Scholar] [CrossRef]
- National Transportation Safety Board. Aircraft Accident Report: Aloha Airlines Flight 243, Boeing 737-200, N73711; NTSB/AAR-89/03; National Transportation Safety Board: Washington, DC, USA, 1989.
- Aviation Safety Council. Final Report on the Accident of China Airlines Flight CI611 B-18255; ASC-AAR-05-06-001; Aviation Safety Council: Taipei, China, 2005.
- Worden, K.; Farrar, C.R.; Manson, G.; Park, G. The fundamental axioms of structural health monitoring. Proc. R. Soc. A 2007, 463, 1639–1664. [Google Scholar] [CrossRef]
- Jiang, Y.; Tran, T.H.; Williams, L. Machine learning and mixed reality for smart aviation: Applications and challenges. J. Air Transp. Manag. 2023, 111, 102437. [Google Scholar] [CrossRef]
- Shabley, A.; Nikolskaia, K.; Varkentin, V.; Peshkov, R.; Petrova, L. Predicting the destruction of composite materials using machine learning methods. Transp. Res. Procedia 2022, 68, 191–196. [Google Scholar] [CrossRef]
- Mahesh, B. Machine learning algorithms—A review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving aircraft performance using machine learning: A review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Revathi, A.; Kaladevi, R.; Ramana, K.; Jhaveri, R.H.; Rudra Kumar, M.; Sankara Prasanna Kumar, M. Early detection of cognitive decline using machine learning algorithm and cognitive ability test. Secur. Commun. Netw. 2022, 2022, 4190023. [Google Scholar] [CrossRef]
- Shan Lee, V.L.; Gan, K.H.; Tan, T.P.; Abdullah, R. Semi-supervised learning for sentiment classification using small number of labeled data. Procedia Comput. Sci. 2019, 161, 577–584. [Google Scholar] [CrossRef]
- Li, Y.F.; Liang, D.M. Safe semi-supervised learning: A brief introduction. Front. Comput. Sci. 2019, 13, 669–676. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep cybersecurity: A comprehensive overview from neural network and deep learning perspective. SN Comput. Sci. 2021, 2, 154. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N.; Manohar, K.; Aravkin, A.Y.; Morgansen, K.; Klemisch, J.; Goebel, N.; Buttrick, J.; Poskin, J.; Blom-Schieber, A.W.; et al. Data-driven aerospace engineering: Reframing the industry with machine learning. AIAA J. 2021, 59, 2820–2847. [Google Scholar] [CrossRef]
- Malekloo, A.; Ozer, E.; AlHamaydeh, M.; Girolami, M. Machine learning and structural health monitoring overview with emerging technology and high-dimensional data source highlights. Struct. Health Monit. 2022, 21, 1906–1955. [Google Scholar] [CrossRef]
- Ray, S. A quick review of machine learning algorithms. In Proceedings of the International Conference on Machine Learning, Big Data, Cloud and Parallel Computing: Trends, Perspectives and Prospects (ComITCon), Faridabad, India, 14–16 February 2019; pp. 35–39. [Google Scholar] [CrossRef]
- Bag, A. A comparative study of regression algorithms for predicting graduate admission to a university. Res. Gate 2020. [Google Scholar] [CrossRef]
- Saleh, H.; Layous, J.A. Machine learning—Regression. Res. Gate 2022. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Cunningham, P.; Delany, S.J. K-Nearest neighbour classifiers—A tutorial. ACM Comput. Surv. 2021, 54, 128. [Google Scholar] [CrossRef]
- Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A brief review of nearest neighbor algorithm for learning and classification. In Proceedings of the International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 1255–1260. [Google Scholar] [CrossRef]
- Bharadiya, J.P. A review of Bayesian machine learning principles, methods, and applications. Int. J. Innov. Sci. Res. Technol. 2023, 8, 2033–2038. [Google Scholar] [CrossRef]
- Magris, M.; Iosifidis, A. Bayesian learning for neural networks: An algorithmic survey. Artif. Intell. Rev. 2023, 56, 11773–11823. [Google Scholar] [CrossRef]
- Leibfried, F.; Dutordoir, V.; John, S.; Durrande, N. A tutorial on sparse Gaussian processes and variational inference. arXiv 2020, arXiv:2012.13962. [Google Scholar] [CrossRef]
- Gadd, C.; Wade, S.; Shah, A.A. Pseudo-marginal Bayesian inference for Gaussian process latent variable models. Mach. Learn. 2021, 110, 1105–1143. [Google Scholar] [CrossRef]
- Melo, J. Gaussian Processes for Regression: A Tutorial. Aston University ePrints. 2011. Available online: http://eprints.aston.ac.uk/651/ (accessed on 23 August 2025).
- Alvarez-Montoya, J.; Carvajal-Castrillón, A.; Sierra-Pérez, J. In-flight and wireless damage detection in a UAV composite wing using fiber optic sensors and strain field pattern recognition. Mech. Syst. Signal Process. 2020, 136, 106526. [Google Scholar] [CrossRef]
- Califano, A.; Chandarana, N.; Grassia, L.; D’Amore, A.; Soutis, C. Damage detection in composites by artificial neural networks trained by using in situ distributed strains. Appl. Compos. Mater. 2020, 27, 657–671. [Google Scholar] [CrossRef]
- Fuentes, R.; Gardner, P.; Mineo, C.; Rogers, T.J.; Pierce, S.G.; Worden, K.; Dervilis, N.; Cross, E.J. Autonomous ultrasonic inspection using Bayesian optimisation and robust outlier analysis. Mech. Syst. Signal Process. 2020, 145, 106897. [Google Scholar] [CrossRef]
- Bergmayr, T.; Höll, S.; Kralovec, C.; Schagerl, M. A framework for physics-driven generation of feature data for strain-based damage detection in aerospace sandwich structures. J. Compos. Mater. 2022, 56, 4081–4099. [Google Scholar] [CrossRef]
- Bergmayr, T.; Höll, S.; Kralovec, C.; Schagerl, M. Local residual random forest classifier for strain-based damage detection and localization in aerospace sandwich structures. Compos. Struct. 2023, 304, 116331. [Google Scholar] [CrossRef]
- Jovel, J.; Greiner, R. An introduction to machine learning approaches for biomedical research. Front. Med. 2021, 8, 771607. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Ikotun, A.M.; Oyelade, O.O.; Abualigah, L.; Agushaka, J.O.; Eke, C.I.; Akinyelu, A.A. A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Eng. Appl. Artif. Intell. 2022, 110, 104743. [Google Scholar] [CrossRef]
- Li, T.; Rezaeipanah, A.; Tag El Din, E.S.M. An ensemble agglomerative hierarchical clustering algorithm based on clusters clustering technique and the novel similarity measurement. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 3828–3842. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Ran, X.; Xi, Y.; Lu, Y.; Wang, X.; Lu, Z. Comprehensive survey on hierarchical clustering algorithms and the recent developments. Artif. Intell. Rev. 2023, 56, 8219–8264. [Google Scholar] [CrossRef]
- Shetty, P.; Singh, S. Hierarchical clustering: A survey. Int. J. Appl. Res. 2021, 7, 178–181. [Google Scholar] [CrossRef]
- Oti, E.U.; Olusola, M.O.; Eze, F.C.; Enogwe, S.U. Comprehensive review of K-means clustering algorithms. Int. J. Adv. Sci. Res. Eng. 2021, 7, 64–69. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H. A clustering method based on K-means algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The K-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Iqbal, T.; Elahi, A.; Wijns, W.; Shahzad, A. Exploring unsupervised machine learning classification methods for physiological stress detection. Front. Med. Technol. 2022, 4, 782756. [Google Scholar] [CrossRef] [PubMed]
- Tharwat, A. Principal component analysis: A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 197. [Google Scholar] [CrossRef]
- Malik, M.R.; Obando Vega, P.; Coussement, A.; Parente, A. Combustion modeling using principal component analysis: A posteriori validation on Sandia flames D, E and F. Proc. Combust. Inst. 2021, 38, 2635–2643. [Google Scholar] [CrossRef]
- Ahmad, N.B.; Alias, U.F.; Mohamad, N.; Yusof, N. Map clustering for student browsing behaviour analysis. Procedia Comput. Sci. 2019, 163, 550–559. [Google Scholar] [CrossRef]
- Tsoulfidis, L.; Athanasiadis, I. A new method of identifying key industries: A principal component analysis. J. Econ. Struct. 2022, 11, 16. [Google Scholar] [CrossRef]
- Sawant, S.; Sethi, A.; Banerjee, S.; Tallur, S. Unsupervised learning framework for temperature compensated damage identification and localization in ultrasonic guided wave SHM with transfer learning. Ultrasonics 2023, 130, 106931. [Google Scholar] [CrossRef] [PubMed]
- Qiao, S.; Huang, M.; Liang, Y.J.; Zhang, S.Z.; Zhou, W. Damage mode identification in carbon/epoxy composite via machine learning and acoustic emission. Polym. Compos. 2023, 44, 2427–2440. [Google Scholar] [CrossRef]
- Andraju, L.B.; Raju, G. Damage characterization of CFRP laminates using acoustic emission and digital image correlation: Clustering, damage identification and classification. Eng. Fract. Mech. 2023, 277, 108993. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Leman, Z.; Baharudin, B.T.H.T. State-of-the-art ensemble learning and unsupervised learning in fatigue crack recognition of glass fiber reinforced polyester composite (GFRP) using acoustic emission. Ultrasonics 2023, 132, 106998. [Google Scholar] [CrossRef] [PubMed]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.E.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Chen, G.; Jin, S. An overview of neural network. Am. J. Neural Netw. Appl. 2019, 5, 7. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendez, Y.A.D.; Lopes Alexandrino, P.S.; Cunha, S.S.; Ancelotti, A.C. A review of vibration-based inverse methods for damage detection and identification in mechanical structures using optimization algorithms and ANN. Arch. Comput. Methods Eng. 2019, 26, 883–897. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Maier, H.R.; Galelli, S.; Razavi, S.; Castelletti, A.; Rizzoli, A.; Athanasiadis, I.N.; Sànchez-Marrè, M.; Acutis, M.; Wu, W.; Humphrey, G.B. Exploding the myths: An introduction to artificial neural networks for prediction and forecasting. Environ. Model. Softw. 2023, 167, 105776. [Google Scholar] [CrossRef]
- Mijwil, M.M. Artificial neural networks advantages and disadvantages. Mesopotamian J. Big Data 2021, 2021, 29–31. [Google Scholar] [CrossRef]
- Jiang, J.H.; Wang, Z. Damage detection of composite laminates based on deep learnings. Front. Phys. 2024, 12, 1456236. [Google Scholar] [CrossRef]
- Prajapati, K.K.; Ghosh, A.; Mitra, M. Semi-supervised generative adversarial network (SGAN) for damage detection in a composite plate using guided wave responses. Mech. Syst. Signal Process. 2025, 232, 112686. [Google Scholar] [CrossRef]
- Pollastro, A.; Testa, G.; Bilotta, A.; Prevete, R. Semi-supervised detection of structural damage using variational autoencoder and a one-class support vector machine. IEEE Access 2023, 11, 67098–67112. [Google Scholar] [CrossRef]
- Lin, J.; Ma, H. Structural damage detection based on the correlation of variational autoencoder neural networks using limited sensors. Sensors 2024, 24, 2616. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zhai, P.; Mosalam, K.M. Balanced semi-supervised generative adversarial network for damage assessment from low-data imbalanced-class regime. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1094–1113. [Google Scholar] [CrossRef]
- Chen, C.; Fu, H.; Zheng, Y.; Tao, F.; Liu, Y. The advance of digital twin for predictive maintenance: The role and function of machine learning. J. Manuf. Syst. 2023, 71, 581–594. [Google Scholar] [CrossRef]
- Sarker, I.H. Deep learning: A comprehensive overview on techniques, taxonomy, applications and research directions. SN Comput. Sci. 2021, 2, 372. [Google Scholar] [CrossRef]
- Kufel, J.; Bargieł-Łączek, K.; Kocot, S.; Koźlik, M.; Bartnikowska, W.; Janik, M.; Czogalik, Ł.; Dudek, P.; Magiera, M.; Lis, A.; et al. What is machine learning, artificial neural networks and deep learning?—Examples of practical applications in medicine. Diagnostics 2023, 13, 2582. [Google Scholar] [CrossRef]
- Phung, V.H.; Rhee, E.J. A high-accuracy model average ensemble of convolutional neural networks for classification of cloud image patches on small datasets. Appl. Sci. 2019, 9, 4500. [Google Scholar] [CrossRef]
- Sublime, J.; Kalinicheva, E. Automatic post-disaster damage mapping using deep-learning techniques for change detection: Case study of the Tohoku tsunami. Remote Sens. 2019, 11, 1123. [Google Scholar] [CrossRef]
- Liao, Y.; Qing, X.; Wang, Y.; Zhang, F. Damage localization for composite structure using guided wave signals with Gramian angular field image coding and convolutional neural networks. Compos. Struct. 2023, 312, 116871. [Google Scholar] [CrossRef]
- Rautela, M.; Senthilnath, J.; Moll, J.; Gopalakrishnan, S. Combined two-level damage identification strategy using ultrasonic guided waves and physical knowledge assisted machine learning. Ultrasonics 2021, 115, 106451. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Gao, Y.; Li, Z.; Hu, Y.; Xuan, F. A Hybrid Deep Learning Framework Based on Diffusion Model and Deep Residual Neural Network for Defect Detection in Composite Plates. Appl. Sci. 2023, 13, 105843. [Google Scholar] [CrossRef]
- Berghout, T.; Vural, T.; Naciri, R. Military training aircraft structural health monitoring leveraging an innovative biologically inspired feedback mechanism for neural networks. Machines 2025, 13, 179. [Google Scholar] [CrossRef]
- Moradi, M.; Broer, A.; Chiachío, J.; Benedictus, R.; Loutas, T.H.; Zarouchas, D. Intelligent health indicator construction for prognostics of composite structures utilizing a semi-supervised deep neural network and SHM data. Eng. Appl. Artif. Intell. 2023, 117, 105502. [Google Scholar] [CrossRef]
- Moradi, M.; Chiachío, J.; Zarouchas, D. Developing Health Indicators for Composite Structures Based on a Two-Stage Semi-Supervised Machine Learning Model Using Acoustic Emission Data. In Proceedings of the 10th ECCOMAS Thematic Conference on Smart Structures and Materials, Patras, Greece, 3–5 July 2023; pp. 923–934. [Google Scholar] [CrossRef]
- Vrtač, T.; Ocepek, D.; Česnik, M.; Čepon, G.; Boltežar, M. A hybrid modeling strategy for training data generation in machine learning-based structural health monitoring. Mech. Syst. Signal Process. 2024, 207, 110937. [Google Scholar] [CrossRef]
- Entezami, A.; Arslan, A.N.; De Michele, C.; Behkamal, B. Online hybrid learning methods for real-time structural health monitoring using remote sensing and small displacement data. Remote Sens. 2022, 14, 3357. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; Kerfriden, P.; van der Meer, F.P. Machine learning of evolving physics-based material models for multiscale solid mechanics. Mech. Mater. 2023, 184, 104707. [Google Scholar] [CrossRef]
- Pop, M.; Tudose, M.; Visan, D.; Bocioaga, M.; Botan, M.; Banu, C.; Salaoru, T. A machine learning-driven wireless system for structural health monitoring. INCAS Bull. 2024, 16, 77–93. [Google Scholar] [CrossRef]
- Spencer, B.F.; Sim, S.H.; Kim, R.E.; Yoon, H. Advances in artificial intelligence for structural health monitoring: A comprehensive review. KSCE J. Civ. Eng. 2025, 29, 100203. [Google Scholar] [CrossRef]
- Xu, Y.; Bansal, P.; Wang, P.; Li, Y. Physics-informed machine learning for system reliability analysis and design with partially observed information. Reliab. Eng. Syst. Saf. 2025, 254, 110598. [Google Scholar] [CrossRef]
- Cross, E.J.; Gibson, S.J.; Jones, M.R.; Pitchforth, D.J.; Zhang, S.; Rogers, T.J. Physics-informed machine learning for structural health monitoring. In Structural Integrity; Springer: Cham, Switzerland, 2022; Volume 21, pp. 347–367. [Google Scholar] [CrossRef]
- Cusati, V.; Corcione, S.; Memmolo, V. Potential benefit of structural health monitoring system on civil jet aircraft. Sensors 2022, 22, 7316. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A systematic review of advanced sensor technologies for non-destructive testing and structural health monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Gardner, P.; Fuentes, R.; Dervilis, N.; Mineo, C.; Pierce, S.G.; Cross, E.J.; Worden, K. Machine learning at the interface of structural health monitoring and non-destructive evaluation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190581. [Google Scholar] [CrossRef]
- Towsyfyn, H.; Biguri, A.; Boardman, R.; Blumensath, T. Successes and challenges in non-destructive testing of aircraft composite structures. Chin. J. Aeronaut. 2020, 33, 771–791. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. Available online: https://vbn.aau.dk/en/publications/vibrational-based-inspection-of-civil-engineering-structures (accessed on 9 February 2024).
- Ganjdoust, F.; Kefal, A.; Tessler, A. A novel delamination damage detection strategy based on inverse finite element method for structural health monitoring of composite structures. Mech. Syst. Signal Process. 2023, 192, 110202. [Google Scholar] [CrossRef]
- Gariya, N.; Prasad, B.; Kumar, P. FEM based analysis of soft polymer composites with crack. Mater. Today Proc. 2020, 28, 2426–2430. [Google Scholar] [CrossRef]
- Gharehbaghi, V.R.; Noroozinejad Farsangi, E.; Noori, M.; Yang, T.Y.; Li, S.; Nguyen, A.; Málaga-Chuquitaype, C.; Gardoni, P.; Mirjalili, S. A critical review on structural health monitoring: Definitions, methods, and perspectives. Arch. Comput. Methods Eng. 2022, 29, 2209–2235. [Google Scholar] [CrossRef]
- Golub, M.V.; Fomenko, S.I.; Shpak, A.N.; Gu, Y.; Wang, Y.; Zhang, C. Semi-analytical hybrid approach for modelling smart structures and guided wave-based SHM systems for a laminate with multiple delaminations and surface-mounted inhomogeneities. Appl. Math. Model. 2023, 120, 812–832. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Sikdar, S.; Ziaja, D.; Jurek, M.; Soman, R.; Malinowski, P. A global-local damage localization and quantification approach in composite structures using ultrasonic guided waves and active infrared thermography. Smart Mater. Struct. 2023, 32, 045001. [Google Scholar] [CrossRef]
- Cai, J.; Qiu, L.; Yuan, S.; Shi, L.; Liu, P.; Liang, D. Structural health monitoring for composite materials. In Composite Materials—Applications in Engineering; Hu, N., Ed.; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Machado, M.A.; Carvalho, M.S.; Vidal, C. Embedded sensors for structural health monitoring: Methodologies and applications review. Sensors 2022, 22, 8320. [Google Scholar] [CrossRef]
- Saeedifar, M.; Mansvelder, J.; Mohammadi, R.; Zarouchas, D. Using passive and active acoustic methods for impact damage assessment of composite structures. Compos. Struct. 2019, 226, 111252. [Google Scholar] [CrossRef]
- Dipietrangelo, F.; Nicassio, F.; Scarselli, G. Structural health monitoring for impact localisation via machine learning. Mech. Syst. Signal Process. 2022, 183, 109621. [Google Scholar] [CrossRef]
- Dipietrangelo, F.; Nicassio, F.; Scarselli, G. Impact characterization on thin structures using machine learning approaches. Chin. J. Aeronaut. 2023, 37, 30–44. [Google Scholar] [CrossRef]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric transducer-based structural health monitoring for aircraft applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Guo, J.K.; Mo, H.; Zhou, X.; Han, Y. Fiber optic sensing technology and vision sensing technology for structural health monitoring. Sensors 2023, 23, 4334. [Google Scholar] [CrossRef] [PubMed]
- Saifan, A.A.A.; Rawat, K.S.; Pathak, B.; Reddy, V.P.; Chaudhary, S.; Anand, A.V.; Nijhawan, G.; Kamil, A.H. Recent advancement in composite material structurally integrated fibre optic damage assessment system. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Goossens, S.; De Pauw, B.; Geernaert, T.; Salmanpour, M.S.; Khodaei, Z.S.; Karachalios, E.; Saenz-Castillo, D.; Thienpont, H.; Berghmans, F. Aerospace-grade surface mounted optical fibre strain sensor for structural health monitoring on composite structures evaluated against in-flight conditions. Smart Mater. Struct. 2019, 28, 065008. [Google Scholar] [CrossRef]
- Di Palma, P.; Leone, M.; Russo, M.; Iadicicco, A.; Cavaccini, G.; Consales, M.; Cusano, A.; Campopiano, S. Bonding quality monitoring of carbon fiber reinforced plastics bonded structures by fiber Bragg gratings. Opt. Laser Technol. 2023, 161, 109119. [Google Scholar] [CrossRef]
- Okagawa, S.; Bernus, P.; Noran, O. Realtime health monitoring of composite structures using FBG sensors. IFAC-Pap. 2022, 55, 157–162. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, G.; Guo, Y.; Kuang, Y.; Liu, H. Investigation of the temperature compensation of FBGs encapsulated with different methods and subjected to different temperature change rates. J. Light. Technol. 2019, 37, 917–926. [Google Scholar] [CrossRef]
- Guo, G. Superstructure fiber Bragg gratings for simultaneous temperature and strain measurement. Optik 2019, 182, 331–340. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, D.; Wang, X.; Zhang, J.; Wu, H.; Qing, X.; Wang, Y. FBG-based strain monitoring and temperature compensation for composite tank. Aerosp. Sci. Technol. 2022, 127, 107724. [Google Scholar] [CrossRef]
- Jia, Z.; Dang, S.; Yu, D.; Fan, W. Cantilever vibration sensor based on fiber Bragg grating temperature compensation. Opt. Fiber Technol. 2023, 75, 103183. [Google Scholar] [CrossRef]
- Boateng, E.K.G.; Schubel, P.; Umer, R. Thermal isolation of FBG optical fibre sensors for composite cure monitoring. Sens. Actuators A Phys. 2019, 287, 158–167. [Google Scholar] [CrossRef]
- Ju, M.; Dou, Z.; Li, J.W.; Qiu, X.; Shen, B.; Zhang, D.; Yao, F.Z.; Gong, W.; Wang, K. Piezoelectric materials and sensors for structural health monitoring: Fundamental aspects, current status, and future perspectives. Sensors 2023, 23, 543. [Google Scholar] [CrossRef] [PubMed]
- Janeliukstis, R.; Mironovs, D. Smart composite structures with embedded sensors for load and damage monitoring—A review. Mech. Compos. Mater. 2021, 57, 131–152. [Google Scholar] [CrossRef]
- Alexopoulos, N.D.; Bartholome, C.; Poulin, P.; Marioli-Riga, Z. Structural health monitoring of glass fiber reinforced composites using embedded carbon nanotube (CNT) fibers. Compos. Sci. Technol. 2010, 70, 260–271. [Google Scholar] [CrossRef]
- Gino, M.E.; Selleri, G.; Cocchi, D.; Brugo, T.M.; Testoni, N.; De Marchi, L.; Zucchelli, A.; Fabiani, D.; Focarete, M.L. On the design of a piezoelectric self-sensing smart composite laminate. Mater. Des. 2022, 219, 110783. [Google Scholar] [CrossRef]
- Montazerian, H.; Rashidi, A.; Milani, A.S.; Hoorfar, M. Integrated sensors in advanced composites: A critical review. Crit. Rev. Solid State Mater. Sci. 2020, 45, 187–238. [Google Scholar] [CrossRef]
- Konka, H.P.; Wahab, M.A.; Lian, K. The effects of embedded piezoelectric fiber composite sensors on the structural integrity of glass-fiber-epoxy composite laminate. Smart Mater. Struct. 2012, 21, 015016. [Google Scholar] [CrossRef]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y. Integration of piezoelectric transducers (PZT and PVDF) within polymer-matrix composites for structural health monitoring applications: New success and challenges. Int. J. Smart Nano Mater. 2020, 11, 343–369. [Google Scholar] [CrossRef]
- Grabowski, K.; Srivatsa, S.; Vashisth, A.; Mishnaevsky, L.; Uhl, T. Recent advances in MXene-based sensors for structural health monitoring applications: A review. Measurement 2022, 189, 110575. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Y.; Lu, S.; Zhang, H.; Zhao, Z.; Ma, C.; Ma, K.; Wang, X. Lifetime health monitoring of fiber reinforced composites using highly flexible and sensitive MXene/CNT film sensor. Sens. Actuators A Phys. 2021, 332, 113148. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, S.; Wang, S.; Wen, K.; Shi, C.; Zhang, J.; Zhao, D.; Han, Y.; Chen, X.; Li, B.; et al. Embedding stretchable, mesh-structured piezoresistive sensor for in-situ damage detection of glass fiber-reinforced composite. Compos. Sci. Technol. 2023, 233, 109926. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, X.; Yan, J.; Wang, Y.; Qing, X. Real-time life-cycle monitoring of composite structures using piezoelectric-fiber hybrid sensor network. Sensors 2021, 21, 8213. [Google Scholar] [CrossRef] [PubMed]
- Negoita, M.; Hothazie, M. A Machine Learning-Based Approach for Predicting Aerodynamic Coefficients Using Deep Neural Networks and CFD Data. INCAS Bull. 2024, 16, 91–104. [Google Scholar] [CrossRef]
- Bao, P.; Yi, W.; Zhu, Y.; Shen, Y.; Chai, B.X. STHFD: Spatial–Temporal Hypergraph-Based Model for Aero-Engine Bearing Fault Diagnosis. Aerospace 2025, 12, 612. [Google Scholar] [CrossRef]
- Philibert, M.; Yao, K.; Gresil, M.; Soutis, C. Lamb waves-based technologies for structural health monitoring of composite structures for aircraft applications. Eur. J. Mater. 2022, 2, 436–474. [Google Scholar] [CrossRef]
- Carrino, S.; Nicassio, F.; Scarselli, G. Development and application of an in-flight structural health monitoring system. Proc. Meet. Acoust. 2019, 38, 065011. [Google Scholar] [CrossRef]
- Patil, S.; Reddy, D.M. Impact damage assessment in carbon fiber reinforced composite using vibration-based new damage index and ultrasonic C-scanning method. Structures 2020, 28, 638–650. [Google Scholar] [CrossRef]
- Chaupal, P.; Rajendran, P. A review on recent developments in vibration-based damage identification methods for laminated composite structures: 2010–2022. Compos. Struct. 2023, 311, 116809. [Google Scholar] [CrossRef]
- Schagerl, M.; Viechtbauer, C.; Schaberger, M. Optimal placement of fiber optical sensors along zero-strain trajectories to detect damages in thin-walled structures with highest sensitivity. Struct. Health Monit. 2015. [Google Scholar] [CrossRef]
- Kralovec, C.; Schagerl, M. Review of structural health monitoring methods regarding a multi-sensor approach for damage assessment of metal and composite structures. Sensors 2020, 20, 826. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Giovanis, D.G.; Kopsaftopoulos, F. Guided wave-based structural awareness under varying operating states via manifold representations. arXiv 2025, arXiv:2504.11235. [Google Scholar] [CrossRef]
- Ochôa, P.A.; Groves, R.M.; Benedictus, R. Effects of high-amplitude low-frequency structural vibrations and machinery sound waves on ultrasonic guided wave propagation for health monitoring of composite aircraft primary structures. J. Sound Vib. 2020, 475, 115289. [Google Scholar] [CrossRef]
- Giannakeas, I.N.; Mazaheri, F.; Bacarreza, O.; Khodaei, Z.S.; Aliabadi, F.M.H. Probabilistic residual strength assessment of smart composite aircraft panels using guided waves. Reliab. Eng. Syst. Saf. 2023, 237, 109338. [Google Scholar] [CrossRef]
- Jin, H.; Wang, Y.; Sun, H.; Li, W.; Qing, X. Identification and imaging of multi-defects on a complicated composite structure by ultrasonic guided wave. Polym. Test. 2022, 106, 107466. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, T.; Schröder, K.U. Development of a piezoelectric transducer-based integrated structural health monitoring system for impact monitoring and impedance measurement. Appl. Sci. 2020, 10, 2062. [Google Scholar] [CrossRef]
- Amin, M.S.; Salem, M.A.M. Depolarization diagnosis of PWAS used for EMI based structural health monitoring system for composite plates. IOP Conf. Ser. Mater. Sci. Eng. 2019, 610, 012018. [Google Scholar] [CrossRef]
- Wirtz, S.F.; Beganovic, N.; Söffker, D. Investigation of damage detectability in composites using frequency-based classification of acoustic emission measurements. Struct. Health Monit. 2019, 18, 1207–1218. [Google Scholar] [CrossRef]
- Spyrou, E.D.; Tsenis, T.; Kappatos, V. Acousto-ultrasonic analysis of defects in composite specimens used in transportation domain. J. Meas. Eng. 2021, 9, 117–127. [Google Scholar] [CrossRef]
- Li, W.; Guo, S.; Liu, Y.; Shen, Z.; Xiong, Y.; Gao, F.; Hughes, D.J.; Lin, J. Structural health monitoring of composites joint reinforced by acoustic emission based smart composite fasteners. Compos. Commun. 2022, 33, 101213. [Google Scholar] [CrossRef]
- Mironovs, D.; Rucevskis, S.; Dzelzitis, K. Prospects of structural damage identification using modal analysis and anomaly detection. Procedia Struct. Integr. 2021, 37, 410–416. [Google Scholar] [CrossRef]
- Mironov, A.; Doronkin, P. The demonstrator of structural health monitoring system of helicopter composite blades. Procedia Struct. Integr. 2021, 37, 241–249. [Google Scholar] [CrossRef]
- Winklberger, M.; Kralovec, C.; Schagerl, M. Development of aircraft spoiler demonstrators for cost-efficient investigations of SHM technologies under quasi-realistic loading conditions. Aerospace 2021, 8, 320. [Google Scholar] [CrossRef]
- Bergmayr, T.; Winklberger, M.; Kralovec, C.; Schagerl, M. Structural health monitoring of aerospace sandwich structures via strain measurements along zero-strain trajectories. Eng. Fail. Anal. 2021, 126, 105454. [Google Scholar] [CrossRef]
- Grassia, L.; Iannone, M.; Califano, A.; D’Amore, A. Strain based method for monitoring the health state of composite structures. Compos. Part B Eng. 2019, 176, 107253. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; Ho-Khac, H.; De Roeck, G.; Bui-Tien, T.; Abdel Wahab, M. Efficient artificial neural networks based on a hybrid metaheuristic optimization algorithm for damage detection in laminated composite structures. Compos. Struct. 2021, 262, 113339. [Google Scholar] [CrossRef]
- Song, R.; Sun, L.; Gao, Y.; Peng, C.; Wu, X.; Lv, S.; Wei, J.; Jiang, M. Global-local feature cross-fusion network for ultrasonic guided wave-based damage localization in composite structures. Sens. Actuators A Phys. 2023, 362, 114659. [Google Scholar] [CrossRef]
- Zhu, J.; Qing, X.; Liu, X.; Wang, Y. Electromechanical impedance-based damage localization with novel signatures extraction methodology and modified probability-weighted algorithm. Mech. Syst. Signal Process. 2020, 146, 107001. [Google Scholar] [CrossRef]
- Nokhbatolfoghahai, A.; Navazi, H.M.; Groves, R.M. Use of dictionary learning for damage localization in complex structures. Mech. Syst. Signal Process. 2022, 180, 109394. [Google Scholar] [CrossRef]
- Zhao, C.; Wen, Y.; Zhu, J.; Li, T. Localization of surface dent deformation and inter-laminated damage in CFRP laminates under low-velocity impact behavior based on multi-channel one-dimensional convolutional gated recurrent unit. Meas. J. Int. Meas. Confed. 2023, 221, 113503. [Google Scholar] [CrossRef]
- Huang, L.; Zeng, L.; Lin, J.; Zhang, N. Baseline-free damage detection in composite plates using edge-reflected Lamb waves. Compos. Struct. 2020, 247, 112423. [Google Scholar] [CrossRef]
- Seventekidis, P.; Giagopoulos, D. A combined finite element and hierarchical Deep learning approach for structural health monitoring: Test on a pin-joint composite truss structure. Mech. Syst. Signal Process. 2021, 157, 107735. [Google Scholar] [CrossRef]
- Rautela, M.; Gopalakrishnan, S. Ultrasonic guided wave based structural damage detection and localization using model assisted convolutional and recurrent neural networks. Expert Syst. Appl. 2021, 167, 114189. [Google Scholar] [CrossRef]
- Lin, M.; Guo, S.; He, S.; Li, W.; Yang, D. Structure health monitoring of a composite wing based on flight load and strain data using deep learning method. Compos. Struct. 2022, 286, 115305. [Google Scholar] [CrossRef]
- Perfetto, D.; Rezazadeh, N.; Aversano, A.; De Luca, A.; Lamanna, G. Composite Panel Damage Classification Based on Guided Waves and Machine Learning: An Experimental Approach. Appl. Sci. 2023, 13, 10017. [Google Scholar] [CrossRef]
- Tang, L.; Li, Y.; Bao, Q.; Hu, W.; Wang, Q.; Su, Z.; Yue, D. Quantitative identification of damage in composite structures using sparse sensor arrays and multi-domain-feature fusion of guided waves. Meas. J. Int. Meas. Confed. 2023, 208, 112482. [Google Scholar] [CrossRef]
- Zeng, X.; Zhao, B.; Liu, X.; Yu, Y.; Guo, J.; Qing, X. Lamb wave-based damage assessment for CFRP composite structures using a CHMM-based damage localization algorithm and a damage quantitative expression. Mech. Syst. Signal Process. 2023, 184, 109750. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, X.; Yan, J.; Zhao, B.; Qing, X. Lamb Wave-Based Damage Localization and Quantification Algorithms for CFRP Composite Structures. Compos. Struct. 2022, 295, 115849. [Google Scholar] [CrossRef]
- Amini, M.; Rahmani, A. Machine learning process evaluating damage classification of composites. Int. J. Sci. Adv. Technol. 2023, 9, 240–250. [Google Scholar]
- Gholizadeh, S. Damage Analysis and Prediction in Glass Fiber Reinforced Polyester Composite Using Acoustic Emission and Machine Learning. J. Robot. Autom. Res. 2022, 3, 131–141. [Google Scholar] [CrossRef]
- Duan, Q.; Ye, B.; Zou, Y.; Hua, R.; Feng, J.; Shi, X. Probability-Based Diagnostic Imaging of Fatigue Damage in Carbon Fiber Composites Using Sparse Representation of Lamb Waves. Electronics 2023, 12, 1148. [Google Scholar] [CrossRef]
- Pagani, A.; Enea, M.; Carrera, E. Damage detection in laminated composites by neural networks and high order finite elements. In Proceedings of the American Society for Composites—Thirty-Sixth Technical Conference on Composite Materials, Virtual, 20–22 September 2021; Volume 1, pp. 597–607. [Google Scholar] [CrossRef]
- Shirazi, M.I.; Khatir, S.; Benaissa, B.; Mirjalili, S.; Wahab, M.A. Damage assessment in laminated composite plates using modal Strain Energy and YUKI-ANN algorithm. Compos. Struct. 2023, 303, 116272. [Google Scholar] [CrossRef]
- Ghrib, M.; Rébillat, M.; Roches, G.V.D.; Mechbal, N. Automatic damage type classification and severity quantification using signal based and nonlinear model based damage sensitive features. J. Process Control. 2019, 83, 136–146. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, S.; Malik, M.K.; Chronopoulos, D.; Chiachío, J. Bayesian damage localization and identification based on a transient wave propagation model for composite beam structures. Compos. Struct. 2021, 267, 113849. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Eleftheroglou, N.; Milanoski, D.; Broer, A.; Zarouchas, D.; Loutas, T. A novel strain-based health indicator for the remaining useful life estimation of degrading composite structures. Compos. Struct. 2023, 306, 116579. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Milanoski, D.; Eleftheroglou, N.; Broer, A.; Zarouchas, D.; Loutas, T. Acoustic emission-based remaining useful life prognosis of aeronautical structures subjected to compressive fatigue loading. Eng. Struct. 2023, 290, 116391. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Fytsilis, E.; Yue, N.; Broer, A.; Milanoski, D.; Zarouchas, D.; Loutas, T. A data driven methodology for upscaling remaining useful life predictions: From single- to multi-stiffened composite panels. Compos. Part C Open Access 2023, 11, 100366. [Google Scholar] [CrossRef]
- Galanopoulos, G.; Milanoski, D.; Broer, A.; Zarouchas, D.; Loutas, T. Health monitoring of aerospace structures utilizing novel health indicators extracted from complex strain and acoustic emission data. Sensors 2021, 21, 5701. [Google Scholar] [CrossRef]
- Ben-Yelun, I.; Díaz-Lago, M.; Saucedo-Mora, L.; Sanz, M.Á.; Callado, R.; Montáns, F.J. Self-learning locally-optimal hypertuning using maximum entropy, and comparison of machine learning approaches for estimating fatigue life in composite materials of the aerospace industry. Eng. Struct. 2023, 283, 115829. [Google Scholar] [CrossRef]
- Lee, H.; Lim, H.J.; Skinner, T.; Chattopadhyay, A.; Hall, A. Automated fatigue damage detection and classification technique for composite structures using Lamb waves and deep autoencoder. Mech. Syst. Signal Process. 2021, 163, 108148. [Google Scholar] [CrossRef]
- Wang, M.; He, M.; Liang, Z.; Wu, D.; Wang, Y.; Qing, X.; Wang, Y. Fatigue damage monitoring of composite laminates based on acoustic emission and digital image correlation techniques. Compos. Struct. 2023, 321, 117239. [Google Scholar] [CrossRef]
- Ai, L.; Soltangharaei, V.; Bayat, M.; Van Tooren, M.; Ziehl, P. Detection of impact on aircraft composite structure using machine learning techniques. Meas. Sci. Technol. 2021, 32, 045003. [Google Scholar] [CrossRef]
- Ai, L.; Soltangharaei, V.; Anay, R.; Van Tooren, M.J.L.; Ziehl, P. Data-Driven Source Localization of Impact on Aircraft Control Surfaces. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Yu, H.; Seno, A.H.; Khodaei, Z.S.; Aliabadi, M.H.F. Structural Health Monitoring Impact Classification Method Based on Bayesian Neural Network. Polymers 2022, 14, 3947. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Liang, D. Impact localization system of composite structure based on recurrence quantification analysis by using FBG sensors. Opt. Fiber Technol. 2019, 49, 7–15. [Google Scholar] [CrossRef]
- Tabatabaeian, A.; Jerkovic, B.; Harrison, P.; Marchiori, E.; Fotouhi, M. Barely visible impact damage detection in composite structures using deep learning networks with varying complexities. Compos. Part B Eng. 2023, 264, 110907. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Khodaei, Z.S. A convolutional neural network for impact detection and characterization of complex composite structures. Sensors 2019, 19, 24933. [Google Scholar] [CrossRef] [PubMed]
- Damm, A.M.; Spitzmüller, C.; Raichle, A.T.S.; Bühler, A.; Weißgraeber, P.; Middendorf, P. Deep learning for impact detection in composite plates with sparsely integrated sensors. Smart Mater. Struct. 2020, 29, 095006. [Google Scholar] [CrossRef]
- Jung, K.C.; Chang, S.H. Advanced deep learning model-based impact characterization method for composite laminates. Compos. Sci. Technol. 2021, 207, 108713. [Google Scholar] [CrossRef]
- Cuomo, S.; De Simone, M.E.; Andreades, C.; Ciampa, F.; Meo, M. Machine learning for impact detection on composite structures. Mater. Today Proc. 2019, 34, 93–98. [Google Scholar] [CrossRef]
- Seno, A.H.; Aliabadi, M.H.F. Impact localisation in composite plates of different stiffness impactors under simulated environmental and operational conditions. Sensors 2019, 19, 3659. [Google Scholar] [CrossRef]
- Seno, A.H.; Khodaei, Z.S.; Aliabadi, M.H.F. Passive sensing method for impact localisation in composite plates under simulated environmental and operational conditions. Mech. Syst. Signal Process. 2019, 129, 20–36. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, B.; Lyu, Q.; Xie, W.; Guo, Z.; Wang, B. Compression after multiple impact strength of composite laminates prediction method based on machine learning approach. Aerosp. Sci. Technol. 2023, 136, 108243. [Google Scholar] [CrossRef]
- Nicassio, F.; Dipietrangelo, F.; Scarselli, G. Energy evaluation and passive damage detection for structural health monitoring in aerospace structures using machine learning models. Sensors 2025, 25, 4942. [Google Scholar] [CrossRef]
- Humer, A.; Grasboeck, L.; Benjeddou, A. Localization of impacts on thin-walled structures by recurrent neural networks: End-to-end learning from real-world data. arXiv 2025. [Google Scholar] [CrossRef]
- Liu, Z.; Ardabilian, M.; Zine, A.; Ichchou, M. Crack damage identification of a thick composite sandwich structure based on Gaussian Processes classification. Compos. Struct. 2021, 255, 112825. [Google Scholar] [CrossRef]
- Budiman, B.A.; Budijanto, H.; Adziman, F.; Triawan, F.; Wirawan, R.; Nurprasetio, I.P. On predicting crack length and orientation in twill-woven CFRP based on limited data availability using a physics-based, high fidelity machine learning approach. Compos. Part C Open Access 2023, 11, 100371. [Google Scholar] [CrossRef]
- Zara, A.; Belaidi, I.; Khatir, S.; Brahim, A.O.; Boutchicha, D.; Wahab, M.A. Damage detection in GFRP composite structures by improved artificial neural network using new optimization techniques. Compos. Struct. 2023, 305, 116475. [Google Scholar] [CrossRef]
- Manujesh, B.J.; Prajna, M.R. Damage detection and classification for sandwich composites using machine learning. Mater. Today Proc. 2022, 52, 702–709. [Google Scholar] [CrossRef]
- Shirazi, M.I.; Khatir, S.; Boutchicha, D.; Wahab, M.A. Feature extraction and classification of multiple cracks from raw vibrational responses of composite beams using 1D-CNN network. Compos. Struct. 2024, 327, 117701. [Google Scholar] [CrossRef]
- Zhu, K.; Cao, W.; Ran, C.; Gu, B. A novel automatic crack classification algorithm of 3-D woven composites based on deep-learning U-Net model. Eng. Fract. Mech. 2023, 289, 109488. [Google Scholar] [CrossRef]
- Mardanshahi, A.; Nasir, V.; Kazemirad, S.; Shokrieh, M.M. Detection and classification of matrix cracking in laminated composites using guided wave propagation and artificial neural networks. Compos. Struct. 2020, 246, 112403. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, L.; Song, Z.; Gao, H.; Zhou, W.; Liu, J.; Tao, R. Strength prediction and progressive damage analysis of carbon fiber reinforced polymer-laminate with circular holes by an efficient Artificial Neural Network. Compos. Struct. 2022, 296, 115835. [Google Scholar] [CrossRef]
- Candon, M.; Esposito, M.; Fayek, H.; Levinski, O.; Koschel, S.; Joseph, N.; Carrese, R.; Marzocca, P. Advanced multi-input system identification for next generation aircraft loads monitoring using linear regression, neural networks and deep learning. Mech. Syst. Signal Process. 2022, 171, 108809. [Google Scholar] [CrossRef]
- Wang, Z.; Chegdani, F.; Yalamarti, N.; Takabi, B.; Tai, B.; El Mansori, M.; Bukkapatnam, S. Acoustic emission characterization of natural fiber reinforced plastic composite machining using a random forest machine learning model. J. Manuf. Sci. Eng. Trans. ASME 2020, 142, 031003. [Google Scholar] [CrossRef]
- An, H.; Youn, B.D.; Kim, H.S. A methodology for sensor number and placement optimization for vibration-based damage detection of composite structures under model uncertainty. Compos. Struct. 2022, 279, 114863. [Google Scholar] [CrossRef]
- Hao, W.; Huang, Y.; Zhao, G. Acoustic sources localization for composite plate using arrival time and BP neural network. Polym. Test. 2022, 115, 107754. [Google Scholar] [CrossRef]
- Sikdar, S.; Ostachowicz, W.; Kundu, A. Deep learning for automatic assessment of breathing-debonds in stiffened composite panels using non-linear guided wave signals. Compos. Struct. 2023, 312, 116876. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.Z.; Wu, J.; Wang, Y. Zero-faulty sample machinery fault detection via relation network with out-of-distribution data augmentation. Eng. Appl. Artif. Intell. 2025, 141, 109753. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.Z.; Deng, Z.; Wu, J. Shrinkage mamba relation network with out-of-distribution data augmentation for rotating machinery fault detection and localization under zero-faulty data. Mech. Syst. Signal Process. 2025, 224, 112145. [Google Scholar] [CrossRef]
- Yang, X.; Deng, X.; Zhang, H.; Zou, Y.; Yang, J. Enhancing robustness of data-driven SHM models: Adversarial training with circle loss. arXiv 2024, arXiv:2406.14232. [Google Scholar] [CrossRef]
- Farooq, E.; Milano, M.; Borghesi, A. Federated Transfer Learning for Anomaly Detection in HPC Systems: First Real-World Validation on a Tier-0 Supercomputer. Expert Syst. Appl. 2025, 298, 129754. [Google Scholar] [CrossRef]
- Zhan, S.; Huang, L.; Luo, G.; Zheng, S.; Gao, Z.; Chao, H.C. A Review on Federated Learning Architectures for Privacy-Preserving AI: Lightweight and Secure Cloud–Edge–End Collaboration. Electronics 2025, 14, 2512. [Google Scholar] [CrossRef]
- Tang, R.; Zhang, S.; Wu, W.; Zhang, S.; Han, Z. Explainable deep learning based ultrasonic guided wave pipe crack identification method. Meas. J. Int. Meas. Confed. 2023, 206, 112277. [Google Scholar] [CrossRef]
- Movsessian, A.; Cava, D.G.; Tcherniak, D. Interpretable Machine Learning in Damage Detection Using Shapley Additive Explanations. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2022, 8, 021101. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, J.; Hua, J.; Zhang, T.; Tong, T. Attention-based interpretable prototypical network towards small-sample damage identification using ultrasonic guided waves. Mech. Syst. Signal Process. 2023, 188, 109990. [Google Scholar] [CrossRef]
- Kosova, F.; Altay, Ö.; Ünver, H.Ö. Structural health monitoring in aviation: A comprehensive review and future directions for machine learning. Nondestruct. Test. Eval. 2024, 40, 1–60. [Google Scholar] [CrossRef]
- European Union Aviation Safety Agency (EASA). Artificial Intelligence Roadmap 2.0; EASA: Cologne, Germany, 2023. [Google Scholar]
- EASA. Concept Paper: Guidance for Level 1 & Level 2 Machine Learning Applications, Issue 02; EASA: Cologne, Germany, 2025. [Google Scholar]
- Federal Aviation Administration (FAA). Roadmap to AI/ML at the FAA; FAA: Washington, DC, USA, 2023.
- Pedraza, A.; Pérez, M.; Herrero, J.; Valenzuela, C. AI-based impact location in structural health monitoring for aerospace application evaluation using explainable artificial intelligence techniques. Electronics 2025, 14, 1975. [Google Scholar] [CrossRef]




| Method | Typical Aerospace SHM Application | Strengths | Limitations |
|---|---|---|---|
| Support Vector Machines (SVMs) | Damage detection in composite plates using Lamb-wave features | High accuracy with small datasets; effective for binary classification | Requires labeled data; performance drops with noise or nonlinear damage states |
| Random Forests (RFs) | Impact energy classification in composite coupons; strain-based crack detection | Robust to noise; interpretable feature importance; fast inference (onboard suitability) | Less effective at learning complex feature hierarchies |
| k-Nearest Neighbors (k-NN) | Localization of low-velocity impacts in CFRP panels | Simple, no training phase; intuitive | Sensitive to feature scaling; computationally heavy for large datasets |
| Principal Component Analysis (PCA) | Novelty detection under varying flight loads and temperatures | No labels required; effective for dimensionality reduction | Sensitive to environmental and operational variability (EOCs) |
| Self-Organizing Maps (SOMs) | Clustering of acoustic emission data for damage characterization | Captures nonlinear structures in high-dimensional data | Interpretation not straightforward; prone to false alarms |
| Autoencoders (Unsupervised DL) | Detection of delamination in CFRPs without labelled data | Learns compact, task-specific latent representations | Higher false positives; requires large healthy-condition datasets |
| Architecture | Typical Aerospace SHM Case | Strengths | Limitations | Training Cost | Inference Cost |
|---|---|---|---|---|---|
| Multilayer Perceptron (MLP) | Strain-based damage detection in stiffened composite panels | Simple and interpretable; effective on small datasets | Limited feature extraction capacity; prone to overfitting | Low Scales with a number of layers/neurons; efficient on vibration/guided-wave features. | Very low Feasible on embedded devices (FPGA/MCU) |
| Convolutional Neural Networks (CNNs) | Impact localization using acoustic emission or Lamb-wave imaging | Learns spatial features; excellent accuracy in impact and imaging tasks | Needs large datasets; computationally demanding | Medium–High Cost grows with kernel size, channels, and input resolution; GPU recommended. | Medium Can be optimized via pruning/quantization |
| Recurrent Neural Networks (RNNs)/LSTMs/GRUs | Fatigue life prediction and remaining useful life (RUL) estimation | Captures temporal dependencies; effective for sequence modeling | Training instabilities; requires long time-series datasets | High Sequential training; scales with sequence length × hidden size | Medium–High Depends on input sequence length |
| Graph Neural Networks (GNNs) | Sensor network data fusion in distributed SHM of large airframes | Naturally handles graph-structured sensor layouts | Still emerging; limited aerospace datasets available | High Scales with a number of nodes/edges; computationally demanding for large structures. | Medium–High Inference costly if graph updates in real time |
| Generative Adversarial Networks (GANs)/Diffusion Models (DDPMs) | Data augmentation for rare impact or defect classes in composites | Expands dataset diversity; mitigates class imbalance | May generate unrealistic data; training complexity | Very high Adversarial training (generator + discriminator) requires long, unstable convergence | Medium Single pass at inference |
| Autoencoders/Variational Autoencoders (VAEs) | Unsupervised delamination detection; feature learning from guided-wave signals | Learns compact feature embeddings; effective for novelty detection | Sensitive to sensor noise; may reconstruct damage as “healthy” | Medium Similar to MLP/CNN depending on encoder complexity | Low Fast reconstruction suitable for real-time novelty detection |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [26] | Data-driven | Damage detection on a composite sandwich wing’s front spar | SOM PCA | Accuracy of 98.1% |
| [27] | Data-driven | Damage detection in a carbon/epoxy plate | ANN | High resolution and generalization to any structure |
| [28] | Data-driven | Damage detection in a composite panel | Bayesian optimization algorithm | Reduction of time and computational costs |
| [29] | Model-based | Damage detection in a composite sandwich aeronautical spoiler | MLP | Numerical and experimental results demonstrate high efficiency |
| [137] | Model-based | Damage detection in composite laminates | ANN Metaheuristic optimization algorithm | Higher accuracy with respect to traditional ANNs |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [65] | Data-driven | Damage localization in a CFRP composite plate | PAA GAF CNN | Localization error of 7.58% |
| [138] | Data-driven | Damage localization in a composite panel | 1D-CNN gMLP | Small localization error |
| [139] | Data-driven | Damage localization in a composite sandwich | MDPI | High accuracy in detecting and visualizing damage position |
| [140] | Data-driven | Damage localization for complex composite structures | Imaging algorithm | Minimum localization error |
| [141] | Data-driven | Damage localization in a CFRP composite plate | DCNN recurrent regression algorithm | High accuracy and resolution. Only a few required sensors. |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [30] | Model-based | Damage detection and localization in a composite sandwich aeronautical spoiler | RF | High performance on numerical data; slightly weaker on experimental validation |
| [45] | Data-driven | Damage detection and localization in a CFRP composite panel | CAE TL | The method is scalable to any material |
| [66] | Data-driven | Damage detection and localization in a CFRP composite panel | CNN | Accuracies of 99.1% (detection) and 99.3% (localization) for damages |
| [142] | Data-driven | Damage detection and localization in a CFRP composite specimens | Imaging algorithm | Multipath Lamb waves reduce sensor requirements while maintaining accuracy |
| [143] | Model-based | Damage detection and localization in CFRP pin-joined truss structures | Hierarchical CNN | Model generalizes well compared with non-hierarchical approaches |
| [144] | Model-based | Damage detection and localization in a carbon/epoxy laminate | 1D-CNN 2D-CNN CNN LSTM | 2D-CNN for damage detection. CNN and LSTM for damage localization |
| [145] | Model-based | Damage detection and localization in the Airbus A350 composite wing | FEM + CNN | Accuracy of 99% in damage detection |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [46] | Data-driven | Damage classification in carbon/epoxy composite specimens | PCA K-Means SVM | Similar accuracy in detecting the type of damage |
| [47] | Data-driven | Damage classification in CFRP composite laminates | K-Means | The algorithm distinguishes the different damage modes |
| [67] | Data-driven | Damage detection and classification in CFRP composite plates | GAN DDPM DenseNet | Highest accuracy for the DDPM+DenseNet combination |
| [68] | Data-driven | Component-level SHM in military trainer | CNN-RM | Higher testing accuracy by introducing feedback connections |
| [146] | Data-driven | Damage localization and quantification in a CFRP composite panel | Supervised classification algorithms | Bagged Trees, with the highest accuracy for localization KNN, with the highest accuracy for quantification |
| [147] | Data-driven | Damage localization and quantification in a glass/epoxy composite plate | SVM | High accuracy with only a few PZT transducers |
| [148] | Data-driven | Damage localization and quantification in a CFRP composite panel | Imaging algorithm | Simple and intuitive proposed methods easily adaptable to online monitoring of composite structures |
| [149] | Data-driven | Damage localization and quantification in a CFRP composite panel | CHMM + quantitative imaging | 2D-CNN for damage detection; CNN and LSTM for damage localization |
| [150] | Data-driven | Damage localization and quantification in a CFRP composite layups | KNN SVM DT RF | Better DT performance with time domain features Better RF performance with frequency domain features |
| [151] | Data-driven | Damage classification in GFRP composites | Linear regression K-Means | The models correctly predict the type of damage, starting with both labelled and unlabeled data |
| [152] | Data-driven | Damage localization and quantification in a CFRP composite laminates | Bayesian algorithm Imaging algorithm | Good performance in detecting and visualizing damage |
| [153] | Model-based | Damage localization and quantification in composite structures | ANN | The network correctly predicts damage position and severity |
| [154] | Model-based | Damage quantification in a composite plate | YUKI-ANN | High accuracy and low computational time |
| [155] | Hybrid | Damage diagnosis in a CFRP composite plate and a composite beam | PCA SVM | SVM performance improves using NMB feature |
| [156] | Model-based | Damage detection, diagnosis of CFRP composite beams | Metropolis-Hastings algorithm | Working on raw data, reaching a high accuracy |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [48] | Data-driven | Fatigue life estimation of GFRP composites | XGBoost LightGBM CatBoost K-Means | XGBoost prove to be the best algorithm. The results show an agreement between predicted and actual values |
| [69] | Data-driven | Health index evaluation of a carbon/epoxy composite plate | SDNN Bayesian | The extracted HIs meet the prognostic criteria |
| [70] | Data-driven | RUL prediction of composite panels | PCA, MLP Bayesian | RUL estimation is improved by considering a time-dependent model for HI evaluation |
| [157] | Data-driven | RUL evaluation of CFRP composite panels | GA GPR | The method is material-independent; it can be generalized to any SHM application |
| [158] | Data-driven | RUL evaluation of CFRP composite panels | GPR BNN | RUL estimation is more accurate when utilizing 10 features instead of 1; GPR requires less training time than BNN |
| [159] | Data-driven | RUL evaluation of multi-stiffened panels | GPR LSTM | The RUL estimation is close to the real one, but strongly depends on HIs |
| [160] | Data-driven | Health index evaluation of stiffened carbon/epoxy composite panels | PCA | HI3, HI4, vHI1, and vHI2 meet the Mo criterion, but not the Pr criterion. The two AE-based HIs meet the Pr criterion, but not the Mo criterion |
| [161] | Data-driven | Fatigue damage index prediction for CFRP composite coupons | ME KNN XGBoost NN | The proposed ME algorithm proves to be better than the others, and presents lower computational time |
| [162] | Data-driven | Fatigue damage diagnosis of a CFRP composite plate | DAE DBSCAN | The method does not require manual feature extraction; hence computation times are reduced |
| [163] | Data-driven | Fatigue damage mode clustering in CFRP open-hole laminated beams | AE + DIC correlation | When trained on AE data, the algorithm can predict the fatigue failure in real time, compared to DIC data |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [164] | Data-driven | Impact detection and localization on a composite aircraft elevator | RF SAE ANN | Accuracy of 98.3%, 99.2%, and 96% for RF, SAE, and ANN |
| [165] | Data-driven | Impact localization in a composite aircraft elevator | Two SAE networks | Accuracy of 98% in classifying the impact zone; accuracy of 99.2% in localizing the impact |
| [166] | Data-driven | Impacts energy levels classification and uncertainty quantification in a composite plate | BNN ANN Multi-ANN | The algorithms can classify the energy levels and quantify the uncertainty for the perpendicular impacts Low performance arises for angle impacts |
| [167] | Data-driven | Localization of LVI in a composite plate | GA | Average localization error of 25.27 mm on a 500 × 500 mm plate |
| [168] | Data-driven | BVID recognition in a composite coupon | Four DL algorithm | ResNet best model to perform damage detection. Performance improves by embedding sensors within the structure |
| [169] | Data-driven | Impact localization and characterization in composite plates | CNN | The method accuracy is between 94.3% and 100% in predicting the impact location, while it is over 98.3% in classifying impact energy |
| [170] | Data-driven | Impact localization and characterization in CFRP composite plates | CNN | Accuracy of 99.76% and 97.04% for localization and characterization with MEMS data Accuracy of 99.58% and 98.68% for localization and characterization with PZT data |
| [171] | Data-driven | Impact localization and characterization in smart composite samples | CNN Bayesian optimization algorithm | Localization average error of 13.8% Classification average error of 11.3% |
| [172] | Data-driven | Impact localization in CFRP composite plate | Localization algorithm | The localization error for three drop heights, namely 50, 100, and 150 mm, is 8.8 mm, 9.5 mm, and 9.8 mm for a 300 × 300 mm plate |
| [173] | Data-driven | Impact localization in a composite plate | NSET ANN | The proposed method has an accuracy similar to that of the ANN-NSET method for hard impacts, while it is superior for soft impacts |
| [174] | Data-driven | Impact localization in flat and curved composite plates | NSET ANN | High accuracy of the ANN-NSET method, which is not affected by number of sensors and plate geometry |
| [175] | Model-based | Compression after impact strength prediction of carbon/glass hybrid laminates | XGBoost | Error of 3.55% in predicting the CAI strength |
| Article | Approach | Scope | Algorithms | Results |
|---|---|---|---|---|
| [176] | Data-driven | Impact energy and damage detection on aerospace panels | Polynomial regression ANN | Successful regression for impact energy, classification for damage detection |
| [177] | Data-driven | Thin-walled structures, thin-walled shells | RNN (GRU-based) | High localization accuracy with limited sensors, end-to-end training |
| [178] | Model-based | Crack damage detection in a composite sandwich plate | GP | Best performance when employing three sensors With only one sensor, the accuracy is 100%, but misclassification can arise |
| [179] | Model-based | Crack length and orientation prediction of CFRP twill-woven plates | Polynomial regression ANN | Polynomial regression proves to be better than ANN |
| [180] | Model-based | Crack length evaluation of GFRP composite specimens | E-Jaya-ANN | The algorithm reaches the highest accuracy with eight hidden neurons |
| [181] | Data-driven | Crack identification in sandwich composites | SVM KNN DCNN | Accuracy of 78.23%, 85.56%, and 94.33% for SVM, KNN, and DCNN |
| [182] | Model-based | Classification of location and severity of cracks in GFRP composite beams | 1D-CNN | Accuracy 95% and 93% for single/double damage classification With merged data to train the algorithm, accuracy of 92% after optimizing the hyperparameters |
| [183] | Data-driven | Crack classification in 3D woven composites | U-Net | Accuracy of more than 88% in crack classification |
| [184] | Data-driven | Matrix cracking classification in glass/epoxy laminates | SVM LVQ MLP | SVM and LVQ outperformed MLP, with SVM having the highest accuracy, at 91.7% |
| [185] | Model-based | Mechanical deformation, strength, and progressive damage prediction of a CFRP composite laminate with circular holes | ANN | Good performance and time reduction in global monitoring |
| [186] | Data-driven | Bending and torsional load spectra prediction on an aircraft wing | ARX, ARMAX, CFN, TDN, LRN, NXN LSTM, Bi-LSTM | Bending loads can be predicted by the auto-regressive models and ANNs, while torsional loads require the use of RNNs Tip torsional loads can be predicted only by Bi-LSTM |
| [187] | Data-driven | Real-time monitoring of NFRP composites during the machining phase | RF | RF shows better performance, with an accuracy of 94% in classifying cutting or non-cutting Accuracy of 95% in distinguishing fiber orientations towards the cutting orientation |
| [188] | Model-based | Optimization of number and orientation of sensors | NSGA-II GPR | The method can optimize the sensors layout The model is validated by conducting a delamination detection |
| [189] | Hybrid | Localization of acoustic sources in a composite laminate | BPN | Accuracy of 100% when trained on numerical data, while accuracy is lower when trained on experimental data |
| [190] | Hybrid | Breathing-debond assessment in fiber-reinforced stiffened composite panels | CNN CWT | Accuracy of 85.6% when trained on experimental data improved to 95.9% on training with higher harmonic signals |
| SHM Task | ML Approach | Strengths | Weaknesses/Challenges | Typical TRL |
|---|---|---|---|---|
| Damage Detection | Supervised Learning (SVM, RF, Decision Trees) | High accuracy with labeled data; interpretable in classical ML; robust for known damage modes | Requires large, labeled datasets; poor generalization to unseen damage types | 4–6 |
| Unsupervised Learning (Clustering, PCA, Autoencoders) | No labels needed; good for novelty detection; adaptable to changing conditions | Higher false-positive rate; difficult to tune thresholds; less explainable | 3–5 | |
| Deep Learning (CNN, 1D/2D) | Learns directly from raw signals/images; handles complex patterns | High data/computational demand; “black-box” nature; certification barriers | 3–5 | |
| Damage Localization | Model-Based ML (FEM + ML hybrid) | Incorporates physics; fewer experimental datasets needed; interpretable | Requires accurate structural model; sensitive to modelling errors | 4–6 |
| Deep Learning (CNN, RNN, LSTM) | Captures spatial/temporal patterns; good for guided-wave data | Large training datasets needed; performance degrades under sensor drift | 3–5 | |
| Probabilistic Imaging + ML | Provides visual output; intuitive for operators | Dependent on sensor density/placement; computationally intensive | 4–5 | |
| Damage Classification and Quantification | Ensemble Methods (RF, Gradient Boosting) | High accuracy; handles mixed feature sets well; robust to noise | Requires hand-crafted features; still needs labelled data | 4–6 |
| Deep Neural Networks + Data Augmentation (GAN, DDPM) | Handles multiple damage types; reduces manual feature extraction | Synthetic data may not match flight conditions; heavy compute cost | 3–5 | |
| Hybrid PCA + ML | Reduces feature dimensionality; improves interpretability | May discard subtle features if poorly tuned | 4–6 | |
| Fatigue Prognosis/RUL Estimation | Gaussian Process Regression (GPR) | Captures uncertainty; good for small datasets; interpretable | Limited scalability to very large datasets | 4–6 |
| Recurrent Networks (LSTM, GRU) | Models time dependence; captures degradation trends | Needs long-term monitoring data; prone to overfitting | 3–5 | |
| Semi-supervised/Transfer Learning | Leverages small, labelled datasets; adaptable to new structures | Performance depends on domain similarity; not yet standardized in aerospace | 2–4 | |
| Multi-Task SHM | Digital Twin + ML Hybrid | Combines simulation and real data; supports multiple SHM tasks | High setup cost; needs reliable real-time data integration | 2–4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarselli, G.; Nicassio, F. Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review. Sensors 2025, 25, 6136. https://doi.org/10.3390/s25196136
Scarselli G, Nicassio F. Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review. Sensors. 2025; 25(19):6136. https://doi.org/10.3390/s25196136
Chicago/Turabian StyleScarselli, Gennaro, and Francesco Nicassio. 2025. "Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review" Sensors 25, no. 19: 6136. https://doi.org/10.3390/s25196136
APA StyleScarselli, G., & Nicassio, F. (2025). Machine Learning for Structural Health Monitoring of Aerospace Structures: A Review. Sensors, 25(19), 6136. https://doi.org/10.3390/s25196136







