Tuberculosis Detection from Cough Recordings Using Bag-of-Words Classifiers
Abstract
1. Introduction
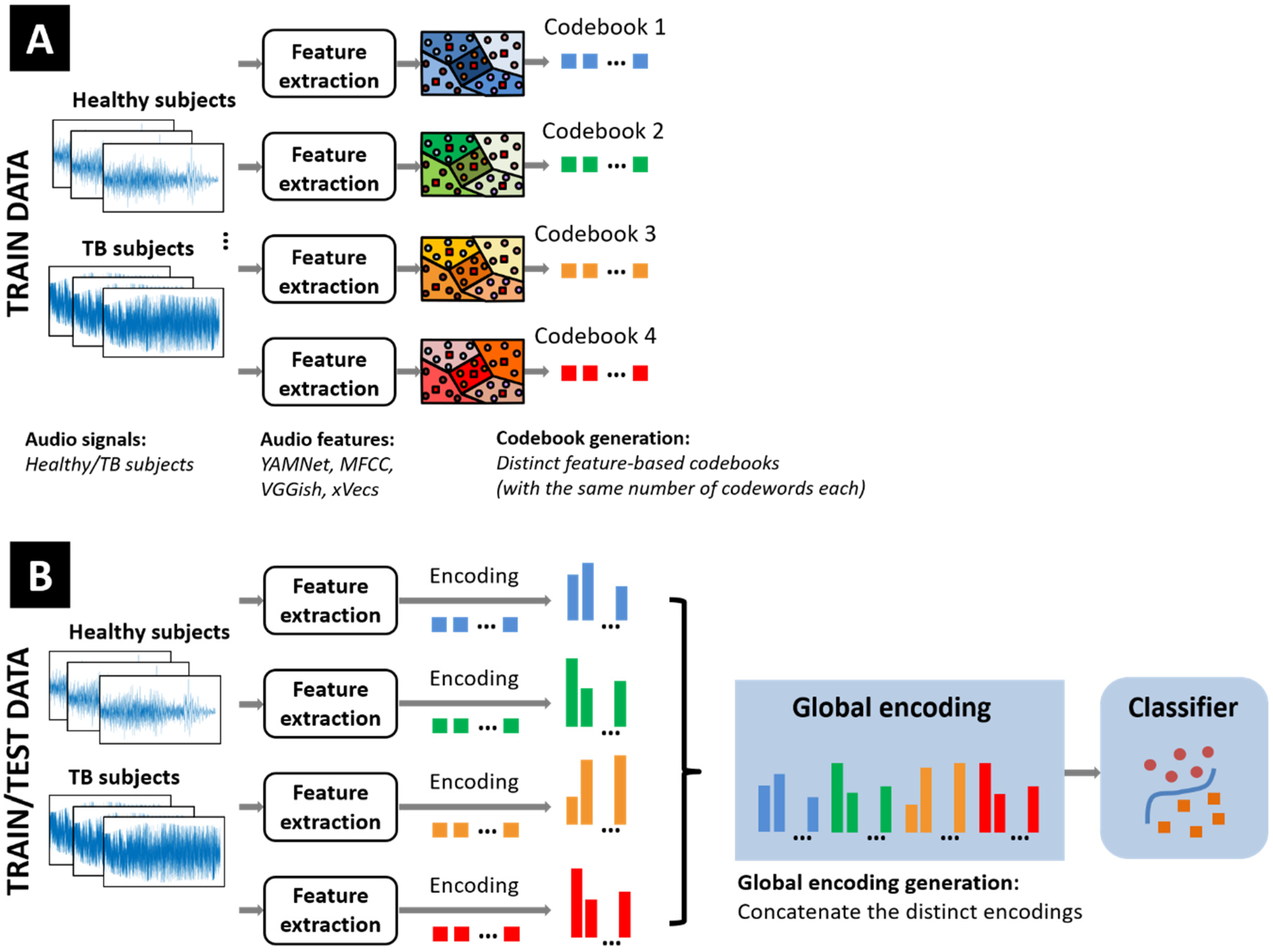
2. Bag-of-Words Classification Models for Tuberculosis Detection
2.1. Overview of BoW Models
- (a)
- Computation of specific (typically, hand-crafted) feature vectors extracted from successive (fixed-length) temporal intervals from the time series under study. In case several distinct datasets are used (e.g., for external set performance validation), all data follow a similar processing procedure, using identical setup parameters.
- (b)
- A set of prototype vectors representative of the feature set distribution is further generated. Those form a codebook including an application-specific number of codewords, typically obtained by employing various clustering algorithms.
- (c)
- A single or, more generally, a combination of specific codewords is next assigned to each feature vector. Special properties of the selected codewords may be imposed by the various encoding algorithms introduced in the literature (e.g., seeking the sparsest subset of codewords that approximates a given feature vector).
- (d)
- Counting the frequency of codeword appearances and computing the corresponding histogram provides a compact description of a given time series. One of the key advantages of BoW models is that the approach can accommodate variable-length time series. As such, the resulting histograms may exhibit variable dynamic ranges, hence the need for using scale-normalization procedures.
- (e)
- The final classification step may consider various models and specific distance measures, some of which are particularly useful when dealing with histogram-type data [28].
2.2. Data Processing and Feature Extraction
- (a)
- Mel-frequency spectrogram coefficients computed from 50% overlapping 1 s long audio segments. Distinct spectrograms were generated for each segment with a window size of 25 ms, a window hop of 10 ms, and a periodic Hanning window. A total of 64 Mel bins covering the frequency range from 50 Hz to 4 kHz were used, and after converting the mel-spectrogram into a log scale, we obtained 64 × 96 images per segment. The distinct spectrograms originating from multiple cough bursts acquired from the same human subject were concatenated along the mel band dimension.
- (b)
- Two additional feature types are obtained by intercepting the outputs of specific inner layers of a couple of (pre-trained) convolutional neural network models frequently used in audio applications, the input of which is given by the mel spectrograms described above. The first option is the YAMNet model [32], which yields 1024-long feature vectors by reading the output of the last layer before the classification module (the layer is called global_average_pooling2d in MATLAB R2023b). The model has been pre-trained to identify 521 distinct audio classes, including cough, using the AudioSet-YouTube corpus [32]. As such, it has also been considered a viable solution for segmenting audio recordings and eliminating pauses between actual cough bursts. The second option considers the VGGish model (inspired by the well-known VGG-type image classification architectures) [33], by reading the output of the EmbeddingBatch layer that returns a set of 128-long feature vectors.
- (c)
- x-vectors have emerged as a performant speaker identification approach [34], but have also been successfully used in various extra-linguistic tasks. The vectors are computed from successive 1 s long audio segments and a window hop of 0.1 s, extracted from the output of the first fully connected layer of the pre-trained model described in [34]. The resulting 512-long vectors are further reduced to a 150-long common length by linear projection using a pre-trained linear discriminant analysis matrix [34].
2.3. Codebook Generation
2.4. Encoding Procedure
2.5. Similarity Measures
2.6. Classifiers
3. Experimental Results
3.1. Training Datasets
| Dataset | No. Subjects | Sensor Type | Sampling Rate | Access | Remarks |
|---|---|---|---|---|---|
| Wallacedene [17] | 16 TB, 35 non-TB | Condenser microphone | 44.1 kHz | private | various numbers of cough events per recording |
| Brooklyn [47] | 17 TB, 21 healthy | Condenser microphone | 44.1 kHz | private | controlled indoor booth |
| CIDRZ [22] | 46 TB, 183 non-TB | Variable quality smartphones | 192 kHz | private | three single coughs and one sequence of multiple coughs |
| Swaasa [48] | 278 TB, 289 non-TB | smartphones and tablets | 44.1 kHz | private | 10 s recordings, noise filtering |
| Xu [19] | 141 TB, 152 healthy, 52 other resp. diseases | smartphone | 44.1 kHz | private | quiet room, augmentation used |
| Sharma [18] | 103 TB, 46 non-TB | 3 microphone types | 16 kHz, 44.1 kHz | public | various audio bandwidths |
| CODA TB DREAM Challenge [46] | 297 TB, 808 healthy | smartphones with the Hyfe app | 44.1 kHz | upon request | 2143 patients across 7 countries, 0.5 s segments |
| Xu [49] | 70 TB, 74 healthy | smartphone | 44.1 kHz | public | 0.35 s multiple cough events |
3.2. Effect of the Sampling Frequency
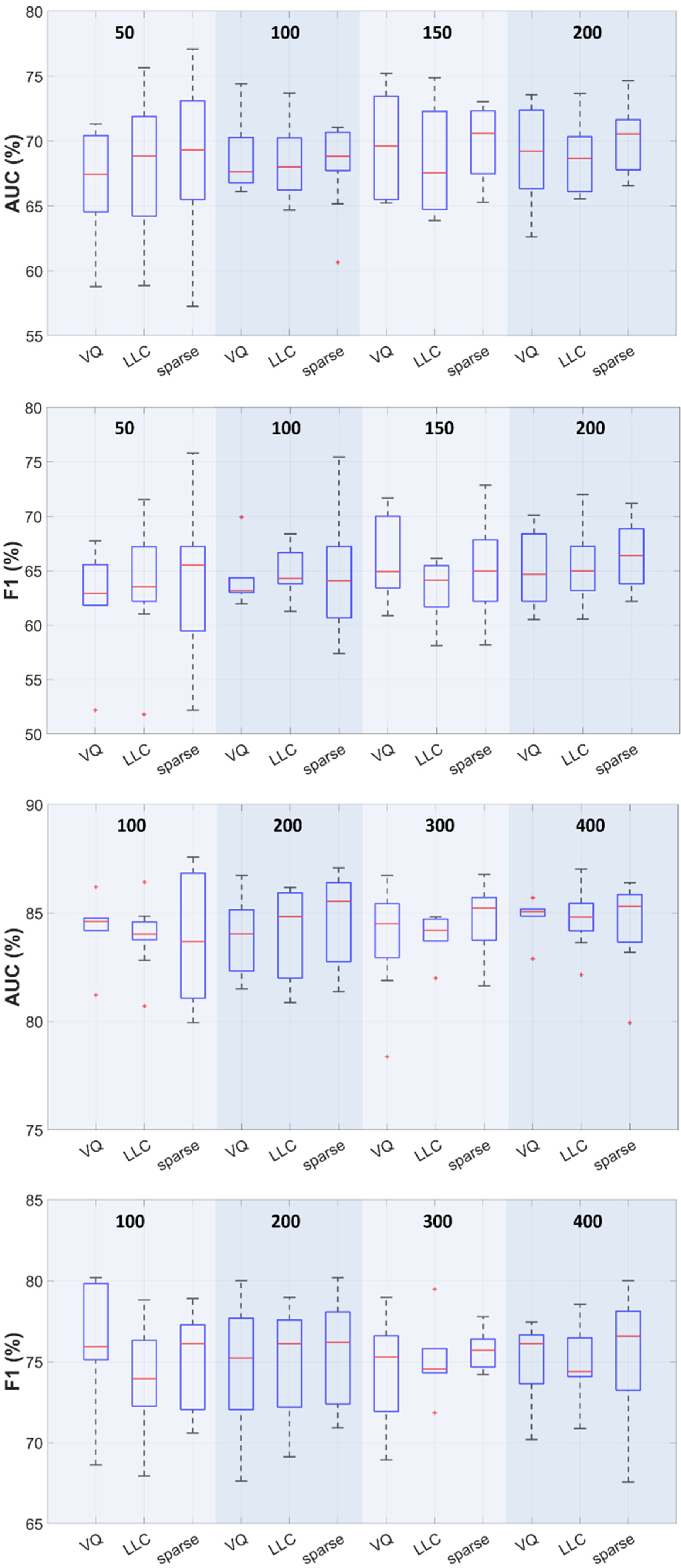
3.3. Effect of the Feature Set Type
3.4. Effect of the Encoding Procedure
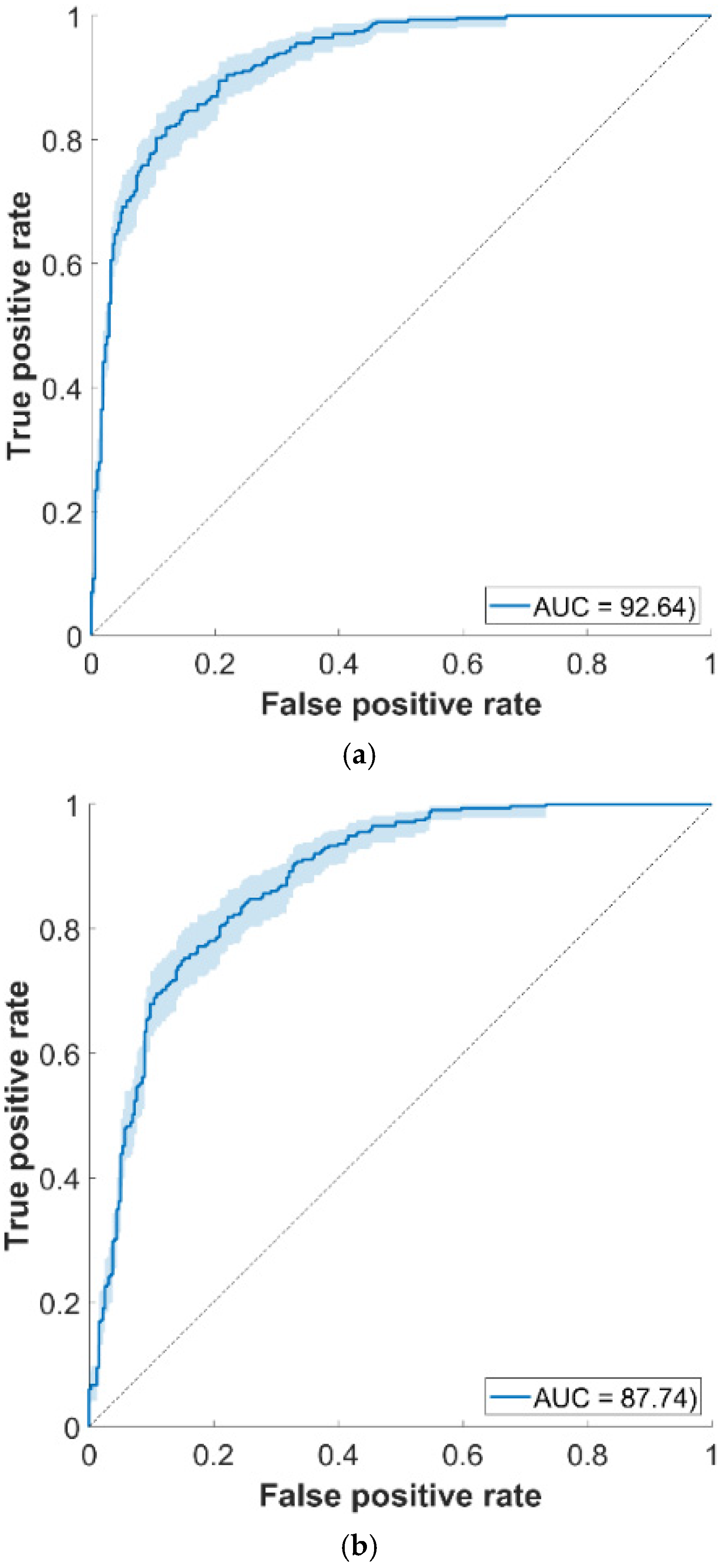
3.5. External Set Validation
3.6. Comparison Against Other Approaches
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hayman, J. Mycobacterium ulcerans: An infection from Jurassic time? Lancet 1984, 324, 1015–1016. [Google Scholar] [CrossRef]
- Cave, A.J.E. The evidence for the incidence of tuberculosis in ancient Egypt. Br. J. Tuberc. 1939, 33, 142–152. [Google Scholar] [CrossRef]
- Morse, D. Tuberculosis. In Diseases in Antiquity. A Survey of the Diseases, Injuries and Surgery of Early Populations; Brothwell, D.J., Sandison, A.T., Eds.; Charles C. Thomas Publisher: Springfield, IL, USA, 1967. [Google Scholar]
- Daniel, T.M. The history of tuberculosis. Resp. Med. 2006, 100, 1862–1870. [Google Scholar] [CrossRef] [PubMed]
- Barberis, I.; Bragazzi, N.L.; Galluzzo, L.; Martini, M. The history of tuberculosis: From the first historical records to the isolation of Koch’s bacillus. J. Prev. Med. Hyg. 2017, 58, E9–E12. [Google Scholar] [PubMed]
- World Health Organization. Available online: https://www.who.int/news-room/fact-sheets/detail/tuberculosis (accessed on 10 March 2025).
- Koch, R. Die Atiologic der Tuberkulose. Berl. Klin. Wochenschr. 1862, 15, 221–230. [Google Scholar]
- World Health Organization. WHO Consolidated Guidelines on Tuberculosis: Module 3: Diagnosis: Tests for TB Infection. Available online: https://www.who.int/publications/i/item/9789240056084 (accessed on 11 March 2025).
- Hansun, S.; Argha, A.; Bakhshayeshi, I.; Wicaksana, A.; Alinejad-Rokny, H.; Fox, G.J.; Marks, G.B. Diagnostic performance of artificial intelligence–based methods for tuberculosis detection: Systematic review. J. Med. Internet Res. 2025, 27, e69068. [Google Scholar] [CrossRef]
- Nansamba, B.; Nakatumba-Nabende, J.; Katumba, A.; Kateete, D.P. A systematic review on application of multimodal learning and explainable AI in tuberculosis detection. IEEE Access 2025, 13, 62198–62221. [Google Scholar] [CrossRef]
- Chawla, N.W.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Korpáš, J.; Sadloňová, J.; Vrabec, M. Analysis of the cough sound: An overview. Pulm. Pharm. 1996, 9, 261–268. [Google Scholar] [CrossRef]
- Frost, G.; Theron, G.; Niesler, T. TB or not TB? Acoustic cough analysis for tuberculosis classification. In Proceedings of the Interspeech, Incheon, Republic of Korea, 18–22 September 2022. [Google Scholar]
- Copppock, H.; Nicholson, G.; Kiskin, I.; Koutra, V.; Baker, K.; Budd, J.; Holmes, C. Audio-based AI classifiers show no evidence of improved COVID-19 screening over simple symptoms checkers. Nat. Mach. Intell. 2024, 6, 229–242. [Google Scholar] [CrossRef]
- Wynants, L.; Van Calster, B.; Collins, G.S.; Riley, R.D.; Heinze, G.; Schuit, E.; Bonten, M.M.J.; Dahly, D.L.; Damen, J.A.; Debray, T.P.A.; et al. Prediction models for diagnosis and prognosis of COVID-19: Systematic review and critical appraisal. BMJ 2020, 369, m1328. [Google Scholar] [CrossRef]
- Zimmer, A.J.; Ugarte-Gil, C.; Pathri, R.; Dewan, P.; Jaganath, D.; Cattamanchi, A.; Pai, M.; Lapierre, S.G. Making cough count in tuberculosis care. Nat. Comm. Med. 2022, 2, 83. [Google Scholar] [CrossRef]
- Pahar, M.; Klopper, M.; Reeve, B.; Warren, R.; Theron, G.; Niesler, T. Automatic cough classification for tuberculosis screening in a real-world environment. Phys. Meas. 2021, 42, 105014. [Google Scholar] [CrossRef]
- Sharma, M.; Nduba, V.; Njagi, L.N.; Murithi, W.; Mwongera, Z.; Hawn, T.R.; Patel, S.N.; Horne, D.J. TBscreen: A passive cough classifier for tuberculosis screening with a controlled dataset. Sci. Adv. 2024, 10, eadi0282. [Google Scholar] [CrossRef]
- Xu, W.; Yuan, H.; Lou, X.; Chen, Y.; Liu, F. DMRNet Based tuberculosis screening with cough sound. IEEE Access 2023, 12, 3960–3968. [Google Scholar] [CrossRef]
- Pahar, M.; Theron, G.; Niesler, T. Automatic tuberculosis detection in cough patterns using NLP-style cough embeddings. In Proceedings of the ICEET, Kuala Lumpur, Malaysia, 27–28 October 2022. [Google Scholar]
- Rajasekar, S.J.S.; Balaraman, A.R.; Balaraman, D.V.; Ali, S.M.; Narasimhan, K.; Krishnasamy, N.; Perumal, V. Detection of tuberculosis using cough audio analysis: A deep learning approach with capsule networks. Discov. Artif. Intell. 2024, 4, 77. [Google Scholar] [CrossRef]
- Baur, S.; Nabulsi, Z.; Weng, W.H.; Garrison, J.; Blankemeier, L.; Fishman, S.; Chen, C.; Kakarmath, S.; Maimbolwa, M.; Sanjase, N.; et al. HeAR—Health Acoustic Representations. Available online: https://arxiv.org/abs/2403.02522 (accessed on 15 March 2025).
- Pavel, I.; Ciocoiu, I.B. COVID-19 detection from cough recordings using Bag-of-Words classifiers. Sensors 2023, 23, 4996. [Google Scholar] [CrossRef] [PubMed]
- Pavel, I.; Ciocoiu, I.B. Multiday personal identification and authentication using electromyogram signals and Bag-of-Words classification models. IEEE Sens. J. 2024, 24, 42373–42383. [Google Scholar] [CrossRef]
- Lin, J.; Keogh, E.; Wei, L.; Lonardi, S. Experiencing SAX: A novel symbolic representation of time series. Data Min. Knowl. Discov. 2007, 15, 107–144. [Google Scholar] [CrossRef]
- Baydogan, M.G.; Runger, G.; Tuv, E. A bag-of-features framework to classify time series. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2796–2802. [Google Scholar] [CrossRef]
- Dance, C.; Willamowski, J.; Fan, L.; Bray, C.; Csurka, G. Visual categorization with bags of keypoints. In Proceedings of the ECCV International Workshop on Statistical Learning in Computer Vision, Prague, Czech Republic, 16 May 2004; pp. 1–16. [Google Scholar]
- Wang, J.; Liu, P.; She, M.F.; Nahavandi, S.; Kouzani, A. Bag-of-words representation for biomedical time series classification. Biomed. Signal Proc. Control 2013, 8, 634–644. [Google Scholar] [CrossRef]
- Ribeiro, M.; Singh, S.; Guestrin, C. Why should I trust you?: Explaining the predictions of any classifier. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, San Diego, CA, USA, 12–17 June 2016; pp. 1135–1144. [Google Scholar]
- Eyben, F.; Wöllmer, M.; Schuller, B. openSMILE—The Munich versatile and fast open-source audio feature extractor. In Proceedings of the ACM Multimedia, Florence, Italy, 25–29 October 2010. [Google Scholar]
- Librosa. Available online: https://librosa.org/ (accessed on 15 March 2025).
- Gemmeke, J.F.; Ellis, D.P.W.; Freedman, D.; Jansen, A.; Lawrence, W.; Moore, R.C.; Plakal, M.; Ritter, M. Audio Set: An ontology and human-labeled dataset for audio events. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.; Gemmeke, J.F.; Jansen, A.; Moore, C.; Plakal, M.; Platt, D.; Saurous, R.; Seybold, B.; et al. CNN architectures for large-scale audio classification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Snyder, D.; Garcia-Romero, D.; Sell, G.; Povey, D.; Khudanpur, S. x-vectors: Robust DNN embeddings for speaker recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the SODA ’07, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Lewicki, M.S.; Sejnowski, T.J. Learning over complete representations. Neural Comput. 2000, 12, 337–365. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, R.; Bruckstein, A.M.; Elad, M. Dictionaries for sparse representation modeling. Proc. IEEE 2010, 98, 1045–1057. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Wang, J.; Yang, J.; Yu, K.; Lv, F.; Huang, T.; Gong, Y. Locality-constrained linear coding for image classification. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 July 2010; pp. 3360–3367. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- LIBSVM—A Library for Support Vector Machines. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 15 March 2025).
- Vedaldi, A.; Zisserman, A. Efficient additive kernels via explicit feature maps. IEEE Trans. Patt. Anal. Mach. Intell. 2012, 34, 480–492. [Google Scholar] [CrossRef]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. Safe-level-SMOTE: Safe-level-synthetic minority over-sampling technique for handling the class imbalanced problem. In Proceedings of the PAKDD, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5476. [Google Scholar]
- Lella, K.K.; PJA, A. Automatic covid-19 disease diagnosis using 1D convolutional neural network and augmentation with human respiratory sound based on parameters: Cough, breath, and voice. AIMS Public Health 2021, 8, 240–264. [Google Scholar] [CrossRef]
- Huddart, S.; Yadav, V.; Sieberts, S.K.; Omberg, L.; Raberahona, M.; Rakotoarivelo, R.; Lyimo, I.N.; Lweno, O.; Christopher, D.J.; Nhung, N.V.; et al. A dataset of solicited cough sound for tuberculosis triage testing. Sci. Data 2024, 11, 1149. [Google Scholar] [CrossRef]
- Pahar, M.; Klopper, M.; Reeve, B.; Warren, R.; Theron, G.; Diacon, A.; Niesler, T. Automatic tuberculosis and COVID-19 cough classification using deep learning. In Proceedings of the ICECET, Prague, Czech Republic, 20–22 July 2022. [Google Scholar]
- Yellapu, G.D.; Rudraraju, G.; Sripada, N.R.; Mamidgi, B.; Jalukuru, C.; Firmal, P.; Yechuri, V.; Varanasi, S.; Peddireddi, V.S.; Bhimarasetty, D.M.; et al. Development and clinical validation of Swaasa AI platform for screening and prioritization of pulmonary TB. Sci. Rep. 2023, 13, 4740. [Google Scholar] [CrossRef]
- Xu, W.; Bao, X.; Lou, X.; Liu, X.; Chen, Y.; Zhao, X.; Zhang, C.; Pan, C.; Liu, W.; Liu, F. Feature fusion method for pulmonary tuberculosis patient detection based on cough sound. PLoS ONE 2024, 19, e0302651. [Google Scholar] [CrossRef]
- Xia, T.; Spathis, D.; Brown, C.; Grammenos, A.; Han, J.; Hasthanasombat, A.; Bondareva, E.; Dang, T.; Floto, A.; Cicuta, P.; et al. COVID-19 Sounds: A large-scale audio dataset for digital respiratory screening. In Proceedings of the NeurIPS, Virtual, 6–14 December 2021. [Google Scholar]
- Coppock, H.; Akman, A.; Bergler, C.; Gerczuk, M.; Brown, C.; Chauhan, J.; Grammenos, A.; Hasthanasombat, A.; Spathis, D.; Xia, T.; et al. A summary of the ComParE COVID-19 challenges. Front. Digit. Health 2023, 5, 1058163. [Google Scholar] [CrossRef] [PubMed]
- Botha, G.H.R.; Theron, G.; Warren, R.M.; Klopper, M.; Dheda, K.; van Helden, P.; Niesler, T.R. Detection of tuberculosis by automatic cough sound analysis. Phys. Meas. 2018, 39, 045005. [Google Scholar] [CrossRef]
- Magni, C.; Chellini, E.; Lavorini, F.; Fontana, G.A.; Widdicombe, J. Voluntary and reflex cough: Similarities and differences. Pulm. Pharmacol. Ther. 2011, 24, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Nadeau, C.; Bengio, Y. Inference for the generalization error. Mach. Learn. 2003, 52, 239–281. [Google Scholar] [CrossRef]
- Bouckaert, R.; Frank, E. Evaluating the replicability of significance tests for comparing learning algorithms. In Proceedings of the Advances in Knowledge Discovery and Data Mining, Sydney, Australia, 26–28 May 2004. [Google Scholar]

| Dataset parameters | Subjects per Class | Accuracy | Sensitivity | Specificity | Precision | F1-Score | AUC (CI) |
|---|---|---|---|---|---|---|---|
| Sampling rate: 16 kHz Filter: 50 Hz–4 kHz | 290 | 63.4 ± 3.8 | 67.9 ± 7.2 | 59 ± 6.4 | 62.4 ± 3.8 | 64.9 ± 4.2 | 66.7 (63.1–70.2) |
| 600 | 74.2 ± 4.2 | 61.1 ± 7.7 | 87.3 ± 3.6 | 82.8 ± 4.5 | 70.2 ± 5.8 | 82.7 (80.7–84.7) | |
| Sampling rate: 44.1 kHz Filter: 50 Hz–4 kHz | 290 | 65.8 ± 2.6 | 67.9 ± 5.1 | 63.6 ± 5 | 65.2 ± 2.8 | 66.4 ± 3 | 70.3 (67.1–71.7) |
| 600 | 77.2 ± 3.1 | 70.4 ± 5 | 84 ± 3 | 81.5 ± 3.2 | 75.5 ± 3.7 | 84.5 (83–86) | |
| Sampling rate: 44.1 kHz Filter: 50 Hz–15 kHz | 290 | 64.6 ± 4.2 | 66.2 ± 6.4 | 63.1 ± 5.2 | 64.7 ± 5.8 | 65.1 ± 3.7 | 69.5 (65.8–73.3) |
| 600 | 75.7 ± 3.7 | 63.6 ± 6.9 | 87.8 ± 2.4 | 83.9 ± 3 | 72.2 ± 5.1 | 84.5 (82–87.3) |
| Dataset | Subjects per Class | No. CodeWords | Accuracy | Sensitivity | Specificity | Precision | F1-Score | AUC (CI) |
|---|---|---|---|---|---|---|---|---|
| Sharma [18] | 110 | 50 | 75.9 (±6) | 74.5 (±6.9) | 77.2 (±6.2) | 78 (±6.8) | 75.7 (±5.1) | 83.9 (78.7–89.2) |
| CODA [46] | 290 | 200 | 65.8 (±2.7) | 67.9 (±5.1) | 63.6 (±5) | 65.2 (±2.8) | 66.4 (±3) | 70.3 (67.1–71.7) |
| CODA + SMOTE | 600 | 400 | 77.2 (±3.1) | 70.4 (±5) | 84 (±3) | 81.5 (±3.3) | 75.5 (±3.7) | 84.5 (83–86) |
| CODA + Sharma | 600 | 400 | 73.1 (±4.1) | 63.8 (±4.6) | 82.5 (±5.2) | 76.7 (±5.2) | 77.2 (±5.5) | 83 (81–85) |
| Dataset | Subjects per Class | No. Codewords | Accuracy | Sensitivity | Specificity | Precision | F1-Score | AUC |
|---|---|---|---|---|---|---|---|---|
| T1 | 315 | 200 | 83.9 | 78.1 | 89.8 | 80 | 84.8 | 92.6 |
| T2 | 315 | 200 | 78.1 | 70.1 | 85.4 | 74.3 | 79.4 | 87.7 |
| T3 (YAMNet + xVecs) | 137 | 200 | 56.6 | 54 | 59.3 | 57 | 55.4 | 57 |
| Reference | Features/Classifier | No. Subjects | Validation | Performances | Remarks |
|---|---|---|---|---|---|
| Baur et al. [22] | Self-supervised deep learning/masked autoencoders | 24 TB, 240 non-TB | Internal | AUC: 0.739 | Robustness against recording devices |
| G.H.R. Botha et al. [52] | Log-spectral energies + MFCC/Logistic regression | 17 TB, 21 healthy | Internal | Accuracy: 0.80/0.63 AUC: 0.81/0.71 for log-spectral energy/MFCC | Sequential forward search used for selecting the best features |
| CODA TB DREAM Challenge [46] | CNN on spectrograms; Selected features from Librosa library + Gradient Boosting Decision Tree | 297 TB, 808 healthy | Internal | AUC: 0.689–0.743 across algorithms | 50 Hz–15 kHz audio range, random resampling to cope with data imbalance |
| M. Pahar et al. [17] | MFCCs, log-filterbank energies, zero-crossing rate, kurtosis/ Logistic regression | 16 TB, 35 non-TB | Internal | Accuracy: 0.845 ACC: 0.863 ± 0.06 | Sequential forward search for best feature selection |
| Sharma et al. [18] | CNN on scalograms | 103 TB, 46 non-TB | Internal | AUC: 0.61–0.86 | Experiments using 3 distinct mic types |
| G.D. Yellapu et al. [48] | MFCC, spectral, chroma, contrast, statistical moments/CNN, ANN | 278 TB, 289 non-TB | External | Accuracy: 0.78 AUC: 0.9 | Selected features Explainability using LIME |
| G. Frost et al. [13] | Mel-spectrograms, Linear filter-bank energies, and MFCC + BiLSTM | 28 TB, 46 non-TB | Internal | Accuracy: 0.68–0.8 AUC: 0.769–0.862 | Data augmentation |
| S.J.S. Rajasekar et al. [21] | Spectrograms + HOG features/capsule networks | 297 TB, 808 healthy | Internal | Accuracy: 0.89–0.97 AUC: 0.81–0.97 | Spectral subtraction to reduce noise |
| Present paper | MFCC, YAMNet, VGGish, x-Vecs/BoW | up to 600 per class | External | Accuracy: 0.65–0.77 AUC: 0.70–0.84 | Data augmentation, input fusion |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavel, I.; Ciocoiu, I.B. Tuberculosis Detection from Cough Recordings Using Bag-of-Words Classifiers. Sensors 2025, 25, 6133. https://doi.org/10.3390/s25196133
Pavel I, Ciocoiu IB. Tuberculosis Detection from Cough Recordings Using Bag-of-Words Classifiers. Sensors. 2025; 25(19):6133. https://doi.org/10.3390/s25196133
Chicago/Turabian StylePavel, Irina, and Iulian B. Ciocoiu. 2025. "Tuberculosis Detection from Cough Recordings Using Bag-of-Words Classifiers" Sensors 25, no. 19: 6133. https://doi.org/10.3390/s25196133
APA StylePavel, I., & Ciocoiu, I. B. (2025). Tuberculosis Detection from Cough Recordings Using Bag-of-Words Classifiers. Sensors, 25(19), 6133. https://doi.org/10.3390/s25196133






