PIV-FlowDiffuser: Transfer-Learning-Based Denoising Diffusion Models for Particle Image Velocimetry
Abstract
1. Introduction
- The denoising diffusion model (PIV-FlowDiffuser) is applied to PIV for the first time. PIV-FlowDiffuser employs an explicit correction mechanism that refines the estimated flow field iteratively, thereby reducing overall measurement errors.
- Transfer learning technique is employed to train deep models for PIV prediction, i.e., fine-tuning a pre-trained FlowDiffuser model from the computer vision domain. This approach leverages the robust feature extraction and flow reconstruction capabilities obtained through pre-training, potentially reducing the need for extensive labeled PIV data. Consequently, this enables accurate PIV estimation with reduced training time and enhances the model’s generalization performance.
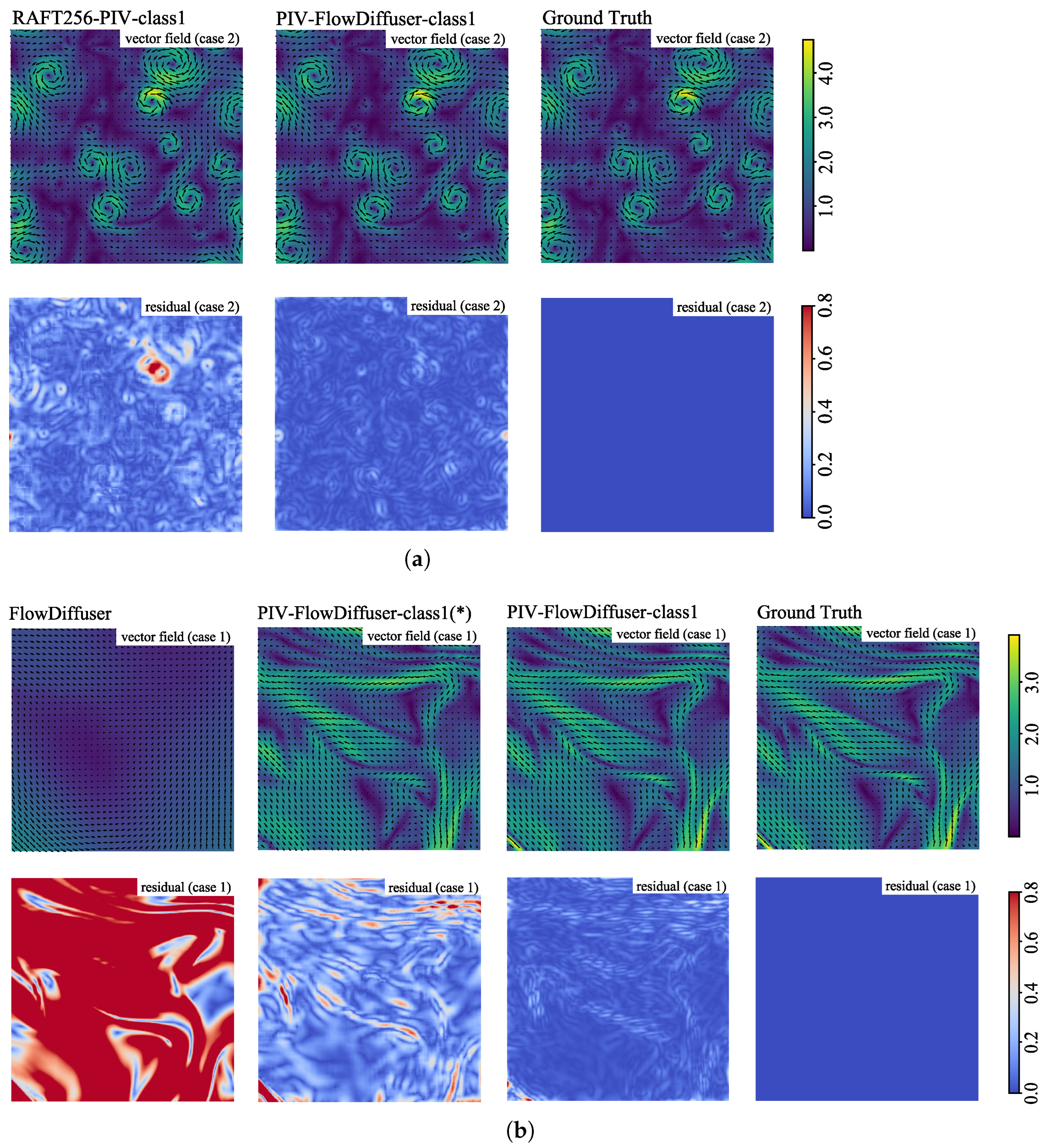
- The feasibility of our PIV-FlowDiffuser model was validated through extensive synthetic and practical PIV images. Compared to the existing RAFT256-PIV model, our PIV-FlowDiffuser demonstrates decreased measurement errors, as evidenced by lower residuals in visualizations. Specifically, it achieves a reduction in the average endpoint error (AEE). Furthermore, the model exhibits superior accuracy on previously unseen data, indicating excellent generalization performance.
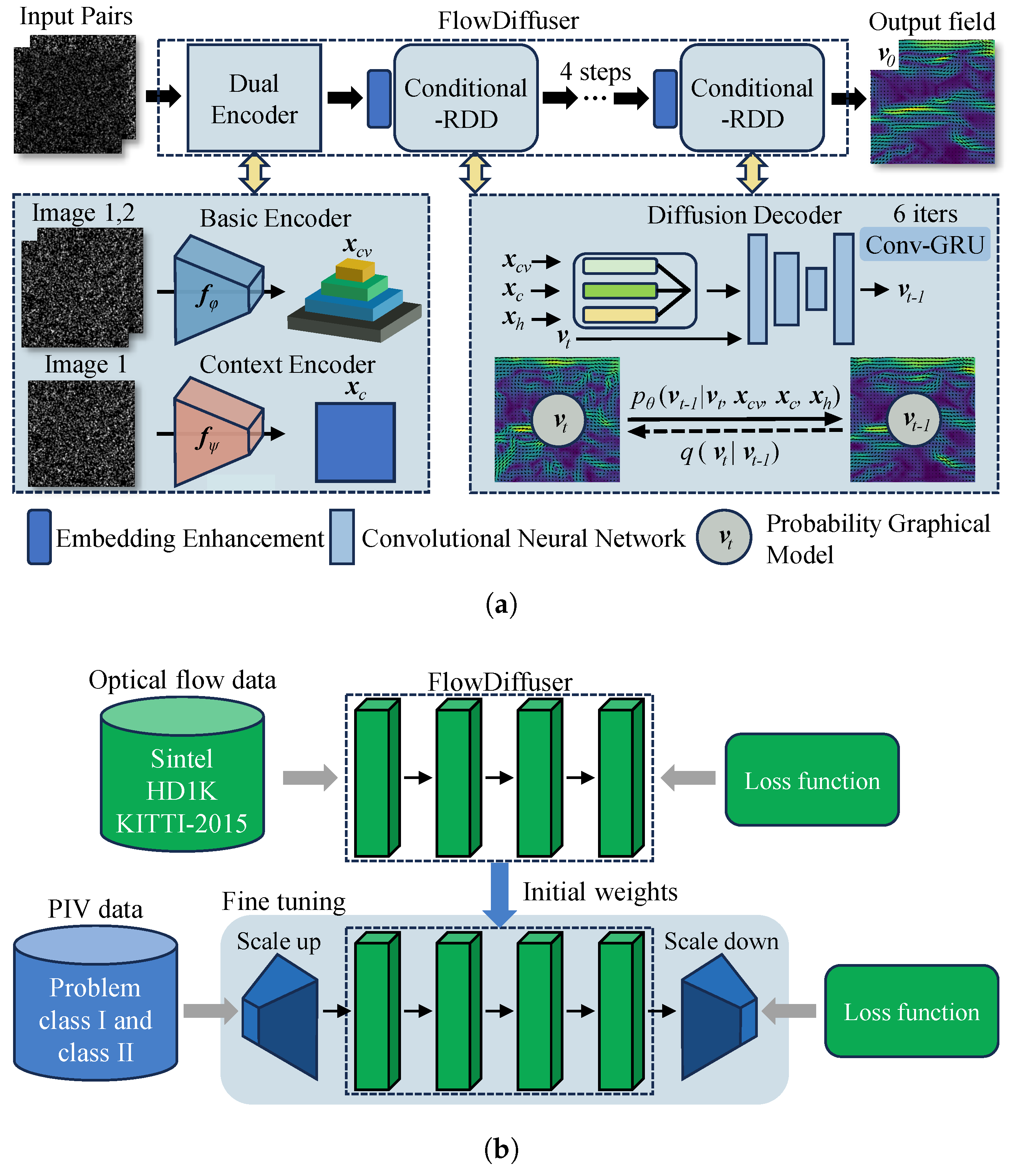
2. Transfer-Learning-Based Denoising Diffusion Models for PIV
2.1. The FlowDiffuser Model for PIV
2.2. Transfer-Learning-Based Training
2.3. Datasets
3. Experimental Arrangement
3.1. Evaluation Metrics
3.2. Baseline Methods
4. Results and Discussions
4.1. Accuracy Performance on Synthetic Images
4.2. Generalization to Out-of-Domain Dataset
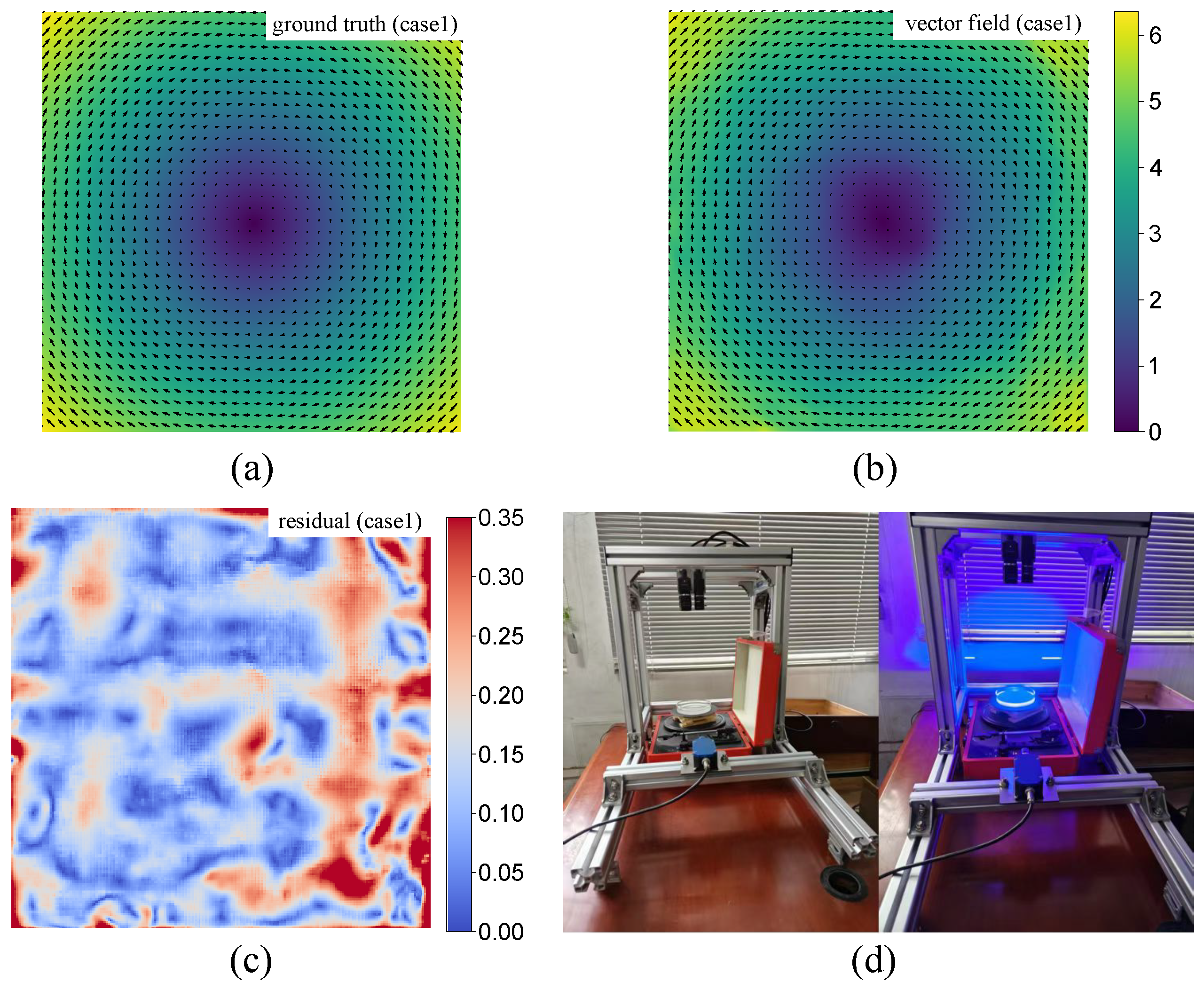
4.3. Performance on Practical PIV Images
4.4. Experiments on Computational Cost
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adrian, R.J. Scattering particle characteristics and their effect on pulsed laser measurements of fluid flow: Speckle velocimetry vs. particle image velocimetry. Appl. Opt. 1984, 23, 1690–1691. [Google Scholar] [CrossRef] [PubMed]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Panciroli, R.; Shams, A.; Porfiri, M. Experiments on the water entry of curved wedges: High speed imaging and particle image velocimetry. Ocean Eng. 2015, 94, 213–222. [Google Scholar] [CrossRef]
- Bardera, R.; Barcala-Montejano, M.; Rodríguez-Sevillano, A.; León-Calero, M. Wind flow investigation over an aircraft carrier deck by PIV. Ocean Eng. 2019, 178, 476–483. [Google Scholar] [CrossRef]
- Capone, A.; Di Felice, F.; Pereira, F.A. On the flow field induced by two counter-rotating propellers at varying load conditions. Ocean Eng. 2021, 221, 108322. [Google Scholar] [CrossRef]
- Lee, Y.; Zhang, S.; Li, M.; He, X. Blind inverse gamma correction with maximized differential entropy. Signal Process. 2022, 193, 108427. [Google Scholar] [CrossRef]
- Lee, Y.; Gu, F.; Gong, Z.; Pan, D.; Zeng, W. Surrogate-based cross-correlation for particle image velocimetry. Phys. Fluids 2024, 36, 087157. [Google Scholar] [CrossRef]
- Kähler, C.J.; Astarita, T.; Vlachos, P.P.; Sakakibara, J.; Hain, R.; Discetti, S.; La Foy, R.; Cierpka, C. Main results of the 4th International PIV Challenge. Exp. Fluids 2016, 57, 97. [Google Scholar] [CrossRef]
- Sciacchitano, A. Uncertainty quantification in particle image velocimetry. Meas. Sci. Technol. 2019, 30, 092001. [Google Scholar] [CrossRef]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1379. [Google Scholar] [CrossRef]
- Corpetti, T.; Heitz, D.; Arroyo, G.; Mémin, E.; Santa-Cruz, A. Fluid experimental flow estimation based on an optical-flow scheme. Exp. Fluids 2006, 40, 80–97. [Google Scholar] [CrossRef]
- Pan, C.; Xue, D.; Xu, Y.; Wang, J.; Wei, R. Evaluating the accuracy performance of Lucas-Kanade algorithm in the circumstance of PIV application. Sci. China Phys. Mech. Astron. 2015, 58, 104704. [Google Scholar] [CrossRef]
- Zhong, Q.; Yang, H.; Yin, Z. An optical flow algorithm based on gradient constancy assumption for PIV image processing. Meas. Sci. Technol. 2017, 28, 055208. [Google Scholar] [CrossRef]
- Wang, H.; He, G.; Wang, S. Globally optimized cross-correlation for particle image velocimetry. Exp. Fluids 2020, 61, 228. [Google Scholar] [CrossRef]
- Lee, Y.; Mei, S. Diffeomorphic particle image velocimetry. IEEE Trans. Instrum. Meas. 2021, 71, 5000310. [Google Scholar] [CrossRef]
- Ai, J.; Chen, Z.; Li, J.; Lee, Y. Rethinking asymmetric image deformation with post-correction for particle image velocimetry. Phys. Fluids 2025, 37, 017122. [Google Scholar] [CrossRef]
- Wereley, S.T.; Meinhart, C.D. Second-order accurate particle image velocimetry. Exp. Fluids 2001, 31, 258–268. [Google Scholar] [CrossRef]
- Scarano, F. Iterativeimage deformation methods in PIV. Meas. Sci. Technol. 2001, 13, R1. [Google Scholar] [CrossRef]
- Scharnowski, S.; Kähler, C.J. Particle image velocimetry-classical operating rules from today’s perspective. Opt. Lasers Eng. 2020, 135, 106185. [Google Scholar] [CrossRef]
- Liu, T.; Merat, A.; Makhmalbaf, M.; Fajardo, C.; Merati, P. Comparison between optical flow and cross-correlation methods for extraction of velocity fields from particle images. Exp. Fluids 2015, 56, 166. [Google Scholar] [CrossRef]
- Lee, Y.; Yang, H.; Yin, Z. PIV-DCNN: Cascaded deep convolutional neural networks for particle image velocimetry. Exp. Fluids 2017, 58, 171. [Google Scholar] [CrossRef]
- Cai, S.; Liang, J.; Gao, Q.; Xu, C.; Wei, R. Particle image velocimetry based on a deep learning motion estimator. IEEE Trans. Instrum. Meas. 2019, 69, 3538–3554. [Google Scholar] [CrossRef]
- Zhang, M.; Piggott, M.D. Unsupervised learning of particle image velocimetry. In Proceedings of the High Performance Computing: ISC High Performance 2020 International Workshops, Frankfurt, Germany, 21–25 June 2020; Revised Selected Papers 35. Springer: Berlin/Heidelberg, Germany, 2020; pp. 102–115. [Google Scholar]
- Wang, H.; Yang, Z.; Li, B.; Wang, S. Predicting the near-wall velocity of wall turbulence using a neural network for particle image velocimetry. Phys. Fluids 2020, 32, 115105. [Google Scholar] [CrossRef]
- Lagemann, C.; Lagemann, K.; Mukherjee, S.; Schröder, W. Deep recurrent optical flow learning for particle image velocimetry data. Nat. Mach. Intell. 2021, 3, 641–651. [Google Scholar] [CrossRef]
- Yu, C.; Luo, H.; Bi, X.; Fan, Y.; He, M. An effective convolutional neural network for liquid phase extraction in two-phase flow PIV experiment of an object entering water. Ocean Eng. 2021, 237, 109502. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Wang, S. Dense velocity reconstruction from particle image velocimetry/particle tracking velocimetry using a physics-informed neural network. Phys. Fluids 2022, 34, 017116. [Google Scholar] [CrossRef]
- Yu, C.; Fan, Y.; Bi, X.; Kuai, Y.; Chang, Y. Deep dual recurrence optical flow learning for time-resolved particle image velocimetry. Phys. Fluids 2023, 35, 045104. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, X.; Sun, Z.; Xu, S. An unsupervised deep learning model for dense velocity field reconstruction in particle image velocimetry (PIV) measurements. Phys. Fluids 2023, 35, 077108. [Google Scholar] [CrossRef]
- Cai, S.; Gray, C.; Karniadakis, G.E. Physics-informed neural networks enhanced particle tracking velocimetry: An example for turbulent jet flow. IEEE Trans. Instrum. Meas. 2024, 73, 2519109. [Google Scholar] [CrossRef]
- Yu, C.; Chang, Y.; Liang, X.; Liang, C.; Xie, Z. Deep learning for particle image velocimetry with attentional transformer and cross-correlation embedded. Ocean Eng. 2024, 292, 116522. [Google Scholar] [CrossRef]
- Reddy, Y.A.; Wahl, J.; Sjödahl, M. Twins-PIVNet: Spatial attention-based deep learning framework for particle image velocimetry using Vision Transformer. Ocean Eng. 2025, 318, 120205. [Google Scholar] [CrossRef]
- Ji, K.; An, Q.; Hui, X. Cross-correlation-based convolutional neural network with velocity regularization for high-resolution velocimetry of particle images. Phys. Fluids 2024, 36, 077117. [Google Scholar] [CrossRef]
- Cai, S.; Zhou, S.; Xu, C.; Gao, Q. Dense motion estimation of particle images via a convolutional neural network. Exp. Fluids 2019, 60, 73. [Google Scholar] [CrossRef]
- Yu, C.; Bi, X.; Fan, Y.; Han, Y.; Kuai, Y. LightPIVNet: An effective convolutional neural network for particle image velocimetry. IEEE Trans. Instrum. Meas. 2021, 70, 2510915. [Google Scholar] [CrossRef]
- Zhang, W.; Nie, X.; Dong, X.; Sun, Z. Pyramidal deep-learning network for dense velocity field reconstruction in particle image velocimetry. Exp. Fluids 2023, 64, 12. [Google Scholar] [CrossRef]
- Ji, K.; Hui, X.; An, Q. High-resolution velocity determination from particle images via neural networks with optical flow velocimetry regularization. Phys. Fluids 2024, 36, 037101. [Google Scholar] [CrossRef]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 23–30. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Luo, A.; Li, X.; Yang, F.; Liu, J.; Fan, H.; Liu, S. Flowdiffuser: Advancing optical flow estimation with diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 19167–19176. [Google Scholar]
- Qin, R.; Zhang, G.; Tang, Y. On the transferability of learning models for semantic segmentation for remote sensing data. arXiv 2023, arXiv:2310.10490. [Google Scholar] [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A comparison review of transfer learning and self-supervised learning: Definitions, applications, advantages and limitations. Expert Syst. Appl. 2024, 242, 122807. [Google Scholar] [CrossRef]
- Hu, Y.; Jia, Q.; Yao, Y.; Lee, Y.; Lee, M.; Wang, C.; Zhou, X.; Xie, R.; Yu, F.R. Industrial internet of things intelligence empowering smart manufacturing: A literature review. IEEE Internet Things J. 2024, 11, 19143–19167. [Google Scholar] [CrossRef]
- Han, X.; Zhang, Z.; Ding, N.; Gu, Y.; Liu, X.; Huo, Y.; Qiu, J.; Yao, Y.; Zhang, A.; Zhang, L.; et al. Pre-trained models: Past, present and future. AI Open 2021, 2, 225–250. [Google Scholar] [CrossRef]
- Teed, Z.; Deng, J. Raft: Recurrent all-pairs field transforms for optical flow. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 402–419. [Google Scholar]
- Oquab, M.; Bottou, L.; Laptev, I.; Sivic, J. Learning and transferring mid-level image representations using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1717–1724. [Google Scholar]
- Chang, H.; Han, J.; Zhong, C.; Snijders, A.M.; Mao, J.H. Unsupervised transfer learning via multi-scale convolutional sparse coding for biomedical applications. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 1182–1194. [Google Scholar] [CrossRef]
- Smith, L.N.; Topin, N. Super-convergence: Very fast training of neural networks using large learning rates. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications, Baltimore, MD, USA, 15–17 April 2019; Volume 11006, pp. 369–386. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Rubbert, A.; Albers, M.; Schröder, W. Streamline segment statistics propagation in inhomogeneous turbulence. Phys. Rev. Fluids 2019, 4, 034605. [Google Scholar] [CrossRef]
- Sharmin, N.; Brad, R. Optimal filter estimation for Lucas-Kanade optical flow. Sensors 2012, 12, 12694–12709. [Google Scholar] [CrossRef]
- Lu, J.; Yang, H.; Zhang, Q.; Yin, Z. An accurate optical flow estimation of PIV using fluid velocity decomposition. Exp. Fluids 2021, 62, 78. [Google Scholar] [CrossRef]
- Hui, T.W.; Tang, X.; Loy, C.C. Liteflownet: A lightweight convolutional neural network for optical flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8981–8989. [Google Scholar]
- Huang, Z.; Shi, X.; Zhang, C.; Wang, Q.; Cheung, K.C.; Qin, H.; Dai, J.; Li, H. Flowformer: A transformer architecture for optical flow. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 668–685. [Google Scholar]
- Scharnowski, S.; Kähler, C.J. On the effect of curved streamlines on the accuracy of PIV vector fields. Exp. Fluids 2013, 54, 1435. [Google Scholar] [CrossRef][Green Version]
- Wald, Y.; Feder, A.; Greenfeld, D.; Shalit, U. On calibration and out-of-domain generalization. Adv. Neural Inf. Process. Syst. 2021, 34, 2215–2227. [Google Scholar][Green Version]



| Method | Backstep | JHTDB | DNS | Cylinder | SQG |
|---|---|---|---|---|---|
| WIDIM | 0.034 | 0.084 | 0.304 | 0.083 | 0.457 |
| PIV-DCNN | 0.049 | 0.117 | 0.334 | 0.100 | 0.479 |
| PIV-LiteFlowNet-en | 0.033 | 0.075 | 0.122 | 0.049 | 0.126 |
| RAFT256-PIV-class1 | 0.016 | 0.137 | 0.093 | 0.014 | 0.117 |
| Twins-PIV-class1 | 0.013 | 0.092 | 0.056 | 0.012 | 0.091 |
| PIV-FlowDiffuser-class1(*) | 0.041 | 0.111 | 0.148 | 0.091 | 0.208 |
| PIV-FlowDiffuser-class1 | 0.007 | 0.029 | 0.039 | 0.019 | 0.052 |
| Method | Backstep | JHTDB | DNS | Cylinder | SQG | Uniform | Other |
|---|---|---|---|---|---|---|---|
| RAFT256-PIV-class2 | 0.131 | 0.476 | 0.646 | 0.124 | 0.593 | 0.174 | 0.380 |
| FlowFormer-PIV-class2 | 0.377 | 0.680 | 1.316 | 0.297 | 1.042 | 0.850 | 1.406 |
| PIV-FlowDiffuser-class2 | 0.155 | 0.296 | 0.565 | 0.138 | 0.466 | 0.328 | 0.587 |
| Method | Problem Class 1 | Problem Class 2 | ||||
|---|---|---|---|---|---|---|
| AEE | RMSE | AAE | AEE | RMSE | AAE | |
| RAFT256-PIV-class1 | 0.0866 | 0.0741 | 0.1631 | 4.7564 | 5.4709 | 1.6131 |
| FlowFormer-PIV-class1 | 0.3608 | 0.2956 | 0.3412 | 1.2518 | 1.4561 | 0.4236 |
| PIV-FlowDiffuser-class1 | (0.0352) | (0.0273) | (0.1283) | 0.5537 | 0.7279 | 0.2683 |
| RAFT256-PIV-class2 | 0.2107 | 0.1726 | 0.2644 | 0.3540 | 0.4502 | 0.2380 |
| FlowFormer-PIV-class2 | 0.4205 | 0.3483 | 0.3890 | 0.7662 | 0.9180 | 0.3365 |
| PIV-FlowDiffuser-class2 | 0.1021 | 0.0848 | 0.1667 | (0.3124) | (0.3921) | (0.1795) |
| Method | Device | Training-Time (h) | Average Inference Time (s) |
|---|---|---|---|
| WIDIM | - | - | 0.86 |
| PIV-DCNN | - | - | 2.23 |
| PIV-LiteFlowNet-en | - | - | 0.13 |
| RAFT256-PIV | Two NVIDIA Quadro RTX 6000 GPUs | ∼18 (from scratch) | 0.08 |
| Twins-PIV-class1 | Two NVIDIA Quadro RTX 8000 GPUs | ∼21 (from scratch) | 0.08 |
| Twins-PIV-class2 | Two NVIDIA Quadro RTX 8000 GPUs | ∼32 (from scratch) | 0.08 |
| FlowFormer-PIV-class1 | One NVIDIA GeForce RTX 3090 GPU | ∼0.5 (fine-tuning) | 0.05 |
| FlowFormer-PIV-class2 | One NVIDIA GeForce RTX 3090 GPU | ∼1.5 (fine-tuning) | 0.05 |
| PIV-FlowDiffuser-class1 | One NVIDIA GeForce RTX 3090 GPU | ∼2.0 (fine-tuning) | 0.27 |
| PIV-FlowDiffuser-class2 | One NVIDIA GeForce RTX 3090 GPU | ∼5.0 (fine-tuning) | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Wang, J.; Hu, J.; Ai, J.; Lee, Y. PIV-FlowDiffuser: Transfer-Learning-Based Denoising Diffusion Models for Particle Image Velocimetry. Sensors 2025, 25, 6077. https://doi.org/10.3390/s25196077
Zhu Q, Wang J, Hu J, Ai J, Lee Y. PIV-FlowDiffuser: Transfer-Learning-Based Denoising Diffusion Models for Particle Image Velocimetry. Sensors. 2025; 25(19):6077. https://doi.org/10.3390/s25196077
Chicago/Turabian StyleZhu, Qianyu, Junjie Wang, Jeremiah Hu, Jia Ai, and Yong Lee. 2025. "PIV-FlowDiffuser: Transfer-Learning-Based Denoising Diffusion Models for Particle Image Velocimetry" Sensors 25, no. 19: 6077. https://doi.org/10.3390/s25196077
APA StyleZhu, Q., Wang, J., Hu, J., Ai, J., & Lee, Y. (2025). PIV-FlowDiffuser: Transfer-Learning-Based Denoising Diffusion Models for Particle Image Velocimetry. Sensors, 25(19), 6077. https://doi.org/10.3390/s25196077






