Eliminate Dynamic Error of A-PNAS High-Precision Time Synchronization Using Multi-Sensor Combination
Abstract
1. Introduction
2. Analysis of Dynamic Error Impact in Time Synchronization of A-PNAS
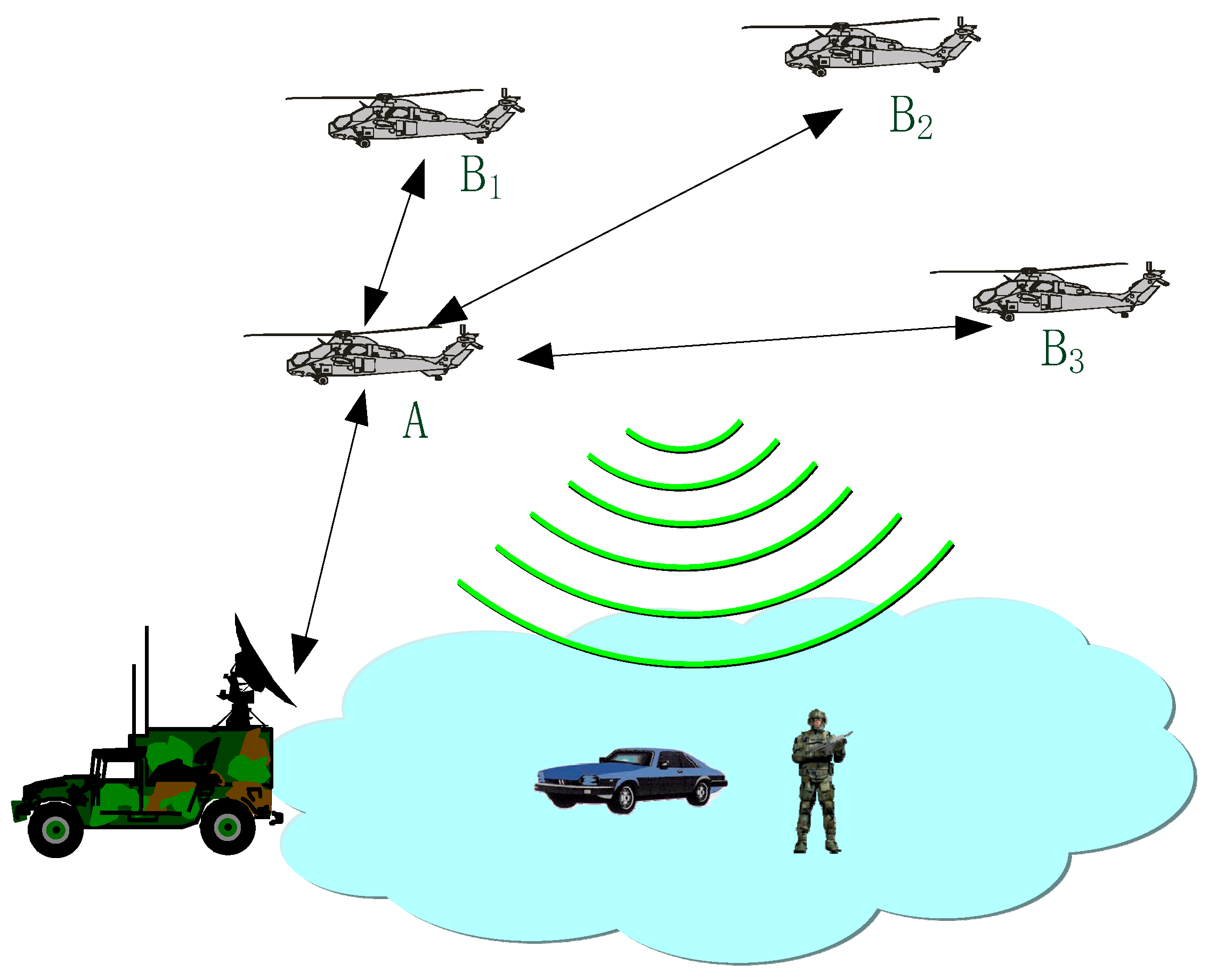
2.1. High-Precision Time Synchronization Requirements of A-PNAS
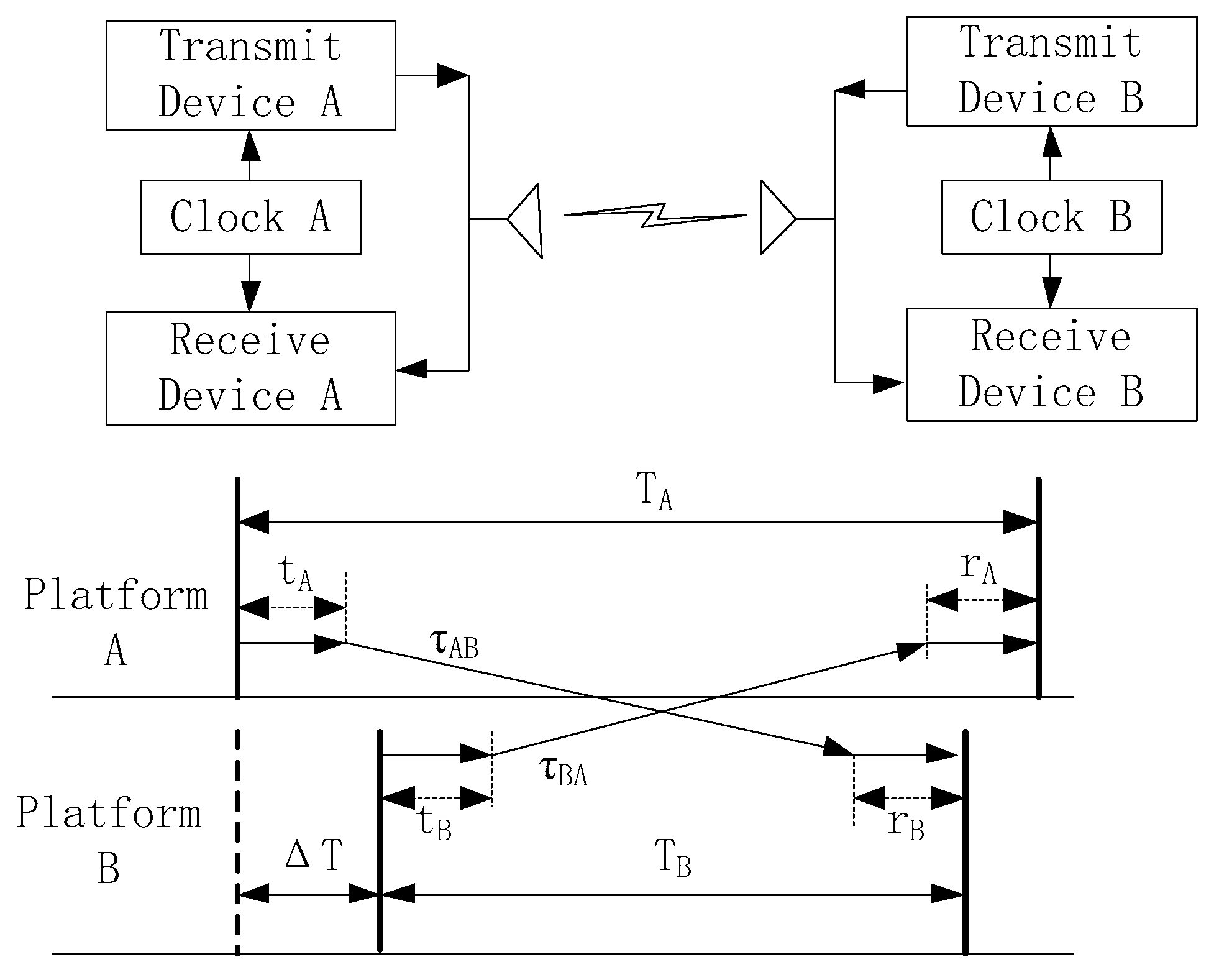
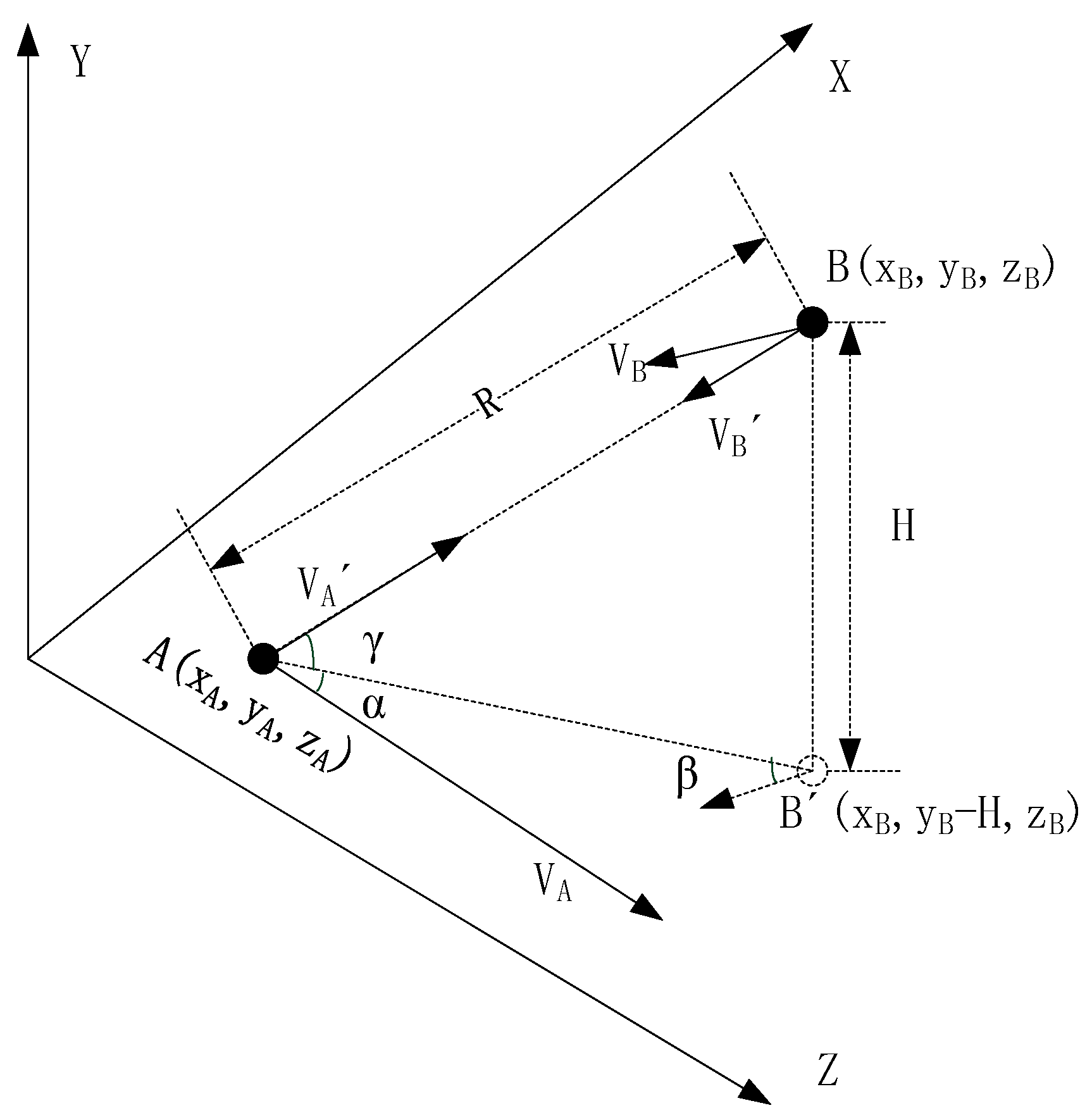
2.2. Bidirectional Time Synchronization Between Airborne Platforms
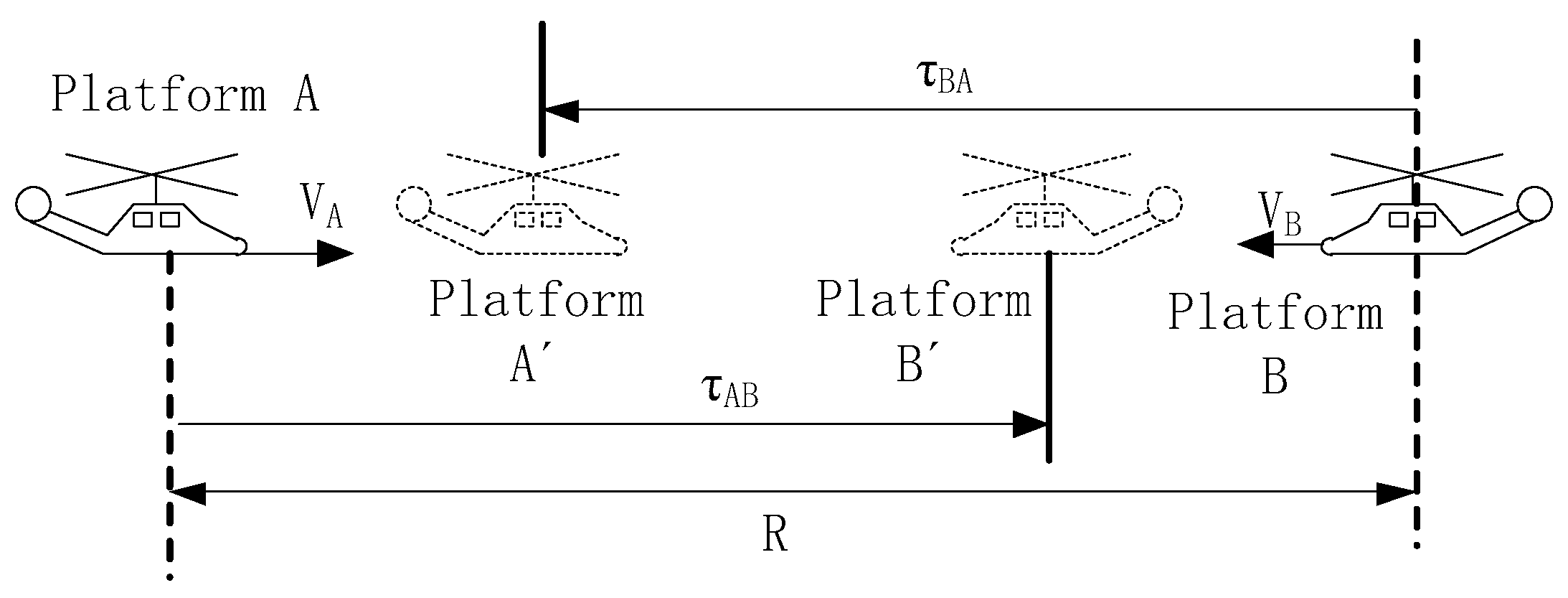
2.3. Analysis of Dynamic Errors and Their Impact
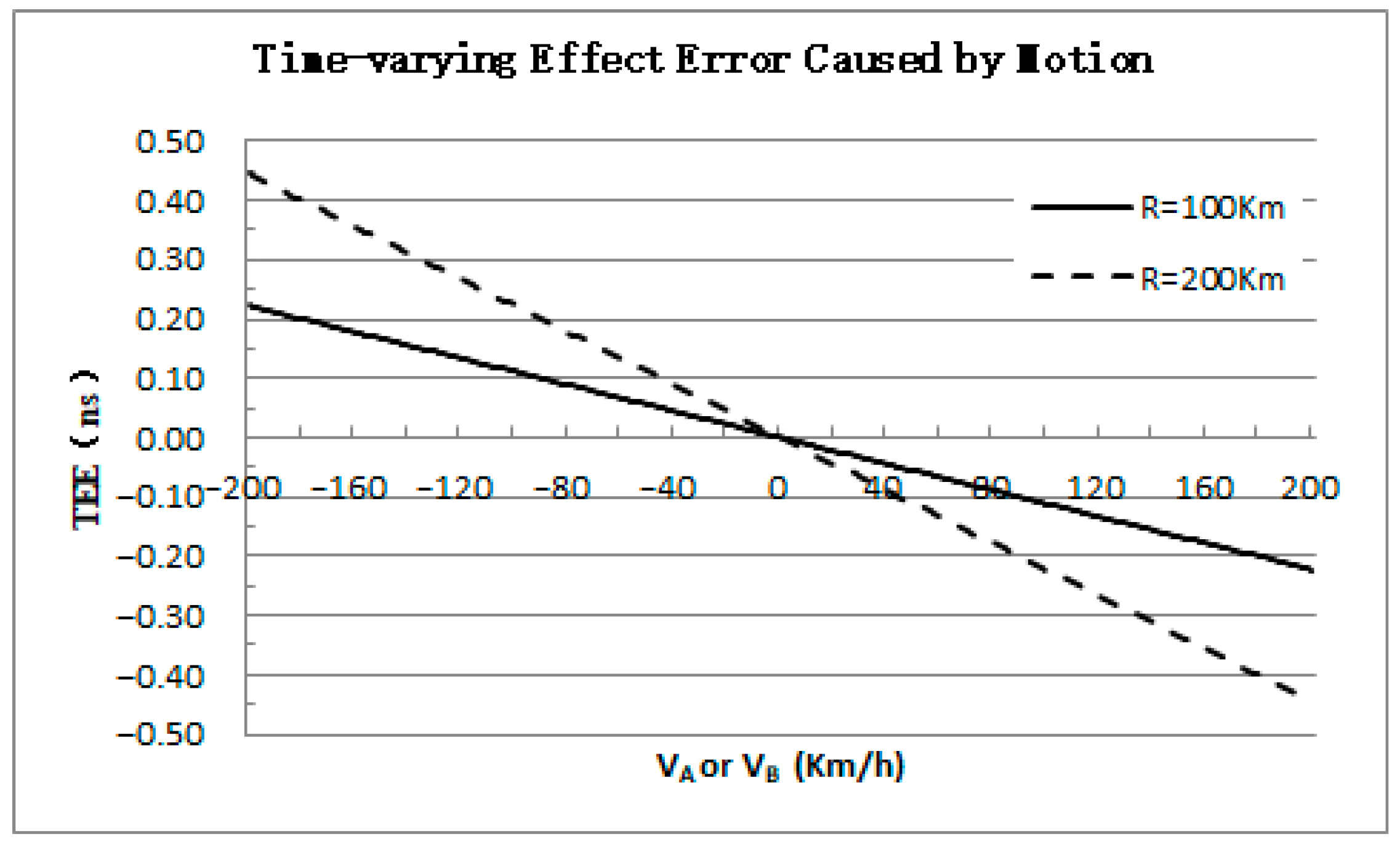
2.3.1. The Time-Varying Effect Error Caused by Motion
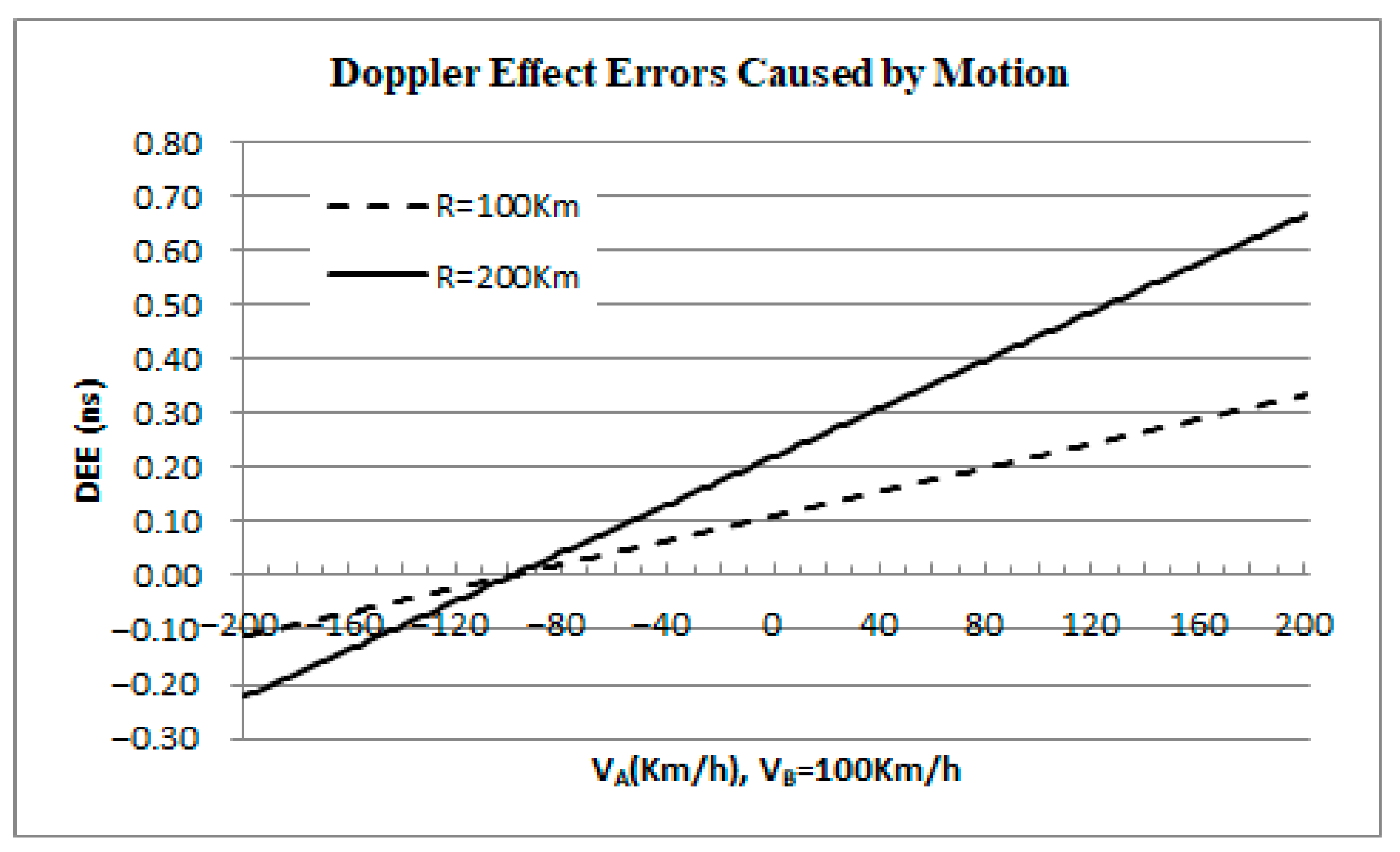
2.3.2. Relativistic Doppler Effect Error Caused by Motion
3. Dynamic Error Model of Time Synchronization
4. Analysis of Dynamic Error Estimation Accuracy and Correction Residuals
4.1. Selection of Velocity Measurement Sensors and Estimation Accuracy of Related Dynamic Error
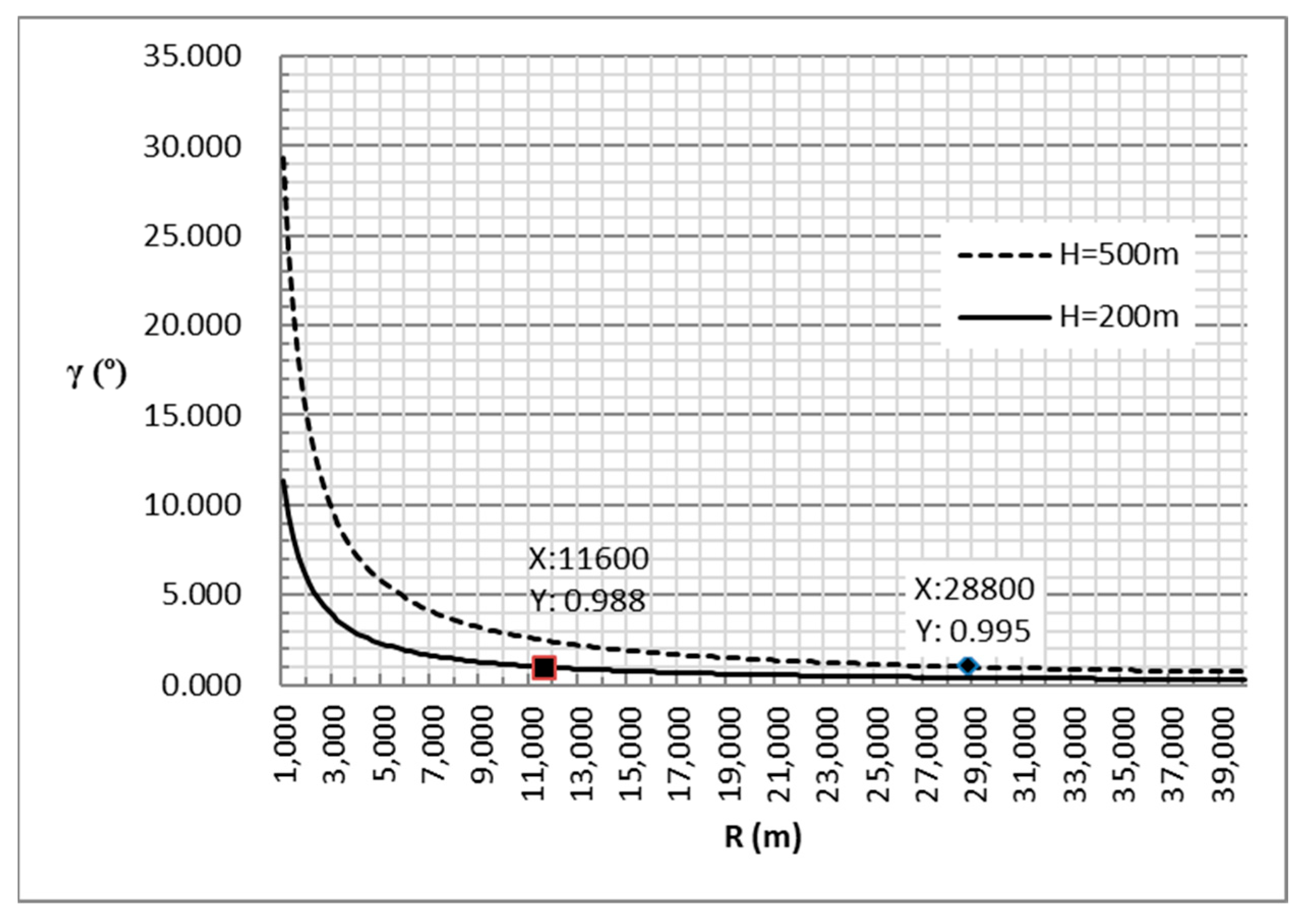
4.2. Selection of Relative Position Measurement Sensors and Estimation Accuracy of Related Dynamic Error
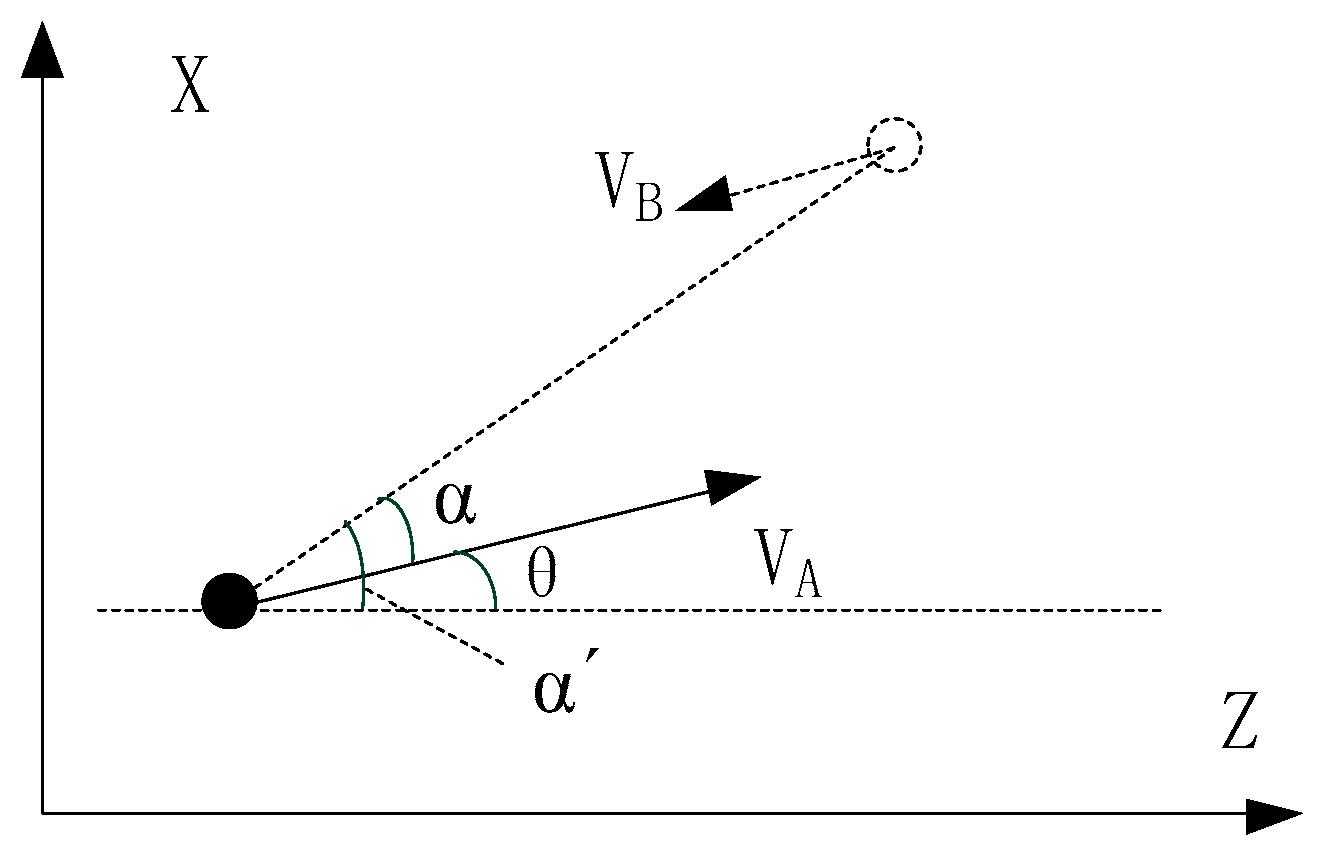
4.3. Selection of Motion Angle Measurement Sensor and Estimation Accuracy of Related Dynamic Error
4.4. The Comprehensive Residual Error of Using Multiple Sensors to Correct Dynamic Errors
5. Data Preprocessing and Dynamic Error Correction Flow
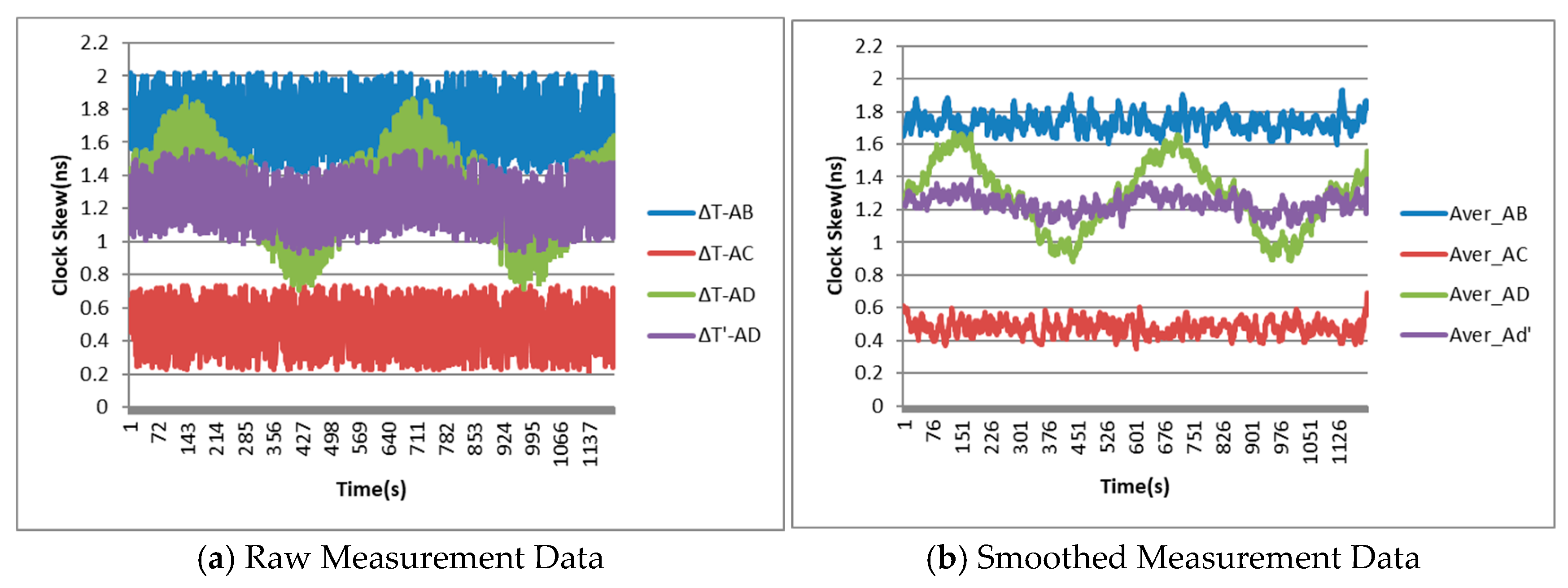
5.1. Observation Data Preprocessing
5.2. Multi-Sensor Combination Dynamic Error Correction Processing Flow
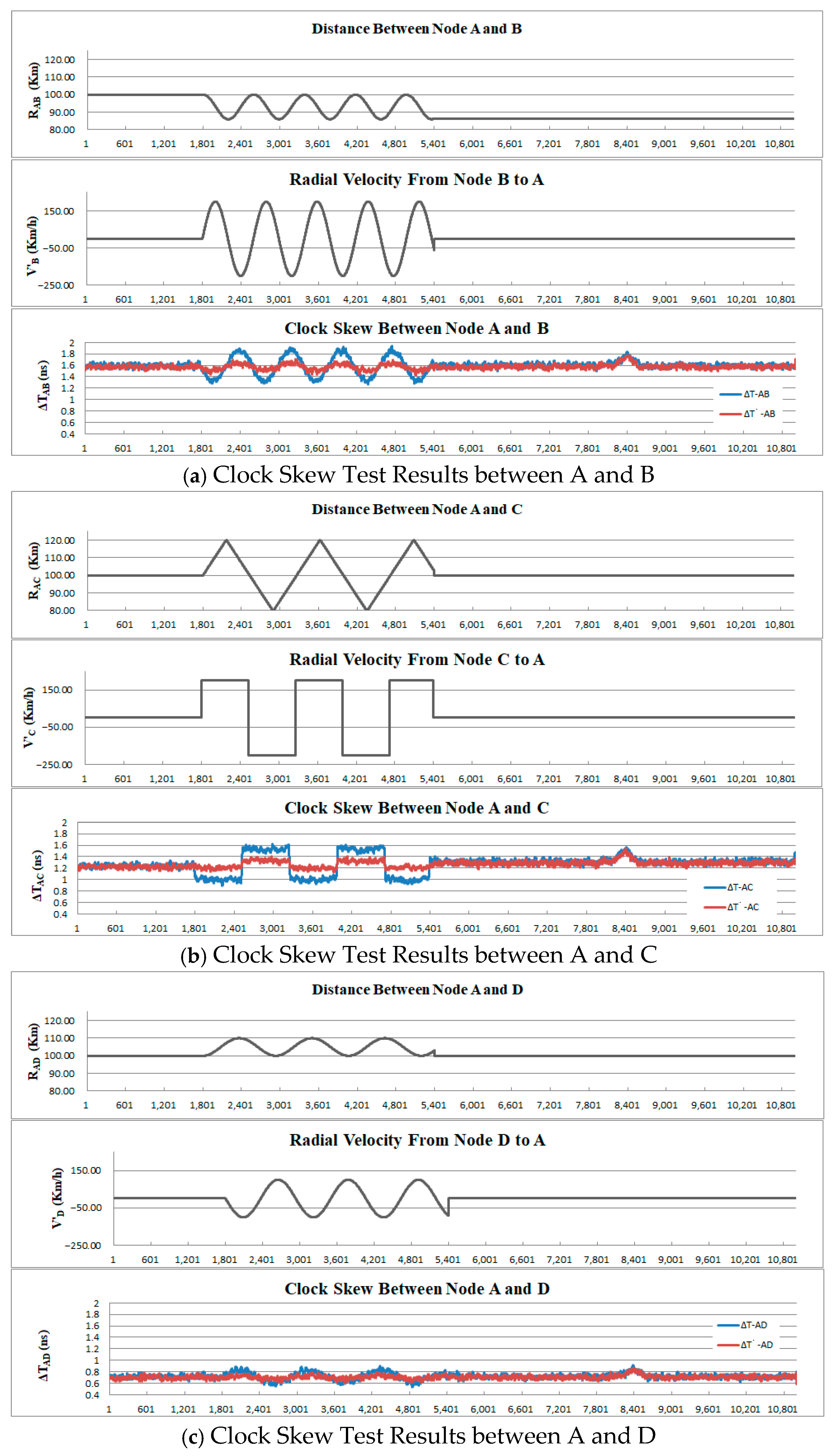
5.3. Simulation Tests and Verification
- (1)
- After the system started and operated for half an hour, the slave nodes B, C, and D started to enter the movement state.
- (2)
- The slave node B performed an anticlockwise circular motion with a radius of 7 km and a speed of 200 km/h.
- (3)
- The slave node C moved at a constant speed in a straight line with a speed of 150 km/h, making round trips within a range of ±20 km.
- (4)
- The slave node D performed a clockwise circular motion with a radius of 5 km and a speed of 100 km/h.
- (5)
- The process of movement simulation lasted for one hour, after which the distance remained at its final state.
5.4. Comparison with Existing Time Synchronization Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dou, J.; Xu, B.; Dou, L. Impact Assessment of the Asynchronous Clocks Between Reference and User Receivers in Differential Pseudolite Navigation System. IEEE Sens. J. 2021, 21, 403–411. [Google Scholar] [CrossRef]
- Gao, H.; Deng, Z.; Wang, L.; Shi, L. Coverage Analysis of Air-based Regional Augmentation System for BD Satellite Navigation Signal. Radio Eng. 2021, 47, 45–47. [Google Scholar]
- Yu, B.; He, C. Assessment of Air-ground Cooperation Pseudolites Augmentation System. J. Huazhong Univ. Sci. & Technol. (Nat. Sci. Ed.) 2017, 45, 113–117. [Google Scholar]
- Han, P.; Guo, C.; Li, S.; Yu, J.; Chen, F. Emergency Communication Relay Deployment Based on UAV. Comput. Appl. Softw. 2024, 41, 140–148. [Google Scholar]
- Dong, K.; Xu, W. Application Research and Development Trend of Firefighting Drone. Mod. Manuf. Technol. Equip. 2023, 8, 78–80. [Google Scholar]
- Xu, Z.; Wang, B.; Yun, X.; Wang, X. Stable relay selection method under an uncertain preference ordinal for UAV in post-disaster. J. Xidian Univ. 2022, 49, 32–41. [Google Scholar]
- Zhao, Q.; Zhu, C.; Qian, F.; Yang, Z.; He, W. Research on Application Development of Small and Medium-sized Shipborne UAVs on Ships. Ordnance Ind. Autom. 2023, 42, 69–75. [Google Scholar]
- Kabiri, M.; Cimarelli, C.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. A Review of Radio Frequency Based Localisation for Aerial and Ground Robits with 5G Future Perspectives. Sensors 2023, 23, 188. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Li, T.; Li, Y. Radio Frequency Based Distributed System for Noncooperative UAV Classification and Positioning. J. Inf. Intell. 2024, 2, 42–51. [Google Scholar] [CrossRef]
- Ko, S.-W.; Chea, H.; Han, K.; Lee, S.; Seo, D.-W.; Huang, K. V2X-Based Vehicular Positioning: Opportunities, Challenges, and Future Directions. Wirel. Commun. 2021, 28, 144–151. [Google Scholar] [CrossRef]
- Seijo, O.; Val, I.; Luvisotto, M.; Pang, Z. Clock synchronization for Wireless Time-Sensitiv Networking: A March from Microsecond to Nanosecond. IEEE Ind. Electron. Mag. 2021, 16, 35–43. [Google Scholar] [CrossRef]
- Yang, F.; Fan, J.; Ma, J.; Ma, Z.; Wu, X.; Liao, B. Time Syachronization Technology and Precision Analysis ov Navigation Enhanced Pseudolite. Navig. Psiotioning Timing 2021, 8, 132–136. [Google Scholar]
- Chen, J.; Peng, L.; Huang, Q. Time Synchronization Mechanism for Locata Positioning System. GNSS World China 2018, 43, 54–58. [Google Scholar]
- Ming, Z.; Pang, H.; Xu, Y.; Zhang, L.; Zhang, W. Estimating Clock Skew with One-Way Timestamps. IEEE Commun. Lett. 2022, 26, 2591–2595. [Google Scholar] [CrossRef]
- Pranger, S.; Haynes, M.S.; Moghaddam, M. Wireless Sub-nanosecond RF Synchronization for Distributed Ultrawideband Software-Defined Radar Networks. IEEE Trans. Microw. Theory Technol. 2020, 68, 4787–4804. [Google Scholar] [CrossRef]
- Merlo, J.M.; Mghabghab, A.R.; Nanzer, J.A. Wireless Picosecond Time Synchronization for Distributed Antenna Arrays. IEEE Trans. Microw. Theory Technol. 2023, 71, 1720–1731. [Google Scholar] [CrossRef]
- Yu, X.; Wang, D.; Li, Z.; Zhao, H. High Accuracy Physical Time Synchronization Method Based on Two-Way Comparison. Acta Aeronaut. Astronaut. Sin. 2019, 40, 203–217. [Google Scholar]
- Huang, F.; Chen, Y.; Li, T.; Shan, Q.; Zhang, J.; Cai, C. Analysis and Correction to the Influence of Satellite Motion on the Measurement of Inter-Sallite Two-Way Clock Offset. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 3. [Google Scholar] [CrossRef]
- Bai, Y.; Lu, X.; Gao, T. An Improved Algorithm for Inter-Satellite Link Time Synchronization Based on Single-Point Paeudo-Rang Reduction. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1044–1052. [Google Scholar]
- Liu, G.; Lei, M. Research on an improved dual one-way ranging measurement UAV time synchronization method. Wirel. Internet Technol. 2023, 20, 121–124. [Google Scholar]
- Zhang, R.; Liu, C.; Cheng, J.; Ding, Y. A Multi-Stage Compensation Bidirectional Time Synchronization Algorithm for UAV Cluster. Comput. Simul. 2021, 38, 327–331. [Google Scholar]
- Müller, P.; Berger, D.; Sarperi, L. Nanosecond Time Synchronization over a 2.4 GHz Long-Range Wireless Link. Sensors 2025, 25, 1961. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Duan, B.; Xu, Q.; Pan, W.; Ma, W.; Shao, S. High precision time synchronization between nodes under motion scenario of UAV platforms. J. Xidian Univ. 2024, 51, 19–29. [Google Scholar]
- Zha, G.; Xiong, X. Spread-Spectrum Communication; XiDian University Press: Xi′an, China, 1990; pp. 132–133. [Google Scholar]
- China Satellite Navigation Office. Beidou Navigation Satellite System Open Service Performance Stardard (Version 3.0); China Satellite Navigation Office: Beijing, China, 2021; pp. 16–17. [Google Scholar]
- Shang, Y.; Zhang, D.; Wang, L.; Li, Z.; Li, S. A High-precision Time Synchronization Algorithm for Aviation Swarm Task Cooperation. In Proceedings of the IEEE 2nd International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 27–29 May 2022; pp. 779–784. [Google Scholar]

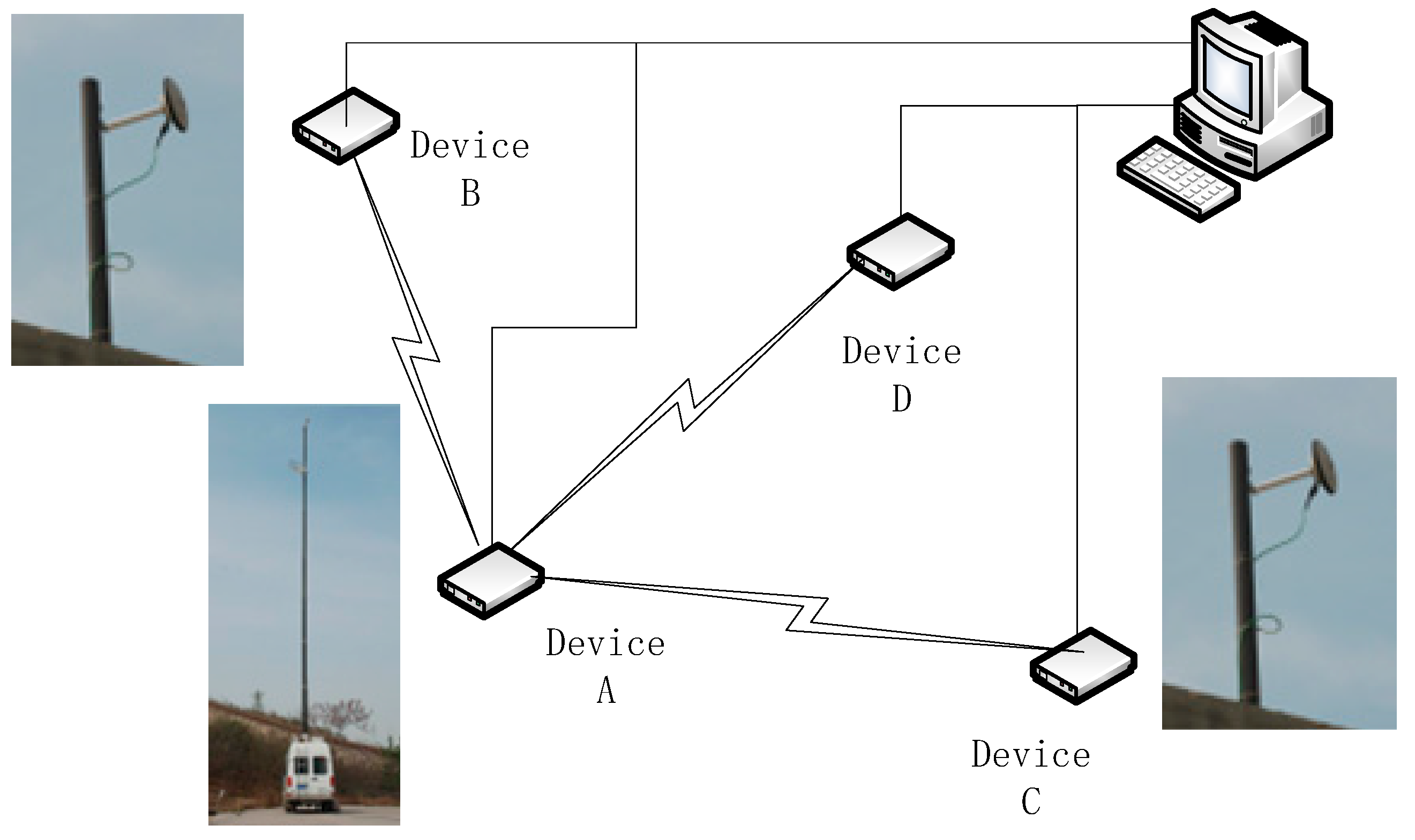
| Garde | Positioning Accuracy | Rate Accuracy | Application |
|---|---|---|---|
| Navigation | ≤0.1n mile (185 m) (in one hour) | ≤0.01 m/s (in one hour) | Aircraft Inertial Navigation System Spacecraft orbit control |
| ≤1n mile (1.85 km) (in 10 h) | ≤0.1 m/s (in 10 h) | ||
| Tactical | ≤1 Km (in one hour) | ≤0.1 m/s (in one hour) | Drone navigation Ship combination navigation, Missile guidance |
| ≤10 m (GNSS assistant) | ≤1 m/s (in 10 h) | ||
| Industrial | ≤10 m (in ten minutes) | ≤0.5 m/s (in one minutes) | Industrial robot, UAV Trajectory planning (GNSS assistance needed) |
| ≥1 Km (after one hour) | ≥30 m/s (after one hour) | ||
| Consumer | ≥10 m (be depended on GNSS or Wi-Fi) | ≤5 m/s (in one second) | Personal attire Low costs UAV attitude assistance. |
| — | ≥50 m/s (after 10 s) |
| Service Scheme | Positioning Accuracy Standard (95%) | Constraints | |
|---|---|---|---|
| Single-frequency or dual-frequency | Average globally, Horizontal | ≤9 m | The elevation mask is 5 degrees; Usage constraints are met, and healthy SISs are used for calculation; The statistical value of any 7-day positioning errors of all points in the global region; Excludes transmission errors and user segment errors. |
| Average globally, Vertical | ≤10 m | ||
| Single-frequency or dual-frequency | Horizontal error at the worst point. | ≤15 m | The elevation mask is 5 degrees; Usage constraints are met, and healthy satellite signals are used for calculation; The statistical value of any 7-day positioning errors of the world’s worst position; Excludes transmission errors and user segment errors. |
| Vertical error at the worst point. | ≤22 m | ||
| Angel Measurement Sensors | Error | Advantage | Limitation |
|---|---|---|---|
| Magnetic Compass | Unable to Output | Simple | Extremely Susceptible to Interference |
| Electronic Compass | 0.5°~2° | Easy to Integrate | Requires Regular Calibration |
| Strap-down Inertial Navigation System (SINS) | <0.1°/h (With Compensation); Without Compensation, the Accumulated Error over 10 h Amounts to Approximately 10°. | High Short-term Accuracy | Long-term Work Leads to Obvious Accumulation of Errors. |
| GNSS/INS Combination | Very Low (error < 0.1°) | High Precision | All-weather Operation, Relying on Satellite Signals |
| Doppler Radar | Medium (error 1°~3°) | Anti-obstruction | Affected by the Terrain The Equipment is Complex |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Tao, H.; Hao, F.; Liu, Y.; Wang, Z. Eliminate Dynamic Error of A-PNAS High-Precision Time Synchronization Using Multi-Sensor Combination. Sensors 2025, 25, 6028. https://doi.org/10.3390/s25196028
Wang Z, Tao H, Hao F, Liu Y, Wang Z. Eliminate Dynamic Error of A-PNAS High-Precision Time Synchronization Using Multi-Sensor Combination. Sensors. 2025; 25(19):6028. https://doi.org/10.3390/s25196028
Chicago/Turabian StyleWang, Zhenling, Haihong Tao, Fang Hao, Yilong Liu, and Zhengyong Wang. 2025. "Eliminate Dynamic Error of A-PNAS High-Precision Time Synchronization Using Multi-Sensor Combination" Sensors 25, no. 19: 6028. https://doi.org/10.3390/s25196028
APA StyleWang, Z., Tao, H., Hao, F., Liu, Y., & Wang, Z. (2025). Eliminate Dynamic Error of A-PNAS High-Precision Time Synchronization Using Multi-Sensor Combination. Sensors, 25(19), 6028. https://doi.org/10.3390/s25196028





