Author Contributions
Conceptualization: C.R., H.H., M.T., P.G. and T.G.; Methodology: C.R., J.F., H.H., L.B., M.T., N.J., P.G., T.H. and T.G.; Software: J.F., L.B. and N.J.; Validation: C.R., J.F., H.H., L.B., M.T., N.J., P.G., T.H. and T.G.; Formal analysis: J.F., L.B., N.J. and T.H.; Investigation: J.F., L.B., N.J. and T.H.; Resources: C.R., J.F., H.H., L.B., M.T., N.J., P.G., T.H. and T.G.; Data curation: J.F., L.B., N.J. and T.H.; Writing—original draft preparation: C.R., J.F., H.H., L.B., M.T., N.J., P.G., T.H. and T.G.; Writing—review and editing: C.R., J.F., H.H., L.B., M.T., N.J., P.G., T.H. and T.G.; Visualization: J.F., L.B., N.J. and T.H.; Supervision: C.R., H.H., M.T., P.G. and T.G.; Project administration: P.G.; Funding acquisition: C.R., H.H., M.T., P.G. and T.G. All authors have read and agreed to the published version of the manuscript.
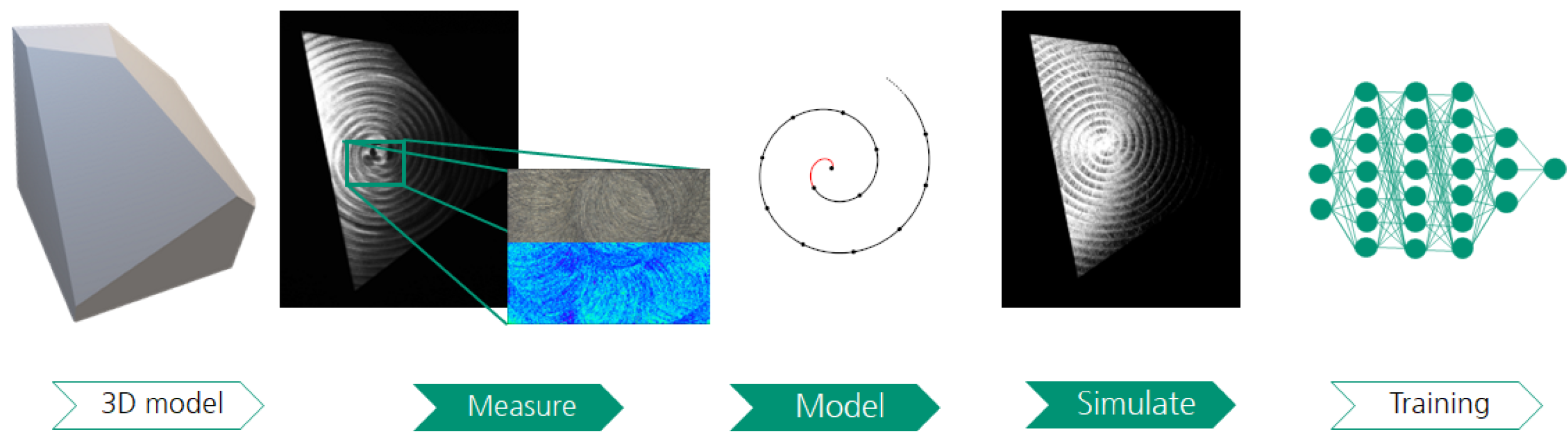
Figure 1.
SYNOSIS synthesis pipeline. Based on a 3D model of an object, spatial properties of the surface texture are measured. Surface topography and manufacturing parameters are used to develop a mathematical model that is capable of reproducing the texture as a normal map. Multiple realizations of the texture are generated by varying the parameters and are applied onto the 3D model of the object that has been altered to include surface defects of varying types and sizes. During the simulation step, the final image is computed based on the interaction between the acquisition environment (light, camera), object geometry, and texture normal map. This process is repeated an arbitrary amount of times. The parameters that are defining the texture and surface defects are varied to generate a training dataset that is sufficient in terms of both image quantity and content variance.
Figure 1.
SYNOSIS synthesis pipeline. Based on a 3D model of an object, spatial properties of the surface texture are measured. Surface topography and manufacturing parameters are used to develop a mathematical model that is capable of reproducing the texture as a normal map. Multiple realizations of the texture are generated by varying the parameters and are applied onto the 3D model of the object that has been altered to include surface defects of varying types and sizes. During the simulation step, the final image is computed based on the interaction between the acquisition environment (light, camera), object geometry, and texture normal map. This process is repeated an arbitrary amount of times. The parameters that are defining the texture and surface defects are varied to generate a training dataset that is sufficient in terms of both image quantity and content variance.
Figure 2.
Examples of the three textures considered in this paper: surface finishing by sandblasting, parallel milling, and spiral milling.
Figure 2.
Examples of the three textures considered in this paper: surface finishing by sandblasting, parallel milling, and spiral milling.
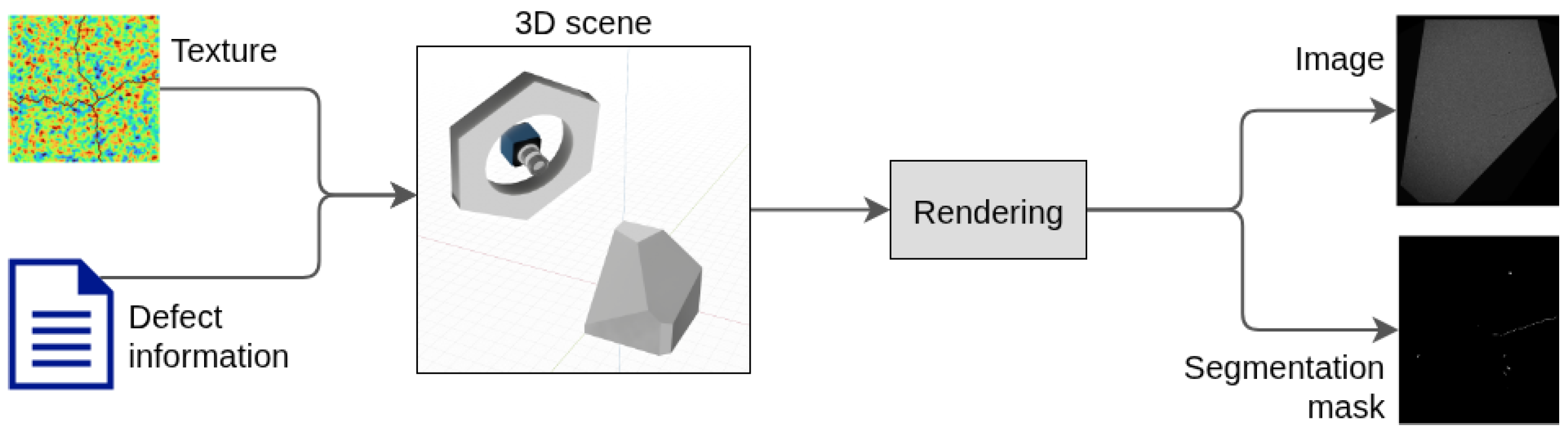
Figure 3.
Image synthesis overview. The texture and defect information are joined with the 3D scene to perform rendering and to generate an image. The defect information is varied to perform photo-realistic image synthesis of both defected and defect-free object instances. In case of defected instances, pixel-precise defect annotations are automatically created.
Figure 3.
Image synthesis overview. The texture and defect information are joined with the 3D scene to perform rendering and to generate an image. The defect information is varied to perform photo-realistic image synthesis of both defected and defect-free object instances. In case of defected instances, pixel-precise defect annotations are automatically created.
Figure 4.
Left: defected synthetic image. Middle: defect annotations. Right: defected synthetic image with annotations as a red overlay.
Figure 4.
Left: defected synthetic image. Middle: defect annotations. Right: defected synthetic image with annotations as a red overlay.
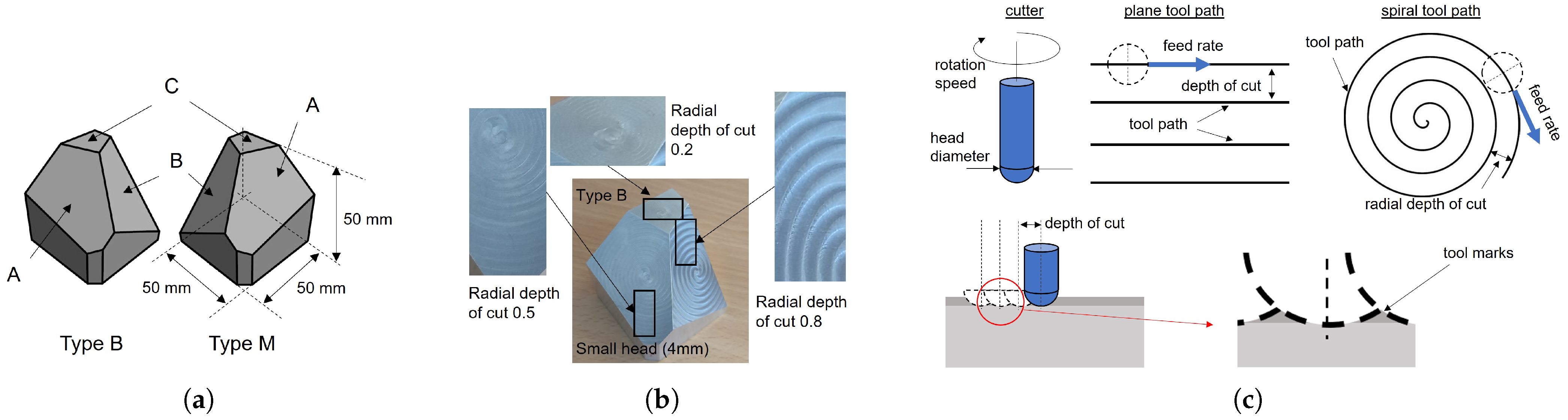
Figure 5.
Illustration of the test object used in the project, the milling processes, and a test object with milled surfaces. (a) Drawing of the base test bodies. (b) Example picture of a type B test body with spiral milled surfaces. (c) Sketch of the milling processes and its main parameters.
Figure 5.
Illustration of the test object used in the project, the milling processes, and a test object with milled surfaces. (a) Drawing of the base test bodies. (b) Example picture of a type B test body with spiral milled surfaces. (c) Sketch of the milling processes and its main parameters.
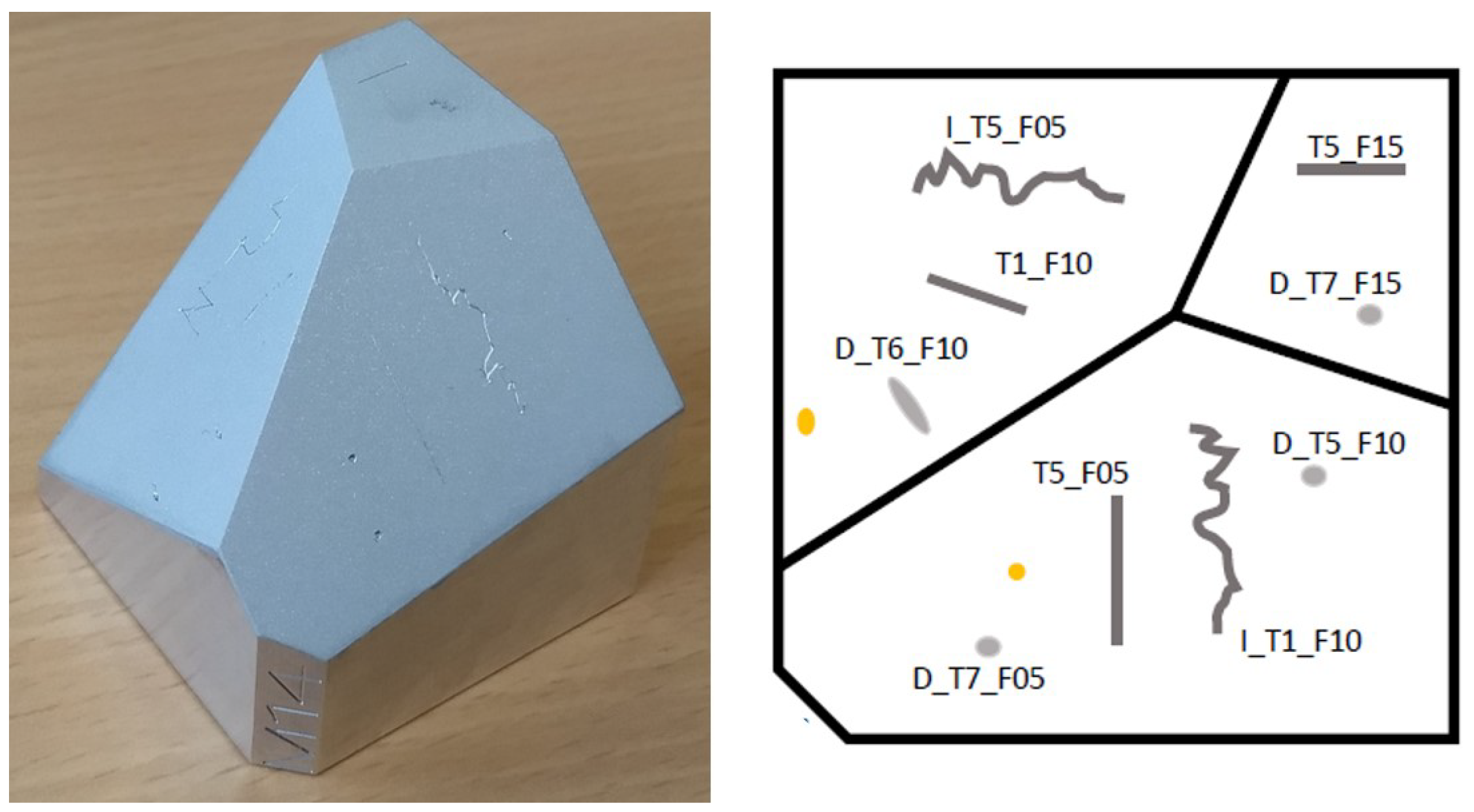
Figure 6.
Test object type M after sandblasting and the subsequently introduced defects with different types and sizes.
Figure 6.
Test object type M after sandblasting and the subsequently introduced defects with different types and sizes.
Figure 7.
Real images of the object’s surface with defects. Top row: 20-degree angle from the perpendicular view. Bottom row: 40-degree angle from the perpendicular view. (a) Test body 14, face A. (b) Test body 17, face A. (c) Test body 27, face A. (d) Test body 21, face A. (e) Test body 14, face A. (f) Test body 17, face A. (g) Test body 27, face A. (h) Test body 21, face A.
Figure 7.
Real images of the object’s surface with defects. Top row: 20-degree angle from the perpendicular view. Bottom row: 40-degree angle from the perpendicular view. (a) Test body 14, face A. (b) Test body 17, face A. (c) Test body 27, face A. (d) Test body 21, face A. (e) Test body 14, face A. (f) Test body 17, face A. (g) Test body 27, face A. (h) Test body 21, face A.
Figure 8.
Topography measurements of sandblasted and milled surfaces. (a) Parallel milled surface using a milling head diameter of 4 mm and a radial depth of cut of 0.5. Small imaged region (left) is with a pixel size of 0.44 µm, and the large imaged region (right) is with a pixel size of 1.75 µm. (b) Sandblasted surface using pressure of bar (left) and 6 bar (right). Imaged region is with a pixel size of 1.75 µm.
Figure 8.
Topography measurements of sandblasted and milled surfaces. (a) Parallel milled surface using a milling head diameter of 4 mm and a radial depth of cut of 0.5. Small imaged region (left) is with a pixel size of 0.44 µm, and the large imaged region (right) is with a pixel size of 1.75 µm. (b) Sandblasted surface using pressure of bar (left) and 6 bar (right). Imaged region is with a pixel size of 1.75 µm.
Figure 9.
Optical 3D measurements of the milled surfaces using different parameter settings. Imaged region is with a pixel size of 7 µm. Best viewed digitally. (a) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (b) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.8. (c) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (d) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.2.
Figure 9.
Optical 3D measurements of the milled surfaces using different parameter settings. Imaged region is with a pixel size of 7 µm. Best viewed digitally. (a) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (b) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.8. (c) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (d) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.2.
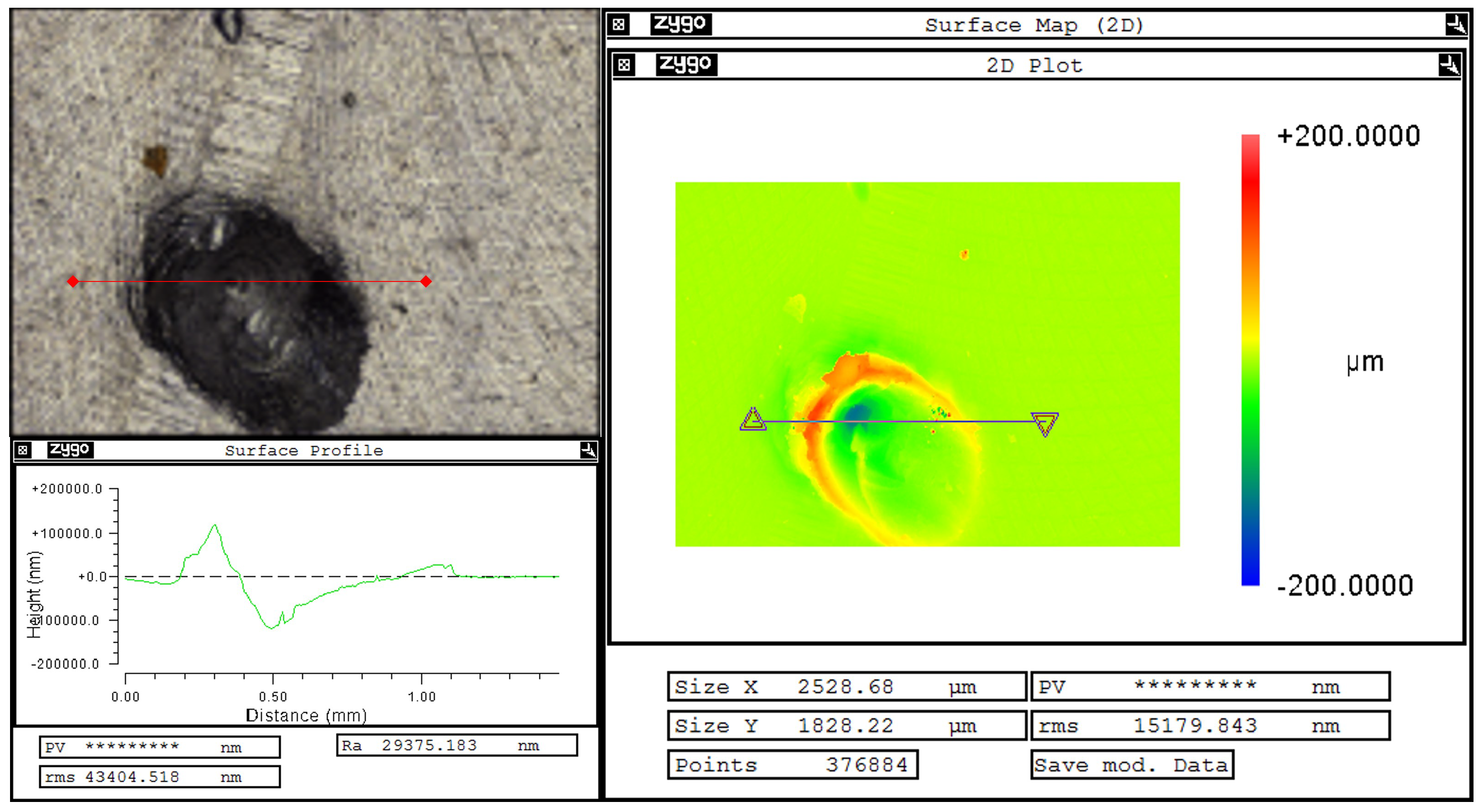
Figure 10.
Software GUI with the optical 3D (top left) and topography (right) measurement with 2D intersection of the height profile (bottom left), which is marked in the topography measurement of a defect created using the indentor with a load of 500 g.
Figure 10.
Software GUI with the optical 3D (top left) and topography (right) measurement with 2D intersection of the height profile (bottom left), which is marked in the topography measurement of a defect created using the indentor with a load of 500 g.
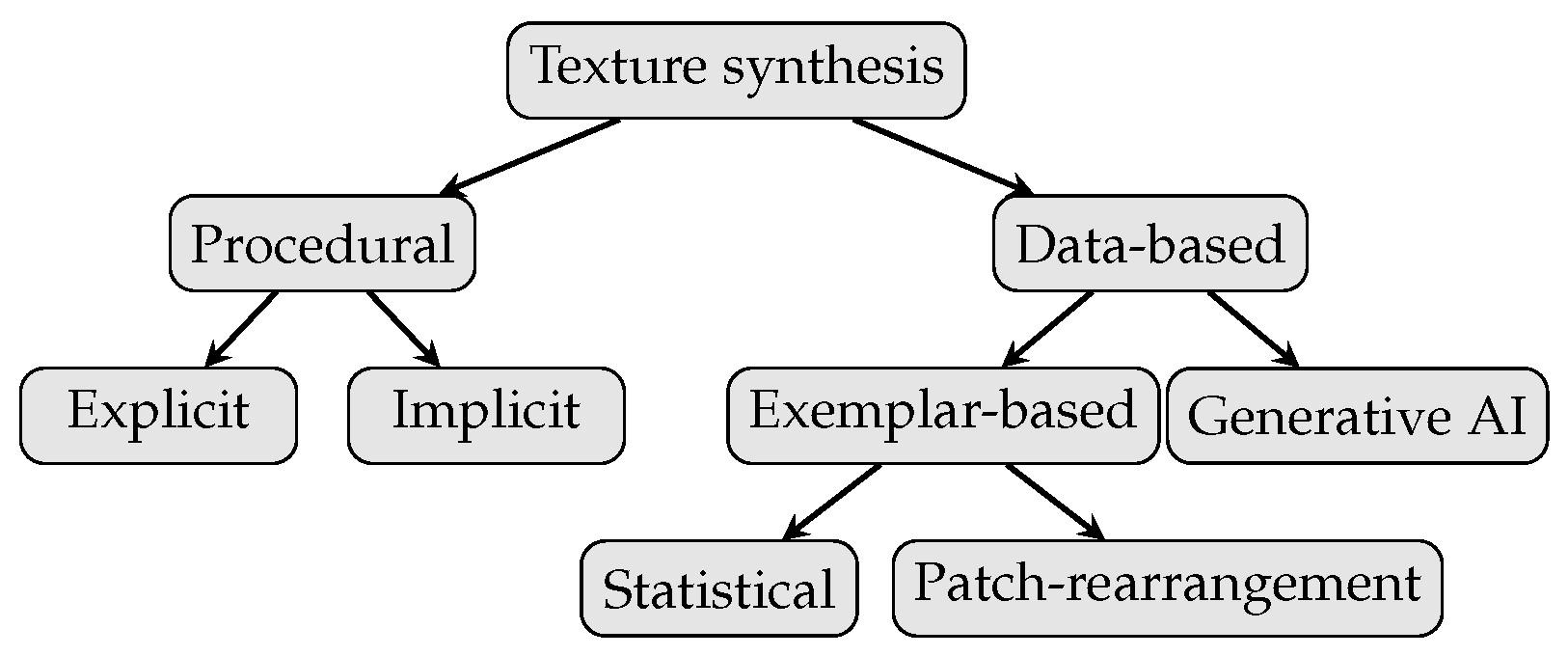
Figure 11.
Classification of computer graphics methods for texture synthesis.
Figure 11.
Classification of computer graphics methods for texture synthesis.
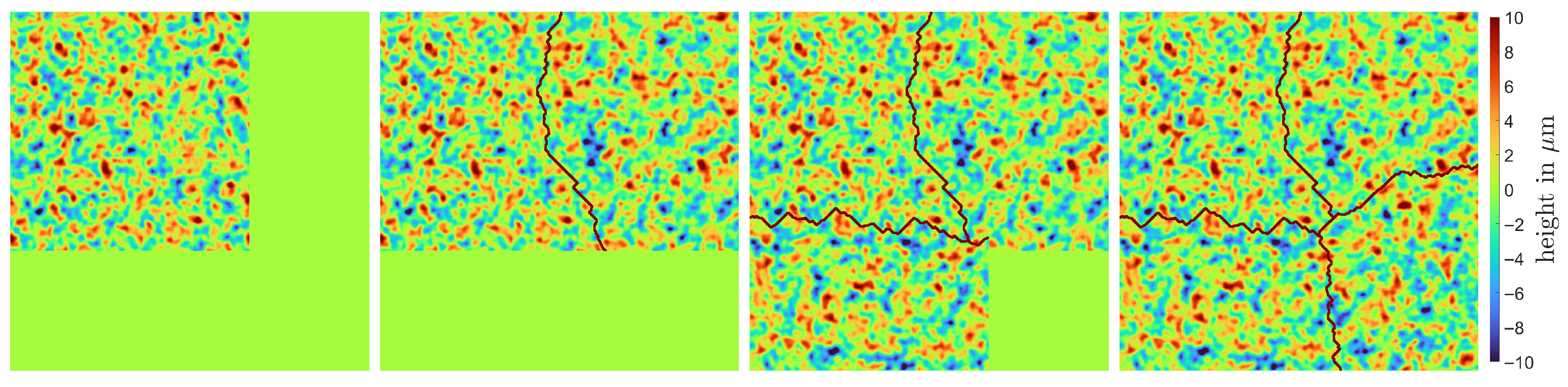
Figure 12.
Illustration of EF stitching marking the minimal path in each step. Patches have a size of , and the overlap region width is 256 pixels. The imaged region is approximately .
Figure 12.
Illustration of EF stitching marking the minimal path in each step. Patches have a size of , and the overlap region width is 256 pixels. The imaged region is approximately .
Figure 13.
Overview of model generating milled surfaces. (a) Edge path (top) and its approximation (bottom). (b) Sub-models for one ring (left) and interaction of multiple rings (right).
Figure 13.
Overview of model generating milled surfaces. (a) Edge path (top) and its approximation (bottom). (b) Sub-models for one ring (left) and interaction of multiple rings (right).
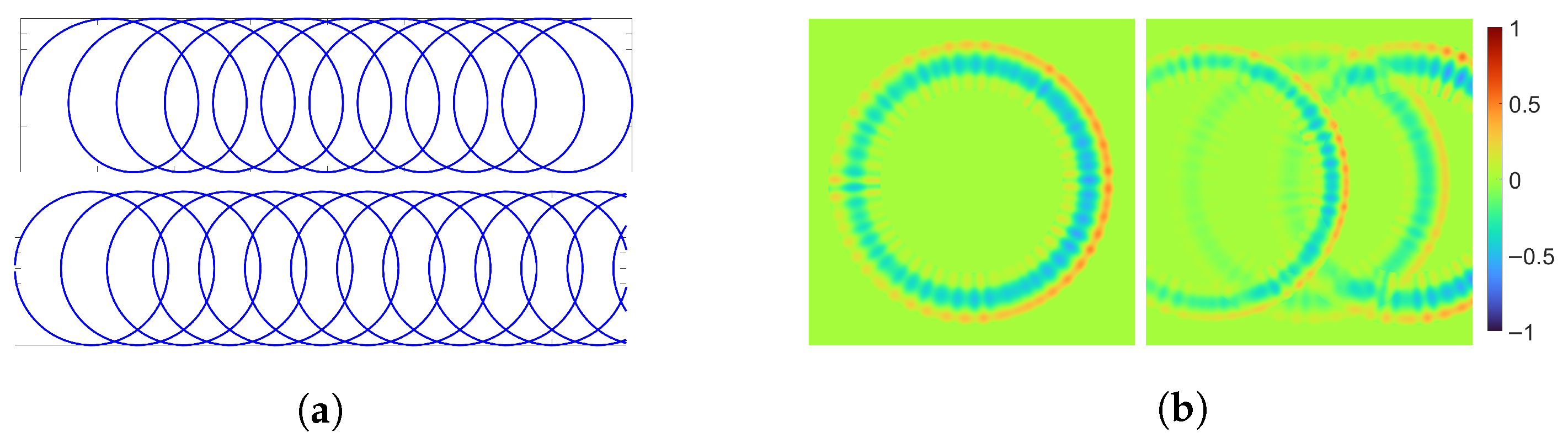
Figure 14.
Tool paths with center points. (a) Parallel milling. (b) Spiral milling.
Figure 14.
Tool paths with center points. (a) Parallel milling. (b) Spiral milling.
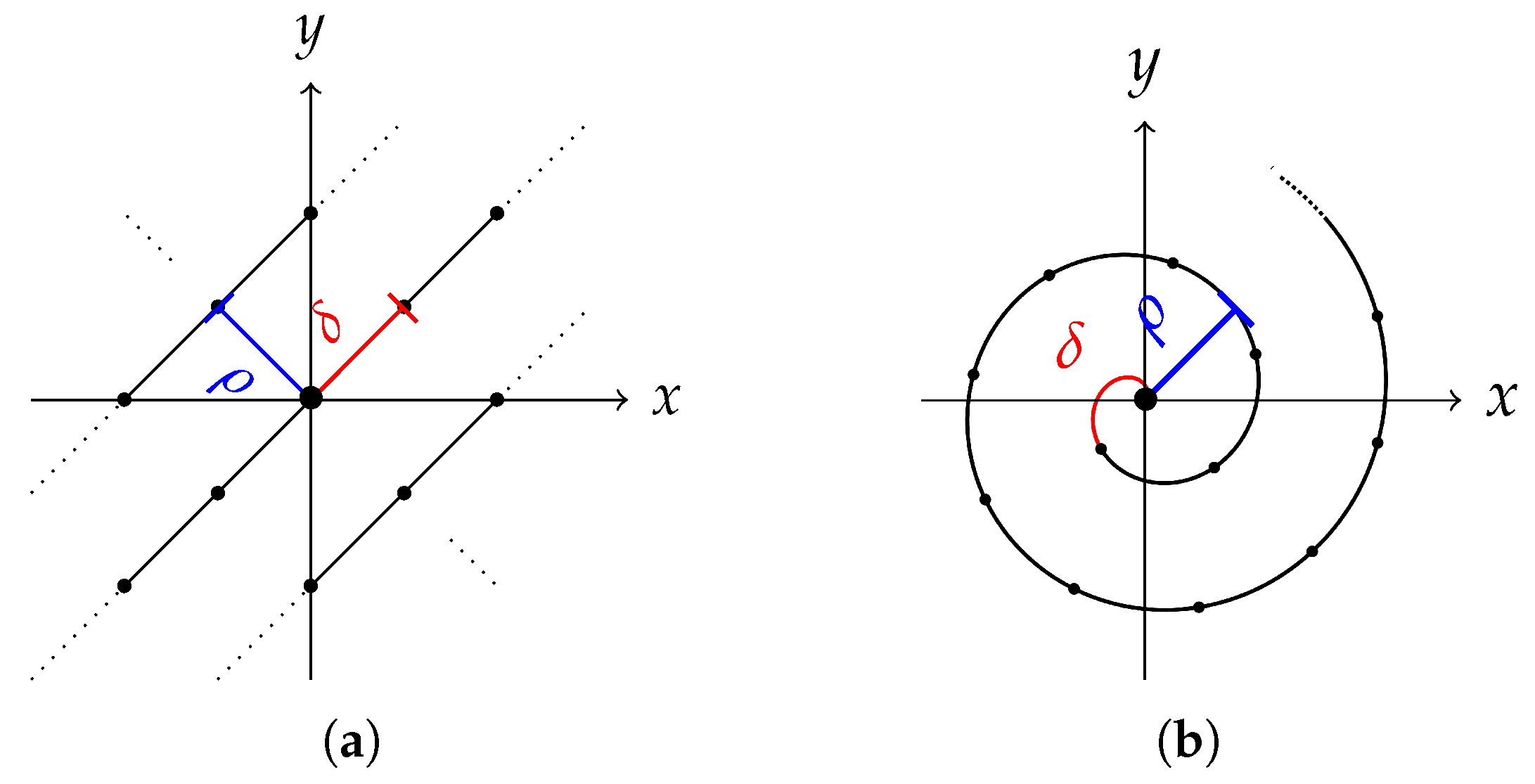
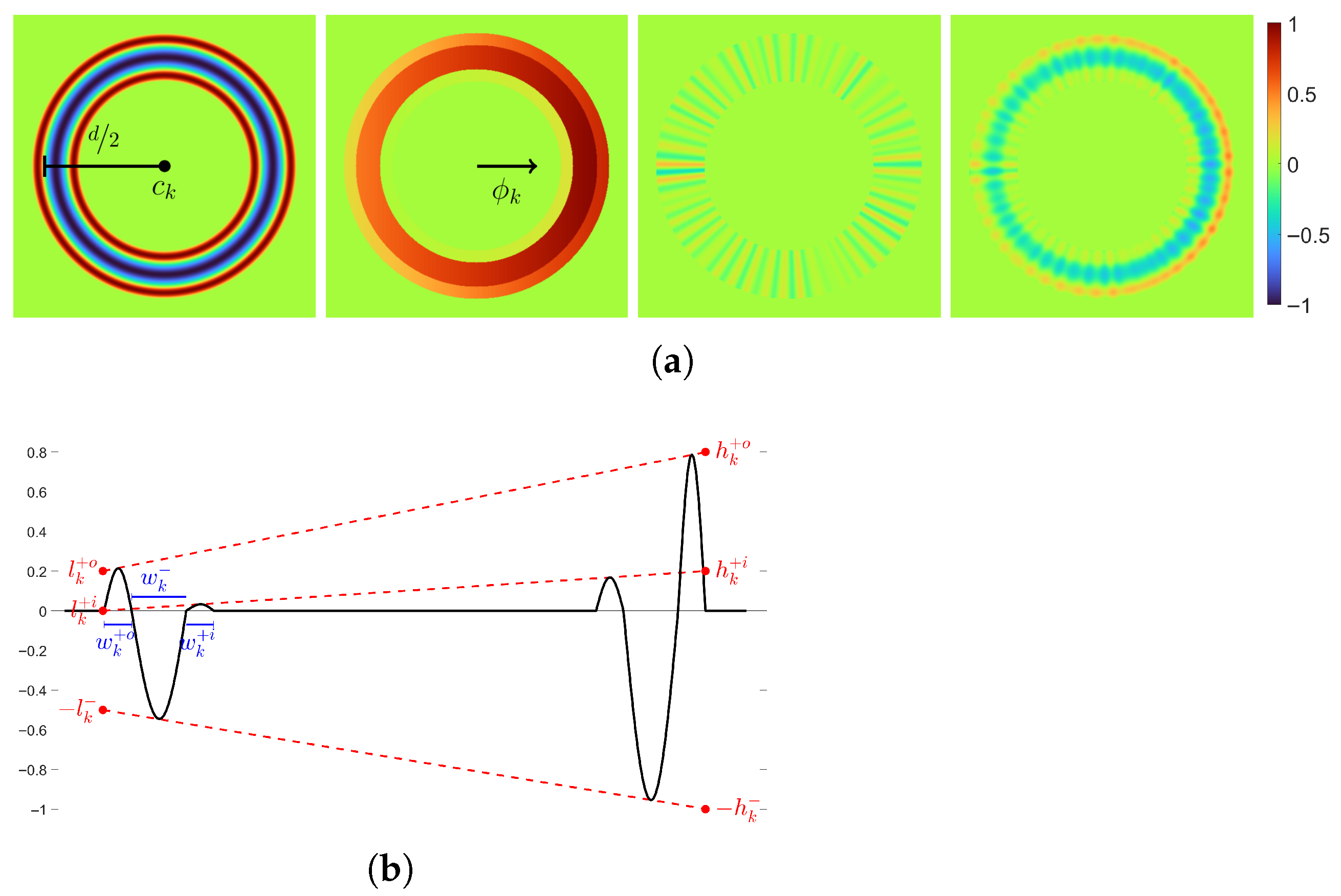
Figure 15.
Illustration of sub-model for ring appearance with explanation of its parameters. (a) Sub-model for ring appearance using , from left to right: , , , and . (b) The 1D intersection of the ring displaying the tilting mechanism: .
Figure 15.
Illustration of sub-model for ring appearance with explanation of its parameters. (a) Sub-model for ring appearance using , from left to right: , , , and . (b) The 1D intersection of the ring displaying the tilting mechanism: .
Figure 16.
Sub-model for rings’ interactions using (no tilting), from left to right: , , , .
Figure 16.
Sub-model for rings’ interactions using (no tilting), from left to right: , , , .
Figure 17.
Adapted simulated milled surfaces generated with different parameter configurations. Imaged region is . (a) Parallel milling using mm, , and mm. (b) Parallel milling using mm, , and mm. (c) Parallel milling using mm, , and mm. (d) Parallel milling using mm, , and mm. (e) Parallel milling using mm, , and mm. (f) Spiral milling using mm, , and mm.
Figure 17.
Adapted simulated milled surfaces generated with different parameter configurations. Imaged region is . (a) Parallel milling using mm, , and mm. (b) Parallel milling using mm, , and mm. (c) Parallel milling using mm, , and mm. (d) Parallel milling using mm, , and mm. (e) Parallel milling using mm, , and mm. (f) Spiral milling using mm, , and mm.
Figure 18.
Real (top) and synthetic (bottom) crops of defects on different surfaces: sandblasted (left), parallel milling (middle), and spiral milling (right). The synthetic images are displayed before the application of pre-processing.
Figure 18.
Real (top) and synthetic (bottom) crops of defects on different surfaces: sandblasted (left), parallel milling (middle), and spiral milling (right). The synthetic images are displayed before the application of pre-processing.
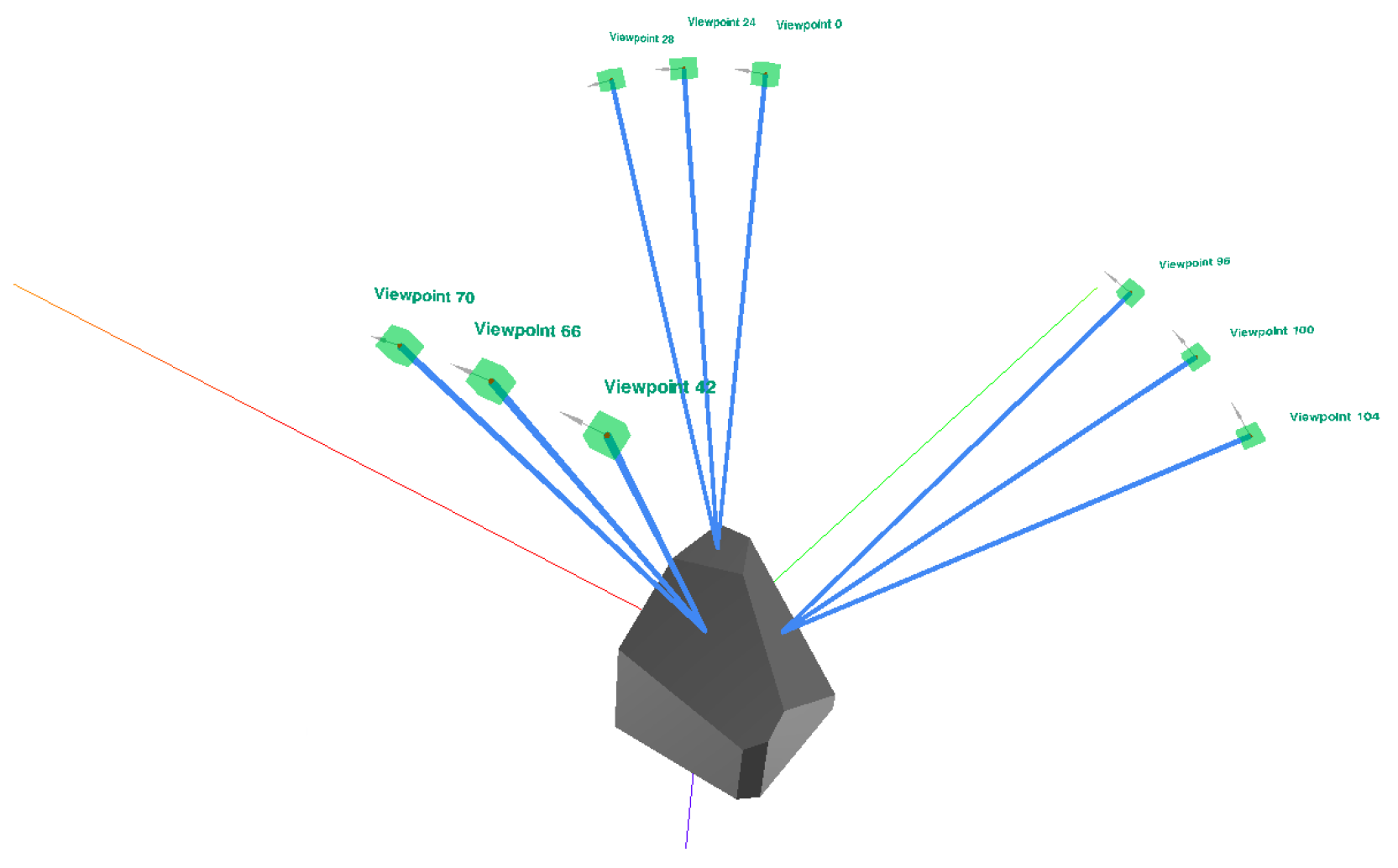
Figure 19.
Visualization of the viewpoints used for inspection. The blue line shows the optical axis of the camera and has the length of the focusing distance.
Figure 19.
Visualization of the viewpoints used for inspection. The blue line shows the optical axis of the camera and has the length of the focusing distance.
Figure 20.
Non-defective representative image samples from the dual dataset. The upper image is synthetic, and the lower image is real. The images represent face A, viewed at a 20-degree angle from the perpendicular view. Selected synthetic images closely match the structures in real images. (a) Sandblasting, 2.5 bar. (b) Sandblasting, 6 bar. (c) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (d) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (e) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.5. (f) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.8. (g) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (h) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (i) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.5. (j) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.8.
Figure 20.
Non-defective representative image samples from the dual dataset. The upper image is synthetic, and the lower image is real. The images represent face A, viewed at a 20-degree angle from the perpendicular view. Selected synthetic images closely match the structures in real images. (a) Sandblasting, 2.5 bar. (b) Sandblasting, 6 bar. (c) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (d) Parallel milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (e) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.5. (f) Parallel milling: a head diameter of 8 mm and a radial depth of cut of 0.8. (g) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.5. (h) Spiral milling: a head diameter of 4 mm and a radial depth of cut of 0.8. (i) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.5. (j) Spiral milling: a head diameter of 8 mm and a radial depth of cut of 0.8.
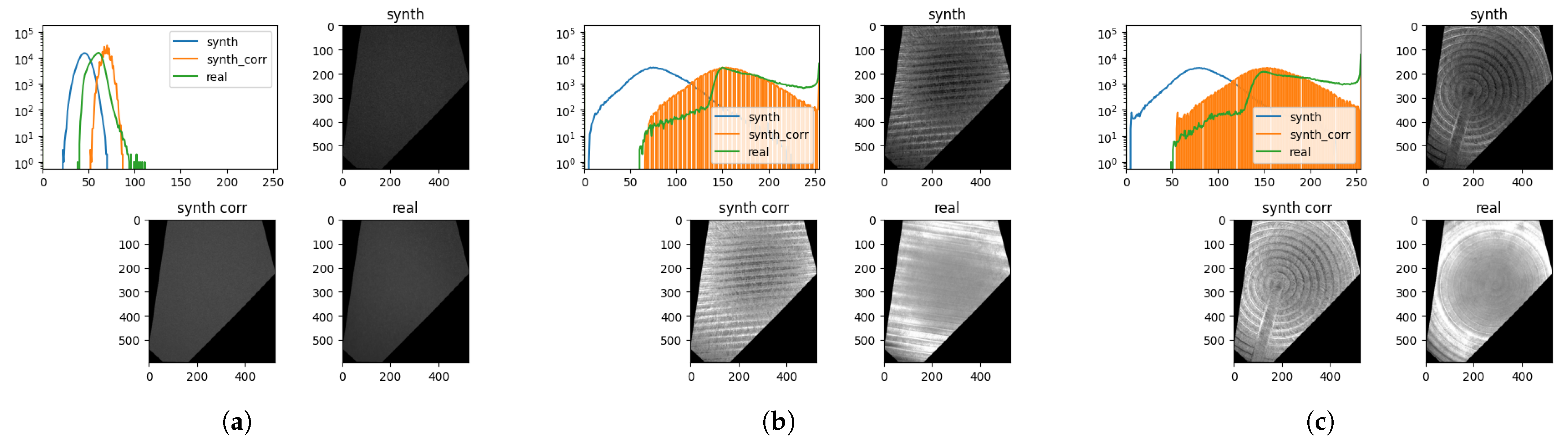
Figure 21.
Examples of the differences made by intensity correction of synthetic images. Each example shows the image histograms, the original synthetic image (synth), the corrected synthetic image (synth_corr), and the closest matching real image (real). (a) Sandblasted, (b) parallel milling, and (c) spiral milling.
Figure 21.
Examples of the differences made by intensity correction of synthetic images. Each example shows the image histograms, the original synthetic image (synth), the corrected synthetic image (synth_corr), and the closest matching real image (real). (a) Sandblasted, (b) parallel milling, and (c) spiral milling.
Table 1.
Parameter settings for surface processing.
Table 1.
Parameter settings for surface processing.
| Technique | Parameter | Values |
|---|
| milling | Milling head’s diameter | 4 mm, 8 mm |
| | Radial depth of the cut | 0.2, 0.5, 0.8 |
| | Path | parallel, spiral |
| sandblasting | Pressure | 2.5 bar, 6 bar |
Table 2.
Overview of all parameters needed for the milling model, including their meaning and choices thereof. Choose
for normally distributed parameters. Known parameters are highlighted (
Table 1).
Table 2.
Overview of all parameters needed for the milling model, including their meaning and choices thereof. Choose
for normally distributed parameters. Known parameters are highlighted (
Table 1).
| | Notation | Definition | Meaning | Distribution | Parameter | Values |
|---|
| Pattern | | rings’ center points | determined by tool path | | | , |
| d | diameter of ring | diameter of milling head | | | |
| defines (distance between neighboring tool paths) | amount of overlap of neighboring tool paths | | | |
| increase distance between neighboring tool paths | distance between blade and outer edge of tool | | | |
| distance between center points | depends on feed rate and tool’s rotational speed | | | mm |
| amount of rings with changed order | | | | |
| Appearance | | width of indentation | width of cutting edge | |
|
|
| width of inner accumulation | depends on edges’ sharpness | |
|
|
| width of outer accumulation | depends on edges’ sharpness | |
|
|
| tilting direction | depends on tool path | | | computed by ck |
| , | minimal/maximal scaling of indentation depth | cutting depth with tilting | |
| ,
|
| , | minimal/maximal scaling of inner accumulation height | depends on edges’ sharpness | |
| ,
|
| , | minimal/maximal scaling of outer accumulation height | depends on edges’ sharpness | |
| ,
|
| number of sine curves | | | | |
| frequency of sine curves | | | | |
| shift of sine curves | | | | |
| Interaction | | minimal value convex combination | | |
|
|
| maximal value convex combination | | |
|
|
Table 3.
Defect quantities and specification ranges obtained from approximate measurements of their correspondents in physical samples with a gentle increase in ranges to model the expected unobserved defects.
Table 3.
Defect quantities and specification ranges obtained from approximate measurements of their correspondents in physical samples with a gentle increase in ranges to model the expected unobserved defects.
| Parameter | Small Dent | Big Dent | Flat Scratch | Curvy Scratch |
|---|
| Quantity | 5 | 3 | 2 | 2 |
| Diameter | [0.02, 0.2] | [0.2, 1.0] | [0.02, 0.2] | [0.02, 0.1] |
| Elongation | [1, 2] | [1, 4] | - | - |
| Depth | [0.05, 0.2] | [0.2, 1.0] | - | - |
| Path length | - | - | [5, 20] | [10, 20] |
| Step size | - | - | 0.1 | 1.0 |
Table 4.
Texture parameter ranges used to modify the default values (highlighted) given in
Table 2. The standard deviations were chosen by the
rule such that the desired ranges of the random variables are obtained. Hence, we set
.
Table 4.
Texture parameter ranges used to modify the default values (highlighted) given in
Table 2. The standard deviations were chosen by the
rule such that the desired ranges of the random variables are obtained. Hence, we set
.
| Parameter | Set of Values |
|---|
| Ring center points noise () | |
| Ring distance () | |
| Ring flip probability () | |
| Ring width noise () | |
| Ring depth noise () | |
| Cosine curves number () | |
Table 5.
Domain similarities averaged within and across texture types, bound to interval . Histogram WD, MAE, and LPIPS were inverted to be interpreted as the degree of similarity.
Table 5.
Domain similarities averaged within and across texture types, bound to interval . Histogram WD, MAE, and LPIPS were inverted to be interpreted as the degree of similarity.
| Method | Sandblasted | Parallel | Spiral | All |
|---|
| 1—HistWD | 0.980 | 0.932 | 0.942 | 0.946 |
| 1—MAE | 0.807 | 0.681 | 0.655 | 0.696 |
| SSIM | 0.896 | 0.561 | 0.585 | 0.638 |
| 1—LPIPS | 0.916 | 0.660 | 0.686 | 0.722 |
Table 6.
Task similarities between texture groups. The domains represent the experiment training → testing domains, with the real (Re) and synthetic (Sy) domains. Fine-tuning (ft) was performed using real data after training on synthetic data.
Table 6.
Task similarities between texture groups. The domains represent the experiment training → testing domains, with the real (Re) and synthetic (Sy) domains. Fine-tuning (ft) was performed using real data after training on synthetic data.
| Texture | Domains | mP | mR | mF1 | mIoU |
|---|
| Sandblasted | Sy → Sy | 57.0 | 53.1 | 54.7 | 37.7 |
| Sy → Re | 34.0 | 64.3 | 41.7 | 26.3 |
| Sy + ft → Re | 60.1 | 71.9 | 65.5 | 49.6 |
| Re → Re | 57.9 | 61.9 | 59.1 | 42.6 |
| Parallel | Sy → Sy | 57.1 | 39.6 | 45.6 | 29.6 |
| Sy → Re | 26.5 | 23.0 | 23.5 | 13.8 |
| Sy + ft → Re | 52.6 | 33.4 | 38.3 | 23.9 |
| Re → Re | 50.3 | 34.5 | 40.8 | 25.8 |
| Spiral | Sy → Sy | 59.5 | 39.7 | 47.6 | 31.3 |
| Sy → Re | 35.2 | 22.1 | 26.4 | 15.5 |
| Sy + ft → Re | 49.5 | 40.1 | 43.9 | 28.4 |
| Re → Re | 50.6 | 43.1 | 46.2 | 30.7 |
| All | Sy → Sy | 59.4 | 46.0 | 51.5 | 34.7 |
| Sy → Re | 32.2 | 31.3 | 31.6 | 18.9 |
| Sy + ft → Re | 59.0 | 49.1 | 53.1 | 36.1 |
| Re → Re | 59.0 | 48.2 | 52.6 | 35.8 |