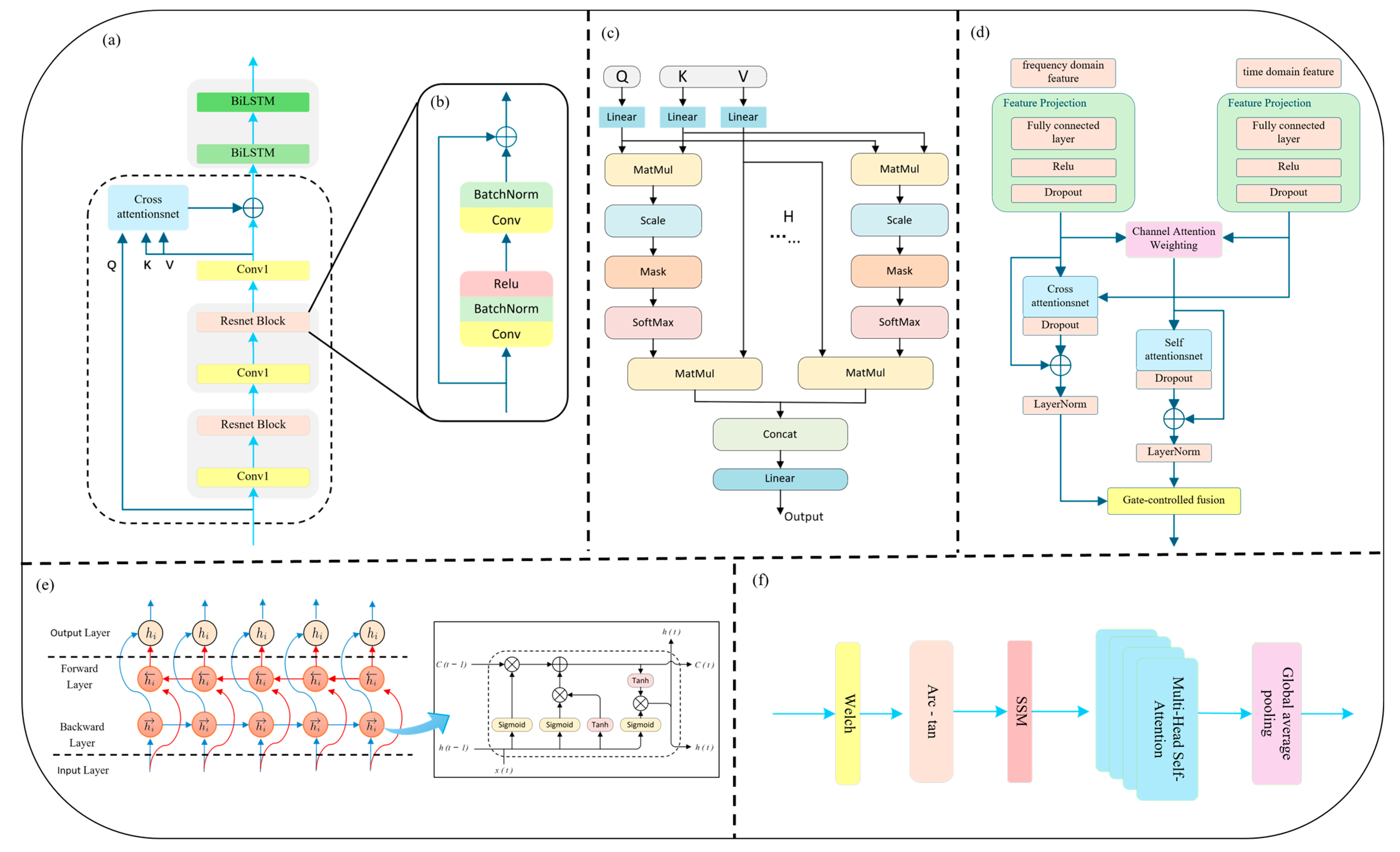
To fully capture the multiscale and multi-domain characteristics of PPG signals, a dual-branch feature extraction module is designed, composed of time-domain and frequency-domain sub-networks. These two branches focus, respectively, on modeling rhythmic dynamics in the temporal dimension and energy distribution patterns in the frequency domain, thereby enhancing the model’s accuracy and robustness in arrhythmia recognition.
2.2.1. Time-Domain Feature Extraction
In the time-domain branch, we introduce a novel Cross-Scale Residual Attention (CSRA) mechanism to enhance the network’s sensitivity to rhythm variations and mitigate the limitations of conventional deep convolutional structures in modeling long-range dependencies and multi-scale temporal patterns. In the field of deep learning, the traditional CNN + LSTM architecture has been widely used for temporal sequence modeling, with CNNs excelling at capturing local structures and LSTMs handling sequential dependencies. However, CNNs typically have limited receptive fields, and deep stacking can lead to vanishing gradients. Meanwhile, standard LSTM architectures are insufficient in capturing bidirectional rhythm dynamics, thus limiting their ability to model complex arrhythmic behavior. To address these challenges, we incorporate a residual network backbone with skip connections that enable direct information flow between shallow and deep layers. This alleviates gradient degradation, accelerates convergence, and enables deeper network depth without performance loss. Each residual block consists of two 1D convolutional layers, combined with Batch Normalization [
29] and ReLU activation [
30], forming a multi-scale learning unit that preserves both low-level detail and high-level abstraction (see
Figure 2b).
To further enhance temporal contextual modeling, an Interactive Attention Mechanism is integrated atop the residual structure. This mechanism is designed to model the relationships between two distinct sequences by allowing one (the query) to attend to another (the key-value pair), thus enabling dynamic cross-time information fusion and feature reweighting. The detailed computation is defined in Equation (1):
Here, , , and represent the query, key, and value matrices, respectively. The term denotes the dimensionality of the key vectors. The product computes the dot-product similarity between the queries and keys, resulting in an attention score matrix. Unlike standard self-attention, in which the queries, keys, and values are derived from the same sequence, the formulation in this module allows the queries () to originate from one sequence, while the keys () and values () are drawn from another, enabling cross-sequence interaction and information alignment.
Building upon the above, this study further introduces Multi-Head Attention (MHA) (as illustrated in
Figure 2c), combined with Layer Normalization, to enhance multi-scale temporal modeling. The underlying principles are detailed in Equations (2)–(4). The multi-head attention mechanism enables parallel alignment and aggregation of multimodal features across different subspaces. Each attention head autonomously attends to distinct temporal fragments or frequency bands, improving the model’s sensitivity to various arrhythmic rhythm disruptions. The residual connection ensures smooth information flow, while LayerNorm stabilizes gradient propagation and prevents excessive fitting or degeneration, thus achieving incremental feature enhancement. In this work, we designate the deep residual features as both query (
) and key (
), while the adaptively reconstructed input serves as the value (
), jointly forming a Cross-Scale Interactive Attention (CSIA) module. This structure effectively reinforces the fusion between low-level information and high-level semantic representations.
Here,
denotes the output vector of the
attention head, which captures localized feature representations extracted by that head. The function Attention refers to the scaled dot-product attention mechanism. The matrices
,
, and
are the learnable linear projection weights corresponding to the
head, applied to the query (
), key (
), and value (
), respectively, to map them into distinct subspaces. The parameter
denotes the total number of attention heads.
Here,
denotes the concatenation operation, which merges the output feature vectors from all attention heads (
to
) into a single, larger vector. The matrix
is a linear projection matrix applied to the concatenated features, reducing the dimensionality to the desired output space.
Here, denotes the final output matrix or tensor. refers to the layer normalization operation, which stabilizes training by normalizing intermediate activations. X represents the input tensor to the residual connection.
To address the periodic and non-stationary nature of arrhythmia signals, a Bidirectional LSTM (BiLSTM) layer is employed following the attention module (
Figure 2e). Compared to standard LSTM, BiLSTM captures both past and future dependencies, enhancing modeling of complex rhythms such as atrial fibrillation (AF) and premature ventricular contractions (PVC). Its bidirectional feedback loop improves model robustness against signal interruptions and local noise. As shown in
Figure 2a, the PPG signal is first passed through a 1D causal convolution and max-pooling layer for preliminary feature extraction and downsampling. Two stacked residual blocks then encode deep representations. The original input is reconstructed via global average pooling and a projection layer to serve as the attention Value input. Finally, the output is passed through two BiLSTM layers to capture long-term dependencies and construct a robust time-domain representation for subsequent classification.
2.2.2. Frequency-Domain Feature Extraction
In the analysis of arrhythmias using PPG signals, time-domain features primarily focus on waveform morphology and rhythm variability, such as local fluctuations in R–R intervals, which can effectively reflect irregularities in cardiac rhythms. However, certain types of arrhythmias—such as atrial flutter, high-frequency fibrillations, or harmonic ventricular tachycardia—exhibit persistent and latent spectral patterns that are difficult to capture through time-domain analysis alone. To address this limitation, a dedicated frequency-domain analysis branch is introduced in this study, aiming to extract energy distribution characteristics and spectral stability features. This perspective supplements the time-domain representation, especially in scenarios involving high-frequency disturbances or chronic rhythm disorders. Frequency-domain modeling enables the identification of latent rhythmic structures within PPG signals and facilitates multi-scale rhythm detection. For instance, although atrial fibrillation appears disorganized in the time domain, it often presents as sustained high-frequency energy in the 4–7 Hz band of the frequency spectrum. Different arrhythmic types exhibit distinct characteristics across low-frequency (LF, 0.04–0.15 Hz), high-frequency (HF, 0.15–0.4 Hz), and even higher bands. Frequency-domain networks allow for the parallel monitoring of multiple frequency bands, offering more fine-grained contrast in rhythm intensity than time-domain models.
To effectively model such frequency-specific features, this study proposes a frequency-domain feature extraction branch that integrates Transformer and BiLSTM architectures with arc-tangent nonlinear mapping and self-similarity matrix (SSM) encoding. The overall architecture of the frequency-domain branch is illustrated in
Figure 2f. The proposed method adopts a spectral self-similarity input strategy, in which a self-similarity matrix (SSM) defined as
is introduced as the primary input to the network. Based on standard sinusoidal positional encoding, an additional lightweight convolutional module is appended to perform dynamic adjustment of positional embeddings, allowing the model to learn the superimposed relationships between low-frequency modulations (e.g., respiratory sinus arrhythmia) and high-frequency components within the PPG signal. Specifically, Welch’s Power Spectral Density (PSD) estimation method is employed to decompose the PPG signal into its spectral components. Unlike direct application of the Fast Fourier Transform (FFT), Welch’s method enhances the stability of spectral estimates by reducing the variance through windowing, segment overlap, and averaging operations.
Welch’s method is a classical approach for PSD estimation widely used in signal processing to obtain a smoother and lower-variance power spectrum. The original signal
of length N is divided into K overlapping or non-overlapping segments, each of length L. Each segment
is then multiplied by a window function
. The periodogram of each segment is calculated as follows (Equation (5)):
Here, is the normalization factor representing the window energy. denotes the power spectral estimate of the k segment. is the n sample from the k signal segment. FFT{⋅} refers to the Discrete Fourier Transform (DFT) operation.
Finally, the periodograms of all K segments are averaged pointwise along the frequency axis to obtain the final power spectral estimate, as defined in Equation (6):
Here,
denotes the total number of segments, determined by the original signal length N, segment length L, and overlap ratio. The averaging operation significantly reduces the variance of individual periodograms, resulting in a smoother and more stable spectral estimate. The specific parameters and methodologies of the proposed model are described in detail in the
Supplementary Materials.
Subsequently, an arc-tangent nonlinear mapping is applied to compress the PSD values from the original domain [0, +∞) into the bounded interval (−π/2, +π/2). This transformation mitigates the impact of local energy spikes (e.g., caused by motion artifacts), while preserving the relative energy ranking across frequency bands, thereby enhancing the model’s robustness and sensitivity in frequency-domain representation. The compressed spectrum is further transformed into a Self-Similarity Matrix (SSM) by computing the inner product between spectral vectors. Each element (i, j) in the resulting matrix represents the energy similarity between frequency bands i and j over the entire signal segment. This operation effectively lifts the original 1D spectral structure into a 2D similarity map, emphasizing structural relationships among frequency bands. It enables the model to intuitively capture rhythmic patterns such as spectral resonance, inter-frequency transitions, and repetitive spectral motifs, thereby enhancing the representation of spectral heterogeneity and multi-scale periodicity.
On top of the SSM, a Transformer encoder is introduced to perform deep feature modeling using multi-head self-attention. In this study, four attention heads are employed in parallel to learn non-local dependencies between spectral blocks in different subspaces. This design effectively breaks through the receptive field limitations of local-window methods commonly used in spectral modeling. The output of the Transformer is combined with the original spectral input via residual connections and layer normalization, facilitating stable long-range dependency modeling. A 1 × 1 convolutional layer is subsequently applied to project the channel dimension of the attention output. This layer maintains the lightweight nature of the network while performing cross-channel linear feature fusion. Finally, a bidirectional Long Short-Term Memory (BiLSTM) network is adopted to further model the sequential dynamics along the frequency axis. This architecture is capable of capturing rhythmic transitions such as enhancement–suppression–reemergence across frequency bands, making it especially suitable for detecting complex arrhythmias like atrial fibrillation, high-frequency flutter, and ventricular fibrillation, which often involve frequency drift and localized modulation.
The proposed frequency-domain feature extraction strategy centers on structural similarity modeling and sequential dependency learning. By combining dynamic range compression, structured SSM representation, multi-head attention, and BiLSTM sequence learning, the method systematically extracts multi-scale rhythmic information in the spectral domain of PPG signals. Compared to fully stacked Transformer architectures, this design achieves a favorable trade-off between model capacity and computational efficiency. Coupled with residual connections, dropout regularization, and layer normalization, the model demonstrates strong generalization and anti-overfitting capabilities, making it well-suited for real-time rhythm anomaly detection in wearable PPG applications.