Localization of Buried Polyethylene Gas Pipelines Using Compressional Wave Migration Stacking Imaging
Abstract
1. Introduction
2. Theory
2.1. Basic Theory of Elastic Waves
2.2. Cross-Correlation Theory
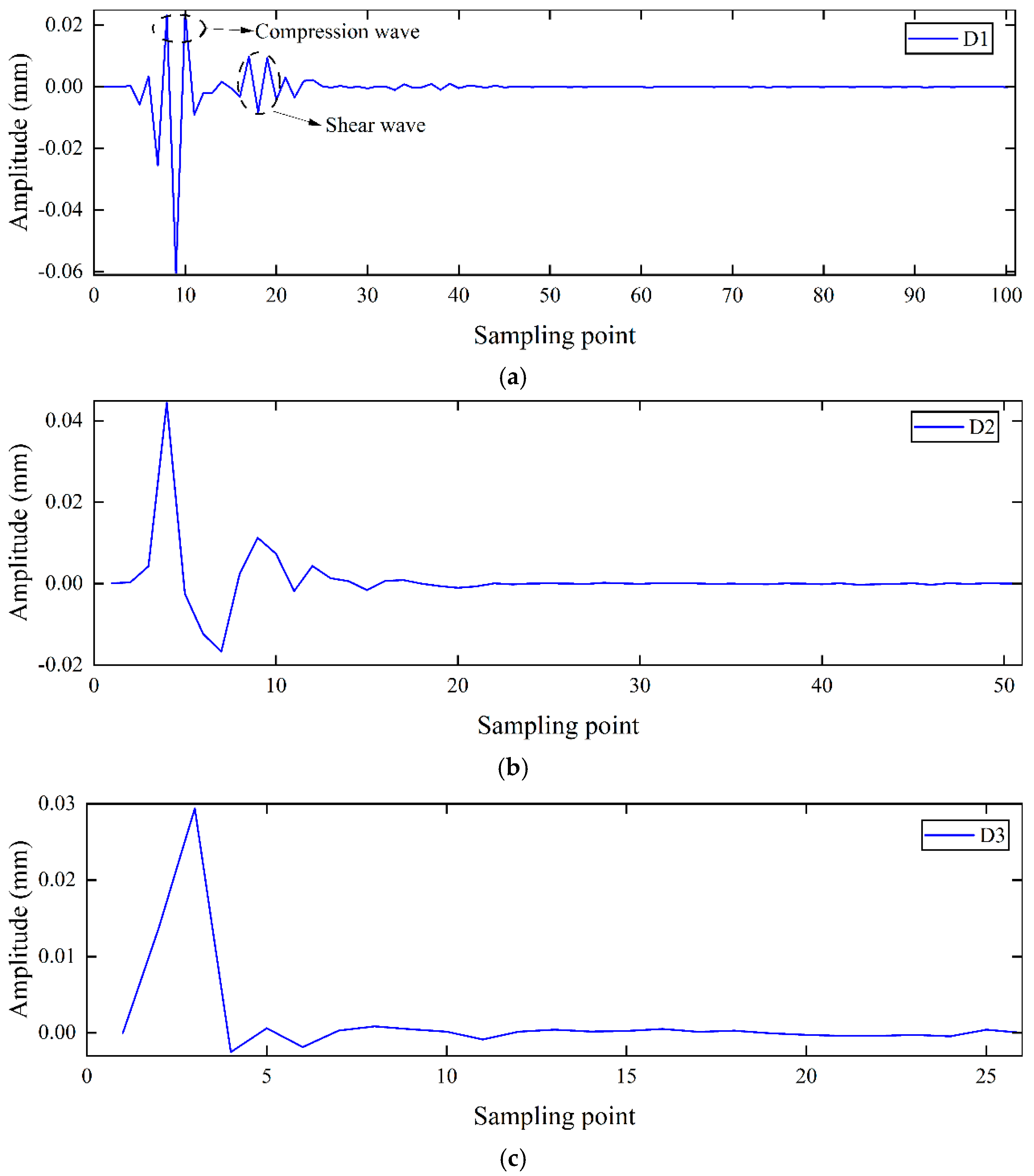
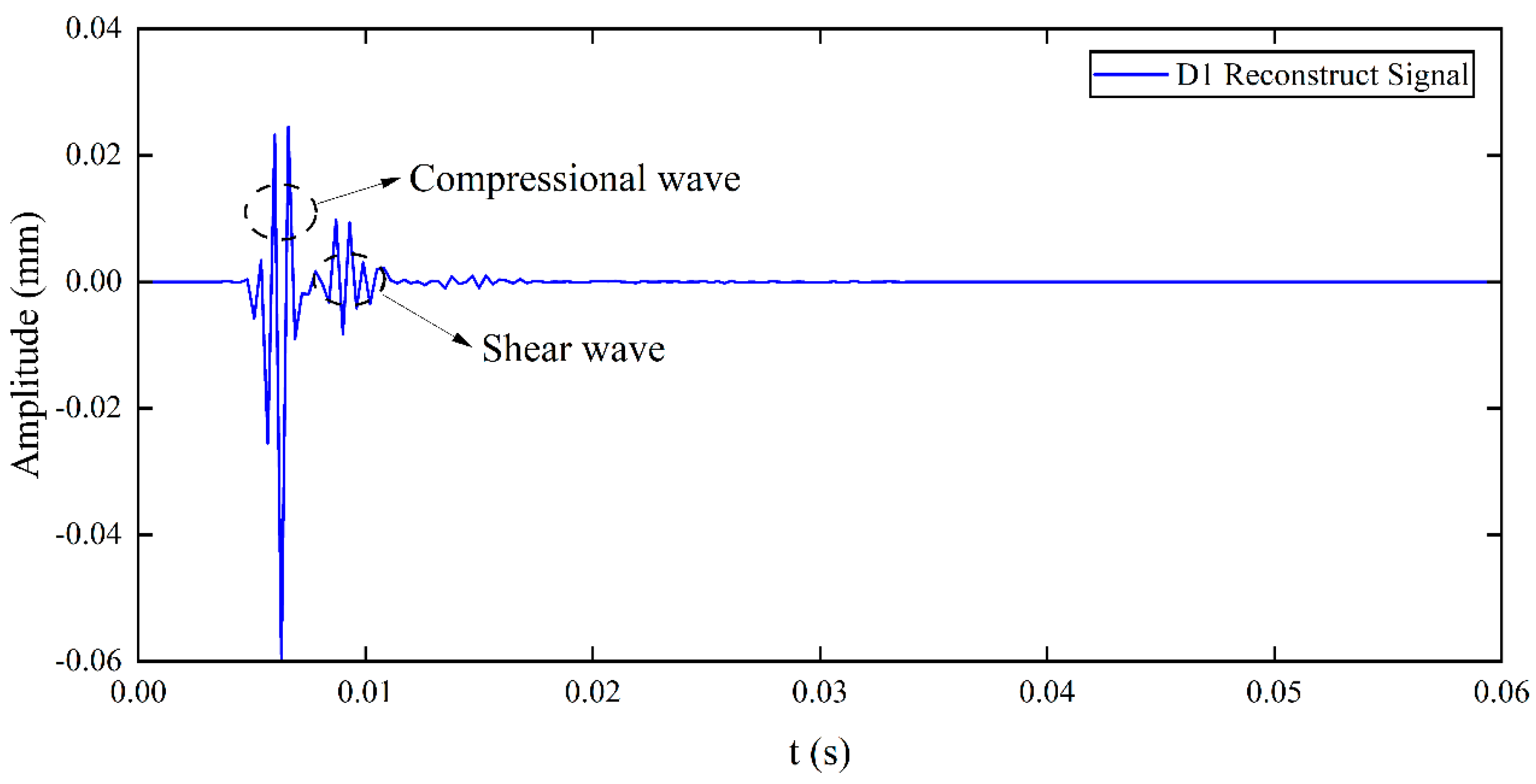
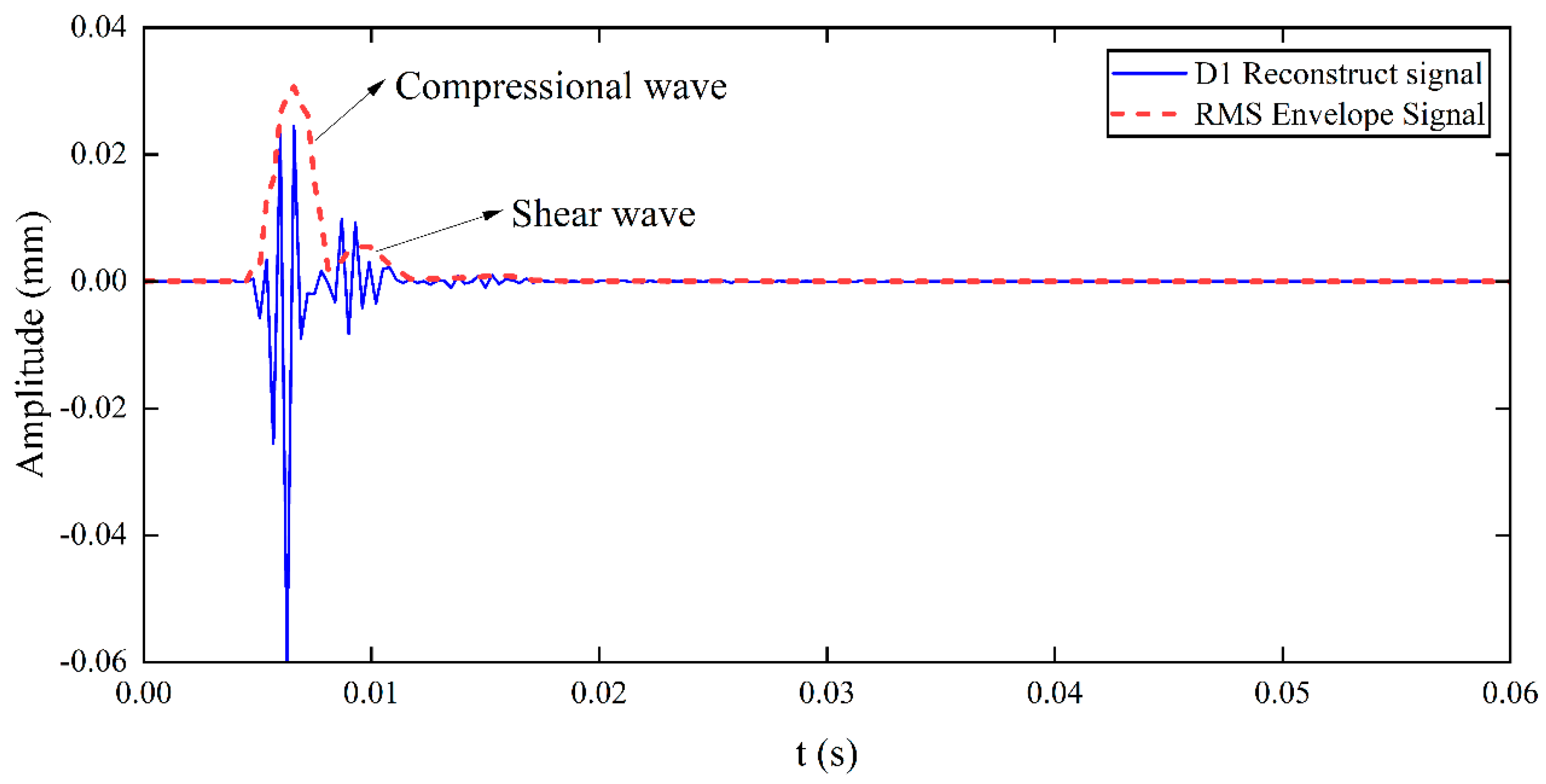
2.3. Wavelet Decomposition Theory
3. Simulation Analysis
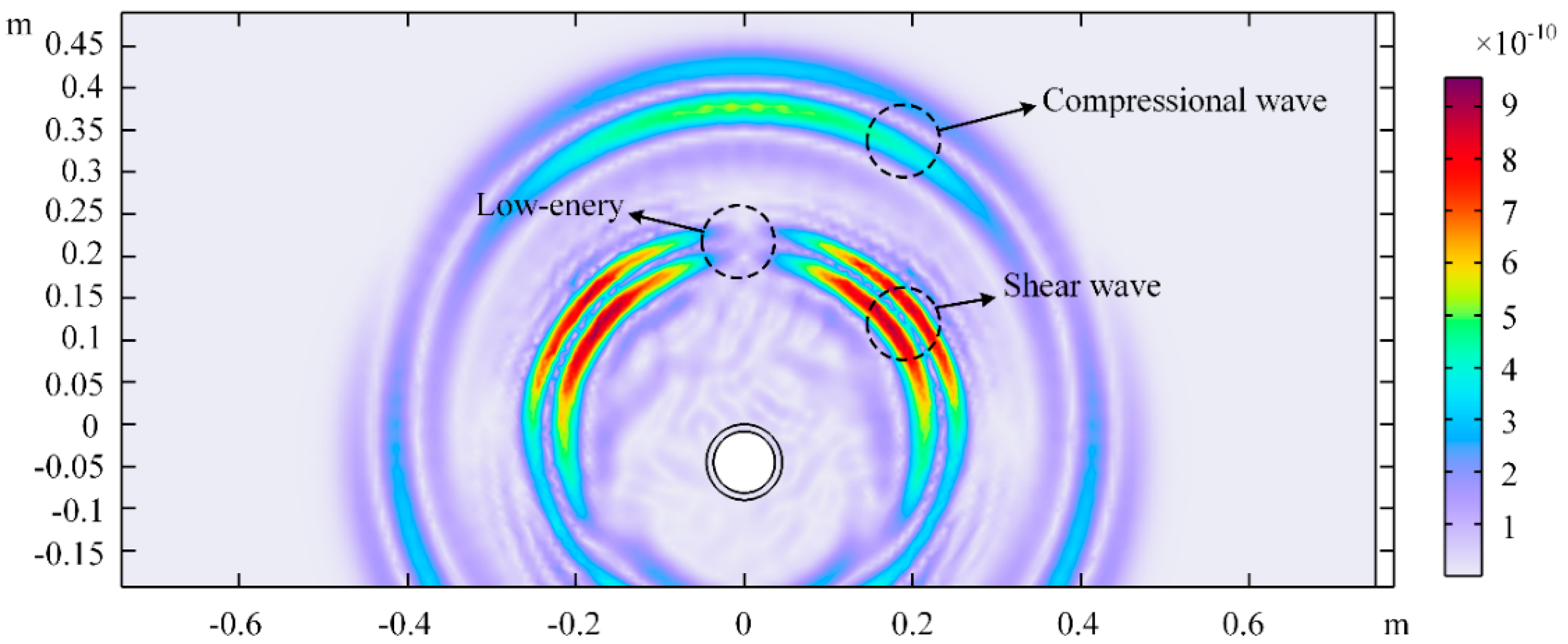
3.1. Simulation Analysis of Elastic Wave Propagation
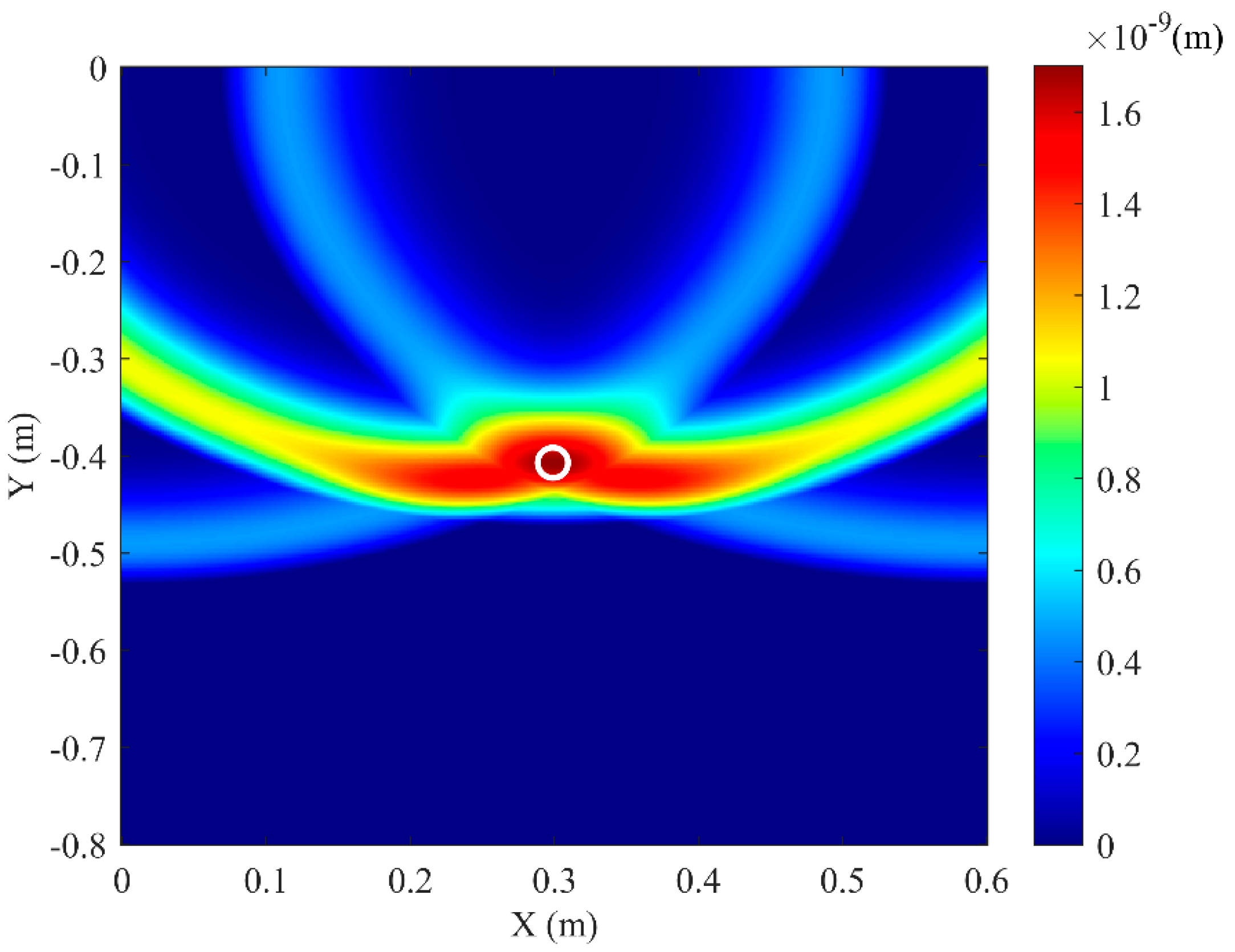
3.2. Localization of Buried PE Pipeline
4. Experimental Verification
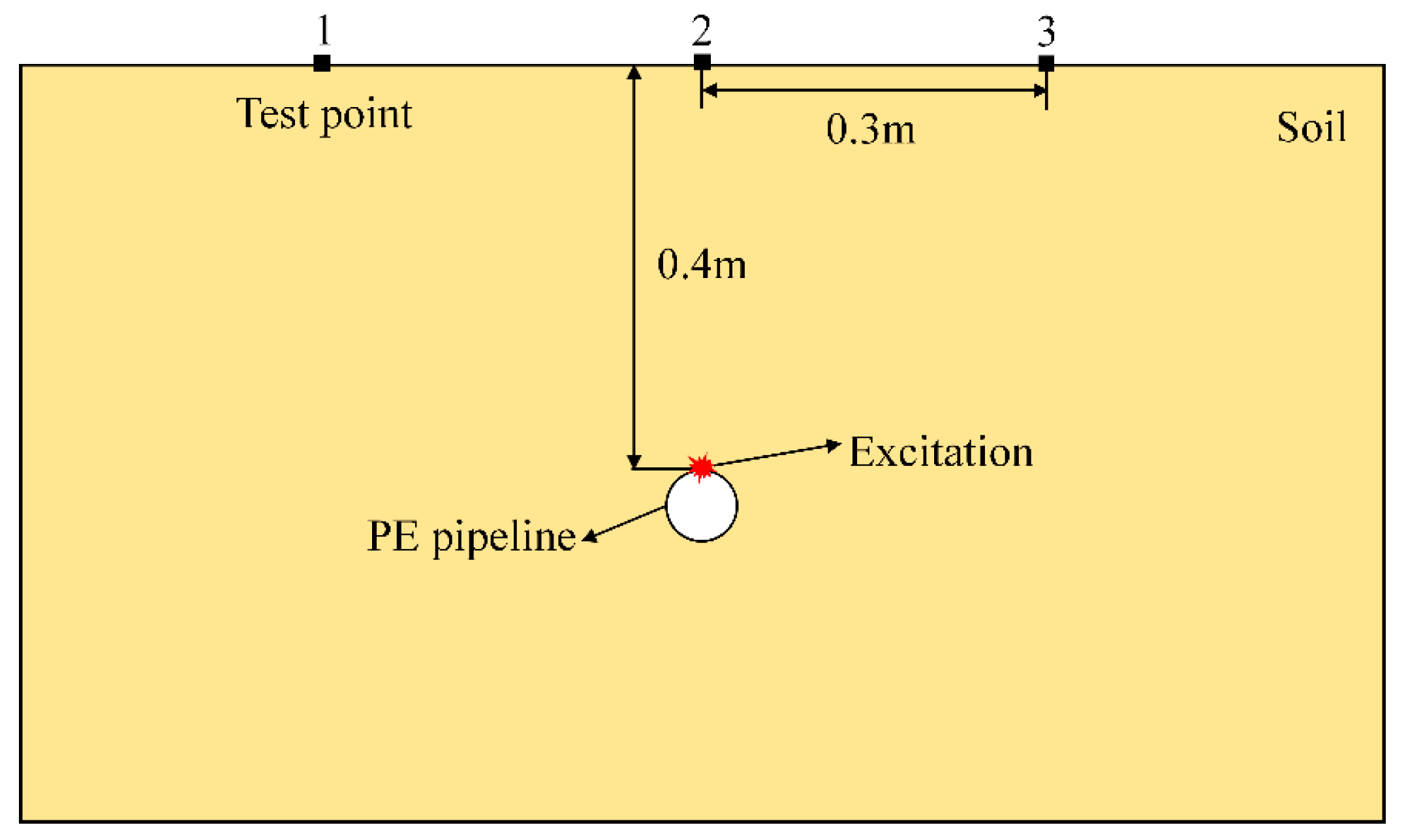
4.1. Experimental Setup
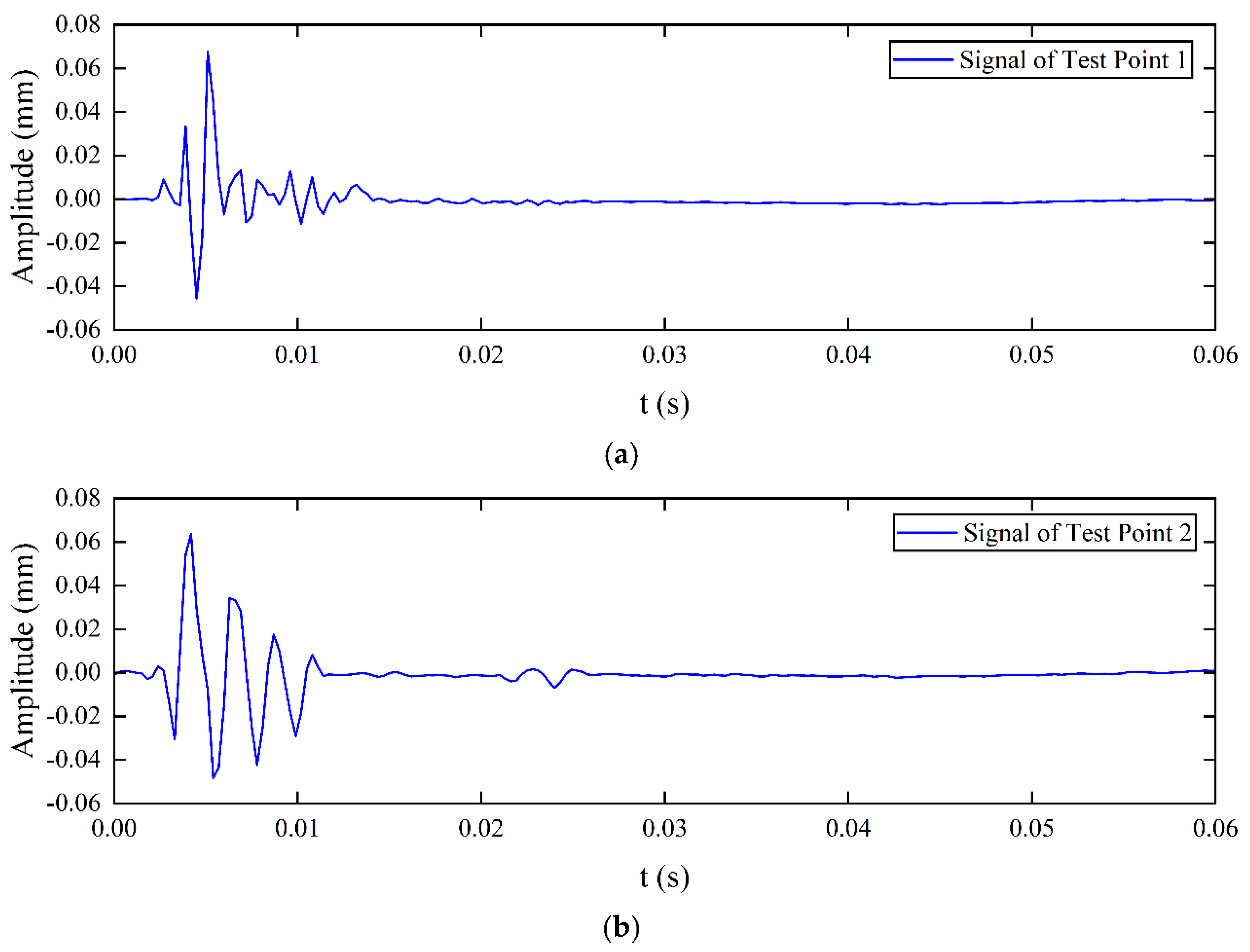
4.2. Signal Processing and Wave Velocity Testing
4.3. Compressional Wave Imaging
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Z.; Tariq, S.; Zayed, T. A comprehensive review of acoustic based leak localization method in pressurized pipelines. Mech. Syst. Signal Process. 2021, 161, 107994. [Google Scholar] [CrossRef]
- Liu, W.; Huang, C.; Wang, Y.; Shi, P.; Cai, G. Seismic Analysis of Connections of Buried Continuous Pipelines. Adv. Civ. Eng. 2020, 2020, 8839380. [Google Scholar] [CrossRef]
- Liu, Y.; Habibi, D.; Chai, D.; Wang, X.; Chen, H.; Gao, Y.; Li, S. A Comprehensive Review of Acoustic Methods for Locating Underground Pipelines. Appl. Sci. 2020, 10, 1031. [Google Scholar] [CrossRef]
- Lin, N.; Sun, X.; Sun, M.; Li, X.; Liu, C.; Chen, S.; Meng, T. Aging Performance and an Improved Evaluation Method for PE80 and PE100 Pipelines for Urban Gas. Appl. Sci. 2024, 14, 9941. [Google Scholar] [CrossRef]
- Hu, G.; Feng, F.; Wang, G.; Pu, Q. Safety evaluation of defective polyethylene pipe under point load: Load ratio calculation method based on J-integral criterion. Theor. Appl. Fract. Mech. 2025, 138, 104914. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Z.; Hu, B.; Ji, Y.; Liang, X. Simulation and experimental study of buried natural gas pipeline leak detection based on sound source characteristics. Therm. Sci. 2024, 28, 101–113. [Google Scholar] [CrossRef]
- Li, P.; Wang, F.; Gao, J.; Lin, D.; Gao, J.; Lu, J.; Qiu, E.; Liu, C.; Hu, J. Failure Mode and the Prevention and Control Technology of Buried PE Pipeline in Service: State of the Art and Perspectives. Adv. Civ. Eng. 2022, 2022, 2228690. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, A.; Usman, M.; Chen, Q.; Xiong, F.; Wu, J.; Chen, H. Underground Pipeline Mapping From Multipositional Data: Data Acquisition Platform and Pipeline Mapping Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4504113. [Google Scholar] [CrossRef]
- Das, Y. Effects of soil electromagnetic properties on metal detectors. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1444–1453. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, C.; Tian, G.; Xiao, X.; Ahmed, J.; Wei, G.; Hu, Z.; Xiang, J.; Robinson, M. Current Trends and Perspectives of Detection and Location for Buried Non-Metallic Pipelines. Chin. J. Mech. Eng. 2021, 34, 97. [Google Scholar] [CrossRef]
- Li, J.; Guo, T.; Leung, H.; Xu, H.; Liu, L.; Wang, B.; Liu, Y. Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar. Sensors 2019, 19, 2913. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Sarkar, S. A review on different pipeline fault detection methods. J. Loss Prev. Process. Ind. 2016, 41, 97–106. [Google Scholar] [CrossRef]
- Xerri, W.; Saracco, G.; Ribodetti, A.; Zomero, L.; Picon, P. Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method. Sensors 2022, 22, 9433. [Google Scholar] [CrossRef]
- Iftimie, N.; Savin, A.; Steigmann, R.; Dobrescu, G.S. Underground Pipeline Identification into a Non-Destructive Case Study Based on Ground-Penetrating Radar Imaging. Remote Sens. 2021, 13, 3494. [Google Scholar] [CrossRef]
- Chun, P.J.; Suzuki, M.; Kato, Y. Iterative application of generative adversarial networks for improved buried pipe detection from images obtained by ground-penetrating radar. Comput. Civ. Infrastruct. Eng. 2023, 38, 2472–2490. [Google Scholar] [CrossRef]
- Ni, Z.-K.; Pan, J.; Shi, C.; Ye, S.; Zhao, D.; Fang, G. DL-Based Clutter Removal in Migrated GPR Data for Detection of Buried Target. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3507205. [Google Scholar] [CrossRef]
- Arendt, B.; Schneider, M.; Mayer, W.; Walter, T. Environmental Influences on the Detection of Buried Objects with a Ground-Penetrating Radar. Remote Sens. 2024, 16, 1011. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Fang, L.; Xu, M. New leak-localization approaches for gas pipelines using acoustic waves. Measurement 2019, 134, 54–65. [Google Scholar] [CrossRef]
- Muggleton, J.M.; Rustighi, E. ‘Mapping the Underworld’: Recent developments in vibro-acoustic techniques to locate buried infrastructure. Geotech. Lett. 2013, 3, 137–141. [Google Scholar] [CrossRef]
- Lobato de Almeida, F.C. Improved Acoustic Methods for Leak Detection in Buried Plastic Water Distribution Pipes. Doctoral Dissertation, University of Southampton, Southampton, UK, 2013. Available online: http://eprints.soton.ac.uk/id/eprint/355964 (accessed on 10 August 2025).
- Sugimoto, T.; Okujima, M. Underground Imaging Using Shear Waves: Stacking Method of the Reflected Scattered Waves. Jpn. J. Appl. Phys. 1996, 35, 3105–3108. [Google Scholar] [CrossRef]
- Muggleton, J.; Brennan, M.; Rogers, C. Point vibration measurements for the detection of shallow-buried objects. Tunn. Undergr. Space Technol. 2014, 39, 27–33. [Google Scholar] [CrossRef]
- Yan, B.; Tian, J.; Meng, X.; Zhang, Z. Vibration Characteristics and Location of Buried Gas Pipeline under the Action of Pulse Excitation. Processes 2023, 11, 2849. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, X.; Sun, T.; Rasool, G.; Ali, A.; Guo, Z.; Zheng, H. Research on Underground Positioning Technology for Buried PE Pipes Based on Acoustic Waveguide Resonance. IEEE Sens. J. 2024, 24, 22896–22906. [Google Scholar] [CrossRef]
- Zhang, A.; Zhong, D.; Xu, Z.; Zhang, H. Research on the positioning of buried polyethylene pipelines considering the acoustic attenuation characteristics. Sci. Rep. 2025, 15, 5826. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Xu, Z.; Zhang, A.; Liu, X.; Sun, P.; Sun, X. Location Method of Buried Polyethylene Gas Pipeline Based on Acoustic Signal Ellipse Method. Sensors 2024, 24, 7302. [Google Scholar] [CrossRef]
- Papandreou, B.; Brennan, M.J.; Rustighi, E. On the detection of objects buried at a shallow depth using seismic wave reflections. J. Acoust. Soc. Am. 2011, 129, 1366–1374. [Google Scholar] [CrossRef]
- Muggleton, J.; Papandreou, B. A shear wave ground surface vibration technique for the detection of buried pipes. J. Appl. Geophys. 2014, 106, 164–172. [Google Scholar] [CrossRef]
- Scott, W.; Schroeder, C.; Martin, J.; Larson, G. Use of elastic waves for the detection of buried land mines. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; pp. 1116–1118. [Google Scholar]
- Qi, Y.; Wang, X.; Yang, L.; Wang, Y.; Guo, Z. A non-excavation detection method for buried PE pipelines based on 3D time-domain stacking focusing of elastic wave reflection. Meas. Sci. Technol. 2023, 35, 025120. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, X.; Yang, X.; Sun, T.; Razzaq, I.; Yang, L.; Wang, Y.; Rasool, G. Nonexcavation Localization Method for Buried PE Pipes Based on Elastic Wave Reflection Imaging and the BPA Method. IEEE Sens. J. 2024, 24, 17987–17998. [Google Scholar] [CrossRef]
- Cui, X.; Gao, Y.; Muggleton, J.; Liu, Y. Superimposed imaging of acoustic wave reflections for the detection of underground nonmetallic pipelines. Mech. Syst. Signal Process. 2024, 209, 111127. [Google Scholar] [CrossRef]
- Cheng, Y.; Ji, T. A Concise Tutorial on Elastic Wave Dynamics; Petroleum Industry Press: Beijing, China, 2014. [Google Scholar]
- Quaegebeur, N.; Padois, T.; Gauthier, P.-A.; Masson, P. Enhancement of time-domain acoustic imaging based on generalized cross-correlation and spatial weighting. Mech. Syst. Signal Process. 2016, 75, 515–524. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Xu, Z.; Zhang, A.; Liu, X.; Sun, P.; Sun, X. Buried PE Pipeline Location Method Based on Double-Tree Complex Wavelet Cross-Correlation Delay. Sensors 2024, 24, 7310. [Google Scholar] [CrossRef]
- Gao, W.; Kong, Q.; Lu, W.; Lu, X. High spatial resolution imaging for damage detection in concrete based on multiple wavelet decomposition. Constr. Build. Mater. 2022, 319, 126057. [Google Scholar] [CrossRef]
- Ge, L.; Wang, T.; Xiao, X.; Wu, J.; Mark, R.; Zhuo, Y.; Yang, G. A new acoustic positioning method for buried PE pipeline based on time-domain superposition. Nat. Gas Ind. 2022, 42, 111–121. [Google Scholar]









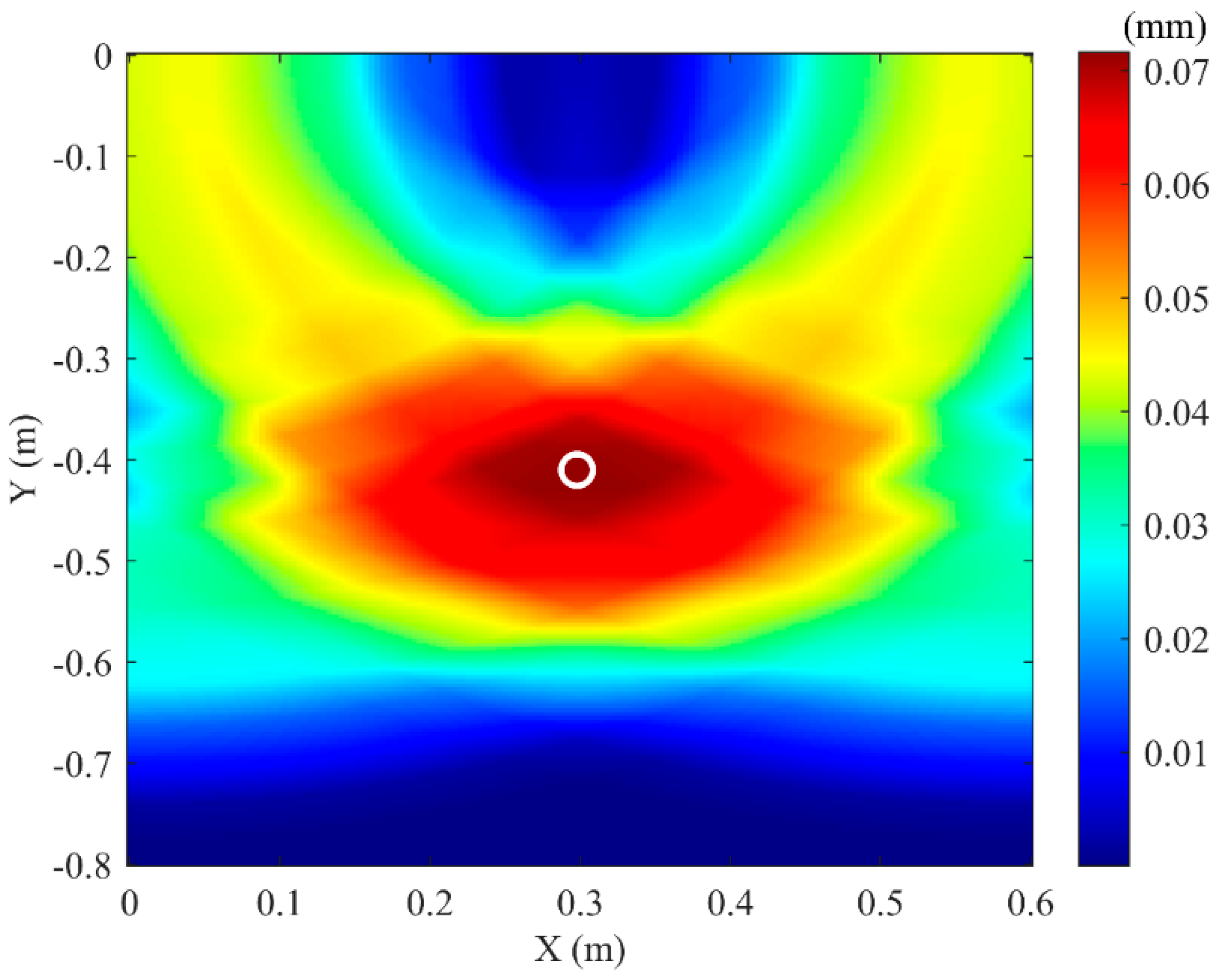
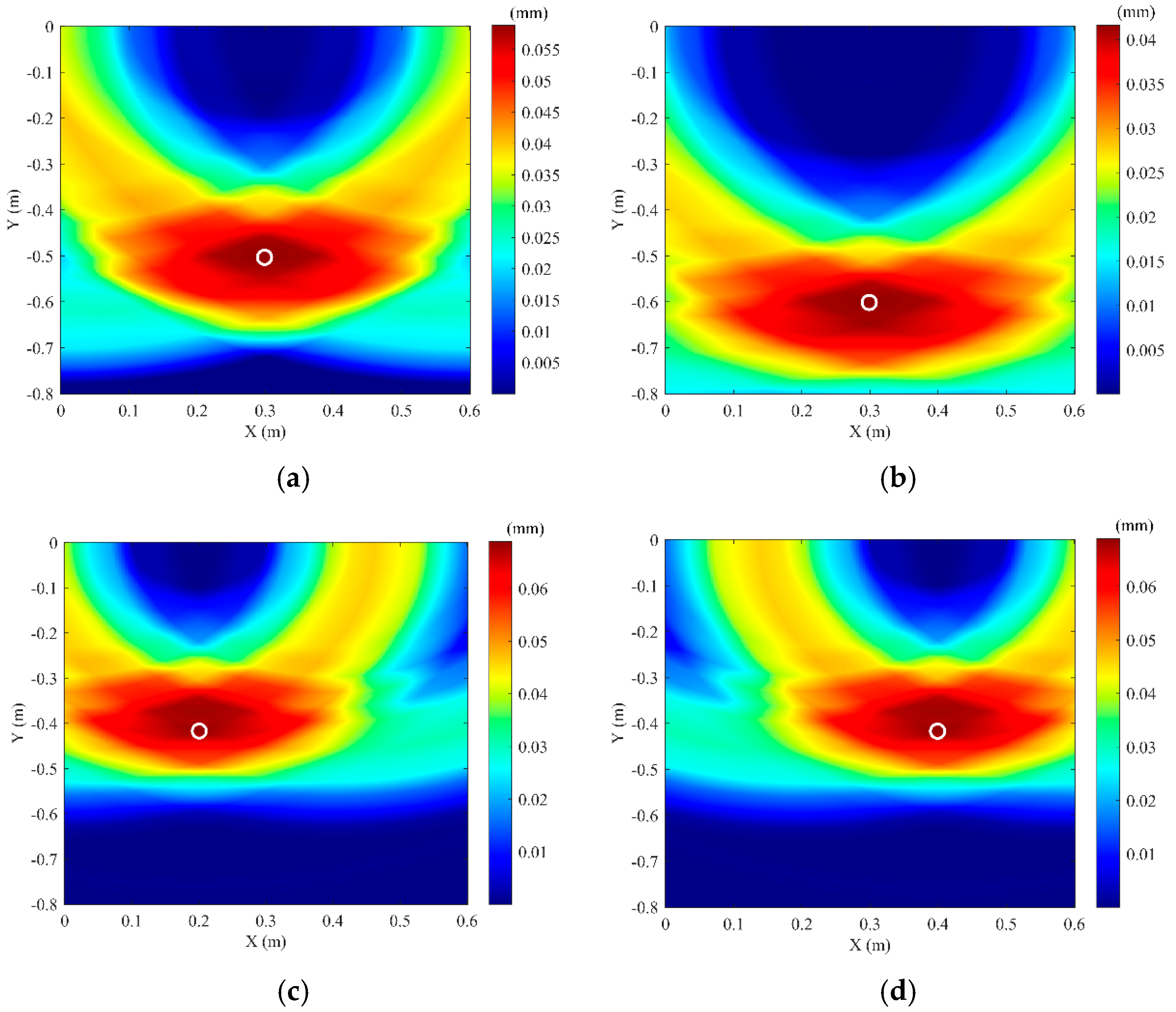
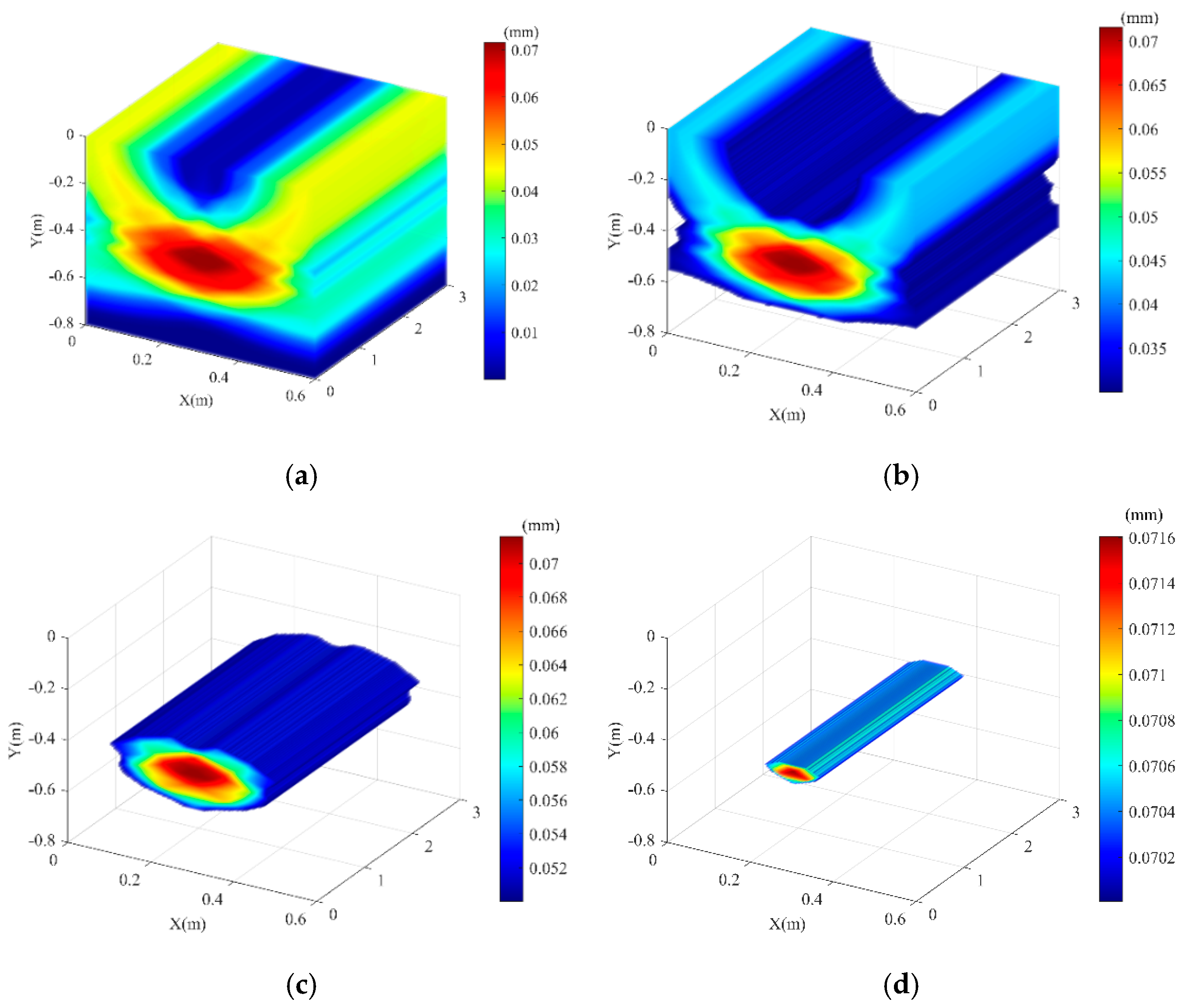
| No. | Pipeline Actual Coordinates | Simulated Localization Coordinates | Error |
|---|---|---|---|
| 1 | (0.3, −0.4) | (0.299, −0.407) | (0.333%, 1.75%) |
| 2 | (0.3, −0.5) | (0.301, −0.505) | (0.333%, 1%) |
| 3 | (0.3, −0.6) | (0.298, −0.604) | (0.667%, 0.667%) |
| 4 | (0.2,−0.4) | (0.2007,−0.417) | (0.35%, 4.25%,) |
| 5 | (0.4,−0.4) | (0.3993,−0.417) | (0.175%, 4.25%) |
| No. | Actual Pre-Buried Pipeline Coordinates | Experimental Imaging Coordinates | Experimental Error |
|---|---|---|---|
| 1 | (0.3, −0.5) | (0.299, −0.503) | (0.333%, 0.6%) |
| 2 | (0.3, −0.6) | (0.299,−0.6015) | (0.333%,0.25%,) |
| 3 | (0.2,−0.4) | (0.201,−0.417) | (0.5%,4.25%) |
| 4 | (0.4,−0.4) | (0.399,−0.417) | (0.25%,4.25%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Liao, J.; Zhong, D.; Li, H.; Han, P.; Song, Z. Localization of Buried Polyethylene Gas Pipelines Using Compressional Wave Migration Stacking Imaging. Sensors 2025, 25, 5826. https://doi.org/10.3390/s25185826
Zhang A, Liao J, Zhong D, Li H, Han P, Song Z. Localization of Buried Polyethylene Gas Pipelines Using Compressional Wave Migration Stacking Imaging. Sensors. 2025; 25(18):5826. https://doi.org/10.3390/s25185826
Chicago/Turabian StyleZhang, Ao, Junfeng Liao, Disheng Zhong, He Li, Ping Han, and Zhenting Song. 2025. "Localization of Buried Polyethylene Gas Pipelines Using Compressional Wave Migration Stacking Imaging" Sensors 25, no. 18: 5826. https://doi.org/10.3390/s25185826
APA StyleZhang, A., Liao, J., Zhong, D., Li, H., Han, P., & Song, Z. (2025). Localization of Buried Polyethylene Gas Pipelines Using Compressional Wave Migration Stacking Imaging. Sensors, 25(18), 5826. https://doi.org/10.3390/s25185826






