An Efficient and Robust Dual-Channel Signal Gluing Method for Atmospheric Lidar
Abstract
1. Introduction
- To address the issue that the complicated design of the advanced IGWO-RSD method leads to long computation and training times, a hybrid and efficient gluing method based on IMWOA and EWM, named IMWOA-EWM, was proposed.
- IMWOA-EWM innovatively adopts the IMWOA optimizer, which integrates advanced techniques such as the nonlinear convergence factor, flight strategy, and optimal neighborhood perturbation. Compared with IGWO utilized in IGWO-RSD, it not only achieves superior global search capabilities but also simplifies predatory behavior and reduces computational complexity.
- Another key innovation of IMWOA-EWM is the use of the EWM method for weight allocation, which notably requires fewer training samples. This significantly reduces the computational load and time overhead compared to the NRS method employed in IGWO-RSD.
- By conducting signal gluing experiments with full-day signals, the robustness and applicable conditions of IMWOA-EWM were discussed, providing guidelines for practical applications.
2. Materials and Methods
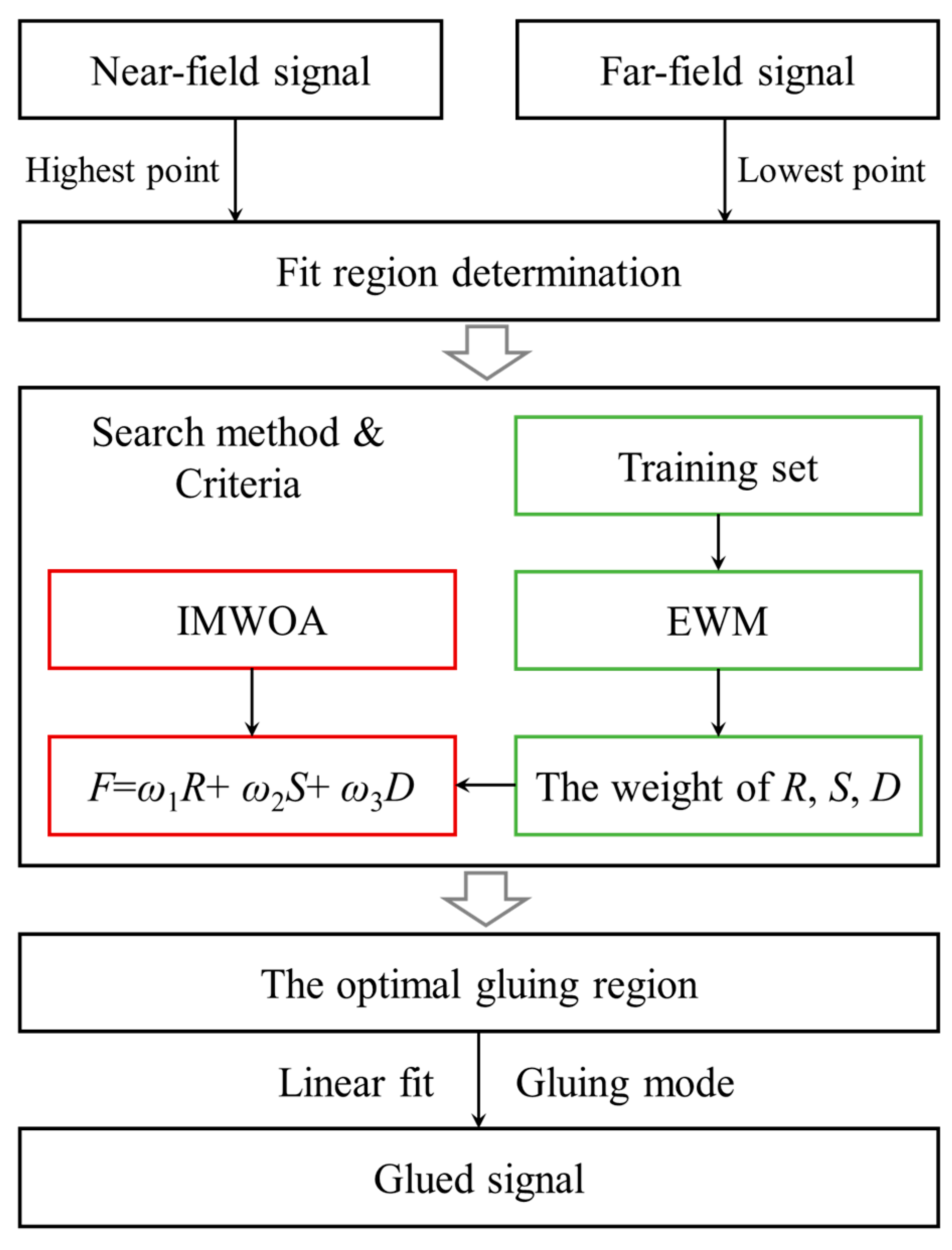
2.1. Basic Idea
2.2. Improved Whale Optimization Algorithm
2.3. Fitness Function
2.4. Entropy Weight Method
- Construct a joint decision evaluation matrix X with n samples and m attribute indexes. Among them, xij indicates the j-th attribute value of the i-th sample. In this paper, m = 3 means that there are three objective functions as attribute indexes.
- Standardize the matrix X to eliminate the dimensional and unit differences among the data. The standardized matrix is denoted by Y, where yij signifies the standardized value corresponding to xij.
- Calculate the specific gravity Pij of yij, which can be defined as
- Compute the weight coefficient ωj of the j-th attribute component based on its entropy value ej and difference coefficient gj, shown by
3. Results
3.1. Data Description
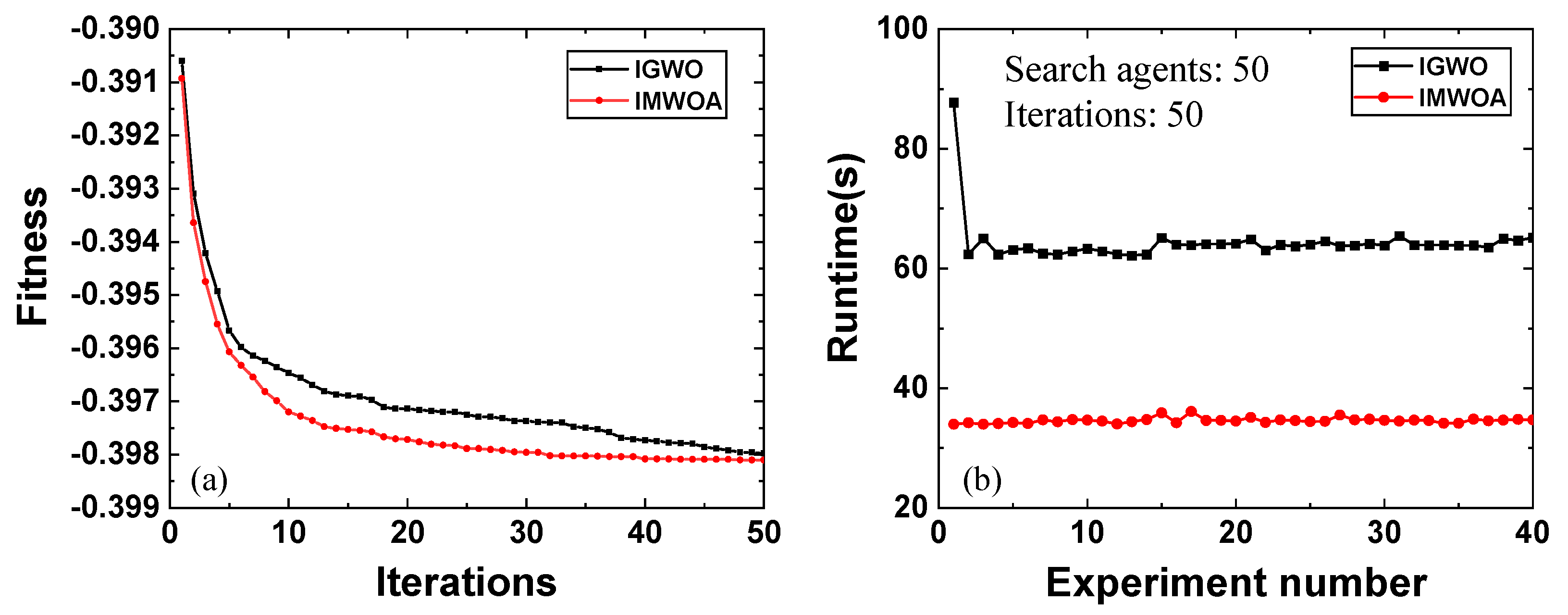
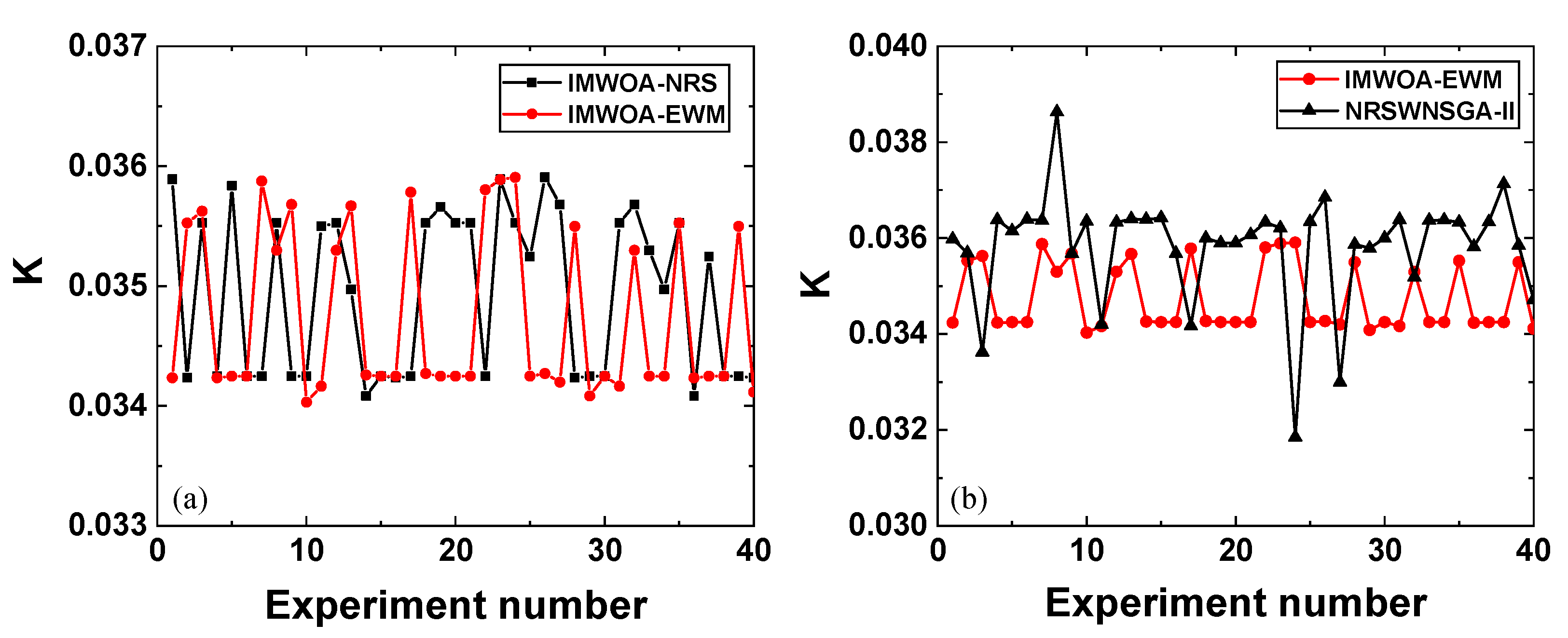
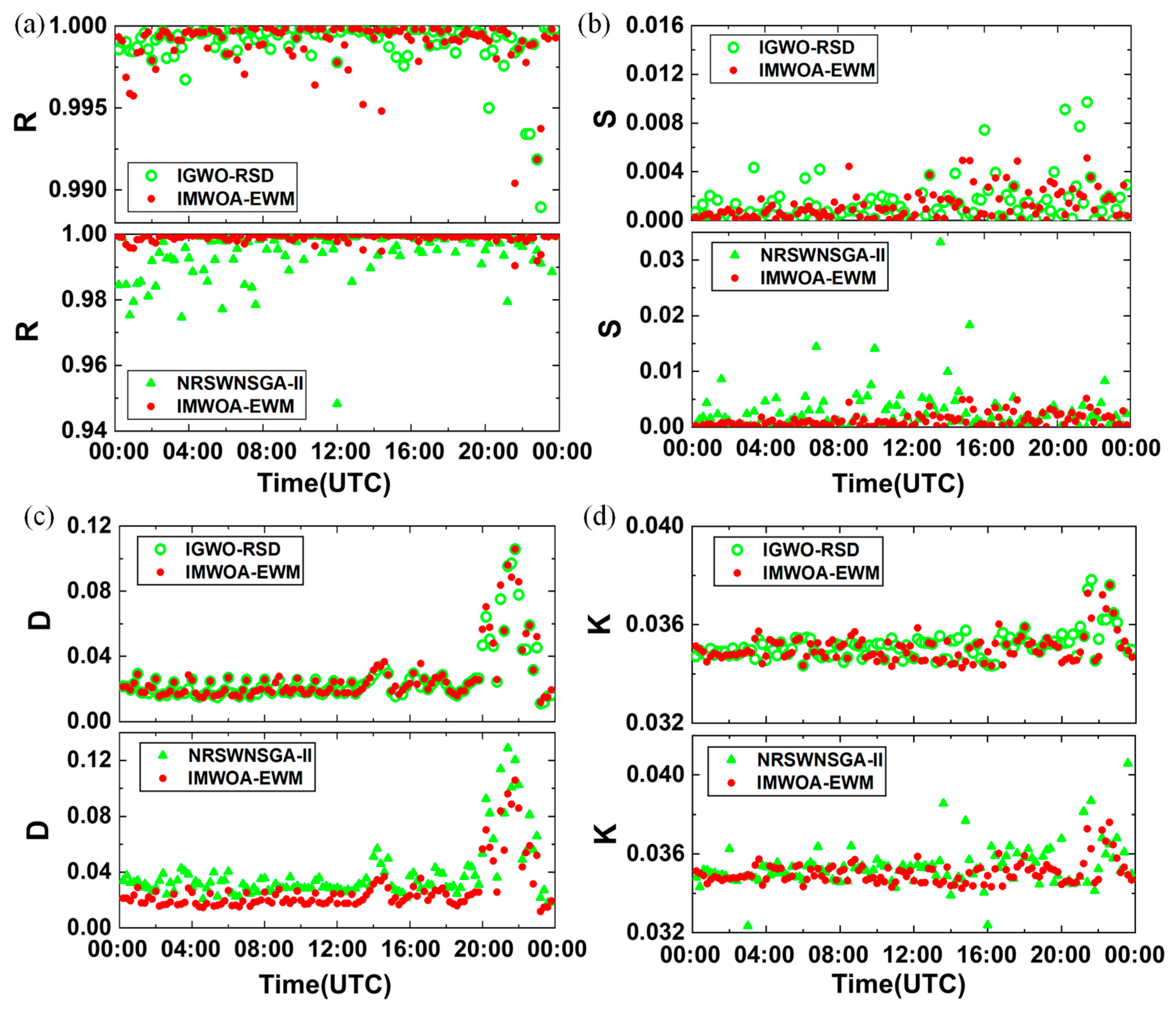
3.2. Performance Comparison of Optimizers
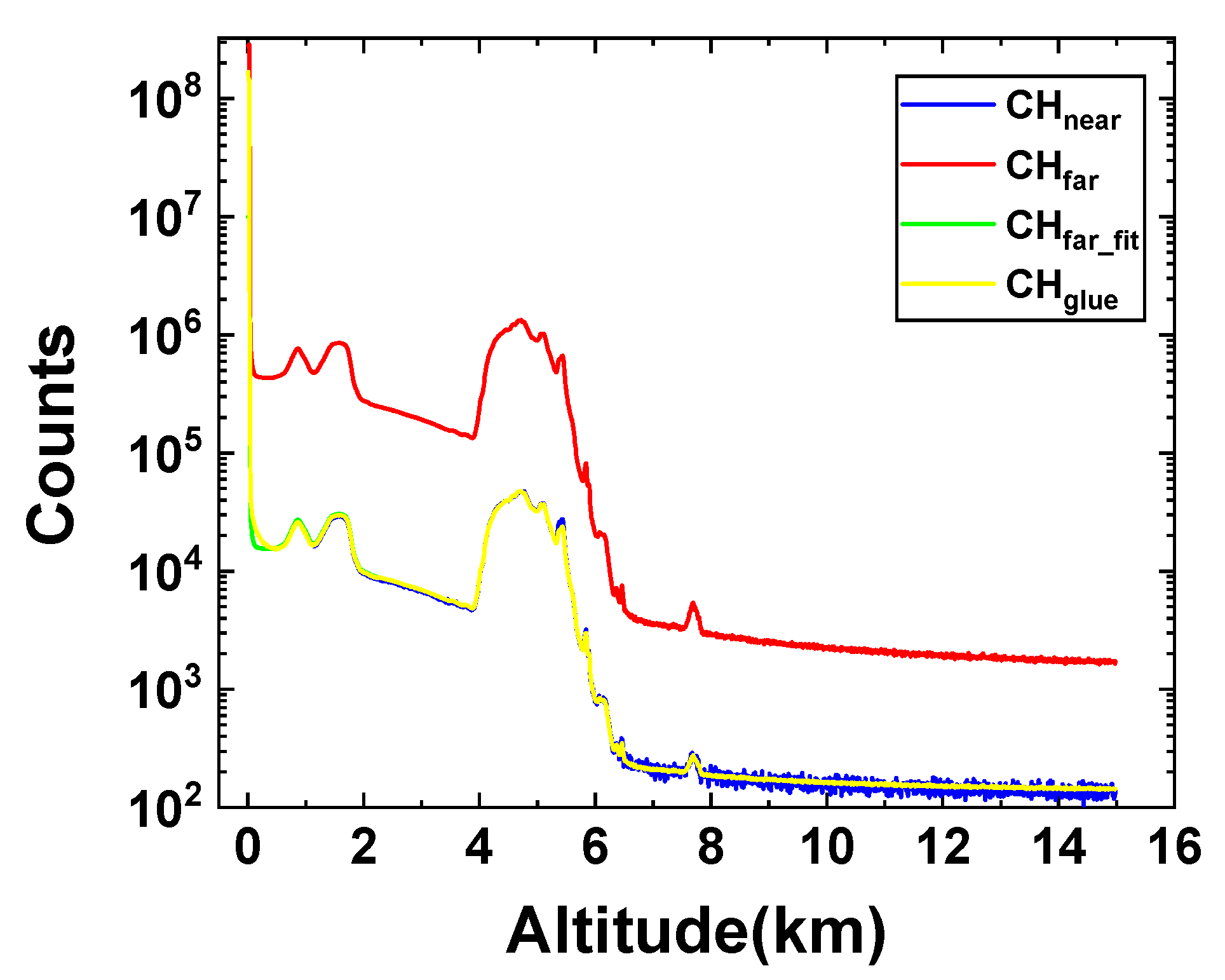
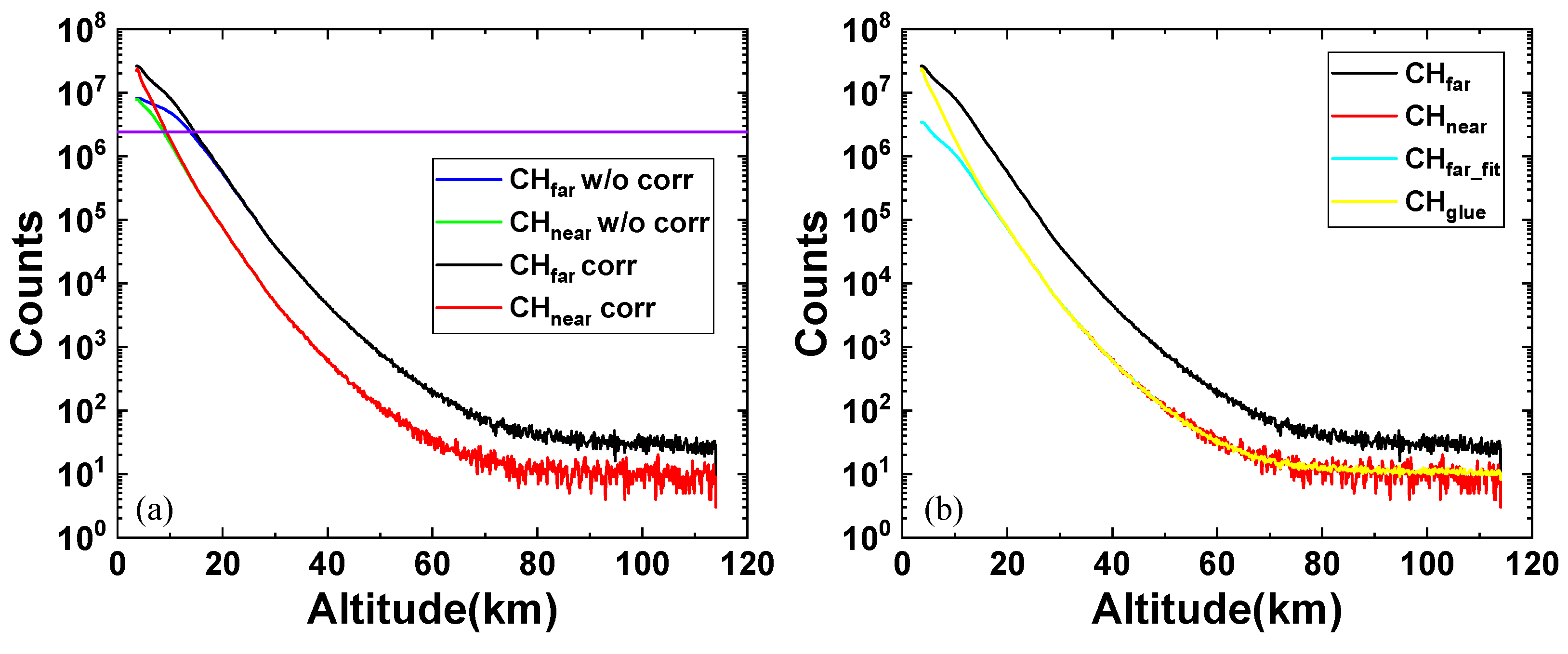
3.3. Verification of Gluing Performance
3.4. Full-Day Gluing Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Zhong, K.; Zhang, X.; Li, F.; Li, X.; Zhang, X.; Yan, Z.; Xu, D.; Yao, J. Measurement Accuracy and Attitude Compensation of Rayleigh Lidar on an Airborne Floating Platform. Remote Sens. 2024, 16, 3308. [Google Scholar] [CrossRef]
- Duan, L. Research on Key Technologies of Signal Processing for Atmospheric Remote Sensing Lidar. Master’s Thesis, Zhejiang University, Hangzhou, China, 2017. [Google Scholar]
- Fu, Y.; Wang, Y.; Zhang, T.; Fan, G.; Liu, W.; Chang, Z.; Qiu, X.; Fang, X.; Tian, Y. Signal Acquisition System with Simultaneous Analog and Photon Counting Measurement for Lidar. Chin. J. Lasers 2015, 42, 318–327. [Google Scholar] [CrossRef]
- Singh, U.N.; Keckhut, P.; McGee, T.J.; Gross, M.R.; Hauchecorne, A.; Fishbein, E.F.; Waters, J.W.; Gille, J.C.; Roche, A.E.; Russell III, J.M. Stratospheric temperature measurements by two collocated NDSC lidars during UARS validation campaign. J. Geophys. Res. Atmos. 1996, 101, 10287–10297. [Google Scholar] [CrossRef]
- Huang, L.; Gong, W.; Li, J.; Mao, F.; Lei, L. Signal splicing of dual-receiver Mie scattering lidar in atmospheric remote sensing. Yaogan Xuebao-J. Remote Sens. 2012, 16, 705–719. [Google Scholar] [CrossRef]
- Kaifler, B.; Kaifler, N. A Compact Rayleigh Autonomous Lidar (CORAL) for the middle atmosphere. Atmos. Meas. Tech. 2021, 14, 1715–1732. [Google Scholar] [CrossRef]
- Kaifler, B.; Rempel, D.; Roßi, P.; Büdenbender, C.; Kaifler, N.; Baturkin, V. A technical description of the Balloon Lidar Experiment BOLIDE. Atmos. Meas. Tech. Discuss. 2020, 13, 5681–5695. [Google Scholar] [CrossRef]
- Alpers, M.; Eixmann, R.; Fricke-Begemann, C.; Gerding, M.; Höffner, J. Temperature lidar measurements from 1 to 105 km altitude using resonance, Rayleigh, and Rotational Raman scattering. Atmos. Chem. Phys. 2004, 4, 793–800. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liu, B.; Li, R. Analysis of saturation signal correction of the troposphere lidar. Chin. Opt. Lett. 2009, 7, 1051–1054. [Google Scholar] [CrossRef]
- Newsom, R.K.; Turner, D.D.; Mielke, B.; Clayton, M.; Ferrare, R.; Sivaraman, C. Simultaneous analog and photon counting detection for Raman lidar. Appl. Opt. 2009, 48, 3903–3914. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, F.; Kong, W.; Yi, Y. Slope characterization in combining analog and photon count data from atmospheric lidar measurements. Appl. Opt. 2014, 53, 7312–7320. [Google Scholar] [CrossRef]
- D’Amico, G.; Amodeo, A.; Mattis, I.; Freudenthaler, V.; Pappalardo, G. EARLINET Single Calculus Chain–technical–Part 1: Pre-processing of raw lidar data. Atmos. Meas. Tech. 2016, 9, 491–507. [Google Scholar] [CrossRef]
- Li, B.; Wei, H.; Zhao, L.; Wang, Y.; Hua, D. Data Splicing Method for LiDAR Detection Temperature Under Fog-Haze Condition. Acta Opt. Sin. 2020, 40, 0928003. [Google Scholar] [CrossRef]
- Gao, F.; Veberič, D.; Stanič, S.; Bergant, K.; Hua, D.-X. Performance improvement of long-range scanning Mie lidar for the retrieval of atmospheric extinction. J. Quant. Spectrosc. Radiat. Transf. 2013, 122, 72–78. [Google Scholar] [CrossRef]
- Walker, M.; Venable, D.; Whiteman, D.N. Gluing for Raman lidar systems using the lamp mapping technique. Appl. Opt. 2014, 53, 8535–8543. [Google Scholar] [CrossRef]
- Gao, F.; Xu, X.; Zhu, Q.; Wang, L.; He, T.; Wang, L.; Stanič, S.; Hua, D. Evaluation and Improvement of Lidar Performance Based on Temporal and Spatial Variance Calculation. Appl. Sci. 2019, 9, 1786. [Google Scholar] [CrossRef]
- Duan, L.; Liu, D.; Zhang, Y.; Cheng, Z.; Luo, J.; Yang, F.; Shen, Y.; Bai, J. Lidar data gluing technology based on hybrid intelligent algorithm. Acta Opt. Sin. 2017, 37, 0601002. [Google Scholar] [CrossRef]
- Li, S.; Wu, T.; Zhong, K.; Zhang, X.; Sun, Y.; Zhang, Y.; Wang, Y.; Li, X.; Xu, D.; Yao, J. Gluing Atmospheric Lidar Signals Based on an Improved Gray Wolf Optimizer. Remote Sens. 2023, 15, 3812. [Google Scholar] [CrossRef]
- Ilya, R. Characterization of a Geiger-Mode Avalanche Photodiode Detector for High Special Resolution Lidar. Master’s Thesis, University of Wisconsin, Madison, WI, USA, 2010. [Google Scholar]
- University of Wisconsin Lidar Group. Available online: https://radiance.ssec.wisc.edu/ (accessed on 15 June 2023).
- Venter, G. Review of optimization techniques. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2010; pp. 1–12. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wu, T.; Zhong, K.; Zhang, X.; Li, X.; Li, S.; Zhang, X.; Yan, Z.; Xu, D.; Yao, J. Noise Reduction for Atmospheric Rayleigh Lidar Based on a Hybrid EEMD–VMD–IMWOA Method with High Retrieval Accuracy. J. Atmos. Ocean. Technol. 2025, 42, 493–507. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy flight trajectory-based whale optimization algorithm for global optimization. IEEE Access 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Li, F.; Su, M.; Li, D. Combination evaluation model based on entropy weight method. In Proceedings of the ICMLCA 2021: 2nd International Conference on Machine Learning and Computer Application, Shenyang, China, 17–19 December 2021; pp. 1–5. [Google Scholar]
- Pham-Gia, T.; Hung, T.L. The mean and median absolute deviations. Math. Comput. Model. 2001, 34, 921–936. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of search agents | 50 | Number of iterations | 50 |
| Weight of R | 0.3952 | The SNR for the highest point | 10 |
| Weight of S | 0.2984 | Time resolution of samples | 1 h |
| Weight of D | 0.3064 | Vertical resolution of samples | 7.5 meter |
| Objective Function | Minimum | Maximum | Median | Median Confidence Interval |
|---|---|---|---|---|
| R | 0.726 | 1 | 0.9992 | 0.998–1 |
| S | 0.0001 | 28.47 | 2.55 | 1.228–3.746 |
| D | 0.0063 | 195.72 | 0.014 | 0.011–0.02 |
| Evaluation Indicators | Value |
|---|---|
| R | 0.9986 |
| S | 0.0023 |
| D | 0.0304 |
| K | 0.1313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Zhong, K.; Zhang, X.; Li, F.; Li, X.; Chen, G.; Xu, D.; Yao, J. An Efficient and Robust Dual-Channel Signal Gluing Method for Atmospheric Lidar. Sensors 2025, 25, 5807. https://doi.org/10.3390/s25185807
Wu T, Zhong K, Zhang X, Li F, Li X, Chen G, Xu D, Yao J. An Efficient and Robust Dual-Channel Signal Gluing Method for Atmospheric Lidar. Sensors. 2025; 25(18):5807. https://doi.org/10.3390/s25185807
Chicago/Turabian StyleWu, Tong, Kai Zhong, Xianzhong Zhang, Fangjie Li, Xinqi Li, Guxi Chen, Degang Xu, and Jianquan Yao. 2025. "An Efficient and Robust Dual-Channel Signal Gluing Method for Atmospheric Lidar" Sensors 25, no. 18: 5807. https://doi.org/10.3390/s25185807
APA StyleWu, T., Zhong, K., Zhang, X., Li, F., Li, X., Chen, G., Xu, D., & Yao, J. (2025). An Efficient and Robust Dual-Channel Signal Gluing Method for Atmospheric Lidar. Sensors, 25(18), 5807. https://doi.org/10.3390/s25185807









