Center of Pressure Analysis of Postural Stability During Repetitive Reaching with Passive Arm-Support Exoskeletons
Abstract
1. Introduction
2. Methods
2.1. Participants
2.2. Exoskeletons Evaluated
2.3. Experimental Task and Design
2.4. Experimental Procedure
2.5. CoP Measurement
2.6. Data Analysis
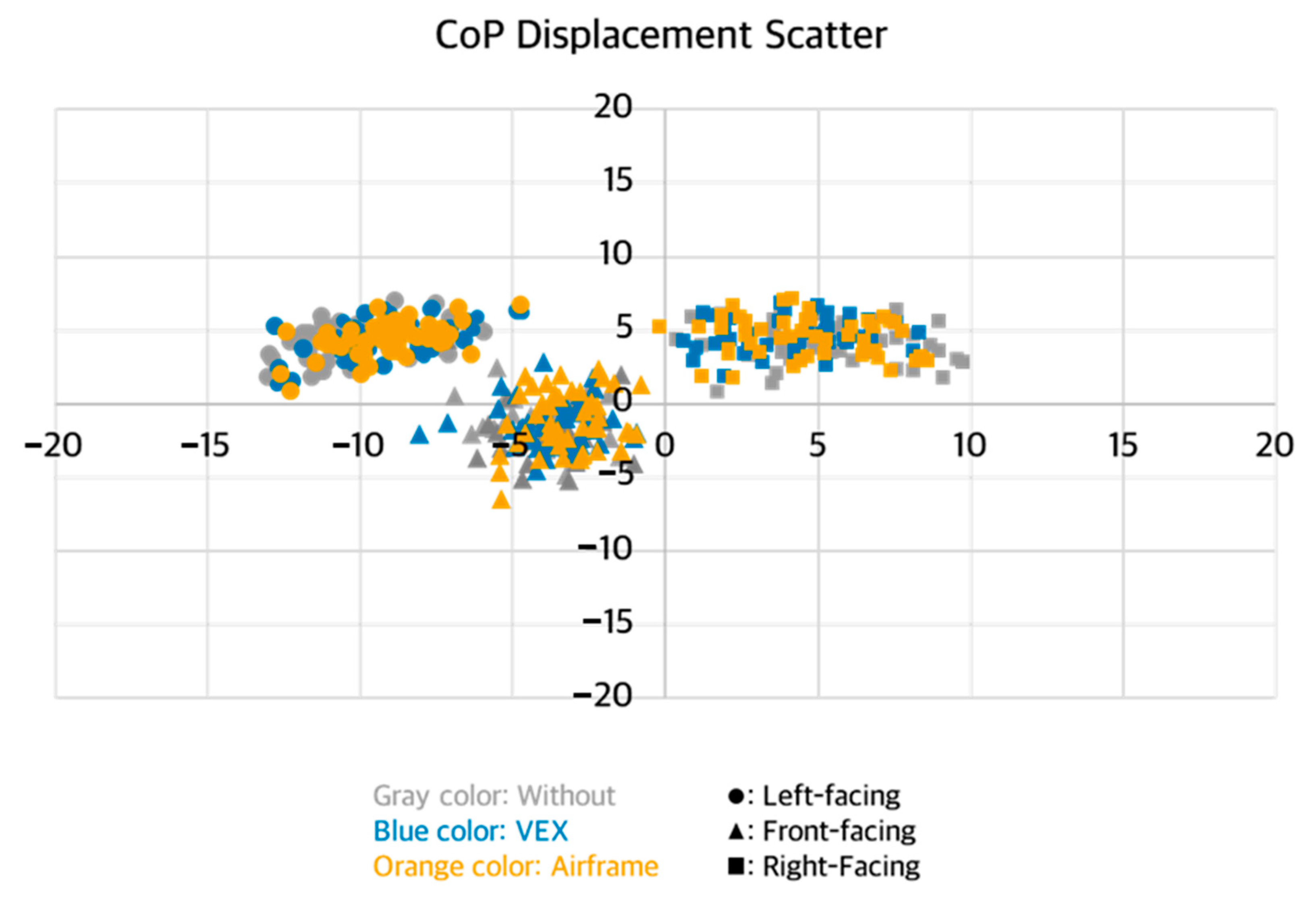
3. Results
3.1. Interaction Effects
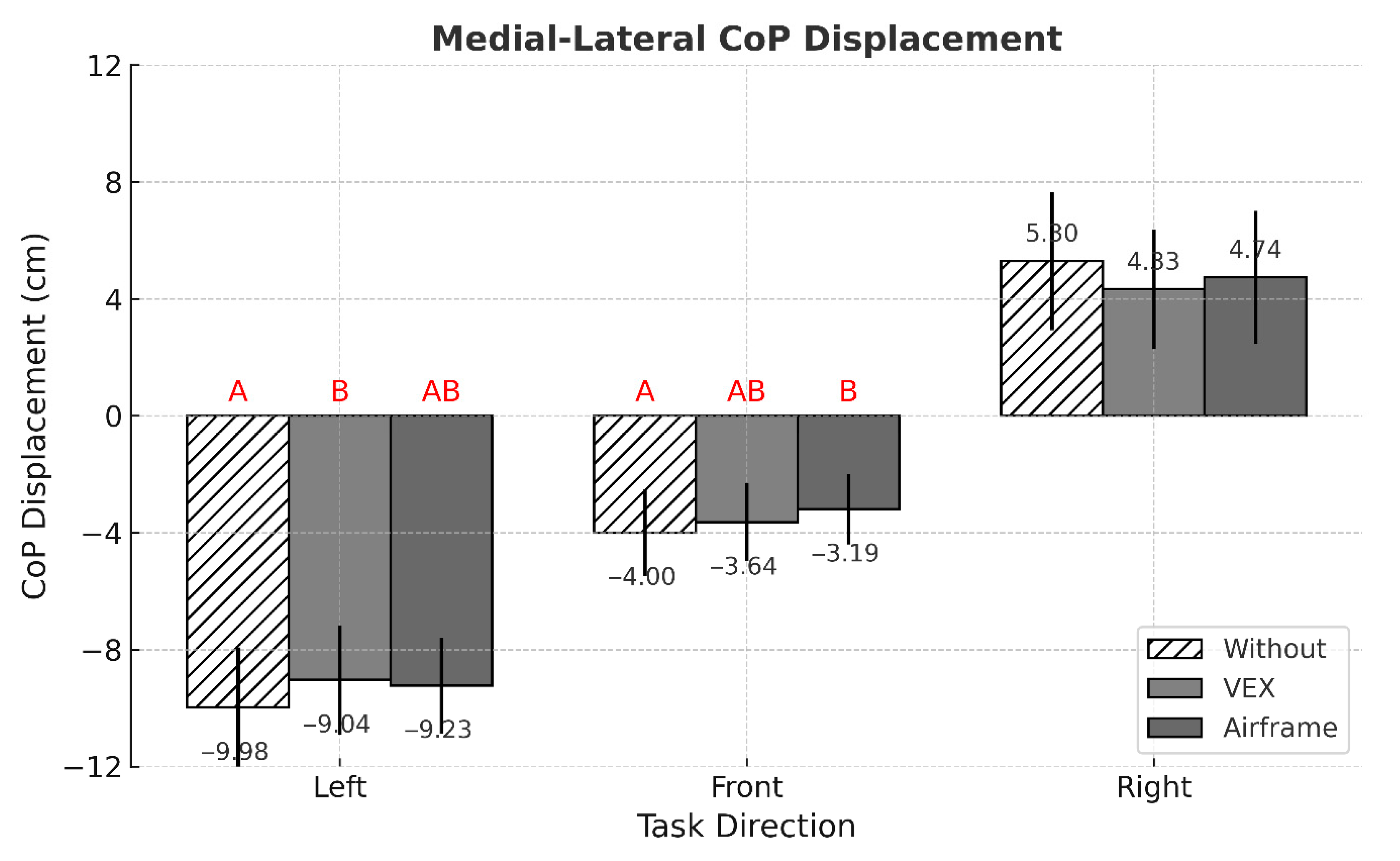
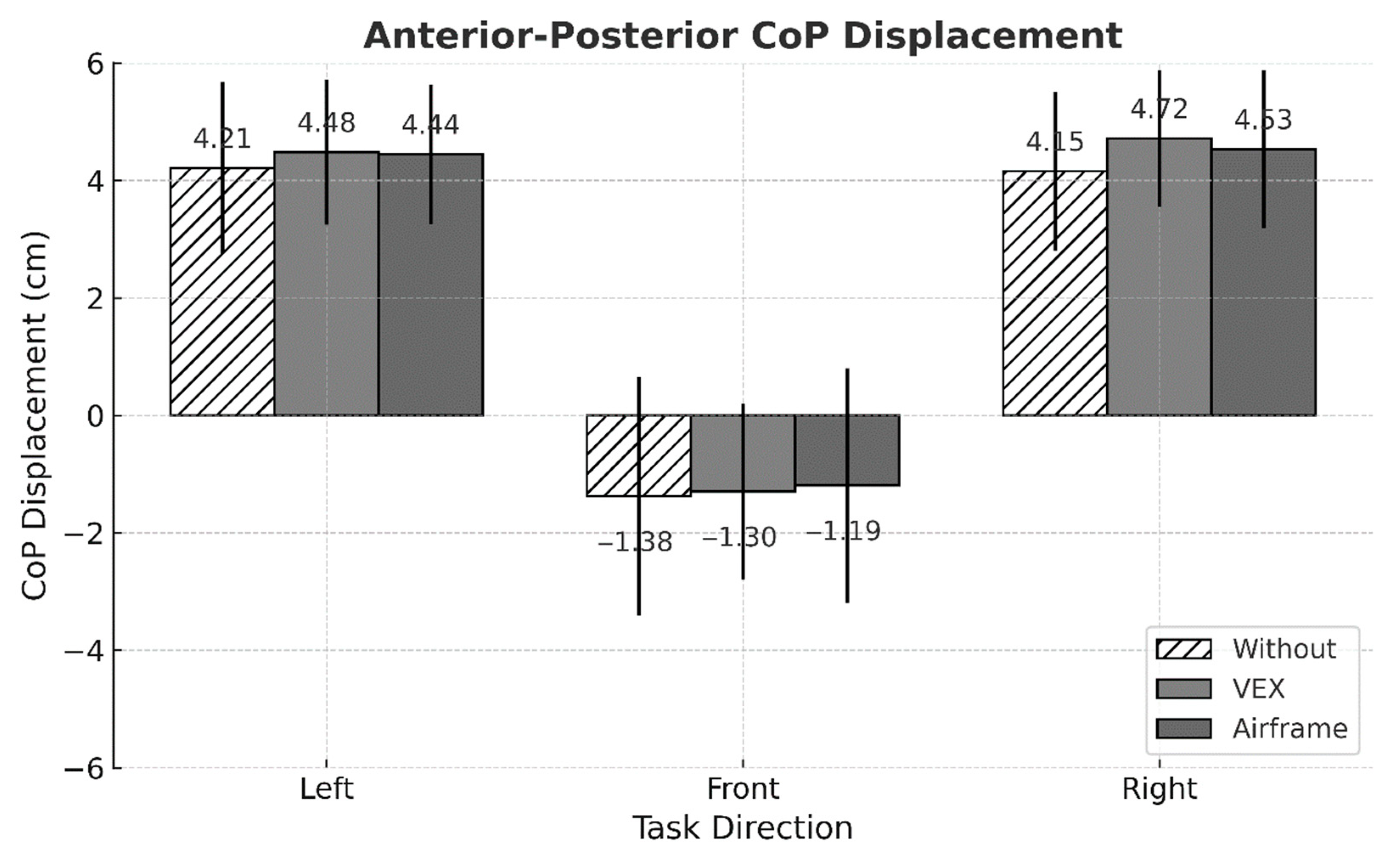
3.2. Intervention
3.3. Task Direction
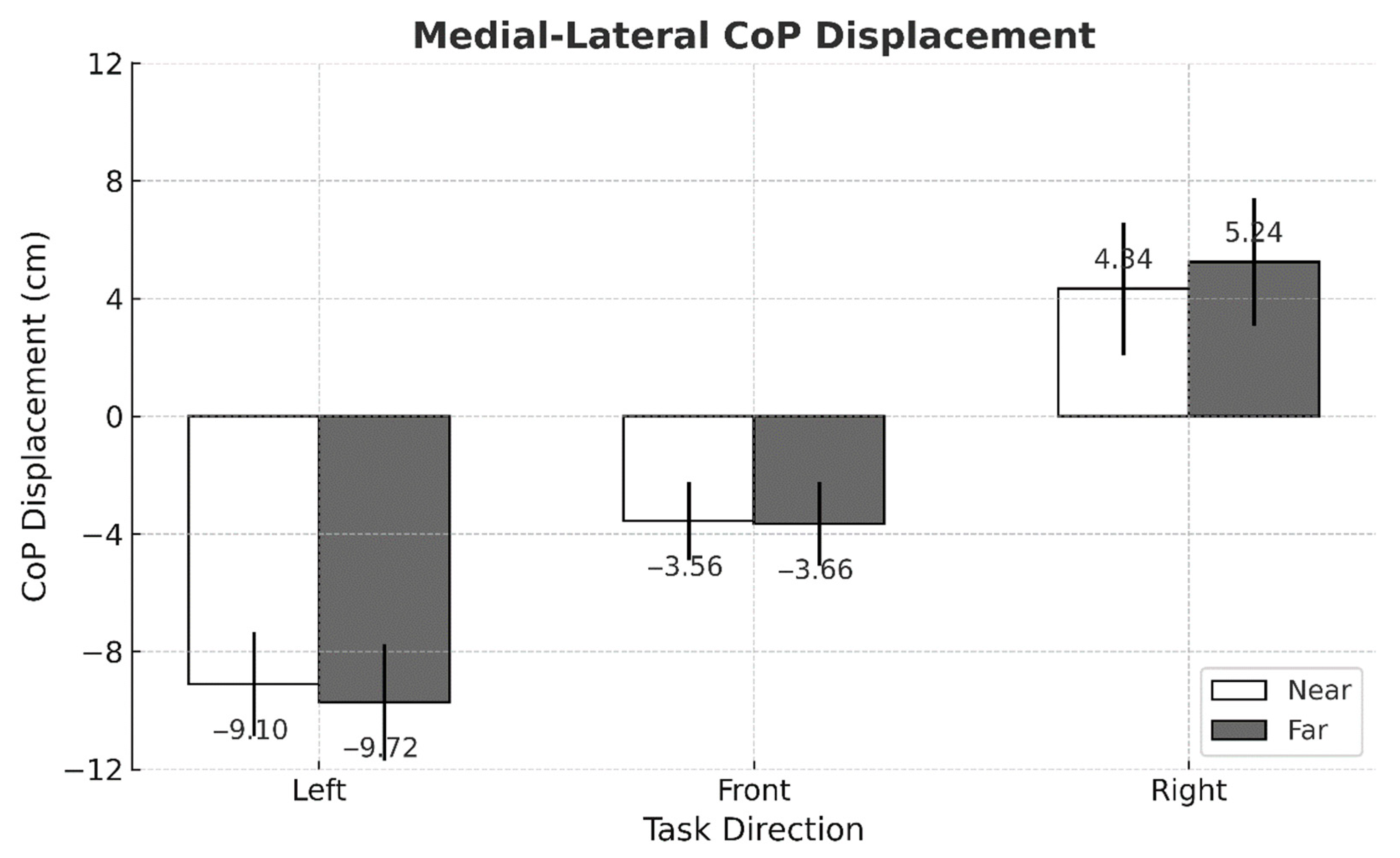
3.4. Working Distance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AP | Anteroposterior |
| APDF | Amplitude Probability Density Function |
| ASE | Arm-Support Exoskeleton |
| BSE | Back-Support Exoskeleton |
| CoP | Center of Pressure |
| EMG | Electromyographic |
| MANOVA | Multivariate Analysis of Variance |
| ML | Mediolateral |
| SNK | Student–Newman–Keuls |
References
- Saito, H.; Kominami, Y.; Yamanaka, M.; Takeda, N.; Fukushima, J. Effects of repetitive reaching movements on performance and postural control. J. Phys. Ther. Sci. 2011, 23, 569–574. [Google Scholar] [CrossRef][Green Version]
- Granata, K.; Wilson, S. Trunk posture and spinal stability. Clin. Biomech. 2001, 16, 650–659. [Google Scholar] [CrossRef]
- Choi, B.; Park, J.; Kim, J.H. Assessment of an arm-support exoskeleton on physical demands, task performance, and usability during simulated agricultural tasks. Int. J. Ind. Ergon. 2024, 101, 103569. [Google Scholar] [CrossRef]
- De Vries, A.W.; Krause, F.; de Looze, M.P. The effectivity of a passive arm support exoskeleton in reducing muscle activation and perceived exertion during plastering activities. Ergonomics 2021, 64, 712–721. [Google Scholar] [CrossRef] [PubMed]
- De Vries, A.; De Looze, M. The effect of arm support exoskeletons in realistic work activities: A review study. J. Ergon. 2019, 9, 255. [Google Scholar]
- Brandt, M.; Jacobsen, S.S.; Skals, S.; Nimb, I.; Ajslev, J.Z.N.; Sundstrup, E.; Andersen, L.L.; Jakobsen, M.D. Technical field-evaluation of exoskeleton-assisted overhead work among carpenters. Appl. Ergon. 2025, 129, 104582. [Google Scholar] [CrossRef] [PubMed]
- Ojelade, A.; Morris, W.; Kim, S.; Kelson, D.; Srinivasan, D.; Smets, M.; Nussbaum, M.A. Three passive arm-support exoskeletons have inconsistent effects on muscle activity, posture, and perceived exertion during diverse simulated pseudo-static overhead nutrunning tasks. Appl. Ergon. 2023, 110, 104015. [Google Scholar] [CrossRef]
- Yin, P.; Yang, L.; Qu, S.; Wang, C. Effects of a passive upper extremity exoskeleton for overhead tasks. J. Electromyogr. Kinesiol. 2020, 55, 102478. [Google Scholar] [CrossRef]
- Maurice, P.; Camernik, J.; Gorjan, D.; Schirrmeister, B.; Bornmann, J.; Tagliapietra, L.; Latella, C.; Pucci, D.; Fritzsche, L.; Ivaldi, S.; et al. Objective and subjective effects of a passive exoskeleton on overhead work. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 28, 152–164. [Google Scholar] [CrossRef]
- De Bock, S.; Rossini, M.; Lefeber, D.; Rodriguez-Guerrero, C.; Geeroms, J.; Meeusen, R.; De Pauw, K. An occupational shoulder exoskeleton reduces muscle activity and fatigue during overhead work. IEEE Trans. Biomed. Eng. 2022, 69, 3008–3020. [Google Scholar] [CrossRef]
- Kim, S.; Nussbaum, M.A. A follow-up study of the effects of an arm support exoskeleton on physical demands and task performance during simulated overhead work. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 163–174. [Google Scholar] [CrossRef]
- Van Engelhoven, L.; Poon, N.; Kazerooni, H.; Barr, A.; Rempel, D.; Harris-Adamson, C. Evaluation of an adjustable support shoulder exoskeleton on static and dynamic overhead tasks. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Chicago, IL, USA, 13–17 October 2018; Volume 62, pp. 804–808. [Google Scholar] [CrossRef]
- Coccia, A.; Capodaglio, E.M.; Amitrano, F.; Gabba, V.; Panigazzi, M.; Pagano, G.; D’Addio, G. Biomechanical effects of using a passive exoskeleton for the upper limb in industrial manufacturing activities: A pilot study. Sensors 2024, 24, 1445. [Google Scholar] [CrossRef]
- Jonathan, E.; Xiong, S. Influence of passive arm-support exoskeleton on static postural balance in load-holding tasks: Effects of supportive force, weight and load location. Ergonomics 2025, 68, 588–601. [Google Scholar] [CrossRef]
- Guittienne, M.; Forestier, N. Differential effect of three types of exoskeletons and handling height on muscular activity, postural control and perceived effort during simulated bedside mobilization task. Appl. Ergon. 2025, 125, 104467. [Google Scholar] [CrossRef]
- Ma, T.; Xiong, S. A novel biomechanical model for predicting ankle moments and assessing static balance in users of shoulder-support exoskeletons. Int. J. Ind. Ergon. 2025, 105, 103688. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, S.; Nussbaum, M.A.; Srinivasan, D. Effects of two passive back-support exoskeletons on postural balance during quiet stance and functional limits of stability. J. Electromyogr. Kinesiol. 2021, 57, 102516. [Google Scholar] [CrossRef]
- Van Engelhoven, L.; Poon, N.; Kazerooni, H.; Rempel, D.; Barr, A.; Harris-Adamson, C. Experimental evaluation of a shoulder-support exoskeleton for overhead work: Influences of peak torque amplitude, task, and tool mass. IISE Trans. Occup. Ergon. Hum. Factors 2019, 7, 250–263. [Google Scholar] [CrossRef]
- Choi, B.; Park, J. Analysis of agricultural applicability of arm-support exoskeletons with simulated orchard pruning and harvesting tasks. J. Electromyogr. Kinesiol. 2025, 82, 103008. [Google Scholar] [CrossRef] [PubMed]
- KATS. Size Korea. Available online: https://sizekorea.kr/human-info/meas-report?measDegree=8 (accessed on 25 July 2025).
- Clark, R.A.; Bryant, A.L.; Pua, Y.; McCrory, P.; Bennell, K.; Hunt, M. Validity and reliability of the Nintendo Wii Balance Board for assessment of standing balance. Gait Posture 2010, 31, 307–310. [Google Scholar] [CrossRef]
- Chang, W.-D.; Chang, W.-Y.; Lee, C.-L.; Feng, C.-Y. Validity and reliability of Wii fit balance board for the assessment of balance of healthy young adults and the elderly. J. Phys. Ther. Sci. 2013, 25, 1251–1253. [Google Scholar] [CrossRef] [PubMed]
- Park, D.-S.; Lee, G. Validity and reliability of balance assessment software using the Nintendo Wii balance board: Usability and validation. J. Neuroeng. Rehabil. 2014, 11, 99. [Google Scholar] [CrossRef]
- Palmieri, R.M.; Ingersoll, C.D.; Stone, M.B.; Krause, B.A. Center-of-pressure parameters used in the assessment of postural control. J. Sport Rehabil. 2002, 11, 51–66. [Google Scholar] [CrossRef]
- Murray, M.; Seireg, A.; Sepic, S.B. Normal postural stability and steadiness: Quantitative assessment. JBJS 1975, 57, 510–516. [Google Scholar] [CrossRef]
- Kirby, R.; Price, N.; MacLeod, D. The influence of foot position on standing balance. J. Biomech. 1987, 20, 423–427. [Google Scholar] [CrossRef]
- Jonsson, B. Measurement and evaluation of local muscular strain in the shoulder during constrained work. J. Hum. Ergol. 1982, 11, 73–88. [Google Scholar] [CrossRef]
- West, S.G.; Finch, J.F.; Curran, P.J. Structural equation models with nonnormal variables: Problems and remedies. In Structural Equation Modeling: Concepts, Issues, and Applications; Hoyle, R.H., Ed.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 1995; pp. 56–75. [Google Scholar]
- Blanca Mena, M.J.; Alarcón Postigo, R.; Arnau Gras, J.; Bono Cabré, R.; Bendayan, R. Non-normal data: Is ANOVA still a valid option? Psicothema 2017, 29, 552–557. [Google Scholar] [CrossRef] [PubMed]
- Olson, C.L. Comparative robustness of six tests in multivariate analysis of variance. J. Am. Stat. Assoc. 1974, 69, 894–908. [Google Scholar] [CrossRef]
- Stevens, J. Applied Multivariate Statistics for the Social Sciences; Mahwah, N.J., Ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2022; Volume 4. [Google Scholar]
- Anderson, M.J. A new method for non-parametric multivariate analysis of variance. Aust. Ecol. 2001, 26, 32–46. [Google Scholar] [CrossRef]
- Richardson, J.T. Eta squared and partial eta squared as measures of effect size in educational research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Kuber, P.M.; Rashedi, E. Effects of a wearable assistive device on postural control and stability during symmetric and asymmetric intermittent trunk flexion tasks. Bioengineering 2025, 12, 456. [Google Scholar] [CrossRef]
- Garcia, G.; Yañez, R.; Espoz, M.; Albuja, C.; Arauz, P.G.; Martin, B.J. Biomechanical and physiological effects of an upper-body exoskeleton during simulated load-carrying on an inclined surface. PLoS ONE 2025, 20, e0325230. [Google Scholar] [CrossRef] [PubMed]
- Park, J. Assessing the Effects of Exoskeleton Use on Balance and Postural Stability. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2021. [Google Scholar]
- Kritzer, T.D.; Lang, C.J.; Holmes, M.W.; Cudlip, A.C. Sex differences in strength at the shoulder: A systematic review. PeerJ 2024, 12, e16968. [Google Scholar] [CrossRef] [PubMed]
- Greggi, C.; Visconti, V.V.; Albanese, M.; Gasperini, B.; Chiavoghilefu, A.; Prezioso, C.; Persechino, B.; Iavicoli, S.; Gasbarra, E.; Iundusi, R.; et al. Work-related musculoskeletal disorders: A systematic review and meta-analysis. J. Clin. Med. 2024, 13, 3964. [Google Scholar] [CrossRef] [PubMed]


| CoP Metrics | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Experimental Factors | MEAN ML | MEAN AP | ML APDF 10 | ML APDF 50 | ML APDF 90 | AP APDF 10 | AP APDF 50 | AP APDF 90 | |
| Intervention | f | 1.217 | 1.765 | 5.879 | 1.749 | 1.543 | 0.204 | 0.148 | 2.197 |
| p | 0.297 | 0.173 | 0.003 | 0.175 | 0.215 | 0.815 | 0.862 | 0.112 | |
| η2p | 0.006 | 0.008 | 0.028 * | 0.008 | 0.007 | 0.001 | 0.001 | 0.011 * | |
| Direction | f | 2162.525 | 698.140 | 13.881 | 360.496 | 256.762 | 142.423 | 39.148 | 18.033 |
| p | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| η2p | 0.913 *** | 0.772 *** | 0.063 ** | 0.636 *** | 0.554 *** | 0.408 *** | 0.159 *** | 0.08 ** | |
| Distance | f | 0.112 | 10.800 | 2.121 | 6.702 | 5.464 | 0.080 | 2.754 | 2.118 |
| p | 0.738 | 0.001 | 0.146 | 0.010 | 0.020 | 0.778 | 0.098 | 0.146 | |
| η2p | 0.000 | 0.025 * | 0.005 | 0.016 * | 0.013 * | 0.000 | 0.007 | 0.005 | |
| Intervention × Direction | f | 3.957 | 0.321 | 1.180 | 0.574 | 0.528 | 0.933 | 0.556 | 0.404 |
| p | 0.004 | 0.864 | 0.319 | 0.682 | 0.715 | 0.445 | 0.695 | 0.806 | |
| η2p | 0.037 * | 0.003 | 0.011 * | 0.006 | 0.005 | 0.009 | 0.005 | 0.004 | |
| Intervention × Distance | f | 0.040 | 0.645 | 1.111 | 0.044 | 0.876 | 0.629 | 0.329 | 0.245 |
| p | 0.960 | 0.525 | 0.330 | 0.957 | 0.417 | 0.534 | 0.720 | 0.783 | |
| η2p | 0.000 | 0.003 | 0.005 | 0.000 | 0.004 | 0.003 | 0.002 | 0.001 | |
| Direction × Distance | f | 6.399 | 0.768 | 0.070 | 0.450 | 1.362 | 2.073 | 7.758 | 6.416 |
| p | 0.002 | 0.465 | 0.932 | 0.638 | 0.257 | 0.127 | <0.001 | 0.002 | |
| η2p | 0.030 * | 0.004 | 0.000 | 0.002 | 0.007 | 0.010 * | 0.036 * | 0.030 * | |
| Intervention × Direction × Distance | f | 0.084 | 0.278 | 0.237 | 0.082 | 0.396 | 1.384 | 0.474 | 0.610 |
| p | 0.987 | 0.892 | 0.918 | 0.988 | 0.812 | 0.239 | 0.755 | 0.655 | |
| η2p | 0.001 | 0.003 | 0.002 | 0.001 | 0.004 | 0.013 * | 0.005 | 0.006 | |
| Postural Stability Metrics | Intervention | p-Value | ||
|---|---|---|---|---|
| Without | VEX | Airframe | ||
| MEAN ML (cm) | −2.84 (±6.60) | −2.78 (±5.78) | −2.56 (±6.00) | 0.297 |
| MEAN AP (cm) | 2.32 (±3.10) | 2.63 (±3.08) | 2.59 (±3.10) | 0.173 |
| ML APDF10 | 0.134 (±0.076) A | 0.116 (±0.061) B | 0.110 (±0.057) B | 0.003 * |
| ML APDF50 | 0.488 (±0.150) | 0.472 (±0.156) | 0.471 (±0.154) | 0.175 |
| ML APDF90 | 0.797 (±0.101) | 0.789 (±0.093) | 0.784 (±0.106) | 0.215 |
| AP APDF10 | 0.184 (±0.094) | 0.186 (±0.094) | 0.181 (±0.094) | 0.815 |
| AP APDF50 | 0.449 (±0.106) | 0.454 (±0.091) | 0.454 (±0.093) | 0.862 |
| AP APDF90 | 0.711 (±0.098) | 0.727 (±0.084) | 0.732 (±0.090) | 0.112 |
| Postural Stability Metrics | Task Direction | p-Value | ||
|---|---|---|---|---|
| Left-Facing | Front-Facing | Right-Facing | ||
| MEAN ML (cm) | −9.41 (±1.89) A | −3.61 (±1.37) B | 4.79 (±2.25) C | <0.001 * |
| MEAN AP (cm) | 4.38 (±1.30) A | −1.29 (±1.85) B | 4.47 (±1.30) A | <0.001 * |
| ML APDF10 | 0.142 (±0.070) A | 0.113 (±0.073) B | 0.105 (±0.044) B | <0.001 * |
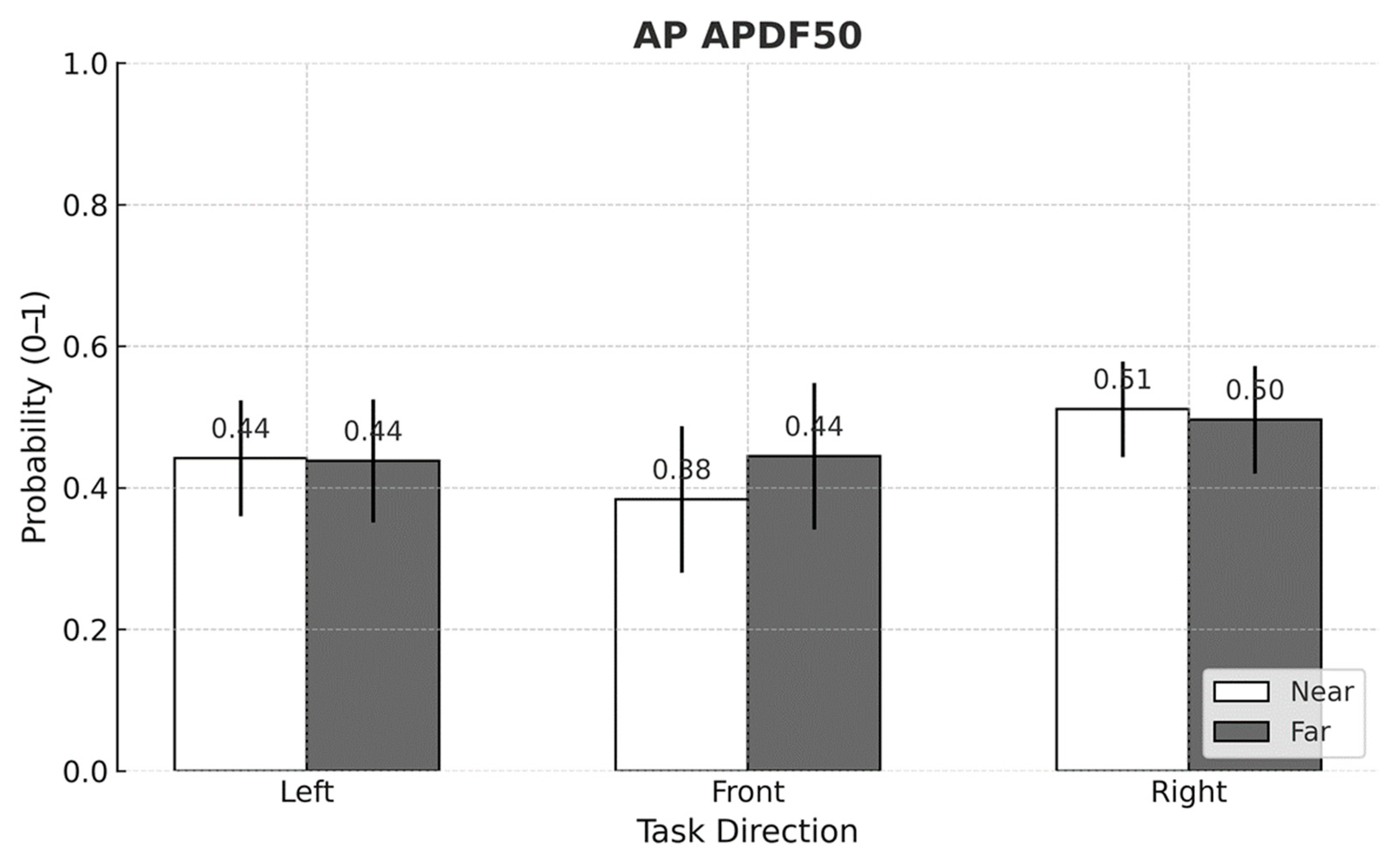
| ML APDF50 | 0.619 (±0.082) A | 0.323 (±0.095) B | 0.490 (±0.103) C | <0.001 * |
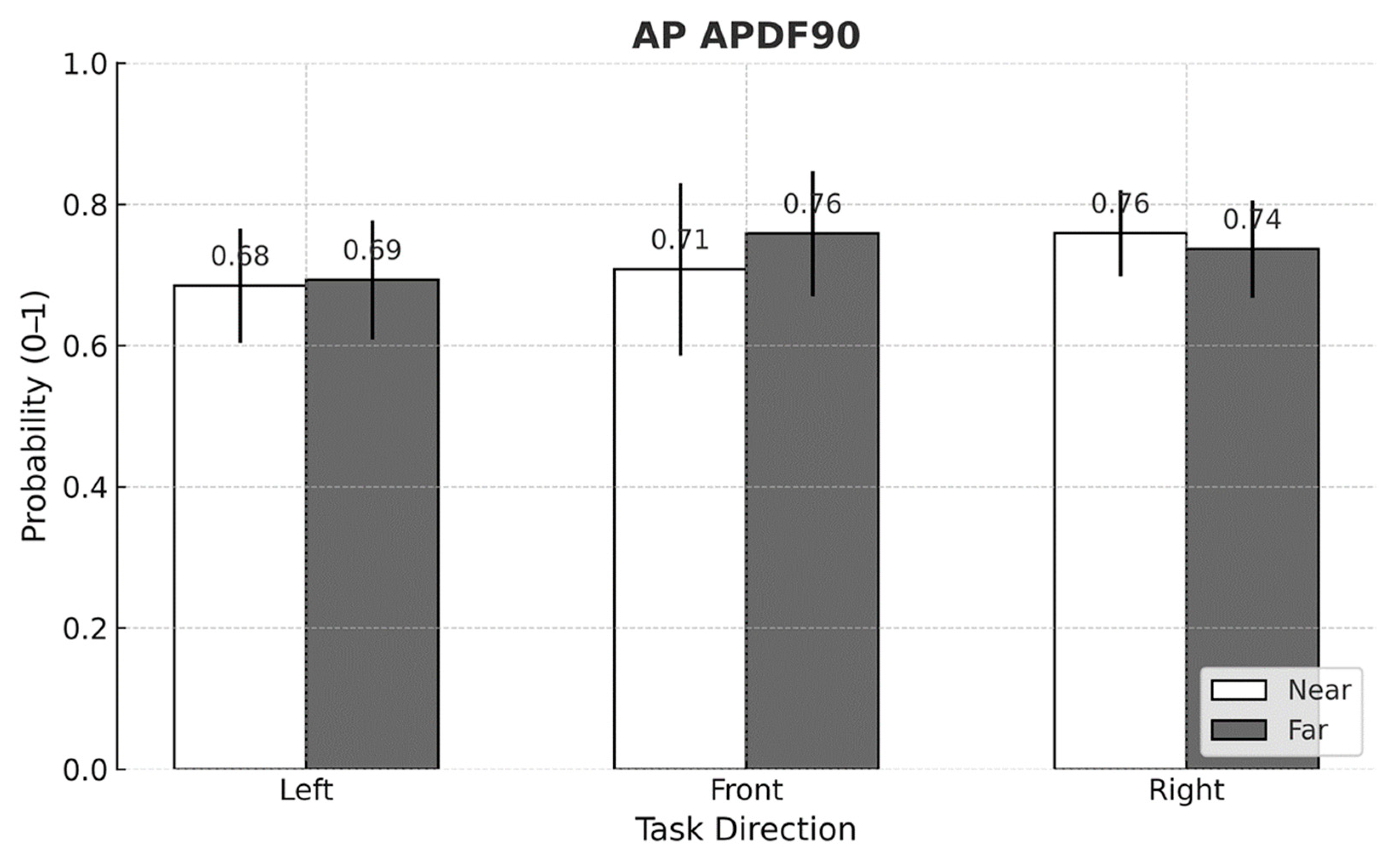
| ML APDF90 | 0.871 (±0.045) A | 0.693 (±0.080) B | 0.808 (±0.073) C | <0.001 * |
| AP APDF10 | 0.210 (±0.081) A | 0.102 (±0.061) B | 0.240 (±0.076) C | <0.001 * |
| AP APDF50 | 0.440 (±0.084) A | 0.414 (±0.108) B | 0.504 (±0.072) C | <0.001 * |
| AP APDF90 | 0.689 (±0.082) A | 0.733 (±0.109) B | 0.748 (±0.066) B | <0.001 * |
| Postural Stability Metrics | Working Distance | p-Value | |
|---|---|---|---|
| Near | Far | ||
| MEAN ML (cm) | −2.78 (±5.82) | −2.68 (±6.43) | 0.738 |
| MEAN AP (cm) | 2.75 (±2.97) | 2.27 (±3.19) | 0.001 * |
| ML APDF10 | 0.116 (±0.063) | 0.124 (±0.068) | 0.146 |
| ML APDF50 | 0.466 (±0.153) | 0.488 (±0.153) | 0.010 * |
| ML APDF90 | 0.783 (±0.105) | 0.798 (±0.095) | 0.020 * |
| AP APDF10 | 0.185 (±0.096) | 0.183 (±0.092) | 0.778 |
| AP APDF50 | 0.445 (±0.100) | 0.460 (±0.093) | 0.098 |
| AP APDF90 | 0.717 (±0.096) | 0.730 (±0.085) | 0.146 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, B.; Park, J. Center of Pressure Analysis of Postural Stability During Repetitive Reaching with Passive Arm-Support Exoskeletons. Sensors 2025, 25, 5650. https://doi.org/10.3390/s25185650
Choi B, Park J. Center of Pressure Analysis of Postural Stability During Repetitive Reaching with Passive Arm-Support Exoskeletons. Sensors. 2025; 25(18):5650. https://doi.org/10.3390/s25185650
Chicago/Turabian StyleChoi, Byungkyu, and Jaehyun Park. 2025. "Center of Pressure Analysis of Postural Stability During Repetitive Reaching with Passive Arm-Support Exoskeletons" Sensors 25, no. 18: 5650. https://doi.org/10.3390/s25185650
APA StyleChoi, B., & Park, J. (2025). Center of Pressure Analysis of Postural Stability During Repetitive Reaching with Passive Arm-Support Exoskeletons. Sensors, 25(18), 5650. https://doi.org/10.3390/s25185650






