Inductive Sensor Characteristics for Conductivity Measurement of Non-Ferromagnetic Metals Based on Single-Layer Solenoid
Abstract
1. Introduction
2. Inductive Sensor Model and Measurement Method
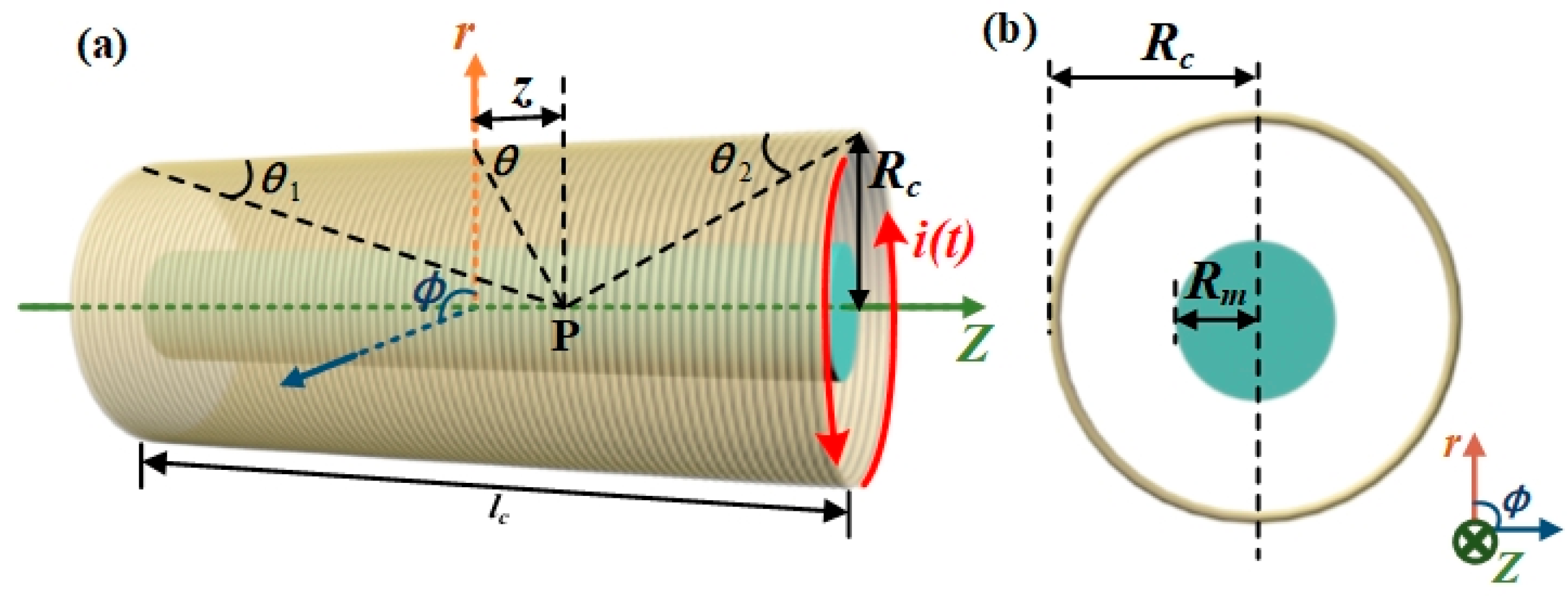
2.1. Inductive Model of the Single-Layer Solenoid with a Finite Length
2.2. Equivalent Model of Electrical Conductivity
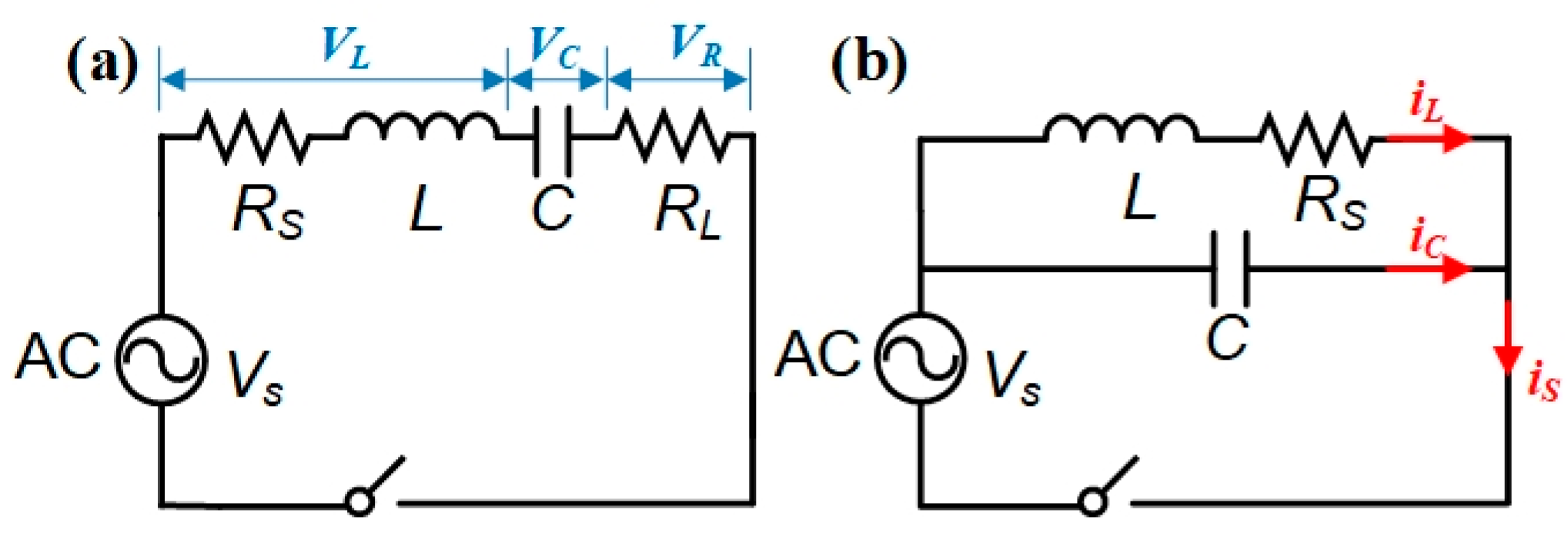
2.3. Measurement Method of Inductance Based on the RLC Resonant Circuit
3. Experimental Results
3.1. The Effect of the Circuit Parameters on the Resonance Frequency
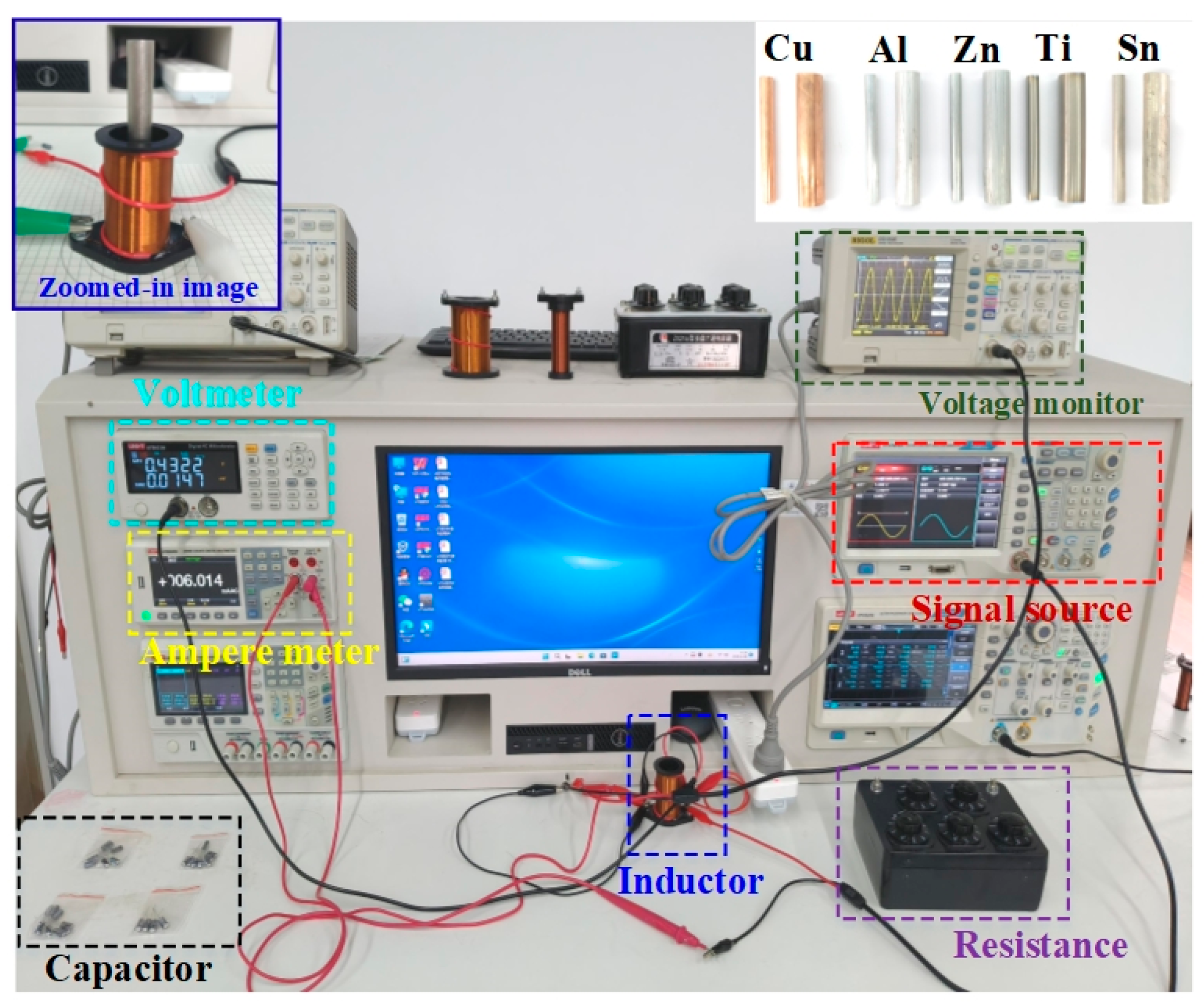
3.1.1. Experimental Setup
3.1.2. The Influence Induced by the Capacitance
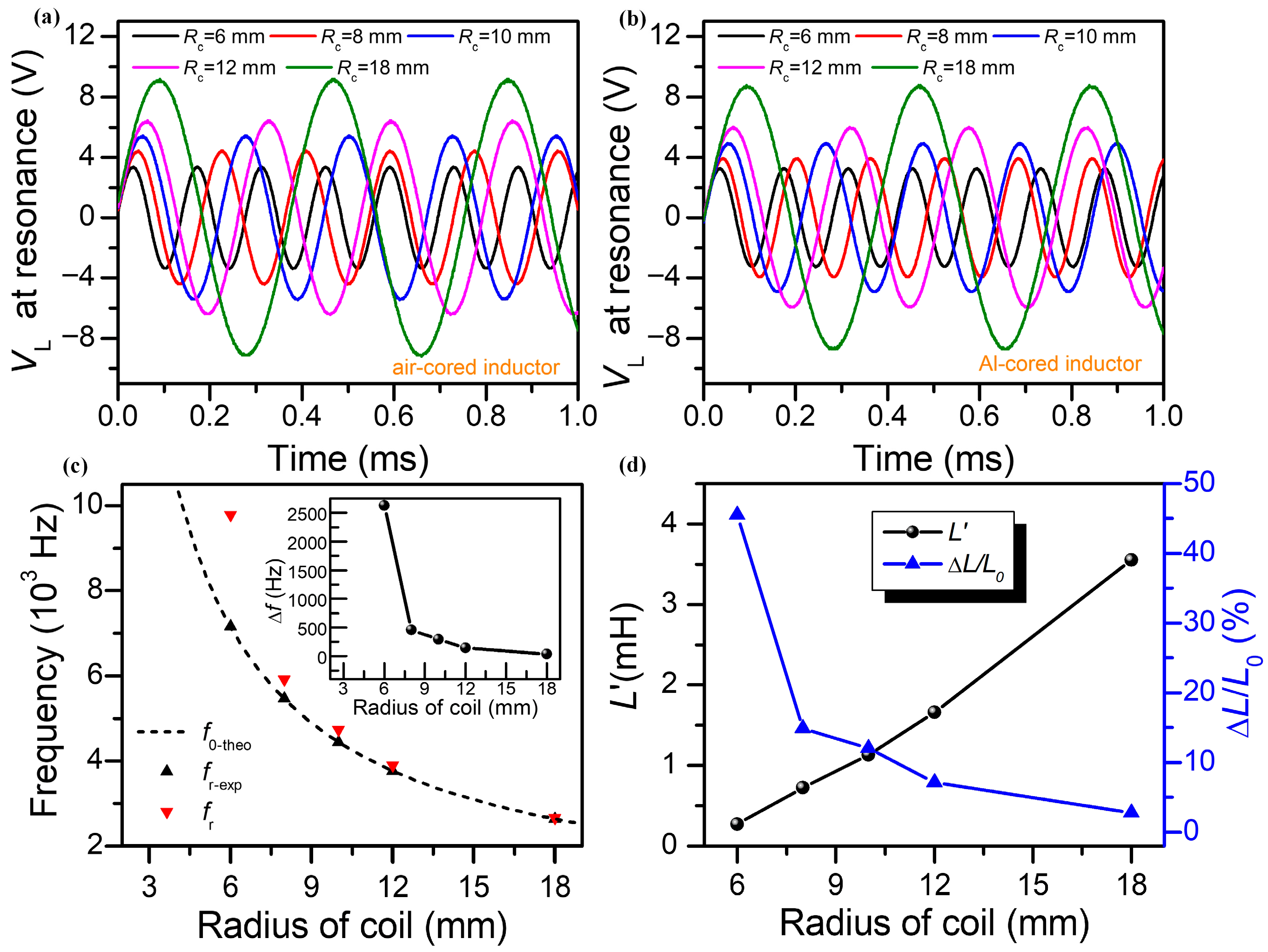
3.2. The Influence Induced by the Coil Radius
3.3. Inductive Response Characteristics of Different Testing Modes
4. Discussion
4.1. Conductivity Measurement Based on the Single-Layer Solenoid Sensor
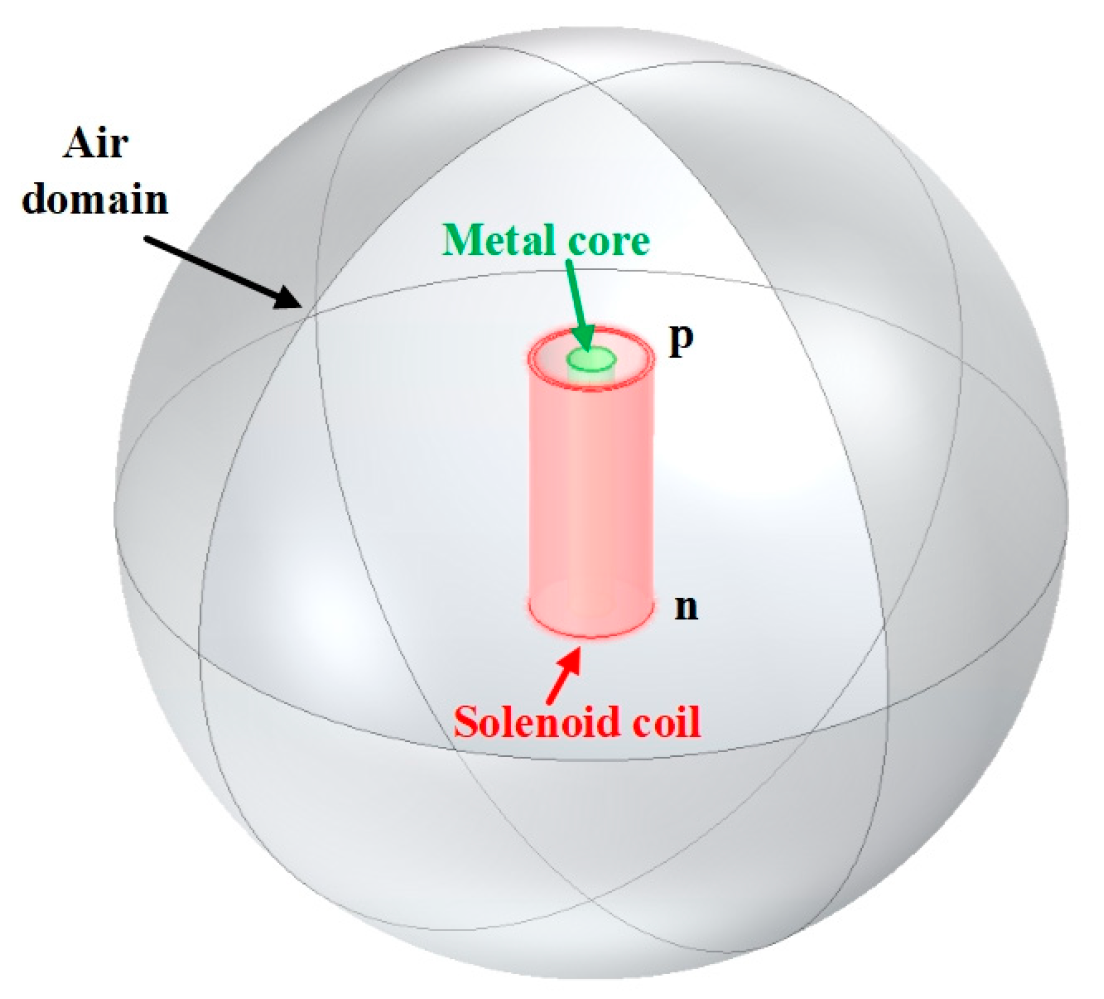
4.2. Simulated Analysis of the Solenoid Sensor
4.3. Relative Standard Deviation and the Relative Error of Conductivity Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, R.; Li, Z.; Deng, G.; Yu, Y.; Shui, J.; Yu, R.; Pan, C.; Liu, X. Anisotropic magnetic liquid metal film for wearable wireless electromagnetic sensing and smart electromagnetic interference shielding. Nano Energy 2022, 92, 106700. [Google Scholar] [CrossRef]
- Farag, E.H.; Toyserkani, E.; Khamesee, M.B. Non-destructive testing using eddy current sensors for defect detection in additively manufactured titanium and stainless-steel parts. Sensors 2022, 22, 5440. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Z.; Lyu, Y.; Zhao, L. Experimental investigation of inductive sensor characteristic for blade tip clearance measurement at high temperature. Sensors 2019, 19, 3694. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Xie, F.; Zhang, H. Defect imaging curved surface based on flexible eddy current array sensor. Measurement 2020, 151, 107280. [Google Scholar] [CrossRef]
- Zhao, G.; Huang, Y.; Zhang, W.; Wang, C.; Chen, J. Advances in high-precision displacement and thickness measurement based on eddy current sensors: A review. Measurement 2025, 243, 116410. [Google Scholar] [CrossRef]
- Guan, A.; Wang, H.; Jin, H.; Chu, W.; Guo, Y. An experimental apparatus for simultaneously measuring Seebeck coefficient and electrical resistivity from 100 K to 600 K. Rev. Sci. Instrum. 2013, 84, 043903. [Google Scholar] [CrossRef]
- Nandihalli, N. A short account of thermoelectric film characterization techniques. Mater. Today Phys. 2023, 36, 101173. [Google Scholar] [CrossRef]
- Xu, W.; Yang, C.; Yu, H.; Jin, X.; Guo, B.; Shan, D. Microcrack healing in non-ferrous metal tubes through eddy current pulse treatment. Sci. Rep. 2018, 8, 6016. [Google Scholar] [CrossRef]
- Zhao, B.; Du, Y.; Yan, Z.; Rao, L.; Chen, G.; Yuan, M.; Yang, L.; Zhang, J.; Che, R. Structural defects in phase-regulated high-entropy oxides toward superior microwave absorption properties. Adv. Funct. Mater. 2023, 33, 2209924. [Google Scholar] [CrossRef]
- Striggow, K.; Dankert, R. The exact theory of inductive conductivity sensors for oceanographic application. IEEE J. Oceanic Eng. 1985, 10, 175–179. [Google Scholar] [CrossRef]
- Rabbani, G.; Smeaton, C.; Cheema, M.; Galagedara, L. Evaluation and estimation of boreal podzol soil nutrient concentrations using electromagnetic induction sensors. Comput. Electron. Agric. 2025, 236, 110448. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Xuan, W.; Huang, S.; You, B.; Li, W.; Sun, L.; Jin, H.; Wang, X.; Dong, S. Conjunction of triboelectric nanogenerator with induction coils as wireless power sources and self-powered wireless sensors. Nat. Commun. 2020, 11, 58. [Google Scholar] [CrossRef]
- Wang, H.; Li, W.; Feng, Z. Noncontact thickness measurement of metal films using eddy-current sensors immune to distance variation. IEEE Trans. Instrum. Meas. 2014, 64, 2557–2564. [Google Scholar] [CrossRef]
- Iguez, J.; Raposo, V.; Zazo, M. Non-contact conductivity measurements in non-ferromagnetic pipes and rods: The choice of working frequency. Sens. Lett. 2009, 7, 387–389. [Google Scholar] [CrossRef]
- Íñiguez, J.; Raposo, V.; Zazo, M. Measurement of electrical conductivity in nonferromagnetic tubes and rods at low frequencies. Am. J. Phys. 2009, 77, 949–953. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, H.; Xiao, X.; Ma, Q.; Li, H.; Tian, G.; Gao, B.; Wu, J. RLC parameters measurement and fusion for high-sensitivity inductive sensors. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Feng, S.; Liu, N.; Wang, T. Analysis of single-coil resonant seawater conductivity measuring model. Electr. Meas. Technol. 2024, 47, 37–43. [Google Scholar] [CrossRef]
- Wang, T.; Liu, N.; Feng, S.; Kong, Y.; Zhao, J. Effect of seawater conductivity on impedance parameters of planar coils in magnetically coupledsystems. IEEE Instrum. Meas. Mag. 2025, 28, 69–76. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, H.; Wang, M.; Chen, H. Differentiation of nonferrous metal particles in lubrication oil using an electrical conductivity measurement-based inductive sensor. Rev. Sci. Instrum. 2018, 89, 025002. [Google Scholar] [CrossRef]
- Fu, T.; Zhao, H.; Xu, J.; Gu, Y. Multi-physical field state characterization of CFRP tube based on heating mode of built-in induction coil. J. Mater. Sci. 2023, 58, 3187–3207. [Google Scholar] [CrossRef]
- Wang, C.; Liang, X.; Guo, Q.; Ye, J. Measurement of equivalent conductivity and permeability of liquid-solid mixture based on single-layer coil. IEEE Sens. J. 2020, 21, 3163–3171. [Google Scholar] [CrossRef]
- Borovik, S.; Kuteynikova, M.; Sekisov, Y. Reducing the impact of influence factors on the measurement results from single-coil eddy current sensors. Sensors 2022, 23, 351. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, X.; Li, Y.; Zhu, T.; Hutchins, D.; Li, W.; Chen, G. A combined inductive and capacitive non-destructive evaluation technique using a single spiral coil sensor. IEEE Sens. J. 2021, 21, 18187–18196. [Google Scholar] [CrossRef]
- Ganesh, M.; Ravan, M.; Amineh, R.K. Electromagnetic induction imaging at multiple depths with a single coil. IEEE Trans. Instrum. Meas. 2021, 70, 4502809. [Google Scholar] [CrossRef]
- Abu-Nabah, B.A.; Nagy, P.B. High-frequency eddy current conductivity spectroscopy for residual stress profiling in surface-treated nickel-base superalloys. NDT E Int. 2007, 40, 405. [Google Scholar] [CrossRef]
- Gupta, M.; Khan, M.A.; Butola, R.; Singari, R.M. Advances in applications of Non-Destructive Testing (NDT): A review. Adv. Mater. Process. Technol. 2022, 8, 2286–2307. [Google Scholar] [CrossRef]
- Bernieri, A.; Betta, G.; Ferrigno, L. Characterization of an eddy-current-based system for nondestructive testing. IEEE Trans. Instrum. Meas. 2002, 51, 241–245. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, C. Ferromagnetic metal particle detection including calculation of particle magnetic permeability based on micro inductive sensor. IEEE Sens. J. 2020, 21, 447–454. [Google Scholar] [CrossRef]
- Harms, J.; Kern, T.A. Theory and modeling of eddy current type inductive conductivity sensors. Eng. Proc. 2021, 6, 37. [Google Scholar] [CrossRef]
- Kral, J.; Smid, R.; Ramos, H.M.G.; Ribeiro, A.L. The lift-off effect in eddy currents on thickness modeling and measurement. IEEE Trans. Instrum. Meas. 2013, 62, 2043–2049. [Google Scholar] [CrossRef]
- Hofmann, T.; Helbig, T.; Schindler, F.; Salgo, N.; Brzezińska, M.; Greiter, M.; Kiessling, T.; Wolf, D.; Vollhardt, A.; Kabaši, A. Reciprocal skin effect and its realization in a topolectrical circuit. Phys. Rev. Res. 2020, 2, 023265. [Google Scholar] [CrossRef]
- Xia, Z.; Huang, R.; Chen, Z.; Yu, K.; Zhang, Z.; Salas-Avila, J.R.; Yin, W. Eddy current measurement for planar structures. Sensors 2022, 22, 8695. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Zhang, Z.; Yin, W.; Tytko, G. Sloping-invariance for nonferrous metallic slabs at multiple frequencies by eddy current sensors. IEEE Access 2021, 9, 59949–59956. [Google Scholar] [CrossRef]




| Parameter | Value | Description |
|---|---|---|
| N | 480 | Number of turns in the coil |
| lc (mm) | 60 | Length of the coil |
| Rc (mm) | 6, 8, 10, 12, 18 | Radius of the coil |
| lm (cm) | 10 | Length of the metal rod |
| Rm (mm) | 2–10 | Radius of the metal rod |
| RS (Ω) | ~0 | Resistance of the coil |
| RL (Ω) | 10 | Load resistance |
| C (µF) | 1.0, 3.3, 4.7, 6.8, 10 | Capacitance |
| L (mH) | 1/ | Inductance of the solenoid |
| VS (V) | 3 | Amplitude of the voltage source |
| fr (Hz) | 1/ | Resonant frequency |
| ωr (Hz) | 1/ | Resonant angular frequency |
| Metal | Reference Data | Proposed Data | |||||
|---|---|---|---|---|---|---|---|
| In Series Mode | In Parallel Mode | ||||||
(107 S/m) | Measured (107 S/m) | RSD (%) | RE (%) | Measured (107 S/m) | RSD (%) | RE (%) | |
| Cu | 5.86 | 5.68 | 9.51 | −3.07 | 5.79 | 5.92 | −1.20 |
| Al | 3.79 | 3.85 | 7.38 | 1.58 | 3.65 | 2.76 | −3.69 |
| Zn | 1.71 | 1.88 | 10.55 | 9.94 | 1.84 | 6.39 | 7.60 |
| Sn | 0.89 | 0.96 | 1.86 | 7.86 | 0.93 | 1.40 | 4.49 |
| Ti | 0.23 | 0.26 | 5.90 | 13.04 | 0.25 | 8.03 | 8.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Han, Z.; Chen, Y.; Li, S.; Li, H.; Shen, H.; Xu, C. Inductive Sensor Characteristics for Conductivity Measurement of Non-Ferromagnetic Metals Based on Single-Layer Solenoid. Sensors 2025, 25, 5566. https://doi.org/10.3390/s25175566
Wang H, Han Z, Chen Y, Li S, Li H, Shen H, Xu C. Inductive Sensor Characteristics for Conductivity Measurement of Non-Ferromagnetic Metals Based on Single-Layer Solenoid. Sensors. 2025; 25(17):5566. https://doi.org/10.3390/s25175566
Chicago/Turabian StyleWang, Huan, Ziyi Han, Yongjian Chen, Shuyu Li, Haoran Li, Hao Shen, and Chunlong Xu. 2025. "Inductive Sensor Characteristics for Conductivity Measurement of Non-Ferromagnetic Metals Based on Single-Layer Solenoid" Sensors 25, no. 17: 5566. https://doi.org/10.3390/s25175566
APA StyleWang, H., Han, Z., Chen, Y., Li, S., Li, H., Shen, H., & Xu, C. (2025). Inductive Sensor Characteristics for Conductivity Measurement of Non-Ferromagnetic Metals Based on Single-Layer Solenoid. Sensors, 25(17), 5566. https://doi.org/10.3390/s25175566









