MECO: Mixture-of-Expert Codebooks for Multiple Dense Prediction Tasks
Abstract
1. Introduction
- We propose an end-to-end multi-task learning framework that learns task-generic and task-specific codebooks via vector quantization, disentangling shared representations into a discrete latent space for task-specific features
- We introduce a Mixture-of-Expert Codebooks design that substantially improves computational efficiency by replacing multiple expert modules in MoE with lightweight codebooks
- We present a real-world driving dataset for embedded environments, enabling evaluation of the proposed method’s efficiency gains and maintained task performance over prior approaches
2. Related Work
2.1. Multi-Task Learning
2.2. Mixture-of-Experts
2.3. Vector Quantization
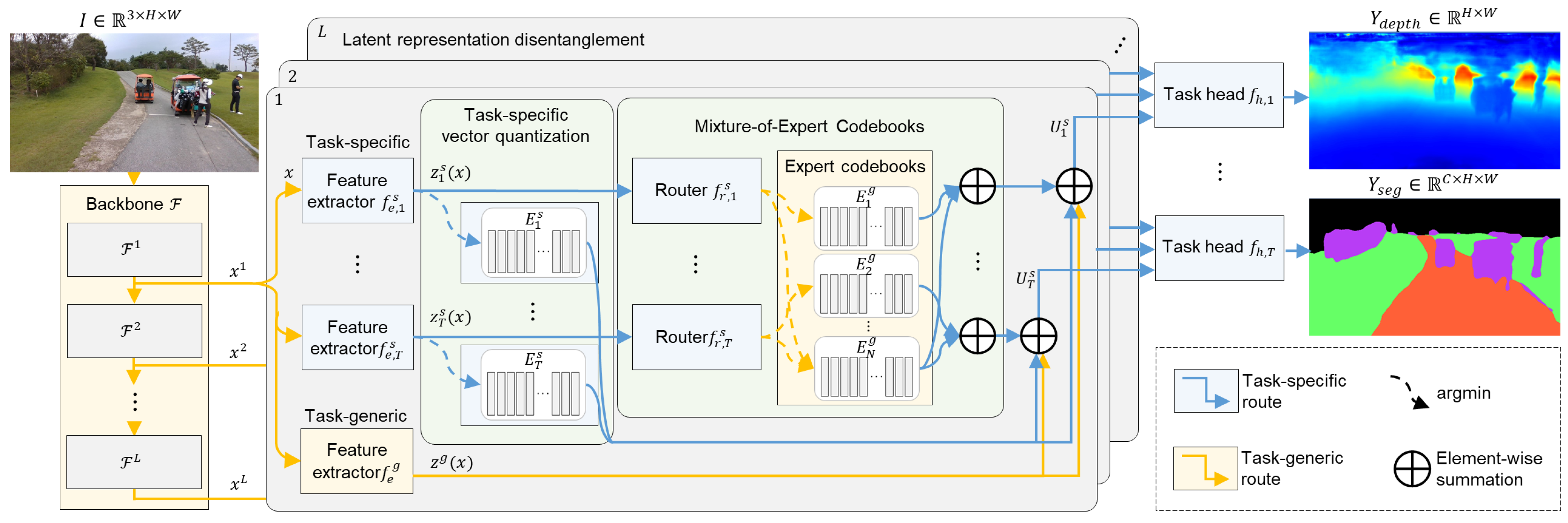
3. Method
3.1. Preliminaries: Mixture-of-Experts
3.2. The MTL Model Architecture
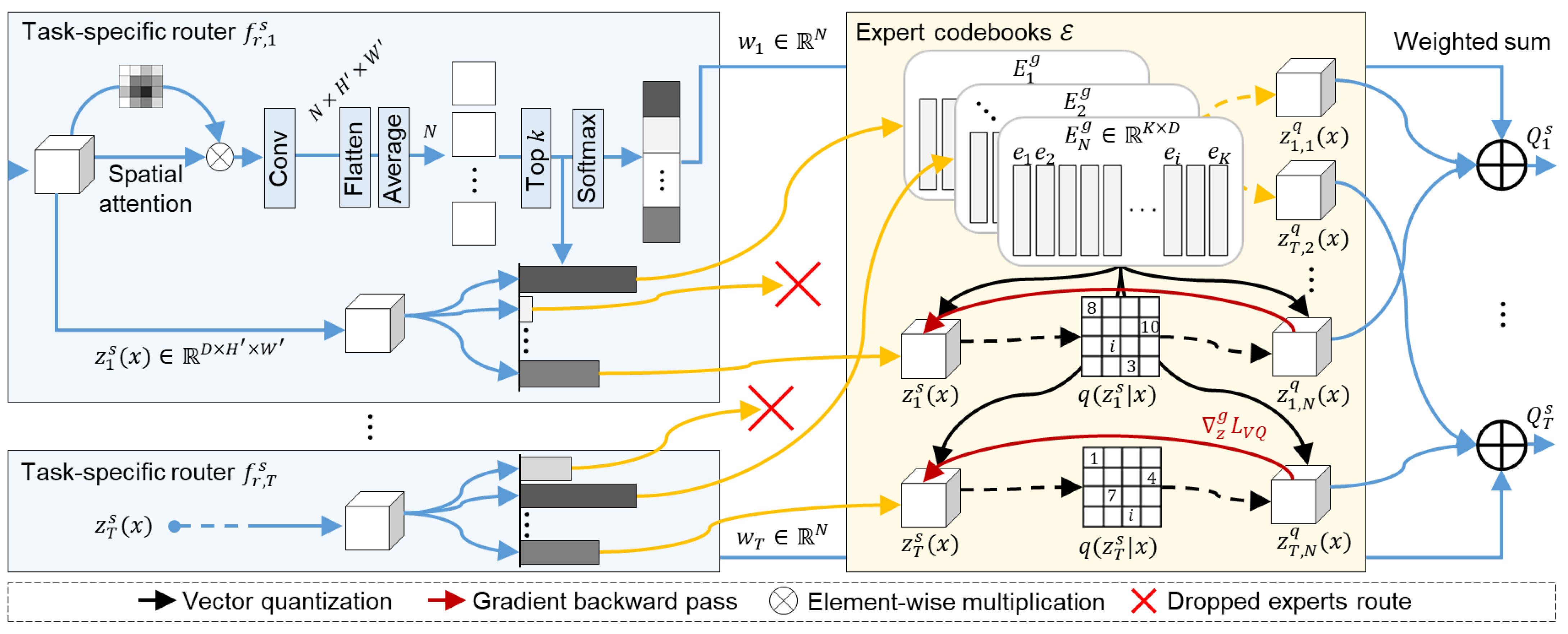
3.3. Mixture-of-Expert Codebooks
3.4. Task-Specific Vector Quantization
3.5. Loss Function
4. Results
4.1. Real-World Driving Dataset
4.2. Experiment Environments
4.3. Hyperparameters and Evaluation Metrics
4.4. Experimental Results on Real-World Dataset
4.5. Computational Complexity
4.6. Ablation Study
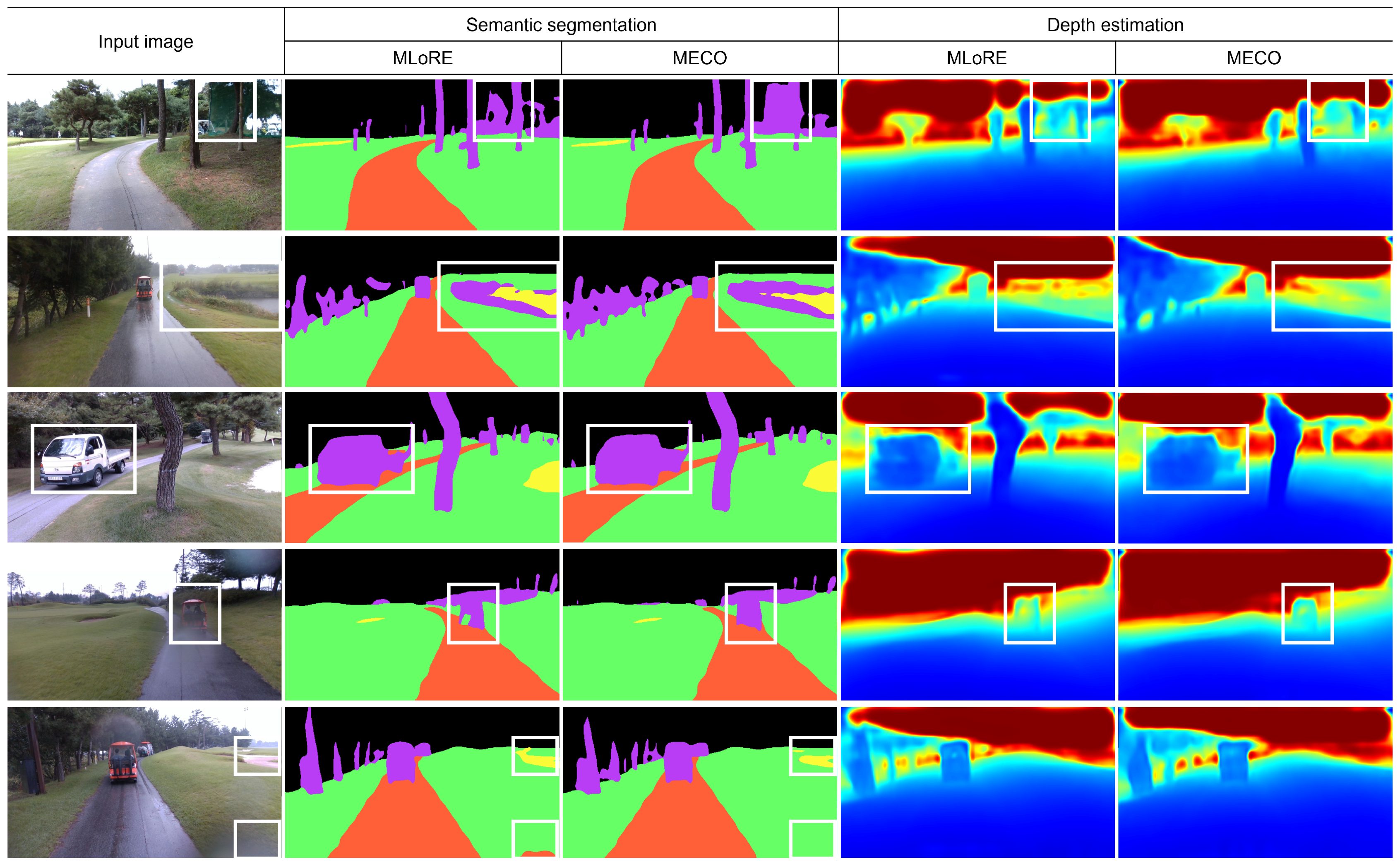
4.7. Qualitative Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Liu, L.; Tang, J.; Yu, B.; Wang, Y.; Shi, W. Edge computing for autonomous driving: Opportunities and challenges. Proc. IEEE 2019, 107, 1697–1716. [Google Scholar] [CrossRef]
- Zhang, F.S.; Ge, D.Y.; Song, J.; Xiang, W.J. Outdoor scene understanding of mobile robot via multi-sensor information fusion. J. Ind. Inf. Integr. 2022, 30, 100392. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2366–2374. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 4015–4026. [Google Scholar]
- Yang, L.; Kang, B.; Huang, Z.; Xu, X.; Feng, J.; Zhao, H. Depth anything: Unleashing the power of large-scale unlabeled data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 10371–10381. [Google Scholar]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Huang, J.; Rathod, V.; Sun, C.; Zhu, M.; Korattikara, A.; Fathi, A.; Fischer, I.; Wojna, Z.; Song, Y.; Guadarrama, S.; et al. Speed/accuracy trade-offs for modern convolutional object detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7310–7311. [Google Scholar]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Ruder, S. An overview of multi-task learning in deep neural networks. arXiv 2017, arXiv:1706.05098. [Google Scholar] [CrossRef]
- Vandenhende, S.; Georgoulis, S.; Proesmans, M.; Dai, D.; Gool, L.V. Revisiting Multi-Task Learning in the Deep Learning Era. arXiv 2020, arXiv:2004.13379. [Google Scholar]
- Liu, S.; Johns, E.; Davison, A.J. End-to-end multi-task learning with attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1871–1880. [Google Scholar]
- Misra, I.; Shrivastava, A.; Gupta, A.; Hebert, M. Cross-stitch networks for multi-task learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3994–4003. [Google Scholar]
- Xu, D.; Ouyang, W.; Wang, X.; Sebe, N. Pad-net: Multi-tasks guided prediction-and-distillation network for simultaneous depth estimation and scene parsing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 675–684. [Google Scholar]
- Vandenhende, S.; Georgoulis, S.; Van Gool, L. Mti-net: Multi-scale task interaction networks for multi-task learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 527–543. [Google Scholar]
- Vandenhende, S.; Georgoulis, S.; Van Gansbeke, W.; Proesmans, M.; Dai, D.; Van Gool, L. Multi-task learning for dense prediction tasks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3614–3633. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, Z.; Yi, X.; Chen, J.; Hong, L.; Chi, E.H. Modeling task relationships in multi-task learning with multi-gate mixture-of-experts. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1930–1939. [Google Scholar]
- Yang, Y.; Jiang, P.T.; Hou, Q.; Zhang, H.; Chen, J.; Li, B. Multi-task dense prediction via mixture of low-rank experts. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 27927–27937. [Google Scholar]
- Kim, I.; Lee, J.; Kim, D. Learning mixture of domain-specific experts via disentangled factors for autonomous driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 1148–1156. [Google Scholar]
- Shazeer, N.; Mirhoseini, A.; Maziarz, K.; Davis, A.; Le, Q.; Hinton, G.; Dean, J. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv 2017, arXiv:1701.06538. [Google Scholar]
- Ye, H.; Xu, D. Taskexpert: Dynamically assembling multi-task representations with memorial mixture-of-experts. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 21828–21837. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the 29th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Van Den Oord, A.; Vinyals, O.; Kavukcuoglu, K. Neural discrete representation learning. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6309–6318. [Google Scholar]
- Ye, H.; Xu, D. Inverted pyramid multi-task transformer for dense scene understanding. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 514–530. [Google Scholar]
- Tang, A.; Shen, L.; Luo, Y.; Yin, N.; Zhang, L.; Tao, D. Merging multi-task models via weight-ensembling mixture of experts. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 47778–47799. [Google Scholar]
- Gray, R. Vector quantization. IEEE ASSP Mag. 1984, 1, 4–29. [Google Scholar] [CrossRef]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv 2013, arXiv:1308.3432. [Google Scholar] [CrossRef]
- Jiao, L.; Lai, Q.; Li, Y.; Xu, Q. Vector quantization prompting for continual learning. Adv. Neural Inf. Process. Syst. 2024, 37, 34056–34076. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef] [PubMed]
- Fnu, N.; Bansal, A. Understanding the architecture of vision transformer and its variants: A review. In Proceedings of the 2024 1st International Conference on Innovative Engineering Sciences and Technological Research (ICIESTR), Muscat, Oman, 14–15 May 2024; pp. 1–6. [Google Scholar]
- Tsai, D.; Worrall, S.; Shan, M.; Lohr, A.; Nebot, E. Optimising the selection of samples for robust lidar camera calibration. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2631–2638. [Google Scholar]
- Lee, J.H.; Han, M.K.; Ko, D.W.; Suh, I.H. From big to small: Multi-scale local planar guidance for monocular depth estimation. arXiv 2019, arXiv:1907.10326. [Google Scholar]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like transformer for efficient semantic segmentation of remote sensing urban scene imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Lin, B.; Jiang, W.; Chen, P.; Zhang, Y.; Liu, S.; Chen, Y.C. MTMamba: Enhancing multi-task dense scene understanding by mamba-based decoders. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2024; pp. 314–330. [Google Scholar]
- Lin, B.; Jiang, W.; Chen, P.; Liu, S.; Chen, Y.C. MTMamba++: Enhancing Multi-Task Dense Scene Understanding via Mamba-Based Decoders. IEEE Trans. Pattern Anal. Mach. Intell. 2025, Early Access. [Google Scholar] [CrossRef] [PubMed]

| Notation | Description | Notation | Description | Notation | Description | Notation | Description |
|---|---|---|---|---|---|---|---|
| I | Input RGB image | t | Task index | h | Task-specific head | n | Expert index |
| Y | Dense prediction output | s | Task-specific component | U | Aggregated features | K | Number of codewords |
| Height and width of the input image | g | Task-generic component | Q | Aggregated VQ features | i-th codeword | ||
| Height and width of the feature map | q | Quantized vector | Feature representation | w | Router weight vector | ||
| M | Number of tokens () | L | Number of ViT layers | z | Latent vector | k | Number of top-k selection |
| m | Spatial position index (VQ) | l | ViT layer index | VQ function of expert codebook | Set of selected expert indices | ||
| D | Feature dimension | f | Functions of modules | VQ function of task codebook | |||
| Loss function | e | Extractor | E | Codebook | |||
| T | Number of tasks | r | Task-specific router | N | Number of experts |
| Task | Method | Depth Estimation ↓ | Semantic Segmentation ↑ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE Log | Abs Rel | Sq Rel | Background | Fairway | Hazard | Road | Obstacle | mIoU (%) | ||
| Single | BTS [35] | 2.758 | 0.195 | 0.129 | 0.541 | - | - | - | - | - | - |
| UNetFormer [36] | - | - | - | - | 82.37 | 93.86 | 65.79 | 95.83 | 52.61 | 78.09 | |
| Multiple | MTMamba [37] | 2.185 | 0.181 | 0.115 | 0.453 | 82.99 | 93.12 | 50.66 | 94.87 | 54.21 | 75.17 |
| MTMamba++ [38] | 2.850 | 0.210 | 0.129 | 0.579 | 84.03 | 93.93 | 56.31 | 95.56 | 55.46 | 77.06 | |
| MLoRE [18] | 2.198 | 0.157 | 0.101 | 0.358 | 85.65 | 94.16 | 61.81 | 96.50 | 59.99 | 79.63 | |
| MECO (ours) | 2.224 | 0.159 | 0.102 | 0.367 | 85.62 | 94.23 | 62.90 | 96.71 | 60.68 | 80.03 | |
| Method | FLOPs (T) | #Params (M) | FPS |
|---|---|---|---|
| MLoRE [18] | 1.453 | 509.58 | 7.61 |
| MECO (ours) | 1.034 | 416.14 | 11.20 |
| N | k | Abs Rel | mIoU (%) | FLOPs (T) | #Params (M) |
|---|---|---|---|---|---|
| 5 | 3 | 0.110 | 79.57 | 1.034 | 400.35 |
| 10 | 6 | 0.108 | 79.60 | 1.034 | 408.25 |
| 15 | 9 | 0.102 | 80.03 | 1.034 | 416.14 |
| 20 | 12 | 0.099 | 79.68 | 1.034 | 422.46 |
| Routing | Codebook Update | Abs Rel | mIoU (%) |
|---|---|---|---|
| Soft | EMA | 0.112 | 79.17 |
| Top-k | EMA | 0.103 | 79.15 |
| Top-k | Dictionary loss | 0.102 | 80.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, G.; Lee, S.J. MECO: Mixture-of-Expert Codebooks for Multiple Dense Prediction Tasks. Sensors 2025, 25, 5387. https://doi.org/10.3390/s25175387
Hwang G, Lee SJ. MECO: Mixture-of-Expert Codebooks for Multiple Dense Prediction Tasks. Sensors. 2025; 25(17):5387. https://doi.org/10.3390/s25175387
Chicago/Turabian StyleHwang, Gyutae, and Sang Jun Lee. 2025. "MECO: Mixture-of-Expert Codebooks for Multiple Dense Prediction Tasks" Sensors 25, no. 17: 5387. https://doi.org/10.3390/s25175387
APA StyleHwang, G., & Lee, S. J. (2025). MECO: Mixture-of-Expert Codebooks for Multiple Dense Prediction Tasks. Sensors, 25(17), 5387. https://doi.org/10.3390/s25175387






