Enhancing LiDAR–IMU SLAM for Infrastructure Monitoring via Dynamic Coplanarity Constraints and Joint Observation
Abstract
1. Introduction
- Design of a ground point cloud extraction algorithm based on angular thresholding, which effectively distinguishes ground from non-ground points through vertical angular analysis of LiDAR point clouds frame-by-frame. This significantly enhances the accuracy and robustness of ground point cloud extraction, thereby improving practical applicability in engineering applications.
- Development of a ground constraint module that exploits the local planar consistency prior inherent in urban infrastructure environments, incorporating coplanarity assessment functionality. By conditionally activating ground constraints, this approach effectively filters outliers, mitigates pose estimation drift, and enhances system robustness and reliability.
- Integration of ground constraints with traditional LiDAR point cloud registration constraints through joint optimization to obtain optimal pose estimates, enabling construction of high-precision point cloud maps.
2. Related Work
2.1. Filter-Based SLAM Approaches
2.2. Optimization-Based SLAM Approaches
3. Proposed Method
3.1. Overview of FAST-LIO2
3.2. Ground Extraction
- Dynamic search truncation: Points that are too close to or too far from the LiDAR center (<0.3 m or >50 m) are skipped to avoid ego-body interference and long-range measurement noise.
- Cross-obstacle detection: A radial distance ratio threshold is introduced. When the ratio of radial distances between adjacent points exceeds this threshold, the pair is considered to span an obstacle, and the current column search is terminated, as formulated below:
- Invalid point tolerance: Points with NaN (Not a Number) values are automatically skipped to prevent computational failures during processing.
3.3. Ground Constraint
3.3.1. Plane Parameterization and Residual Definition
3.3.2. Coordinate Transformation and Observation Model
- Initial calibration:
- 2.
- Transformation to world coordinate system:
- 3.
- Transformation to current frame LiDAR coordinate system:
3.3.3. Transformation to Current Frame LiDAR Coordinate System
3.4. Joint Observation
4. Experiment and Results
4.1. Experimental Setups
4.1.1. Self-Built Platform and Self-Collected Dataset
4.1.2. Public M2DGR Dataset
4.2. Evaluation Metrics and Baseline Algorithms
- A-LOAM [17]: A-LOAM is a code implementation and optimized version of the original LOAM algorithm, which mainly improves the readability and implementation efficiency of the code;
- LeGO-LOAM [22]: A lightweight LiDAR odometry and mapping algorithm optimized for ground-based applications;
- LIO-SAM [23]: A tightly coupled LiDAR-inertial odometry approach based on smoothing and mapping;
- Fast-LIO2 [27]: The baseline algorithm on which our proposed method is based is an advanced, tightly coupled LIO (LiDAR-inertial odometry) system.
4.3. Results and Discussion
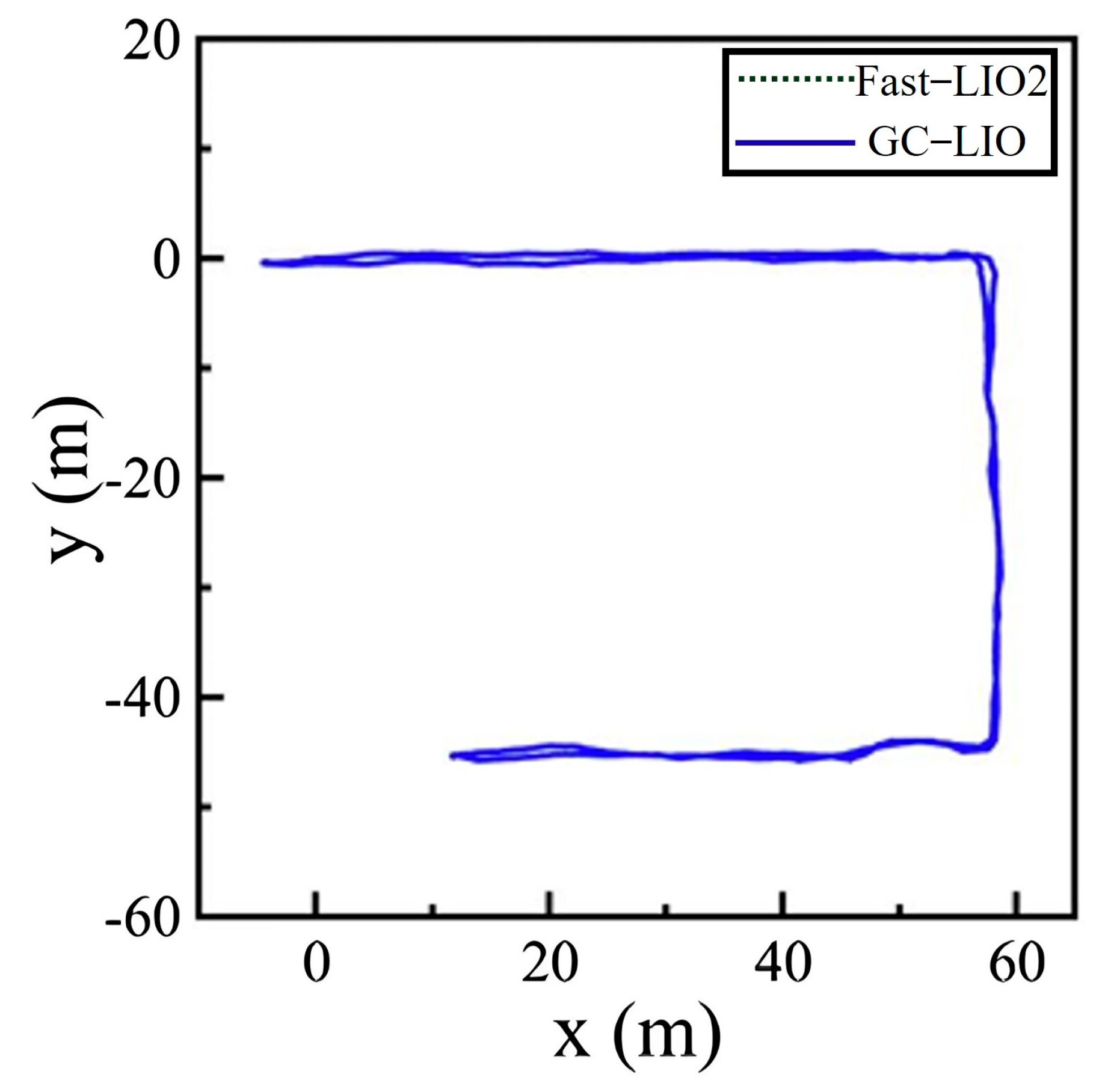
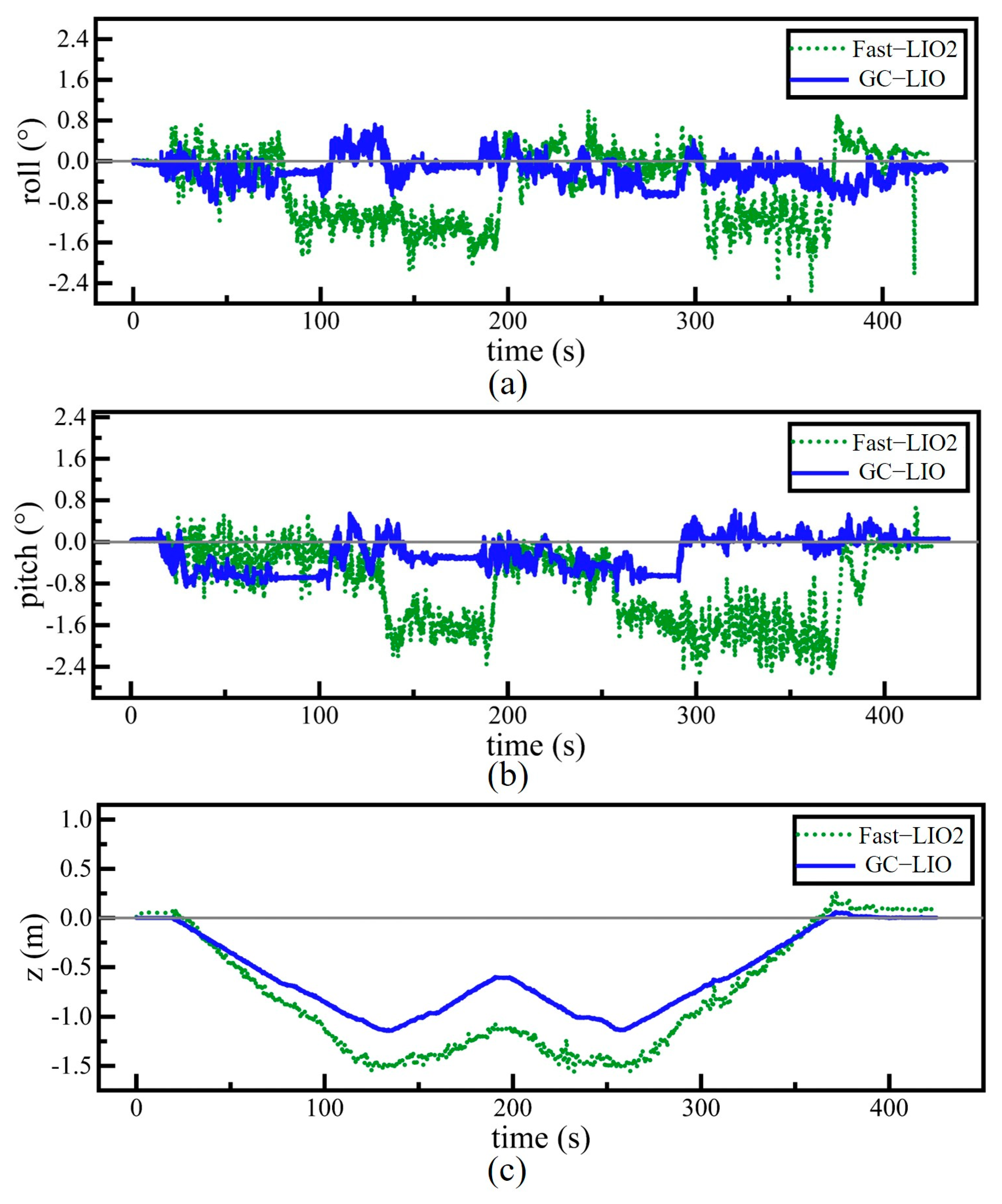
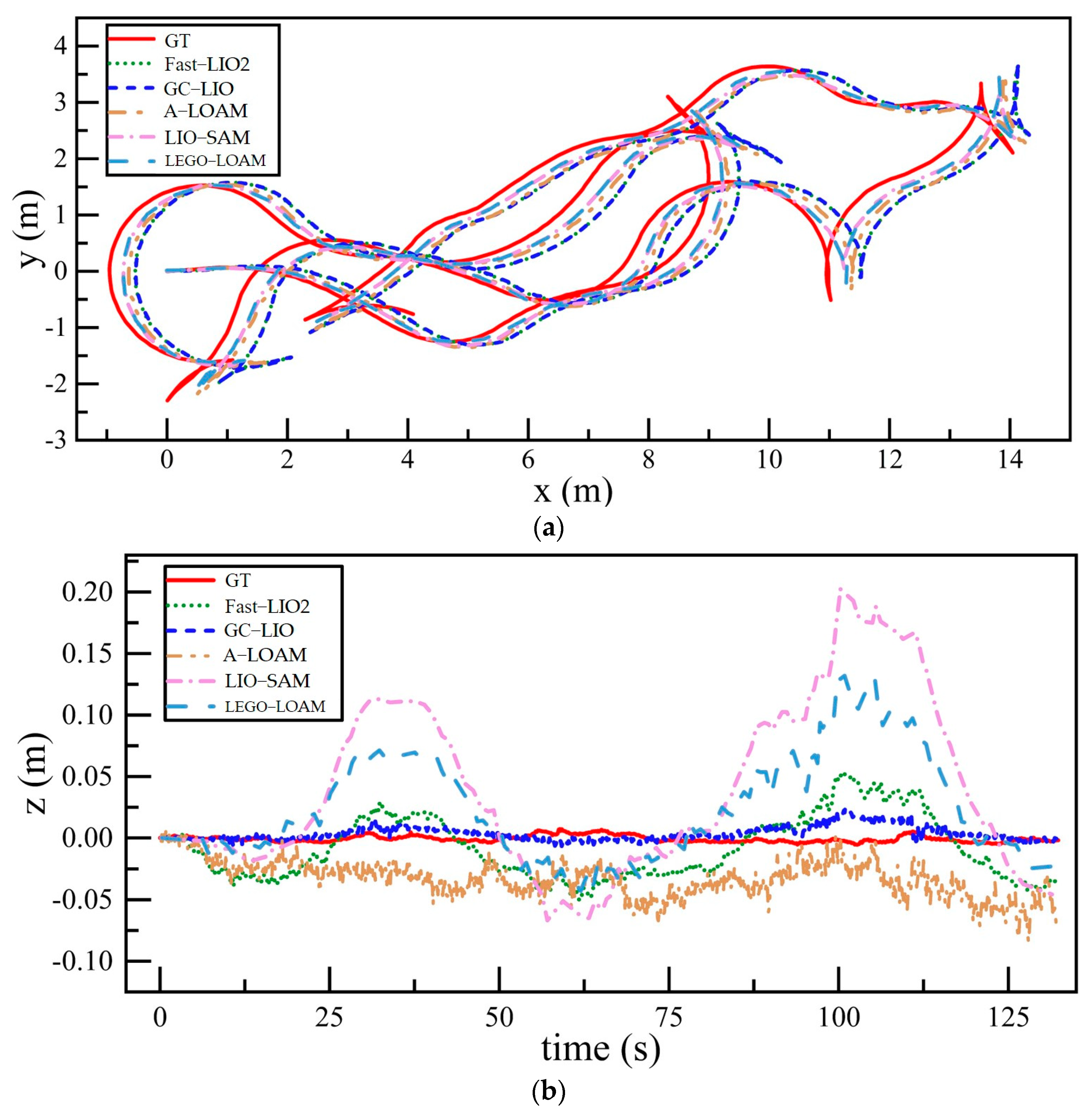
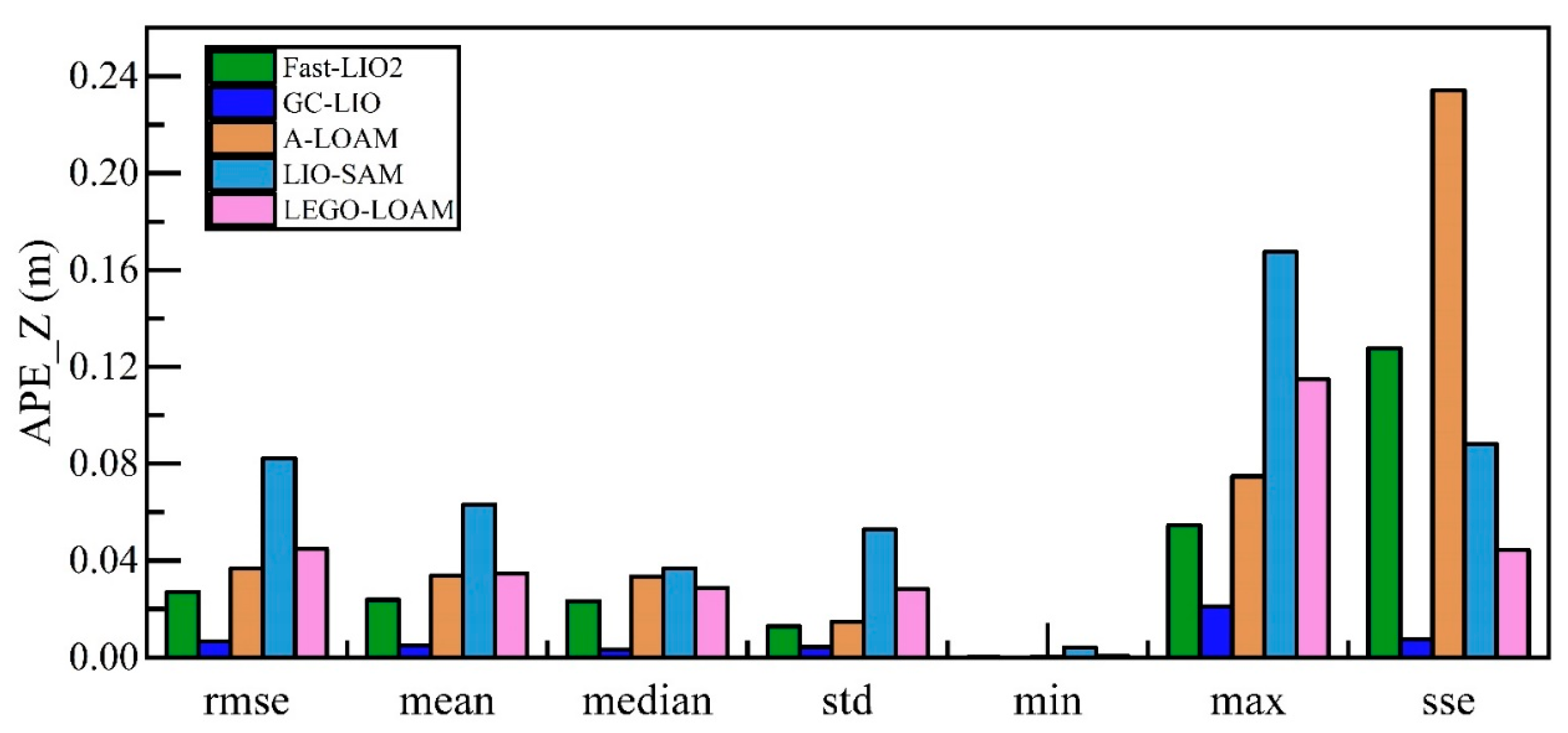
4.3.1. Analysis of Accuracy
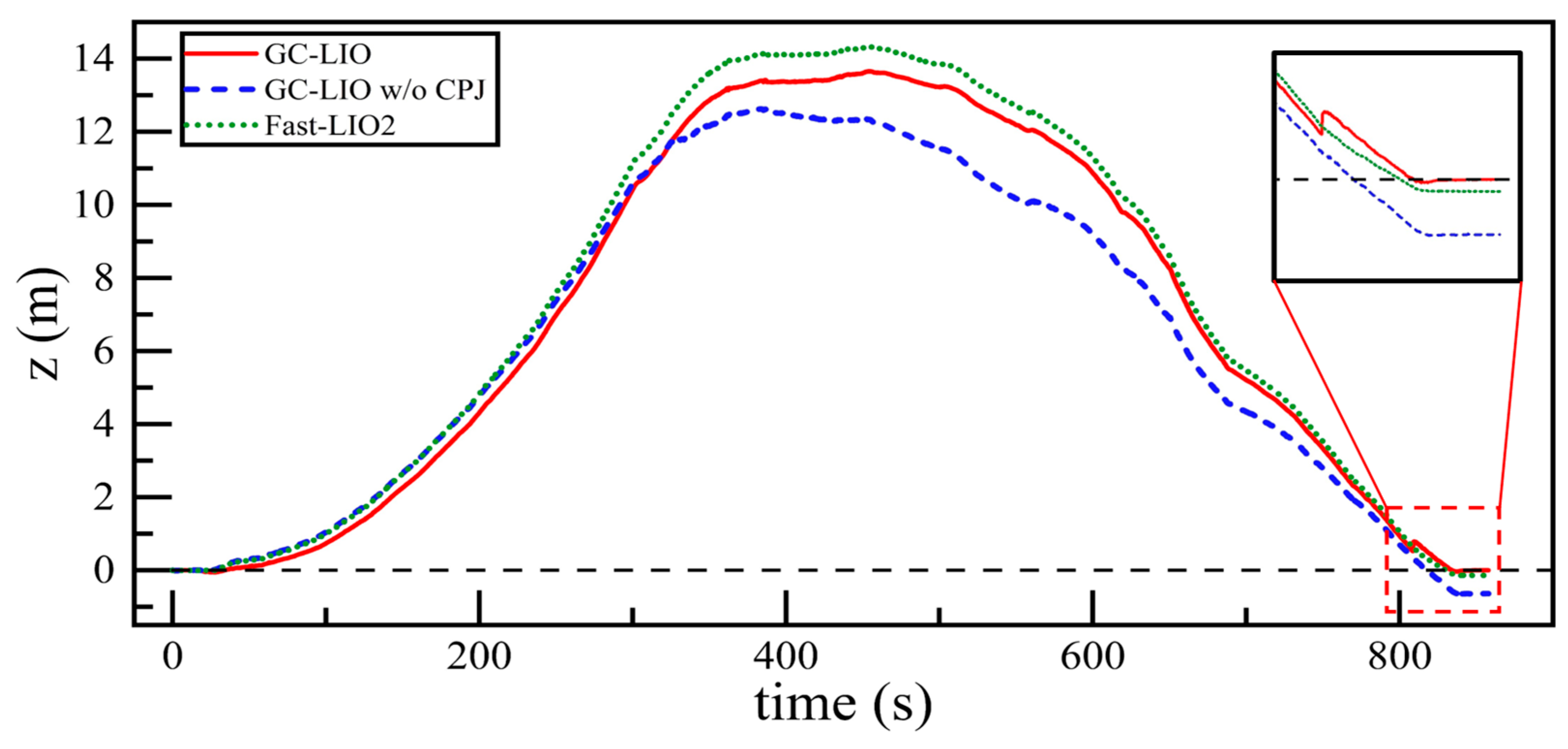
4.3.2. Ablation Experiment
- The complete version of our proposed method (GC-LIO);
- A variant of our method with the coplanarity judgment module disabled (referred to as GC-LIO w/o CPJ);
- The baseline algorithm Fast-LIO2.
5. Conclusions and Future Work
- In scenarios with abrupt ground elevation changes or continuously varying slopes, the current static ground constraint module may experience degraded positioning accuracy due to failure of the local planar assumption.
- The global map consistency optimization capability of the existing algorithm requires further improvement, along with enhanced robustness against dynamic obstacles.
- In addition, it should be noted that hardware selection has a non-negligible influence on the experimental results. The LiDAR sensors used in this work have relatively sparse vertical resolution, which directly affects the strength of vertical geometric constraints and may limit performance in certain environments. While our proposed ground constraint mitigates this weakness, sensors with denser vertical channels could further improve accuracy. Moreover, the IMU precision and synchronization quality also contribute to the overall stability of the system. Regarding field tests, the evaluation scenarios—although representative—mainly feature structured environments with sufficient planar regions. More diverse and unstructured field conditions should be considered in the future to comprehensively assess robustness and generalization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Stilla, U. Toward Building and Civil Infrastructure Reconstruction from Point Clouds: A Review on Data and Key Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2857–2885. [Google Scholar] [CrossRef]
- Kim, P.; Chen, J.; Cho, Y.K. SLAM-Driven Robotic Mapping and Registration of 3D Point Clouds. Autom. Constr. 2018, 89, 38–48. [Google Scholar] [CrossRef]
- Koide, K.; Miura, J.; Menegatti, E. A Portable Three-Dimensional LIDAR-Based System for Long-Term and Wide-Area People Behavior Measurement. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419841532. [Google Scholar] [CrossRef]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Paris, France, 2020; pp. 8899–8906. [Google Scholar]
- Laconte, J.; Deschênes, S.-P.; Labussière, M.; Pomerleau, F. Lidar Measurement Bias Estimation via Return Waveform Modelling in a Context of 3D Mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8100–8106. [Google Scholar]
- Smith, R.C.; Cheeseman, P. On the Representation and Estimation of Spatial Uncertainty. Int. J. Robot. Res. 1986, 5, 56–68. [Google Scholar] [CrossRef]
- Chatila, R.; Laumond, J. Position Referencing and Consistent World Modeling for Mobile Robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 1985; Volume 2, pp. 138–145. [Google Scholar]
- Neira, J.; Tardos, J.D. Data Association in Stochastic Mapping Using the Joint Compatibility Test. IEEE Trans. Robot. Autom. 2001, 17, 890–897. [Google Scholar] [CrossRef]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM: A Factored Solution to the Simultaneous Localization and Mapping Problem. In Proceedings of the AAAI National Conference on Artificial Intelligence, Edmonton, AB, Canada, 28 July–1 August 2002; AAAI Press: Edmonton, AB, Canada, 2002; pp. 593–598. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM 2.0: An Improved Particle Filtering Algorithm for Simultaneous Localization and Mapping That Provably Converges. In IJCAI’03, Proceedings of the 18th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2003. [Google Scholar]
- Lu, F.; Milios, E. Globally Consistent Range Scan Alignment for Environment Mapping. Auton. Robot. 1997, 4, 333–349. [Google Scholar] [CrossRef]
- Gutmann, J.-S.; Konolige, K. Incremental Mapping of Large Cyclic Environments. In Proceedings of the 1999 IEEE International Symposium on Computational Intelligence in Robotics and Automation, Monterey, CA, USA, 8–9 November 1999; CIRA’99 (Cat. No.99EX375). IEEE: Monterey, CA, USA, 1999; pp. 318–325. [Google Scholar]
- Kschischang, F.R.; Loeliger, H.-A. Factor Graphs and the Sum-Product Algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Kretzschmar, H.; Stachniss, C.; Grisetti, G. Efficient Information-Theoretic Graph Pruning for Graph-Based SLAM with Laser Range Finders. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Sunderhauf, N.; Protzel, P. Towards a Robust Back-End for Pose Graph SLAM. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; IEEE: St Paul, MN, USA, 2012; pp. 1254–1261. [Google Scholar]
- Saeedi, S.; Paull, L.; Trentini, M.; Li, H. Multiple Robot Simultaneous Localization and Mapping. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: San Francisco, CA, USA, 2011; pp. 853–858. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems (RSS), University of California, Berkeley, CA, USA, 12–16 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Dubé, R.; Cramariuc, A.; Dugas, D.; Nieto, J.; Siegwart, R.; Cadena, C. SegMap: 3D Segment Mapping Using Data-Driven Descriptors. In Proceedings of the Robotics: Science and Systems XIV; Robotics: Science and Systems Foundation, Pittsburgh, PA, USA, 26–30 June 2018. Paper 3. [Google Scholar] [CrossRef]
- Behley, J.; Stachniss, C. Efficient Surfel-Based SLAM Using 3D Laser Range Data in Urban Environments. In Proceedings of the Robotics: Science and Systems XIV; Robotics: Science and Systems Foundation, Pittsburgh, PA, USA, 26–30 June 2018. Paper 16. [Google Scholar] [CrossRef]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguere, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-Based Semantic SLAM. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), The Venetian Macao, Macau, 3–8 November 2019; IEEE: Macau, China, 2019; pp. 4530–4537. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-Time Loop Closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Stockholm, Sweden, 2016; pp. 1271–1278. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Madrid, Spain, 2018; pp. 4758–4765. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-Coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; IEEE: Las Vegas, NV, USA, 2020; pp. 5135–5142. [Google Scholar]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. LVI-SAM: Tightly-Coupled Lidar-Visual-Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Xi’an, China, 2021; pp. 5692–5698. [Google Scholar]
- Liu, Z.; Zhang, F. BALM: Bundle Adjustment for Lidar Mapping. IEEE Robot. Autom. Lett. 2021, 6, 3184–3191. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. FAST-LIO2: Fast Direct LiDAR-Inertial Odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. R3 LIVE: A Robust, Real-Time, RGB-Colored, LiDAR-Inertial-Visual Tightly-Coupled State Estimation and Mapping Package. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Philadelphia, PA, USA, 23 May 2022; pp. 10672–10678. [Google Scholar]
- Zheng, C.; Xu, W.; Zou, Z.; Hua, T.; Yuan, C.; He, D.; Zhou, B.; Liu, Z.; Lin, J.; Zhu, F.; et al. FAST-LIVO2: Fast, Direct LiDAR–Inertial–Visual Odometry. IEEE Trans. Robot. 2025, 41, 326–346. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Q.; Cheng, K.; Hao, T.; Yang, X. SDV-LOAM: Semi-Direct Visual–LiDAR Odometry and Mapping. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11203–11220. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, L.; Shen, Y.; Zhou, Y. D-LIOM: Tightly-Coupled Direct LiDAR-Inertial Odometry and Mapping. IEEE Trans. Multimed. 2023, 25, 3905–3920. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, C.; Li, C.; Zhang, Y.; Shi, Y.; Zhang, W. A Tightly-Coupled LIDAR-IMU SLAM Method for Quadruped Robots. Meas. Control 2024, 57, 1004–1013. [Google Scholar] [CrossRef]
- Li, Q.; Yu, X.; Queralta, J.P.; Westerlund, T. Robust Multi-Modal Multi-LiDAR-Inertial Odometry and Mapping for Indoor Environments. arXiv 2023, arXiv:2303.02684. [Google Scholar]
- Zhang, H.; Du, L.; Bao, S.; Yuan, J.; Ma, S. LVIO-Fusion:Tightly-Coupled LiDAR-Visual-Inertial Odometry and Mapping in Degenerate Environments. IEEE Robot. Autom. Lett. 2024, 9, 3783–3790. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. R3LIVE++: A Robust, Real-Time, Radiance Reconstruction Package With a Tightly-Coupled LiDAR-Inertial-Visual State Estimator. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 11168–11185. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, Z.; Liu, A.; Shao, K.; Guo, Q.; Wang, C. LVI-Fusion: A Robust Lidar-Visual-Inertial SLAM Scheme. Remote Sens. 2024, 16, 1524. [Google Scholar] [CrossRef]
- Cai, Y.; Ou, Y.; Qin, T. Improving SLAM Techniques with Integrated Multi-Sensor Fusion for 3D Reconstruction. Sensors 2024, 24, 2033. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Li, A.; Li, T.; Yu, W.; Zou, D. M2DGR: A Multi-Sensor and Multi-Scenario SLAM Dataset for Ground Robots. IEEE Robot. Autom. Lett. 2022, 7, 2266–2273. [Google Scholar] [CrossRef]
- Lv, J.; Xu, J.; Hu, K.; Liu, Y.; Zuo, X. Targetless Calibration of LiDAR-IMU System Based on Continuous-Time Batch Estimation. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021. [Google Scholar]









| Specifications | Parameters |
|---|---|
| Dimensions | |
| Rotation Rate | 10 Hz |
| Accuracy | |
| Horizontal field of view | |
| Vertical field of view | (+ to −) |
| Vertical angular resolution | |
| Horizontal angular resolution | |
| Measurement range | Up to 100 m |
| Specifications | Parameters |
|---|---|
| Dimensions | |
| Sampling Rate | Up to 1 kHz |
| Accelerometer resolution | 0.001 g |
| Gyroscope resolution | |
| Weight | 78 g |
| Interface | USB, RS-232 |
| Transducers | Model | Key Parameters |
|---|---|---|
| LiDAR | Velodyne VLP-32C | Horizontal Field of View (H-FoV): 360°, Vertical Field of View (V-FoV): −30° to +10°, Rotation Rate: 10 Hz, Max Range: 200 m, Ranging Accuracy: 3 cm, Horizontal Angular Resolution: 0.2° |
| RBG Camera | FLIR Pointgrey CM3-U3-13Y3C-CS | Resolution: 1280 × 1024, H-FoV: 190°, V-FoV: 190°, Frame Rate: 15 Hz |
| GNSS | Ublox M8T | System: GPS/BeiDou, Sampling Rate: 1 Hz |
| Infrared Camera | PLUG 617 | Resolution: 640 × 512, H-FoV: 90.2°, V-FoV: 70.6°, Frame Rate: 25 Hz |
| VI Sensor | Realsense d435i | RGB/Depth Resolution: 640 × 480, H-FoV: 69°, V-FoV: 42.5°, Frame Rate: 15 Hz, IMU: 6-axis, 200 Hz |
| Event Camera | Inivation DVXplorer | Resolution: 640 × 480, Frame Rate: 15 Hz |
| IMU | Handsfree A9 | Axes: 9-axis, Sampling Rate: 150 Hz |
| GNSS-IMU | Xsens Mti 680 G | GNSS-RTK, Localization Precision: 2 cm, Sampling Rate: 100 Hz, IMU: 9-axis, 100 Hz |
| Laser Scanner | Leica MS60 | Localization Precision: 1 mm + 1.5 ppm |
| Motion-capture System | Vicon Vero 2.2 | Localization Accuracy: 1 mm, Sampling Rate: 50 Hz |
| Algorithm | Sequence | ||||
|---|---|---|---|---|---|
| 01 | 02 | 03 | 04 | 05 | |
| Fast-LIO2 | 0.027 | 0.068 | 0.094 | 0.076 | 0.102 |
| GC-LIO | 0.007 | −0.002 | 0.013 | −0.003 | 0.027 |
| Algorithm | Error Type | |||||
|---|---|---|---|---|---|---|
| RMSE | Mean | Median | Min | Max | SSE | |
| Fast-LIO2 | 0.027 | 0.024 | 0.023 | 0.000 | 0.055 | 0.128 |
| A-LOAM | 0.036 | 0.034 | 0.033 | 0.000 | 0.075 | 0.234 |
| LIO-SAM | 0.082 | 0.063 | 0.037 | 0.004 | 0.167 | 0.088 |
| LEGO-LOAM | 0.045 | 0.035 | 0.029 | 0.001 | 0.115 | 0.044 |
| GC-LIO | 0.007 | 0.005 | 0.003 | 0.000 | 0.021 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Chen, J.; Liang, Y.; Liu, W.; Peng, Y. Enhancing LiDAR–IMU SLAM for Infrastructure Monitoring via Dynamic Coplanarity Constraints and Joint Observation. Sensors 2025, 25, 5330. https://doi.org/10.3390/s25175330
Feng Z, Chen J, Liang Y, Liu W, Peng Y. Enhancing LiDAR–IMU SLAM for Infrastructure Monitoring via Dynamic Coplanarity Constraints and Joint Observation. Sensors. 2025; 25(17):5330. https://doi.org/10.3390/s25175330
Chicago/Turabian StyleFeng, Zhaosheng, Jun Chen, Yaofeng Liang, Wenli Liu, and Yongfeng Peng. 2025. "Enhancing LiDAR–IMU SLAM for Infrastructure Monitoring via Dynamic Coplanarity Constraints and Joint Observation" Sensors 25, no. 17: 5330. https://doi.org/10.3390/s25175330
APA StyleFeng, Z., Chen, J., Liang, Y., Liu, W., & Peng, Y. (2025). Enhancing LiDAR–IMU SLAM for Infrastructure Monitoring via Dynamic Coplanarity Constraints and Joint Observation. Sensors, 25(17), 5330. https://doi.org/10.3390/s25175330






