An Integrated Quasi-Zero-Stiffness Mechanism with Arrayed Piezoelectric Cantilevers for Low-Frequency Vibration Isolation and Broadband Energy Harvesting
Abstract
1. Introduction
2. Structure Design and Parameter Optimization
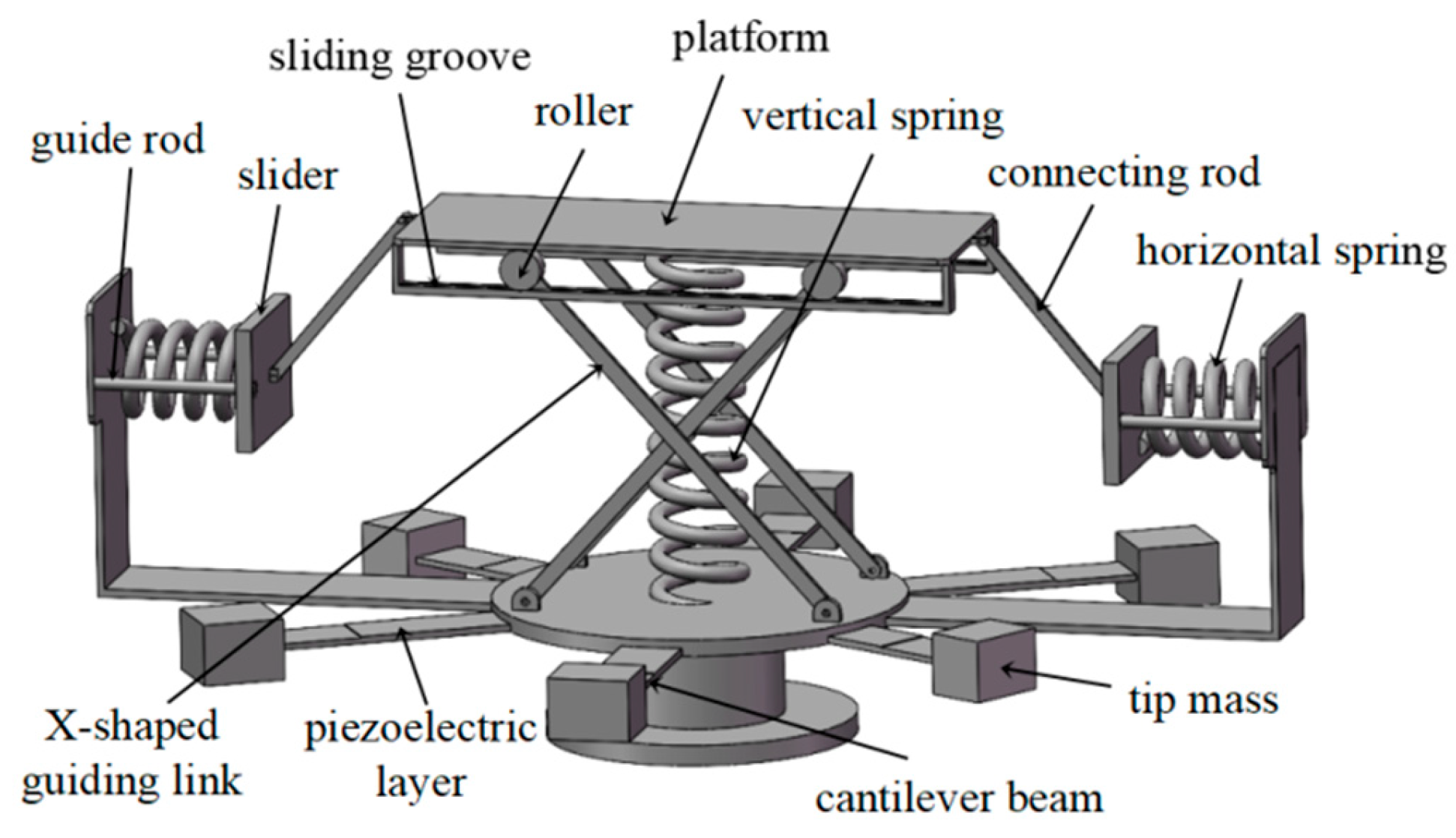
2.1. Conceptual Design
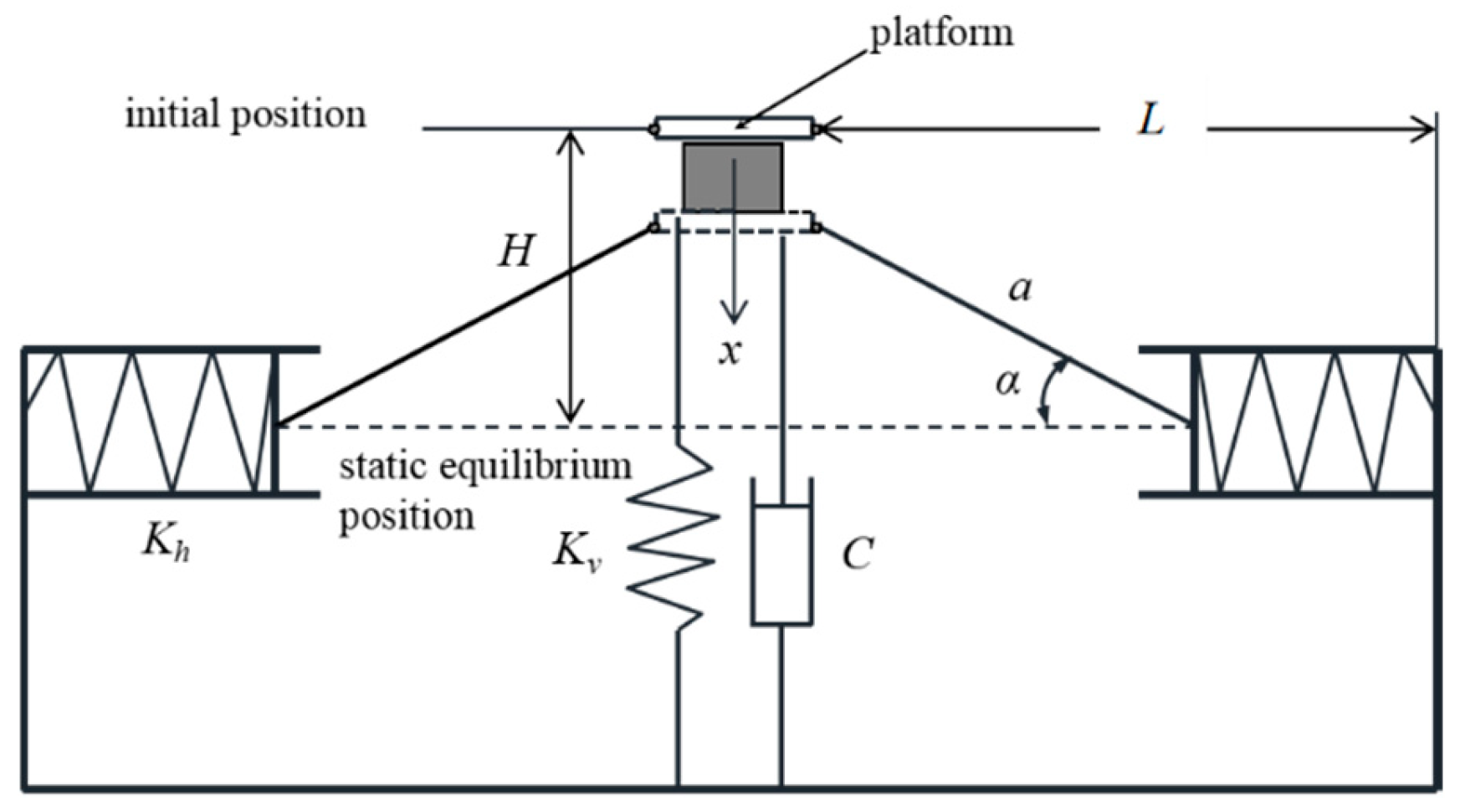
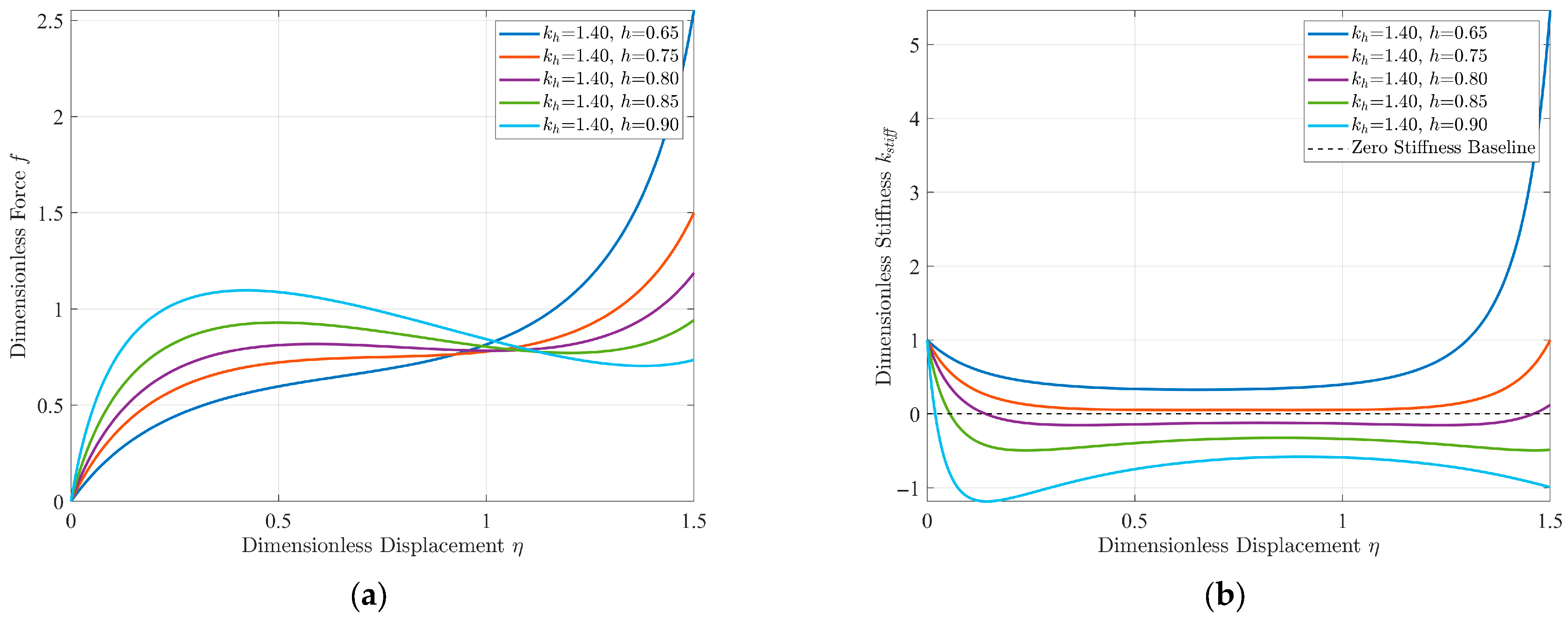
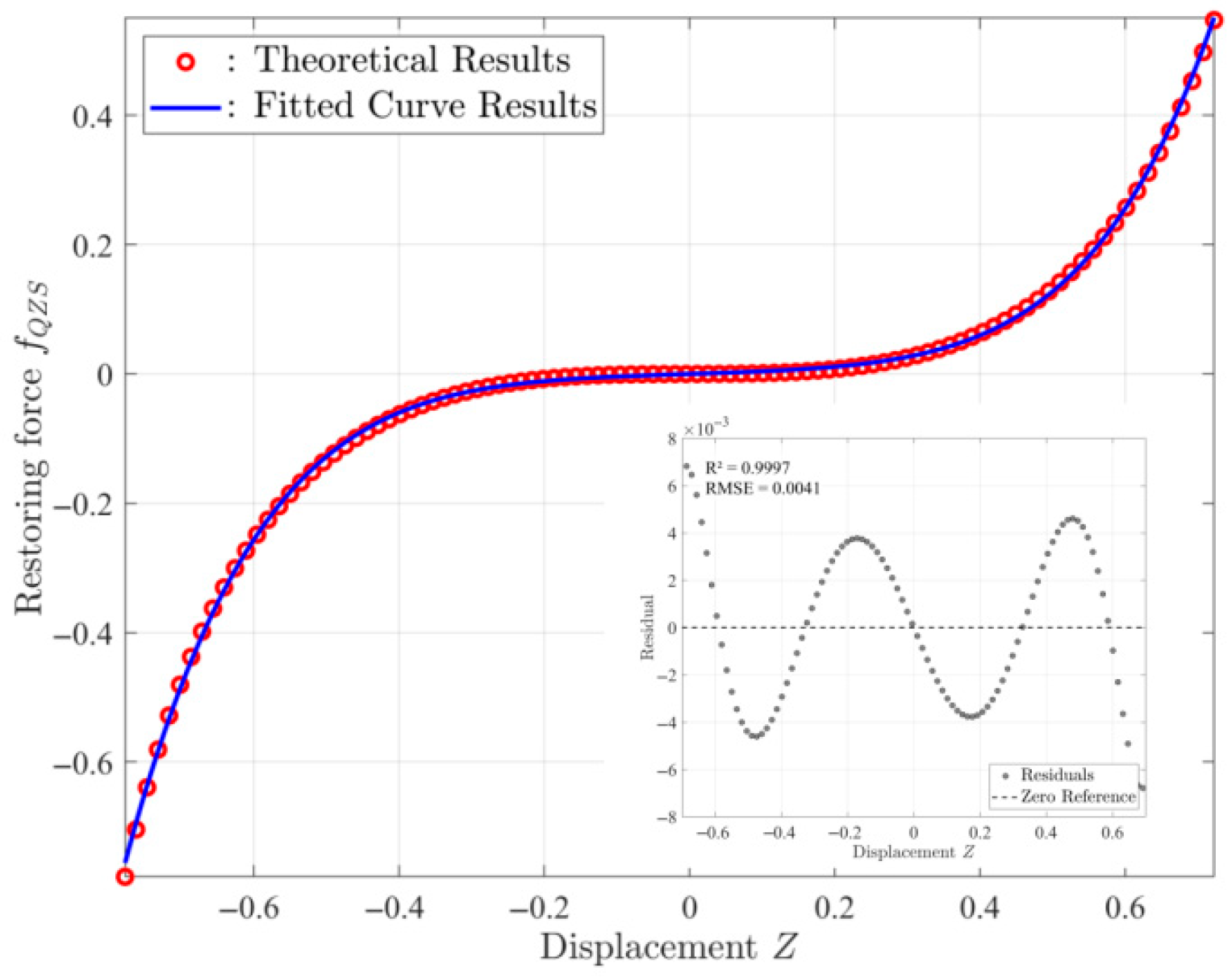
2.2. Stiffness Analysis of QZS Structure
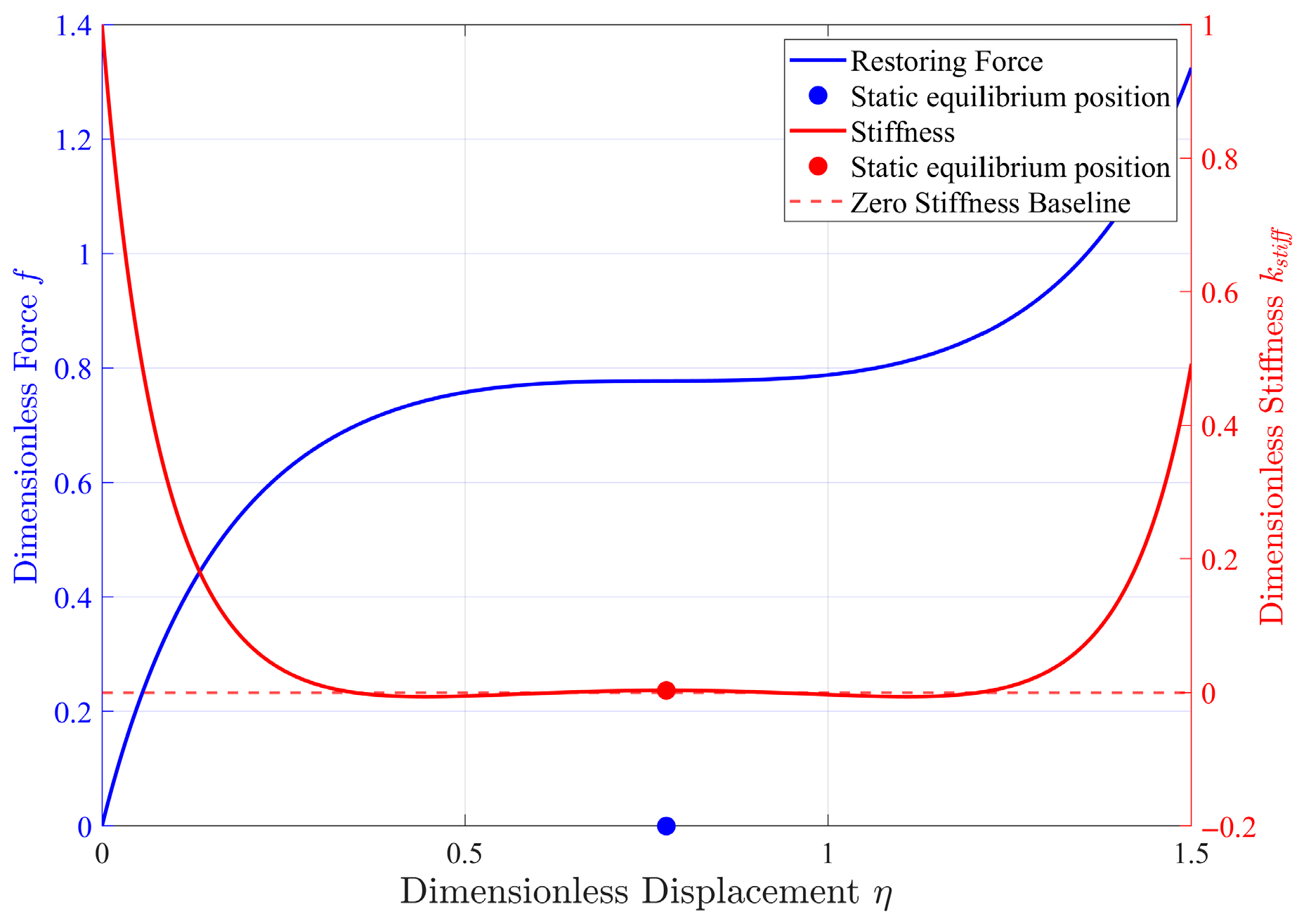
2.3. Multi-Objective Optimization and Optimal Parameter Determination
3. Dynamic Modeling and Analysis
3.1. Dynamic Model
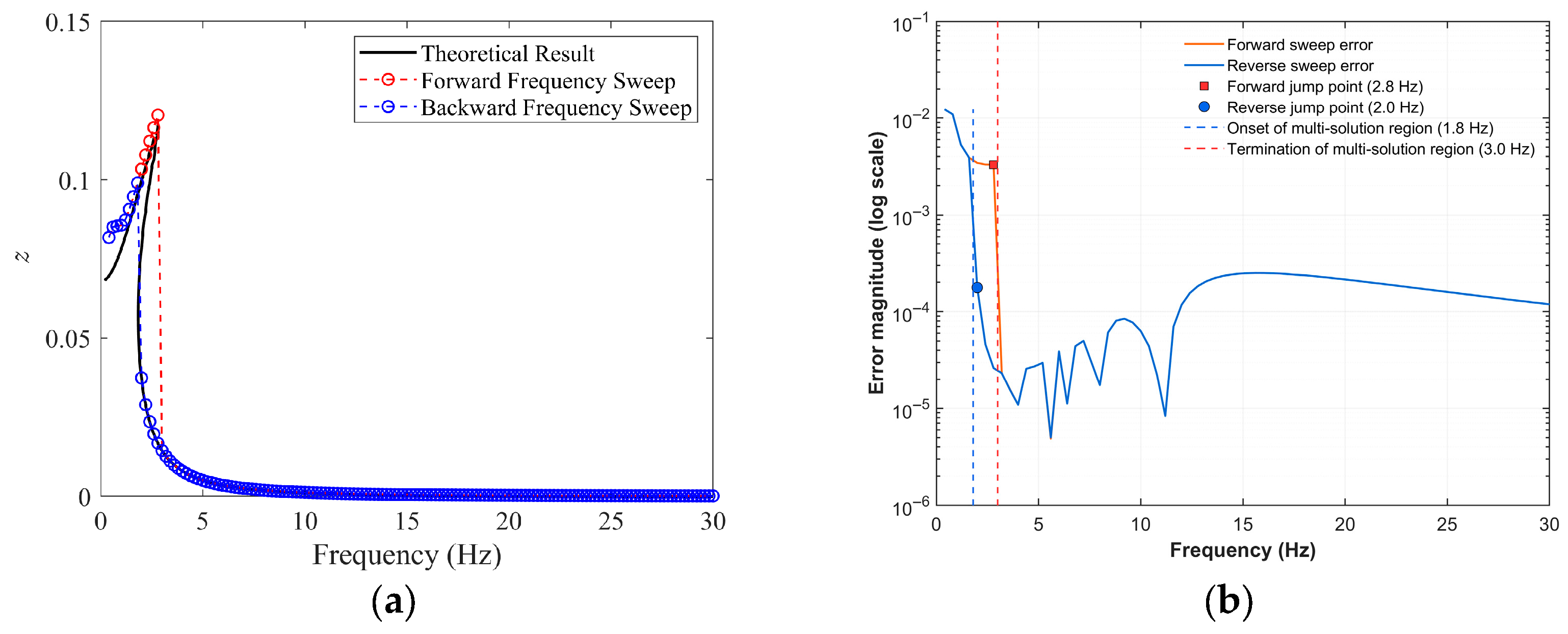
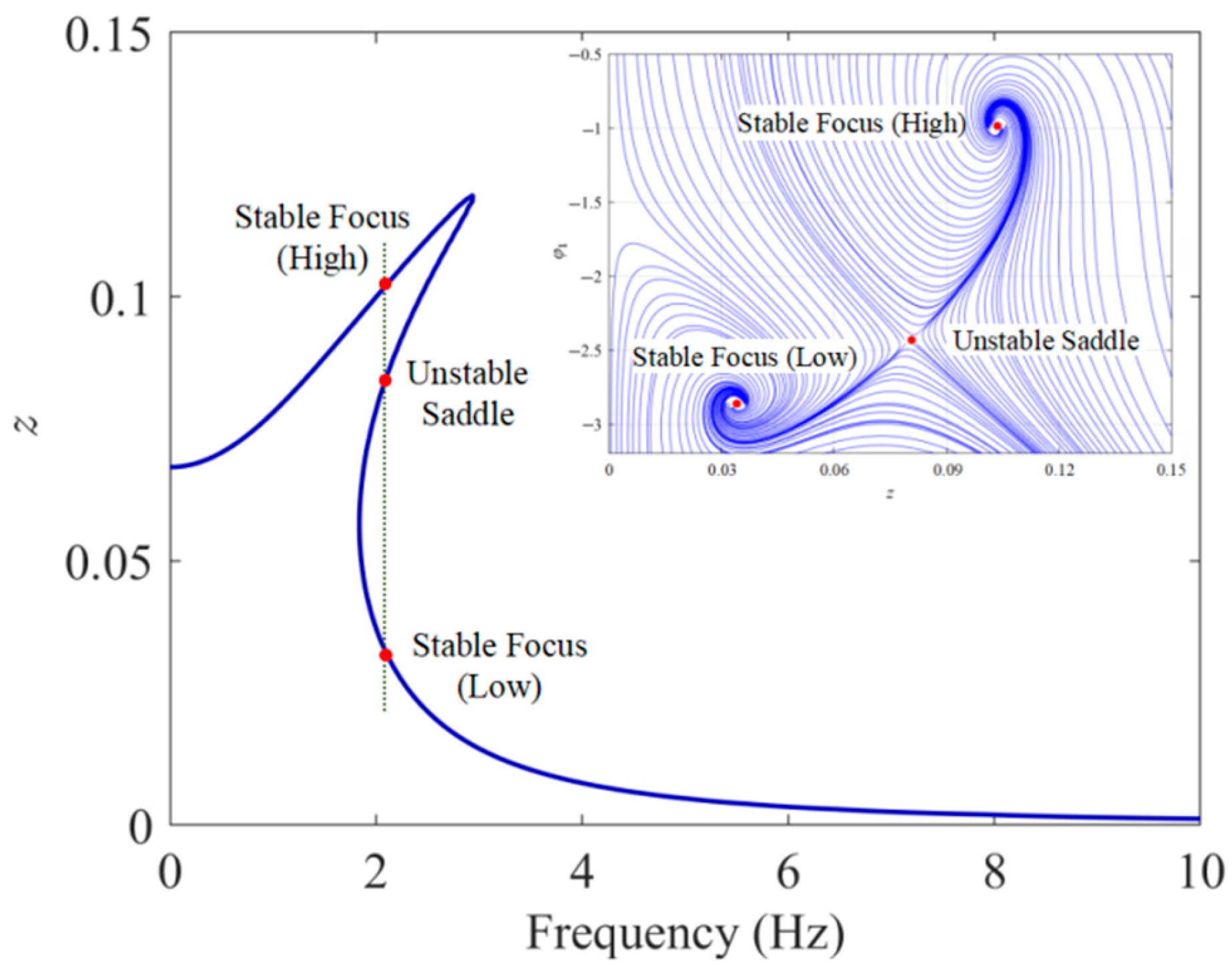
3.2. HBM-Based Solution
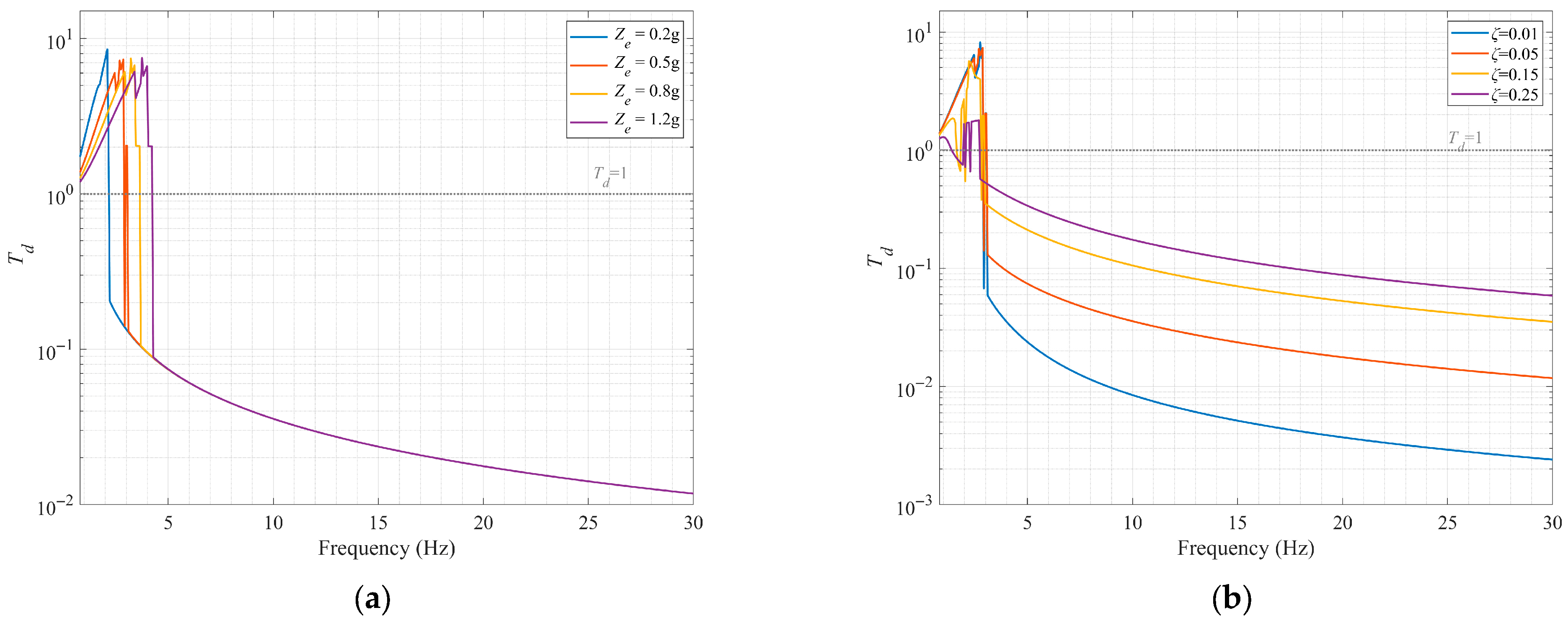
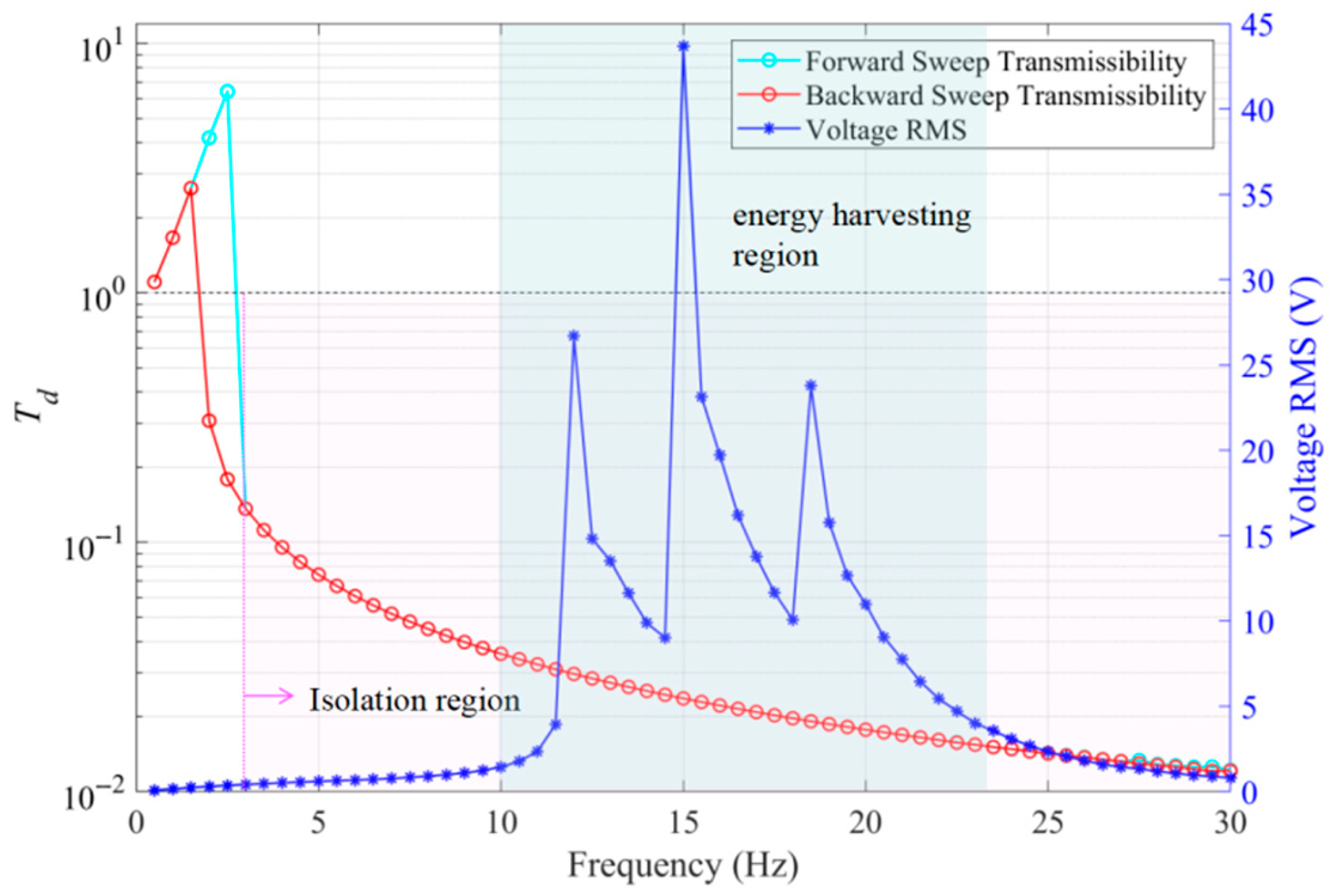
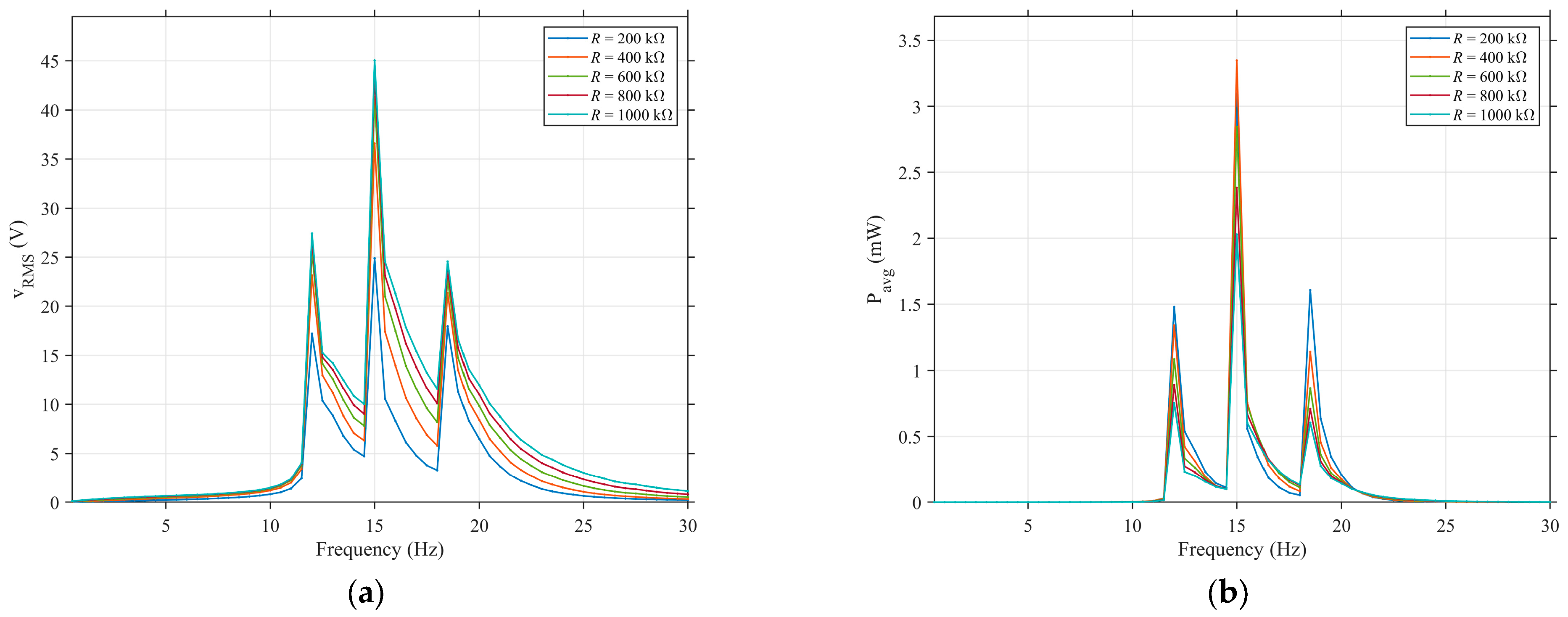
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Zhou, R.; Yang, Q. Recent Advances in Quasi-Zero Stiffness Vibration Isolation Systems: An Overview and Future Possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E.; Thanh, C.L.; Riahi, M.K. Advancements and Emerging Trends in Integrating Machine Learning and Deep Learning for SHM in Mechanical and Civil Engineering: A Comprehensive Review. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 419. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-Low Frequency Vibration Energy Harvesting: Mechanisms, Enhancement Techniques, and Scaling Laws. Energy Convers. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E. Vibration-Based Crack Prediction on a Beam Model Using Hybrid Butterfly Optimization Algorithm with Artificial Neural Network. Front. Struct. Civ. Eng. 2022, 16, 976–989. [Google Scholar] [CrossRef]
- Patil, R.; Joladarashi, S.; Kadoli, R. Bending and Vibration Studies of FG Porous Sandwich Beam with Viscoelastic Boundary Conditions: FE Approach. Mech. Adv. Mater. Struct. 2023, 30, 3588–3607. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.; Waters, T.P.; Lopes, V. Force and Displacement Transmissibility of a Nonlinear Isolator with High-Static-Low-Dynamic-Stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Zhao, F.; Cao, S.; Luo, Q.; Ji, J. Enhanced Design of the Quasi-Zero Stiffness Vibration Isolator with Three Pairs of Oblique Springs: Theory and Experiment. J. Vib. Control. 2022, 29, 2049–2063. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Hua, H. On the Characteristics of a Quasi-Zero Stiffness Isolator Using Euler Buckled Beam as Negative Stiffness Corrector. J. Sound Vib. 2013, 332, 3359–3376. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Song, C.; Gu, H.; Ji, W. Dynamic Characteristics of a Quasi-Zero Stiffness Vibration Isolator with Nonlinear Stiffness and Damping. Arch. Appl. Mech. 2019, 89, 1743–1759. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wu, C. A State-of-the-Art Review on Low-Frequency Nonlinear Vibration Isolation with Electromagnetic Mechanisms. Appl. Math. Mech.-Engl. Ed. 2022, 43, 1045–1062. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C. Dynamic Analysis of the Effects of Self-Weight Induced Structural and Damping Nonlinearity on the Performance of an Origami-Inspired Vibration Isolator. J. Sound Vib. 2023, 547, 117538. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.X.; Wang, S.; Zhao, L.C.; Wu, Z.Y.; Zhang, W.M. Bio-Inspired Toe-Like Structure for Low-Frequency Vibration Isolation. Mech. Syst. Signal Process. 2022, 162, 108010. [Google Scholar] [CrossRef]
- Jiang, G.; Zang, H.; Xiong, Y.; Shen, Y.; Guo, Z.; Yang, Y.; Li, M. Design and Vibration Reduction Performance Analysis of a 6-DOF Nonlinear Vibration Isolation Platform by Employing Bio-Inspired Multi-Joint X-Structure. Nonlinear Dyn. 2025, 113, 21119–21150. [Google Scholar] [CrossRef]
- Nie, X.; Tan, T.; Yan, Z.; Yan, Z.; Wang, L. Revised Method of Multiple Scales for 1:2 Internal Resonance Piezoelectric Vibration Energy Harvester Considering the Coupled Frequency. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107018. [Google Scholar] [CrossRef]
- Harte, P.; Blokhina, E.; Feely, O.; Fournier-Prunaret, D.; Galayko, D. Electrostatic Vibration Energy Harvesters with Linear and Nonlinear Resonators. Int. J. Bifurc. Chaos. 2014, 24, 1430030. [Google Scholar] [CrossRef]
- Foong, F.M.; Thein, C.K.; Yurchenko, D. Important Considerations in Optimising the Structural Aspect of a SDOF Electromagnetic Vibration Energy Harvester. J. Sound Vib. 2020, 482, 115470. [Google Scholar] [CrossRef]
- Tan, D.; Zhou, J.; Wang, K.; Ouyang, H.; Zhao, H. Sliding-Impact Bistable Triboelectric Nanogenerator for Enhancing Energy Harvesting from Low-Frequency Intrawell Oscillation. Mech. Syst. Signal Process. 2023, 184, 109731. [Google Scholar] [CrossRef]
- Mori, K.; Horibe, T.; Ishikawa, S.; Shindo, Y.; Narita, F. Characteristics of Vibration Energy Harvesting Using Giant Magnetostrictive Cantilevers with Resonant Tuning. Smart Mater. Struct. 2015, 24, 125032. [Google Scholar] [CrossRef]
- Kandukuri, T.R.; Liao, C.; Occhipinti, L.G. Modeling and Optimization of Energy Harvesters for Specific Applications Using COMSOL and Equivalent Spring Models. Sensors 2024, 24, 7509. [Google Scholar] [CrossRef]
- Ooi, B.L.; Gilbert, J.M.; Aziz, A.R.A. Analytical and Finite-Element Study of Optimal Strain Distribution in Various Beam Shapes for Energy Harvesting Applications. Acta Mech. Sin. 2016, 32, 670–683. [Google Scholar] [CrossRef]
- Ellouz, H.; Jrad, H.; Wali, M.; Dammak, F. Numerical Modeling of Geometrically Nonlinear Responses of Smart Magneto-Electro-Elastic Functionally Graded Double Curved Shallow Shells Based on Improved FSDT. Comput. Math. Appl. 2023, 151, 271–287. [Google Scholar] [CrossRef]
- Fang, S.; Miao, G.; Chen, K.; Xing, J.; Zhou, S.; Yang, Z.; Liao, W.H. Broadband Energy Harvester for Low-Frequency Rotations Utilizing Centrifugal Softening Piezoelectric Beam Array. Energy 2022, 241, 122833. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Wang, K.; Chang, Y.; Xu, D.; Wen, G. Bio-Inspired Bistable Piezoelectric Vibration Energy Harvester: Design and Experimental Investigation. Energy 2021, 228, 120595. [Google Scholar] [CrossRef]
- Chen, T.T.; Wang, K.; Cheng, L.; Pan, H.B.; Cui, H.C.; Zhou, J.X. Theoretical and Experimental Research on a Quasi-Zero-Stiffness-Enabled Nonlinear Piezoelectric Energy Harvester. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107863. [Google Scholar] [CrossRef]
- Davis, P.B.; McDowell, M.D. Combined Euler Column Vibration Isolation and Energy Harvesting. Smart Mater. Struct. 2017, 26, 055001. [Google Scholar] [CrossRef]
- Mofidian, S.M.; Bardaweel, H. A Dual-Purpose Vibration Isolator Energy Harvester: Experiment and Model. Mech. Syst. Signal Process. 2019, 118, 360–376. [Google Scholar] [CrossRef]
- Diala, U.; Mofidian, S.M.M.; Lang, Z.Q.; Bardaweel, H. Analysis and Optimal Design of a Vibration Isolation System Combined with Electromagnetic Energy Harvester. J. Intell. Mater. Syst. Struct. 2019, 30, 2382–2395. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q.J.; Hao, Z.F. A Novel Nonlinear Mechanical Oscillator and Its Application in Vibration Isolation and Energy Harvesting. Mech. Syst. Signal Process. 2021, 155, 107636. [Google Scholar] [CrossRef]
- Zou, D.L.; Liu, G.Y.; Rao, Z.S.; Tan, T.; Zhang, W.M.; Liao, W.H. A Device Capable of Customizing Nonlinear Forces for Vibration Energy Harvesting, Vibration Isolation, and Nonlinear Energy Sink. Mech. Syst. Signal Process. 2021, 147, 107101. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Wu, D.; Ding, H.; Chen, L.Q. Vibration Isolation and Energy Harvesting Integrated in a Stewart Platform with High Static and Low Dynamic Stiffness. Appl. Math. Model. 2021, 89, 249–267. [Google Scholar] [CrossRef]
- Cao, D.X.; Guo, X.Y.; Hu, W.H. A Novel Low-Frequency Broadband Piezoelectric Energy Harvester Combined with a Negative Stiffness Vibration Isolator. J. Intell. Mater. Syst. Struct. 2019, 30, 1105–1114. [Google Scholar] [CrossRef]
- Liu, C.R.; Zhao, R.; Yu, K.P.; Lee, H.P.; Liao, B.P. A Quasi-Zero-Stiffness Device Capable of Vibration Isolation and Energy Harvesting Using Piezoelectric Buckled Beams. Energy 2021, 233, 121146. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhao, L.; Ding, H.; Chen, L.Q. A Dual-Functional Metamaterial for Integrated Vibration Isolation and Energy Harvesting. J. Sound Vib. 2021, 509, 116251. [Google Scholar] [CrossRef]
- Li, Y.; Baker, E.; Reissman, T.; Sun, C.; Liu, W.K. Design of Mechanical Metamaterials for Simultaneous Vibration Isolation and Energy Harvesting. Appl. Phys. Lett. 2017, 111, 251903. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Lin, Q.; Xu, D.; Wen, G. A Compact Quasi-Zero-Stiffness Device for Vibration Suppression and Energy Harvesting. Int. J. Mech. Sci. 2023, 250, 108284. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, R.; Yu, K.; Lee, H.P.; Liao, B. Simultaneous Energy Harvesting and Vibration Isolation via Quasi-Zero-Stiffness Support and Radially Distributed Piezoelectric Cantilever Beams. Appl. Math. Model. 2021, 100, 152–169. [Google Scholar] [CrossRef]
- Banerjee, P.; Dalela, S.; Balaji, P.S.; Murugan, S.; Kumaraswamidhas, L.A. Simultaneous Vibration Isolation and Energy Harvesting Using Quasi-Zero-Stiffness-Based Metastructure. Acta Mech. 2023, 234, 3337–3359. [Google Scholar] [CrossRef]
- Tuo, J.; Zheng, S.S.; Chen, X.; Wang, B.; Qi, W. Design of a Quasi-Zero Stiffness Vibration Isolation and Energy Harvesting Integrated Seat Suspension. J. Vib. Eng. Technol. 2025, 13, 3. [Google Scholar] [CrossRef]
- Fang, S.; Chen, K.; Zhao, B.; Lai, Z.; Zhou, S.; Liao, W.H. Simultaneous Broadband Vibration Isolation and Energy Harvesting at Low Frequencies with Quasi-Zero Stiffness and Nonlinear Monostability. J. Sound Vib. 2023, 553, 29. [Google Scholar] [CrossRef]
- Xing, Z.Y.; Yang, X.D. A Combined Vibration Isolation System Capable of Isolating Large Amplitude Excitation. Nonlinear Dyn. 2024, 112, 2523–2544. [Google Scholar] [CrossRef]
- Liu, T.; Li, A. An Innovative Three-Dimensional QZS Vibration Isolator and Multi-Stage Vibration Isolation Platform Design. Mech. Syst. Signal Process. 2025, 237, 113070. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Magagnini, E.; Brahim, A.O.; Osmani, A.; Khatir, S.; Abualigah, L. Advancing Structural Integrity Prediction with Optimized Neural Network and Vibration Analysis. J. Struct. Integr. Maint. 2024, 9, 2390258. [Google Scholar] [CrossRef]
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E.; Cuong-Le, T. Enhancing Damage Detection Using Reptile Search Algorithm-Optimized Neural Network and Frequency Response Function. J. Vib. Eng. Technol. 2025, 13, 88. [Google Scholar] [CrossRef]
- Kim, J.E. On the Equivalent Mass-Spring Parameters and Assumed Mode Cantilevered Beam with Mass. J. Mech. Sci. Technol. 2017, 31, 1073–1078. [Google Scholar] [CrossRef]




| Symbol | Meaning | Value |
|---|---|---|
| m | Mass of the payload (including the platform) | 50 kg |
| a | Length of the linkage | 0.15 m |
| L | Distance between the payload and the constraint surfaces on both sides | 0.194 m |
| H | Distance from the loading platform to the static equilibrium position under no-load condition | 0.1166 m |
| Kv | Stiffness of the vertical spring | 24,525 N/m |
| Lh0 | Original length of the horizontal spring | 0.1 m |
| Kh | Stiffness of the horizontal spring | 32,947 N/m |
| ζ | Damping ratio | 0.05 |
| G | Number of parallel piezoelectric oscillator groups | 3 |
| ng | Number of piezoelectric oscillators per group | 2 |
| ρ | Density of the cantilever beam substrate | 7850 kg/m3 |
 | Elastic stiffness coefficient of the substrate | 37 GPa |
| Lb1,2,3 | Length of the cantilever beam | 0.1 m, 0.11 m, 0.12 m |
| mt1,2,3 | Tip mass of the beam | 0.08 kg, 0.12 kg, 0.13 kg |
| Lp1,2,3 | Length of the piezoelectric layer | 0.06 m, 0.07 m, 0.08 m |
| b | Width of the beam and piezoelectric layer | 0.02 m |
| hb | Thickness of the cantilever beam | 0.003 m |
| hp | Thickness of the piezoelectric layer | 0.0005 m |
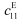 | Stiffness of the piezoelectric layer under zero electric field | 1.26 × 1011 Pa |
| e31 | Piezoelectric coefficient | −5.2 C/m2 |
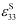 | Dielectric constant | 3.0 × 10−8 F/m |
| Θ1,2,3 | Electromechanical coupling coefficient | −0.000900 C/m, −0.000945 C/m, −0.000980 C/m |
| Cp1,2,3 | Piezoelectric capacitance | 7.2 × 10−9 F, 8.4 × 10−9 F, 9.6 × 10−9 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Sun, A.; He, J. An Integrated Quasi-Zero-Stiffness Mechanism with Arrayed Piezoelectric Cantilevers for Low-Frequency Vibration Isolation and Broadband Energy Harvesting. Sensors 2025, 25, 5180. https://doi.org/10.3390/s25165180
Guo K, Sun A, He J. An Integrated Quasi-Zero-Stiffness Mechanism with Arrayed Piezoelectric Cantilevers for Low-Frequency Vibration Isolation and Broadband Energy Harvesting. Sensors. 2025; 25(16):5180. https://doi.org/10.3390/s25165180
Chicago/Turabian StyleGuo, Kangkang, Anjie Sun, and Junhai He. 2025. "An Integrated Quasi-Zero-Stiffness Mechanism with Arrayed Piezoelectric Cantilevers for Low-Frequency Vibration Isolation and Broadband Energy Harvesting" Sensors 25, no. 16: 5180. https://doi.org/10.3390/s25165180
APA StyleGuo, K., Sun, A., & He, J. (2025). An Integrated Quasi-Zero-Stiffness Mechanism with Arrayed Piezoelectric Cantilevers for Low-Frequency Vibration Isolation and Broadband Energy Harvesting. Sensors, 25(16), 5180. https://doi.org/10.3390/s25165180







