Threat Assessment of Buried Objects Using Single-Frequency Microwave Measurements
Abstract
1. Introduction
2. Background and Related Work
3. Materials and Methods
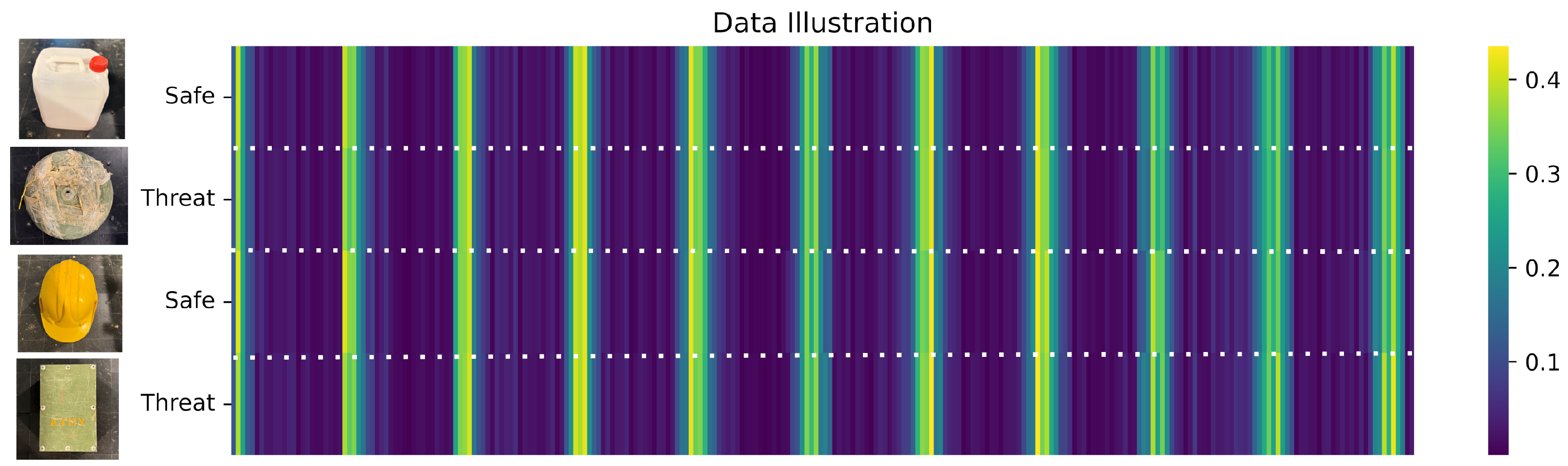
3.1. Data Gathering
3.2. Model and Experiments
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| DL | Deep Learning |
| LOOCV | Leave-One-Out Cross-Validation |
| ML | Machine Learning |
| RELU | Rectified Linear Unit |
| GPR | Ground Penetrating Radar |
References
- Mandal, J.; Goel, M.D.; Agarwal, A.K. Surface and buried explosions: An explorative review with recent advances. Arch. Comput. Methods Eng. 2021, 28, 4815–4835. [Google Scholar] [CrossRef]
- Srimuk, P.; Boonpoonga, A.; Kaemarungsi, K.; Athikulwongse, K.; Dentri, S. Implementation of and experimentation with ground-penetrating radar for real-time automatic detection of buried improvised explosive devices. Sensors 2022, 22, 8710. [Google Scholar] [CrossRef]
- Rafaels, K.A.; Gillich, P.J.; Ehlers, R.Z.; Duvall, P.S. Lower leg injuries in dismounted military personnel from buried explosives. In Proceedings of the IRCOBI Conference, Gothenburg, Sweden, 11–13 September 2013. [Google Scholar]
- Kislov, M.A.; Chauhan, M.; Krupin, K.N.; Kildyushov, E.M.; Zotkin, D.A. Forensic pathological characteristics of explosion trauma in confined space terrorist mass fatalities classified with a 3-dimensional model. Leg. Med. 2022, 58, 102090. [Google Scholar] [CrossRef]
- Pastorino, M. Microwave Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Doğu, S.; Akıncı, M.N.; Çayören, M.; Akduman, İ. Truncated singular value decomposition for through-the-wall microwave imaging application. IET Microwaves Antennas Propag. 2020, 14, 260–267. [Google Scholar] [CrossRef]
- Akıncı, M.N. An efficient sampling method for cross-borehole GPR imaging. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1857–1861. [Google Scholar] [CrossRef]
- Zhang, X.; Tortel, H.; Ruy, S.; Litman, A. Microwave imaging of soil water diffusion using the linear sampling method. IEEE Geosci. Remote Sens. Lett. 2011, 8, 421–425. [Google Scholar] [CrossRef]
- Counts, T.; Gurbuz, A.C.; Scott, W.R.; McClellan, J.H.; Kim, K. Multistatic ground-penetrating radar experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Paul, S.; Akhtar, M.J. A novel piecewise Riccati-based SAR microwave imaging technique for the detection of objects inside the layered media. IEEE Trans. Instrum. Meas. 2023, 72, 8002710. [Google Scholar] [CrossRef]
- Meaney, P.M.; Paulsen, K.D.; Hartov, A.; Crane, R.K. An active microwave imaging system for reconstruction of 2-D electrical property distributions. IEEE Trans. Biomed. Eng. 1995, 42, 1017–1026. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.S.; Schiessl, A.; Gumbmann, F.; Tiebout, M.; Methfessel, S.; Schmidt, L.-P. Advanced microwave imaging. IEEE Microw. Mag. 2012, 13, 26–43. [Google Scholar] [CrossRef]
- Mohammed, B.J.; Bialkowski, K.; Mustafa, S.; Abbosh, A. Investigation of noise effect on image quality in microwave head imaging systems. IET Microwaves Antennas Propag. 2015, 9, 200–205. [Google Scholar] [CrossRef]
- Shao, W.; Du, Y. Microwave imaging by deep learning network: Feasibility and training method. IEEE Trans. Antennas Propag. 2020, 68, 5626–5635. [Google Scholar] [CrossRef]
- Zardi, F.; Tosi, L.; Salucci, M.; Massa, A. A physics-driven AI approach for microwave imaging of breast tumors. IEEE Trans. Antennas Propag. 2025, 73, 4661–4676. [Google Scholar] [CrossRef]
- Shah, P.; Moghaddam, M. Super resolution for microwave imaging: A deep learning approach. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 849–850. [Google Scholar]
- Zhang, J.; Sharma, R.; García-Fernández, M.; Álvarez-Narciandi, G.; Abbasi, M.A.B.; Yurduseven, O. Deep learning for sensing matrix prediction in computational microwave imaging with coded-apertures. IEEE Access 2024, 12, 16844–16855. [Google Scholar] [CrossRef]
- Yurt, R.; Torpi, H.; Kizilay, A.; Koziel, S.; Pietrenko-Dabrowska, A.; Mahouti, P. Buried object characterization by data-driven surrogates and regression-enabled hyperbolic signature extraction. Sci. Rep. 2023, 13, 5717. [Google Scholar] [CrossRef]
- Yurt, R.; Torpi, H.; Kizilay, A.; Koziel, S.; Mahouti, P. Variable data structures and customized deep learning surrogates for computationally efficient and reliable characterization of buried objects. Sci. Rep. 2024, 14, 14898. [Google Scholar] [CrossRef] [PubMed]
- Gharamohammadi, A.; Shaker, G.; Crowley, M. Artificial intelligence to detect buried objects. Authorea Prepr. 2023. [Google Scholar] [CrossRef]
- Sezgin, M.; Alpdemir, M.N. Classification of buried objects using deep learning on GPR data. In Proceedings of the 2023 IEEE International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 29 April–1 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 01–05. [Google Scholar]
- Barkataki, N.; Tiru, B.; Sarma, U. A CNN model for predicting size of buried objects from GPR B-Scans. J. Appl. Geophys. 2022, 200, 104620. [Google Scholar] [CrossRef]
- Chiu, C.-C.; Chien, W.; Yu, K.-X.; Chen, P.-H.; Lim, E.H. Electromagnetic imaging for buried conductors using deep convolutional neural networks. Appl. Sci. 2023, 13, 6794. [Google Scholar] [CrossRef]
- Yurt, R.; Torpi, H.; Mahouti, P.; Kizilay, A.; Koziel, S. Buried object characterization using ground penetrating radar assisted by data-driven surrogate-models. IEEE Access 2023, 11, 13309–13323. [Google Scholar] [CrossRef]
- Alshamy, H.M.; Abdul Sadah, J.W.; Saeed, T.R. Recognizing of the A-Scan Image of a Buried Object Using a Deep Network. In Proceedings of the 2nd International Conference on Advances in Engineering Science and Technology (AEST), Babil, Iraq, 24–25 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 752–757. [Google Scholar]
- Chiu, C.-C.; Chien, W.; Li, C.-L.; Chen, P.-H.; Yu, K.-X.; Lim, E.H. Generative Adversarial Network Applied to Electromagnetic Imaging of Buried Objects. Sens. Mater. 2024, 36, 2925–2941. [Google Scholar] [CrossRef]
- Priya, C.N.N.; Ashok, S.D.; Maji, B.; Kumaran, K.S. Deep learning based thermal image processing approach for detection of buried objects and mines. Eng. J. 2021, 25, 61–67. [Google Scholar] [CrossRef]
- Jafuno, D.; Mian, A.; Ginolhac, G.; Stelzenmuller, N. Classification of Buried Objects from Ground Penetrating Radar Images by using Second Order Deep Learning Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 3185–3197. [Google Scholar] [CrossRef]
- Haynes, M.; Moghaddam, M. Vector Green’s Function for S-Parameter Measurements of the Electromagnetic Volume Integral Equation. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1100–1103. [Google Scholar] [CrossRef]
- Akinci, M.N.; Çağlayan, T.; Özgür, S.; Alkaşı, U.; Ahmadzay, H.; Abbak, M.; Çayören, M.; Akduman, İ. Qualitative Microwave Imaging with Scattering Parameters Measurements. IEEE Trans. Microw. Theory Tech. 2015, 63, 2730–2740. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Heaton, J. Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep Learning. Genet. Program. Evolvable Mach. 2018, 19, 305–307. [Google Scholar] [CrossRef]
- Javid, A.M.; Das, S.; Skoglund, M.; Chatterjee, S. A ReLU dense layer to improve the performance of neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2810–2814. [Google Scholar]
- Waoo, A.A.; Soni, B.K. Performance analysis of sigmoid and ReLU activation functions in deep neural network. In Intelligent Systems: Proceedings of SCIS 2021; Springer: Singapore, 2021; pp. 39–52. [Google Scholar]
- Li, H.; Li, J.; Guan, X.; Liang, B.; Lai, Y.; Luo, X. Research on overfitting of deep learning. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS), Macao, China, 13–16 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 78–81. [Google Scholar]
- Garbin, C.; Zhu, X.; Marques, O. Dropout vs. batch normalization: An empirical study of their impact to deep learning. Multimed. Tools Appl. 2020, 79, 12777–12815. [Google Scholar] [CrossRef]





| Validation Type | Accuracy | F1 Score | Recall |
|---|---|---|---|
| Dataset Split | 0.988636364 | 0.923076923 | 0.857142857 |
| LOOCV | 0.998284734 | 0.989473684 | 0.979166667 |
| K-Fold (K = 5) | 0.994572321 | 0.928328401 | 0.865817302 |
| Depth (cm) | Accuracy | F1 Score | Recall |
|---|---|---|---|
| 10 | 1.0 | 1.0 | 1.0 |
| 15 | 0.993562232 | 0.869565217 | 0.833333333 |
| 20 | 0.995708155 | 0.916666667 | 0.916666667 |
| 25 | 0.997854077 | 0.956521739 | 0.916666667 |
| Model | Accuracy | F1 Score | Recall |
|---|---|---|---|
| CNN | 0.9205 | 0.0 | 0.0 |
| DRN | 0.9164 | 0.0 | 0.0 |
| EfficientNet | 0.9013 | 0.0 | 0.0 |
| Proposed Network | 0.998284734 | 0.989473684 | 0.979166667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayat, İ.H.; Yarimay, G.; Doğu, S.; Akduman, İ. Threat Assessment of Buried Objects Using Single-Frequency Microwave Measurements. Sensors 2025, 25, 5132. https://doi.org/10.3390/s25165132
Bayat İH, Yarimay G, Doğu S, Akduman İ. Threat Assessment of Buried Objects Using Single-Frequency Microwave Measurements. Sensors. 2025; 25(16):5132. https://doi.org/10.3390/s25165132
Chicago/Turabian StyleBayat, İbrahim Halil, Gülçin Yarimay, Semih Doğu, and İbrahim Akduman. 2025. "Threat Assessment of Buried Objects Using Single-Frequency Microwave Measurements" Sensors 25, no. 16: 5132. https://doi.org/10.3390/s25165132
APA StyleBayat, İ. H., Yarimay, G., Doğu, S., & Akduman, İ. (2025). Threat Assessment of Buried Objects Using Single-Frequency Microwave Measurements. Sensors, 25(16), 5132. https://doi.org/10.3390/s25165132









