Sensitivity Analysis of Component Parameters in Dual-Channel Time-Domain Correlated UWB Fuze Receivers Under Parametric Deviations
Abstract
1. Introduction

- (1)
- The inability to pinpoint key contributors to performance fluctuations in multi-component circuits.
- (2)
- (3)
- Empirical tolerance allocation mechanisms that trigger excessive utilization of premium-grade components, lacking quantitative cost–performance optimization frameworks.
2. Receiver Modeling Under Parameter Deviations
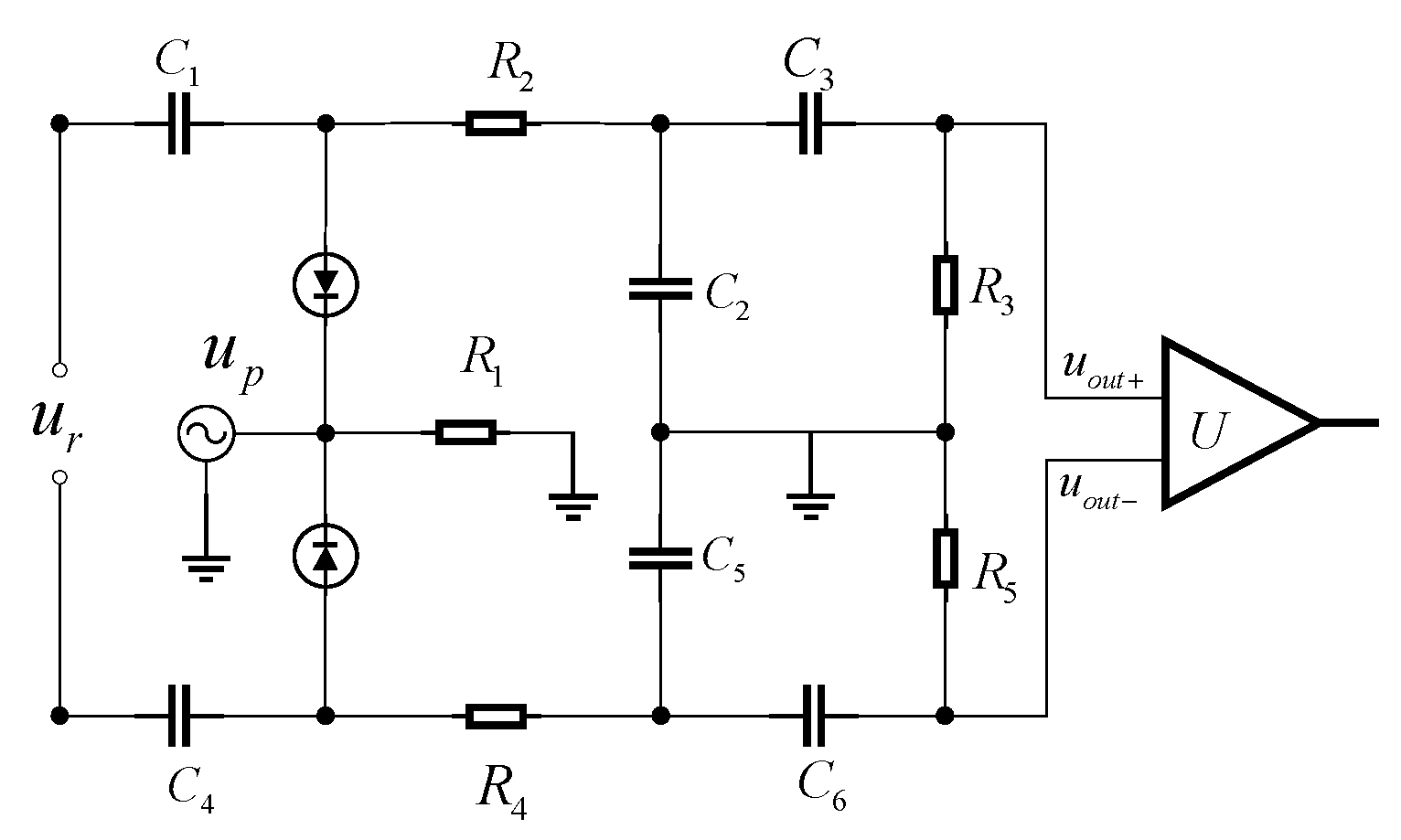
2.1. Operational Framework of Dual-Path Correlated Receiver
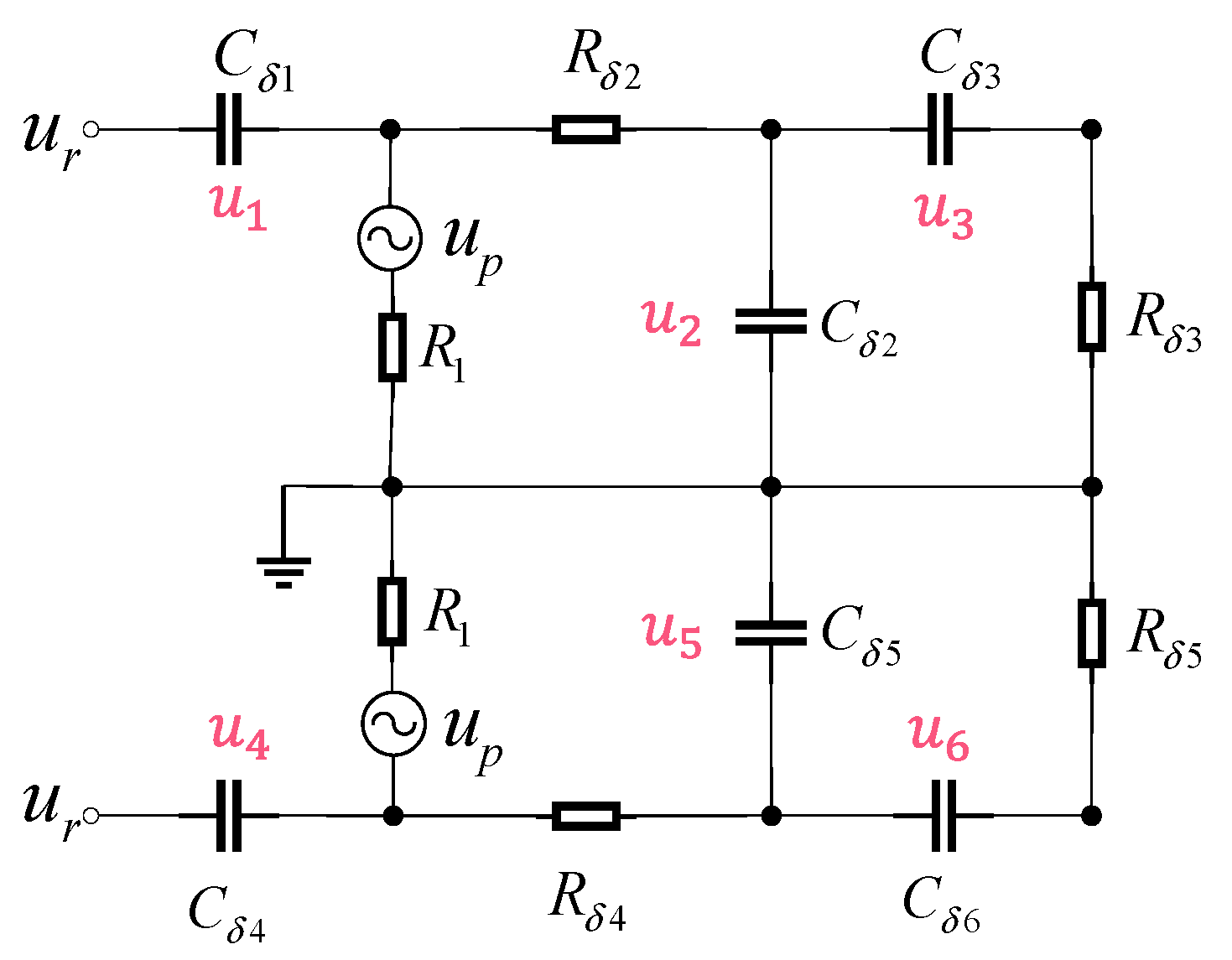
2.2. Receiver Model Based on Tolerance
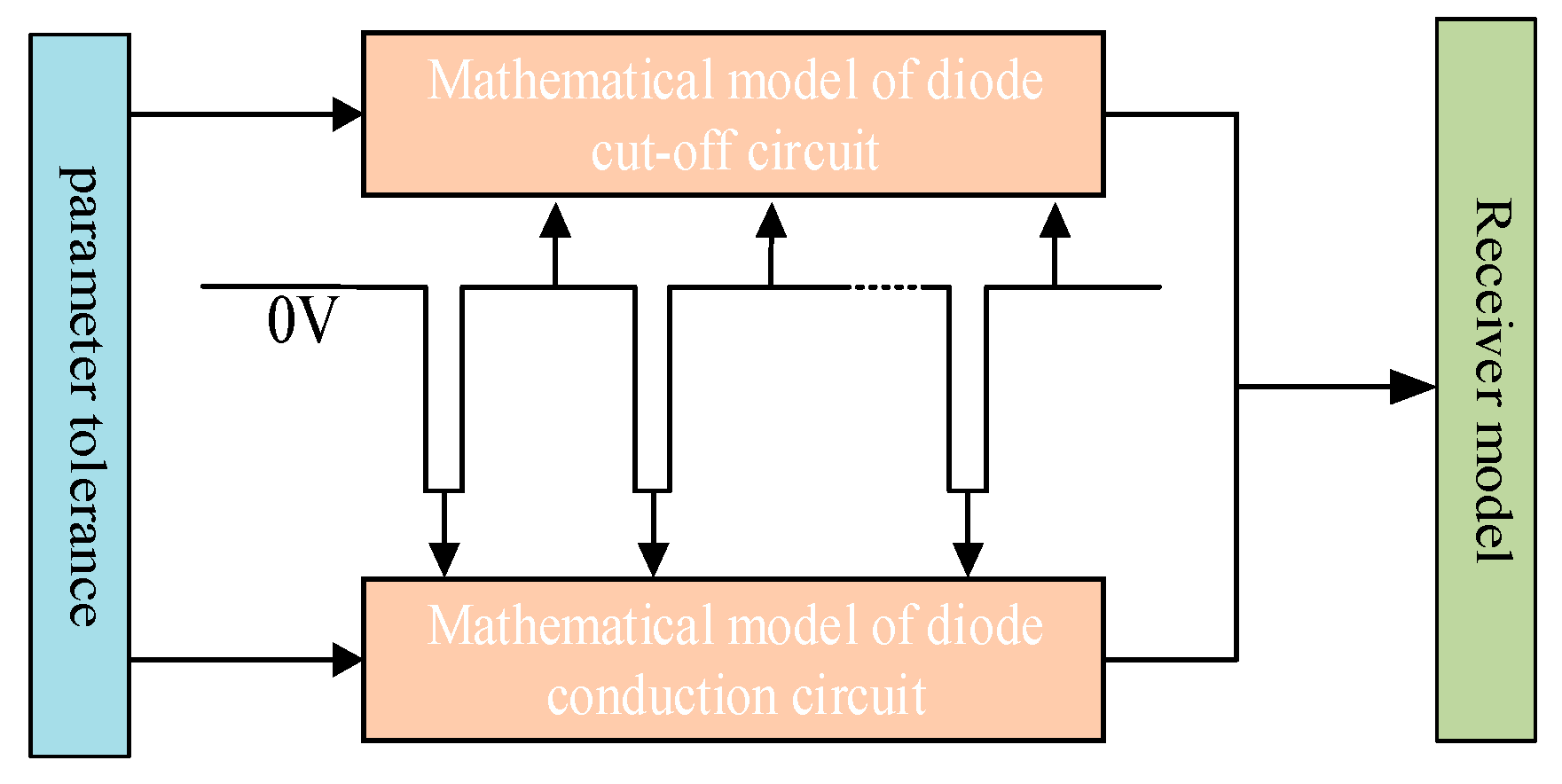
2.2.1. Diode Conduction Mode Under Parameter Deviation
2.2.2. Diode Cutoff Mode Under Parameter Deviation
3. Sensitivity Analysis
- (1)
- Local Sensitivity Analysis (LSA)
- (2)
- Global Sensitivity Analysis (GSA)
3.1. Local Sensitivity Analysis Based on Modified Morris Screening Method
- (a)
- Morris Local Sensitivity Analysis
- (b)
- PDM Local Sensitivity Analysis
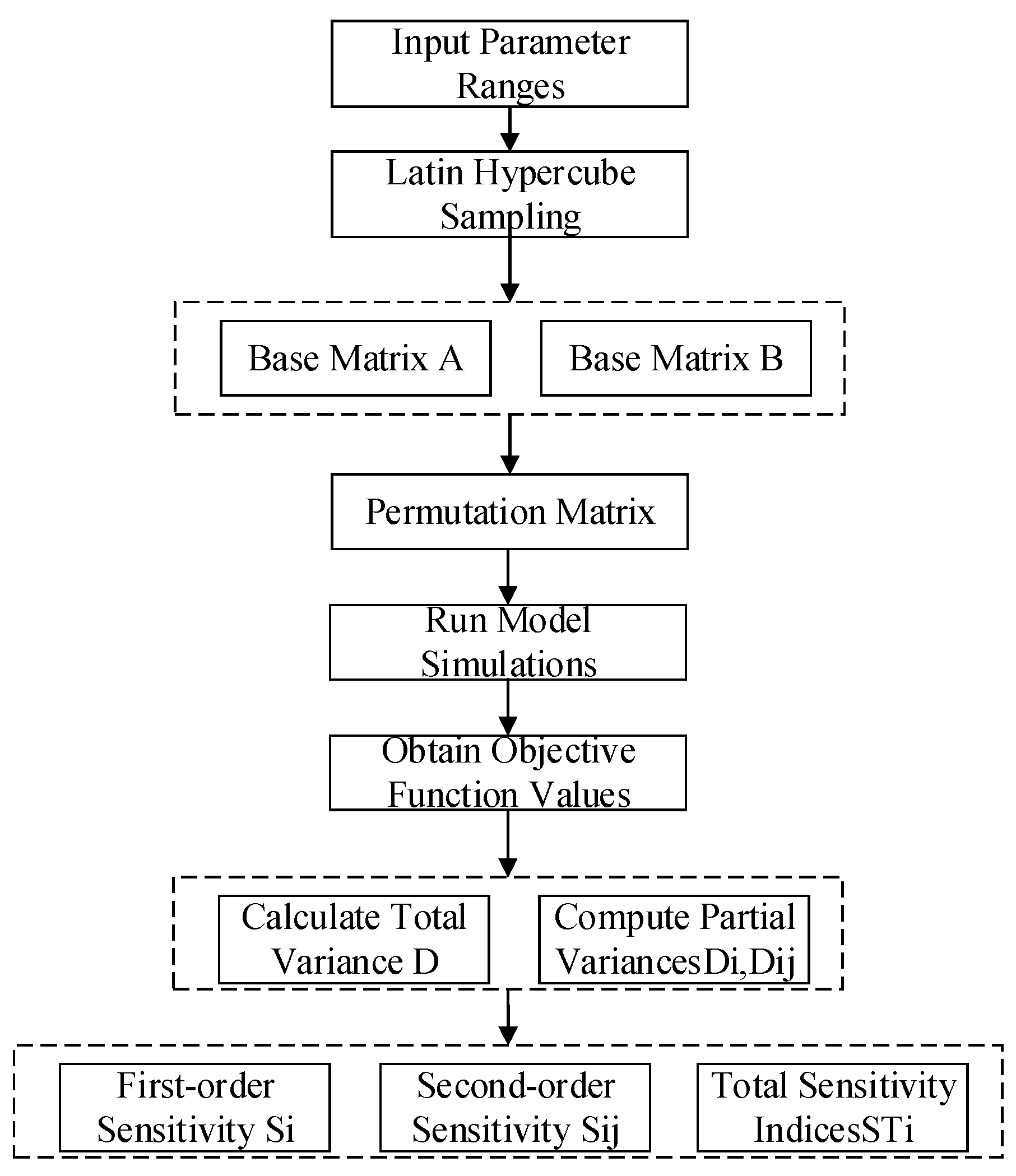
3.2. Global Sensitivity Analysis Based on LHS-Sobol Method
4. Physics-Based Modeling and Hardware Testing
- (a)
- The effect of single-component tolerance variations on receiver output noise.
- (b)
- The collective influence of stochastic multi-parameter variations on output noise performance.
4.1. Effect of Single Component on Circuit Performance
4.2. Impact of Full-Circuit Component Tolerances
4.3. Experimental Hardware Verification
4.4. Comparison of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UWB | Ultra-Wideband |
| SNR | Signal-to-Noise Ratio |
| RF | Radio Frequency |
| MMW | Millimeter-Wave |
| SA | Sensitivity Analysis |
| GSA | Global Sensitivity Analysis |
| LSA | Local Sensitivity Analysis |
| PRCC | Partial Rank Correlation Coefficient |
| PDM | Partial Derivative Method |
| OAT | One-Factor-at-a-Time |
| LHS | Latin Hypercube Sampling |
References
- Cui, Z.Z.; Song, S.H.; Xu, L.X. Principle of Proximity Fuze; Beijing Institute of Technology Press: Beijing, China, 2009. [Google Scholar]
- Dong, E.; Hao, X.; Yan, X.; Yu, H. Research on interference mechanism of swept-frequency jamming to UWB radio fuze. Acta Armamentarii 2023, 44, 1006–1014. [Google Scholar]
- Meng, Q.; Song, Y.; Li, S.Y.; Zhuang, Y. Resilient Tightly Coupled INS/UWB Integration Method for Indoor UAV Navigation under Challenging Scenarios. Def. Technol. 2022, 18, 185–196. [Google Scholar] [CrossRef]
- Wu, K.; Yang, B.; Hao, S.; Liang, Y.; Huang, Z. Modulated Radio Frequency Stealth Waveforms for Ultra-Wideband Radio Fuzes. Entropy 2024, 26, 605. [Google Scholar] [CrossRef]
- Li, M.; Huang, Z.H. Research on Relation between Sampling Pulse Width and Output Signal Amplitude for Ultra-wideband Radio Fuze. Acta Armamentarii 2016, 37, 1989. [Google Scholar]
- Yan, Y.; Cui, Z. Anti-jamming Performance of Ultra Wideband Radio Fuze. Acta Armamentarii 2010, 31, 13–17. [Google Scholar]
- Leon, G.; Koptev, D.S. Evaluation of Influence of the Radio Receiving Devices Heterodynes Functioning Quality on the Quadrature Amplitude Modulation Digital Signals Reception Noise Immunity. IEEE Trans. Wirel. Commun. 2023, 22, 5123–5136. [Google Scholar]
- Zhao, D.; Suo, Y.; Liu, X.; Zhang, D.; Kou, Y. Tolerance Simulation and Optimization Technology for Aircraft Assembly Based on Key Characteristics. In Proceedings of the 2024 IEEE 6th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 24–26 May 2024; pp. 552–556. [Google Scholar]
- Qin, C.; Jin, Y.; Tian, M.; Ju, P.; Zhou, S. Comparative study of global sensitivity analysis and local sensitivity analysis in power system parameter identification. Energies 2023, 16, 5915. [Google Scholar] [CrossRef]
- Zhao, G.; Yin, J.; Wu, L.; Feng, Z. Ultrastable and low-noise self-compensation method for circuit thermal drift of eddy current sensors based on analog multiplier. IEEE Trans. Ind. Electron. 2020, 67, 5150–5160. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Ren, K.; Qian, W.X. Noise analysis of photoelectric detection circuit based on photodiode reverse bias. Infrared Laser Eng. 2016, 45, 1117003. [Google Scholar]
- Im, S.; Park, S.-G. Thermal noise analysis of switched-capacitor integrators with correlated double sampling. Int. J. Circuit Theory Appl. 2016, 44, 1971–1985. [Google Scholar] [CrossRef]
- Han, Y.; Ma, Y.; Ouyang, L.; Wang, J.; Tu, Y. Integrated multiresponse parameter and tolerance design with model parameter uncertainty. Qual. Reliab. Eng. Int. 2020, 36, 414–433. [Google Scholar] [CrossRef]
- Myeong, I.; Kim, J.; Ko, H.; Song, I.; Kim, Y.; Shin, H. A Simple and Accurate Modeling Method of Channel Thermal Noise Using BSIM4 Noise Models. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 4351–4358. [Google Scholar] [CrossRef]
- Hasan, S.M.N.; Irgens, P.; Murphy, T. Role of Worst-Case Operating Scenario and Component Tolerance in Robust Automotive Electronic Control Module Design. SAE Int. J. Adv. Curr. Pract. Mob. 2024, 6, 270–277. [Google Scholar]
- Fan, J.; Li, Z.; Pan, R.; Sun, K.; Chen, K. Volumetric error modeling and prediction for machine tools based on key component tolerance. Alex. Eng. J. 2023, 73, 61–76. [Google Scholar] [CrossRef]
- Vineela, J.; Praneetha, G.; Harshad, R.; Masrunnisa, K.; Kumar, M.P.; Sandeep, T.S. A Complete Analysis of Tolerance of Component in Analog VLSI Circuits Using Sensitivity. Int. J. Hybrid Inf. Technol. 2016, 9, 9–18. [Google Scholar] [CrossRef]
- Manukian, H.; Nayfeh, O.; Kelly, M. Circuit Component Tolerance of Self-Organizing Logic Gates. In Proceedings of the 2024 20th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Volos, Greece, 9–12 July 2024; pp. 1–5. [Google Scholar]
- Quirós, J.C.; Trivio Cabrera, A.; Escolar Illarramendi, J. Fuzzy-logic based frequency control for a wireless charging robust to component tolerance. IEEE Trans. Power Electron. 2023, 38, 10234–10245. [Google Scholar]
- Wang, Q.; Cheng, L.; Cheng, Z.B. Optimized position and orientation evaluation of wing based on tolerance constraints in aircraft assembly. J. Mech. Eng. 2015, 51, 124–134. [Google Scholar] [CrossRef]
- Peng, J.K.; Ru, Y.; Li, Z.Q.; Chen, L.S.; Li, L.F. Geometric tolerance analysis of monolithic nonplanar ring resonators. Chin. J. Lasers 2025, 52, 1–12. [Google Scholar]
- Jing, T.; Tian, X.T. Multi-objective optimization method for aircraft tolerance allocation based on Monte Carlo-adaptive differential evolution algorithm. Acta Aeronaut. Et Astronaut. Sin. 2022, 43, 425278. [Google Scholar]
- Wang, Y.; Zhai, B.; Gao, S.; Guo, Y.; Shen, C.; Chen, Y.; Zheng, Z.; Song, Y. Data-driven parameter calibration of power system EMT model based on Sobol sensitivity analysis and Gaussian mixture model. IEEE Trans. Power Syst. 2024, 40, 1024–1036. [Google Scholar] [CrossRef]
- Ballester-Ripoll, R.; Leonelli, M. Global Sensitivity Analysis of Uncertain Parameters in Bayesian Networks. Int. J. Approx. Reason. 2025, 180, 109368. [Google Scholar] [CrossRef]
- Liu, J.; Shi, Y.; Ding, C.; Beer, M. Efficient Global Sensitivity Analysis Framework and Approach for Structures with Hybrid Uncertainties. Comput. Methods Appl. Mech. Eng. 2025, 436, 117726. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, X.; Li, X.; Yan, X.; Wan, K. Global Sensitivity Analysis on Accuracy of Aviation Fire Control System via DBN Effectiveness Fitting. Acta Armamentarii 2024, 45, 3430–3444. [Google Scholar]
- Zhang, P.; Deng, S.; Hu, X.; Wang, L.; Wang, Z.; Yuan, X.; Cai, L. Detection performance and sensitivity of logging-while-drilling extra-deep azimuthal resistivity measurement. Chin. J. Geophys. 2021, 64, 2210–2219. [Google Scholar]
- Rajabi, R.; Sun, S.; Wu, B.; Khan, J.; Huang, K. Parameter Sensitivity Analysis in Zinc-Ion Batteries: A Study on Ionic Conductivity, Current Density, and Electrode Properties. J. Power Sources 2025, 589, 233–245. [Google Scholar]
- Long, H.; Luo, X.; Liu, J.; Xiang, H. Distribution Features of Deviation and Determination of a Tolerance Method for Prefabricated Concrete Components. Buildings 2023, 13, 1142. [Google Scholar] [CrossRef]
- Kourehpaz, P.; Molina Hutt, C.; Zsarnoczay, A. Impact of Parameter Selection on Seismic Loss and Recovery Time Estimates: A Variance-Based Sensitivity Analysis. Earthq. Spectra 2025, 41, 1713–1737. [Google Scholar] [CrossRef]
- Huang, Z.H.; Li, Y.L. Ultra-Wideband Proximity Detection Theory; Beijing Institute of Technology Press: Beijing, China, 2019. [Google Scholar]
- Neudeck, P.G.; Spry, D.J.; Krasowski, M.J.; Chang, C.W.; Gonzalez, J.M.; Rajgopal, S.; Prokop, N.F.; Greer, L.C.; Lukco, D.; Maldonado-Rivera, S.; et al. Recent Progress in Extreme Environment Durable SiC JFET-R Integrated Circuit Technology. In Proceedings of the 2023 IMAPs International High Temperature Electronics Conference (HiTEC), Albuquerque, NM, USA, 22–25 May 2023. [Google Scholar]
- Wang, Z.; Gao, J.; Tian, P.; Xie, G. Symmetry degradation of differential circuits induced by uneven gold plating of high-speed connectors in extreme environment. Microw. Opt. Technol. Lett. 2020, 62, 3716–3726. [Google Scholar] [CrossRef]
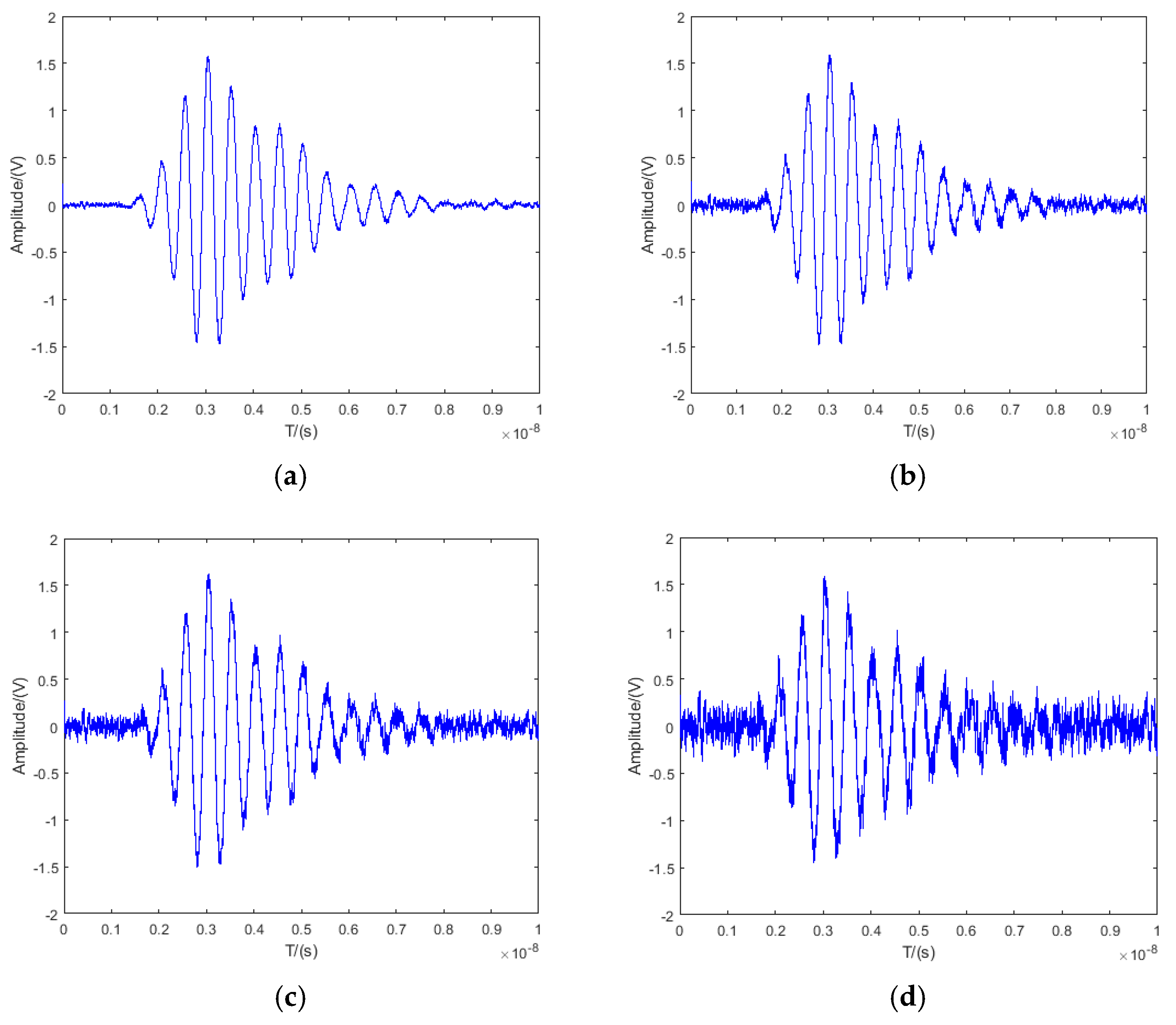



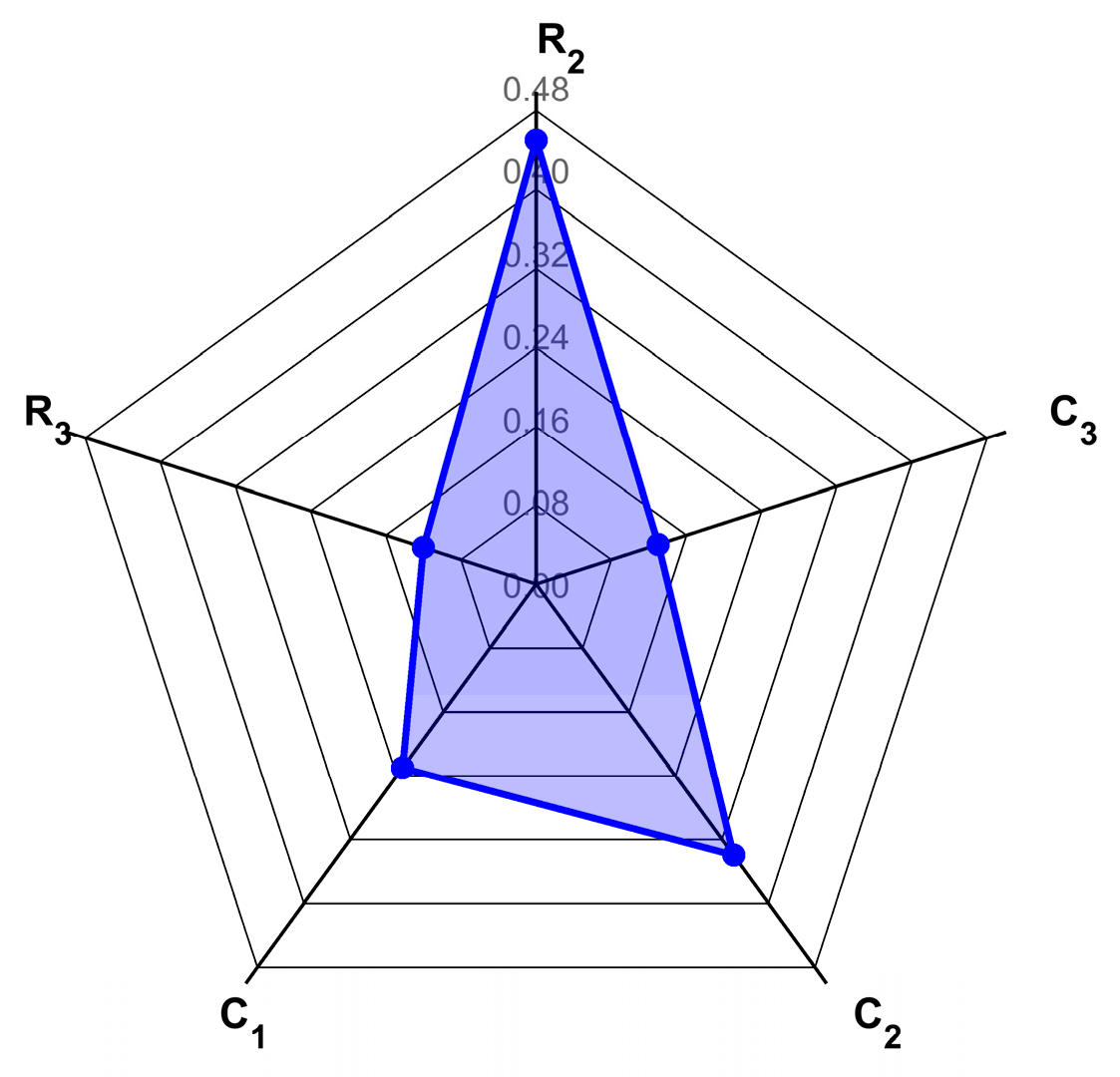
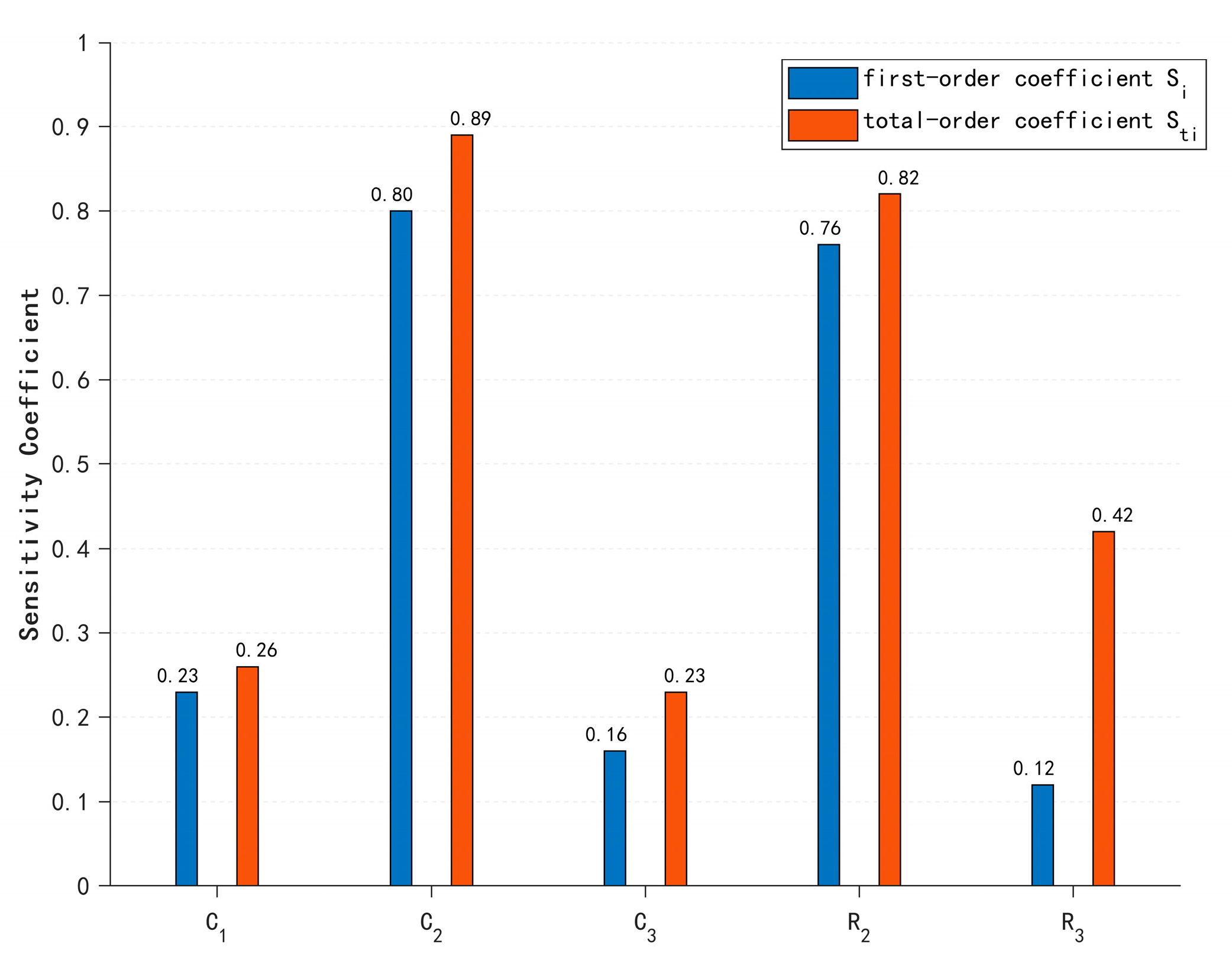
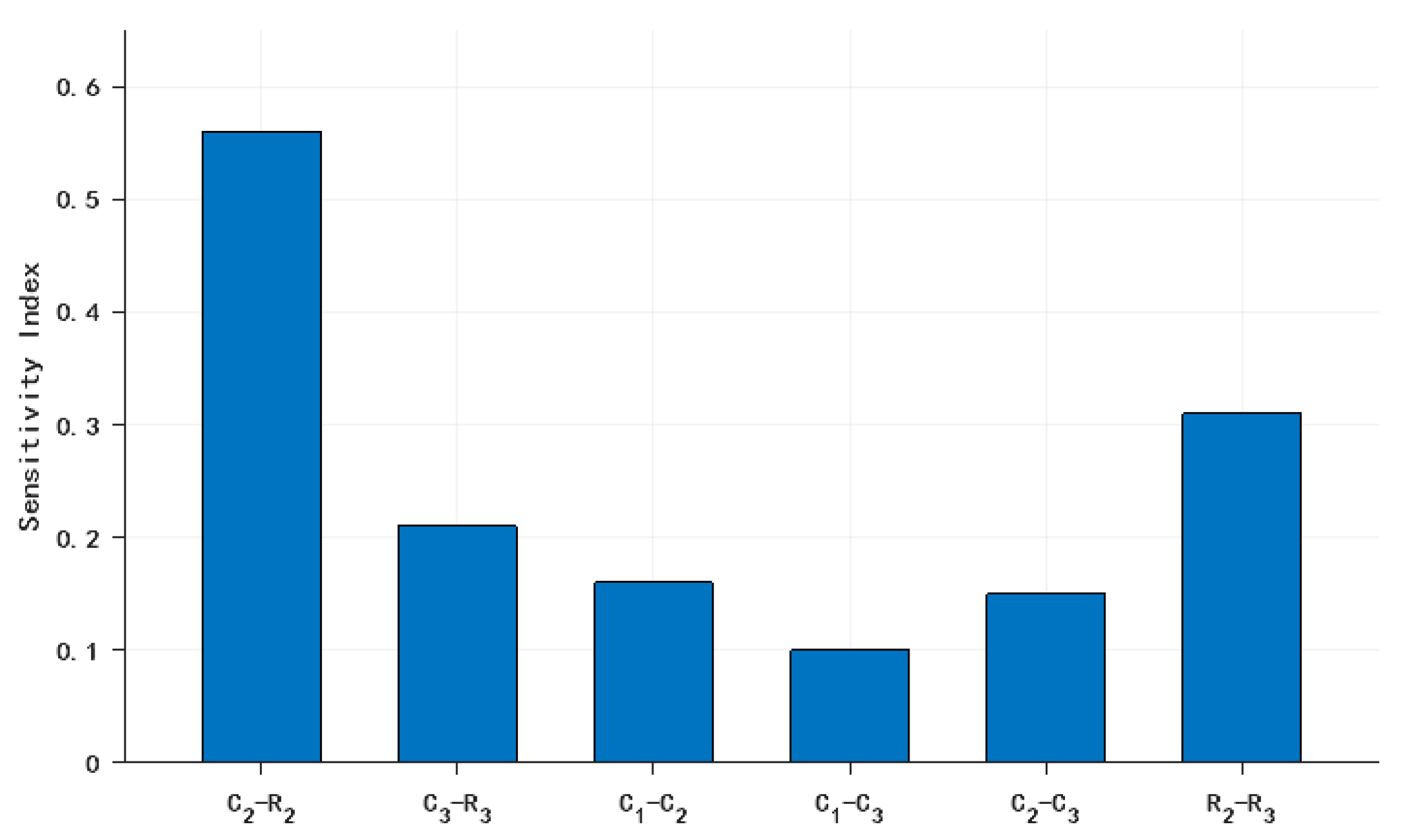

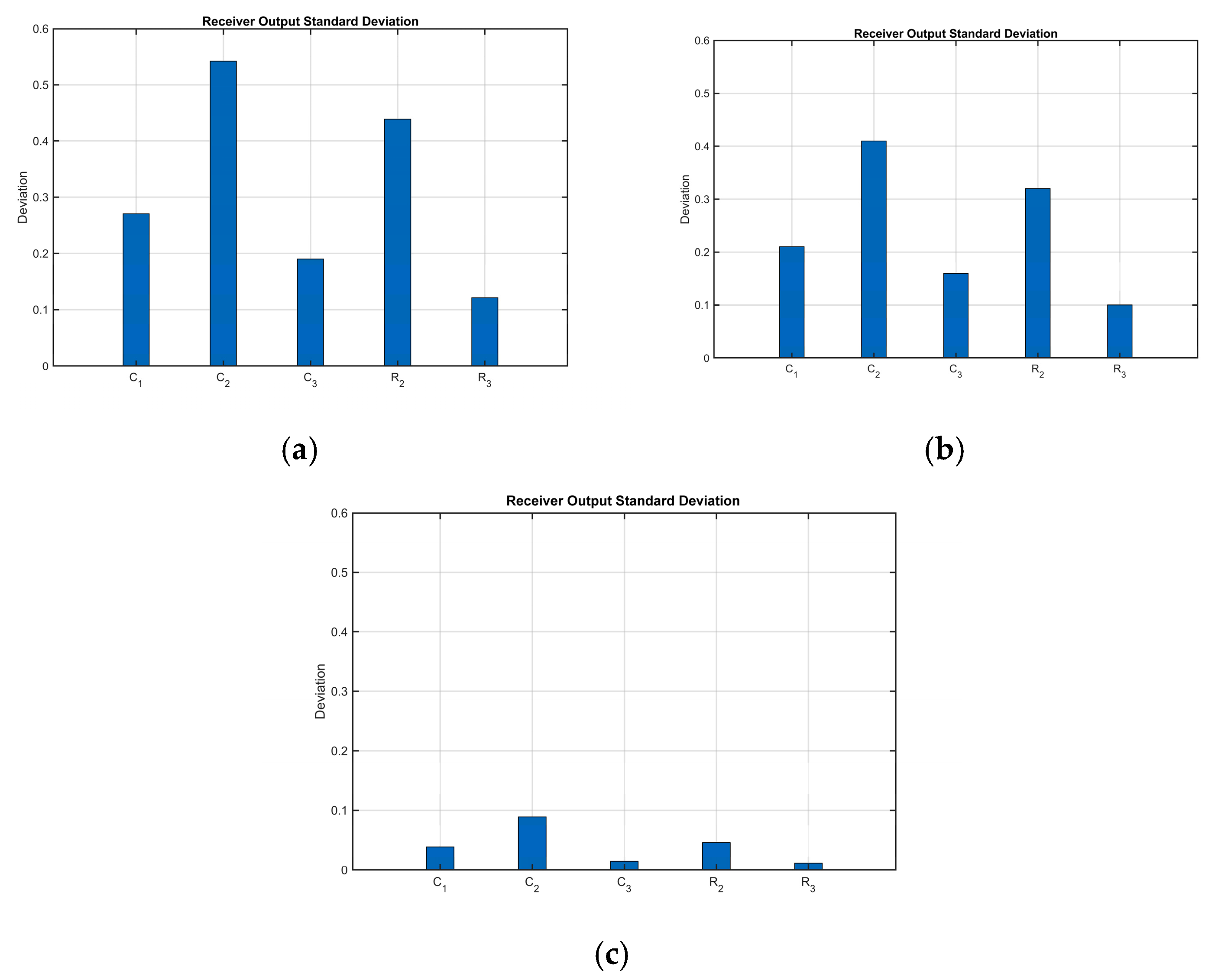

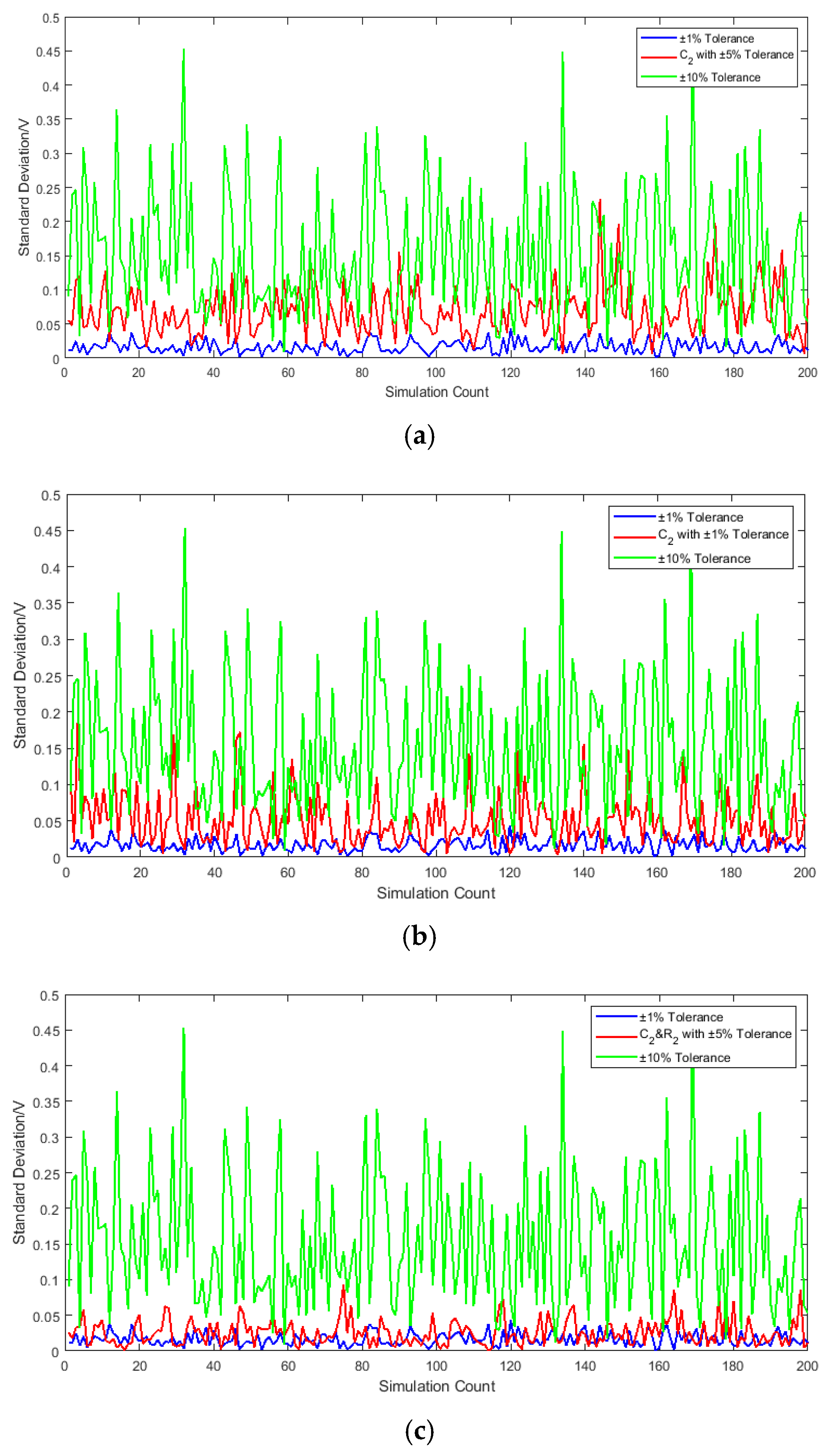

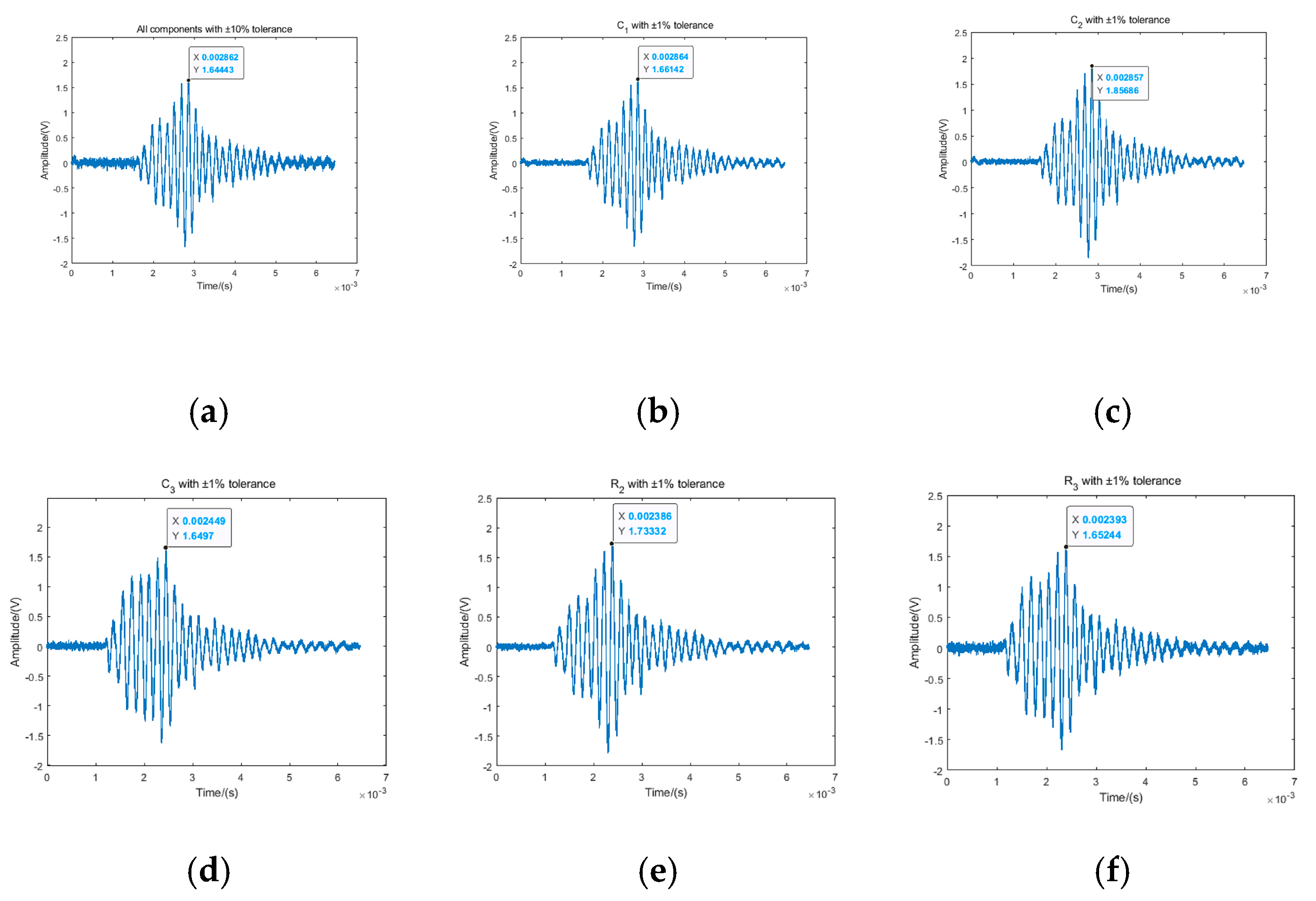
| Symmetry Ratio | ||||
|---|---|---|---|---|
| SNR/dB | 18.58 | 13.18 | 6.49 | −2.16 |
| Class | Sensitivity Coefficient Range | Sensitivity Level |
|---|---|---|
| I | High Sensitivity | |
| II | Sensitive | |
| III | Moderate Sensitivity | |
| IV | Insensitive |
| Morris | PDM | |
|---|---|---|
| 0.23 | 0.21 | |
| 0.46 | 0.48 | |
| 0.13 | 0.16 | |
| 0.35 | 0.32 | |
| 0.12 | 0.11 |
| 10%Tolerance | : ±1% | : ±1% | : ±1% | : ±1% | : ±1% | |
|---|---|---|---|---|---|---|
| SNR/dB | 15.63 | 16.62 | 17.17 | 16.19 | 17.01 | 16.05 |
| Sensitivity Range | Components | Tolerance Strategy |
|---|---|---|
| Critical Sensitivity (STi > 0.3) | R2, C2 | ±1% precision components |
| Moderate Sensitivity (0.2 < STi < 0.3) | C2 | ±5% tolerance components |
| Low Sensitivity (STi < 0.2) | C1, R3, C3 | ±10% commercial components |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Wu, K.; Yang, B.; Hao, S.; Huang, Z. Sensitivity Analysis of Component Parameters in Dual-Channel Time-Domain Correlated UWB Fuze Receivers Under Parametric Deviations. Sensors 2025, 25, 5065. https://doi.org/10.3390/s25165065
Liang Y, Wu K, Yang B, Hao S, Huang Z. Sensitivity Analysis of Component Parameters in Dual-Channel Time-Domain Correlated UWB Fuze Receivers Under Parametric Deviations. Sensors. 2025; 25(16):5065. https://doi.org/10.3390/s25165065
Chicago/Turabian StyleLiang, Yanbin, Kaiwei Wu, Bing Yang, Shijun Hao, and Zhonghua Huang. 2025. "Sensitivity Analysis of Component Parameters in Dual-Channel Time-Domain Correlated UWB Fuze Receivers Under Parametric Deviations" Sensors 25, no. 16: 5065. https://doi.org/10.3390/s25165065
APA StyleLiang, Y., Wu, K., Yang, B., Hao, S., & Huang, Z. (2025). Sensitivity Analysis of Component Parameters in Dual-Channel Time-Domain Correlated UWB Fuze Receivers Under Parametric Deviations. Sensors, 25(16), 5065. https://doi.org/10.3390/s25165065





