A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot
Abstract
1. Introduction
- (1)
- To address the common limitations of traditional trilateration methods under non-line-of-sight (NLOS) and multipath conditions, a geometric residual-weighted UWB ranging model is established. Compared to the conventional trilateration principle, this model integrates multiple sets of residuals to improve the robustness and reliability of raw UWB ranging measurements.
- (2)
- To mitigate zero-bias drift and slip errors in IMU and wheel odometry, a dynamically weighted complementary filtering scheme is designed based on traditional complementary filter principles. This contributes to the short-term pose prediction stability, particularly in dynamic and low-speed motion scenarios.
- (3)
- Development and implementation of a multi-source fusion EKF framework: In the prediction stage, the short-term state estimate is generated by dynamically fusing IMU and wheel odometry through the complementary filter. In the update stage, the optimized UWB ranging data, processed via residual weighting, is introduced as the observation input to the EKF. This supports global state estimation and improves error correction.
2. Overview of Localization Algorithms and Sensor Principles
2.1. IMU-Based Localization Principles
2.2. Overview of Wheel Odometry-Based Position Estimation
2.3. Overview of UWB Positioning Techniques
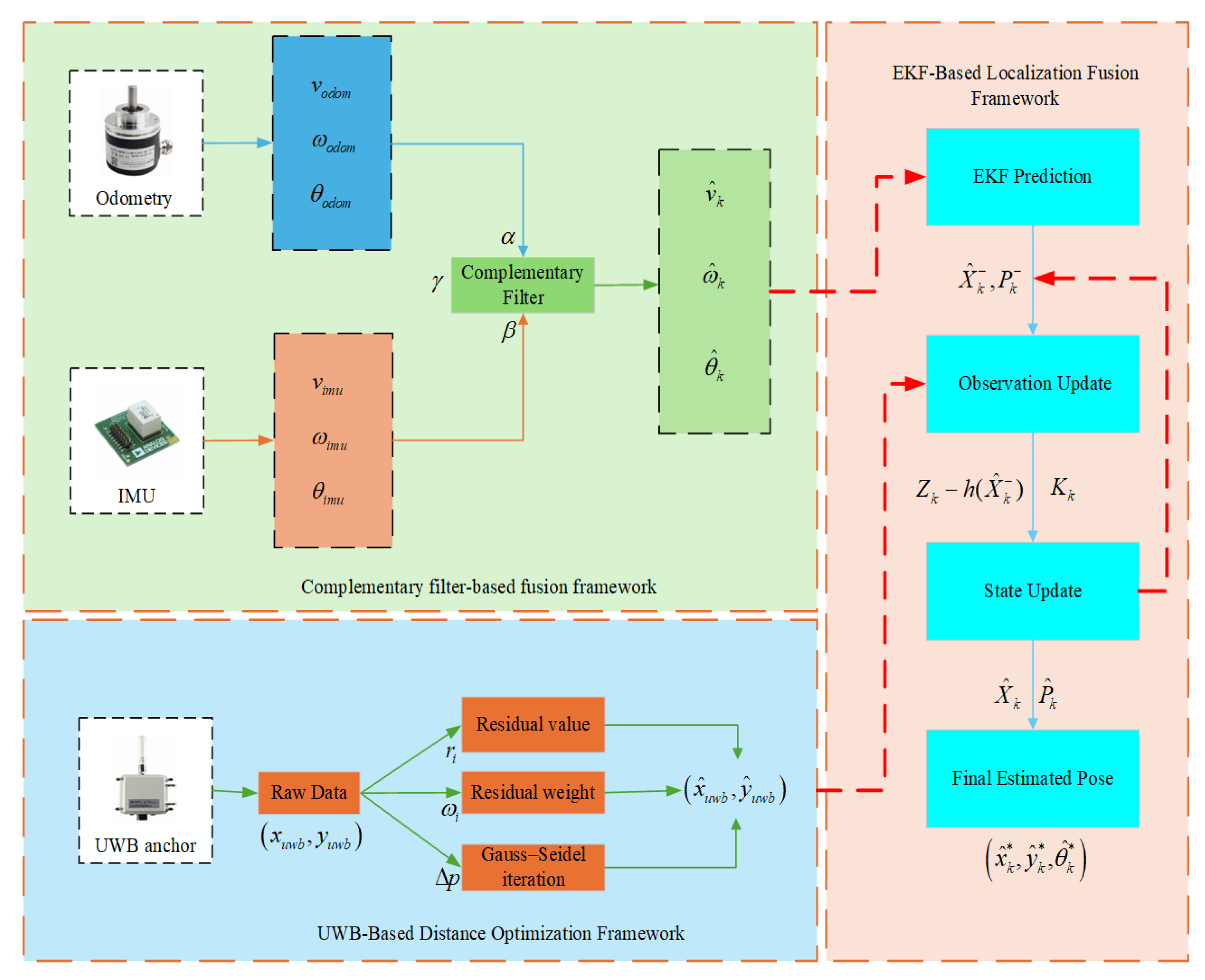
3. Fusion Localization Algorithm Based on IMU-Odom-UWB
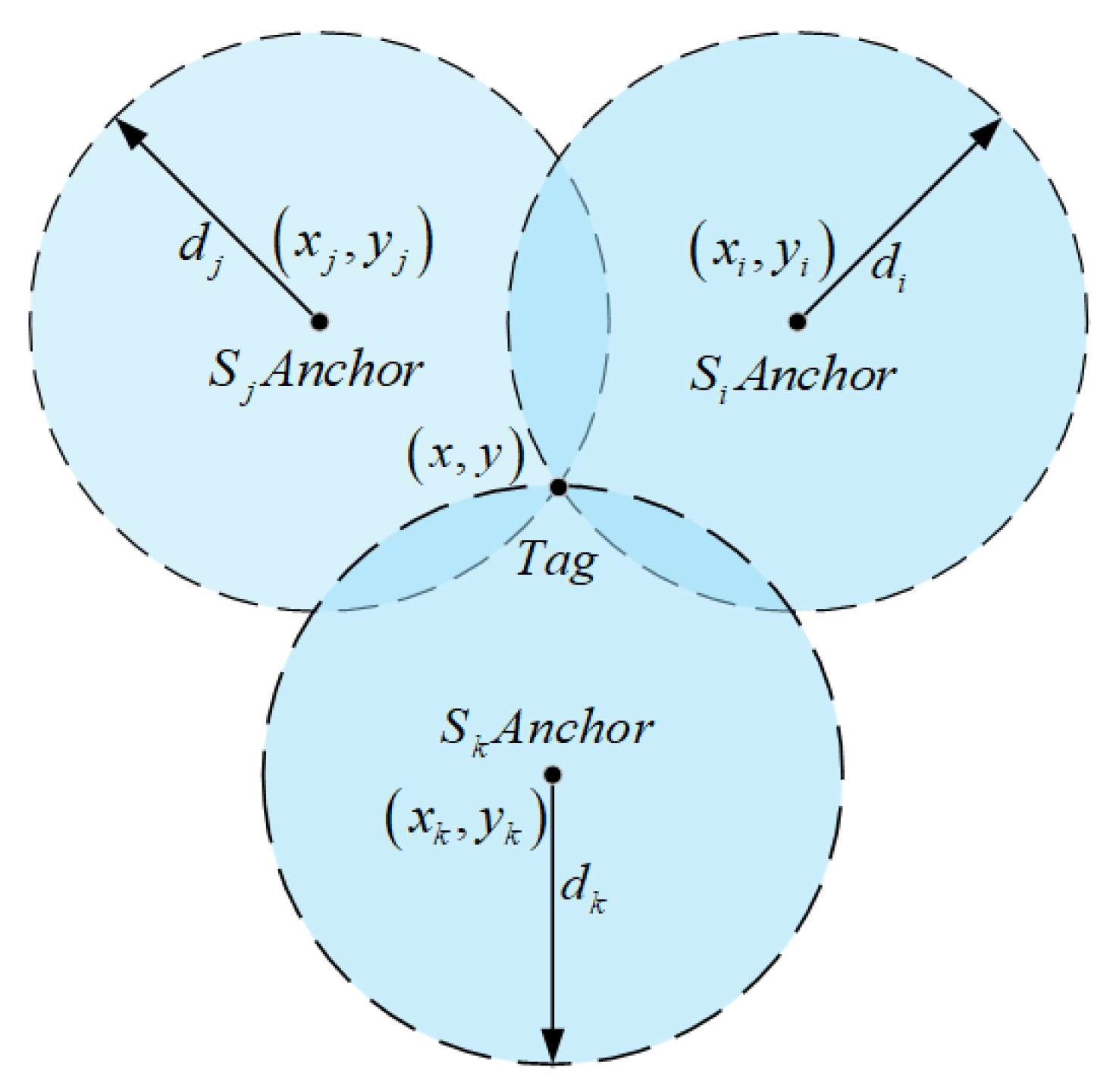
3.1. Establishment of a Geometric Residual Weighted UWB Ranging Model
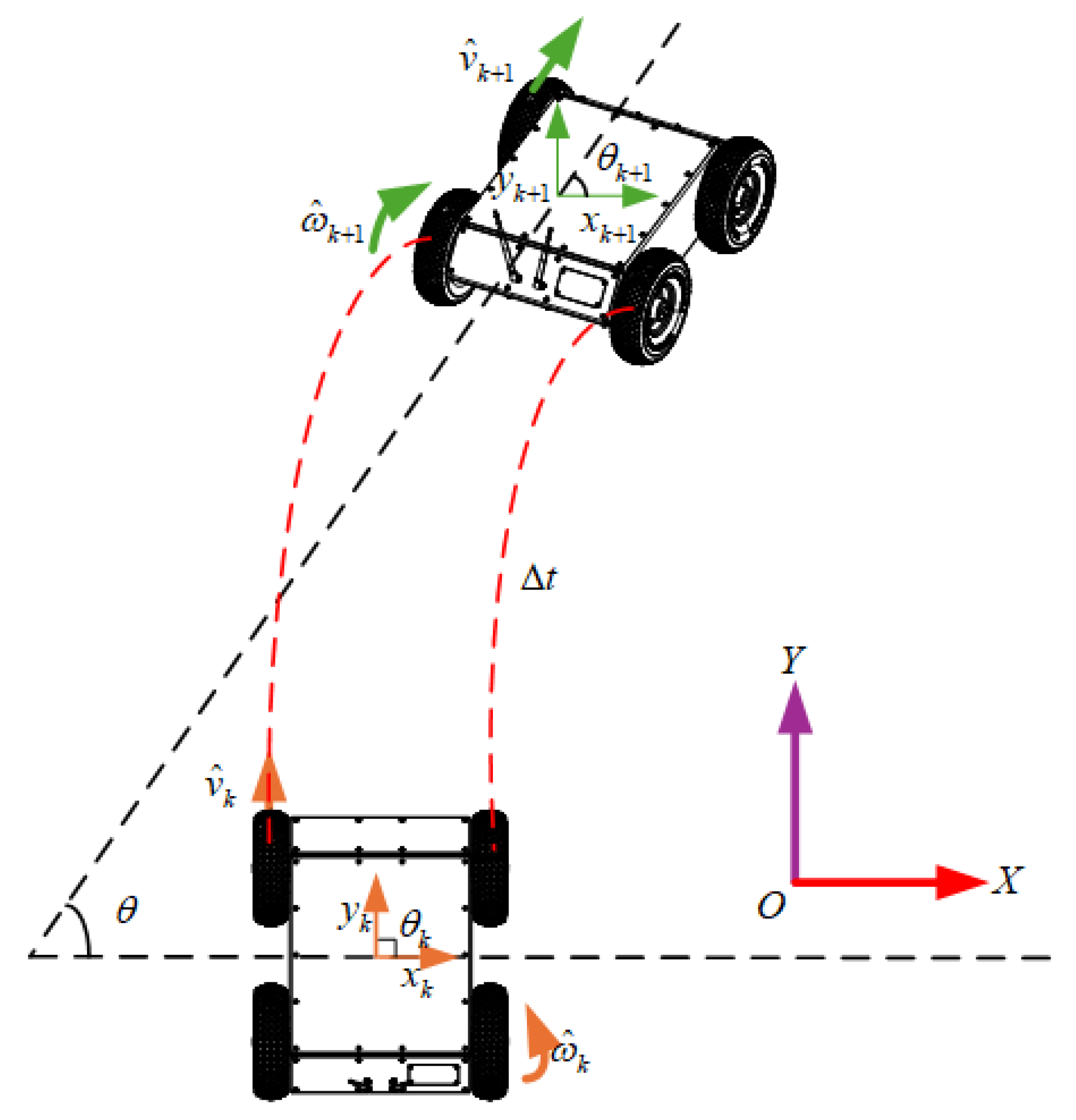
3.2. Design of a Dynamically Weighted Complementary Filter
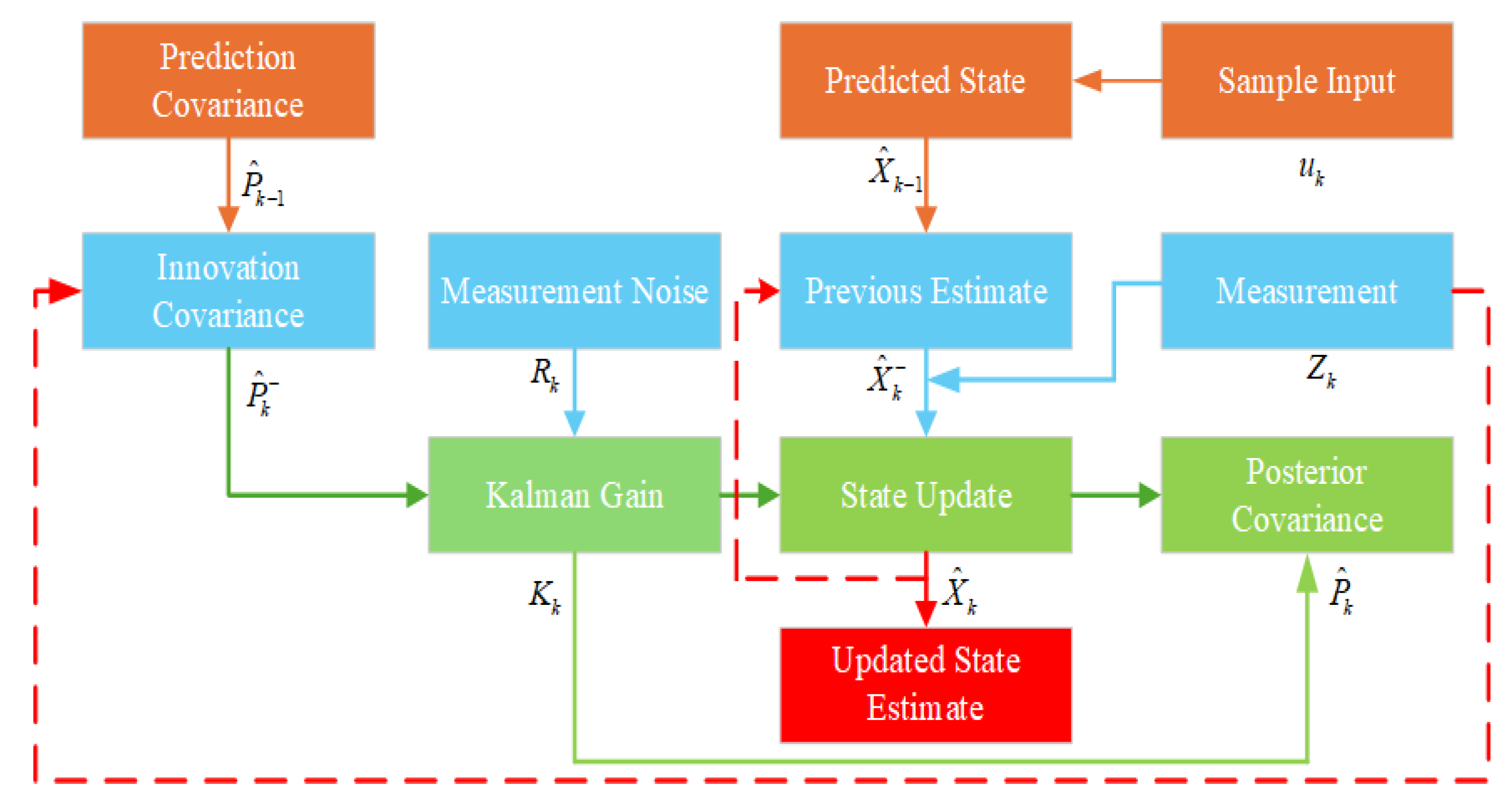
3.3. EKF Fusion Modeling and State Estimation Method
4. Results and Discussion
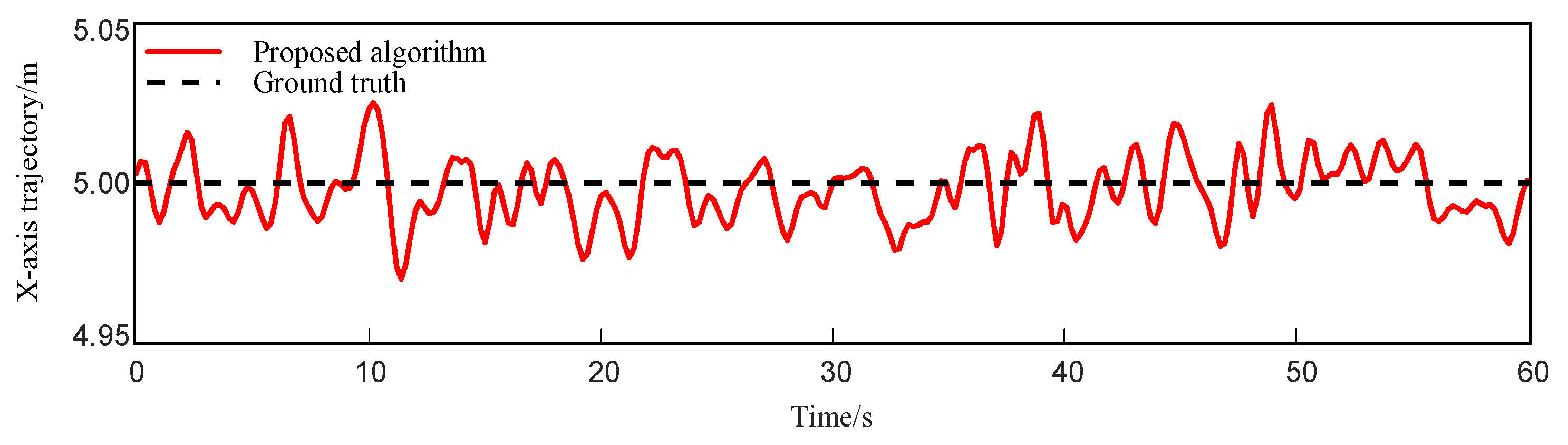
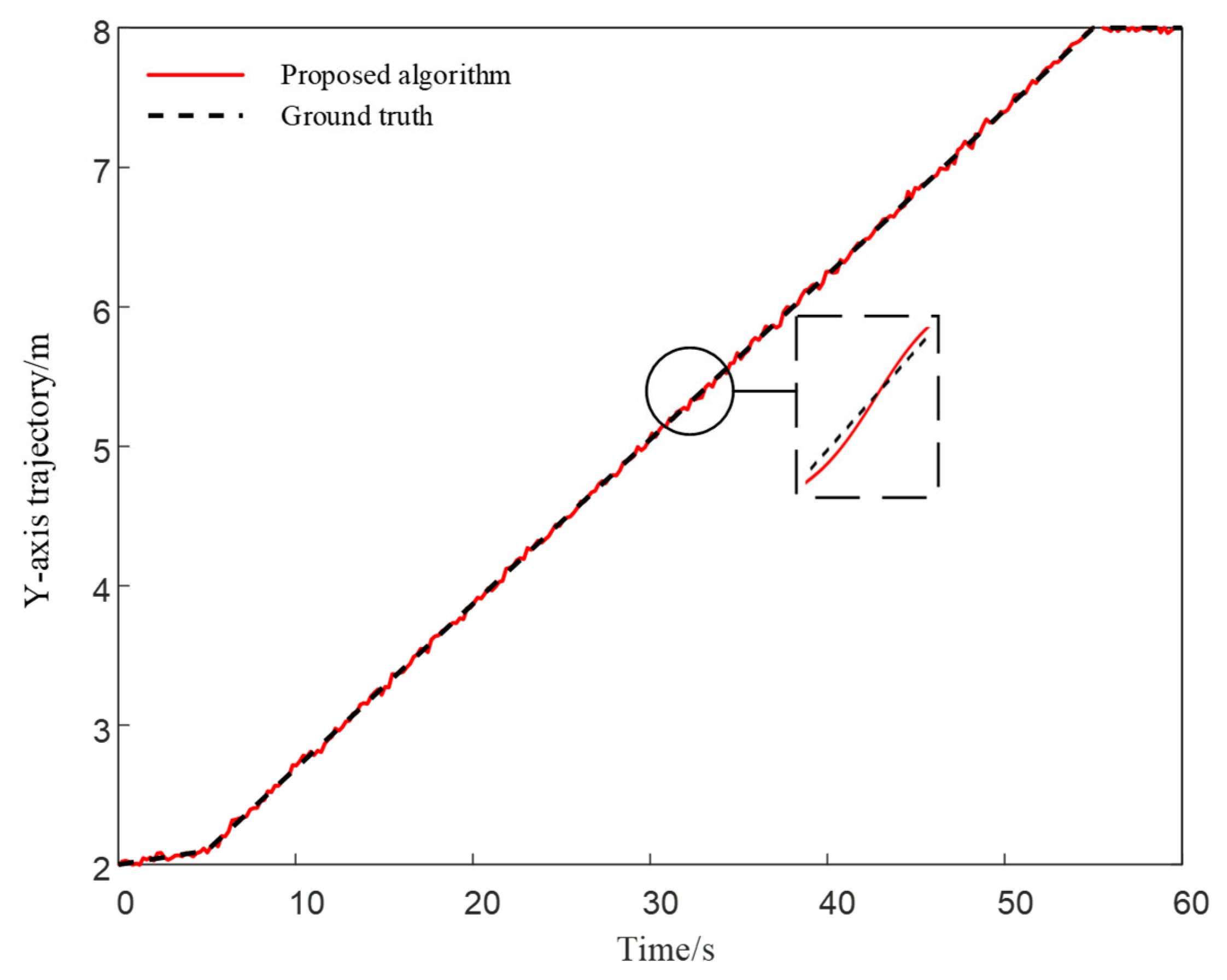
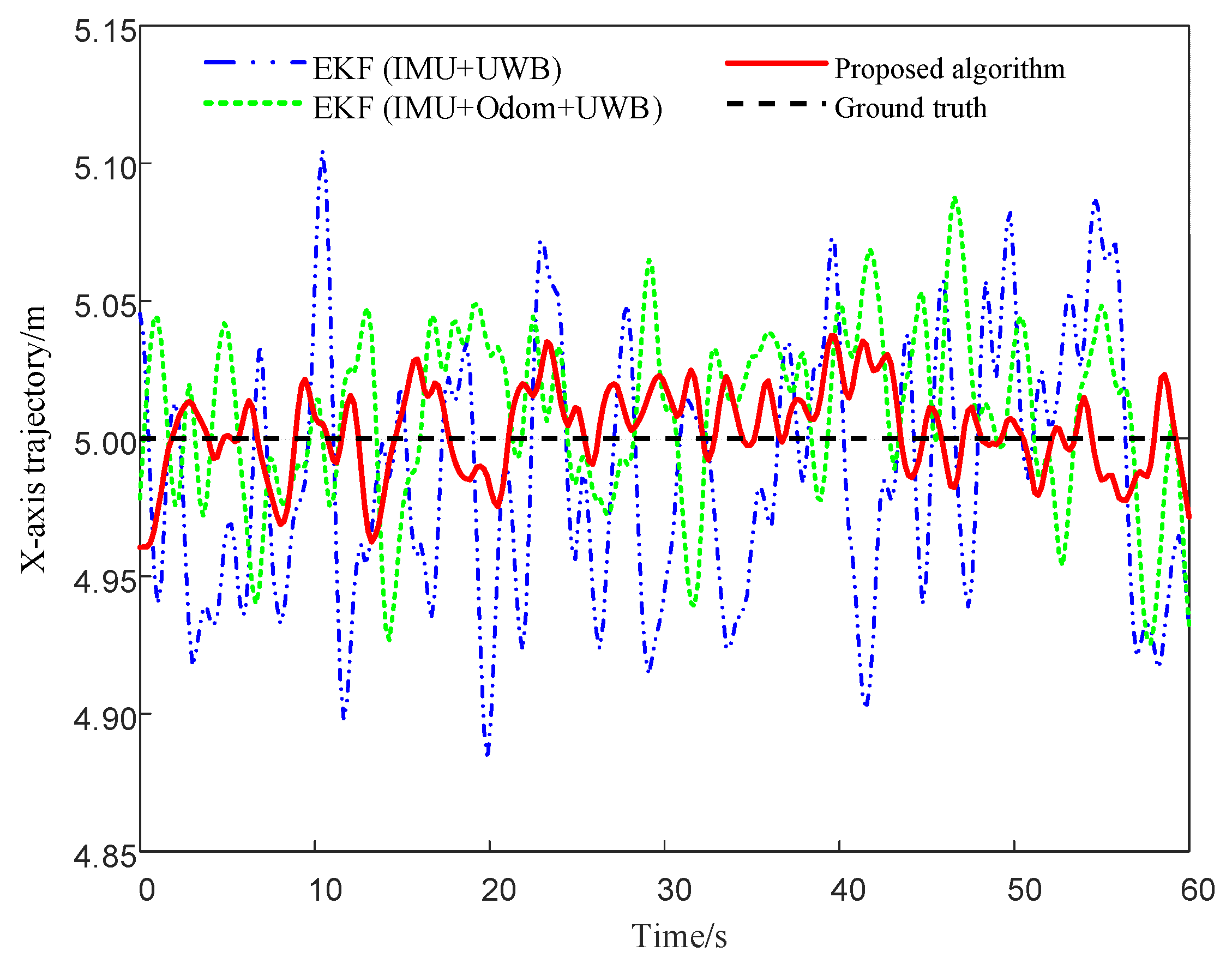
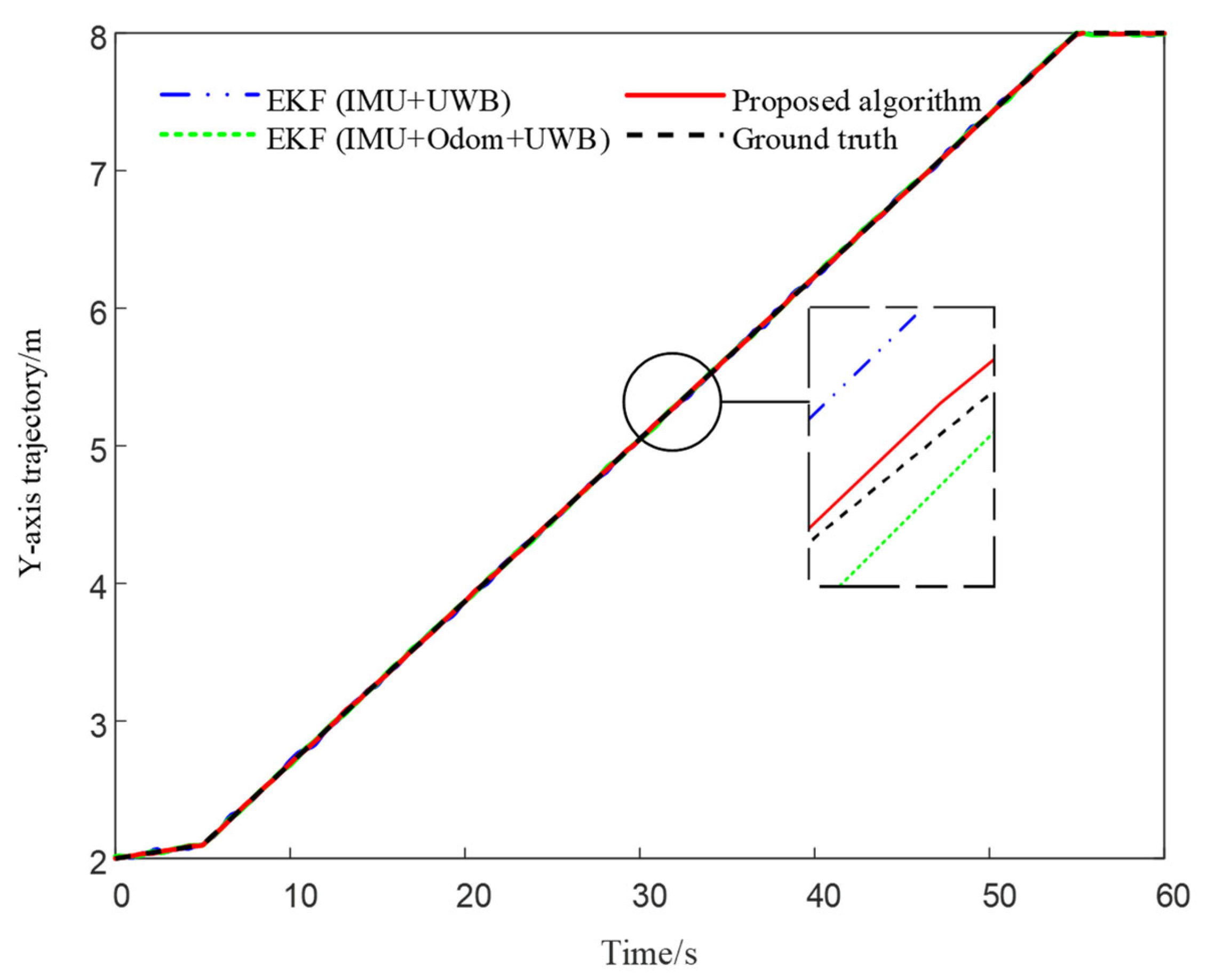
4.1. Straight-Line Trajectory Localization Simulation
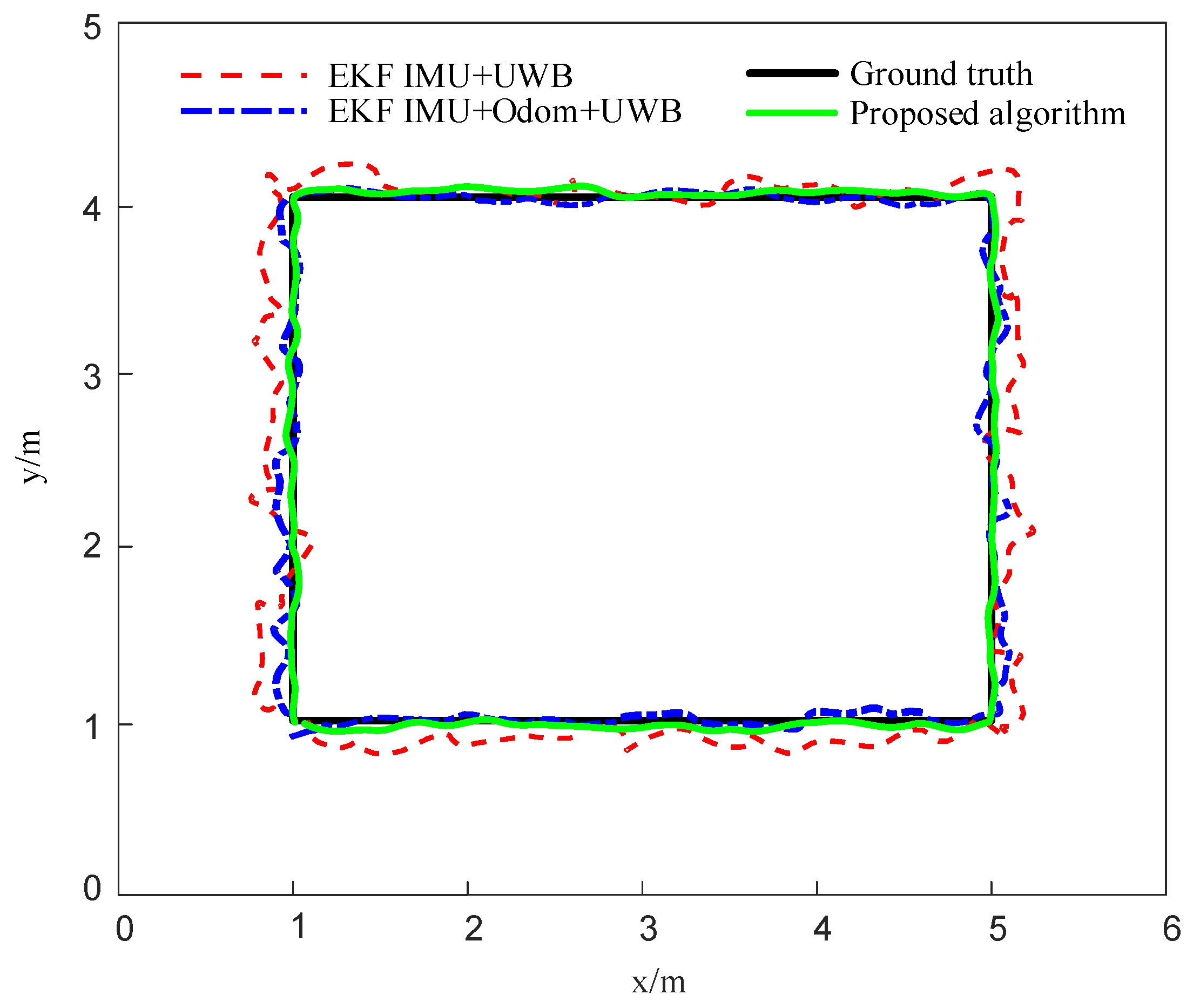
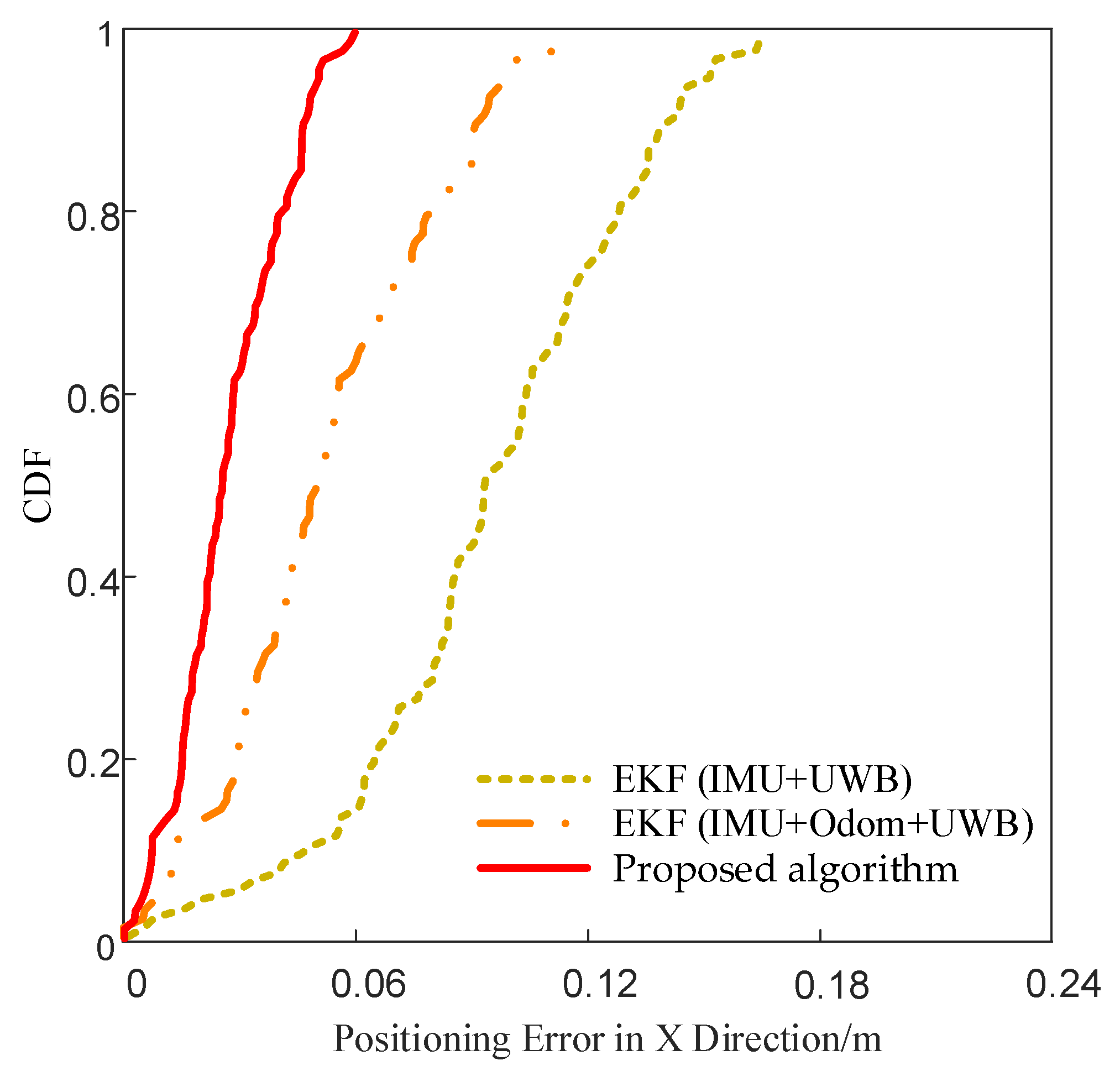
4.2. Closed Trajectory-Based Localization Simulation
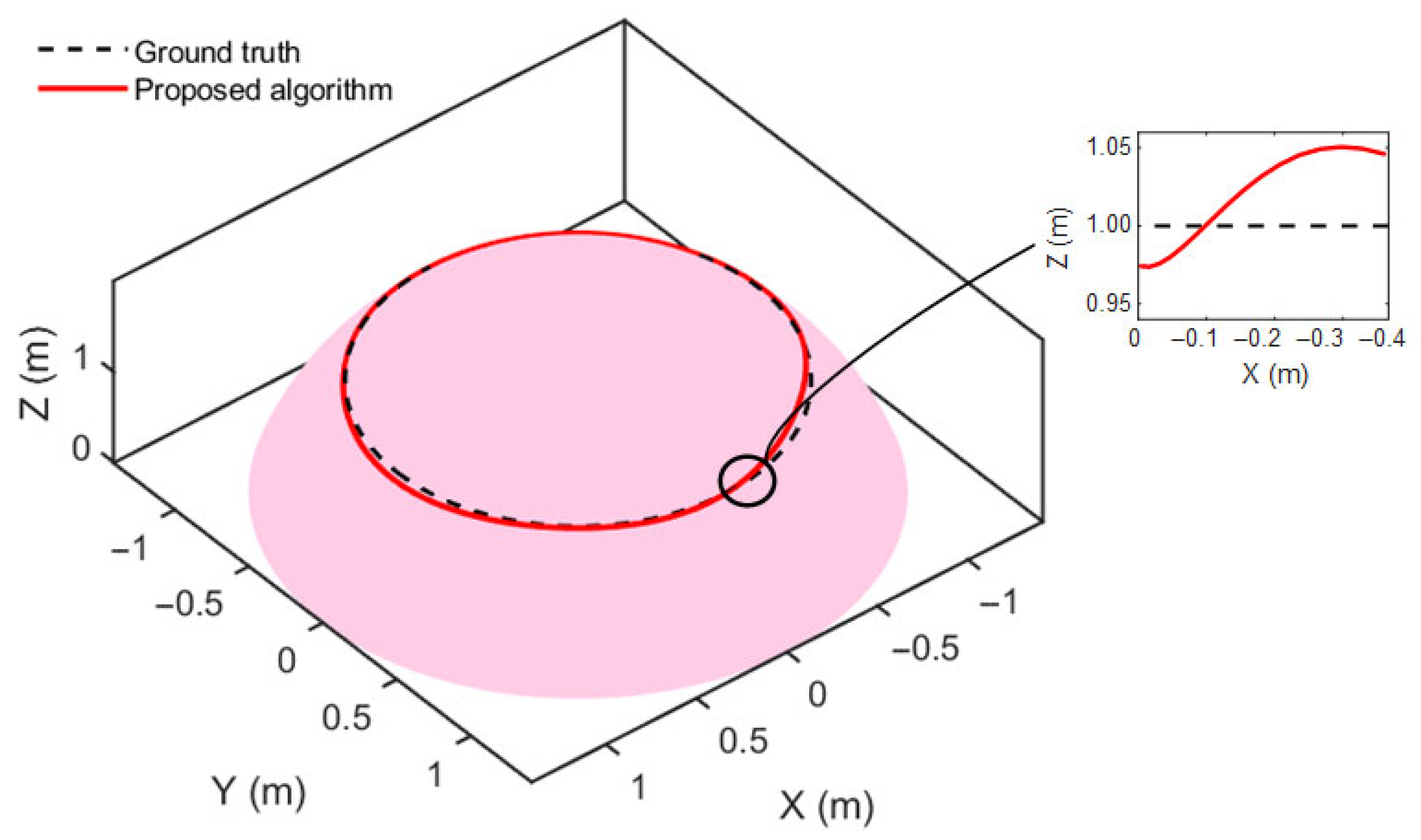
4.3. Localization Simulation on Curved Steel Surfaces
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Y.; Xu, Z.; Lin, Y.; Su, Z.; Ren, W. Design and Technical Development of Wall-Climbing Robots: A Review. J. Bionic Eng. 2022, 19, 877–901. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Feng, J.; Wang, H.; Liu, Z. Automated Wall-Climbing Robot for Concrete Construction Inspection. J. Field Robot. 2023, 40, 110–129. [Google Scholar] [CrossRef]
- Hu, J.; Han, X.; Tao, Y.; Feng, S. A Magnetic Crawler Wall-Climbing Robot with Capacity of High Payload on the Convex Surface. Robotics Auton. Syst. 2022, 148, 103907. [Google Scholar] [CrossRef]
- Jiang, Z.; Ma, Z.; Ju, Z.; Wang, D.; Xu, Y. Design and Analysis of a Wall-Climbing Robot for Passive Adaptive Movement on Variable-Curvature Metal Facades. J. Field Robot. 2023, 40, 94–109. [Google Scholar] [CrossRef]
- Gu, Z.; Gong, Z.; Tan, K.; Liu, Y.; Zhang, Y. Climb-Odom: A Robust and Low-Drift RGB-D Inertial Odometry with Surface Continuity Constraints for Climbing Robots on Freeform Surface. Inf. Fusion 2025, 117, 102880. [Google Scholar] [CrossRef]
- Ullah, I.; Adhikari, D.; Khan, H.; Saeed, M.; Ahmad, W.; Kim, H. Mobile Robot Localization: Current Challenges and Future Prospective. Comput. Sci. Rev. 2024, 53, 100651. [Google Scholar] [CrossRef]
- Yin, J.; Yan, F.; Liu, Y.; Guo, H.; Zhang, X. An Overview of Simultaneous Localisation and Mapping: Towards Multi-Sensor Fusion. Int. J. Syst. Sci. 2024, 55, 550–568. [Google Scholar] [CrossRef]
- Eang, C.; Lee, S. An Integration of Deep Neural Network-Based Extended Kalman Filter (DNN-EKF) Method in Ultra-Wideband (UWB) Localization for Distance Loss Optimization. Sensors 2024, 24, 7643. [Google Scholar] [CrossRef]
- Feng, D.; Peng, J.; Zhuang, Y.; Zhao, Y.; Shen, Y.; Zhang, X. An Adaptive IMU/UWB Fusion Method for NLOS Indoor Positioning and Navigation. IEEE Internet Things J. 2023, 10, 11414–11428. [Google Scholar] [CrossRef]
- Xing, H.; Liu, Y.; Guo, S.; Chen, Y.; Xie, G. A Multi-Sensor Fusion Self-Localization System of a Miniature Underwater Robot in Structured and GPS-Denied Environments. IEEE Sens. J. 2021, 21, 27136–27146. [Google Scholar] [CrossRef]
- Alfonso, L.; De Rango, F.; Fedele, G.; Perri, G.; Talarico, S. CM-SLASM: A Cooperative Multi-Technology Simultaneous Localization and Signal Mapping for Vehicles Indoor Positioning. IEEE Sens. J. 2024. [Google Scholar] [CrossRef]
- Cao, B.; Jiang, M.; Li, M.; Yin, Y.; Wang, H.; Yu, W. Improving Accuracy of the IMU/UWB Fusion Positioning Approach Utilizing ESEKF and VBUKF for Underground Coal Mining Working Face. IEEE Internet Things J. 2025. Early Access. [Google Scholar] [CrossRef]
- Cheng, B.; He, X.; Li, X.; Jin, Z.; Wang, Y. Research on Positioning and Navigation System of Greenhouse Mobile Robot Based on Multi-Sensor Fusion. Sensors 2024, 24, 4998. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Han, K.; Sun, T.; Li, Z.; Wang, L. A Multi-Sensor Fusion Approach for Centimeter-Level Indoor 3D Localization of Wheeled Robots. Meas. Sci. Technol. 2025, 36, 046304. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Gao, R.; Zhang, H.; Zhao, Y. A Multi-Sensor Fusion Positioning Approach for Indoor Mobile Robot Using Factor Graph. Measurement 2023, 216, 112926. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, T.; Sun, Z. An Autonomous Localisation Method of Wall-Climbing Robots on Large Steel Components with IMU and Fixed RGB-D Camera. J. Navig. 2024, 77, 469–484. [Google Scholar] [CrossRef]
- Sun, J.; Sun, W.; Zheng, G.; Yang, K.; Li, S.; Meng, X.; Deng, N.; Tan, C. A Novel UWB/IMU/Odometer-Based Robot Localization System in LOS/NLOS Mixed Environments. IEEE Trans. Instrum. Meas. 2024. preprint. [Google Scholar] [CrossRef]
- Brunacci, V.; De Angelis, A. Fusion of UWB and Magnetic Ranging Systems for Robust Positioning. IEEE Trans. Instrum. Meas. 2023, 73, 1–12. [Google Scholar] [CrossRef]
- Hao, X.; Yang, H.; Xu, Y. Information Fusion for Positioning System with Location Constraint of Camera and UWB. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15978–15989. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X.; Zhong, H.; Liu, Y.; Huang, S. A Dynamic Window-Based UWB-Odometer Fusion Approach for Indoor Positioning. IEEE Sens. J. 2023, 23, 2922–2931. [Google Scholar] [CrossRef]
- Yuan, G.; Shi, S.; Shen, G.; Huang, W.; Wu, C. MIAKF: Motion Inertia Estimated Adaptive Kalman Filtering for Underground Mine Tunnel Positioning. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Ghadimzadeh Alamdari, A.; Zade, F.A.; Ebrahimkhanlou, A. A Review of Simultaneous Localization and Mapping for the Robotic-Based Nondestructive Evaluation of Infrastructures. Sensors 2025, 25, 712. [Google Scholar] [CrossRef]
- Yan , H.; Shuang, G.; Chao, G. FCIHMRT: Feature Cross-Layer Interaction Hybrid Method Based on Res2Net and Transformer for Remote Sensing Scene Classification. Electronics 2023, 12, 4362. [Google Scholar] [CrossRef]
- Nguyen, S.T.; La, K.T.; La, H.M. Agile Robotic Inspection of Steel Structures: A Bicycle-Like Approach with Multisensor Integration. J. Field Robot. 2024, 41, 396–419. [Google Scholar] [CrossRef]
- Otsuki, Y.; Nguyen, S.T.; La, H.M. Autonomous Ultrasonic Thickness Measurement of Steel Bridge Members Using a Climbing Bicycle Robot. J. Eng. Mech. 2023, 149, 04023051. [Google Scholar] [CrossRef]
- Lu, J.; Ye, L.; Zhang, J.; Luo, H.; Li, Z. A New Calibration Method of MEMS IMU Plus FOG IMU. IEEE Sens. J. 2022, 22, 8728–8737. [Google Scholar] [CrossRef]
- Lyu, P.; Wang, B.; Lai, J.; Li, Y.; Zhang, H. A Factor Graph Optimization Method for High-Precision IMU-Based Navigation System. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Tang, H.; Niu, X.; Zhang, T.; Chen, X.; Qin, Y.; Wang, C. OdoNet: Untethered Speed Aiding for Vehicle Navigation without Hardware Wheeled Odometer. IEEE Sens. J. 2022, 22, 12197–12208. [Google Scholar] [CrossRef]
- Wen, Z.; Yang, G.; Cai, Q.; Fan, C.; Zhang, X. A Novel Bluetooth-Odometer-Aided Smartphone-Based Vehicular Navigation in Satellite-Denied Environments. IEEE Trans. Ind. Electron. 2022, 70, 3136–3146. [Google Scholar] [CrossRef]
- Huang, G.; Huang, H.; Zhai, Y.; Luo, X.; Chen, X. Multi-Sensor Fusion for Wheel-Inertial-Visual Systems Using a Fuzzification-Assisted Iterated Error State Kalman Filter. Sensors 2024, 24, 7619. [Google Scholar] [CrossRef]
- Hashim, H.A.; Eltoukhy, A.E.E.; Vamvoudakis, K.G. UWB Ranging and IMU Data Fusion: Overview and Nonlinear Stochastic Filter for Inertial Navigation. IEEE Trans. Intell. Transp. Syst. 2023, 25, 359–369. [Google Scholar] [CrossRef]
- Shalaby, M.A.; Cossette, C.C.; Forbes, J.R.; Xu, C. Reducing Two-Way Ranging Variance by Signal-Timing Optimization. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3718–3724. [Google Scholar] [CrossRef]
- Yan, X.; Yang, X.; Lou, M.; Zhang, Y.; Hu, G. Cooperative Navigation in Unmanned Surface Vehicles with Observability and Trilateral Positioning Method. Ocean Eng. 2024, 306, 118078. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, C. Research on UWB Indoor Positioning System Based on TOF Combined Residual Weighting. Sensors 2023, 23, 1455. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Bao, T.; Xu, B.; Chen, H.; Liu, Z. A Deep Residual Neural Network Framework with Transfer Learning for Concrete Dams Patch-Level Crack Classification and Weakly-Supervised Localization. Measurement 2022, 188, 110641. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Zhang, L.; Guo, G. Sparse Tensor-Based Multiscale Representation for Point Cloud Geometry Compression. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 9055–9071. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| ch1, ch2, ch3, ch4 | (0, 0), (10, 0), (10, 10), (0, 10) m |
| 0.1 m/s | |
| 0 rad/s | |
| 0 rad | |
| 0.01 s | |
| 0.7 | |
| 0.3 | |
| 0.6 | |
| 0.01 rad/s | |
| 0.06 m |
| Number | Sample Point | EKF IMU + UWB | EKF IMU + Odom + UWB | Proposed Algorithm |
|---|---|---|---|---|
| 1 | (1.000, 1.000) | (1.124, 1.093) | (1.080, 1.066) | (1.046, 0.973) |
| 2 | (5.000, 1.000) | (4.891, 1.087) | (5.083, 0.914) | (4.962, 1.068) |
| 3 | (5.000, 4.000) | (5.126, 4.118) | (5.070, 4.082) | (5.049, 4.051) |
| 4 | (1.000, 4.000) | (0.870, 3.883) | (0.926, 3.955) | (1.052, 3.952) |
| Positioning Method | Mean Error in the X Direction (m) | Mean Error in the Y Direction (m) |
|---|---|---|
| EKF (IMU + UWB) | 0.1304 | 0.0962 |
| EKF (IMU + Odom + UWB) | 0.0741 | 0.0688 |
| Proposed algorithm | 0.0462 | 0.0503 |
| Positioning Method | Mean Error in the X Direction (m) | Mean Error in the Y Direction (m) |
|---|---|---|
| EKF (IMU + UWB) | 0.1376 | 0.1182 |
| EKF (IMU + Odom + UWB) | 0.0841 | 0.0763 |
| Proposed algorithm | 0.0578 | 0.0511 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Li, H.; Hui, N.; Zhang, J.; Yue, G. A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot. Sensors 2025, 25, 5051. https://doi.org/10.3390/s25165051
Han X, Li H, Hui N, Zhang J, Yue G. A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot. Sensors. 2025; 25(16):5051. https://doi.org/10.3390/s25165051
Chicago/Turabian StyleHan, Xiaowei, Hao Li, Nanmu Hui, Jiaying Zhang, and Gaofeng Yue. 2025. "A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot" Sensors 25, no. 16: 5051. https://doi.org/10.3390/s25165051
APA StyleHan, X., Li, H., Hui, N., Zhang, J., & Yue, G. (2025). A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot. Sensors, 25(16), 5051. https://doi.org/10.3390/s25165051





