A Blur Feature-Guided Cascaded Calibration Method for Plenoptic Cameras
Abstract
1. Introduction
- For the first time, a geometric observation model of the virtual depth domain is proposed. The geometric relationship between the epipolar lines in the micro-image (MI) and the virtual depth space is used to construct a geometric observation model of the virtual depth domain that is unique to plenoptic cameras.
- A quantification and grading rule for micro-image clarity that accounts for blur-perceived plenoptic features is constructed. The geometric observation mode of the virtual depth domain is used to iteratively filter the outliers and optimize the corner point coordinates in a step-by-step diffusion manner, effectively improving the extraction quality of the corner point features.
- A decoupled and cascaded optimization strategy is proposed for the first time. The central light projection equation of the target MI is constructed to assist in optimizing the parameters of the microlens array (MLA), and redundant observations of the same corner point and adaptive confidence weights that account for blur are established to construct a global nonlinear optimization model. The complexity of the nonlinear function can thus be effectively reduced, avoiding sensitivity to the initial estimated parameters and making it easier to converge to the optimal solution.
2. Related Work
- (1)
- Feature point quality issues
- (2)
- Sensitivity of nonlinear optimization to initial values
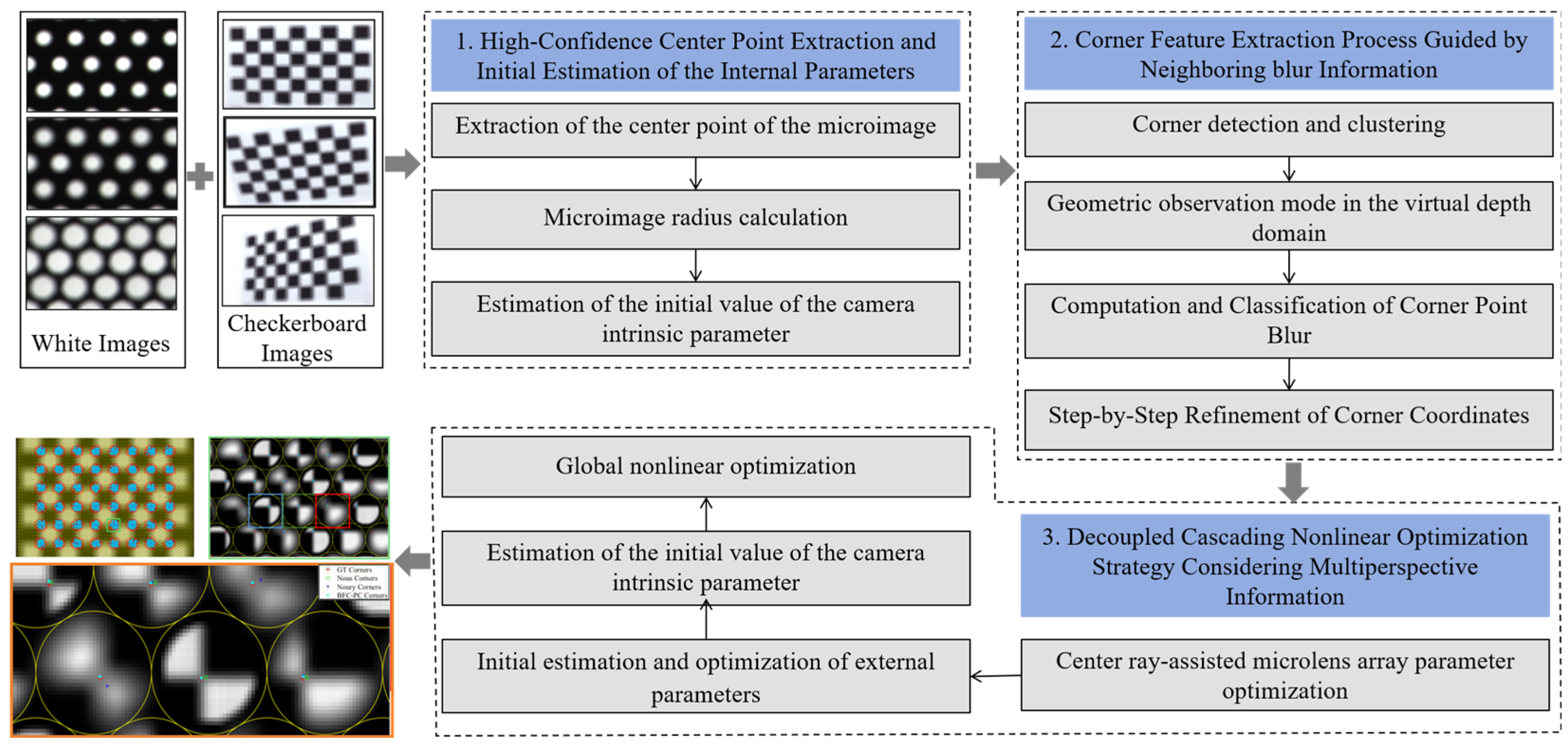
3. Methods
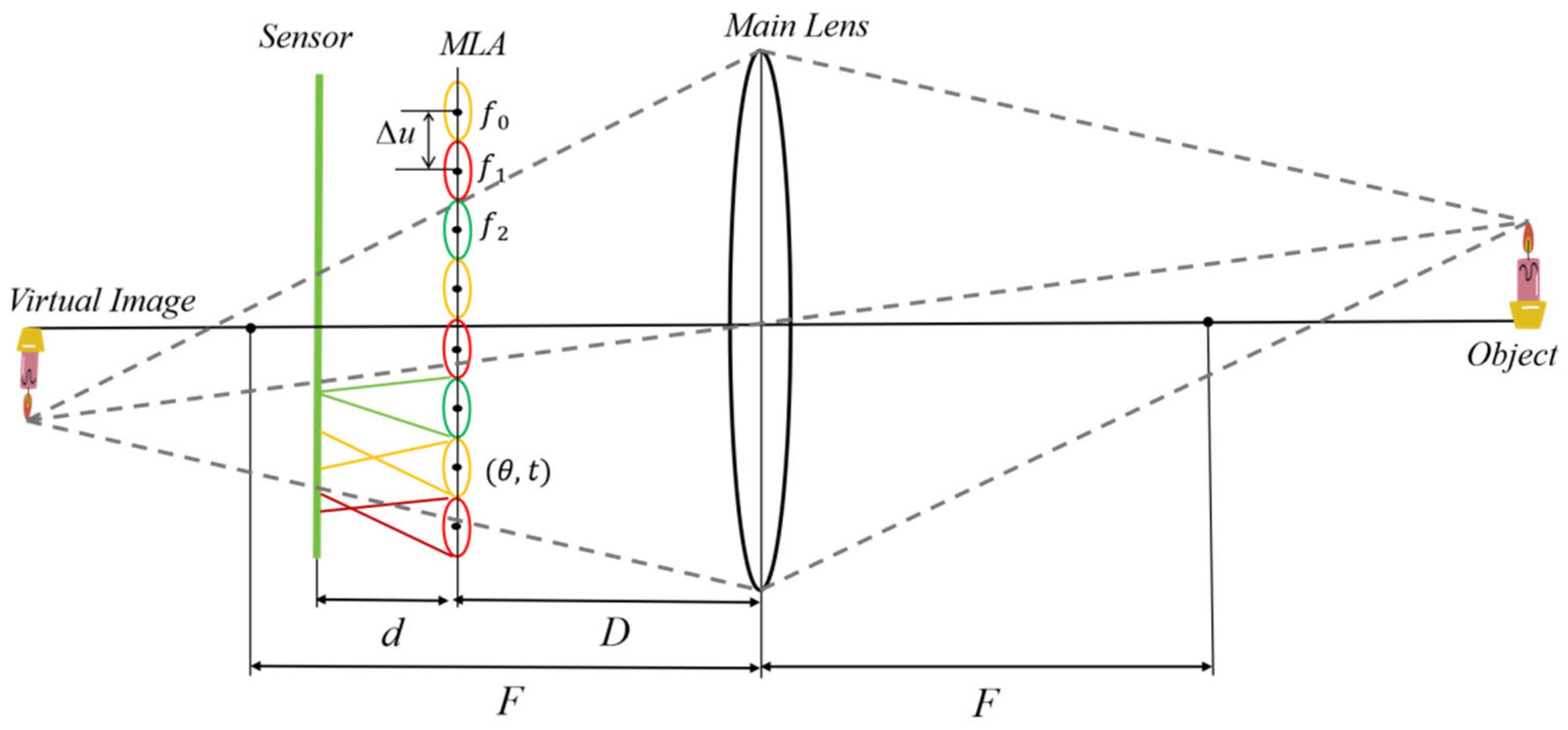
3.1. Micro-Image Central Grid and Initial Intrinsic Parameter Estimation
3.2. Corner Feature Extraction Based on Blur Quantization Under the Virtual Depth Geometric Constraint Model
- (1)
- Blur feature quantization of corner points based on the dual features of light field ray propagation and the image gradient.
- (2)
- Calculation of the initial virtual depth.
- (3)
- Optimization of the corner point coordinates via a diffusion method.
3.3. Nonlinear Optimization Strategy with Hierarchical Decoupling
4. Experiments and Analysis
4.1. Experiment Setup
- 1.
- Hardware EnvironmentThe light field cameras used in the experiments primarily included two multifocal plenoptic cameras, namely, the Raytrix R12 and HR260. The Raytrix R12 is produced by the German company Raytrix, and the HR260 is independently developed by our research group. The detailed specifications of the three light field cameras are as follows:
- (1)
- The main lens used by Raytrix R12 is a Nikon AF Nikkor F/1.8D with a focal length of 50 mm. The MLA consists of 176 × 152 microlenses with three focal lengths arranged crosswise. The sensor is a Basler boA4000-KC with a pixel size of 0.0055 mm, a resolution of 4080 × 3068, and a working distance of approximately 0.1~5 m.
- (2)
- The main lens for the HR260 has a focal length of 105 mm, and the MLA consists of 65 × 50 microlenses with three focal lengths arranged crosswise. The sensor pixel size is 0.0037 mm, the resolution is 6240 × 4168, and the working distance is approximately 0.1~100 m.
- 2.
- Software Environment
- 3.
- DatasetsWe establish three datasets with different focus distances H, obtained from two different light field cameras, with detailed parameter settings as shown in Table 1. Each dataset consists of the following:
- (1)
- White raw plenoptic images captured at different apertures () using a light diffuser mounted on the main objective lens.
- (2)
- Target images captured at different poses (distances and directions), divided into two subsets, one for the calibration process (16 images) and the other for reprojection error evaluation (15 images).
- (3)
- White raw plenoptic images acquired under the same illumination conditions and the same aperture are used for calibration target acquisition for dehalation, as well as calibration targets acquired through controlled translation motion for quantitative evaluation.
- 4.
- Simulation Environment
4.2. Ablation Study
4.2.1. Evaluation Metrics
4.2.2. Experimental Setup
- (1)
- Without neighboring blur-aware corner feature extraction: This configuration evaluates the system’s performance across different datasets when the blur-aware corner feature extraction guided by neighboring views is disabled.
- (2)
- Without principal ray-assisted microlens array parameter optimization: This setting assesses the system’s accuracy on various datasets when the optimization of microlens array parameters using principal rays is not employed.
- (3)
- Without decoupled hierarchical nonlinear optimization: This test examines the system’s accuracy on different datasets when the decoupled hierarchical nonlinear optimization module is omitted.
- (4)
- Full system: This configuration includes all modules, namely the neighboring blur-aware corner feature extraction, principal ray-assisted microlens array parameter optimization, and decoupled hierarchical nonlinear optimization.
4.2.3. Ablation Results and Contribution Impact
- (1)
- Effect of blur-aware corner extraction
- (2)
- Effect of center-ray-assisted MLA optimization
- (3)
- Effect of decoupled nonlinear optimization:
- (4)
- Overall effectiveness:
4.3. Corner Feature Extraction Accuracy Evaluation
- (1)
- As the image blur changes, the Nousias method and Noury method exhibit large fluctuations. Furthermore, the error gradually increases with increasing blur, indicating that the accuracy of these two methods is strongly affected by blur, which also verifies the problem raised in this paper. However, the proposed method performs smoothly, and the accuracies of the three types of corner points are almost the same.
- (2)
- Noury’s method and the proposed method have multiple identical numerical values in terms of the minimum error because the first step of the corner feature extraction strategy proposed in this paper, which is guided by neighboring blur information, uses the template matching algorithm introduced by Noury et al. [15] to detect the corner coordinates of the micro-image. The corner coordinates with the minimum error are the detection results corresponding to the clearest corners. The corner feature extraction strategy uses the coordinates of these clearest corners to construct geometric observations in the virtual depth domain to optimize the coordinates of other corners.
- (3)
- The overall performance of the proposed method is the best in terms of the two indicators of the error mean and standard deviation, as the experimental results for the proposed method are the smallest. Compared with the second-ranked method, the accuracy is improved by 11%, 57%, 60%, 44%, and 43%, respectively, with an average improvement of more than 30%. These improved results can be obtained due to the corner feature extraction strategy guided by neighboring blur information proposed in this paper. This approach uses the geometric relationship between the epipolar lines between micro-images and the virtual depth space to construct a multi constraint model and then, on this basis, constructs a geometric observation model of the virtual depth domain. It next quantifies and grades the degree of blur imaging for multiple corner points in the cluster, in turn iteratively filtering the noise in the cluster according to the step-by-step diffusion method and optimizes the coordinates of the corner points from clear to blur. Therefore, the proposed method refines relatively blurred corner coordinates and effectively improves the extraction quality of corner features.
4.4. Accuracy Assessment of the Intrinsic Calibration Parameters
- (1)
- When the given camera parameters are limited, only the focal length of the main lens is considered. Although the reprojection errors of the Nousias and Liu methods are different, especially the Liu method, which has a better reprojection error performance, the estimated focal length of the main lens is significantly different from the given value, so the accuracy of the estimated intrinsic parameters is questionable.
- (2)
- The focal length of the main lens estimated by the proposed method and the Labussière method is closest to the given value, and the reprojection error of the proposed method is the smallest at approximately 0.5 pixels; however, the reprojection error of the Labussière method can reach 2.080 pixels. Therefore, the proposed method has the best comprehensive performance in terms of calibrating the intrinsic parameters because the proposed method constructs the quantification and classification rules related to the micro-image clarity to account for the blur-perceived full-light characteristics and uses the geometric observation mode of the virtual depth domain to effectively improve the extraction quality for corner features.
- (3)
- Compared with the given main lens focal length parameters, the main lens focal length values estimated by the Nousias and Liu methods are still significantly different from the given values, and the reprojection error is large, even reaching 6 pixels. The main lens focal length values estimated by the Labussière method are all close to the given values, but the reprojection error, an indicator that characterizes the accuracy of the intrinsic parameters, is too large, with a maximum of 20.049 pixels. Therefore, the robust performance of the proposed method is the best because it introduces blur-aware plenoptic features, constructs a step-by-step diffusion corner point optimization model to achieve high-quality extraction of corner point coordinates, and establishes a decoupled stacked intrinsic and extrinsic parameter optimization strategy to ensure the accuracy and robustness of the calibration.
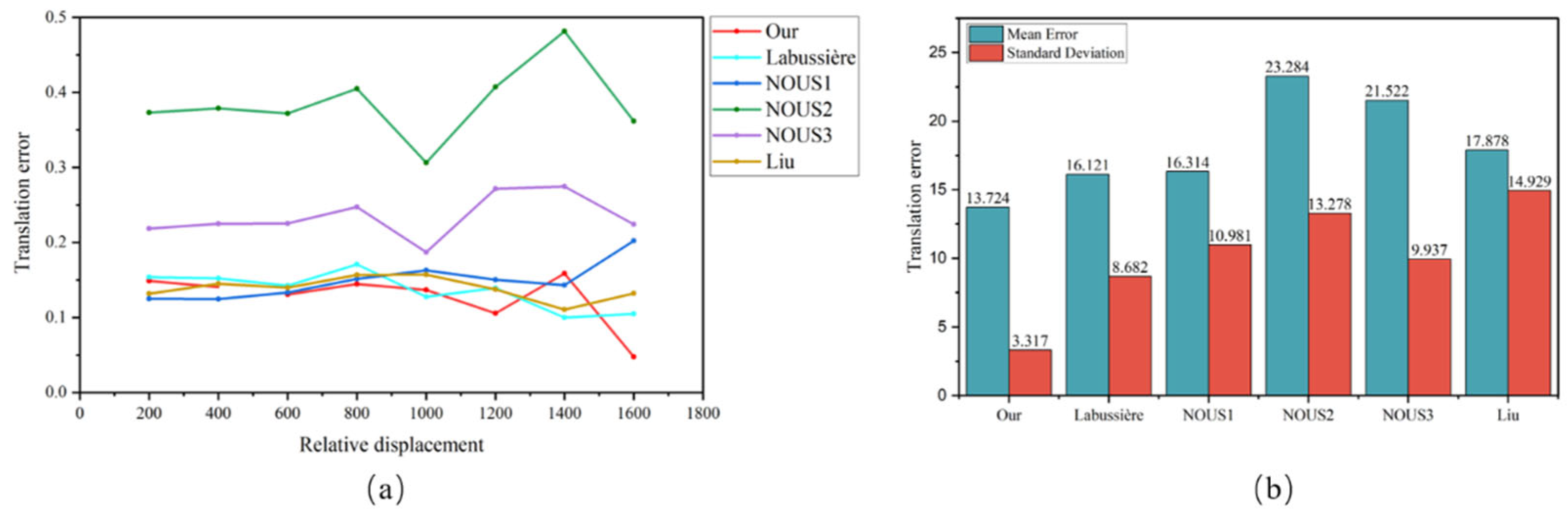
4.5. Comparative Analysis of the Z-Axis Translation Error
- (1)
- Comparative Performance in terms of the Extrinsic Parameter Error
- (2)
- Consistency Analysis via the Standard Deviation
- (3)
- Distance-dependent Performance Analysis
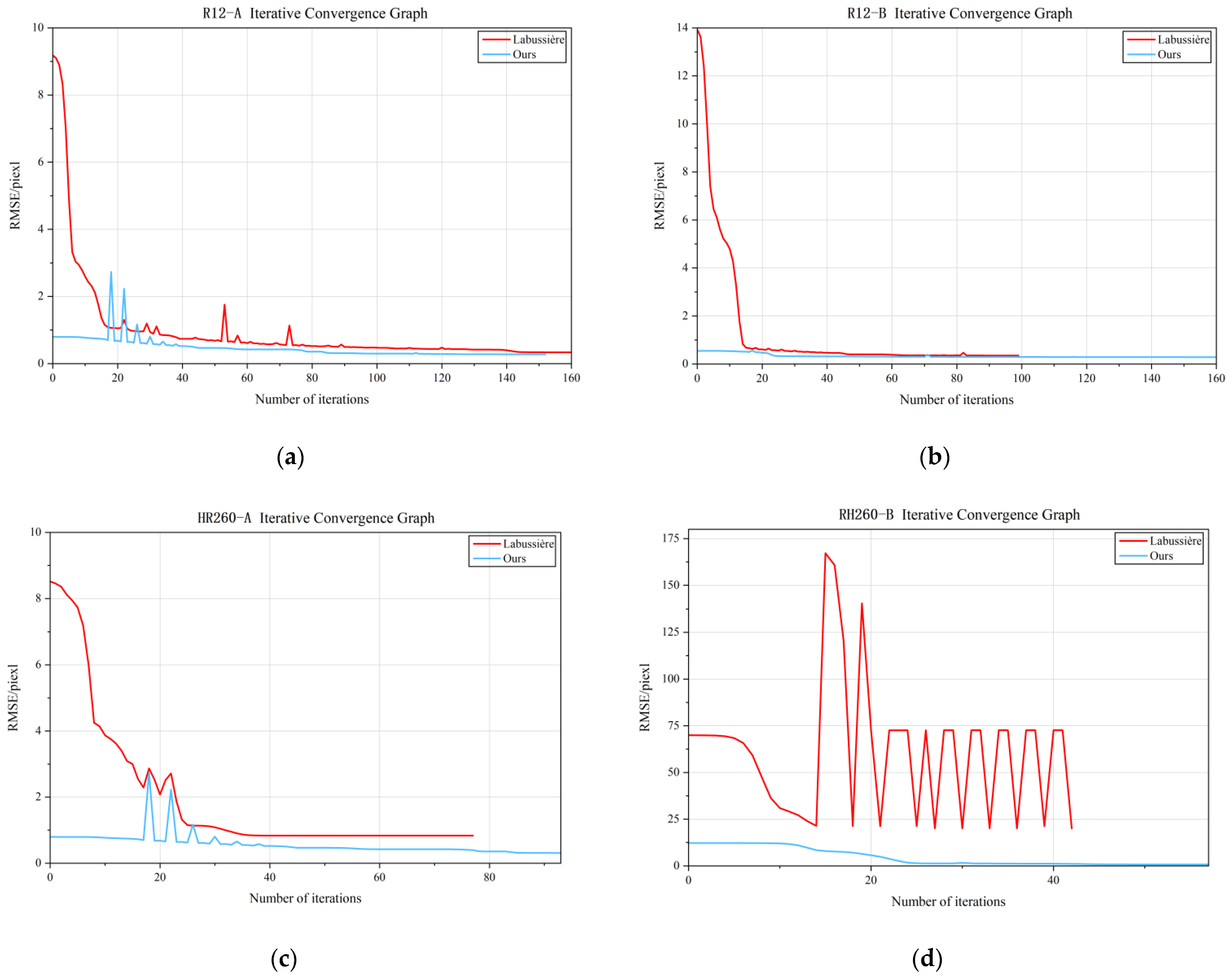
4.6. Runtime Efficiency Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Ji, X.; Dai, Q. Key Technologies of Light Field Capture for 3D Reconstruction in Microscopic Scene. Sci. China Inf. Sci. 2010, 53, 1917–1930. [Google Scholar] [CrossRef]
- Kim, C. 3D Reconstruction and Rendering from High Resolution Light Fields. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2015. [Google Scholar]
- Feng, W.; Qu, T.; Gao, J.; Wang, H.; Li, X.; Zhai, Z.; Zhao, D. 3D Reconstruction of Structured Light Fields Based on Point Cloud Adaptive Repair for Highly Reflective Surfaces. Appl. Opt. 2021, 60, 7086–7093. [Google Scholar] [CrossRef] [PubMed]
- Koch, R.; Pollefeys, M.; Heigl, B.; Van Gool, L.; Niemann, H. Calibration of Hand-Held Camera Sequences for Plenoptic Modeling. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–25 September 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 585–591. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 22, 1330–1334. [Google Scholar] [CrossRef]
- Vaish, V.; Wilburn, B.; Joshi, N.; Levoy, M. Using Plane+ Parallax for Calibrating Dense Camera Arrays. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, p. I–I. [Google Scholar]
- Georgiev, T.; Lumsdaine, A.; Goma, S. Plenoptic Principal Planes. In Proceedings of the Computational Optical Sensing and Imaging, Toronto, ON, Canada, 10–14 July 2011; Optica Publishing Group: Washington, DC, USA, 2011; p. JTuD3. [Google Scholar]
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light Field Photography with a Hand-Held Plenoptic Camera. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2005. [Google Scholar]
- Dansereau, D.G.; Pizarro, O.; Williams, S.B. Decoding, Calibration and Rectification for Lenselet-Based Plenoptic Cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1027–1034. [Google Scholar]
- Bok, Y.; Jeon, H.-G.; Kweon, I.S. Geometric Calibration of Micro-Lens-Based Light Field Cameras Using Line Features. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.; Zhang, X.; Yang, W.; Zhang, C.; Lei, M.; Dong, Z. A Calibration Method for Defocused Cameras Based on Defocus Blur Estimation. Measurement 2024, 235, 115045. [Google Scholar] [CrossRef]
- Johannsen, O.; Heinze, C.; Goldluecke, B.; Perwaß, C. On the Calibration of Focused Plenoptic Cameras. In Time-of-Flight and Depth Imaging. Sensors, Algorithms, and Applications; Grzegorzek, M., Theobalt, C., Koch, R., Kolb, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8200, pp. 302–317. ISBN 978-3-642-44963-5. [Google Scholar]
- Zeller, N.; Quint, F.; Stilla, U. Calibration and Accuracy Analysis of a Focused Plenoptic Camera. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 205–212. [Google Scholar] [CrossRef]
- Nousias, S.; Chadebecq, F.; Pichat, J.; Keane, P.; Ourselin, S.; Bergeles, C. Corner-Based Geometric Calibration of Multi-Focus Plenoptic Cameras. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 957–965. [Google Scholar]
- Noury, C.-A.; Teulière, C.; Dhome, M. Light-Field Camera Calibration from Raw Images. In Proceedings of the 2017 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 29 November–1 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Heinze, C.; Spyropoulos, S.; Hussmann, S.; Perwaß, C. Automated Robust Metric Calibration Algorithm for Multifocus Plenoptic Cameras. IEEE Trans. Instrum. Meas. 2016, 65, 1197–1205. [Google Scholar] [CrossRef]
- Zeller, N.; Noury, C.; Quint, F.; Teulière, C.; Stilla, U.; Dhome, M. Metric Calibration of a Focused Plenoptic Camera Based on a 3D Calibration Target. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 449–456. [Google Scholar]
- O’brien, S.; Trumpf, J.; Ila, V.; Mahony, R. Calibrating Light-Field Cameras Using Plenoptic Disc Features. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 286–294. [Google Scholar]
- Liu, Q.; Xie, X.; Zhang, X.; Tian, Y.; Li, J.; Wang, Y.; Xu, X. Stepwise Calibration of Plenoptic Cameras Based on Corner Features of Raw Images. Appl. Opt. 2020, 59, 4209–4219. [Google Scholar] [CrossRef] [PubMed]
- Labussière, M.; Teulière, C.; Bernardin, F.; Ait-Aider, O. Leveraging Blur Information for Plenoptic Camera Calibration. Int. J. Comput. Vis. 2022, 130, 1655–1677. [Google Scholar] [CrossRef]
- Labussière, M.; Teulière, C.; Bernardin, F.; Ait-Aider, O. Blur Aware Calibration of Multi-Focus Plenoptic Camera. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2020; pp. 2545–2554. [Google Scholar]
- Chen, B.; Xiong, C.; Zhang, Q. CCDN: Checkerboard Corner Detection Network for Robust Camera Calibration. arXiv 2023, arXiv:2302.05097. [Google Scholar] [CrossRef]
- Fleith, A.; Ahmed, D.; Cremers, D.; Zeller, N. LiFCal: Online Light Field Camera Calibration via Bundle Adjustment. In Proceedings of the DAGM German Conference on Pattern Recognition, Heidelberg, Germany, 19–22 September 2023; Springer: Berlin/Heidelberg, Germany, 2024; pp. 120–136. [Google Scholar]
- Liao, K.; Nie, L.; Huang, S.; Lin, C.; Zhang, J.; Zhao, Y.; Gabbouj, M.; Tao, D. Deep Learning for Camera Calibration and beyond: A Survey. arXiv 2023, arXiv:2303.10559. [Google Scholar] [CrossRef]
- Pan, L.; Baráth, D.; Pollefeys, M.; Schönberger, J.L. Global Structure-from-Motion Revisited. In Computer Vision—ECCV 2024; Leonardis, A., Ricci, E., Roth, S., Russakovsky, O., Sattler, T., Varol, G., Eds.; Springer Nature: Cham, Switzerland, 2025; Volume 15098, pp. 58–77. ISBN 978-3-031-73660-5. [Google Scholar]
- Ragonneau, T.M.; Zhang, Z. PDFO: A Cross-Platform Package for Powell’s Derivative-Free Optimization Solvers. Math. Program. Comput. 2024, 16, 535–559. [Google Scholar] [CrossRef]
- Thomason, C.M.; Thurow, B.S.; Fahringer, T.W. Calibration of a Microlens Array for a Plenoptic Camera. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; American Institute of Aeronautics and Astronautics: National Harbor, MD, USA, 2014. [Google Scholar]
- Suliga, P.; Wrona, T. Microlens Array Calibration Method for a Light Field Camera. In Proceedings of the 2018 19th International Carpathian Control Conference (ICCC), Szilvásvárad, Hungary, 28–30 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 19–22. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. Density-Based Spatial Clustering of Applications with Noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 240. [Google Scholar]
- Michels, T.; Petersen, A.; Koch, R. Creating Realistic Ground Truth Data for the Evaluation of Calibration Methods for Plenoptic and Conventional Cameras. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Québec City, QC, Canada, 16–19 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 434–442. [Google Scholar]












| Dataset | H (mm) | Checkerboard | Depth Distance | |||
|---|---|---|---|---|---|---|
| Size (Rows × Cols) | Scale (mm) | Min (mm) | Max (mm) | Step (mm) | ||
| R12-A | 450 | 9 × 5 | 10 | 265 | 385 | 10 |
| R12-B | 1000 | 8 × 5 | 20 | 450 | 900 | 50 |
| R12-C | ∞ | 6 × 4 | 30 | 400 | 1250 | 50 |
| HR260-A | 1500 | 7 × 5 | 35 | 1200 | 2200 | 100 |
| HR260-B | 4000 | 6 × 4 | 40 | 1000 | 2600 | 200 |
| Dataset | Resolution | (Pixels) | D (mm) | D (mm) | (mm) |
|---|---|---|---|---|---|
| R1 | 2000 × 3000 | 23.4 | 101.43 | 1.32 | 1.35/1.62/1.95 |
| R2 | 2000 × 3000 | 60 | 99.62 | 1.32 | 1.34/1.75/2.25 |
| R3 | 6000 × 8000 | 130 | 99.41 | 1.30 | 1.35/1.75/2.25 |
| Configuration | RMSE (Pixel) | ||
|---|---|---|---|
| R12-A | HR260-A | HR260-B | |
| Without neighboring blur-aware corner extraction | 0.936 | 1.541 | 1.945 |
| Without center-ray-assisted microlens array optimization | 0.610 | 1.171 | 14.421 |
| Without decoupled nonlinear optimization | 0.686 | 1.235 | 17.125 |
| Full system (all modules included) | 0.527 | 0.572 | 1.250 |
| Dataset | Method | Type1 | Type2 | Type3 | All |
|---|---|---|---|---|---|
| R1 | Nousias | (0.83, 0.42) (2.28, 0.04) | (0.79, 0.41) (2.22, 0.02) | (0.95, 0.45) (2.56, 0.10) | (0.84,0.43) (2.56,0.02) |
| Noury | (0.81, 0.37) (2.78, 0.03) | (0.82, 0.37) (2.06, 0.01) | (0.90, 0.47) (2.87, 0.03) | (0.84, 0.40) (2.87, 0.01) | |
| BFC-PC | (0.81, 0.37) (2.78, 0.03) | (0.71, 0.24) (1.04, 0.07) | (0.71, 0.23) (1.24, 0.03) | (0.74, 0.29) (2.78, 0.03) | |
| R2 | Nousias | (1.37, 0.69) (3.22, 0.13) | (1.55, 0.76) (3.63, 0.16) | (2.32, 0.88) (3.89, 0.41) | (1.53, 0.78) (3.89, 0.13) |
| Noury | (0.51, 0.33) (2.18, 0.03) | (0.73, 0.39) (2.37, 0.03) | (2.25, 0.80) (2.99, 0.11) | (0.73, 0.59) (2.99, 0.02) | |
| BFC-PC | (0.51, 0.33) (1.39, 0.03) | (0.43, 0.23) (1.12, 0.03) | (0.43, 0.23) (1.35, 0.01) | (0.46, 0.27) (2.18, 0.01) | |
| R3 | Nousias | (1.82, 0.92) (3.93, 0.08) | (2.91, 1.38) (6.26, 0.88) | (3.17, 1.54) (6.01, 0.23) | (2.43, 1.38) (6.26, 0.08) |
| Noury | (1.16, 0.63) (3.15, 0.04) | (2.17, 1.43) (4.83, 0.28) | (2.72, 1.64) (4.95, 0.06) | (1.71, 1.31) (4.95, 0.04) | |
| BFC-PC | (1.16, 0.63) (3.01, 0.04) | (1.11, 0.61) (3.48, 0.06) | (1.16, 0.62) (2.77, 0.10) | (1.14, 0.63) (3.48, 0.04) |
| Datasets | BFC-PC | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu |
|---|---|---|---|---|---|---|
| R12-A | 0.527 (0.080) | 0.856 (0.083) | 0.773 | 0.667 | 0.958 | 0.691 |
| R12-B | 0.421 (0.086) | 0.674 (0.183) | 0.538 | 0.519 | 0.593 | 0.330 |
| R12-C | 0.336 (0.040) | 0.738 (0.041) | 1.287 | 0.681 | 0.411 | 0.338 |
| HR260-A | 0.572 (0.257) | 1.827 (0.293) | 1.624 | 1.432 | 1.316 | 0.681 |
| HR260-B | 1.250 (0.371) | 20.049 (12.866) | 3.296 | 19.175 | 3.514 | 5.849 |
| R12-A (F = 50 mm, H = 450 mm) | ||||||
|---|---|---|---|---|---|---|
| Ours | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu | |
| [] | 50.471 | 49.714 | 61.305 | 62.476 | 63.328 | 58.233 |
| [] | 16.82 | 24.66 | — | — | — | — |
| [] | 2.044 | 2.998 | — | — | — | — |
| [] | 0.717 | 1.063 | — | — | — | — |
| [] | −6.8 | −14.6 | — | — | — | — |
| [] | 0.556 | 6.340 | — | — | — | — |
| ] | 57.520 | 56.701 | 71.131 | 72.541 | 73.530 | 66.985 |
| ] | 10.90 | 10.97 | — | — | — | — |
| ] | 8.419 | 7.887 | — | — | — | — |
| ] | 463.1 | 843. 1 | — | — | — | — |
| ] | 389.2 | 637.1 | — | — | — | — |
| ] | 29.1 | 31.5 | — | — | — | — |
| ] | 127.46 | 127.46 | — | — | — | — |
| ] | 766.26 | 578.18 | — | — | — | — |
| ] | 689.95 | 505.42 | — | — | — | — |
| ] | 855.03 | 552.08 | — | — | — | — |
| ] | 2083.9 | 2070.9 | 1984.9 | 2034.5 | 1973.7 | 2085.8 |
| ] | 1513.8 | 1610.9 | 1482.1 | 1481.0 | 1495.2 | 1590.3 |
| ] | 3,36.48 | 324.77 | 585.16 | 527.59 | 561.93 | 455.30 |
| R12-B (F = 50 mm, H = 450 mm) | ||||||
| Ours | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu | |
| [] | 50.170 | 50.047 | 53.913 | 52.988 | 52.977 | 48.949 |
| [] | −0.419 | 2.900 | — | — | — | — |
| [] | 0.086 | 0.300 | — | — | — | — |
| [] | 0.036 | 0.064 | — | — | — | — |
| [] | 8.46 | 14.13 | — | — | — | — |
| [] | 17.655 | 21.540 | — | — | — | — |
| ] | 52.217 | 52.125 | 56.062 | 55.128 | 55.124 | 50.830 |
| ] | 12.03 | 12.44 | — | — | — | — |
| ] | 6.447 | 5.988 | — | — | — | — |
| ] | 436.9 | 607.2 | — | — | — | — |
| ] | 477.5 | 514.5 | — | — | — | — |
| ] | 38.5 | 46.0 | — | — | — | — |
| ] | 127.46 | 127.45 | — | — | — | — |
| ] | 708.39 | 580.49 | — | — | — | — |
| ] | 646.18 | 504.31 | — | — | — | — |
| ] | 795.08 | 546.36 | — | — | — | — |
| ] | 1877.2 | 1958.3 | 2074.7 | 2094.7 | 1837.0 | 1946.9 |
| ] | 1874.4 | 1802.9 | 1640.2 | 1649.1 | 1620.4 | 1668.7 |
| ] | 337.83 | 336.38 | 447.81 | 401.93 | 414.32 | 324.70 |
| R12-C (F = 50 mm, H = ∞) | ||||||
|---|---|---|---|---|---|---|
| Ours | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu | |
| [] | 50.197 | 50.013 | 51.113 | 49.919 | 50.812 | 44.523 |
| [] | 17.21 | 18.61 | — | — | — | — |
| [] | 3.016 | 2.646 | — | — | — | — |
| [] | 1.406 | 1.038 | — | — | — | — |
| [] | 9.16 | 19.11 | — | — | — | — |
| [] | 7.245 | 7.311 | — | — | — | — |
| ] | 49.424 | 49.362 | 50.331 | 49.067 | 49.882 | 43.819 |
| ] | 12.76 | 13.12 | — | — | — | — |
| ] | 8.153 | 7.446 | — | — | — | — |
| ] | 417.8 | 490.9 | — | — | — | — |
| ] | 389.7 | 388.9 | — | — | — | — |
| ] | 35.1 | 41.1 | — | — | — | — |
| ] | 127.46 | 127.48 | — | — | — | — |
| ] | 650.32 | 569.88 | — | — | — | — |
| ] | 598.01 | 491.71 | — | — | — | — |
| ] | 712.68 | 535.28 | — | — | — | — |
| ] | 1743.7 | 1692.1 | 1966.3 | 1913.8 | 2052.5 | 1845.3 |
| ] | 1562.3 | 1677.8 | 1484.6 | 1487.2 | 1492.7 | 1514.4 |
| ] | 328.63 | 319.53 | 357.80 | 349.99 | 353.26 | 274.00 |
| HR260-A (F = 105 mm, H = 1500 mm) | ||||||
|---|---|---|---|---|---|---|
| Ours | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu | |
| [] | 105.658 | 112.129 | 87.115 | 52.486 | 52.227 | 57.274 |
| [] | −45.06 | 11.82 | — | — | — | — |
| [] | −14.794 | 2.066 | — | — | — | — |
| [] | −9.576 | 1.143 | — | — | — | — |
| [] | 12.08 | −2.21 | — | — | — | — |
| [] | −24.320 | 6.325 | — | — | — | — |
| ] | 109.929 | 109.086 | 89.097 | 50.416 | 49.497 | 54.867 |
| ] | 11.36 | 10.92 | — | — | — | — |
| ] | 7.690 | 7.206 | — | — | — | — |
| ] | 352.7 | 834.6 | — | — | — | — |
| ] | 4752.3 | 3274.3 | — | — | — | — |
| ] | 120.8 | 237.5 | — | — | — | — |
| ] | 351.22 | 349.55 | — | — | — | — |
| ] | 2812.02 | 2365.11 | — | — | — | — |
| ] | 2778.64 | 2333.44 | — | — | — | — |
| ] | 2729.26 | 2297.09 | — | — | — | — |
| ] | 3066.2 | 3186.1 | 3119.2 | 3117.7 | 3098.7 | 2171.7 |
| ] | 2015.7 | 2147.1 | 2084.3 | 2083.7 | 2056.3 | 1608.3 |
| ] | 1584.16 | 1486.54 | 392.60 | 522.90 | 583.80 | 668.50 |
| HR260-B (F = 105 mm, H = 2000 mm) | ||||||
|---|---|---|---|---|---|---|
| Ours | Labussière | NOUS1 | NOUS2 | NOUS3 | Liu | |
| [] | 110.766 | 111.888 | 58.728 | 42.712 | 42.233 | 57.919 |
| [] | −7.78 | 4.38 | — | — | — | — |
| [] | −1.224 | 0.065 | — | — | — | — |
| [] | −0.730 | 0.002 | — | — | — | — |
| [] | −9.03 | −11.29 | — | — | — | — |
| [] | 2.250 | −8.907 | — | — | — | — |
| ] | 107.737 | 106.403 | 56.692 | 0.667 | 58.124 | 54.857 |
| ] | 11.13 | −7.25 | — | — | — | — |
| ] | 8.863 | 16.043 | — | — | — | — |
| ] | 689.2 | 824.7 | — | — | — | — |
| ] | 3087.1 | 3425.9 | — | — | — | — |
| ] | 276.7 | 381.2 | — | — | — | — |
| ] | 350.27 | 349.40 | — | — | — | — |
| ] | 2155.54 | 2588.68 | — | — | — | — |
| ] | 2190.22 | 2546.87 | — | — | — | — |
| ] | 2225.47 | 2506.37 | — | — | — | — |
| ] | 3134.5 | 8168.1 | 3121.9 | 3119.5 | 3122.1 | 1909.2 |
| ] | 1696.6 | −280.7 | 2086.7 | 2088.6 | 2085.2 | 1687.9 |
| ] | 1354.74 | 1639.79 | 526.20 | 1.10 | 2203.80 | 686.00 |
| Dataset | Method | Corner Extraction | Center Ray Optimization (Iterations, Time) | Extrinsic Optimization (Iterations, Time) | Global Nonlinear Optimization (Iterations, Time) |
|---|---|---|---|---|---|
| R12-A | Labussière | 1027 | / | / | (160, 451.26) |
| Ours | 1041 | (6, 8.88) | (98, 20.69) | (152, 378.89) | |
| R12-B | Labussière | 982 | / | / | (100, 284.58) |
| Ours | 1045 | (6, 8.82) | (74, 8.78) | (160, 197.75) | |
| HR260-A | Labussière | 4824 | / | / | (77, 101.68) |
| Ours | 5069 | (5, 0.92) | (250, 19.86) | (93, 64.45) | |
| HR260-B | Labussière | 4809 | / | / | (42, 52.70) |
| Ours | 4970 | (5, 0.91) | (180, 14.45) | (57, 65.48) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Guan, H.; Ni, Q. A Blur Feature-Guided Cascaded Calibration Method for Plenoptic Cameras. Sensors 2025, 25, 4940. https://doi.org/10.3390/s25164940
Liu Z, Guan H, Ni Q. A Blur Feature-Guided Cascaded Calibration Method for Plenoptic Cameras. Sensors. 2025; 25(16):4940. https://doi.org/10.3390/s25164940
Chicago/Turabian StyleLiu, Zhendong, Hongliang Guan, and Qingyang Ni. 2025. "A Blur Feature-Guided Cascaded Calibration Method for Plenoptic Cameras" Sensors 25, no. 16: 4940. https://doi.org/10.3390/s25164940
APA StyleLiu, Z., Guan, H., & Ni, Q. (2025). A Blur Feature-Guided Cascaded Calibration Method for Plenoptic Cameras. Sensors, 25(16), 4940. https://doi.org/10.3390/s25164940





