Machine Learning-Based Assessment of Parkinson’s Disease Symptoms Using Wearable and Smartphone Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Data Preparation
2.3. Feature Extraction
2.4. Examination Metadata
2.5. Feature Selection
2.6. ML Model Training
2.7. Individual Symptom Evaluation
- Single exercise, single sensor from one device—finding which sensor and device combination best captures specific symptoms during different exercises,
- Single exercise—finding which exercise is best at capturing each of the symptoms,
- All exercises and devices—finding out how the models perform at capturing symptoms when all of the data can be used.
2.8. Overall State Evaluation
- Single device—finding which device is more useful in capturing the scope of the disease,
- All collected data—building a complete and optimal model for predicting a patient’s state.
3. Results
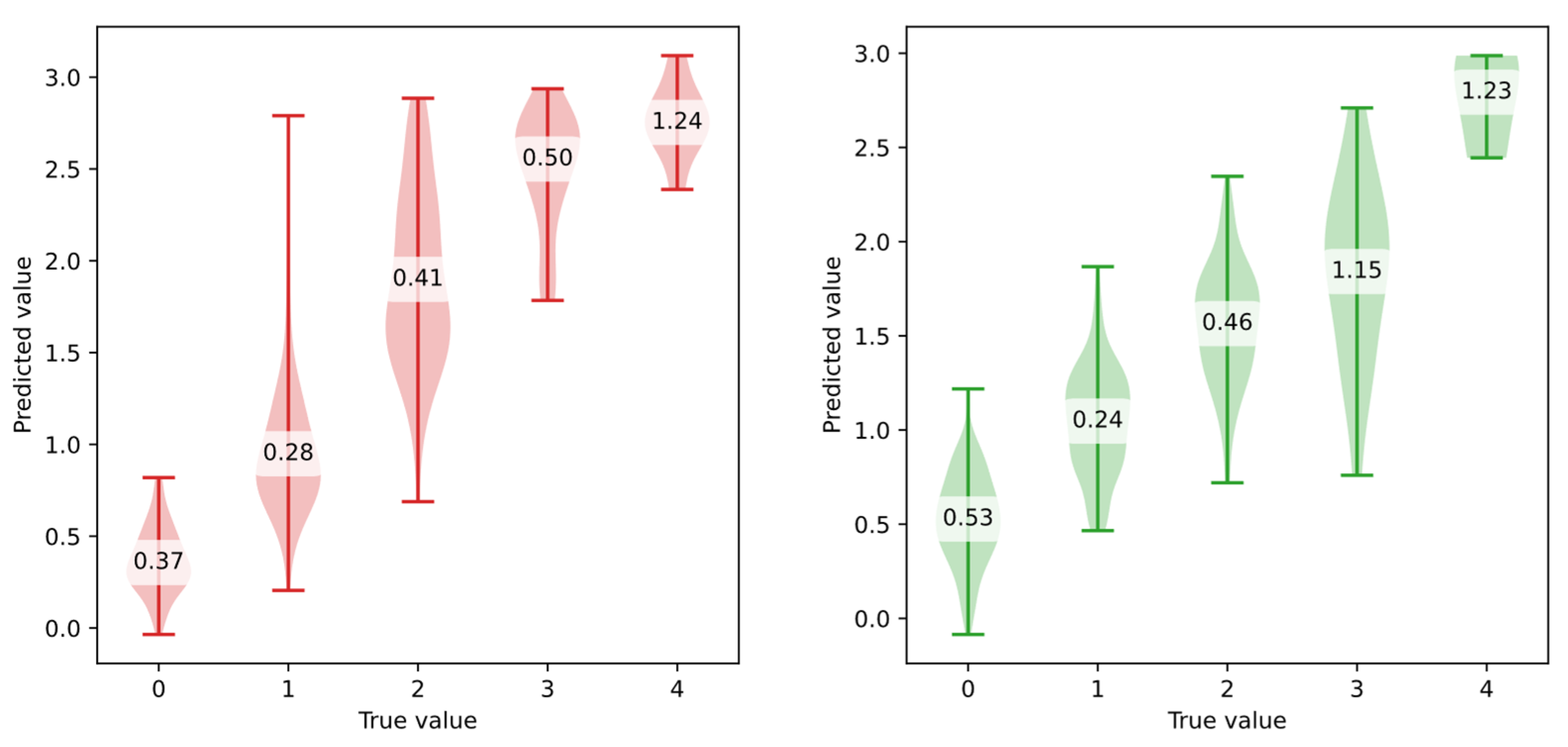
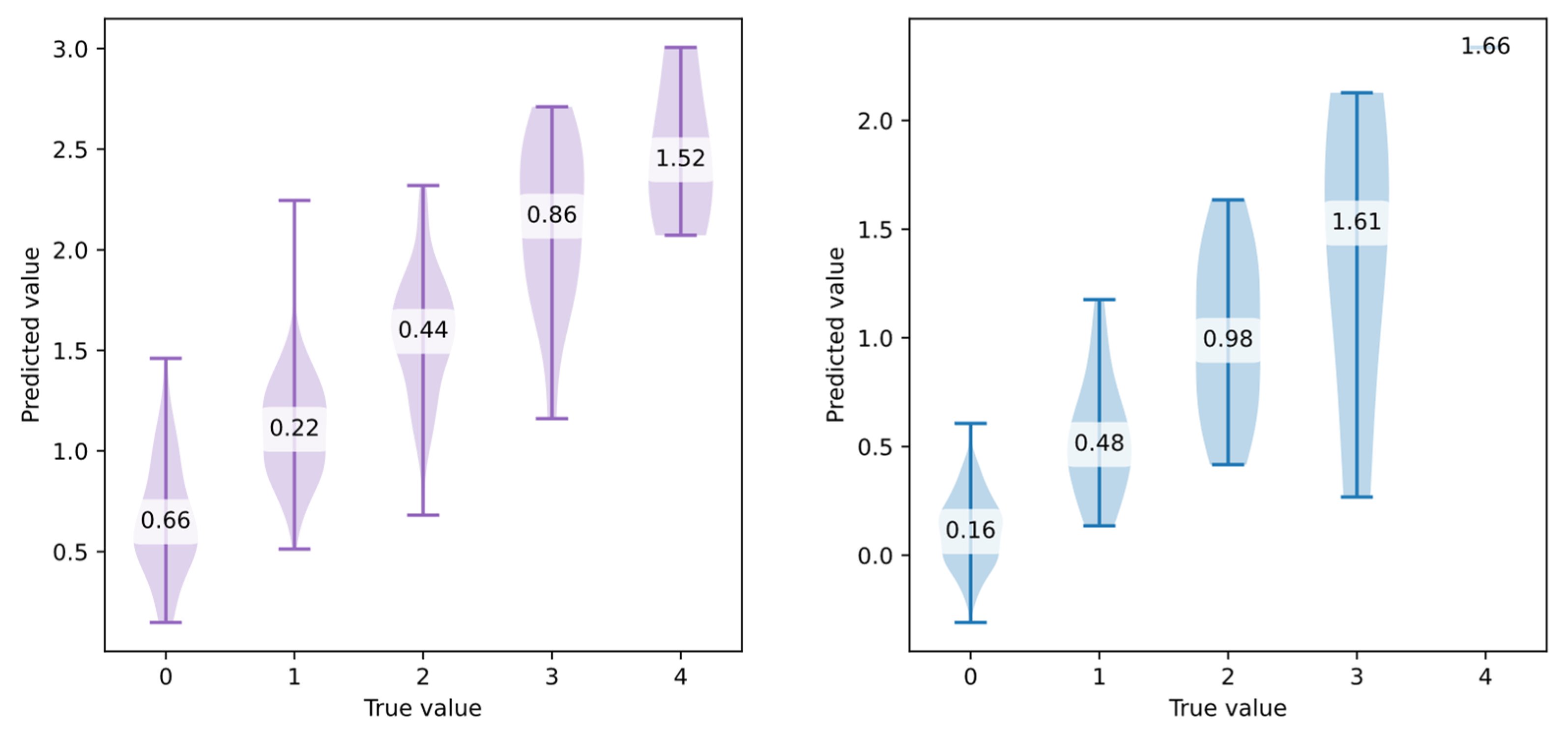
3.1. Individual Symptom Evaluation
- Using post-processing to clip predicted values to the valid range [0, 4],
- Reformulating the problem as a classification task (ordinal classification). However, this would lead to a loss of prediction precision.
- If neural networks were explored, applying a bounded activation function scaled to the target range in the final layer of the model.
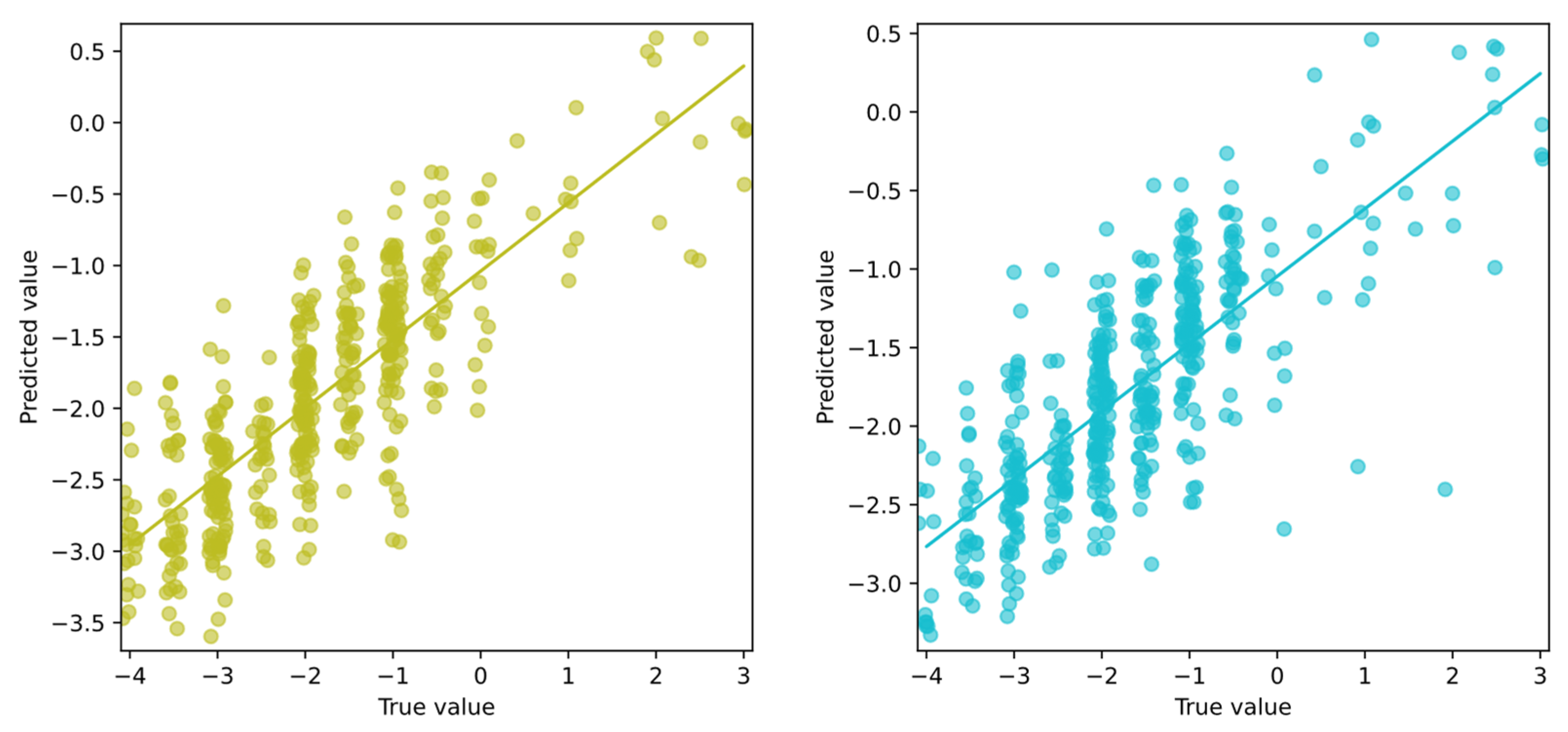
3.2. Overall State Evaluation
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symptom | Split | Dataset | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|---|
| bradykinesia | 10F | MYO-ACC-#1 | XG | 0.157 | 0.417 | 0.666 | 1.194 | 2.215 |
| bradykinesia | LOO | MYO-ACC-#1 | XG | 0.146 | 0.399 | 0.673 | 1.219 | 2.245 |
| bradykinesia | 10F | MYO-ACC-#2 | SVM | 0.222 | 0.477 | 0.630 | 1.170 | 2.075 |
| bradykinesia | LOO | MYO-ACC-#2 | SVM | 0.204 | 0.458 | 0.637 | 1.213 | 2.268 |
| bradykinesia | 10F | MYO-ACC-#3 | SVM | 0.344 | 0.594 | 0.572 | 1.114 | 1.989 |
| bradykinesia | LOO | MYO-ACC-#3 | SVM | 0.317 | 0.565 | 0.593 | 1.003 | 1.461 |
| bradykinesia | 10F | MYO-GYRO-#1 | RF | 0.200 | 0.450 | 0.648 | 1.209 | 2.240 |
| bradykinesia | LOO | MYO-GYRO-#1 | SVM | 0.233 | 0.484 | 0.630 | 1.180 | 2.165 |
| bradykinesia | 10F | MYO-GYRO-#2 | SVM | 0.197 | 0.447 | 0.648 | 1.179 | 2.072 |
| bradykinesia | LOO | MYO-GYRO-#2 | SVM | 0.188 | 0.437 | 0.657 | 1.167 | 1.968 |
| bradykinesia | 10F | MYO-GYRO-#3 | RF | 0.357 | 0.600 | 0.596 | 0.992 | 1.436 |
| bradykinesia | LOO | MYO-GYRO-#3 | XG | 0.408 | 0.639 | 0.570 | 0.896 | 1.187 |
| bradykinesia | 10F | Phone-ACC-#1 | SVM | 0.167 | 0.414 | 0.644 | 1.195 | 2.149 |
| bradykinesia | LOO | Phone-ACC-#1 | SVM | 0.200 | 0.454 | 0.650 | 1.168 | 1.998 |
| bradykinesia | 10F | Phone-ACC-#2 | RF | 0.220 | 0.475 | 0.651 | 1.161 | 2.004 |
| bradykinesia | LOO | Phone-ACC-#2 | SVM | 0.161 | 0.418 | 0.641 | 1.229 | 2.407 |
| bradykinesia | 10F | Phone-ACC-#3 | SVM | 0.400 | 0.638 | 0.547 | 0.956 | 1.402 |
| bradykinesia | LOO | Phone-ACC-#3 | SVM | 0.360 | 0.603 | 0.585 | 0.978 | 1.402 |
| bradykinesia | 10F | Phone-GYRO-#1 | SVM | 0.130 | 0.368 | 0.668 | 1.302 | 2.598 |
| bradykinesia | LOO | Phone-GYRO-#1 | SVM | 0.094 | 0.330 | 0.674 | 1.341 | 2.761 |
| bradykinesia | 10F | Phone-GYRO-#2 | RF | 0.215 | 0.478 | 0.645 | 1.196 | 2.140 |
| bradykinesia | LOO | Phone-GYRO-#2 | SVM | 0.204 | 0.457 | 0.619 | 1.190 | 2.172 |
| bradykinesia | 10F | Phone-GYRO-#3 | XG | 0.342 | 0.590 | 0.578 | 0.970 | 1.531 |
| bradykinesia | LOO | Phone-GYRO-#3 | RF | 0.290 | 0.539 | 0.615 | 1.059 | 1.708 |
| dyskinesia | 10F | MYO-ACC-#1 | XG | 0.248 | 0.516 | 0.275 | 1.399 | 3.219 |
| dyskinesia | LOO | MYO-ACC-#1 | XG | 0.302 | 0.557 | 0.266 | 1.371 | 3.046 |
| dyskinesia | 10F | MYO-ACC-#2 | SVM | 0.263 | 0.599 | 0.269 | 1.539 | 3.493 |
| dyskinesia | LOO | MYO-ACC-#2 | XG | 0.335 | 0.580 | 0.281 | 1.109 | 1.810 |
| dyskinesia | 10F | MYO-ACC-#3 | SVM | 0.259 | 0.542 | 0.260 | 1.615 | 4.305 |
| dyskinesia | LOO | MYO-ACC-#3 | XG | 0.326 | 0.572 | 0.265 | 1.266 | 2.344 |
| dyskinesia | 10F | MYO-GYRO-#1 | XG | 0.359 | 0.600 | 0.253 | 1.209 | 2.179 |
| dyskinesia | LOO | MYO-GYRO-#1 | XG | 0.379 | 0.616 | 0.259 | 1.160 | 2.009 |
| dyskinesia | 10F | MYO-GYRO-#2 | XG | 0.302 | 0.561 | 0.283 | 1.159 | 1.962 |
| dyskinesia | LOO | MYO-GYRO-#2 | RF | 0.298 | 0.557 | 0.270 | 1.379 | 2.862 |
| dyskinesia | 10F | MYO-GYRO-#3 | SVM | 0.145 | 0.432 | 0.294 | 1.724 | 4.493 |
| dyskinesia | LOO | MYO-GYRO-#3 | SVM | 0.166 | 0.457 | 0.320 | 1.709 | 4.421 |
| dyskinesia | 10F | Phone-ACC-#1 | RF | 0.343 | 0.586 | 0.235 | 1.283 | 2.487 |
| dyskinesia | LOO | Phone-ACC-#1 | SVM | 0.355 | 0.641 | 0.240 | 1.379 | 2.837 |
| dyskinesia | 10F | Phone-ACC-#2 | RF | 0.240 | 0.490 | 0.269 | 1.393 | 2.912 |
| dyskinesia | LOO | Phone-ACC-#2 | XG | 0.277 | 0.530 | 0.254 | 1.354 | 2.894 |
| dyskinesia | 10F | Phone-ACC-#3 | RF | 0.125 | 0.385 | 0.315 | 1.355 | 2.636 |
| dyskinesia | LOO | Phone-ACC-#3 | XG | 0.084 | 0.367 | 0.317 | 1.439 | 3.091 |
| dyskinesia | 10F | Phone-GYRO-#1 | RF | 0.385 | 0.622 | 0.228 | 1.238 | 2.353 |
| dyskinesia | LOO | Phone-GYRO-#1 | SVM | 0.348 | 0.625 | 0.237 | 1.291 | 2.475 |
| dyskinesia | 10F | Phone-GYRO-#2 | RF | 0.343 | 0.589 | 0.240 | 1.208 | 2.194 |
| dyskinesia | LOO | Phone-GYRO-#2 | RF | 0.307 | 0.557 | 0.254 | 1.259 | 2.405 |
| dyskinesia | 10F | Phone-GYRO-#3 | RF | 0.236 | 0.485 | 0.274 | 1.399 | 2.903 |
| dyskinesia | LOO | Phone-GYRO-#3 | SVM | 0.191 | 0.471 | 0.284 | 1.585 | 3.655 |
| stiffness | 10F | MYO-ACC-#1 | XG | 0.141 | 0.412 | 0.633 | 1.137 | 1.958 |
| stiffness | LOO | MYO-ACC-#1 | XG | 0.127 | 0.383 | 0.633 | 1.156 | 2.015 |
| stiffness | 10F | MYO-ACC-#2 | RF | 0.165 | 0.408 | 0.602 | 1.204 | 2.224 |
| stiffness | LOO | MYO-ACC-#2 | RF | 0.152 | 0.399 | 0.614 | 1.206 | 2.113 |
| stiffness | 10F | MYO-ACC-#3 | RF | 0.309 | 0.562 | 0.568 | 0.992 | 1.402 |
| stiffness | LOO | MYO-ACC-#3 | XG | 0.360 | 0.600 | 0.543 | 0.869 | 1.073 |
| stiffness | 10F | MYO-GYRO-#1 | XG | 0.132 | 0.400 | 0.621 | 1.168 | 2.051 |
| stiffness | LOO | MYO-GYRO-#1 | SVM | 0.160 | 0.400 | 0.589 | 1.215 | 2.280 |
| stiffness | 10F | MYO-GYRO-#2 | XG | 0.140 | 0.410 | 0.639 | 1.083 | 1.698 |
| stiffness | LOO | MYO-GYRO-#2 | RF | 0.178 | 0.425 | 0.611 | 1.175 | 2.009 |
| stiffness | 10F | MYO-GYRO-#3 | SVM | 0.261 | 0.515 | 0.565 | 1.046 | 1.623 |
| stiffness | LOO | MYO-GYRO-#3 | XG | 0.303 | 0.557 | 0.558 | 0.862 | 1.075 |
| stiffness | 10F | Phone-ACC-#1 | SVM | 0.180 | 0.424 | 0.592 | 1.096 | 1.712 |
| stiffness | LOO | Phone-ACC-#1 | SVM | 0.143 | 0.381 | 0.600 | 1.167 | 1.969 |
| stiffness | 10F | Phone-ACC-#2 | RF | 0.172 | 0.415 | 0.598 | 1.197 | 2.193 |
| stiffness | LOO | Phone-ACC-#2 | RF | 0.180 | 0.424 | 0.593 | 1.179 | 2.120 |
| stiffness | 10F | Phone-ACC-#3 | SVM | 0.272 | 0.529 | 0.569 | 1.046 | 1.591 |
| stiffness | LOO | Phone-ACC-#3 | SVM | 0.250 | 0.512 | 0.572 | 1.049 | 1.574 |
| stiffness | 10F | Phone-GYRO-#1 | XG | 0.172 | 0.439 | 0.604 | 1.034 | 1.575 |
| stiffness | LOO | Phone-GYRO-#1 | SVM | 0.208 | 0.457 | 0.584 | 1.122 | 1.838 |
| stiffness | 10F | Phone-GYRO-#2 | SVM | 0.232 | 0.486 | 0.593 | 1.123 | 1.832 |
| stiffness | LOO | Phone-GYRO-#2 | SVM | 0.242 | 0.494 | 0.579 | 1.131 | 1.962 |
| stiffness | 10F | Phone-GYRO-#3 | SVM | 0.291 | 0.541 | 0.562 | 1.036 | 1.612 |
| stiffness | LOO | Phone-GYRO-#3 | RF | 0.285 | 0.536 | 0.575 | 0.980 | 1.356 |
| tremor | 10F | MYO-ACC-#1 | RF | 0.523 | 0.723 | 0.570 | 0.770 | 0.875 |
| tremor | LOO | MYO-ACC-#1 | SVM | 0.557 | 0.750 | 0.541 | 0.777 | 0.926 |
| tremor | 10F | MYO-ACC-#2 | SVM | 0.535 | 0.732 | 0.544 | 0.800 | 1.017 |
| tremor | LOO | MYO-ACC-#2 | SVM | 0.531 | 0.730 | 0.561 | 0.799 | 0.951 |
| tremor | 10F | MYO-ACC-#3 | RF | 0.293 | 0.548 | 0.683 | 1.054 | 1.634 |
| tremor | LOO | MYO-ACC-#3 | SVM | 0.353 | 0.606 | 0.647 | 0.986 | 1.421 |
| tremor | 10F | MYO-GYRO-#1 | RF | 0.590 | 0.769 | 0.537 | 0.690 | 0.685 |
| tremor | LOO | MYO-GYRO-#1 | RF | 0.596 | 0.773 | 0.523 | 0.698 | 0.720 |
| tremor | 10F | MYO-GYRO-#2 | SVM | 0.524 | 0.726 | 0.565 | 0.821 | 0.996 |
| tremor | LOO | MYO-GYRO-#2 | SVM | 0.544 | 0.739 | 0.552 | 0.785 | 0.912 |
| tremor | 10F | MYO-GYRO-#3 | RF | 0.340 | 0.591 | 0.676 | 0.965 | 1.305 |
| tremor | LOO | MYO-GYRO-#3 | RF | 0.311 | 0.565 | 0.690 | 1.026 | 1.484 |
| tremor | 10F | Phone-ACC-#1 | RF | 0.595 | 0.772 | 0.537 | 0.675 | 0.652 |
| tremor | LOO | Phone-ACC-#1 | XG | 0.616 | 0.786 | 0.514 | 0.652 | 0.642 |
| tremor | 10F | Phone-ACC-#2 | SVM | 0.535 | 0.733 | 0.562 | 0.780 | 0.922 |
| tremor | LOO | Phone-ACC-#2 | SVM | 0.528 | 0.728 | 0.562 | 0.805 | 0.983 |
| tremor | 10F | Phone-ACC-#3 | SVM | 0.323 | 0.573 | 0.679 | 0.985 | 1.396 |
| tremor | LOO | Phone-ACC-#3 | SVM | 0.359 | 0.607 | 0.659 | 0.945 | 1.314 |
| tremor | 10F | Phone-GYRO-#1 | RF | 0.590 | 0.768 | 0.546 | 0.662 | 0.614 |
| tremor | LOO | Phone-GYRO-#1 | RF | 0.566 | 0.752 | 0.553 | 0.696 | 0.673 |
| tremor | 10F | Phone-GYRO-#2 | RF | 0.536 | 0.734 | 0.581 | 0.762 | 0.827 |
| tremor | LOO | Phone-GYRO-#2 | SVM | 0.516 | 0.718 | 0.568 | 0.776 | 0.894 |
| tremor | 10F | Phone-GYRO-#3 | SVM | 0.345 | 0.590 | 0.652 | 0.967 | 1.420 |
| Symptom | Split | Dataset | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|---|
| bradykinesia | 10F | #1 | RF | 0.234 | 0.495 | 0.638 | 1.163 | 2.024 |
| bradykinesia | LOO | #1 | SVM | 0.283 | 0.541 | 0.616 | 1.083 | 1.713 |
| bradykinesia | 10F | #2 | SVM | 0.313 | 0.562 | 0.586 | 1.101 | 1.886 |
| bradykinesia | LOO | #2 | SVM | 0.372 | 0.623 | 0.565 | 1.076 | 1.840 |
| bradykinesia | 10F | #3 | RF | 0.422 | 0.654 | 0.556 | 0.956 | 1.412 |
| bradykinesia | LOO | #3 | SVM | 0.392 | 0.631 | 0.562 | 0.977 | 1.437 |
| dyskinesia | 10F | #1 | SVM | 0.433 | 0.690 | 0.251 | 1.175 | 2.024 |
| dyskinesia | LOO | #1 | SVM | 0.477 | 0.722 | 0.245 | 1.182 | 2.178 |
| dyskinesia | 10F | #2 | RF | 0.386 | 0.624 | 0.245 | 1.181 | 2.015 |
| dyskinesia | LOO | #2 | SVM | 0.338 | 0.641 | 0.271 | 1.440 | 3.098 |
| dyskinesia | 10F | #3 | SVM | 0.197 | 0.488 | 0.279 | 1.668 | 4.251 |
| dyskinesia | LOO | #3 | SVM | 0.296 | 0.603 | 0.289 | 1.557 | 3.771 |
| state(doctor) | 10F | #1 | SVM | 0.370 | 0.610 | 0.823 | 1.463 | 3.489 |
| state(doctor) | LOO | #1 | SVM | 0.384 | 0.627 | 0.819 | 1.459 | 3.383 |
| state(doctor) | 10F | #2 | RF | 0.333 | 0.580 | 0.820 | 1.546 | 3.808 |
| state(doctor) | LOO | #2 | SVM | 0.329 | 0.580 | 0.825 | 1.562 | 3.822 |
| state(doctor) | 10F | #3 | SVM | 0.343 | 0.592 | 0.740 | 1.586 | 3.932 |
| state(doctor) | LOO | #3 | SVM | 0.361 | 0.615 | 0.727 | 1.600 | 3.990 |
| state(patient) | 10F | #1 | SVM | 0.364 | 0.604 | 0.858 | 1.402 | 3.327 |
| state(patient) | LOO | #1 | SVM | 0.383 | 0.623 | 0.859 | 1.385 | 3.241 |
| state(patient) | 10F | #2 | RF | 0.313 | 0.566 | 0.903 | 1.510 | 3.524 |
| state(patient) | LOO | #2 | SVM | 0.328 | 0.582 | 0.868 | 1.514 | 3.911 |
| state(patient) | 10F | #3 | RF | 0.317 | 0.567 | 0.812 | 1.458 | 3.478 |
| state(patient) | LOO | #3 | SVM | 0.361 | 0.607 | 0.771 | 1.498 | 3.646 |
| stiffness | 10F | #1 | RF | 0.244 | 0.511 | 0.566 | 1.108 | 1.784 |
| stiffness | LOO | #1 | RF | 0.212 | 0.469 | 0.575 | 1.125 | 1.831 |
| stiffness | 10F | #2 | RF | 0.228 | 0.483 | 0.590 | 1.118 | 1.816 |
| stiffness | LOO | #2 | SVM | 0.277 | 0.533 | 0.555 | 1.093 | 1.858 |
| stiffness | 10F | #3 | SVM | 0.402 | 0.640 | 0.511 | 0.882 | 1.152 |
| stiffness | LOO | #3 | SVM | 0.439 | 0.672 | 0.503 | 0.860 | 1.085 |
| tremor | 10F | #1 | RF | 0.630 | 0.795 | 0.496 | 0.657 | 0.637 |
| tremor | LOO | #1 | SVM | 0.674 | 0.822 | 0.464 | 0.646 | 0.645 |
| tremor | 10F | #2 | SVM | 0.607 | 0.780 | 0.511 | 0.740 | 0.839 |
| tremor | LOO | #2 | SVM | 0.665 | 0.818 | 0.468 | 0.683 | 0.730 |
| tremor | 10F | #3 | SVM | 0.424 | 0.664 | 0.627 | 0.906 | 1.183 |
| tremor | LOO | #3 | SVM | 0.467 | 0.700 | 0.595 | 0.885 | 1.168 |
References
- Kirmani, B.F.; Shapiro, L.A.; Shetty, A.K. Neurological and Neurodegenerative Disorders: Novel Concepts and Treatment. Aging Dis. 2021, 12, 950. [Google Scholar] [CrossRef]
- Sveinbjornsdottir, S. The Clinical Symptoms of Parkinson’s Disease. J. Neurochem. 2016, 139, 318–324. [Google Scholar] [CrossRef]
- Bloem, B.R.; Okun, M.S.; Klein, C. Parkinson’s Disease. Lancet 2021, 397, 2284–2303. [Google Scholar] [CrossRef]
- de Lau, L.M.; Breteler, M.M. Epidemiology of Parkinson’s Disease. Lancet Neurol. 2006, 5, 525–535. [Google Scholar] [CrossRef]
- Connolly, B.S.; Lang, A.E. Pharmacological Treatment of Parkinson Disease: A Review. JAMA 2014, 311, 1670–1683. [Google Scholar] [CrossRef]
- Giugni, J.C.; Okun, M.S. Treatment of Advanced Parkinson’s Disease. Curr. Opin. Neurol. 2014, 27, 450. [Google Scholar] [CrossRef]
- Lee, T.K.; Yankee, E.L. A Review on Parkinson’s Disease Treatment. Neurosciences 2021, 8, 222–244. [Google Scholar] [CrossRef]
- Yanase, J.; Triantaphyllou, E. A Systematic Survey of Computer-Aided Diagnosis in Medicine: Past and Present Developments. Expert. Syst. Appl. 2019, 138, 112821. [Google Scholar] [CrossRef]
- Shehab, M.; Abualigah, L.; Shambour, Q.; Abu-Hashem, M.A.; Shambour, M.K.Y.; Alsalibi, A.I.; Gandomi, A.H. Machine Learning in Medical Applications: A Review of State-of-the-Art Methods. Comput. Biol. Med. 2022, 145, 105458. [Google Scholar] [CrossRef] [PubMed]
- Oung, Q.W.; Hariharan, M.; Lee, H.L.; Basah, S.N.; Sarillee, M.; Lee, C.H. Wearable Multimodal Sensors for Evaluation of Patients with Parkinson Disease. In Proceedings of the 5th IEEE International Conference on Control System, Computing and Engineering, ICCSCE 2015, Penang, Malaysia, 27–29 November 2015; pp. 269–274. [Google Scholar] [CrossRef]
- Patel, S.; Lorincz, K.; Hughes, R.; Huggins, N.; Growdon, J.; Standaert, D.; Akay, M.; Dy, J.; Welsh, M.; Bonato, P. Monitoring Motor Fluctuations in Patients with Parkinsons Disease Using Wearable Sensors. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 864–873. [Google Scholar] [CrossRef]
- Sieberts, S.K.; Schaff, J.; Duda, M.; Pataki, B.Á.; Sun, M.; Snyder, P.; Daneault, J.F.; Parisi, F.; Costante, G.; Rubin, U.; et al. Crowdsourcing Digital Health Measures to Predict Parkinson’s Disease Severity: The Parkinson’s Disease Digital Biomarker DREAM Challenge. npj Digit. Med. 2021, 4, 53. [Google Scholar] [CrossRef]
- Thomas, I.; Westin, J.; Alam, M.; Bergquist, F.; Nyholm, D.; Senek, M.; Memedi, M. A Treatment-Response Index from Wearable Sensors for Quantifying Parkinson’s Disease Motor States. IEEE J. Biomed. Health Inform. 2018, 22, 1341–1349. [Google Scholar] [CrossRef]
- Griffiths, R.I.; Kotschet, K.; Arfon, S.; Xu, Z.M.; Johnson, W.; Drago, J.; Evans, A.; Kempster, P.; Raghav, S.; Horne, M.K. Automated Assessment of Bradykinesia and Dyskinesia in Parkinson’s Disease. J. Parkinsons Dis. 2012, 2, 47–55. [Google Scholar] [CrossRef]
- Lin, F.; Wang, Z.; Li, Z.; Zhao, H.; Shi, X.; Liu, R.; Li, J.; Peng, D.; Ru, B. Fine-Grained Assessment of Upper-Limb Bradykinesia Through Multimodal Feature Enhancement and Deep Learning. IEEE Trans. Hum. Mach. Syst. 2025, 55, 508–518. [Google Scholar] [CrossRef]
- Rodriguez, F.; Krauss, P.; Kluckert, J.; Ryser, F.; Stieglitz, L.; Baumann, C.; Gassert, R.; Imbach, L.; Bichsel, O. Continuous and Unconstrained Tremor Monitoring in Parkinson’s Disease Using Supervised Machine Learning and Wearable Sensors. Parkinsons Dis. 2024, 2024, 5787563. [Google Scholar] [CrossRef]
- Gutowski, T. Deep Learning for Parkinson’s Disease Symptom Detection and Severity Evaluation Using Accelerometer Signal. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2022), Bruges, Belgium, Online Event, 5–7 October 2022; pp. 271–276. [Google Scholar] [CrossRef]
- Visconti, P.; Gaetani, F.; Zappatore, G.A.; Primiceri, P. Technical Features and Functionalities of Myo Armband: An Overview on Related Literature and Advanced Applications of Myoelectric Armbands Mainly Focused on Arm Prostheses. Int. J. Smart Sens. Intell. Syst. 2018, 11, 1–25. [Google Scholar] [CrossRef]
- Gutowski, T. Optimization of Medicine Dosing in Parkinson’s Disease, Based on Signals from Sensor Measurements; Military University of Technology: Warsaw, Poland, 2024. [Google Scholar]
- Erer, K.S. Adaptive Usage of the Butterworth Digital Filter. J. Biomech. 2007, 40, 2934–2943. [Google Scholar] [CrossRef]
- Bazgir, O.; Frounchi, J.; Habibi, S.A.H.; Palma, L.; Pierleoni, P. A Neural Network System for Diagnosis and Assessment of Tremor in Parkinson Disease Patients. In Proceedings of the 2015 22nd Iranian Conference on Biomedical Engineering, ICBME 2015, Tehran, Iran, 25–27 November 2015; pp. 1–5. [Google Scholar]
- Sejdic, E.; Lowry, K.A.; Bellanca, J.; Redfern, M.S.; Brach, J.S. A Comprehensive Assessment of Gait Accelerometry Signals in Time, Frequency and Time-Frequency Domains. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 603–612. [Google Scholar] [CrossRef]
- Tsipouras, M.G.; Tzallas, A.T.; Rigas, G.; Tsouli, S.; Fotiadis, D.I.; Konitsiotis, S. An Automated Methodology for Levodopa-Induced Dyskinesia: Assessment Based on Gyroscope and Accelerometer Signals. Artif. Intell. Med. 2012, 55, 127–135. [Google Scholar] [CrossRef]
- Alam, M.N.; Johnson, B.; Gendreau, J.; Tavakolian, K.; Combs, C.; Fazel-Rezai, R. Tremor Quantification of Parkinson’s Disease –A Pilot Study. In Proceedings of the IEEE International Conference on Electro Information Technology, IEEE Computer Society, Grand Forks, ND, USA, 19–21 August 2016; pp. 755–759. [Google Scholar]
- Eskofier, B.M.; Lee, S.I.; Daneault, J.F.; Golabchi, F.N.; Ferreira-Carvalho, G.; Vergara-Diaz, G.; Sapienza, S.; Costante, G.; Klucken, J.; Kautz, T.; et al. Recent Machine Learning Advancements in Sensor-Based Mobility Analysis: Deep Learning for Parkinson’s Disease Assessment. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS 2016, Orlando, FL, USA, 16–20 August 2016; pp. 655–658. [Google Scholar] [CrossRef]
- San-Segundo, R.; Zhang, A.; Cebulla, A.; Panev, S.; Tabor, G.; Stebbins, K.; Massa, R.E.; Whitford, A.; de la Torre, F.; Hodgins, J. Parkinson’s Disease Tremor Detection in the Wild Using Wearable Accelerometers. Sensors 2020, 20, 5817. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast Fourier Transforms: A Tutorial Review and a State of the Art. Signal Process 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Fu, Q.; Li, Q.; Ding, W.; Lin, F.; Zheng, Z. Multi-Objective Binary Grey Wolf Optimization for Feature Selection Based on Guided Mutation Strategy. Appl. Soft Comput. 2023, 145, 110558. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Thakur, D.; Biswas, S. Permutation Importance Based Modified Guided Regularized Random Forest in Human Activity Recognition with Smartphone. Eng. Appl. Artif. Intell. 2024, 129, 107681. [Google Scholar] [CrossRef]
- Archana, T.; Sachin, D. Dimensionality Reduction and Classification through PCA and LDA. Int. J. Comput. Appl. 2015, 122, 4–8. [Google Scholar] [CrossRef]
- 1.13. Feature Selection—Scikit-Learn 1.5.0 Documentation. Available online: https://scikit-learn.org/stable/modules/feature_selection.html#selectfrommodel (accessed on 14 June 2024).
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer New York, Inc.: Secaucus, NJ, USA, 2006; ISBN 0387310738. [Google Scholar]
- Naser, M.Z.; Alavi, A.H. Error Metrics and Performance Fitness Indicators for Artificial Intelligence and Machine Learning in Engineering and Sciences. Archit. Struct. Constr. 2021, 3, 499–517. [Google Scholar] [CrossRef]
- Wong, T.T. Performance Evaluation of Classification Algorithms by K-Fold and Leave-One-out Cross Validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, M.B.; Dodel, R.; et al. Movement Disorder Society-Sponsored Revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale Presentation and Clinimetric Testing Results. Mov. Disord. 2008, 23, 2129–2170. [Google Scholar] [CrossRef]
- Westin, J.; Nyholm, D.; Pålhagen, S.; Willows, T.; Groth, T.; Dougherty, M.; Karlsson, M.O. A Pharmacokinetic-Pharmacodynamic Model for Duodenal Levodopa Infusion. Clin. Neuropharmacol. 2011, 34, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Stacy, M.; Bowron, A.; Guttman, M.; Hauser, R.; Hughes, K.; Larsen, J.P.; Le Witt, P.; Oertel, W.; Quinn, N.; Sethi, K.; et al. Identification of Motor and Nonmotor Wearing-off in Parkinson’s Disease: Comparison of a Patient Questionnaire versus a Clinician Assessment. Mov. Disord. 2005, 20, 726–733. [Google Scholar] [CrossRef] [PubMed]
- Kikuya, A.; Tsukita, K.; Sawamura, M.; Yoshimura, K.; Takahashi, R. Distinct Clinical Implications of Patient- Versus Clinician-Rated Motor Symptoms in Parkinson’s Disease. Mov. Disord. 2024, 39, 1799–1808. [Google Scholar] [CrossRef]
- Pratt, J.W. Remarks on Zeros and Ties in the Wilcoxon Signed Rank Procedures. J. Am. Stat. Assoc. 1959, 54, 655–667. [Google Scholar] [CrossRef]

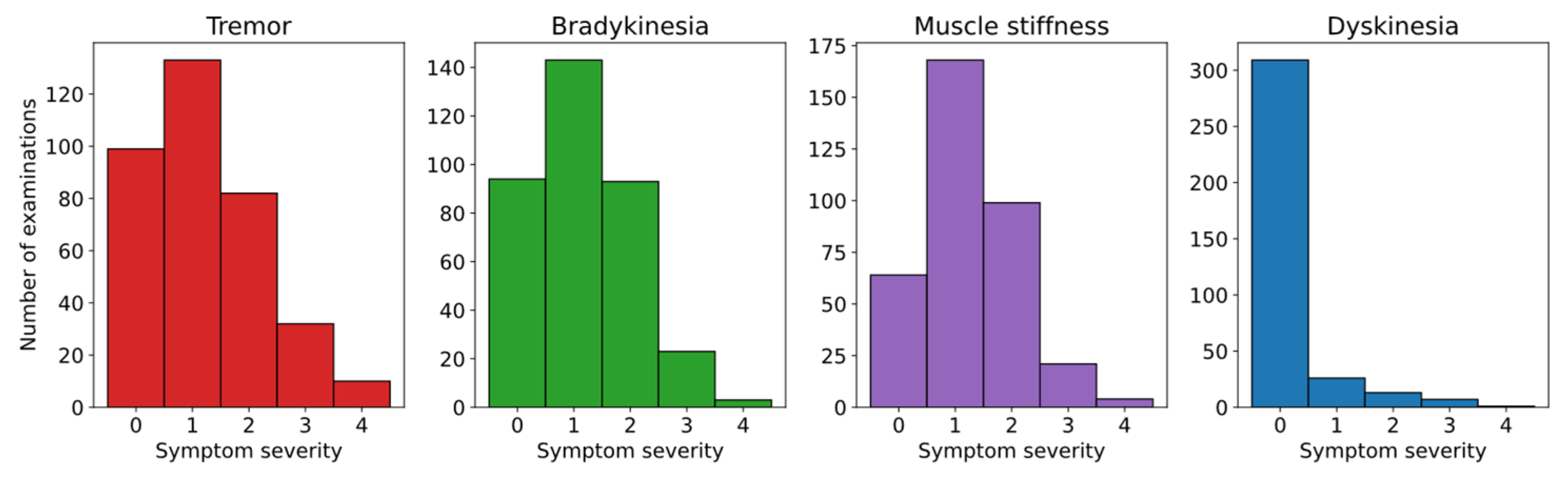

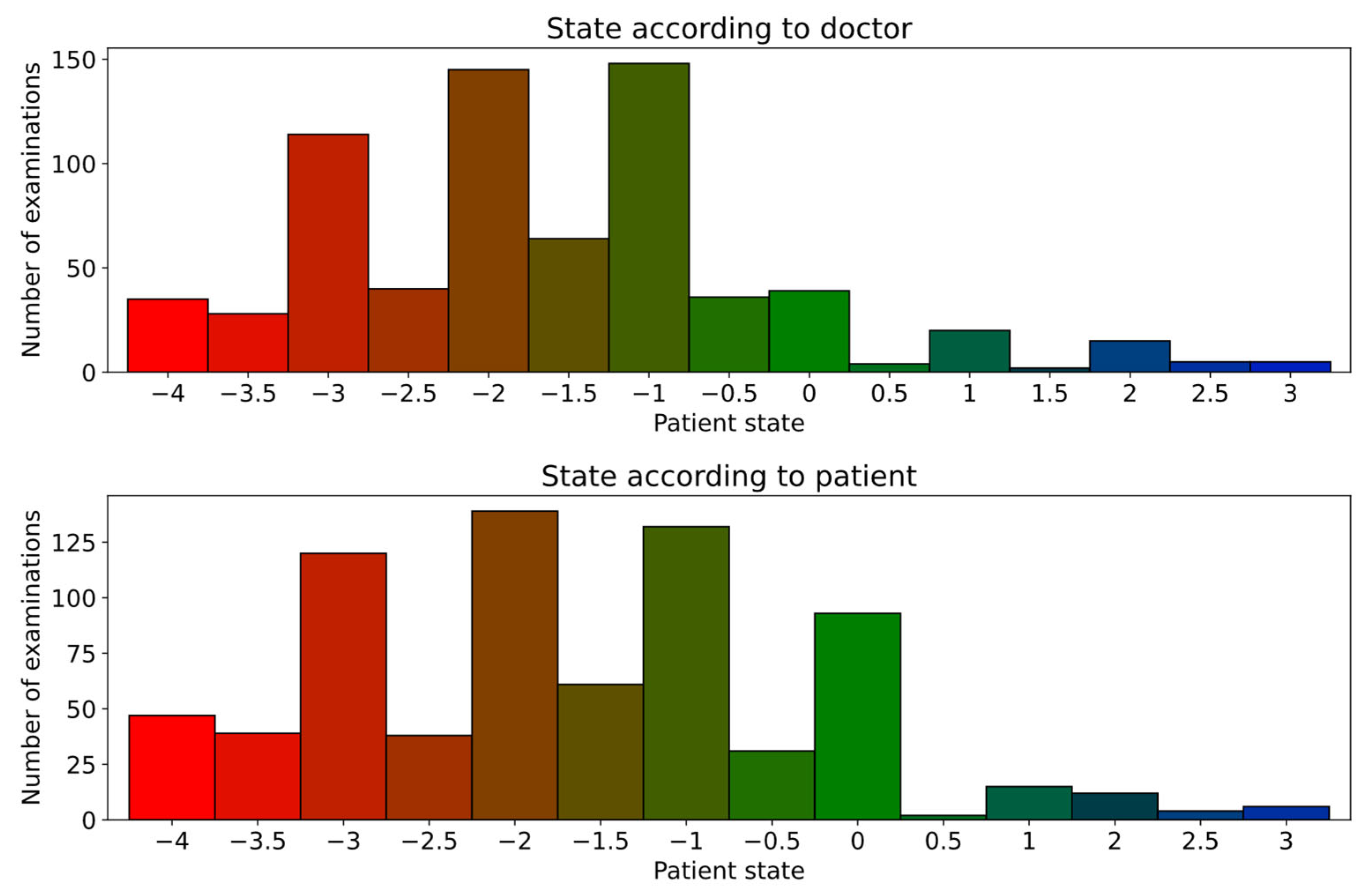
| Characteristic | Value |
|---|---|
| Total number of patients | 241 |
| Age (years) * | 62.0 (11.1) |
| Years since diagnosis * | 10.5 (6.10) |
| Patient sex | 98 female, 143 male |
| Examination count | 739 |
| Examinations per patient * | 3.07 (2.77) |
| States according to clinician * | −1.64 (1.38) |
| States according to patient * | −1.66 (1.42) |
| Examinations with state assessment according to doctor | 700 |
| Examinations with symptom assessment | 356 |
| Feature | Equation/Explanation | |
|---|---|---|
| Time domain | ||
| Mean | (2) | |
| Standard deviation | (3) | |
| Median | The middle value of the sorted signal samples. | |
| Skewness | (4) | |
| Kurtosis | (5) | |
| Max | The maximum value in the signal. | |
| Min | The minimum value in the signal. | |
| Interquartile range | The difference between the 75th and 25th percentiles of the signal. | |
| Approximate entropy | A measure of the regularity and unpredictability of fluctuations in a time series [28]. | |
| Sample entropy | A measure of the likelihood that similar sequences in time-series data remain similar over time [28]. | |
| Power | (6) | |
| Absolute mean difference | (7) | |
| Frequency domain | ||
| Max power | Maximum power found in the PSD. | |
| Max power frequency | The frequency at which the maximum power occurs. | |
| Spectral power | (8) | |
| Weighted mean power | (9) | |
| Kurtosis | (10) | |
| Skewness | (11) | |
| Interquartile range | Interquartile Range of the PSD values. | |
| Spectral centroid | (12) | |
| Name | Description | Source |
|---|---|---|
| affected side | The side of the body more affected by the disease | patient |
| handedness | The dominant hand of the patient | patient |
| groups | Belonging to groups (disease, treatment method) | patient |
| diagnosis | Time since diagnosis to execution of examination | patient + exam |
| age | Age during examination | patient + exam |
| Symptom | Split | Dataset | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|---|
| bradykinesia | 10F | Phone-ACC-#3 | SVM | 0.400 | 0.638 | 0.547 | 0.956 | 1.402 |
| LOO | MYO-GYRO-#3 | XG | 0.408 | 0.639 | 0.570 | 0.896 | 1.187 | |
| dyskinesia | 10F | Phone-GYRO-#1 | RF | 0.385 | 0.622 | 0.228 | 1.238 | 2.353 |
| LOO | Phone-ACC-#1 | SVM | 0.355 | 0.641 | 0.240 | 1.379 | 2.837 | |
| stiffness | 10F | MYO-ACC-#3 | RF | 0.309 | 0.562 | 0.568 | 0.992 | 1.402 |
| LOO | MYO-ACC-#3 | XG | 0.360 | 0.600 | 0.543 | 0.869 | 1.073 | |
| tremor | 10F | Phone-ACC-#1 | RF | 0.595 | 0.772 | 0.537 | 0.675 | 0.652 |
| LOO | Phone-ACC-#1 | XG | 0.616 | 0.786 | 0.514 | 0.652 | 0.642 |
| Symptom | Split | Dataset | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|---|
| bradykinesia | 10F | #3 | RF | 0.422 | 0.654 | 0.556 | 0.956 | 1.412 |
| LOO | #3 | SVM | 0.392 | 0.631 | 0.562 | 0.977 | 1.437 | |
| dyskinesia | 10F | #1 | SVM | 0.433 | 0.69 | 0.251 | 1.175 | 2.024 |
| LOO | #1 | SVM | 0.477 | 0.722 | 0.245 | 1.182 | 2.178 | |
| stiffness | 10F | #3 | SVM | 0.402 | 0.64 | 0.511 | 0.882 | 1.152 |
| LOO | #3 | SVM | 0.439 | 0.672 | 0.503 | 0.860 | 1.085 | |
| tremor | 10F | #1 | RF | 0.630 | 0.795 | 0.496 | 0.657 | 0.637 |
| LOO | #1 | SVM | 0.674 | 0.822 | 0.464 | 0.646 | 0.645 |
| Symptom | Split | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|
| bradykinesia | 10F | SVM | 0.632 | 0.826 | 0.438 | 0.722 | 0.762 |
| LOO | SVM | 0.629 | 0.827 | 0.435 | 0.721 | 0.765 | |
| dyskinesia | 10F | SVM | 0.585 | 0.802 | 0.238 | 0.979 | 1.442 |
| LOO | SVM | 0.567 | 0.790 | 0.245 | 0.983 | 1.432 | |
| stiffness | 10F | SVM | 0.604 | 0.817 | 0.420 | 0.750 | 0.842 |
| LOO | SVM | 0.617 | 0.822 | 0.410 | 0.738 | 0.834 | |
| tremor | 10F | SVM | 0.777 | 0.888 | 0.382 | 0.576 | 0.526 |
| LOO | SVM | 0.780 | 0.887 | 0.378 | 0.561 | 0.498 |
| Symptom | Device, Sensor, Exercise | Hand | Axis | Parameter | Score |
|---|---|---|---|---|---|
| Tremor | Phone-ACC-#1 | Left | Z | Spectral centroid (0–25 Hz) | 0.0269 |
| MYO-GYRO-#1 | Right | Z | Weighted mean power (3–9 Hz) | 0.0261 | |
| MYO-GYRO-#1 | Left | Z | Min of entropy (4 s window) | 0.0242 | |
| MYO-GYRO-#3 | Left | X | Skewness of entropy (4 s window) | 0.0238 | |
| Phone-ACC-#1 | Right | M | Kurtosis (3–9 Hz) | 0.0230 | |
| Bradykinesia | Phone-ACC-#3 | Right | M | Skewness of value range (4 s window) | 0.0406 |
| Phone-ACC-#3 | Left | X | Mean of entropy (4 s window) | 0.0371 | |
| MYO-ACC-#1 | Right | X | Median | 0.0342 | |
| MYO-ACC-#3 | Left | Y | Max power (0–25 Hz) | 0.0335 | |
| Phone-ACC-#3 | Left | Z | Absolute mean difference | 0.0329 | |
| Dyskinesia | Phone-GYRO-#1 | Left | Z | Spectral power | 0.0694 |
| MYO-GYRO-#3 | Right | Z | Interquartile range | 0.0615 | |
| MYO-ACC-#1 | Left | Y | Frequency of max power | 0.0458 | |
| Phone-GYRO-#1 | Left | Z | D1 | 0.0434 | |
| Phone-GYRO-#3 | Right | Y | Mean PSD | 0.0410 | |
| Stiffness | Phone-GYRO-#3 | Right | Z | Max of value range (4 s window) | 0.0685 |
| Phone-ACC-#1 | Left | Y | Absolute mean difference | 0.0504 | |
| Phone-ACC-#3 | Left | Y | Mean PSD (9–14 Hz) | 0.0489 | |
| MYO-ACC-#3 | Left | Z | Skewness | 0.0482 | |
| Phone-GYRO-#1 | Left | Y | Min of entropy (4 s window) | 0.0447 |
| State According to | Split | Dataset | Model | R2 | r | MAE | bMAE | bMSE |
|---|---|---|---|---|---|---|---|---|
| clinician | 10F | All | SVM | 0.543 | 0.767 | 0.617 | 1.309 | 2.786 |
| LOO | SVM | 0.534 | 0.758 | 0.629 | 1.309 | 2.765 | ||
| 10F | MYO | SVM | 0.468 | 0.703 | 0.67 | 1.413 | 3.209 | |
| LOO | SVM | 0.471 | 0.704 | 0.675 | 1.397 | 3.122 | ||
| 10F | Phone | SVM | 0.406 | 0.652 | 0.695 | 1.514 | 3.716 | |
| LOO | SVM | 0.409 | 0.653 | 0.697 | 1.505 | 3.693 | ||
| patient | 10F | All | SVM | 0.610 | 0.816 | 0.603 | 1.144 | 2.232 |
| LOO | SVM | 0.608 | 0.812 | 0.610 | 1.131 | 2.155 | ||
| 10F | MYO | SVM | 0.454 | 0.689 | 0.723 | 1.311 | 2.907 | |
| LOO | SVM | 0.452 | 0.687 | 0.724 | 1.306 | 2.878 | ||
| 10F | Phone | SVM | 0.436 | 0.674 | 0.729 | 1.378 | 3.166 | |
| LOO | SVM | 0.396 | 0.639 | 0.760 | 1.433 | 3.384 |
| According To | Device, Sensor, Exercise | Hand | Axis | Parameter | Score |
|---|---|---|---|---|---|
| clinician | Phone-ACC-#1 | Left | Z | Absolute mean difference | 0.0365 |
| Phone-GYRO-#1 | Left | X | Interquartile range (0–3 Hz) | 0.0313 | |
| MYO-GYRO-#3 | Left | Z | Maximum | 0.0307 | |
| - | - | - | Time since diagnosis | 0.0285 | |
| Phone-GYRO-#1 | Right | X | Weighted mean power (0–3 Hz) | 0.0231 | |
| patient | MYO-ACC-#1 | Left | Y | Skewness (0–25 Hz) | 0.0329 |
| MYO-ACC-#3 | Left | - | Correlation (Y and Z) | 0.0262 | |
| - | - | - | Time since diagnosis | 0.0231 | |
| MYO-GYRO-#1 | Right | - | Correlation (X and Y) | 0.0222 | |
| Phone-ACC-#1 | Left | Z | Spectral centroid (0–25 Hz) | 0.0217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutowski, T.; Stodulska, O.; Ćwiklińska, A.; Gutowska, K.; Kopeć, K.; Betka, M.; Antkiewicz, R.; Koziorowski, D.; Szlufik, S. Machine Learning-Based Assessment of Parkinson’s Disease Symptoms Using Wearable and Smartphone Sensors. Sensors 2025, 25, 4924. https://doi.org/10.3390/s25164924
Gutowski T, Stodulska O, Ćwiklińska A, Gutowska K, Kopeć K, Betka M, Antkiewicz R, Koziorowski D, Szlufik S. Machine Learning-Based Assessment of Parkinson’s Disease Symptoms Using Wearable and Smartphone Sensors. Sensors. 2025; 25(16):4924. https://doi.org/10.3390/s25164924
Chicago/Turabian StyleGutowski, Tomasz, Olga Stodulska, Aleksandra Ćwiklińska, Katarzyna Gutowska, Kamila Kopeć, Marta Betka, Ryszard Antkiewicz, Dariusz Koziorowski, and Stanisław Szlufik. 2025. "Machine Learning-Based Assessment of Parkinson’s Disease Symptoms Using Wearable and Smartphone Sensors" Sensors 25, no. 16: 4924. https://doi.org/10.3390/s25164924
APA StyleGutowski, T., Stodulska, O., Ćwiklińska, A., Gutowska, K., Kopeć, K., Betka, M., Antkiewicz, R., Koziorowski, D., & Szlufik, S. (2025). Machine Learning-Based Assessment of Parkinson’s Disease Symptoms Using Wearable and Smartphone Sensors. Sensors, 25(16), 4924. https://doi.org/10.3390/s25164924







