Fast Anomaly Detection for Vision-Based Industrial Inspection Using Cascades of Null Subspace PCA Detectors
Abstract
1. Introduction
- We introduce a novel anomaly detection framework for industrial inspection that leverages the compact yet robust feature representations of a pretrained MobileNetV2 (known for small memory and computing footprint), eliminating the need for large, complex backbones. Source codes are openly available: https://github.com/4mbilal/Anomaly_Detection (accessed on 22 June 2025).
- We propose a PCA-based technique that specifically exploits near-zero variance features, effectively identifying the null subspace where normal samples project near zero while anomalies stand out, thus enabling efficient and accurate detection.
- We develop a cascaded multi-stage detection strategy, where dual thresholds at each stage rapidly classify clearly normal or anomalous samples, and only ambiguous cases are forwarded for further analysis. This progressive filtering reduces computational load and refines decision boundaries.
- We address practical pre-processing challenges by incorporating tailored image padding and augmentation techniques that mitigate distortion and enhance dataset diversity, especially for classes with limited sample sizes.
- Experimental results on industrial inspection datasets demonstrate that our combined approach not only achieves high accuracy but also significantly reduces computational complexity (20.1 fps on a low-end GPU), making it highly suitable for real-time applications.
2. Literature Review
2.1. Reconstruction-Based Methods
2.2. Embedding-Based Methods
- Memory Bank Methods like SPADE [2] and PatchCore [15] store representative normal features in a “memory bank” similar to K-Nearest Neighbor (KNN) in nature. PatchCore, for instance, focuses on locally aggregated, mid-level feature patches and employs greedy coreset subsampling to reduce redundancy in the memory bank, thereby minimizing storage memory and inference time, which is highly beneficial for industrial applications. Anomaly detection is then performed by comparing input features to these memorized normal features, often using distance metrics like -distance.
- Statistical Distribution Modeling-based methods such as PaDiM [16], describe the normal class through a set of multivariate Gaussian distributions, where each patch position in the feature map is associated with its own distribution. This method is designed to have low time and space complexity at test time, independent of the training dataset size, addressing scalability concerns of KNN-based methods.
- One-Class Classification (OCC) methods explicitly define classification boundaries, such as hyperplanes or hyperspheres [17], to distinguish normal from anomalous data.
- Distribution Transformation methods such as Normalizing Flow (NF) aim to transform the distribution of normal samples into a standard Gaussian distribution, where anomalies are then identified by their low likelihood in this transformed space [18].
- Knowledge Distillation-based approach involves training a student network to mimic the outputs of a fixed pre-trained teacher network using only normal samples [19]. Anomalies are detected by observing discrepancies between the teacher’s and student’s outputs.
2.3. Synthesis-Based Methods
- Image-level anomaly synthesis explicitly simulates anomalies directly on the image itself. Techniques include cutting and pasting normal image regions at random positions, as seen in methods like CutPaste [20]. Other approaches involve seamlessly blending blocks from different images, such as NSA [21], or creating binary masks (e.g., using Perlin noise [4]) and filling them with external textures, such as DRAEM [22]. While this approach can provide detailed anomaly textures, it often suffers from a lack of diversity and realism in the synthesized anomalies. The synthetic appearances may not closely match real defects, and features derived from such synthetic data might deviate significantly from actual normal features, potentially resulting in a loosely bounded normal feature space that could inadvertently classify subtle defects as normal.
- Feature-level anomaly synthesis implicitly simulates anomalies within the feature space extracted by a neural network. This approach is generally more efficient due to the smaller size of feature maps compared to full images. SimpleNet, for instance, generates anomalous features by adding Gaussian noise to normal features, which have first been processed by a “feature adaptor” to reduce domain bias from pre-trained backbones. The network then trains a simple discriminator, often a multi-layer perceptron (MLP), to distinguish between these adapted normal features and the synthesized anomalous features. A key challenge for early feature-level methods was the lack of controllable and directional synthesis, particularly for anomalies that are very similar to normal regions. More advanced methods, such as Global and Local Anomaly co-Synthesis Strategy (GLASS) [23], address this by guiding Gaussian noise with gradient ascent and truncated projection to synthesize “near-in-distribution anomalies” in a controllable manner. This allows for the generation of both “weak anomalies” close to normal points and “strong anomalies” further away. SuperSimpleNet [4] also employs feature-space anomaly generation, using a binarized Perlin noise mask to define regions where Gaussian noise is applied to adapted features, leading to more realistic and spatially coherent synthetic anomalous regions.
2.4. Speed, Memory and Training Requirements
3. Materials and Methods
- PCA-based anomaly detection module that exploits near-zero variance features: by focusing on the eigenvectors corresponding to small eigenvalues, we capture the null space where normal samples project near zero, while anomalous samples exhibit significant deviations.
- A cascaded multi-stage strategy: Instead of combining features from all layers in a single detector, we treat the features from each CNN layer independently in stages which employ dual thresholds to immediately classify clear cases and forward only ambiguous samples to the next stage.
3.1. Leveraging Near-Zero Variance Principal Components for Anomaly Detection
- Mean:
3.2. Cascaded Multi-Stage Anomaly Detection
3.3. Image Pre- and Post-Processing
4. Results
4.1. Experimental Setup
4.2. Anomaly Detection on Standard Datasets
4.3. Inference Speed Comparison
4.4. Ablation Study
4.4.1. CNN Backbone Selection
4.4.2. Role of Specific CNN Layers
4.4.3. PCA Null-Space Size Across Different CNN Layers
4.4.4. Impact of Image Augmentation
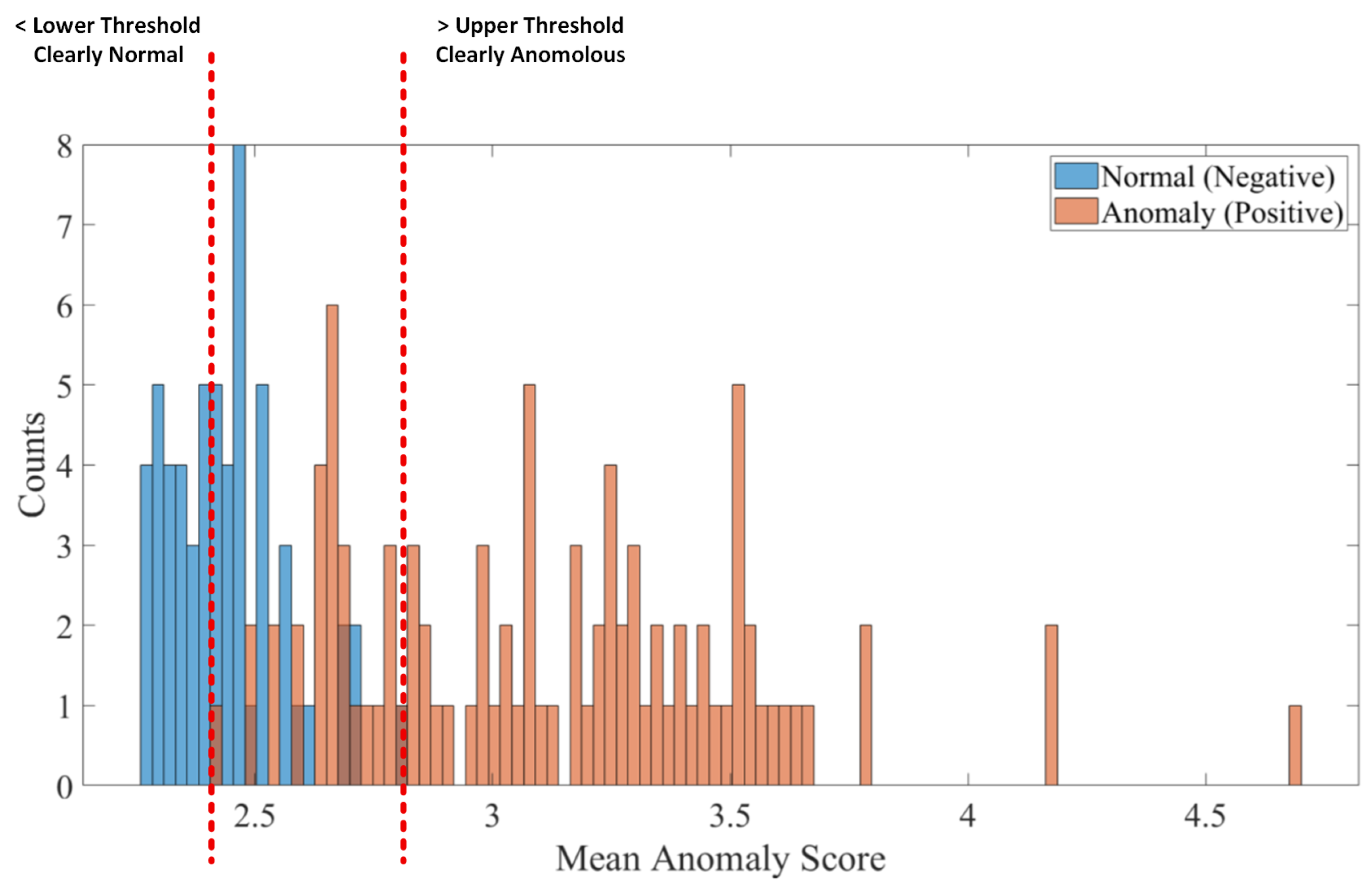
4.5. Threshold Selection in the Cascaded Architecture
4.6. False Positive Analysis
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Li, C.-L.; Yoon, J.; Sohn, K.; Arik, S.O.; Pfister, T. SPADE: Semi-supervised Anomaly Detection under Distribution Mismatch. arXiv 2023, arXiv:2212.00173. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Y.; Xu, Y.; Wang, Z. SimpleNet: A Simple Network for Image Anomaly Detection and Localization. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 20402–20411. [Google Scholar] [CrossRef]
- Rolih, B.; Fučka, M.; Skočaj, D. SuperSimpleNet: Unifying Unsupervised and Supervised Learning for Fast and Reliable Surface Defect Detection. In Pattern Recognition. ICPR 2024; Antonacopoulos, A., Chaudhuri, S., Chellappa, R., Liu, C.L., Bhattacharya, S., Pal, U., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2025; Volume 15310. [Google Scholar] [CrossRef]
- Batzner, K.; Heckler, L.; König, R. EfficientAD: Accurate Visual Anomaly Detection at Millisecond-Level Latencies. arXiv 2024, arXiv:2303.14535. [Google Scholar]
- Vaswani, N.; Chellappa, R. Principal components null space analysis for image and video classification. IEEE Trans. Image Process. 2006, 15, 1816–1830. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Zhang, M.; Cheng, X.; Shi, L.; Gamba, P.; Wang, H. Dynamic low-rank and sparse priors constrained deep autoencoders for hyperspectral anomaly detection. IEEE Trans. Instrum. Meas. 2024, 73, 2500518. [Google Scholar] [CrossRef]
- Berahmand, K.; Daneshfar, F.; Salehi, E.S.; Li, Y.; Xu, Y. Autoencoders and their applications in machine learning: A survey. Artif. Intell. Rev. 2024, 57, 28. [Google Scholar] [CrossRef]
- Zhou, C.; Paffenroth, R.C. Anomaly Detection with Robust Deep Autoencoders. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 665–674. [Google Scholar] [CrossRef]
- An, J.; Cho, S. Variational Autoencoder Based Anomaly Detection Using Reconstruction Probability. arXiv 2015, arXiv:1512.04313. [Google Scholar]
- Rafiee, L.; Fevens, T. Unsupervised Anomaly Detection with a GAN Augmented Autoencoder. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Bratislava, Slovakia, 15–18 September 2020; pp. 479–490. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-Supervised Anomaly Detection via Adversarial Training. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 189–196. [Google Scholar]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery. In Proceedings of the Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; pp. 146–157. [Google Scholar]
- Cheng, X.; Wang, C.; Huo, Y.; Zhang, M.; Wang, H.; Ren, J. Prototype-guided spatial–spectral interaction network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5516517. [Google Scholar] [CrossRef]
- Roth, K.; Pemula, L.; Zepeda, J.; Schölkopf, B.; Brox, T.; Gehler, P. Towards Total Recall in Industrial Anomaly Detection. arXiv 2021, arXiv:2106.08265. [Google Scholar] [CrossRef]
- Defard, T.; Setkov, A.; Loesch, A.; Audigier, R. PaDiM: A Patch Distribution Modeling Framework for Anomaly Detection and Localization. In Proceedings of the Pattern Recognition. ICPR International Workshops and Challenges, ICPR 2021, Virtual Event, 10–15 January 2021; Del Bimbo, A., Cucchiara, R., Sclaroff, S., Farinella, G.M., Mei, T., Bertini, M., Escalante, H.J., Vezzani, R., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2021; Volume 12664. [Google Scholar] [CrossRef]
- Que, Z.; Lin, C.-J. One-Class SVM Probabilistic Outputs. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 6244–6256. [Google Scholar] [CrossRef] [PubMed]
- Chiu, L.-L.; Lai, S.-H. Self-Supervised Normalizing Flows for Image Anomaly Detection and Localization. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 2927–2936. [Google Scholar] [CrossRef]
- Rudolph, M.; Wehrbein, T.; Rosenhahn, B.; Wandt, B. Asymmetric Student-Teacher Networks for Industrial Anomaly Detection. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 2591–2601. [Google Scholar] [CrossRef]
- Li, C.-L.; Sohn, K.; Yoon, J.; Pfister, T. CutPaste: Self-Supervised Learning for Anomaly Detection and Localization. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 9659–9669. [Google Scholar] [CrossRef]
- Schlüter, H.M.; Tan, J.; Hou, B.; Kainz, B. Natural Synthetic Anomalies for Self-supervised Anomaly Detection and Localization. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Zavrtanik, V.; Kristan, M.; Skočaj, D. DRAEM—A Discriminatively Trained Reconstruction Embedding for Surface Anomaly Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 8330–8339. [Google Scholar]
- Chen, Q.; Luo, H.; Lv, C.; Zhang, Z. A Unified Anomaly Synthesis Strategy with Gradient Ascent for Industrial Anomaly Detection and Localization. In Proceedings of the ECCV 2024, Milan, Italy, 29 September–4 October 2024; Lecture Notes in Computer Science (LNCS). Springer: Cham, Switzerland, 2025; Volume 15125, pp. 37–54. [Google Scholar] [CrossRef]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A Comprehensive Real-World Dataset for Unsupervised Anomaly Detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9584–9592. [Google Scholar] [CrossRef]
- Zou, Y.; Jeong, J.; Pemula, L.; Zhang, D.; Dabeer, O. Visual Anomaly (VisA) Dataset. 2024. Available online: https://service.tib.eu/ldmservice/dataset/visual-anomaly--visa--dataset (accessed on 22 June 2025). [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE Computer Society: Los Alamitos, CA, USA; pp. 4510–4520. [Google Scholar]
- Zhe, Q.; Gao, W.; Zhang, C.; Du, G.; Li, Y.; Chen, D. A Hyperspectral Classification Method Based on Deep Learning and Dimension Reduction for Ground Environmental Monitoring. IEEE Access 2025, 13, 29969–29982. [Google Scholar] [CrossRef]
- Yap, Y.S.; Ahmad, M.R. Modified Overcomplete Autoencoder for Anomaly Detection Based on TinyML. IEEE Sens. Lett. 2024, 8, 2504104. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Y.; Wang, X.; Li, W.; Wu, Y.; Zhao, R.; Wu, L. FastFlow: Unsupervised Anomaly Detection and Localization via 2D Normalizing Flows. arXiv 2021, arXiv:2111.07677. [Google Scholar] [CrossRef]






| Class | PaDiM | FastFlow | PatchCore | SimpleNet | SuperSimpleNet | GLASS | Proposed |
|---|---|---|---|---|---|---|---|
| Carpet | 99.8/99.1 | 97.5/92.9 | 98.7/99.0 | 99.7/98.2 | 98.4/- | 99.8/99.6 | 100 ± 0.00/98.4 ± 0.01 |
| Grid | 96.7/97.3 | 100/96.0 | 98.2/98.7 | 99.7/98.8 | 99.3/- | 100/99.4 | 99.2 ± 0.13/97.2 ± 0.06 |
| Leather | 100/99.2 | 100/99.1 | 100/99.3 | 100/99.2 | 100/- | 100/99.8 | 100 ± 0.00/98.6 ± 0.00 |
| Tile | 98.1/94.1 | 99.9/87.3 | 98.7/95.6 | 99.8/97.0 | 99.7/- | 100/99.7 | 99.7 ± 0.11/93 ± 0.01 |
| Wood | 99.2/94.9 | 98.9/93.1 | 99.2/95.0 | 100/94.5 | 99.3/- | 99.9/98.8 | 100 ± 0.00/93.6 ± 0.01 |
| Bottle | 99.1/98.3 | 100/89.3 | 100/98.6 | 100/98.0 | 100/- | 100/99.3 | 100 ± 0.00/97.7 ± 0.00 |
| Cable | 97.1/96.7 | 93.9/89.9 | 99.5/98.4 | 99.9/97.6 | 98.1/- | 99.8/98.7 | 99.1 ± 0.06/97.1 ± 0.00 |
| Capsule | 87.5/98.5 | 98.1/95.4 | 98.1/98.8 | 97.7/98.9 | 98.7/- | 99.9/99.4 | 98.7 ± 1.28/98.4 ± 0.00 |
| Hazelnut | 99.4/98.2 | 98.9/95.6 | 100/98.7 | 100/97.9 | 99.8/- | 100/99.4 | 100 ± 0.00/98.1 ± 0.00 |
| Metal_nut | 96.2/97.2 | 99.6/92.3 | 100/98.4 | 100/98.8 | 99.5/- | 100/99.4 | 99.2 ± 0.05/98.5 ± 0.00 |
| Pill | 90.1/95.7 | 96.7/93.9 | 96.6/97.4 | 99.0/98.6 | 98.1/- | 99.3/99.4 | 96.7 ± 0.21/98.4 ± 0.00 |
| Screw | 97.5/98.5 | 84.5/89.7 | 98.1/99.4 | 98.2/99.3 | 92.9/- | 100/99.5 | 99.6 ± 0.37/98.7 ± 0.02 |
| Toothbrush | 100/98.8 | 89.2/87.0 | 100/98.7 | 99.7/98.5 | 92.2/- | 100/99.3 | 100 ± 0.00/98.7 ± 0.00 |
| Transistor | 94.4/97.5 | 98.5/92.0 | 100/96.3 | 100/97.6 | 99.9/- | 99.9/97.6 | 100 ± 0.00/98.2 ± 0.02 |
| Zipper | 98.6/98.5 | 98.5/93.7 | 99.4/98.8 | 99.9/98.9 | 99.6/- | 100/99.6 | 98.7 ± 0.15/98.1 ± 0.00 |
| Average | 95.8/97.5 | 96.9/92.5 | 99.1/98.1 | 99.6/98.1 | 98.4/- | 99.9/99.3 | 99.4 ± 0.16/97.5 ± 0.01 |
| Class | PaDiM | FastFlow | PatchCore | SimpleNet | SuperSimpleNet | Proposed |
|---|---|---|---|---|---|---|
| Candle | 95.9 | 96.8 | 98.6 | 92.5 | 97.1 | 97.5 ± 0.05 |
| Capsules | 64.2 | 83.0 | 76.4 | 78.9 | 81.5 | 70.2 ± 0.52 |
| Cashew | 89.9 | 90.0 | 97.9 | 91.9 | 93 | 94.1 ± 0.06 |
| Chewing gum | 99.5 | 99.8 | 98. | 99 | 99.3 | 99.5 ± 0.00 |
| Fryum | 88.1 | 98.6 | 94.8 | 95.4 | 96.8 | 93.9 ± 0.02 |
| Macaroni 1 | 81.6 | 94.8 | 95.8 | 94.2 | 93.1 | 88.1 ± 0.05 |
| Macaroni 2 | 70.3 | 80.5 | 77.7 | 71.8 | 75 | 77.0 ± 1.02 |
| PCB 1 | 95.7 | 95.5 | 98.9 | 92.5 | 96.9 | 96.1 ± 0.03 |
| PCB 2 | 89.3 | 96.1 | 97.1 | 93.6 | 97.5 | 94.3 ± 0.02 |
| PCB 3 | 79.3 | 94.0 | 96.3 | 92.6 | 94.4 | 90.5 ± 0.04 |
| PCB 4 | 98.7 | 98.4 | 99.4 | 97.9 | 98.4 | 99.7 ± 0.01 |
| Pipe fryum | 95.9 | 99.6 | 99.7 | 94.6 | 97.6 | 99.6 ± 0.01 |
| Average | 87.4 | 93.9 | 94.3 | 91.2 | 93.4 | 91.7 ± 0.15 |
| Detector | Backbone | Processing Speed (fps) |
|---|---|---|
| PaDiM | ResNet18 | 3.8 |
| PatchCore | ResNet18 | 11.1 |
| PatchCore | ResNet50 | 9.0 |
| SimpleNet | ResNet50 | 17.3 |
| Proposed | MobileNetV2 | 20.1 |
| Backbone | AUROC | Processing Speed (fps) | Model Parameters |
|---|---|---|---|
| MobileNetV2-Block13 | 94.0 | 20.1 | 615 K |
| MobileNetV2-Block11 | 94.0 | 23.2 | 431 K |
| MobileNetV2-Block4 | 96.2 | 23.5 | 42 K |
| ResNet18-Block4 | 91.0 | 22.9 | 2.7 M |
| ResNet18-Block3 | 90.2 | 23.1 | 684 K |
| SqueezeNet-fire8 | 91.0 | 24.3 | 525 K |
| Class | Block 4 | Block 8 | Block 11 | Block 12 | Block 13 |
|---|---|---|---|---|---|
| 192 Channels | 384 Channels | 576 Channels | 576 Channels | 576 Channels | |
| Carpet | 97 | 98.2 | 100 | 99.5 | 98.5 |
| Grid | 95.1 | 98.5 | 97.2 | 95.2 | 70.8 |
| Leather | 99.9 | 100 | 100 | 100 | 100 |
| Tile | 98.9 | 99.2 | 98.7 | 97.6 | 98.3 |
| Wood | 99.6 | 99.5 | 98.8 | 99.3 | 99.2 |
| Bottle | 100 | 100 | 99.8 | 100 | 100 |
| Cable | 94.9 | 96.8 | 91.5 | 96.6 | 98.8 |
| Capsule | 90.5 | 96.1 | 84.4 | 91.2 | 93.3 |
| Hazelnut | 99.3 | 100 | 92 | 99.9 | 99.6 |
| Metal_nut | 96.1 | 98.5 | 96.6 | 97.6 | 96.6 |
| Pill | 95.2 | 93.9 | 81.3 | 88.8 | 88.5 |
| Screw | 86.5 | 98.2 | 79.8 | 82.4 | 77.2 |
| Toothbrush | 100 | 100 | 98.6 | 98.9 | 98.1 |
| Transistor | 98.5 | 100 | 99 | 100 | 99.3 |
| Zipper | 91.4 | 98.2 | 92.6 | 95 | 91.3 |
| Average | 96.2 | 98.5 | 94 | 96.1 | 94 |
| 100% | 90% | 75% | 70% | 65% | |
|---|---|---|---|---|---|
| AUROC | 95.4 | 97.2 | 99.1 | 99.4 | 98.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilal, M.; Hanif, M.S. Fast Anomaly Detection for Vision-Based Industrial Inspection Using Cascades of Null Subspace PCA Detectors. Sensors 2025, 25, 4853. https://doi.org/10.3390/s25154853
Bilal M, Hanif MS. Fast Anomaly Detection for Vision-Based Industrial Inspection Using Cascades of Null Subspace PCA Detectors. Sensors. 2025; 25(15):4853. https://doi.org/10.3390/s25154853
Chicago/Turabian StyleBilal, Muhammad, and Muhammad Shehzad Hanif. 2025. "Fast Anomaly Detection for Vision-Based Industrial Inspection Using Cascades of Null Subspace PCA Detectors" Sensors 25, no. 15: 4853. https://doi.org/10.3390/s25154853
APA StyleBilal, M., & Hanif, M. S. (2025). Fast Anomaly Detection for Vision-Based Industrial Inspection Using Cascades of Null Subspace PCA Detectors. Sensors, 25(15), 4853. https://doi.org/10.3390/s25154853






