Antenna Model with Pattern Optimization Based on Genetic Algorithm for Satellite-Based SAR Mission
Abstract
1. Introduction
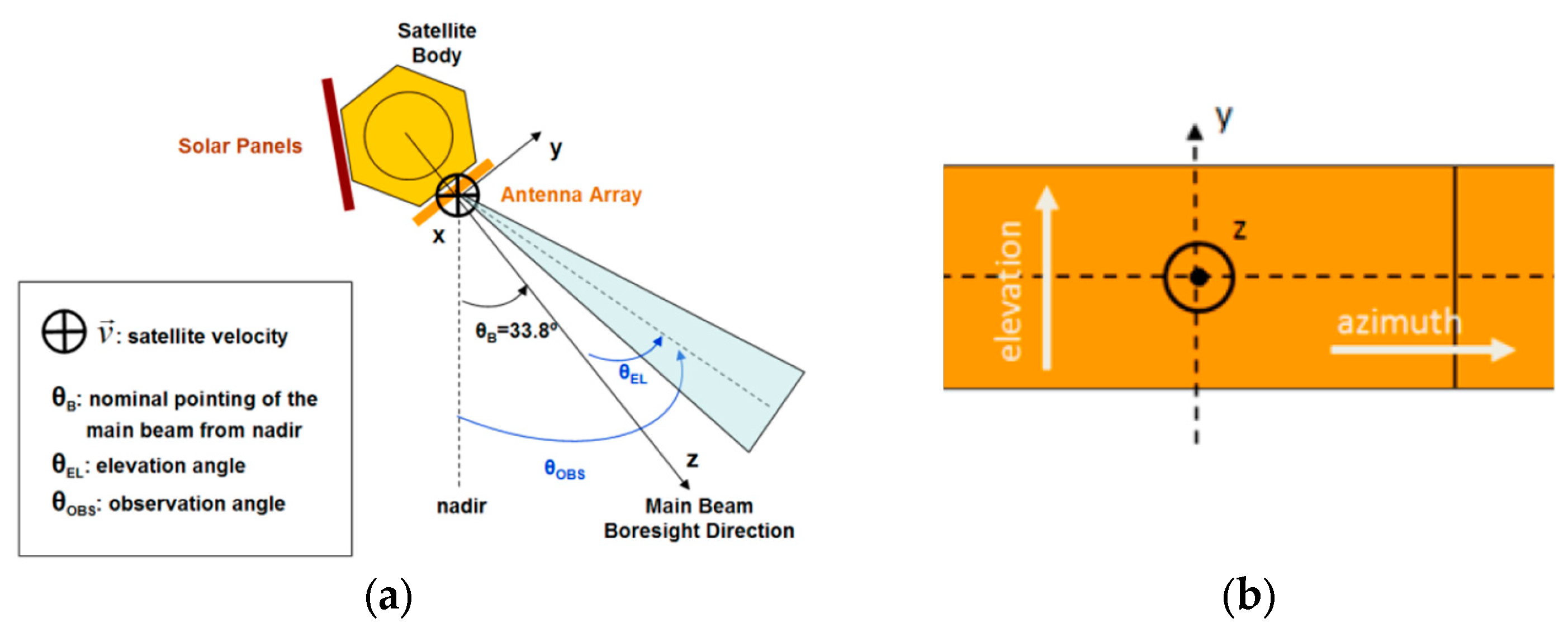
2. The Antenna Model Approach
2.1. The Purpose of the Antenna Model
2.2. The User Interface of the SARAS Antenna Model
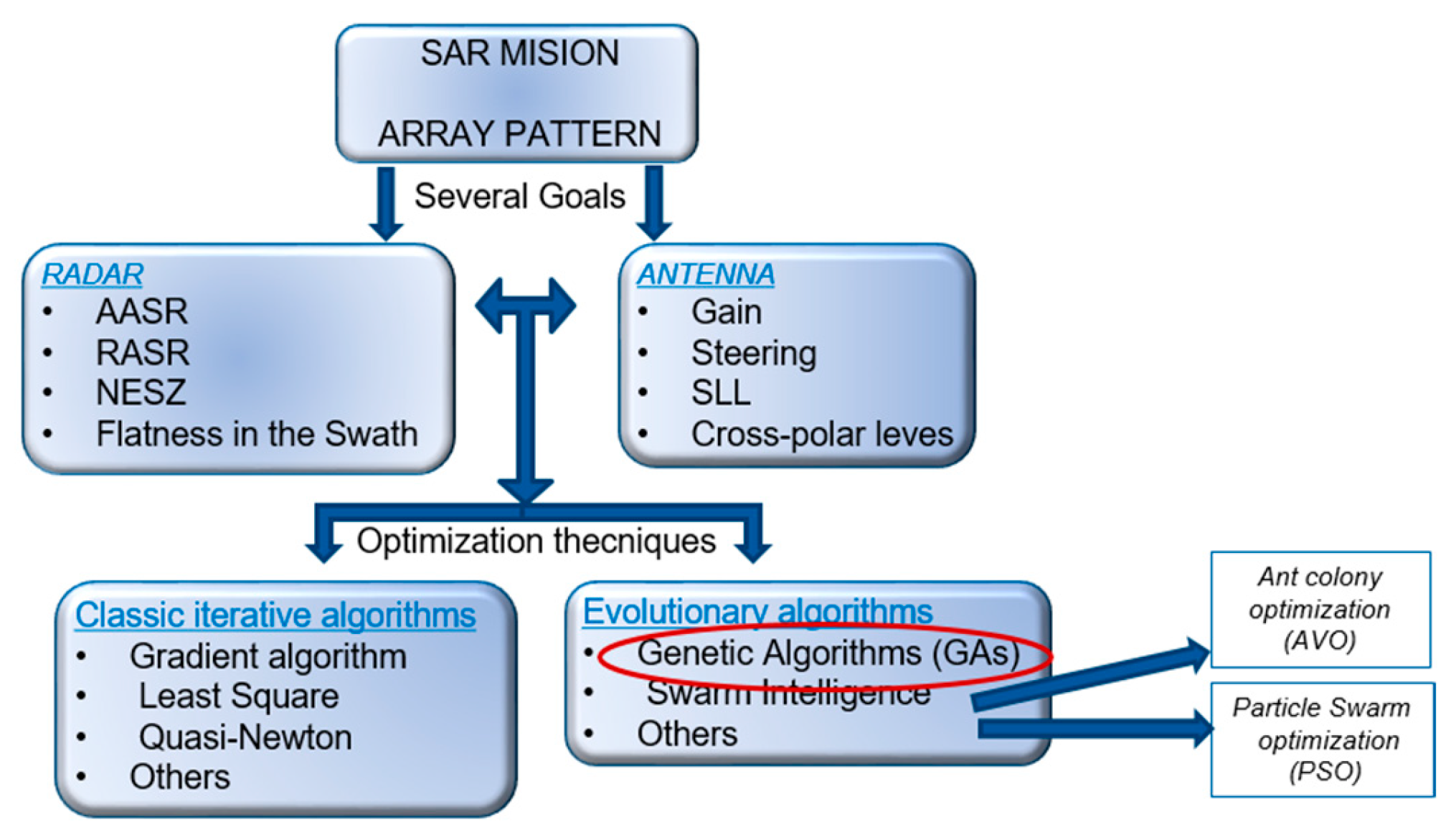
3. The Excitation Coefficient Optimization Tool (AEG) Based on a GA
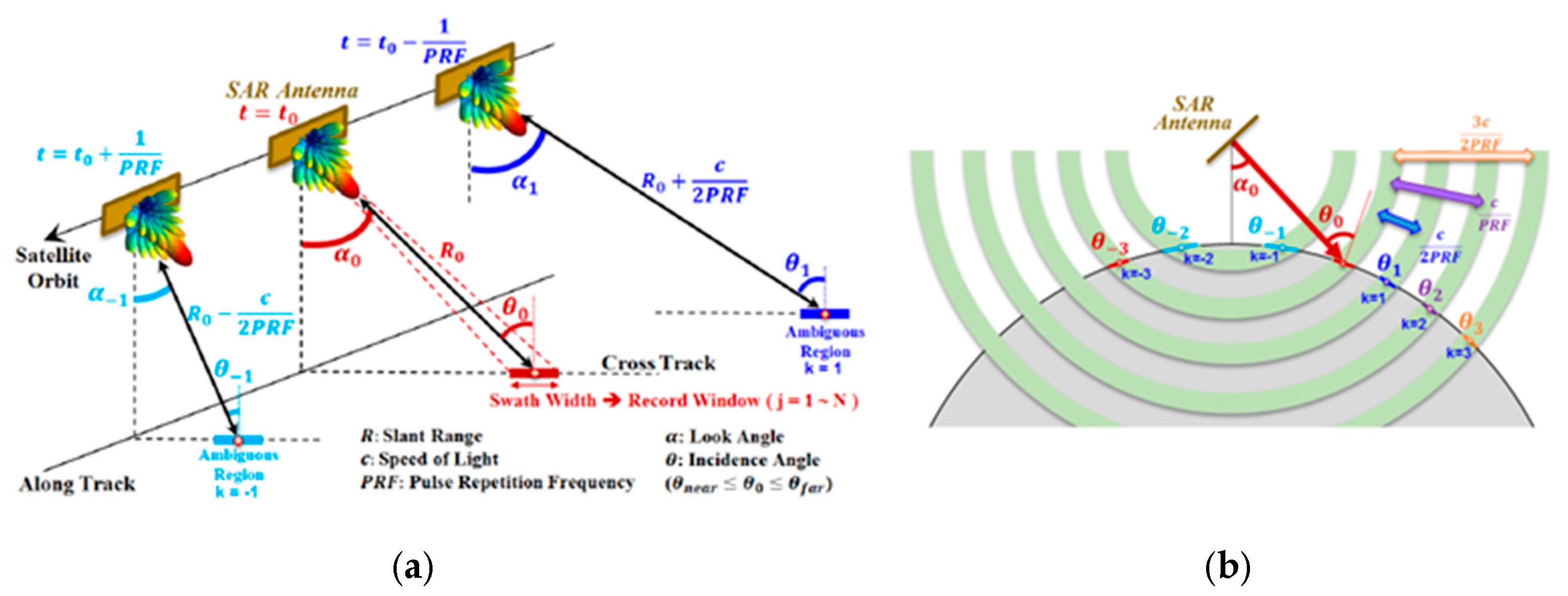
3.1. The Optimization Framework for Phased Arrays in SAR Systems
3.2. The GA Implemented by INTA
3.3. Strategies Implemented for Optimization
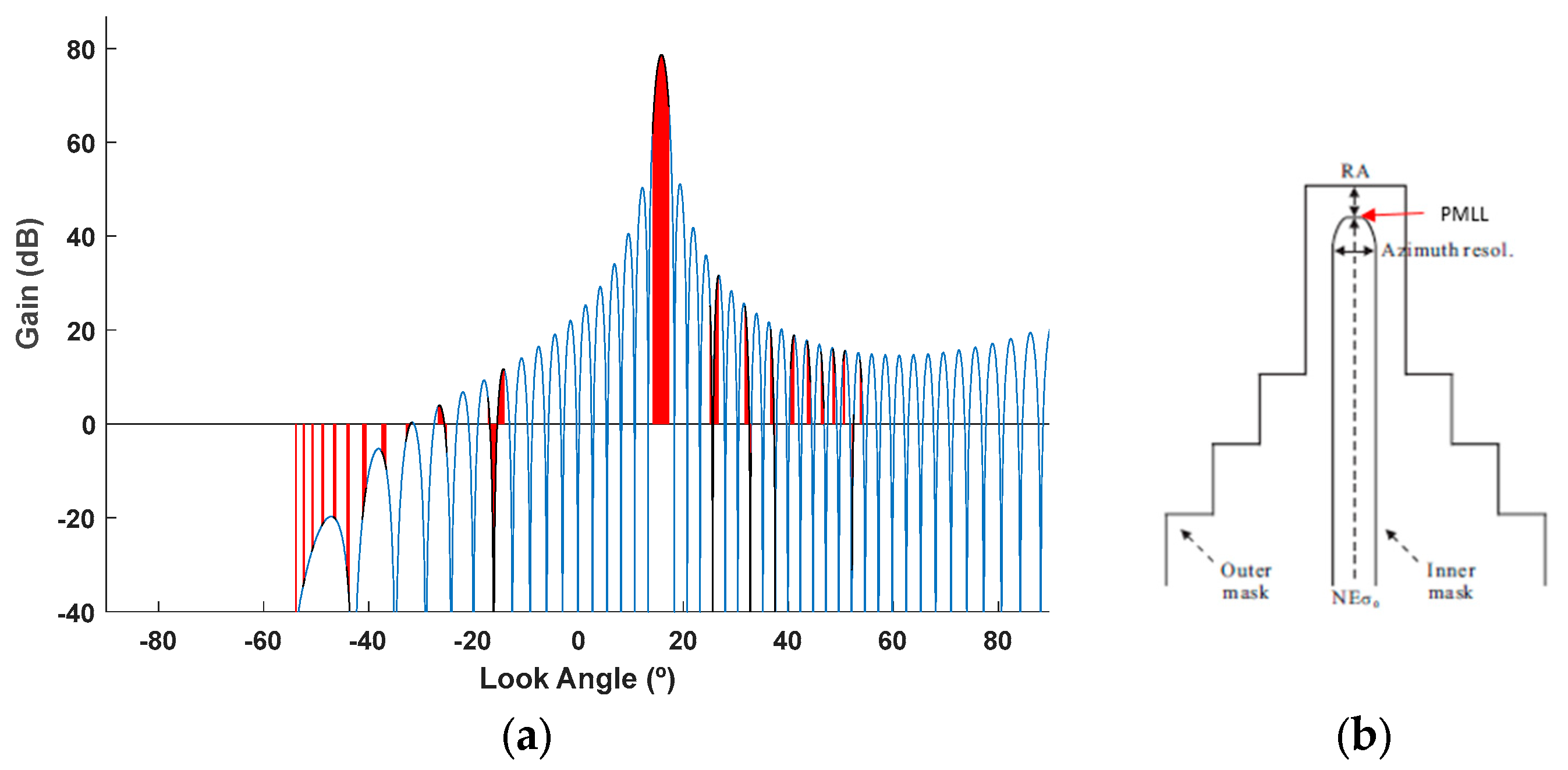
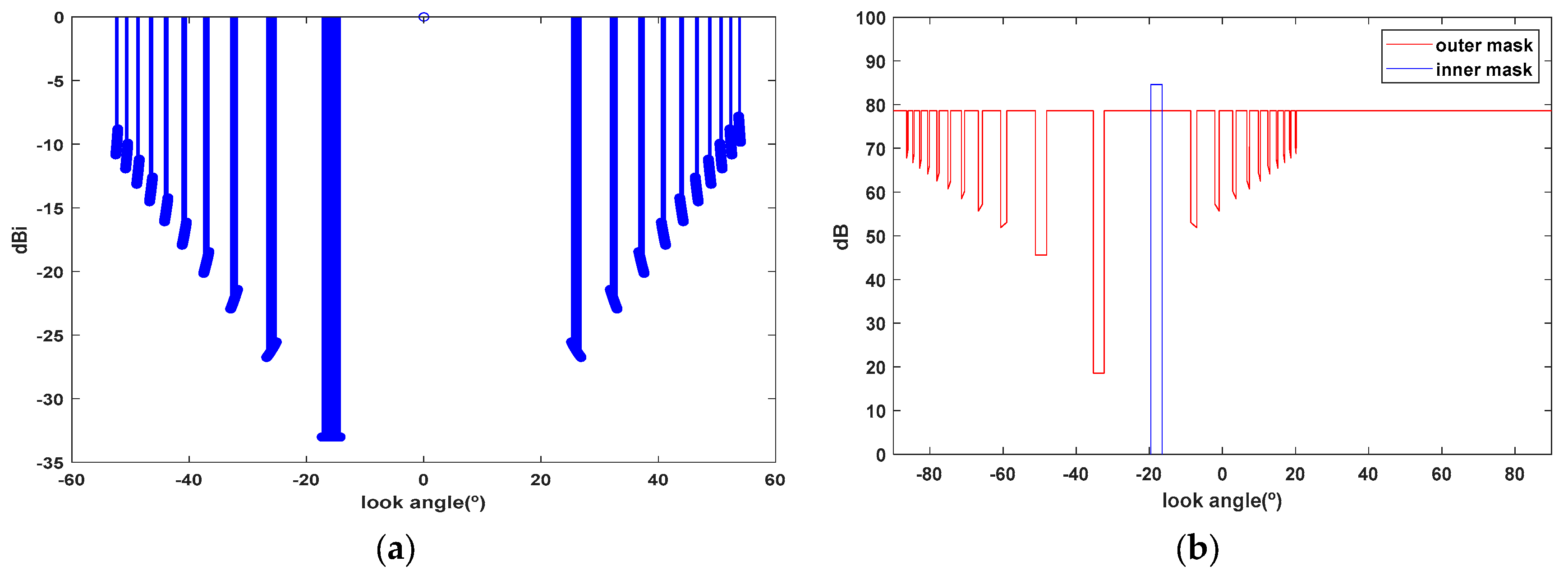
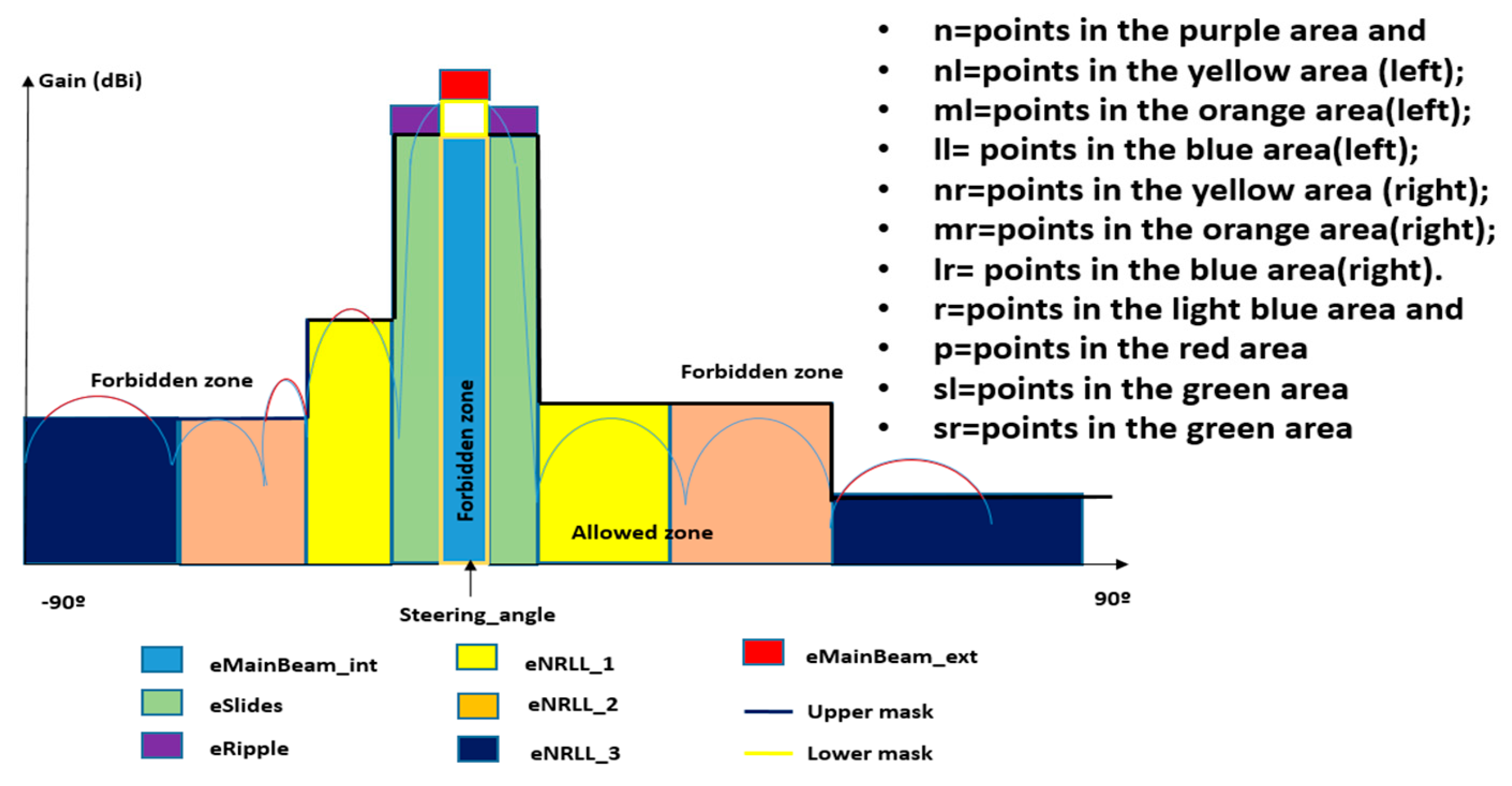
3.4. Mask Definition
3.5. The Cost Function or Fitness
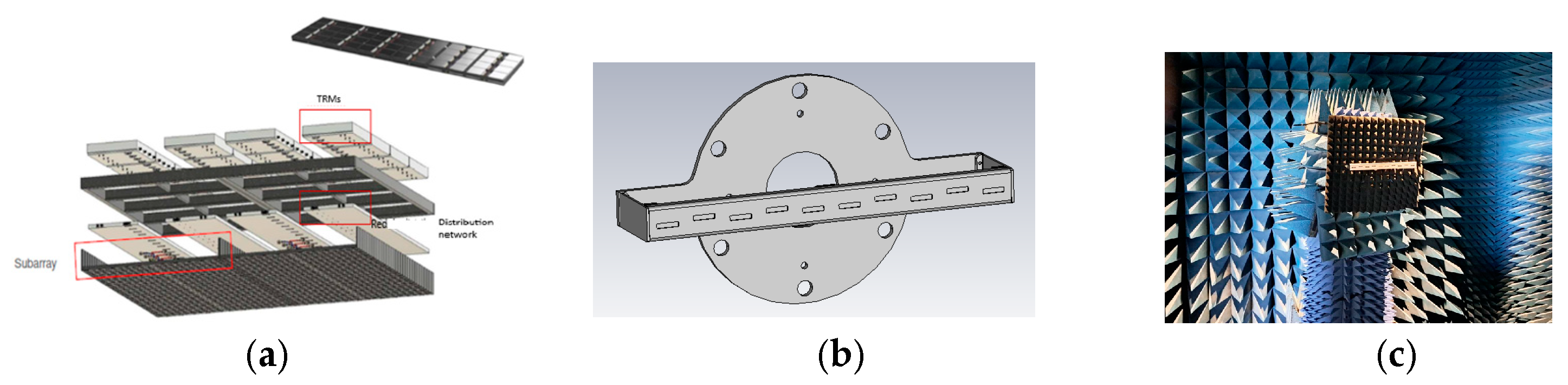
4. Validation of the SARAS Antenna Model with Experimental Data from the PAZ Satellite
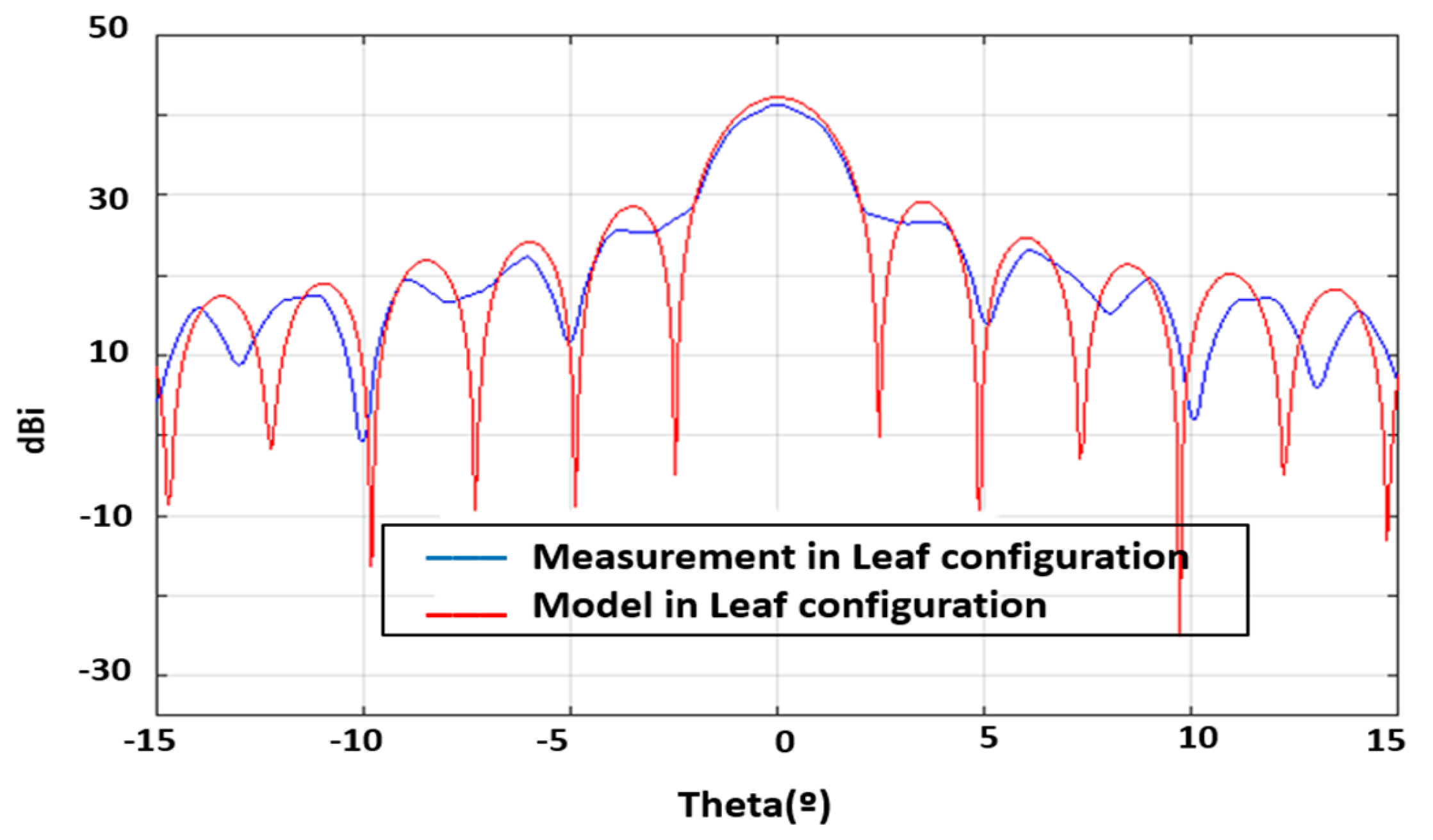
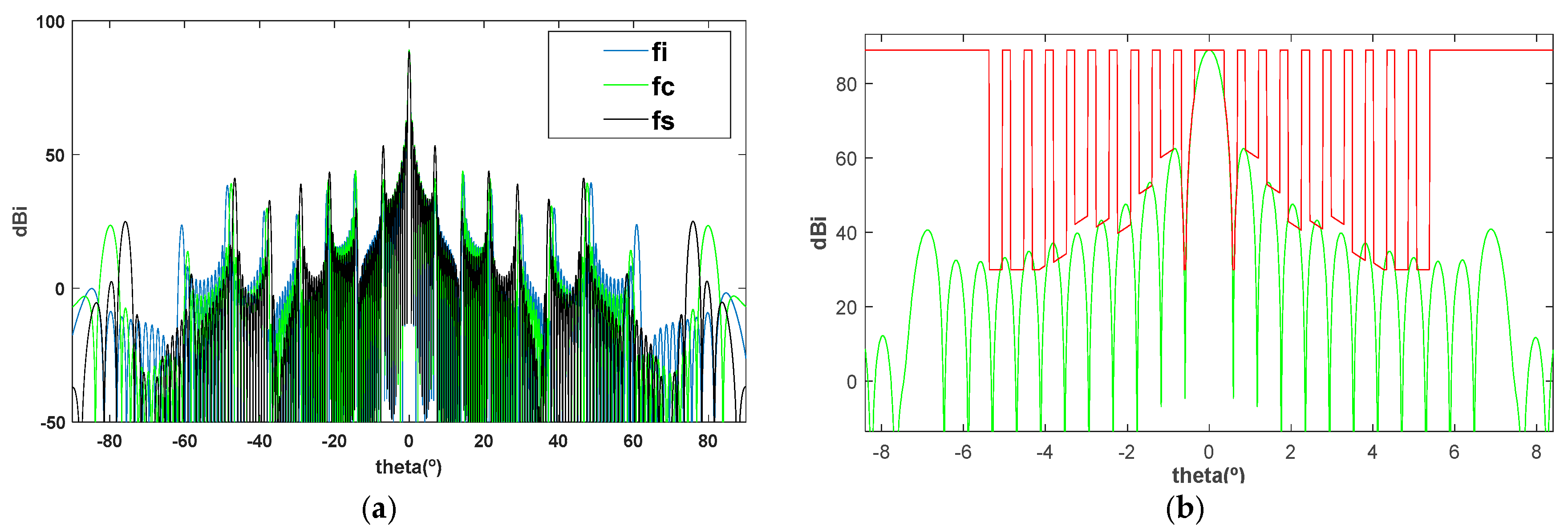
4.1. APG Results and Validation
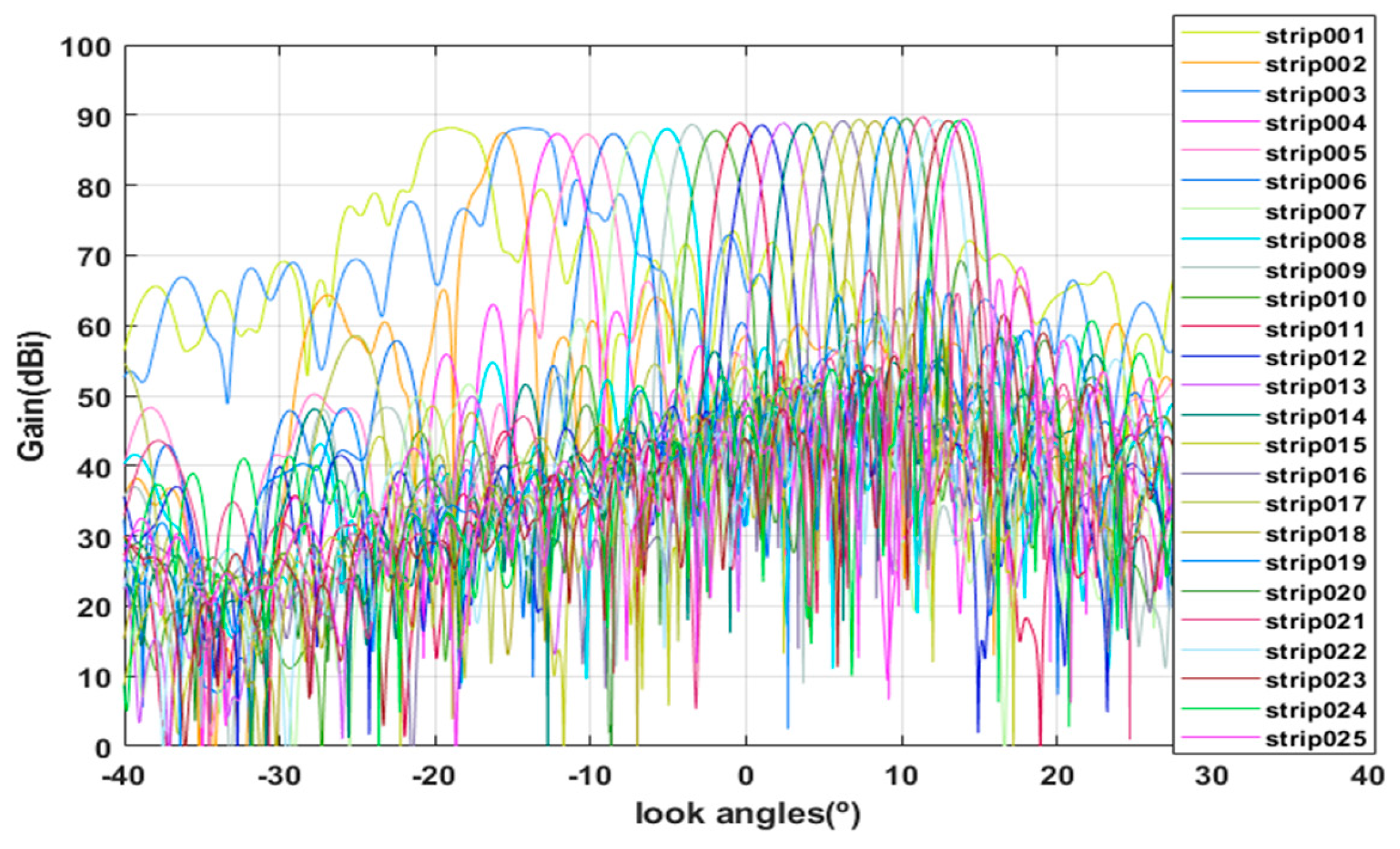
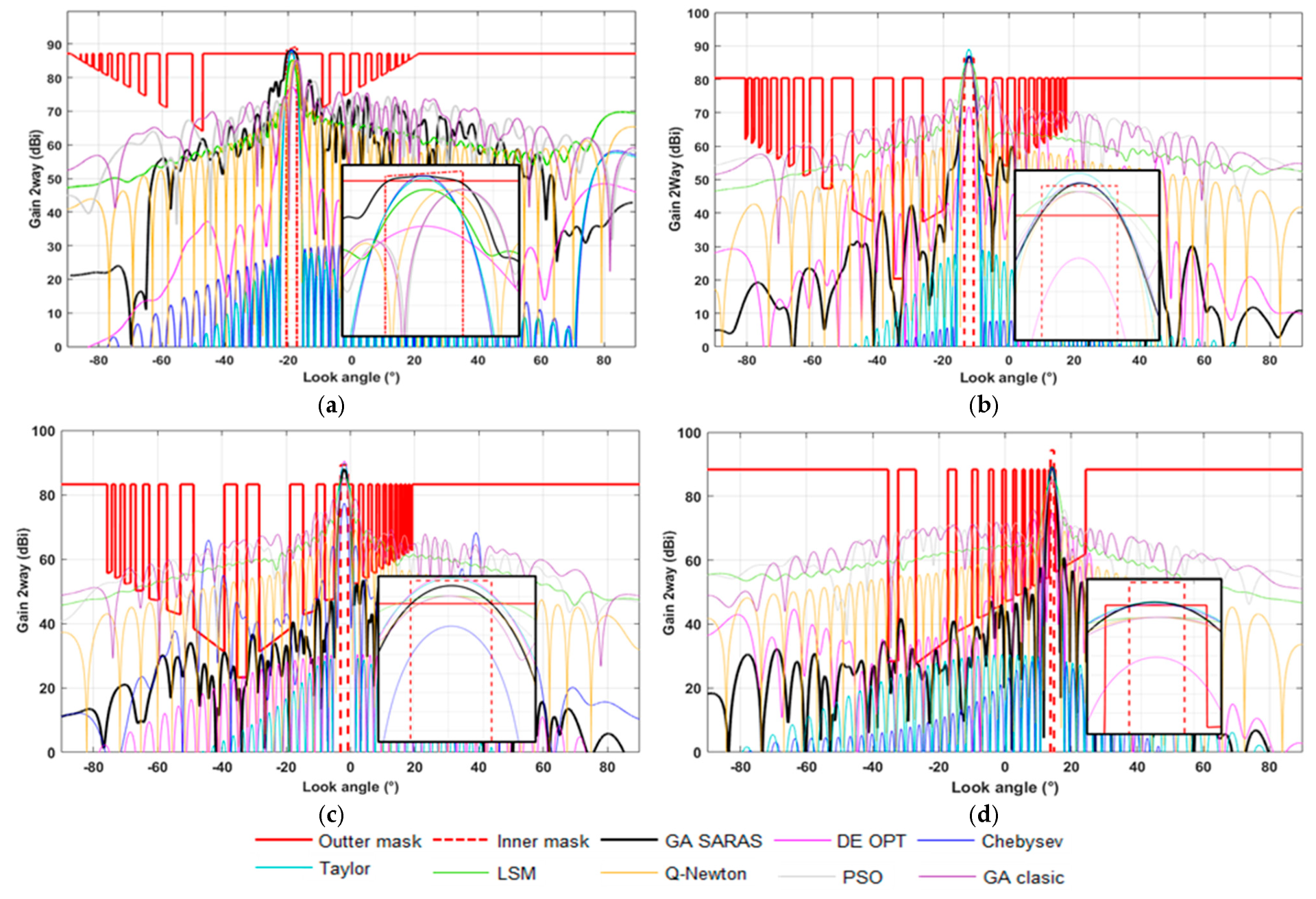
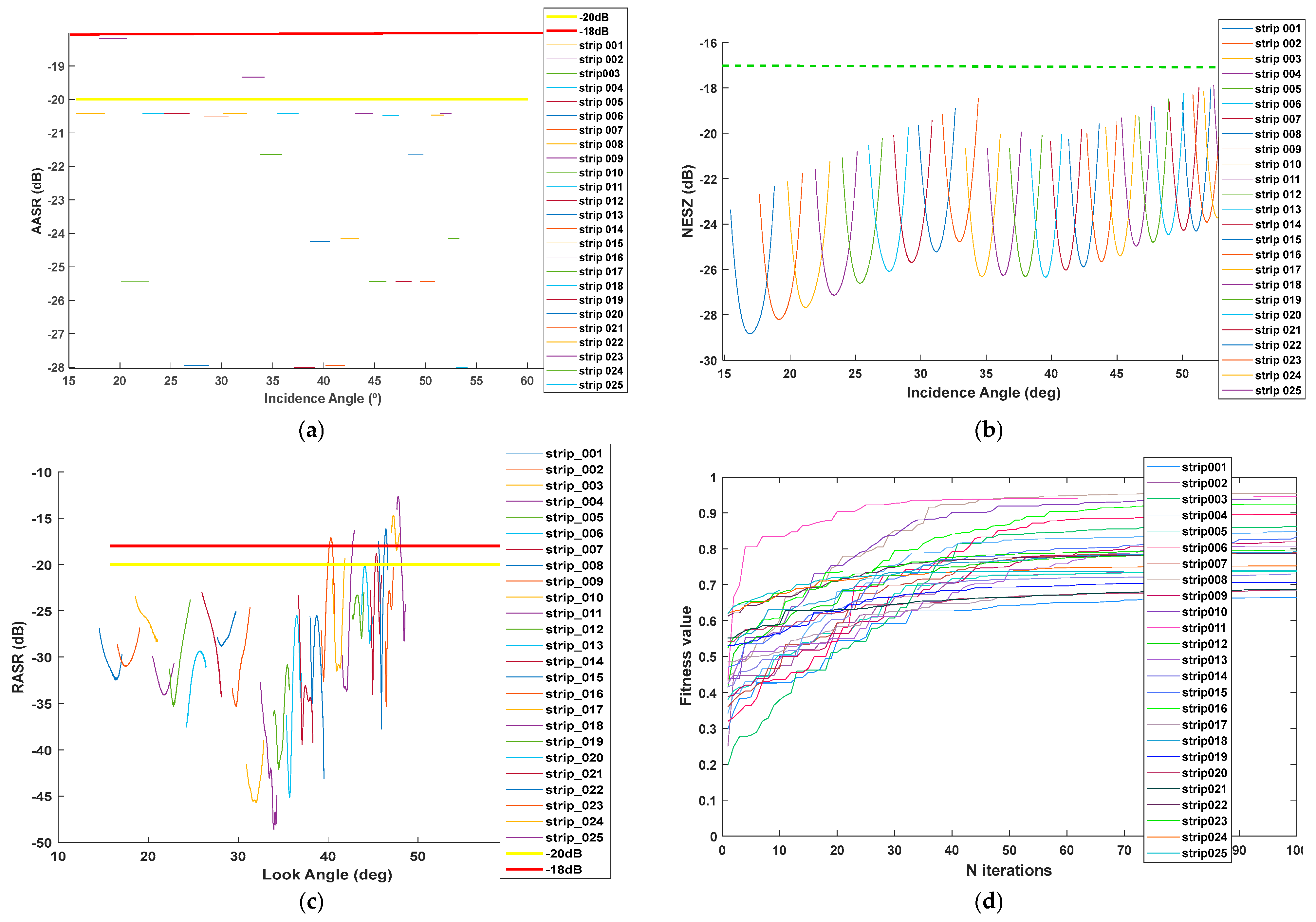
4.2. AEG Results, Beam Synthesis, Comparison, and Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley-Interscience: Hoboken, NJ, USA, 1991. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Henderson, F.M.; Lewis, A.J. Principles and Applications of Imaging Radar. In Manual of Remote Sensing; Wiley: Hoboken, NJ, USA, 1998; Volume 2. [Google Scholar]
- Bachmann, M.; Schwerdt, M.; Brautigam, B. TerraSAR-X Antenna Calibration and Monitoring Based on a Precise Antenna Model. IEEE Trans. Geosci. Remote Sens. 2010, 48, 690–701. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, H.C. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Capece, P.; Torre, A. Space Antenna Handbook; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Barbarossa, S.; Levrini, G. An antenna pattern synthesis technique for spaceborne SAR performance optimization. IEEE Trans. Geosci. Remote Sens. 1991, 29, 254–259. [Google Scholar] [CrossRef]
- Heer, C.; Dumper, K.; Grafmuller, B. SAR antenna beam pattern optimization. In Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment (IGARSS), Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 2263–2265. [Google Scholar]
- Kim, S.Y.; Myung, N.H.; Kang, M.J. Antenna mask design for SAR performance optimization. IEEE Geosci. Remote Sens. Lett. 2009, 6, 443–447. [Google Scholar]
- Kang, M.-S.; Won, Y.-J.; Lim, B.-G.; Kim, K.-T. Efficient synthesis of antenna pattern using improved PSO for spaceborne SAR performance and imaging in presence of element failure. IEEE Sens. J. 2018, 18, 6576–6587. [Google Scholar] [CrossRef]
- Won, Y.-J.; Lee, K.-H.; Lee, J.-H. Performance improvement of spaceborne SAR using antenna pattern synthesis based on quantumbehaved particle swarm optimization. Int. J. Antennas Propag. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Khosravi, M.; Fakharzadeh, M.; Bastani, M.H. Beamforming in SAR satellites for nadir echo suppression. IET Radar Sonar Navigat. 2019, 13, 420–427. [Google Scholar] [CrossRef]
- Ryu, J.; Yi, D.-W.; Kim, S.-Y.; Yoon, G. Suppression of Range Ambiguity in Spaceborne SAR With Elevation Beam Pattern Mask Design. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sánchez-Sevilleja, S.; Poyatos, D.; Masa-Campos, J.L.; Aragón, V.M.; Rodríguez, J.A.; Santiago, A. Design, Development, and Qualification of a Broadband Compact S-Band Antenna for a CubeSat Constellation. Sensors 2025, 25, 1237. [Google Scholar] [CrossRef]
- Rodriguez, M.G.; Muñoz, J.M.C.; Carrasco, E.M.V.; Llorente, N.A. Precursor—ECO: Inta Sar Mission Based on Collaborative Small Satellites. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 1521–1524. [Google Scholar]
- Bachmann, M.; Schwerdt, M.; Bräutigam, B. Accurate Antenna Pattern Modeling for Phased Array Antennas in SAR Applications—Demonstration on TerraSAR-X. Int. J. Antennas Propag. 2009, 2009, 1–9. [Google Scholar] [CrossRef]
- Mailloux, R.J. Phased Array Antenna Handbook, 2nd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Sánchez-Sevilleja, S.; García, M. Antenna Model with Pattern Optimization Based on Genetic Algorithms for Space SAR Systems. In Proceedings of the CEOS SAR Calibration & Validation Workshop 2023, Munich, Germany, 16–18 October 2023. [Google Scholar]
- Sebastian, J.; Dayal, P.; Song, K.-B.; AliAhmad, W. Explicit Calibration of mmWave Phased Arrays with Phase Dependent Errors. arXiv 2021, arXiv:2107.09561. [Google Scholar]
- Goudos, S.K.; Kalialakis, C.; Mittra, R. Evolutionary algorithms applied to antennas and propagation: A review of state of the art. Int. J. Antennas Propag. 2016, 1, 1010459. [Google Scholar] [CrossRef]
- Chaitanya, R.; Raju, G.S.N.; Raju, K.V.S.N.; Rao, P. Antenna Pattern Synthesis Using the Quasi Newton Method, Firefly and Particle Swarm Optimization Techniques. IETE J. Res. 2019, 68, 1148–1156. [Google Scholar] [CrossRef]
- Koh, J.; Lee, W.; Sarkar, T.K.; Salazar-Palma, M. Calculation of Far-Field Radiation Pattern Using Nonuniformly Spaced Antennas by a Least Square Method. IEEE Trans. Antennas Propag 2013, 62, 1572–1578. [Google Scholar] [CrossRef]
- Orazi, H.; Soleimani, H.; Azadkhah, R. Synthesis of linearly polarised patterns of conical arrays by the method of least square. IET Microw. Antennas Propag. 2015, 9, 185–191. [Google Scholar] [CrossRef]
- Kapoor, A.; Mishra, R. Genetic Algorithm Optimized Gain Augmented Dual Band Printed Antenna for Cognitive eHealth Care (IoMT) Applications. In Proceedings of the 2022 IEEE 11th International Conference on Communication Systems and Network Technologies (CSNT), Indore, India, 23–24 April 2022; pp. 6–11. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kumar, S.; Ram, G.; Mandal, D.; Kar, R. Far-Field Radiation Pattern Synthesis of Elliptical Antenna Arrays Using GA and PSO. In Proceedings of the 4th International Conference on Communication, Devices and Computing, Haldia, India, 1–3 March 2023. [Google Scholar] [CrossRef]
- Liang, Z.; Ouyang, J.; Yang, F. A hybrid GA-PSO optimization algorithm for conformal antenna array pattern synthesis. J. Electromagn. Waves Appl. 2018, 32, 1601–1615. [Google Scholar] [CrossRef]
- Johnson, J.M.; Rahmat-Samii, Y. Genetic algorithms in engineering electromagnetics. IEEE Antennas Propag. Mag. 1997, 39, 7–25. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Boeringer, D.W.; Werner, D.H. Particle swarm optimization versus genetic algorithms for phased array synthesis. IEEE Trans. Antennas Propag. 2004, 52, 771–779. [Google Scholar] [CrossRef]
- Durmus, A.; Kurban, R.; Karakose, E. A comparison of swarm-based optimization algorithms in linear antenna array synthesis. J. Comput. Electron 2021, 20, 1520–1531. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Sun, J.; Li, Q. Pattern Synthesis of Linear Antenna Array Using Improved Differential Evolution Algorithm with SPS Framework. Sensors 2020, 20, 5158. [Google Scholar] [CrossRef]
- Al-Sawafi, M.M.S.; Jervase, J.A. A micro-genetic algorithm-based CDMA multi-user detector. In Proceedings of the Conference on Communication Networks and Services Research, Fredericton, NB, Canada, 19–21 May 2004; pp. 175–180. [Google Scholar]
- Mühlenbein, H.; Schlierkamp-Voosen, D. Predictive Models for the Breeder Genetic Algorithm I. Continuous Parameter Optimization. Evol. Comput. 1993, 1, 25–49. [Google Scholar] [CrossRef]
- Wen, X.; Qiu, X.; Han, B.; Ding, C.; Lei, B.; Chen, Q. A Range Ambiguity Suppression Processing Method for Spaceborne SAR with Up and Down Chirp Modulation. Sensors 2018, 18, 1454. [Google Scholar] [CrossRef]
- Chatterjee, S.; Poddar, D.R. Synthesis of linear array using Taylor distribution and Particle Swarm Optimisation. Int. J. Electron. 2015, 102, 514–528. [Google Scholar] [CrossRef]
- Siakavara, K.; Chrysomallis, M.; Fernandez Jambrina, J.L.; Sahalos, J.N. An antenna array synthesis technique by the help of Chebyshev polynomials. Arch. Elektrotechnik 1989, 72, 435–441. [Google Scholar] [CrossRef]








| RASR requirement | −20 dB |
| Satellite altitude/roll angle | 550 km/33.8° |
| Frequency | 9.65G Hz |
| N elevation | 32 |
| N azimuth | 12 |
| Antena size (Wa × La) | 0.75 × 3 m |
| Steering angle | −17.98° |
| NESZ | −17 |
| Swath_BW | 3000 km |
| PRF | 3650 |
| AASR requirement | −17 dB |
| ‘Beam Name’ | ‘Min Look Angle’ | ‘Max Look Angle’ | ‘Swath Width’ | ‘Target PRF’ |
|---|---|---|---|---|
| ‘strip_001’ | 14.26 | 17.35 | ‘30 km’ | 4693.31 |
| ‘strip_002’ | 16.56 | 19.07 | ‘25 km’ | 4538.24 |
| ‘strip_003’ | 18.30 | 21.24 | ‘30 km’ | 5054.86 |
| ‘strip_004’ | 20.25 | 23.10 | ‘30 km’ | 4701.88 |
| ‘strip_005’ | 22.14 | 24.90 | ‘30 km’ | 4693.31 |
| ‘strip_010’ | 30.72 | 33.03 | ‘30 km’ | 5017.93 |
| ‘strip_025’ | 47.64 | 48.57 | ‘22 km’ | 5296.56 |
| ‘PARAM’ | GA SARAS | CHEBY | TAYLOR | QNEWTON | LSM | DE | PSO | |
|---|---|---|---|---|---|---|---|---|
| Strip_001 | NESZ_min (dB) | −27.93 | −29 | −28.4 | −25.6 | −25.9 | −18 | −25.4 |
| AASR (dB) | −19.39 | −19.39 | −19.39 | −19.39 | −19.39 | −19.39 | −19.39 | |
| RASR (dB) | −44.5 | −45.7 | −32.63 | −31 | −22.1 | −35.3 | −14.4 | |
| GAIN (dBi) | 88.2 | 88.2 | 87.6 | 85.2 | 85.7 | 77.2 | 85.4 | |
| BW −3dB (°) | 4.6 | 2.7 | 2.8 | 2.7 | 3.3 | 4.95 | 2.87 | |
| Strip_004 | NESZ_min(dB) | −25.5 | −25.6 | −27.6 | −23.8 | −23.9 | −10.3 | −23.8 |
| AASR (dB) | −19.42 | −19.42 | −19.42 | −19.42 | −19.42 | −19.42 | −19.42 | |
| RASR (dB) | −40.3 | −44.2 | −52.25 | −29.2 | −9.8 | −12.7 | −17.4 | |
| GAIN (dBi) | 86.9 | 87 | 88.9 | 85.1 | 85.21 | 71.7 | 85 | |
| BW −3dB(°) | 2.85 | 2.9 | 2.72 | 3 | 4.7 | 2.23 | 3.77 | |
| Strip_010 | NESZ_min(dB) | −25.4 | −14.9 | −24.4 | −22.8 | −22.8 | −27.9 | −22.7 |
| AASR (dB) | −21.3 | −21.3 | −21.3 | −21.3 | −21.3 | −21.3 | −21.3 | |
| RASR (dB) | −47.9 | −27.2 | −45 | −26.5 | −13.6 | −36.5 | −12.8 | |
| GAIN (dBi) | 87.9 | 77.3 | 89.8 | 85.1 | 85.2 | 90.4 | 85.1 | |
| BW −3dB(°) | 2.5 | 2 | 2.6 | 3 | 4.7 | 2.6 | 3.4 | |
| Strip_025 | NESZ_min | −21.6 | −21.1 | −21.6 | −17.7 | −17.7 | −7.11 | −17.7 |
| AASR (dB) | −27.42 | −27.42 | −27.42 | −27.42 | −27.42 | −27.42 | −27.42 | |
| RASR (dB) | −34.9 | −42 | −45.25 | −15.1 | −7.1 | −2.9 | −5.8 | |
| GAIN (dBi) | 89.1 | 88.6 | 89.2 | 85.3 | 85.21 | 77.7 | 85.2 | |
| BW −3dB(°) | 2.2 | 2.74 | 2.7 | 2.14 | 4.7 | 1.66 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Sevilleja, S.; García-Rodríguez, M.; Masa-Campos, J.L.; Cuerda-Muñoz, J.M. Antenna Model with Pattern Optimization Based on Genetic Algorithm for Satellite-Based SAR Mission. Sensors 2025, 25, 4835. https://doi.org/10.3390/s25154835
Sánchez-Sevilleja S, García-Rodríguez M, Masa-Campos JL, Cuerda-Muñoz JM. Antenna Model with Pattern Optimization Based on Genetic Algorithm for Satellite-Based SAR Mission. Sensors. 2025; 25(15):4835. https://doi.org/10.3390/s25154835
Chicago/Turabian StyleSánchez-Sevilleja, Saray, Marcos García-Rodríguez, José Luis Masa-Campos, and Juan Manuel Cuerda-Muñoz. 2025. "Antenna Model with Pattern Optimization Based on Genetic Algorithm for Satellite-Based SAR Mission" Sensors 25, no. 15: 4835. https://doi.org/10.3390/s25154835
APA StyleSánchez-Sevilleja, S., García-Rodríguez, M., Masa-Campos, J. L., & Cuerda-Muñoz, J. M. (2025). Antenna Model with Pattern Optimization Based on Genetic Algorithm for Satellite-Based SAR Mission. Sensors, 25(15), 4835. https://doi.org/10.3390/s25154835






