Digital Inspection Technology for Sheet Metal Parts Using 3D Point Clouds
Abstract
1. Introduction
2. Digital Inspection Method for Sheet Metal Parts Using 3D Point Clouds
2.1. Acquisition and Preprocessing of Point Cloud Data of Sheet Metal Parts
- ①
- Pass-Through Filtering Algorithm
- ②
- Downsampling and Processing for Improved Voxel Grid Filtering
- (1)
- Suppose that the original point cloud data set P contains N data coordinate points, and the voxel grid method is adopted to perform downsampling on the point cloud data.
- (2)
- Calculate the centroid coordinate points, p(x, y, z), of each non-empty voxel grid and construct a new set of centroid points, pi(xi, yi, zi).
- (3)
- Search each voxel grid according to the KD tree nearest neighbor search method and take the point closest to the centroid in it as the new downsampled point to obtain a new set of centroid points, pi.
2.2. Point Cloud Registration of Sheet Metal Parts
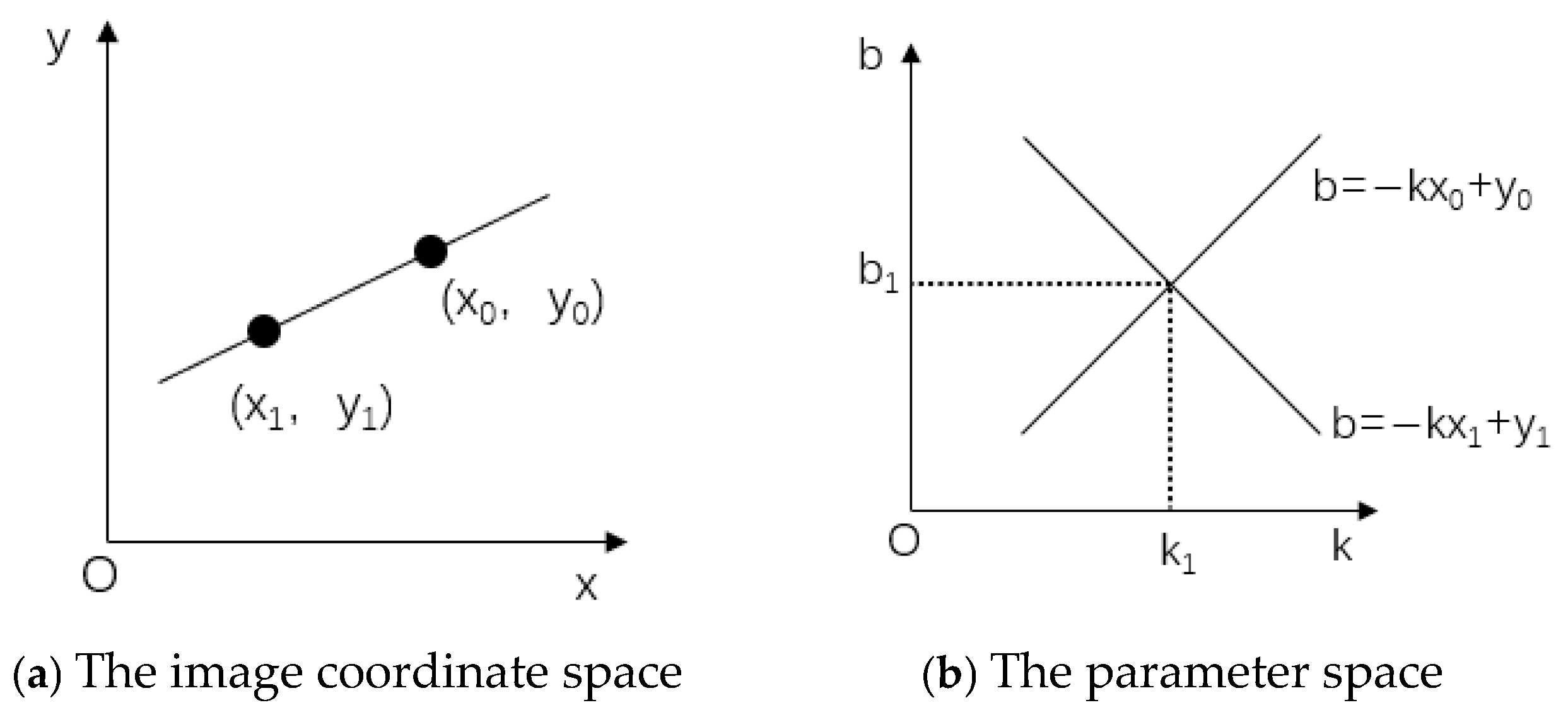
2.2.1. Rough Registration of Point Clouds
- ①
- A local coordinate system is established for each point pi in the point cloud data, and a search radius r is set for all points. An appropriate search radius r needs to be selected based on the actual situation, such as the density of the point cloud.
- ②
- Query all points in the area of radius r centered on each point pi in point cloud data P and calculate the weights wij of these points, as shown in Equation (1):
- ③
- Calculate the covariance matrix of each point pi, as shown in Equation (2):
- ④
- Calculate the eigenvalues of covariance matrix cov(pi) for each point pi in the point cloud data and arrange them in order from largest to smallest.
- ⑤
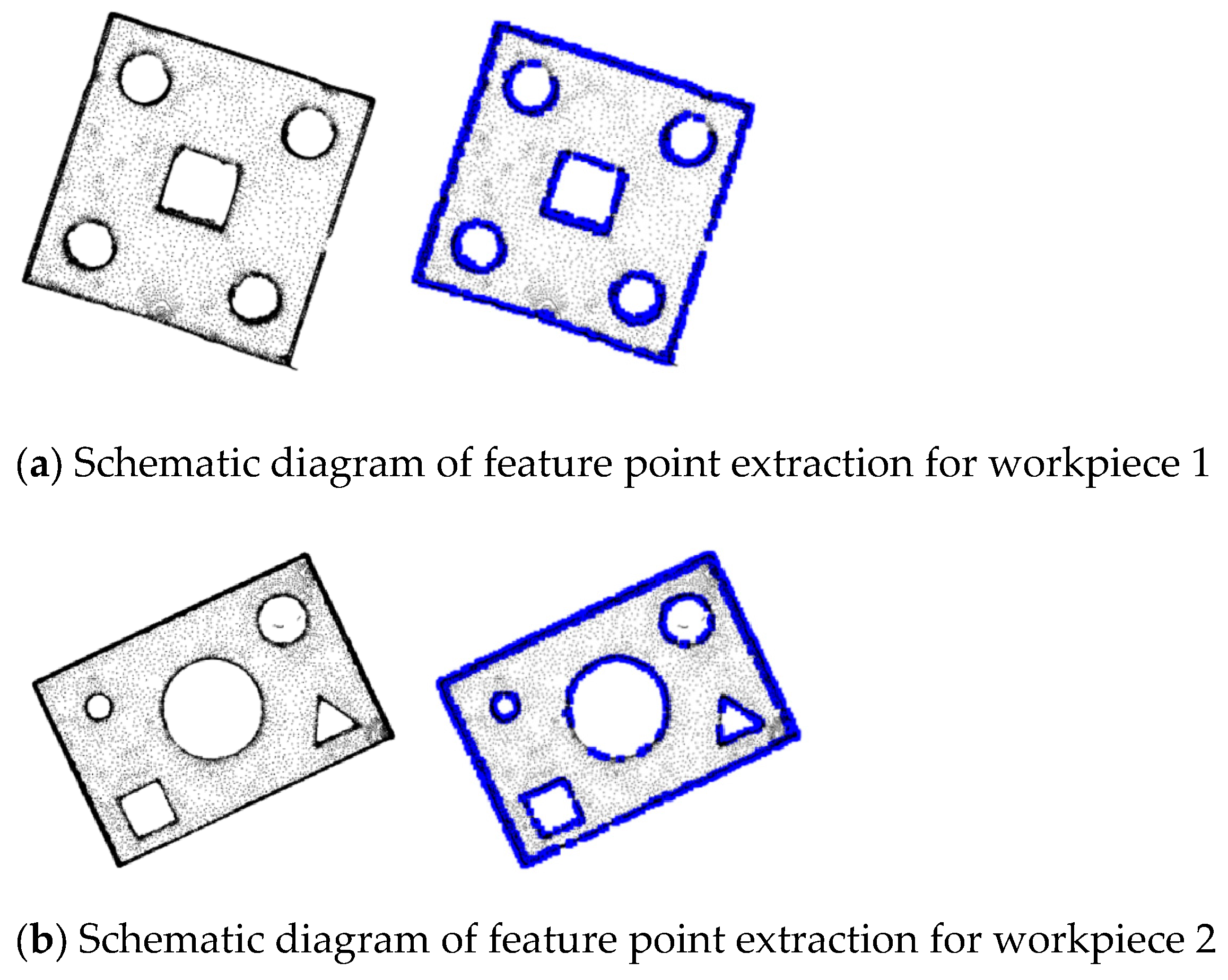
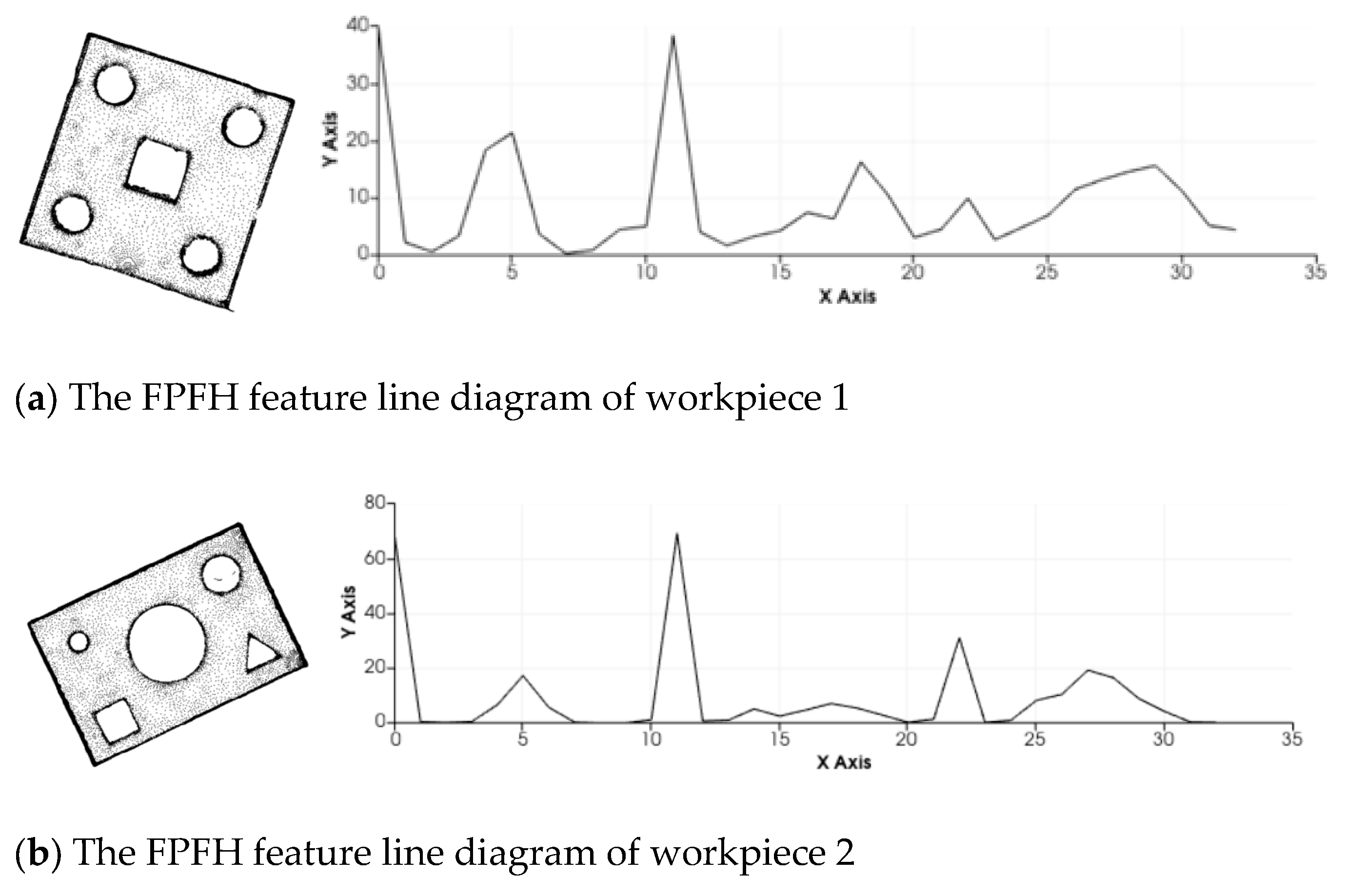
- Set the threshold values and , and the points that meet the screening conditions of Equation (3) are ISS feature points.
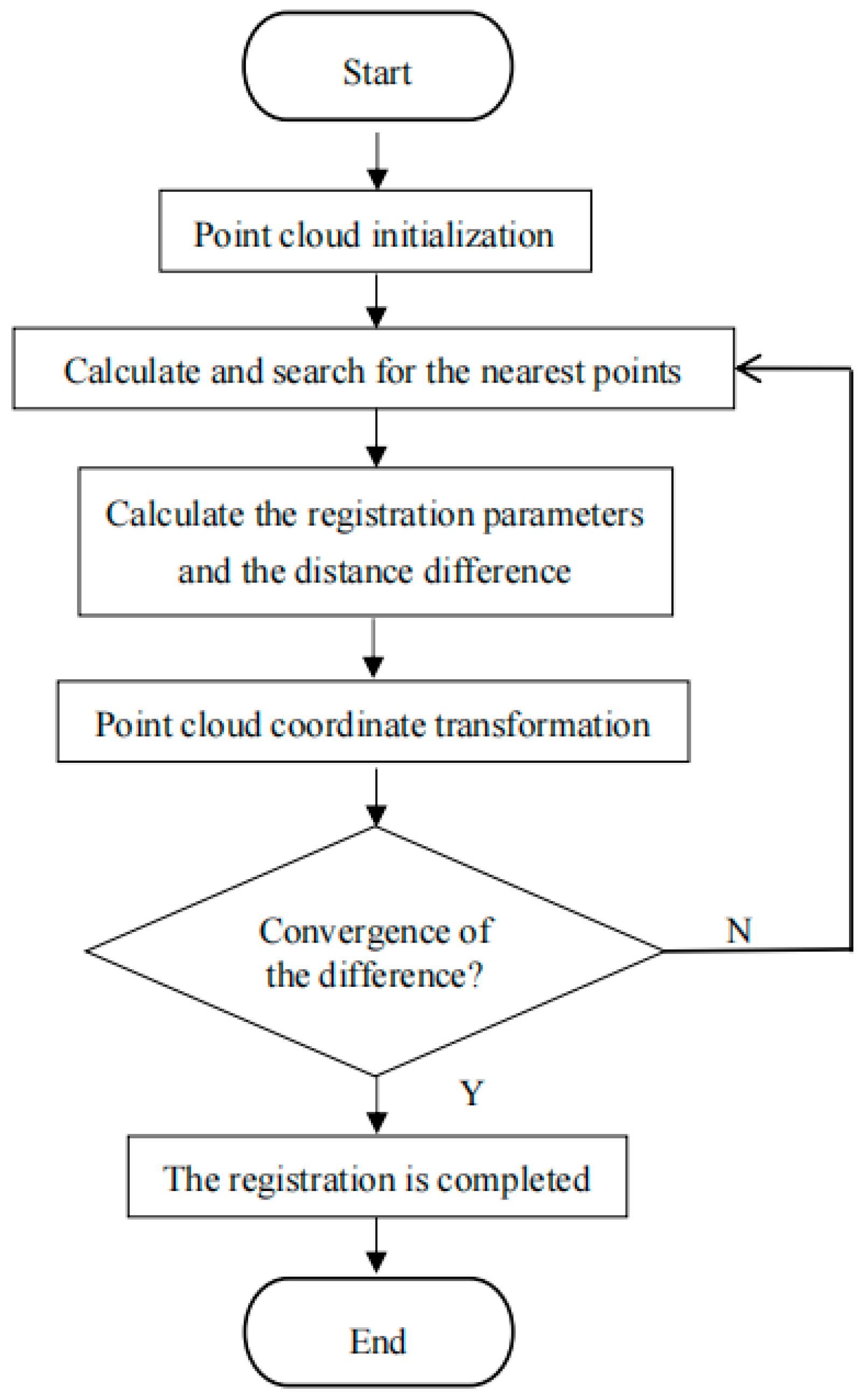
2.2.2. ICP Fine Registration
2.3. A 3D Reconstruction Algorithm for Sheet Metal Parts
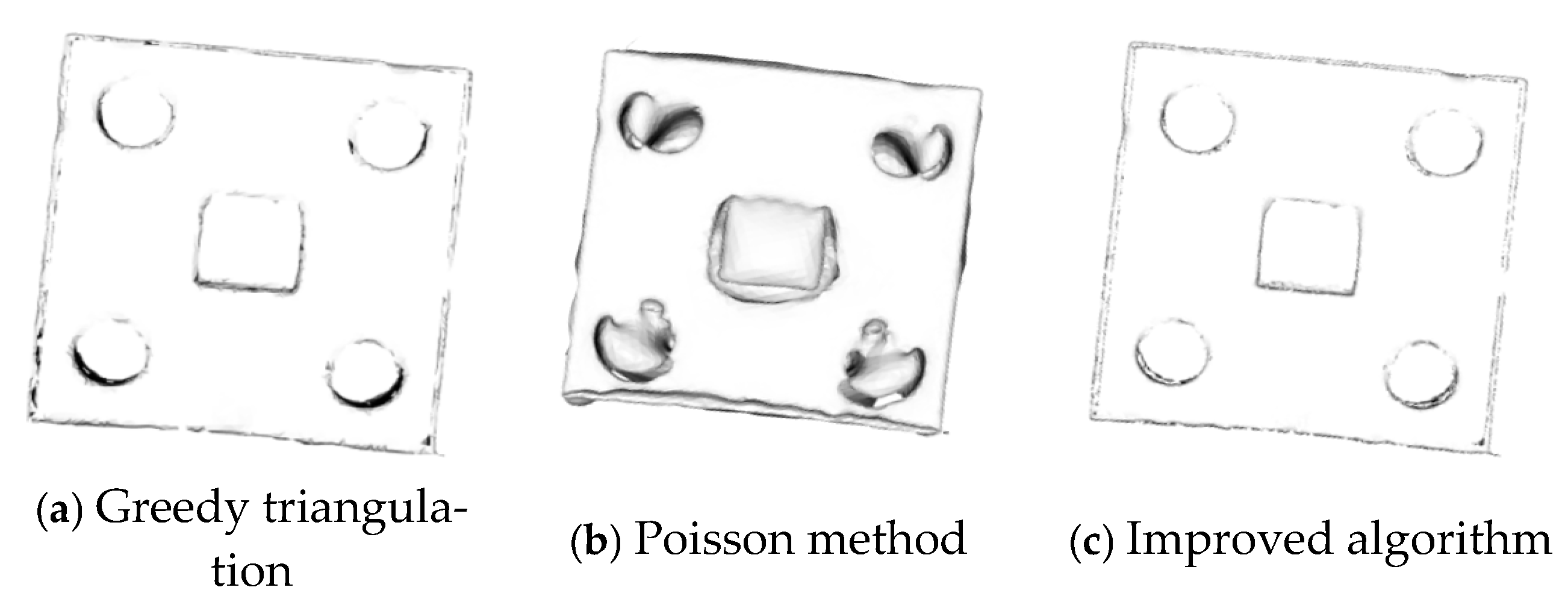
2.3.1. Greedy Projection Triangulation Processing
2.3.2. Poisson Surface Reconstruction Processing
2.3.3. MLS Smoothing Processing
3. Digital Detection Experiments on Sheet Metal Parts Based on 3D Point Clouds
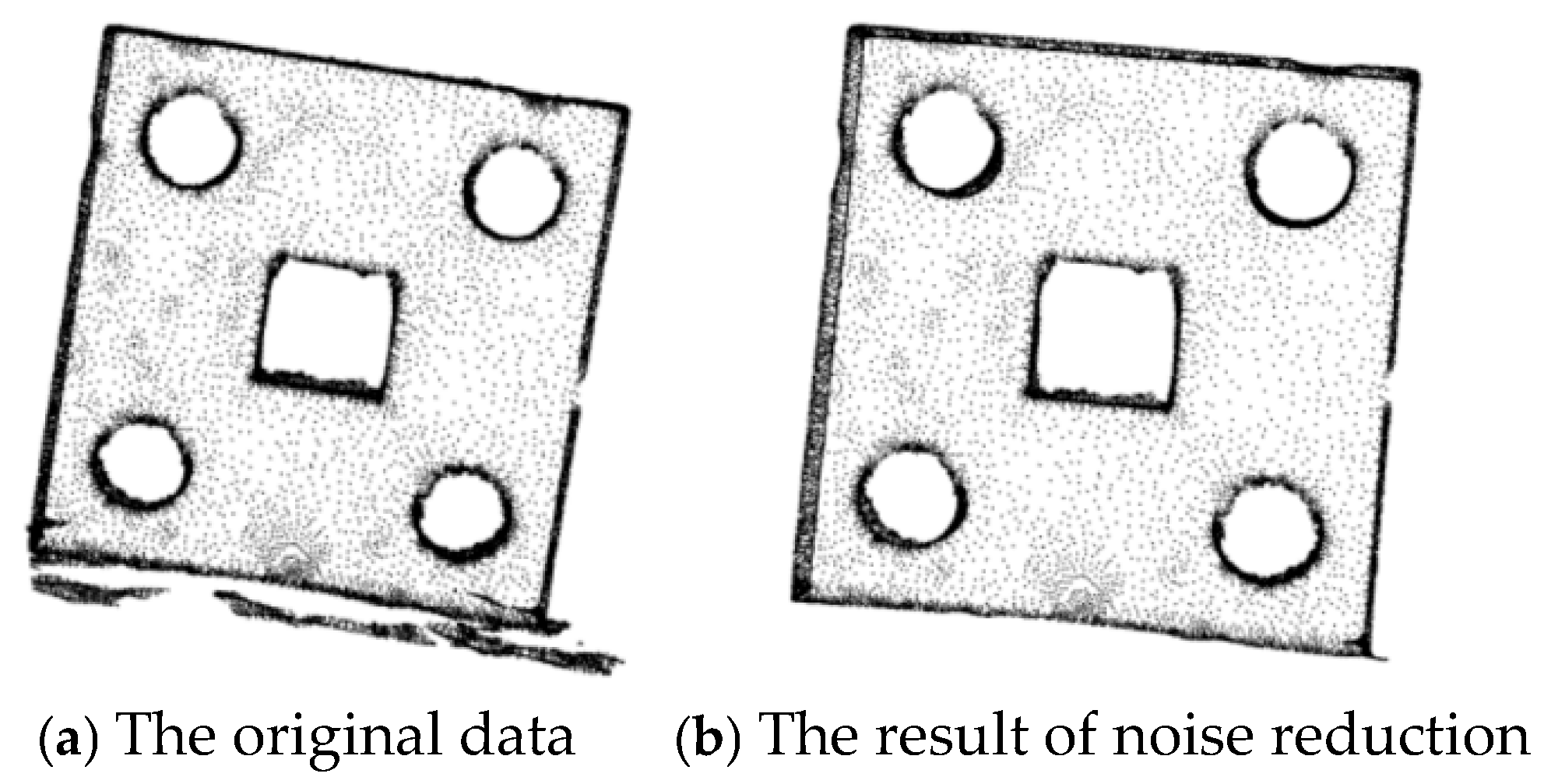
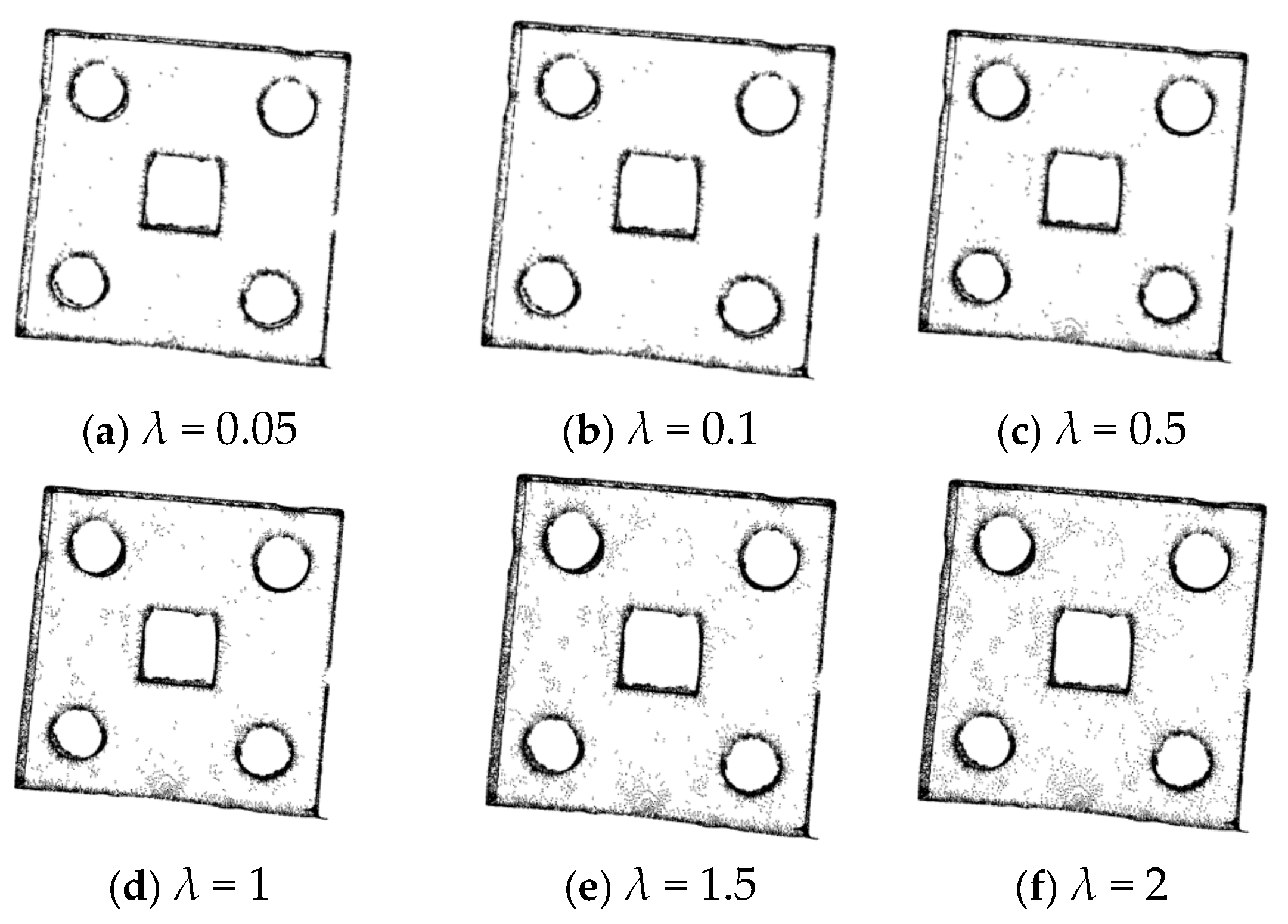
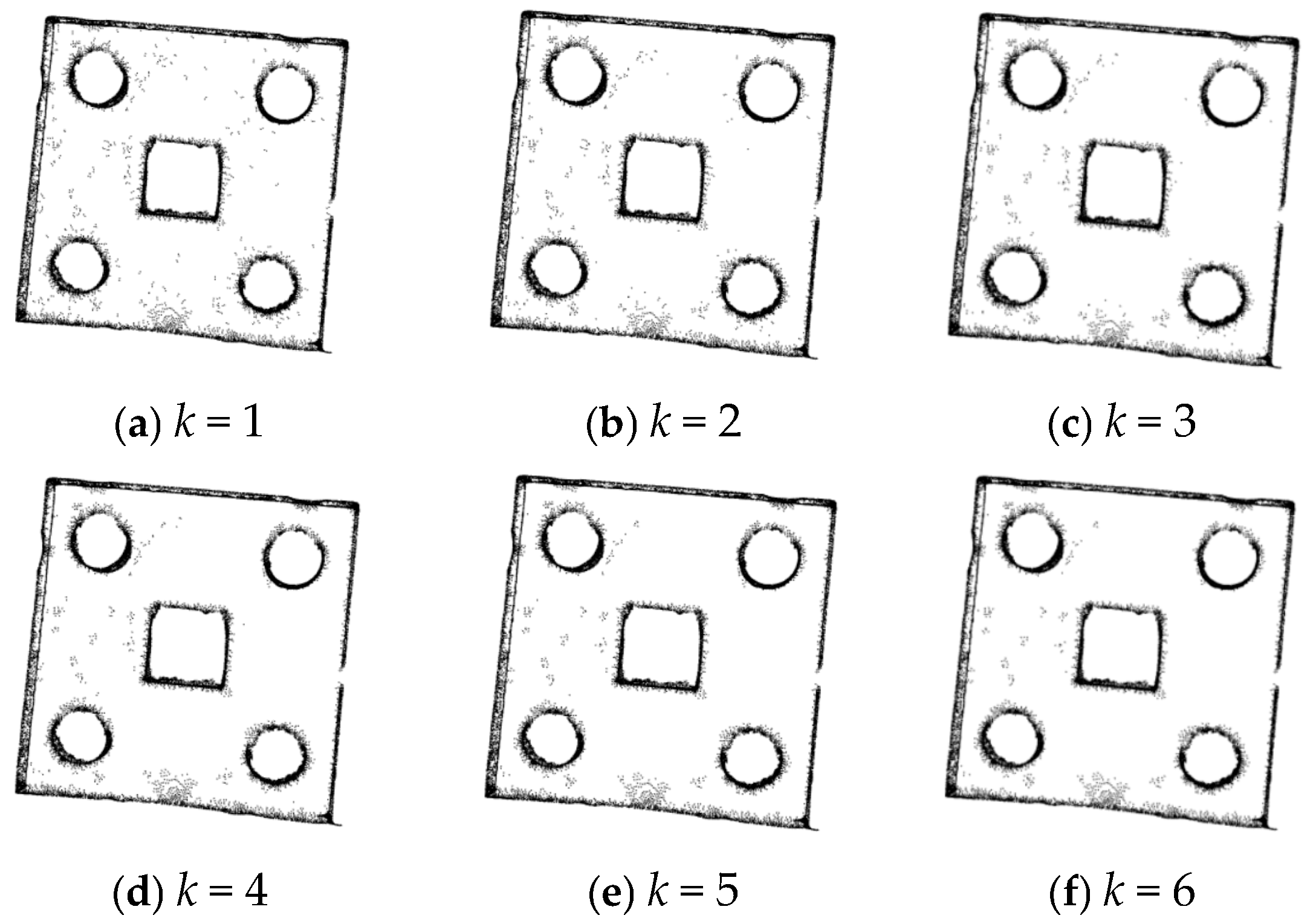
3.1. Experiments on Point Cloud Denoising of Sheet Metal Parts
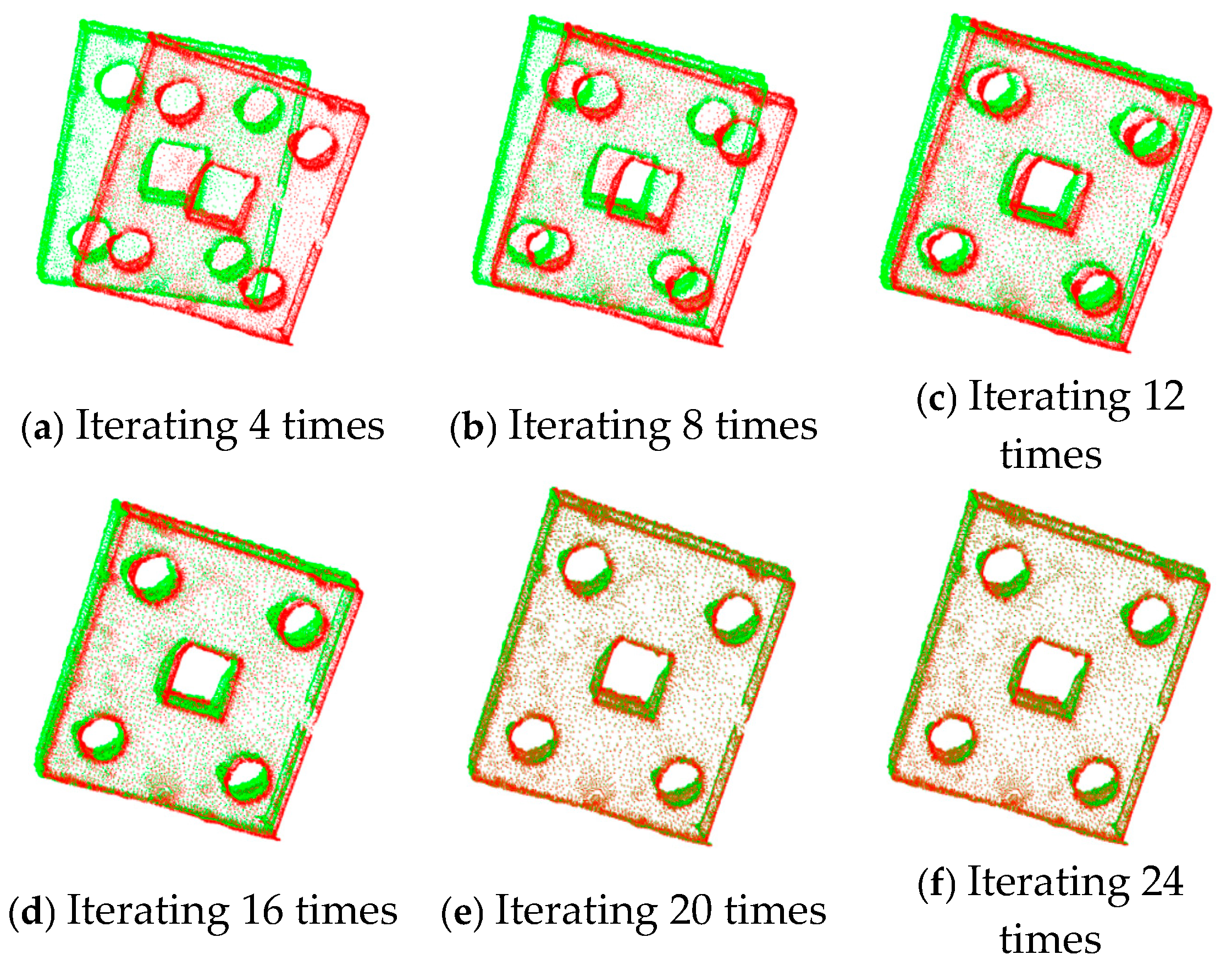
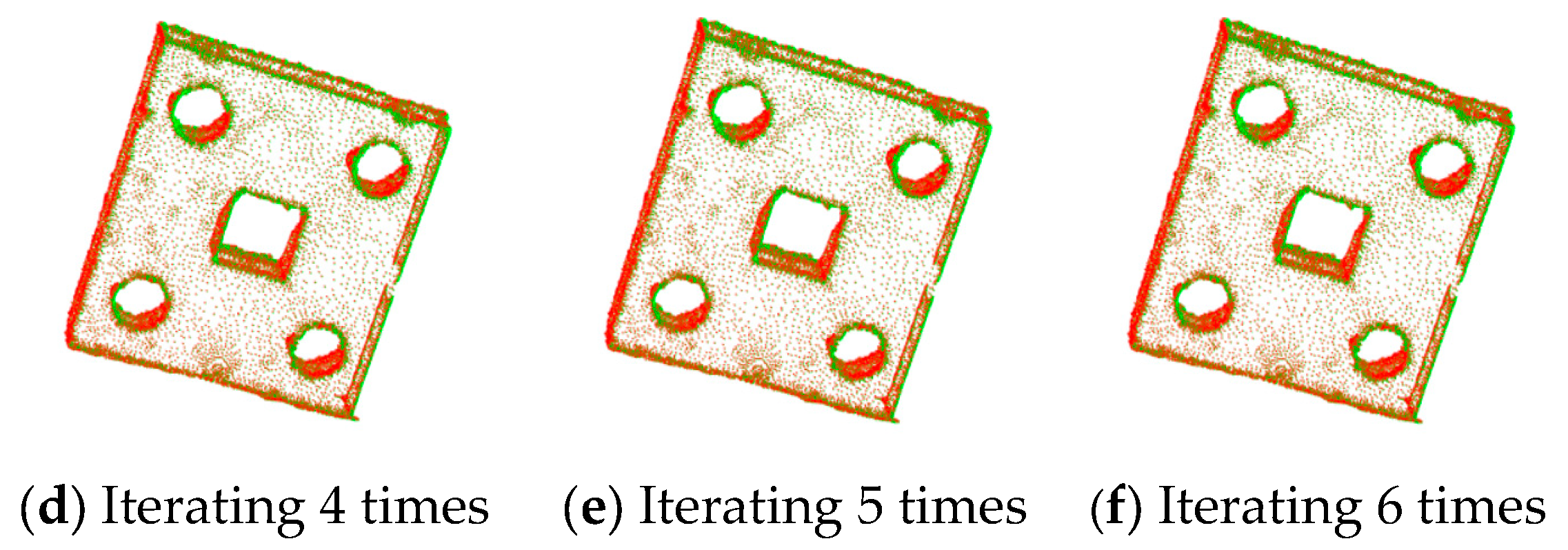
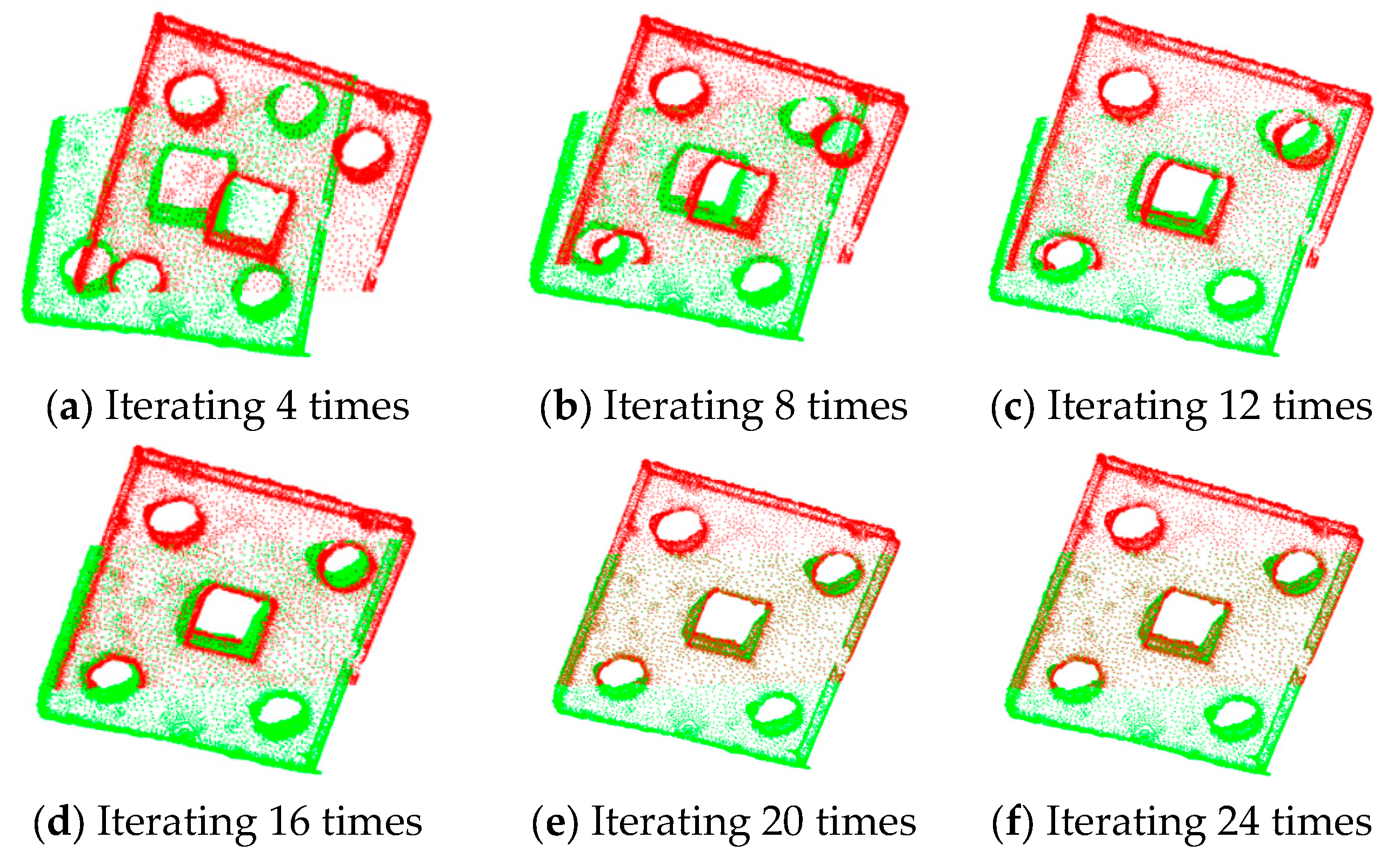
3.2. Registration Experiments on Sheet Metal Parts
3.3. Three-Dimensional Reconstruction Experiments on Sheet Metal Parts
3.4. Digital Detection Experiments on Sheet Metal Parts
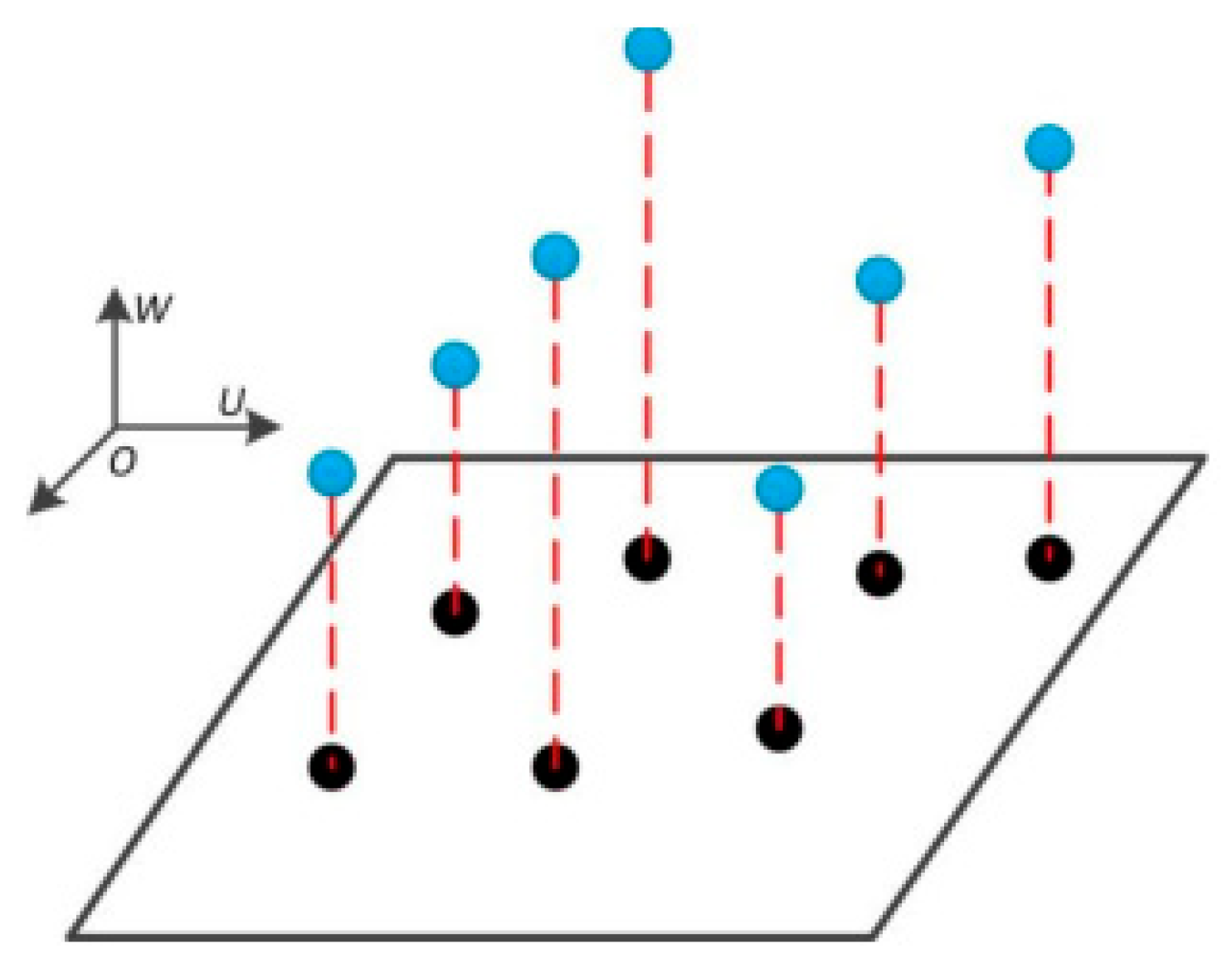
3.4.1. Digital Detection Algorithm
3.4.2. Projection Experiments on Sheet Metal Parts
3.4.3. Experiments on Dimension Measurement of Sheet Metal Parts
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhang, Y.C. Length dimension measurement for large hot forgings based on green laser recognition. Acta Metrol. Sin. 2018, 39, 316–320. [Google Scholar]
- Cheng, Y.B.; Chen, X.H.; Wang, H.B. Uncertainty estimation model of CMM for size measurement. Acta Metrol. Sin. 2016, 37, 462–466. [Google Scholar]
- Lilienblum, E.; Al-Hamadi, A. A structured light approach for 3-D surface reconstruction with a stereo line-scan system. IEEE Trans. Instrum. Meas. 2015, 64, 1258–1266. [Google Scholar] [CrossRef]
- Siekański, P.; Magda, K.; Zagórski, A. On-line laser triangulation scanner for wood logs surface geometry measurement. Sensors 2019, 19, 1074–1079. [Google Scholar] [CrossRef]
- Tong, Q.B.; Jiao, C.Q.; Huang, H.; Li, G.B.; Ding, Z.L.; Yuan, F. An automatic measuring method and system using laser triangulation scanning for screw thread parameters. Meas. Sci. Technol. 2014, 25, 35202–35209. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Jin, C.Q.; Xu, J.; Yang, T.X. Measurement of potato volume with laser triangulation and three-dimensional reconstruction. IEEE Access 2020, 8, 176565–176574. [Google Scholar] [CrossRef]
- Haque, S.M.; Govindu, V.M. Robust feature-preserving denoising of 3D point clouds. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Lyon, France, 25–28 October 2016. [Google Scholar]
- Lee, M.Y.; Lee, S.H.; Jung, K.D.; Lee, S.H.; Kwon, S.C. A novel preprocessing method for dynamic point-cloud compression. Appl. Sci. 2021, 11, 5941–5948. [Google Scholar] [CrossRef]
- Heinzler, R.; Piewak, F.; Schindler, P.; Stork, W. CNN-based lidar point cloud de-noising in adverse weather. IEEE Robot. Autom. Lett. 2020, 5, 2514–2521. [Google Scholar] [CrossRef]
- Ren, Y.J.; Li, T.Z.; Xu, J.K.; Hong, W.W.; Zheng, Y.C.; Fu, B. Overall filtering algorithm for multiscale noise removal from point cloud data. IEEE Access 2021, 9, 110723–110734. [Google Scholar] [CrossRef]
- Zou, B.C.; Qiu, H.D.; Lu, Y.F. Point cloud reduction and denoising based on optimized downsampling and bilateral filtering. IEEE Access 2020, 8, 136316–136326. [Google Scholar] [CrossRef]
- Xu, Z.; Kang, R.; Lu, R.D. 3D reconstruction and measurement of surface defects in prefabricated elements using point clouds. J. Comput. Civil. Eng. 2020, 34, 04020033. [Google Scholar] [CrossRef]
- Makovetskii, A.; Voronin, S.; Kober, V.; Voronin, A. A regularized point cloud registration approach for orthogonal transformations. J. Glob. Optim. 2022, 83, 497–519. [Google Scholar] [CrossRef]
- Koide, K.; Yokozuka, M.; Oishi, S.; Banno, A. Voxelized GICP for fast and accurate 3D point cloud registration. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Young, M.; Pretty, C.; McCulloch, J.; Green, R. Sparse point cloud registration and aggregation with mesh-based generalized iterative closest point. J. Field Robot. 2021, 38, 1078–1091. [Google Scholar] [CrossRef]
- Yu, J.W.; Yu, C.G.; Lin, C.D.; Wei, F.Q. Improved iterative closest point (ICP) point cloud registration algorithm based on matching point pair quadratic filtering. In Proceedings of the 2021 International Conference on Computer, Internet of Things and Control Engineering (CITCE), Guangzhou, China, 12–14 November 2021. [Google Scholar]
- He, Y.W.; Lee, C.H. An improved ICP registration algorithm combining PointNet++ and ICP algorithm. In Proceedings of the 2020 Sixth International Conference on Control, Automation and Robotics (ICCAR), Singapore, Singapore, 20–23 April 2020. [Google Scholar]
- Vizzo, I.; Chen, X.Y.L.; Chebrolu, N.; Behley, J.; Stachniss, C. Poisson surface reconstruction for lidar odometry and mapping. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Maurya, S.R.; Magar, G.M. Performance of greedy triangulation algorithm on reconstruction of coastal dune surface. In Proceedings of the2018 Third International Conference for Convergence in Technology (I2CT), Pune, India, 6–8 April 2018. [Google Scholar]
- Ando, R.; Ozasa, Y.; Guo, W. Robust surface reconstruction of plant leaves from 3D point clouds. Plant Phenomics 2021, 2021, 3184185. [Google Scholar] [CrossRef] [PubMed]
- Gu, R.R.; Sun, A.B.; Li, Y.R.; Wang, Z.Y. An analysis of triangulation reconstruction based on 3D point cloud with geometric features. In Proceedings of the 2021 Tenth International Symposium on Precision Mechanical Measurements, Qingdao, China, 15-17 October 2021. [Google Scholar]
- Xie, Z.P.; Lang, Y.C.; Chen, L.Q. Geometric modeling of rosa roxburghii fruit based on three-dimensional point cloud reconstruction. J. Food Qual. 2021, 2021, 9990499. [Google Scholar] [CrossRef]
- Pan, Y.; Dong, Y.Q.; Wang, D.L.; Chen, A.R.; Ye, Z. Three-dimensional reconstruction of structural surface model of heritage bridges using UAV-based photogrammetric point clouds. Remote Sens. 2019, 11, 1204. [Google Scholar] [CrossRef]
- Liao, L.X.; Zhou, J.D.; Ma, Y.Q.; Liu, Y.B.; Lei, J. A thinning method of building 3D laser point cloud data based on voxel grid. Geomat. Spat. Inf. Technol. 2023, 46, 53–56, 60. [Google Scholar]
- Zhang, Z.L.; Dong, Y.M.; Zhu, J.X.; Lu, J.J. An improved ICP point cloud registration algorithm based on ISS-FPFH features. Appl. Laser 2023, 43, 124–131. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Zhang, M.; Wen, J.H.; Zhang, Z.X.; Zhang, J.Q. Laser points cloud registration using euclidean distance measure. Sci. Surv. Mapp. 2010, 35, 5–8. [Google Scholar]
- Li, Y.; Qu, R.F.; Gu, S.; Xie, Y.M. 3D point cloud registration method of ICP based on k-d tree. Comput. Knowl. Technol. 2022, 18, 82–84. [Google Scholar]
- Liu, X.Y.; Wang, J.; Chang, Q.F.; Wang, X.G. Fast 3D reconstruction of point cloud based on improved greedy projection triangulation algorithm. Laser Infrared 2022, 52, 763–770. [Google Scholar]
- Lu, M.S.; Yao, J.; Dong, S.Y. The poisson surface reconstruction algorithm for normal constraint’s for point cloud data. J. Geomat. 2022, 47, 51–55. [Google Scholar]











| Device Model | EinScan Pro 2X |
|---|---|
| Scanning precision | 0.045 mm |
| Scanning range per single scan | 150 × 120 mm~250 × 200 mm |
| Working center distance | 400 mm |
| Printable data output format | OBJ, STL, ASC, PLY, P3, 3MF |
| Weight of scanning head | 1.13 kg |
| System requirements | Windows 10, 64-bit |
| Serial Number | Number of Point Clouds | λ | k | Number of Point Clouds After Noise Reduction |
|---|---|---|---|---|
| (a) | 20,463 | 0.05 | 1 | 13,713 |
| (b) | 20,463 | 0.1 | 1 | 14,120 |
| (c) | 20,463 | 0.5 | 1 | 16,552 |
| (d) | 20,463 | 1 | 1 | 17,901 |
| (e) | 20,463 | 1.5 | 1 | 18,674 |
| (f) | 20,463 | 2 | 1 | 19,253 |
| Serial Number | Number of Point Clouds | λ | k | Number of Point Clouds After Noise Reduction |
|---|---|---|---|---|
| (a) | 17,901 | 1 | 1 | 17,901 |
| (b) | 17,901 | 1 | 2 | 17,761 |
| (c) | 17,901 | 1 | 3 | 17,687 |
| (d) | 17,901 | 1 | 4 | 17,622 |
| (e) | 17,901 | 1 | 5 | 17,617 |
| (f) | 17,901 | 1 | 6 | 17,616 |
| Algorithm | Number of Point Clouds |
|---|---|
| Initial point clouds | 17,617 |
| Downsampling by the voxel grid algorithm | 3359 |
| Downsampling by the improved algorithm | 3359 |
| Algorithm | Number of Iterations | Registration Error (m) | Time (s) |
|---|---|---|---|
| ICP algorithm | 4 | 8.00264 × 10−5 | 5.936 |
| 8 | 1.93961 × 10−5 | 8.453 | |
| 12 | 5.56931 × 10−6 | 10.867 | |
| 16 | 1.23578 × 10−6 | 13.349 | |
| 20 | 6.96264 × 10−7 | 15.896 | |
| 24 | 2.63578 × 10−7 | 18.345 | |
| Improved algorithm | 1 | 2.46069 × 10−6 | 11.522 |
| 2 | 2.03659 × 10−6 | 11.572 | |
| 3 | 1.60361 × 10−6 | 11.634 | |
| 4 | 1.18995 × 10−6 | 11.681 | |
| 5 | 7.51249 × 10−7 | 11.736 | |
| 6 | 4.22656 × 10−7 | 11.793 |
| Algorithm | Number of Iterations | Registration Error (m) | Time (s) |
|---|---|---|---|
| ICP algorithm | 4 | 7.07786 × 10−5 | 5.032 |
| 8 | 1.89264 × 10−5 | 7.982 | |
| 12 | 6.68919 × 10−6 | 10.975 | |
| 16 | 1.52197 × 10−6 | 14.063 | |
| 20 | 5.69119 × 10−7 | 17.192 | |
| 24 | 2.03491 × 10−7 | 20.038 | |
| Improved algorithm | 1 | 2.59116 × 10−6 | 10.581 |
| 2 | 2.10359 × 10−6 | 10.623 | |
| 3 | 1.68134 × 10−6 | 10.674 | |
| 4 | 1.20319 × 10−6 | 10.716 | |
| 5 | 8.76916 × 10−7 | 10.759 | |
| 6 | 4.95649 × 10−7 | 10.807 |
| Algorithm | Time (s) |
|---|---|
| Greedy triangulation algorithm | 4.368 |
| Poisson algorithm | 4.136 |
| Improved algorithm | 4.697 |
| Size Name | Value Measured by the Universal Tool Microscope (mm) | Pixel Value |
|---|---|---|
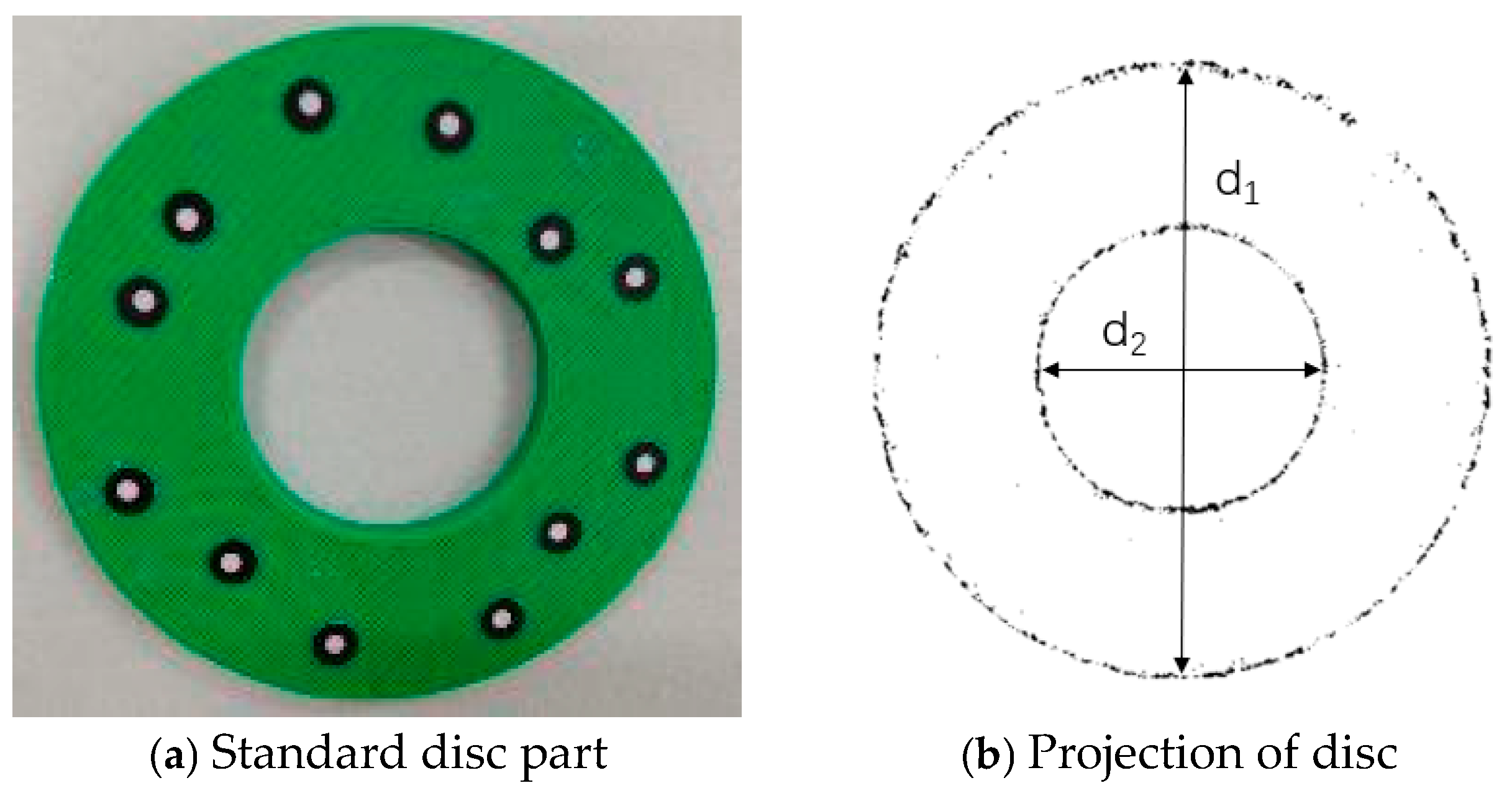
| d1 | 95.9941 | 1517 |
| d2 | 43.9887 | 695 |
| Dimension Annotation | Value Measured by the Universal Tool Microscope (mm) | Measured Value (mm) | Error (mm) |
|---|---|---|---|
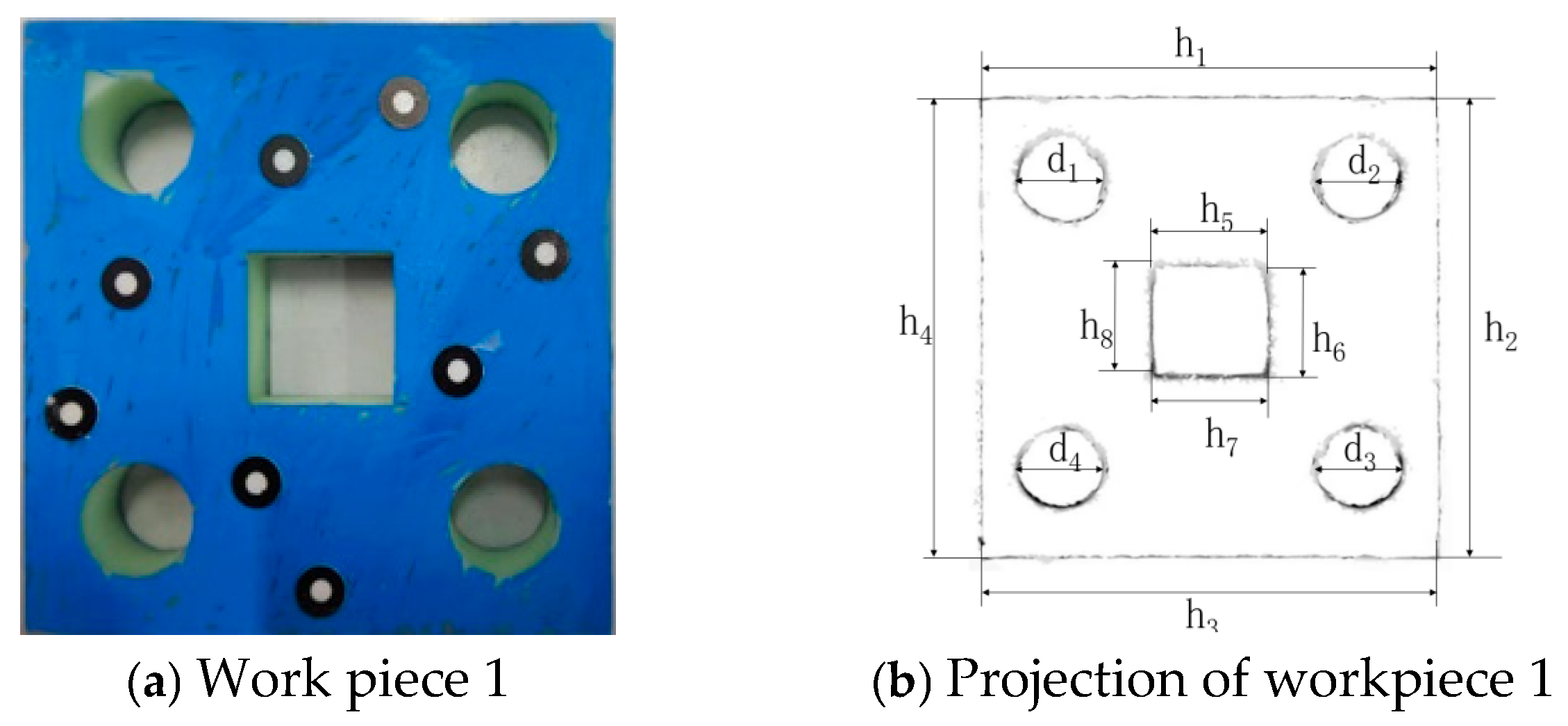
| h1 | 80.0129 | 80.2011 | 0.1882 |
| h2 | 80.0067 | 80.2644 | 0.2577 |
| h3 | 80.0117 | 80.2011 | 0.1894 |
| h4 | 79.9962 | 80.1378 | 0.1416 |
| d1 | 15.0165 | 14.8122 | 0.2043 |
| d2 | 15.0097 | 15.1922 | 0.1825 |
| d3 | 15.0126 | 14.7489 | 0.2637 |
| d4 | 15.0203 | 15.2553 | 0.2350 |
| h5 | 20.0105 | 20.2562 | 0.2457 |
| h6 | 20.0107 | 19.7496 | 0.2611 |
| h7 | 20.0096 | 20.1927 | 0.1831 |
| h8 | 20.0148 | 20.1927 | 0.1779 |
| Dimension Annotation | Value Measured by the Universal Tool Microscope (mm) | Measured Value (mm) | Error (mm) |
|---|---|---|---|
| h1 | 120.0026 | 120.2067 | 0.2041 |
| h2 | 80.0103 | 80.2011 | 0.1908 |
| h3 | 120.0067 | 120.2704 | 0.2637 |
| h4 | 79.9972 | 80.2644 | 0.2672 |
| h5 | 18.0065 | 18.2304 | 0.2239 |
| h6 | 18.0112 | 18.1671 | 0.1559 |
| h7 | 18.0130 | 17.8506 | 0.1624 |
| h8 | 17.9826 | 18.1671 | 0.1845 |
| h9 | 20.0192 | 20.2560 | 0.2368 |
| h10 | 19.9763 | 20.1927 | 0.2164 |
| h11 | 20.0125 | 20.1927 | 0.1802 |
| d1 | 40.0070 | 40.2588 | 0.2518 |
| d2 | 20.0108 | 19.7496 | 0.2612 |
| d3 | 10.0203 | 10.2546 | 0.2343 |
| Dimension Annotation | Value Measured by the Universal Tool Microscope (mm) | Measured Value (mm) | Error (mm) |
|---|---|---|---|
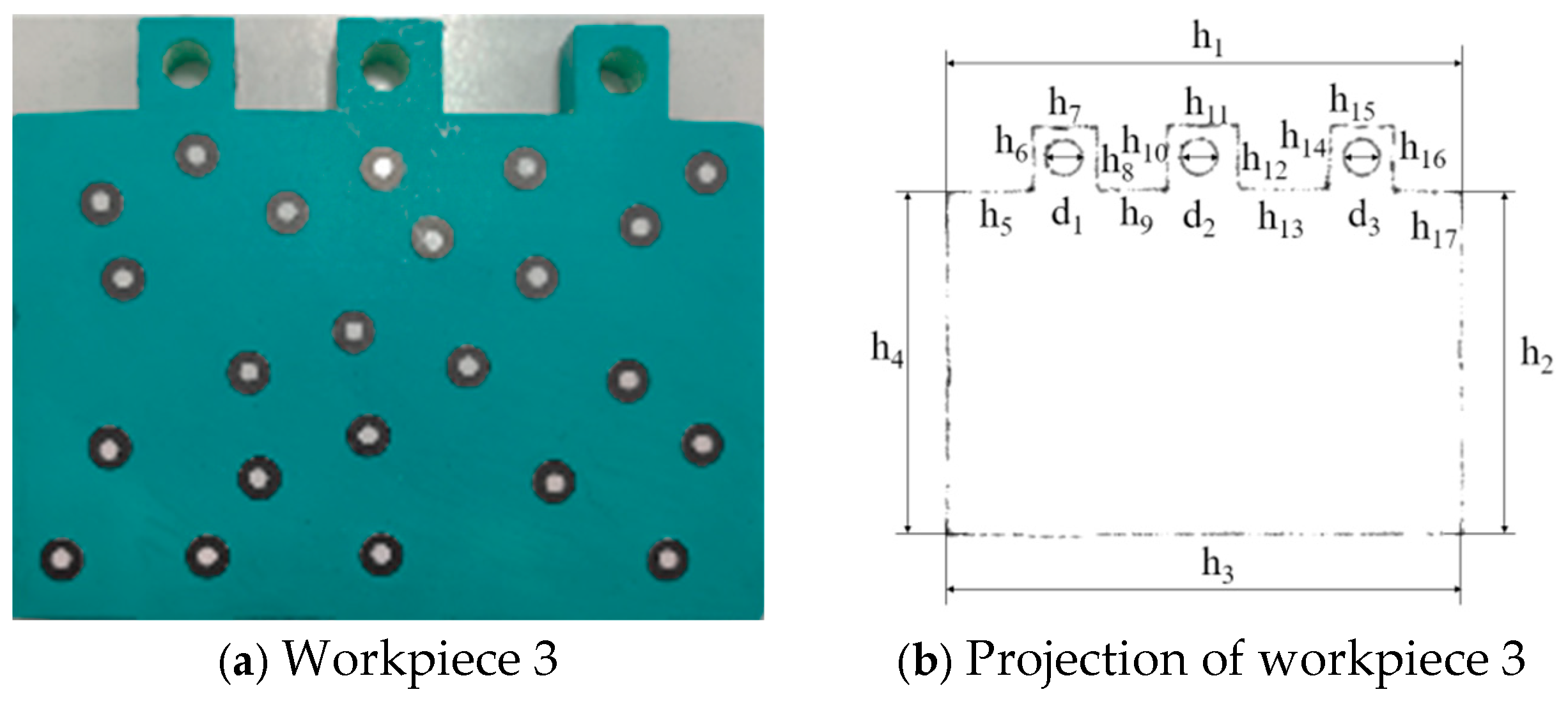
| h1 | 120.0116 | 120.2067 | 0.1951 |
| h2 | 80.0126 | 80.2011 | 0.1885 |
| h3 | 119.9776 | 120.1434 | 0.1658 |
| h4 | 79.9863 | 80.1378 | 0.1515 |
| h5 | 20.0067 | 20.2561 | 0.2494 |
| h6 | 15.0026 | 15.2553 | 0.2527 |
| h7 | 15.0120 | 15.1924 | 0.1804 |
| h8 | 14.9773 | 15.1287 | 0.1514 |
| h9 | 17.9926 | 17.7242 | 0.2684 |
| h10 | 15.0028 | 14.8122 | 0.1906 |
| h11 | 15.0102 | 15.2553 | 0.2451 |
| h12 | 15.0113 | 14.8126 | 0.1987 |
| h13 | 21.0036 | 20.8257 | 0.1779 |
| h14 | 15.0096 | 15.2553 | 0.2457 |
| h15 | 15.0198 | 14.8755 | 0.1443 |
| h16 | 15.0114 | 14.8122 | 0.1992 |
| h17 | 15.9727 | 16.2048 | 0.2321 |
| d1 | 8.0076 | 7.8492 | 0.1584 |
| d2 | 8.0103 | 8.2290 | 0.2187 |
| d3 | 8.0060 | 8.1657 | 0.1597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Tan, D.; Guo, S.; Chen, Z.; Liu, R. Digital Inspection Technology for Sheet Metal Parts Using 3D Point Clouds. Sensors 2025, 25, 4827. https://doi.org/10.3390/s25154827
Guo J, Tan D, Guo S, Chen Z, Liu R. Digital Inspection Technology for Sheet Metal Parts Using 3D Point Clouds. Sensors. 2025; 25(15):4827. https://doi.org/10.3390/s25154827
Chicago/Turabian StyleGuo, Jian, Dingzhong Tan, Shizhe Guo, Zheng Chen, and Rang Liu. 2025. "Digital Inspection Technology for Sheet Metal Parts Using 3D Point Clouds" Sensors 25, no. 15: 4827. https://doi.org/10.3390/s25154827
APA StyleGuo, J., Tan, D., Guo, S., Chen, Z., & Liu, R. (2025). Digital Inspection Technology for Sheet Metal Parts Using 3D Point Clouds. Sensors, 25(15), 4827. https://doi.org/10.3390/s25154827






