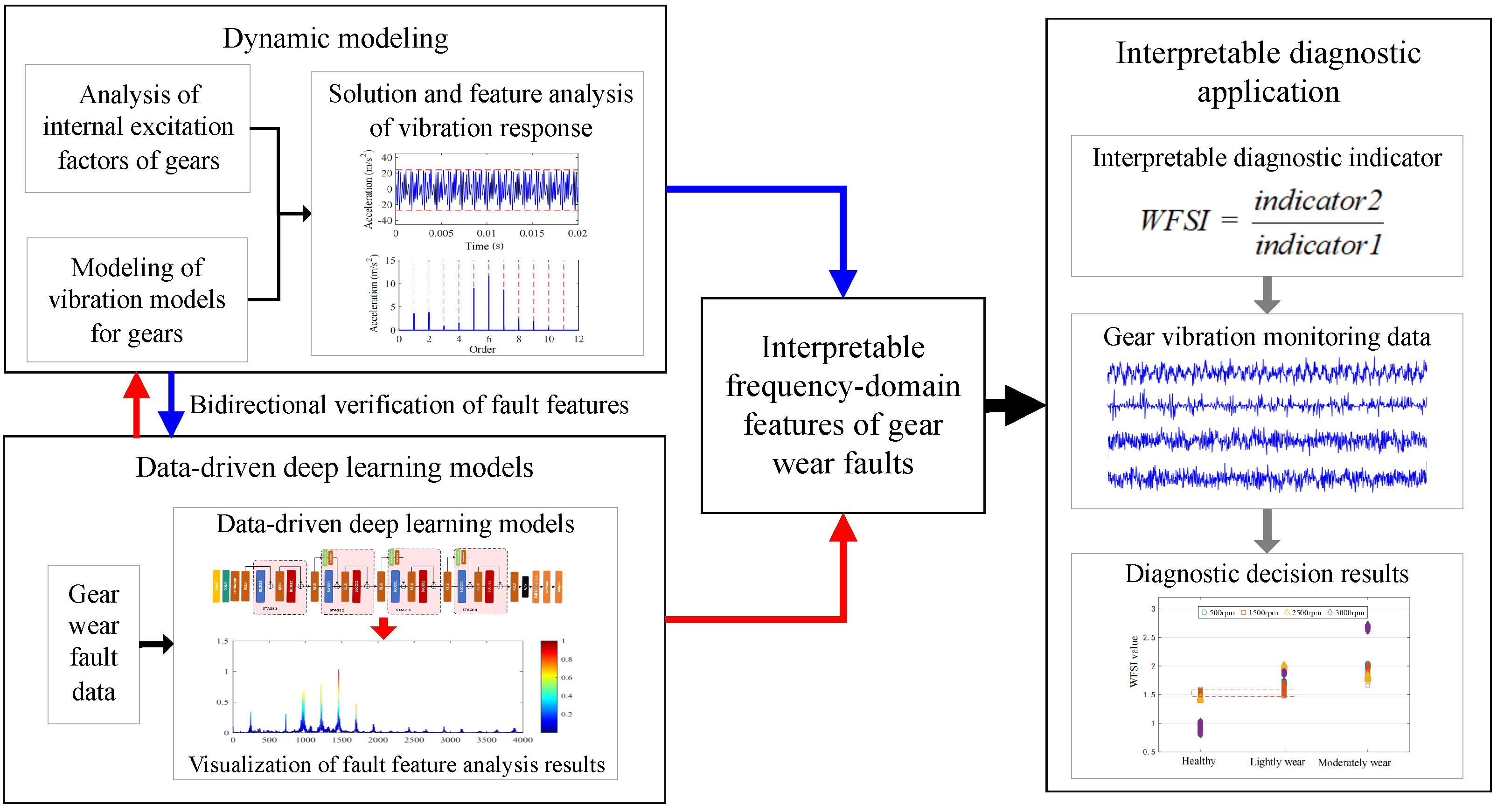
Integrated Explainable Diagnosis of Gear Wear Faults Based on Dynamic Modeling and Data-Driven Representation
Abstract
1. Introduction
- (1)
- A frequency-domain feature extraction method for gear wear faults is proposed, which combines bidirectional verification between dynamic modeling and data-driven representation, achieving physically constrained accurate characterization of gear wear states.
- (2)
- An interpretable quantitative discriminant index for gear wear faults is established based on dynamic mechanisms and deep learning models, enabling accurate identification of gear wear faults under different wear severities.
- (3)
- The effectiveness and superiority of the proposed method for interpretable gear fault diagnosis are verified through gear wear fault experiments.
2. Feature Analysis of Gear Wear Based on Dynamic Modeling
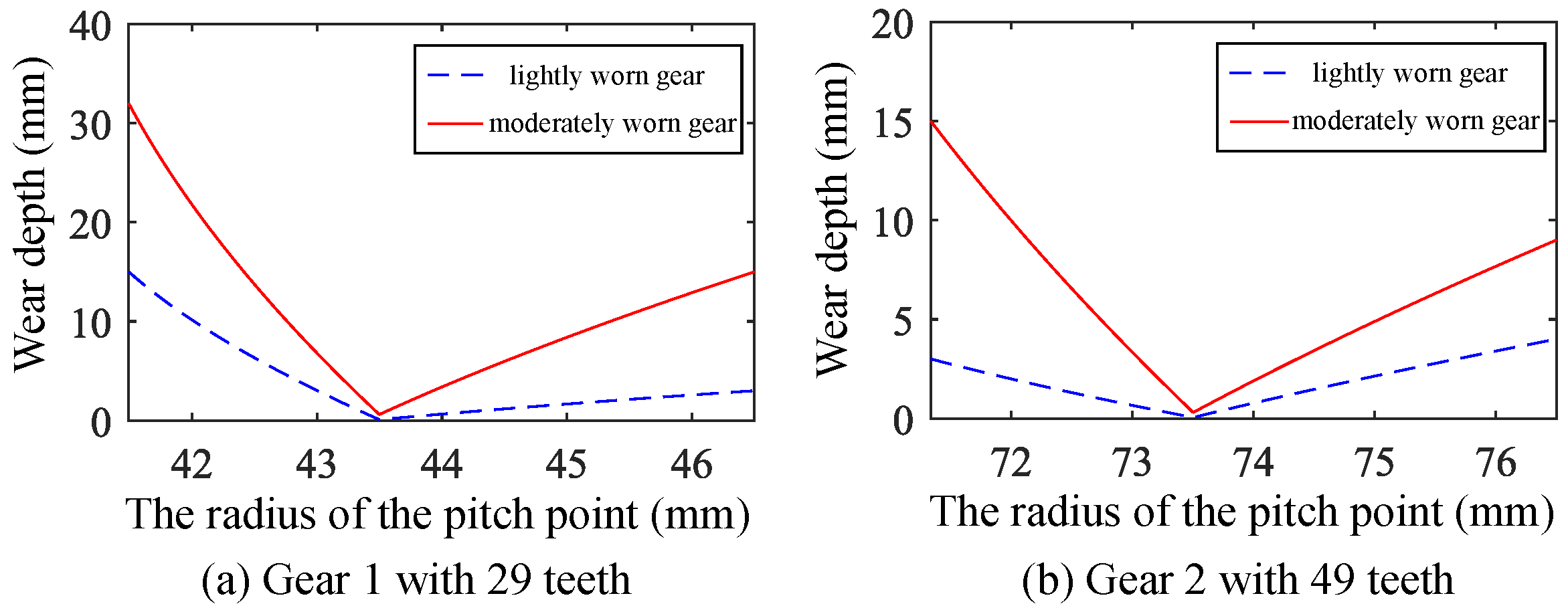
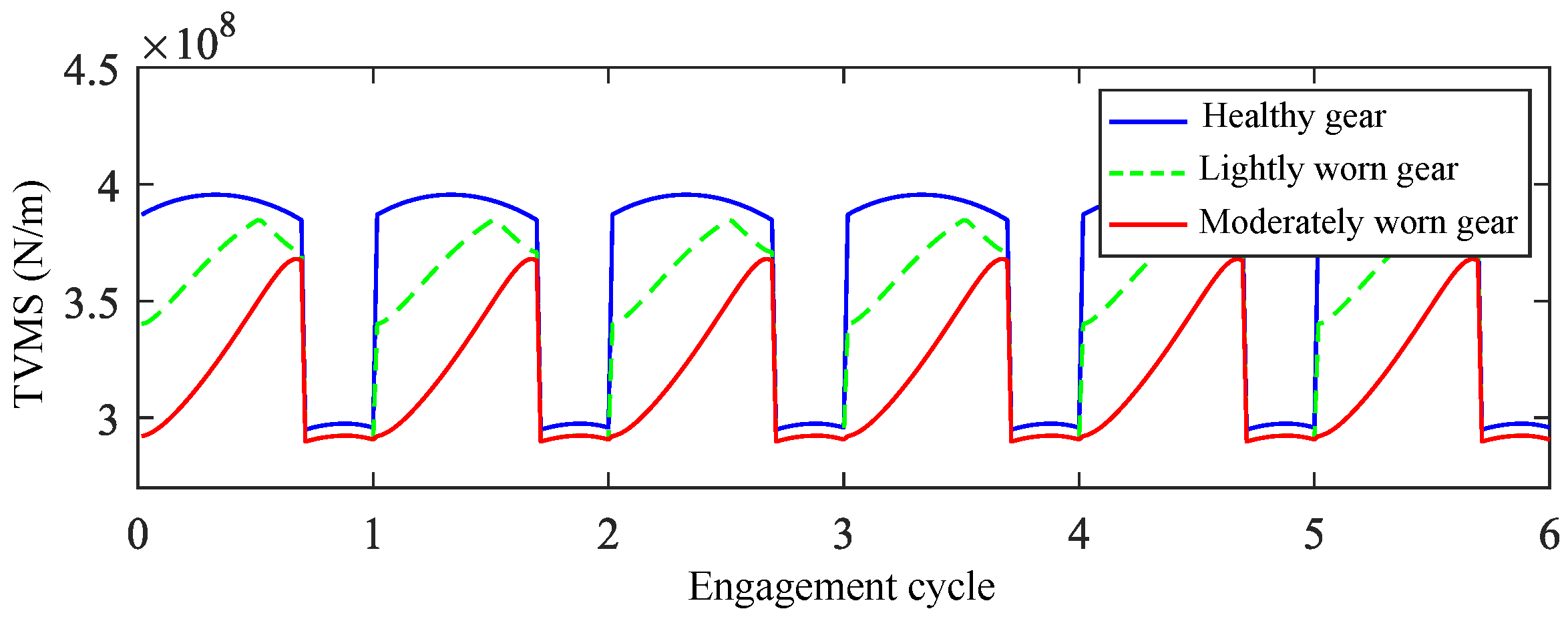
2.1. Effect of Gear Wear on Meshing Stiffness
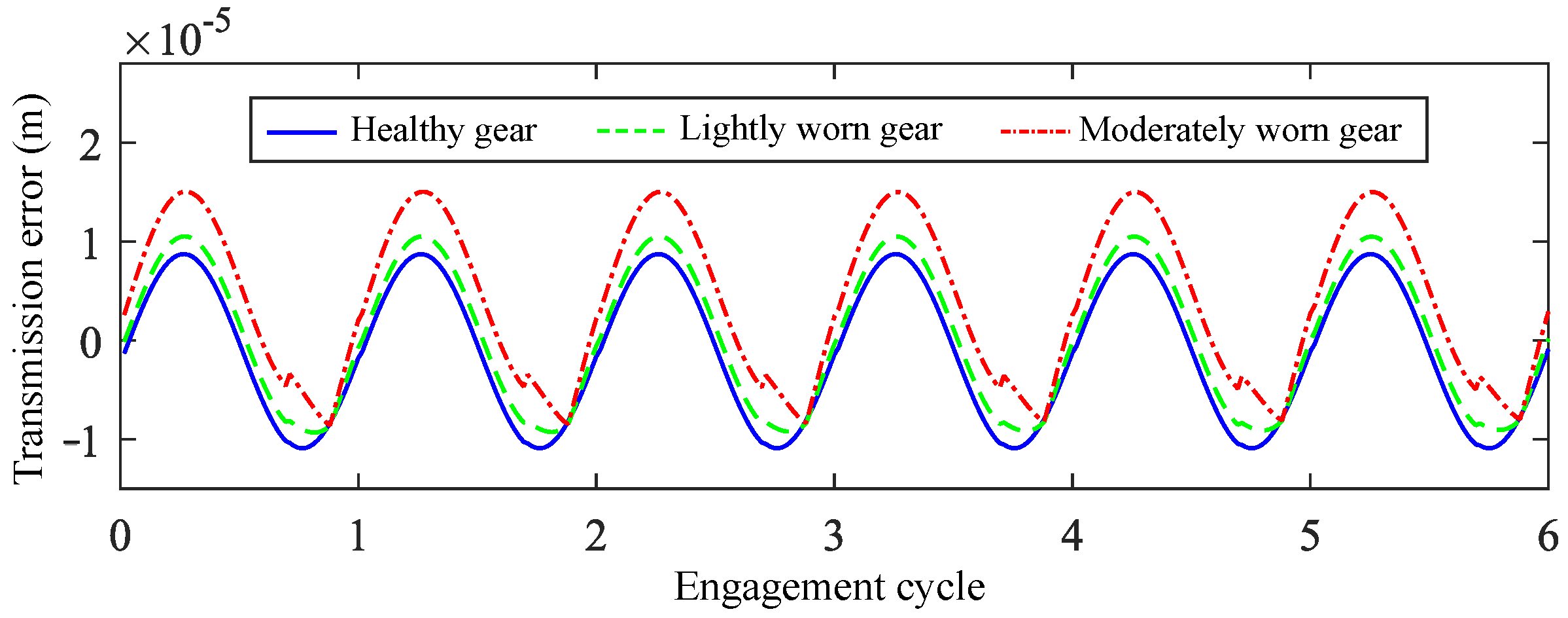
2.2. Effect of Gear Wear on No-Load Static Transmission Error
2.3. Vibration Characteristic Analysis of Gear Wear Based on Dynamic Model
- (1)
- Nodes are created at shaft endpoints and cross-section mutation points (shaft segment nodes).
- (2)
- Nodes are placed at bearing support locations (support nodes).
- (3)
- Nodes are assigned at gear meshing positions (meshing nodes).
- (4)
- Nodes are established at load application points (load nodes).
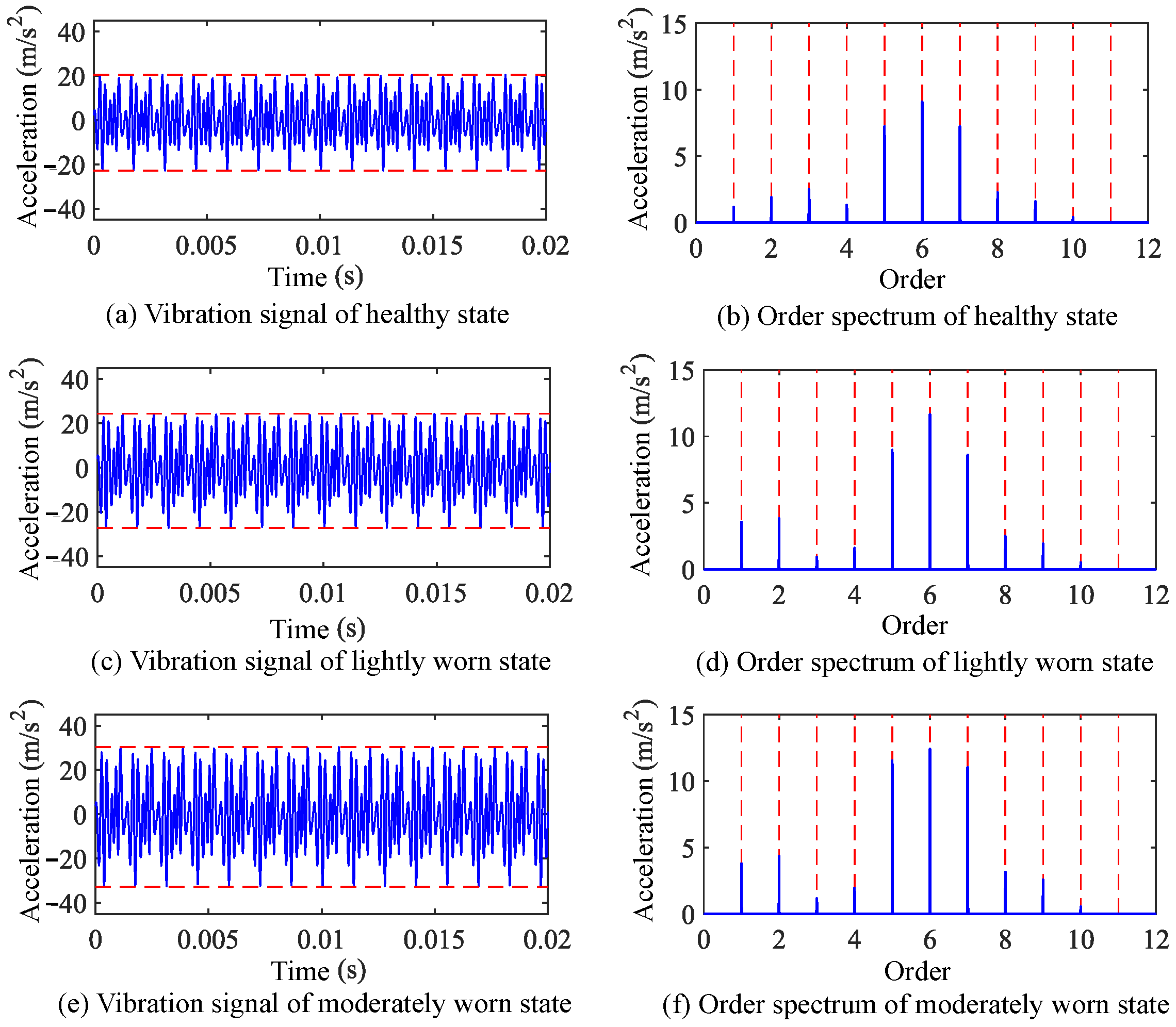
- (1)
- The peak-to-peak value, root mean square value, and kurtosis index of vibration acceleration response all increase.
- (2)
- No new characteristic frequencies or distribution patterns emerge in the response.
- (3)
- The primary changes manifest as a growth in the amplitude of the meshing frequency and its harmonics.
- (4)
- The growth of higher-order meshing frequency components is more pronounced compared to that of lower-order ones.
3. Gear Wear Fault Simulation Experiment
3.1. Introduction to Gear Wear Experiment
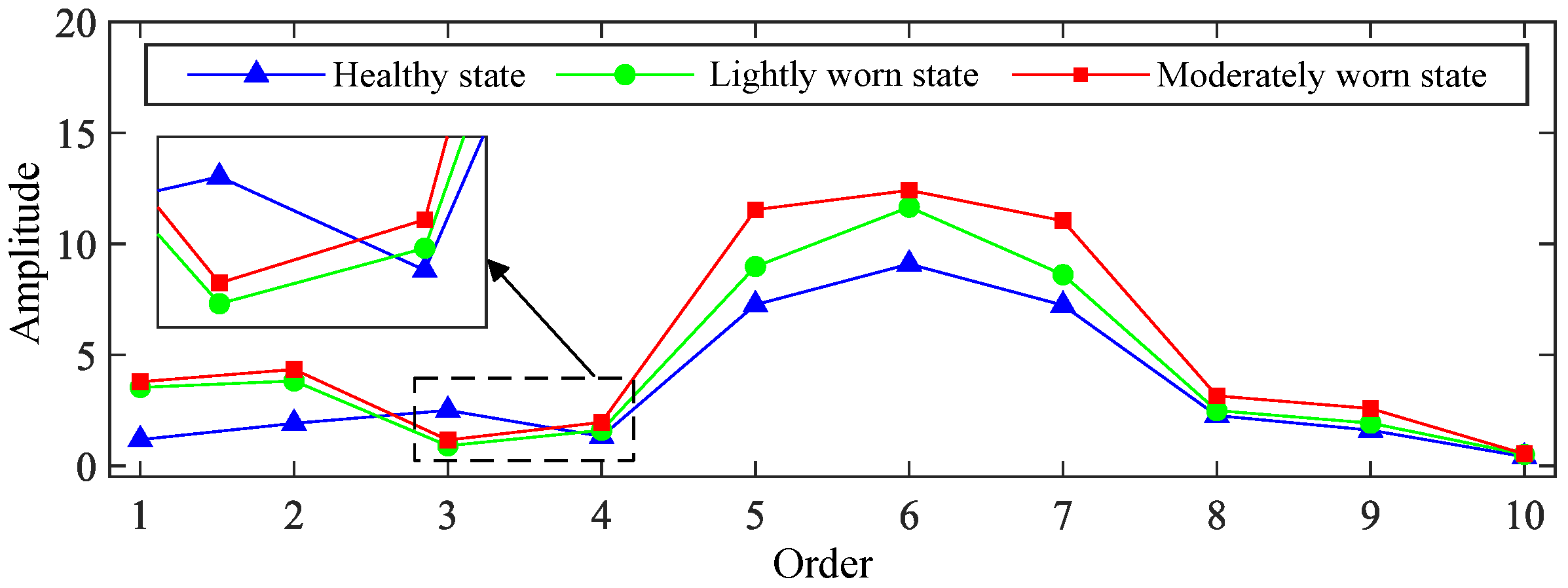
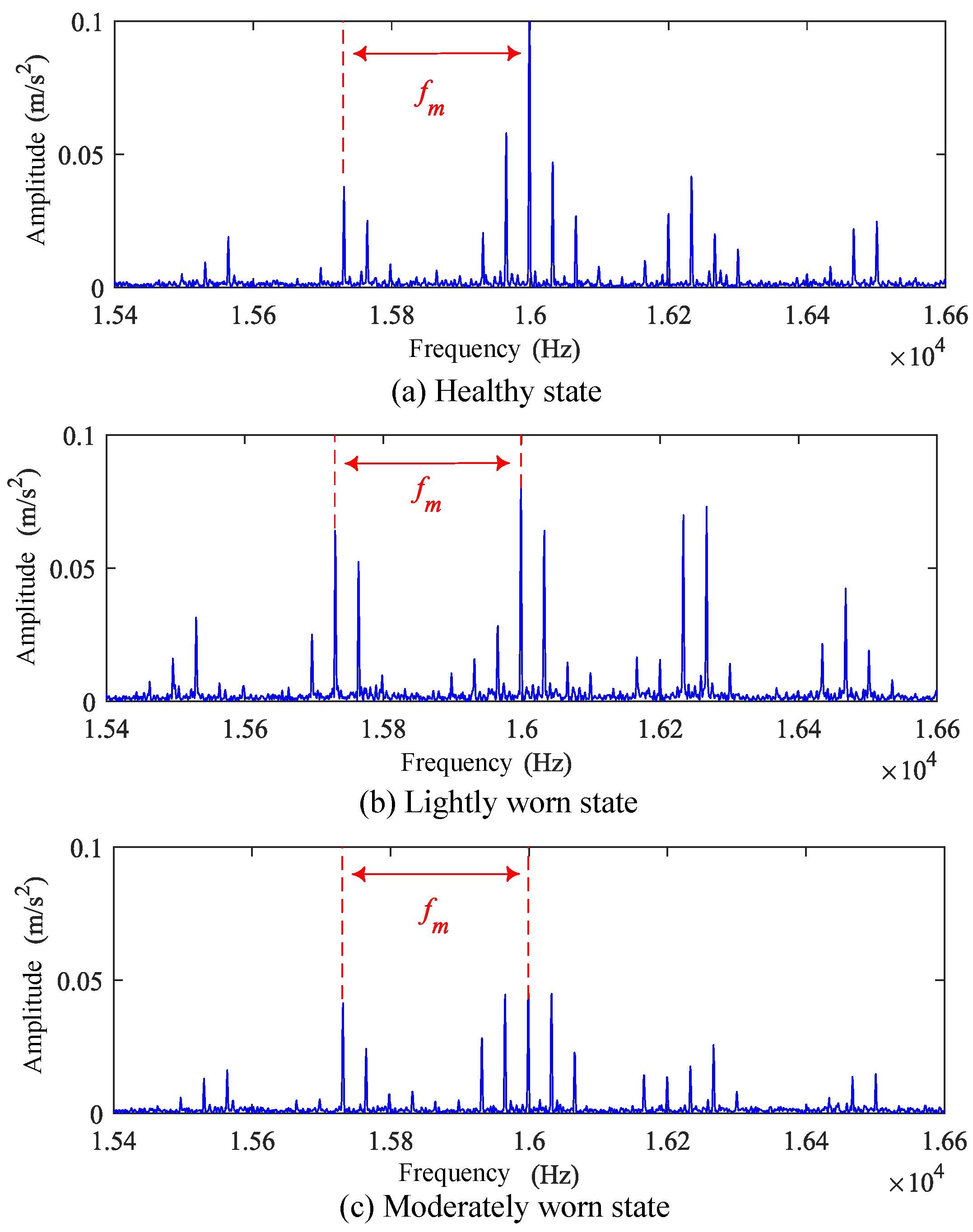
3.2. Analysis of Gear Wear Vibration Signals
4. Data-Driven Analysis of Sensitive Features for Gear Wear Faults
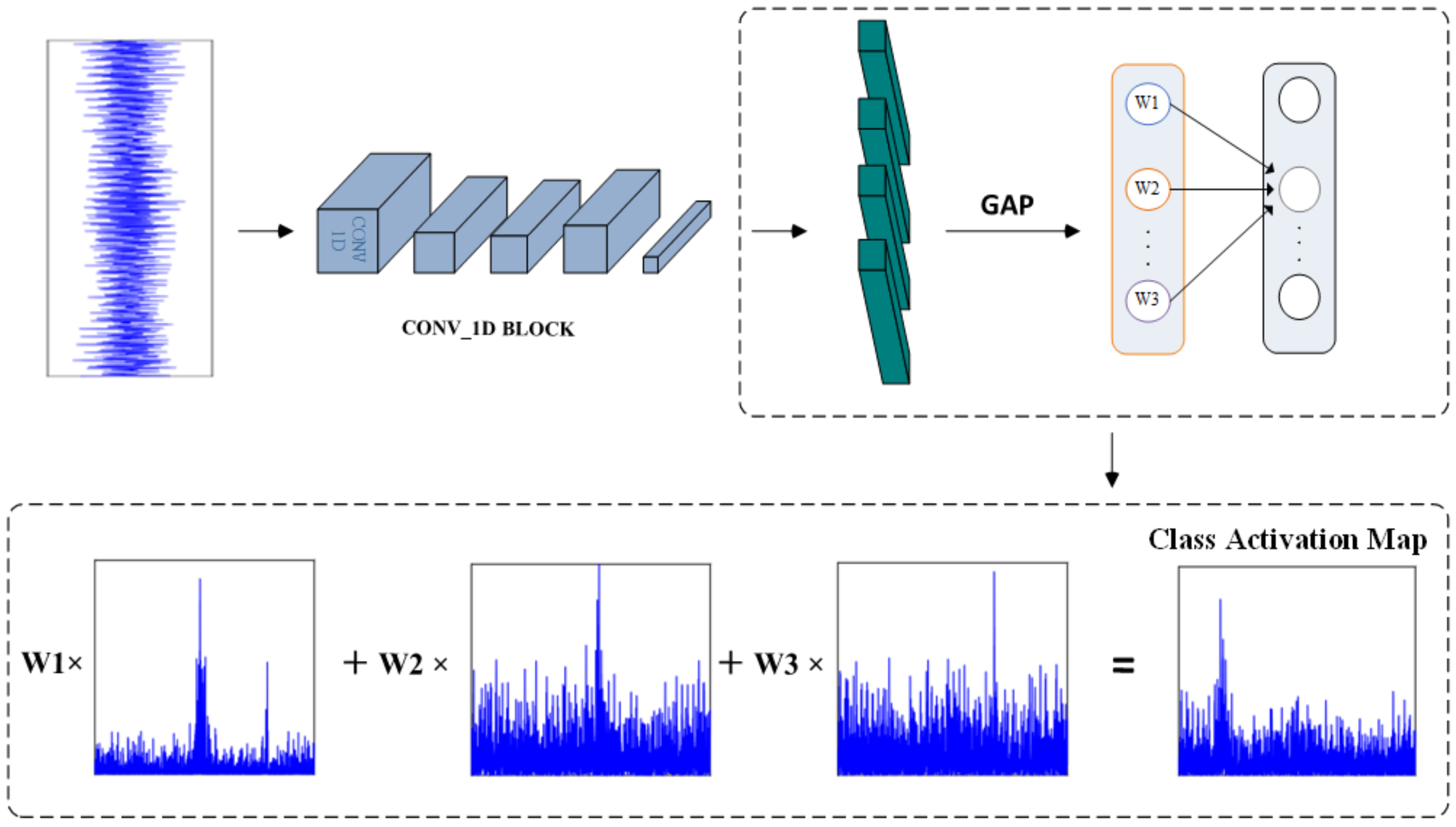
4.1. Data-Driven Model Based on Residual Convolutional Network and Grad-CAM
- (1)
- Load the trained model, input the spectrum sequence sample, and perform forward propagation to obtain class scores .
- (2)
- Fix network parameters, perform backpropagation to calculate the gradient of class scores with respect to the output feature maps of the last convolutional layer, and use the global average of gradients as weights for each channel.
- (3)
- Perform weighted summation of channel weights and feature maps, then apply the activation function to retain positively correlated regions, obtaining the CAM sequence .
- (4)
- Interpolate and upsample the CAM sequence to restore it to the input sample size.
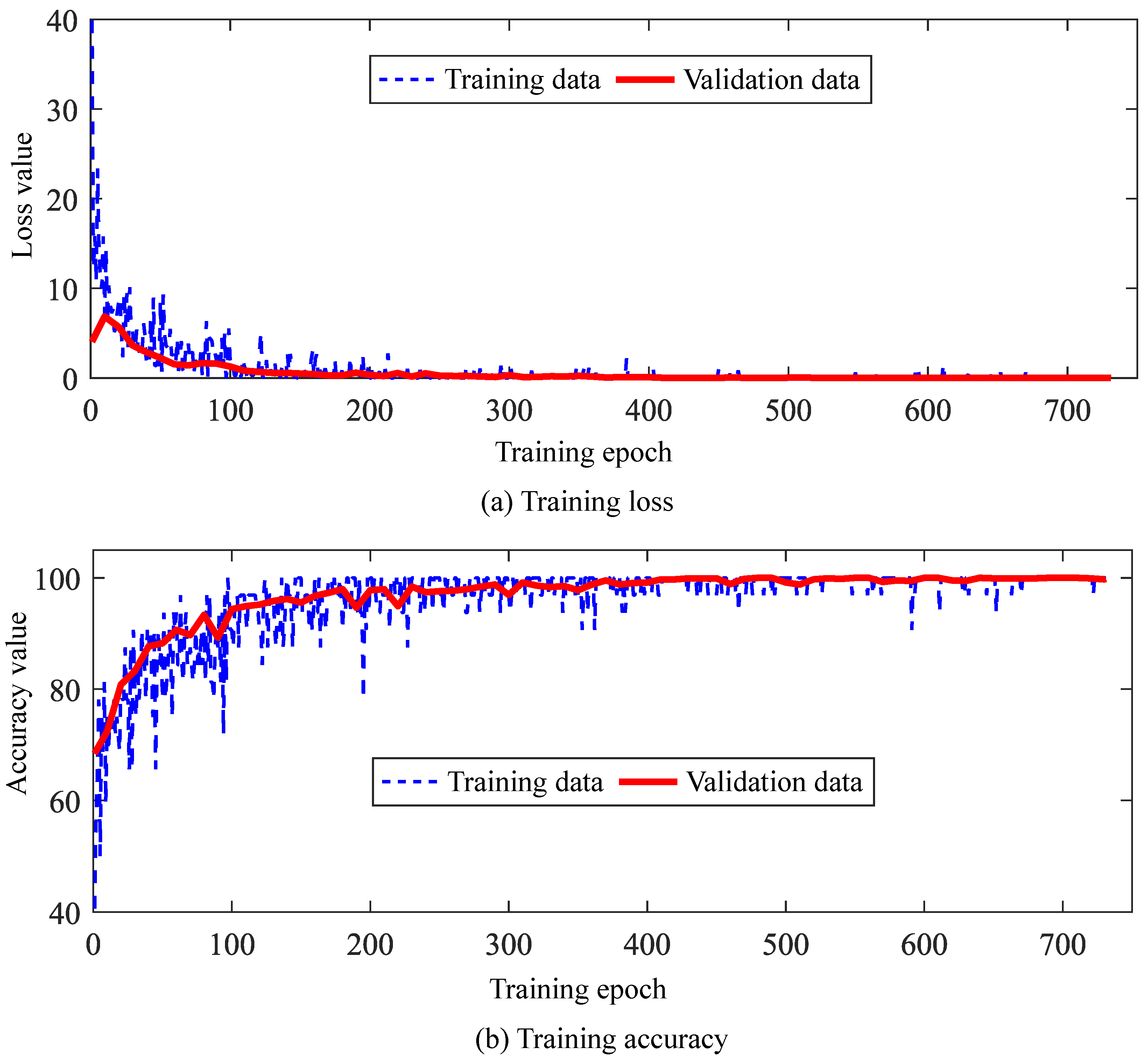
4.2. Data-Driven Model Training and Testing for Gear Wear Faults
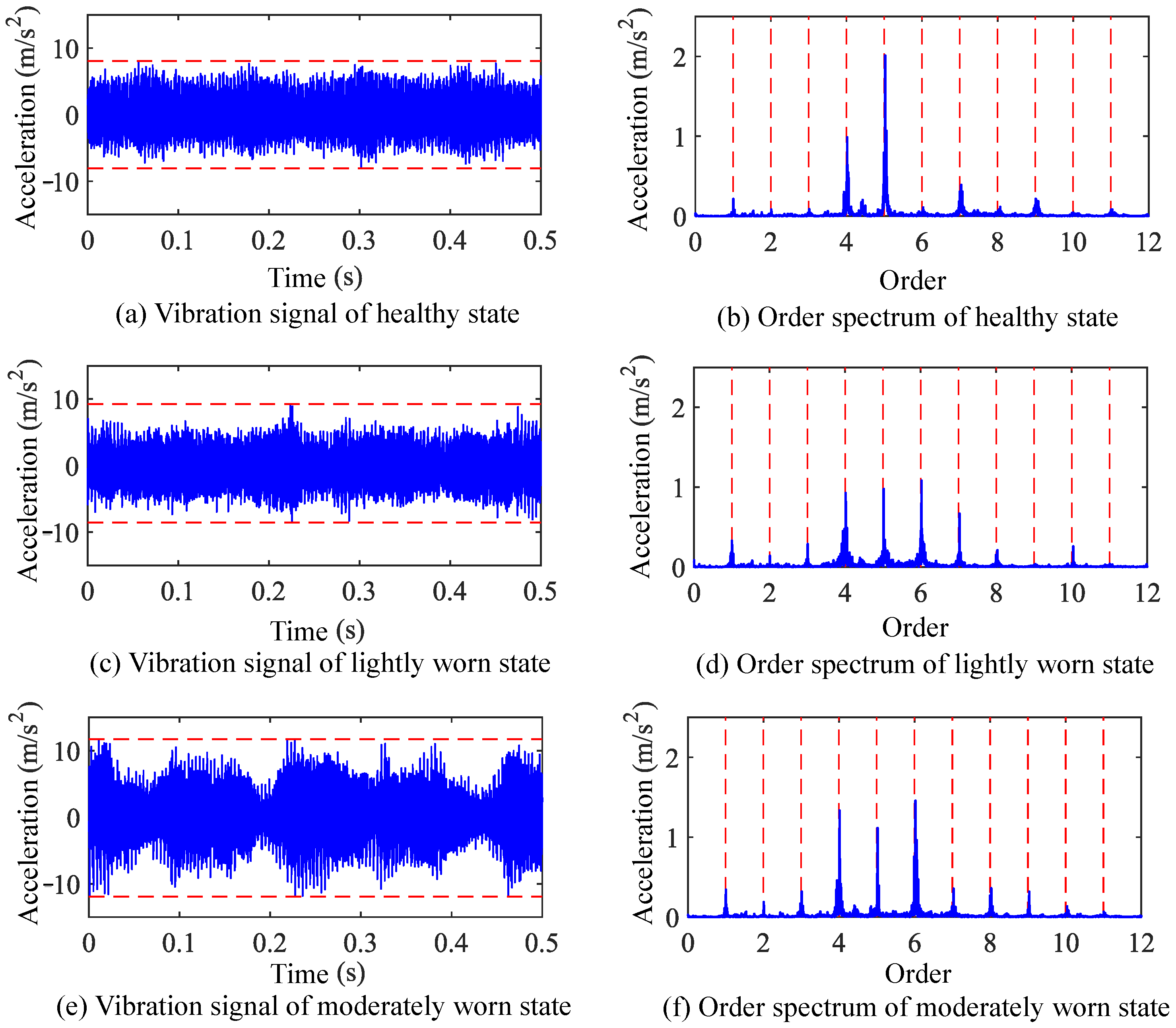
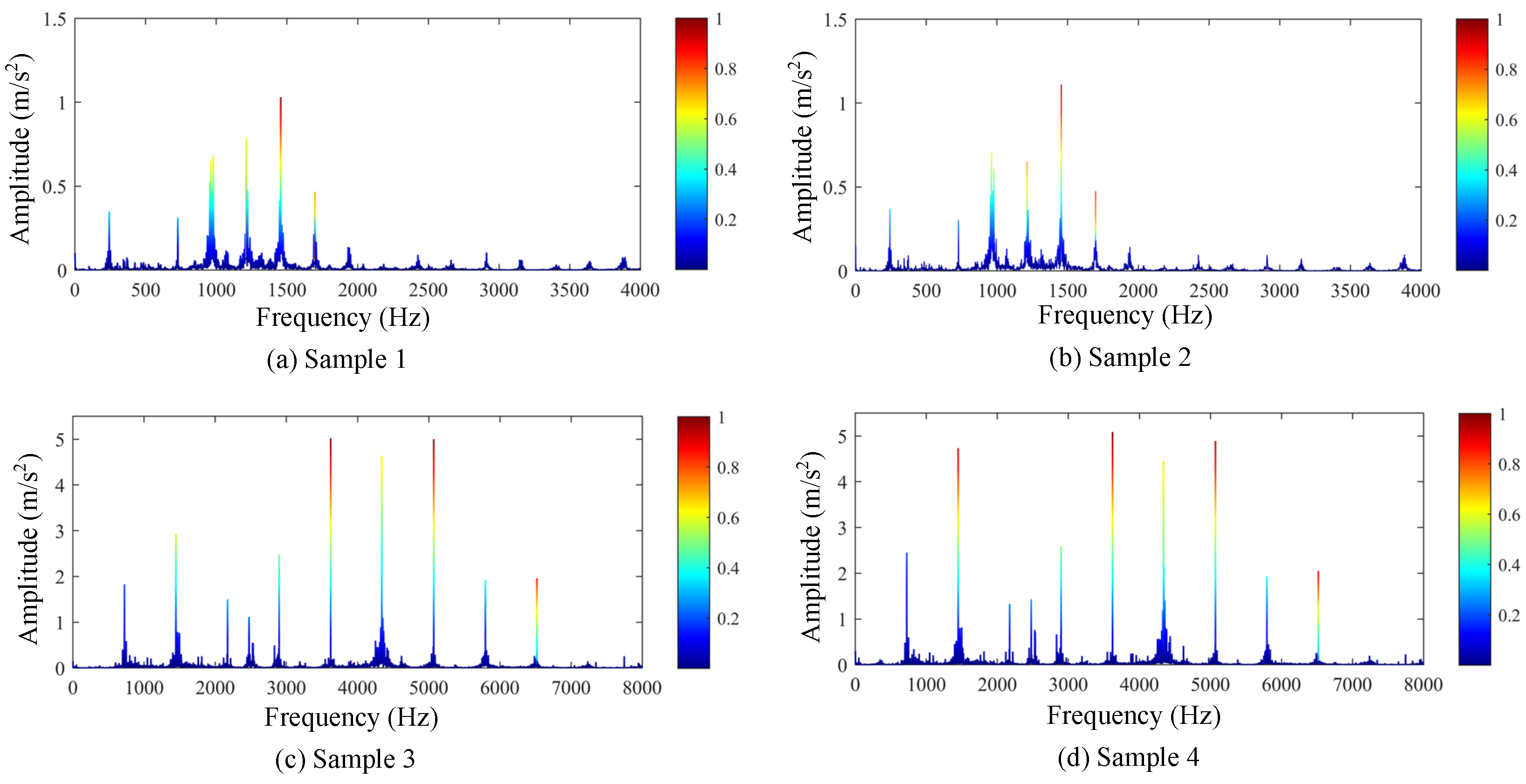
4.3. Visualization Analysis of Sensitive Features for Gear Wear Faults
5. Interpretable Feature Indicator Construction and Diagnostic Application for Gear Wear
- (1)
- The amplitudes of multiple meshing frequency orders increase, and the higher-order meshing frequency amplitudes show more significant growth.
- (2)
- Modulation phenomena with meshing frequency as the modulation frequency become more prominent in high-frequency signal components, and the energy proportion of meshing frequency and its harmonics increases.
5.1. Diagnostic Indicator Design Based on Vibration Signal Characteristics
- (1)
- Calculate the spectrum of the original signal using the Discrete Fourier Transform:
- (2)
- Calculate the first 10 orders of meshing frequency for the current operating condition:where is the driving shaft speed and z is the number of teeth on the driving gear.
- (3)
- For each meshing frequency order , search for the maximum amplitude in the frequency band range within the spectrum sequence:Obtain the amplitude set .
- (4)
- Calculate the mean and standard deviation of set :Define the ratio of mean to standard deviation as the factor :
- (5)
- Filter the signal using a fourth-order Chebyshev IIR filter with a cutoff frequency of , obtaining the filtered signal:
- (6)
- For the filtered signal, construct its analytic signal through the Hilbert transform:where represents the Hilbert transform. Then, extract the envelope signal and perform DFT on the envelope signal to obtain the envelope spectrum of the filtered signal:
- (7)
- Extract the first five orders of meshing frequency amplitudes from the envelope spectrum :Calculate the ratio of the first five orders’ meshing frequency energy to the total envelope spectrum energy, denoted as factor :
- (8)
- The final designed Wear Fault Sensitivity Indicator () is the ratio of to :
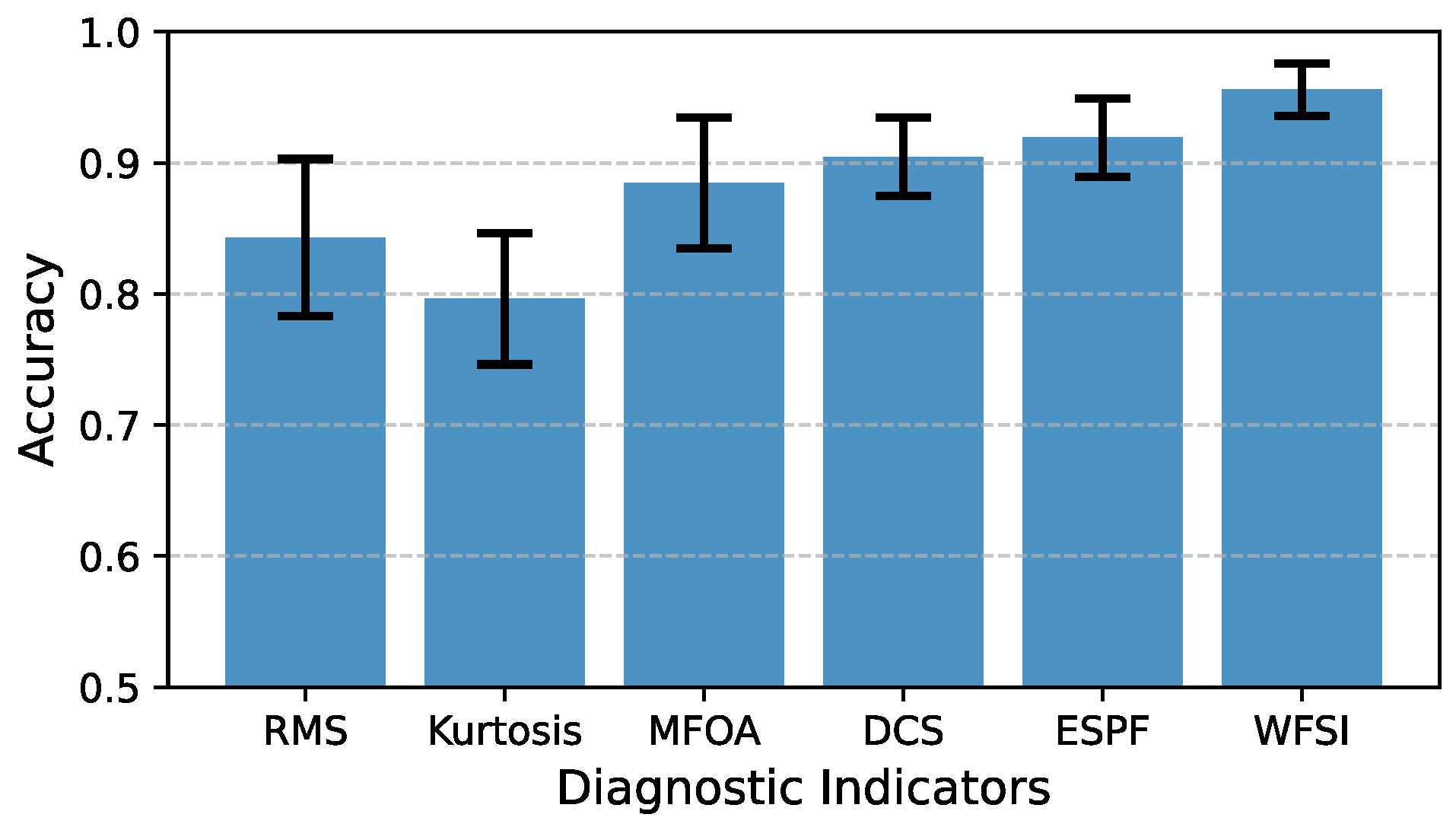
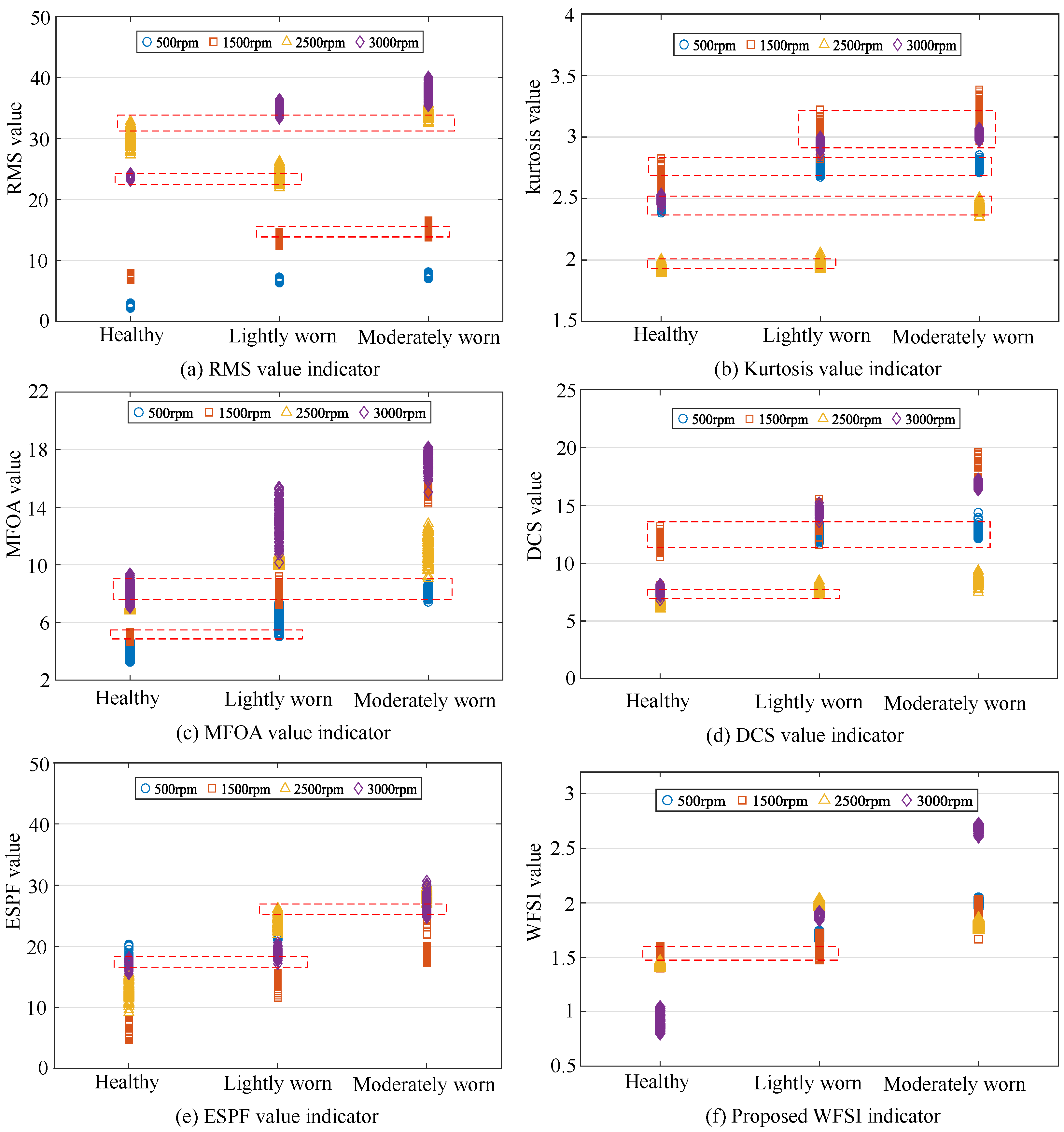
5.2. Analysis of Gear Wear Fault Diagnosis Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Zhong, J.; Li, W.; Bocian, M. Nonlinear dynamic analysis of high-speed gear pair with wear fault and tooth contact temperature for a wind turbine gearbox. Mech. Mach. Theory 2022, 173, 104840. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Y.; Chen, S. Efficient Gearbox Fault Diagnosis Based on Improved Multi-Scale CNN with Lightweight Convolutional Attention. Sensors 2025, 25, 2636. [Google Scholar] [CrossRef]
- Ma, X.; Zhai, K.; Luo, N.; Zhao, Y.; Wang, G. Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism. Sensors 2025, 25, 2978. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Li, Q.; Feng, K.; Qin, Y. Dynamic modeling of spur gear transmission system with evolutive coupling fault of fatigue crack and wear. Eng. Fail. Anal. 2024, 156, 107820. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; An, B.; Sun, R.; Cui, Y. Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors 2025, 25, 2775. [Google Scholar] [CrossRef] [PubMed]
- Liu, X. Vibration modelling and fault evolution symptom analysis of a planetary gear train for sun gear wear status assessment. Mech. Syst. Signal Process. 2022, 166, 108403. [Google Scholar] [CrossRef]
- Gao, X.; Lei, Y.; Yang, X.; Liu, H.; Feng, K.; Wu, T.; Wang, Z. Dynamic interactions of surface wear and tooth crack in gear transmission systems: An investigation of progressive-degradation mechanisms. Wear 2025, 571, 205861. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, H.; Tang, Y.; Liang, G.; Wang, L.; Yang, J. A deterministic model of surface profile degradation for evaluating time-varying mesh stiffness and dynamic responses of spur gear considering tooth surface wear evolution. Mech. Syst. Signal Process. 2025, 225, 112313. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, R.; Hu, Z.; Tang, J.; Sun, Z.; Ning, A.; Yang, S. Dynamic modeling and analysis considering friction-wear coupling of gear system. Int. J. Mech. Sci. 2024, 275, 109343. [Google Scholar] [CrossRef]
- Feng, K.; Xiao, H.; Zhang, J.; Ni, Q. A digital twin methodology for vibration-based monitoring and prediction of gear wear. Wear 2025, 571, 205806. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Xu, M.; Yang, D.; Zhao, Z. Improved deep transfer learning and transmission error based method for gearbox fault diagnosis with limited test samples. Mech. Syst. Signal Process. 2025, 230, 112593. [Google Scholar] [CrossRef]
- Yu, L.; Wang, C.; Wang, C.; Zhang, F.; Luo, H. Periodicity-constrained reweighted generalized minimax-concave regularization and its application in gearbox fault diagnosis. Signal Process. 2025, 234, 110005. [Google Scholar] [CrossRef]
- Duan, X.; Lin, R.; Feng, Z. Spectral Correlation Demodulation Analysis for Fault Diagnosis of Planetary Gearboxes. Sensors 2025, 25, 2694. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Zhang, Y.; Hou, S. Fault diagnosis for wind turbine planetary gearboxes via demodulation analysis based on ensemble empirical mode decomposition and energy separation. Renew. Energy 2012, 47, 112–126. [Google Scholar] [CrossRef]
- Chen, D.; Lin, J.; Li, Y. Modified complementary ensemble empirical mode decomposition and intrinsic mode functions evaluation index for high-speed train gearbox fault diagnosis. J. Sound Vib. 2018, 424, 192–207. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Cheng, Y.; Lu, C. Fault diagnosis of gearbox using empirical mode decomposition and multi-fractal detrended cross-correlation analysis. J. Sound Vib. 2016, 385, 350–371. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, X.; Li, F. High-order synchrosqueezing wavelet transform and application to planetary gearbox fault diagnosis. Mech. Syst. Signal Process. 2019, 131, 126–151. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Cheng, H.; Han, C.; Liu, Y.; Mu, H. Compound faults diagnosis and analysis for a wind turbine gearbox via a novel vibration model and empirical wavelet transform. Renew. Energy 2019, 136, 393–402. [Google Scholar] [CrossRef]
- Zhu, P.; Deng, L.; Tang, B.; Yang, Q.; Li, Q. Digital twin-enabled entropy regularized wavelet attention domain adaptation network for gearboxes fault diagnosis without fault data. Adv. Eng. Inform. 2025, 64, 103055. [Google Scholar] [CrossRef]
- Shao, Z.; Jiang, H.; Zhang, X.; Zhou, J.; Huang, W. PLL-WCAN: Pseudo-label progressive learning guided wavelet class-aware adaptive network for gearbox cross-domain fault diagnosis. Mech. Syst. Signal Process. 2025, 230, 112624. [Google Scholar] [CrossRef]
- Ha, J.M.; Fink, O. Domain knowledge-informed synthetic fault sample generation with health data map for cross-domain planetary gearbox fault diagnosis. Mech. Syst. Signal Process. 2023, 202, 110680. [Google Scholar] [CrossRef]
- Li, Q.; Tang, B.; Deng, L.; Xiong, P.; Zhao, M. Cross-Attribute adaptation networks: Distilling transferable features from multiple sampling-frequency source domains for fault diagnosis of wind turbine gearboxes. Measurement 2022, 200, 111570. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Ye, Z.; Liu, W.; Tang, J. Prior knowledge-informed multi-task dynamic learning for few-shot machinery fault diagnosis. Expert Syst. Appl. 2025, 271, 126439. [Google Scholar] [CrossRef]
- Dong, Y.; Jiang, H.; Jiang, W.; Xie, L. Dynamic normalization supervised contrastive network with multiscale compound attention mechanism for gearbox imbalanced fault diagnosis. Eng. Appl. Artif. Intell. 2024, 133, 108098. [Google Scholar] [CrossRef]
- Kang, J.; Zhu, X.; Shen, L.; Li, M. Fault diagnosis of a wave energy converter gearbox based on an Adam optimized CNN-LSTM algorithm. Renew. Energy 2024, 231, 121022. [Google Scholar] [CrossRef]
- Jia, S.; Sun, D.; Noman, K.; Wang, X.; Li, Y. Lifting wavelet-informed hierarchical domain adaptation network: An interpretable digital twin-driven gearbox fault diagnosis method. Reliab. Eng. Syst. Saf. 2025, 254, 110660. [Google Scholar] [CrossRef]
- Guo, Z.; Du, W.; Liu, Z.; Hu, T.; Yu, Y.; Li, C. Few-shot sample multi-class incremental fault diagnosis for gearbox based on convolutional-attention fusion network. Expert Syst. Appl. 2025, 264, 125918. [Google Scholar] [CrossRef]
- Zhuang, J.; Yan, J.; Huang, C.G.; Jia, M. Residual attention temporal recurrent network for fault diagnosis of gearboxes under limited labeled data. Eng. Appl. Artif. Intell. 2024, 129, 107539. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, B.; Deng, L.; Li, Q. Distillation-enhanced fast neural architecture search method for edge-side fault diagnosis of wind turbine gearboxes. Expert Syst. Appl. 2022, 208, 118049. [Google Scholar] [CrossRef]
- Xia, J.; Huang, R.; Chen, Z.; He, G.; Li, W. A novel digital twin-driven approach based on physical-virtual data fusion for gearbox fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 240, 109542. [Google Scholar] [CrossRef]
- Delvecchio, S.; D’Elia, G.; Dalpiaz, G. On the use of cyclostationary indicators in IC engine quality control by cold tests. Mech. Syst. Signal Process. 2015, 60–61, 208–228. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, W.; Xi Gu, J.; Song, D.; Cheng, Y.; Zhou, Z.; Gu, F.; Ball, A.D. Product envelope spectrum optimization-gram: An enhanced envelope analysis for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 193, 110270. [Google Scholar] [CrossRef]
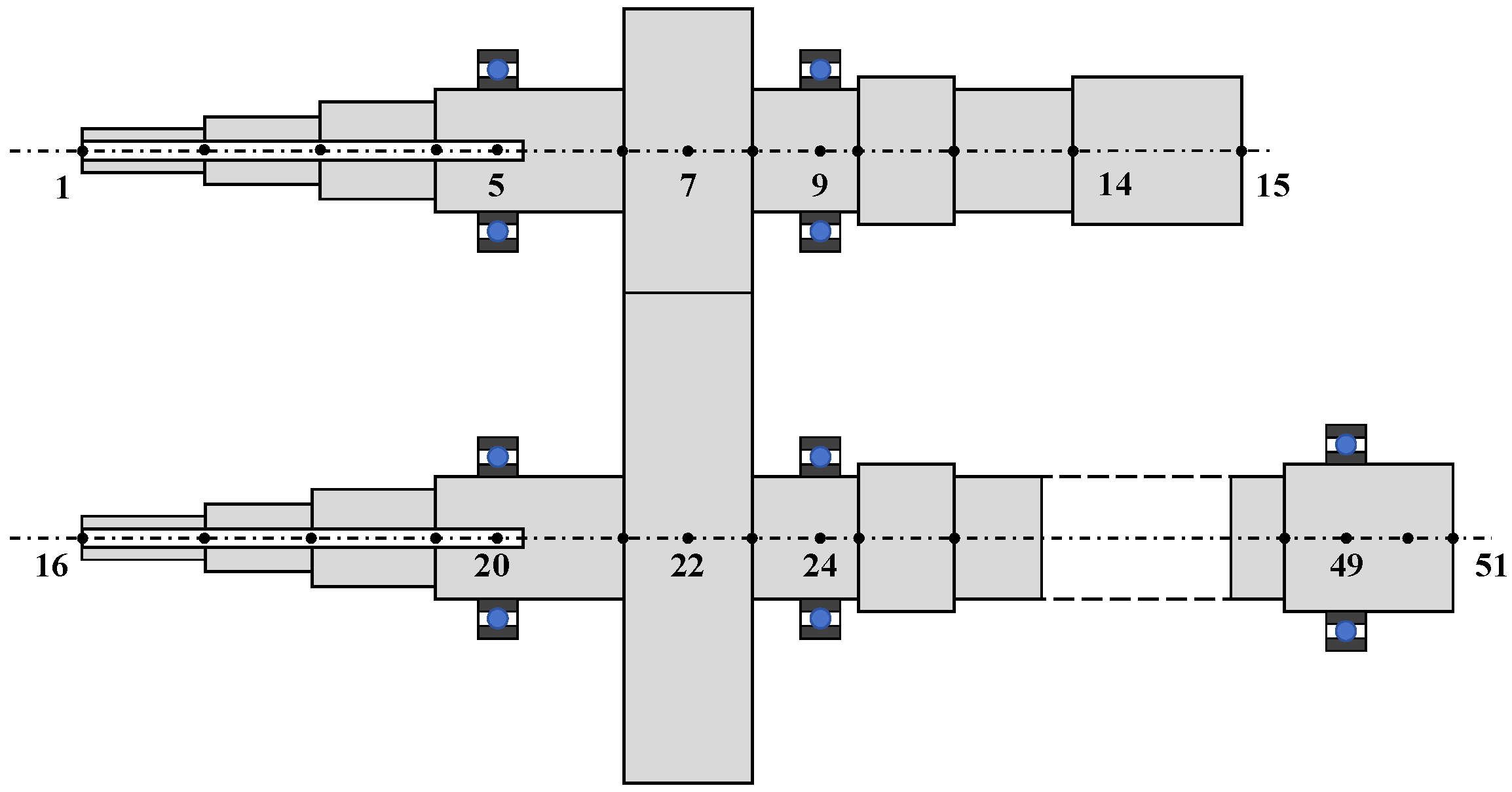



| Parameter | Value |
|---|---|
| Module | 3 |
| Number of Teeth | 29 (Gear 1), 49 (Gear 2) |
| Pressure Angle (°) | 20 |
| Face Width (mm) | 20 |
| Elastic Modulus (GPa) | 206.8 |
| Poisson’s Ratio | 0.3 |
| Node Number | Outer Diameter (mm) | Inner Diameter (mm) | Length (mm) |
|---|---|---|---|
| 1–2 | 16 | 6 | 34 |
| 2–3 | 20 | 6 | 23 |
| 3–4 | 24 | 6 | 20 |
| 4–6 | 30 | 6 | 30 |
| 6–10 | 30 | 0 | 70 |
| 10–11 | 34 | 0 | 25 |
| 11–13 | 35 | 0 | 42 |
| 13–15 | 38 | 0 | 45 |
| 15–17 | 16 | 6 | 34 |
| 17–18 | 20 | 6 | 23 |
| 18–19 | 24 | 6 | 20 |
| 19–21 | 30 | 6 | 30 |
| 21–25 | 30 | 0 | 70 |
| 25–26 | 40 | 0 | 25 |
| 26–48 | 28 | 0 | 500 |
| 48–51 | 30 | 0 | 63 |
| Gear Condition | Test Speed (rpm) | Test Load (Nm) |
|---|---|---|
| Healthy | 500 | 45 |
| Light Wear | 1500 | |
| Moderate Wear | 2500 | |
| 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Zhang, T.; Xu, K.; Tang, J.; Yang, Y. Integrated Explainable Diagnosis of Gear Wear Faults Based on Dynamic Modeling and Data-Driven Representation. Sensors 2025, 25, 4805. https://doi.org/10.3390/s25154805
Zhao Z, Zhang T, Xu K, Tang J, Yang Y. Integrated Explainable Diagnosis of Gear Wear Faults Based on Dynamic Modeling and Data-Driven Representation. Sensors. 2025; 25(15):4805. https://doi.org/10.3390/s25154805
Chicago/Turabian StyleZhao, Zemin, Tianci Zhang, Kang Xu, Jinyuan Tang, and Yudian Yang. 2025. "Integrated Explainable Diagnosis of Gear Wear Faults Based on Dynamic Modeling and Data-Driven Representation" Sensors 25, no. 15: 4805. https://doi.org/10.3390/s25154805
APA StyleZhao, Z., Zhang, T., Xu, K., Tang, J., & Yang, Y. (2025). Integrated Explainable Diagnosis of Gear Wear Faults Based on Dynamic Modeling and Data-Driven Representation. Sensors, 25(15), 4805. https://doi.org/10.3390/s25154805







