A Few-Shot SE-Relation Net-Based Electronic Nose for Discriminating COPD
Abstract
1. Introduction
2. Materials and Environments
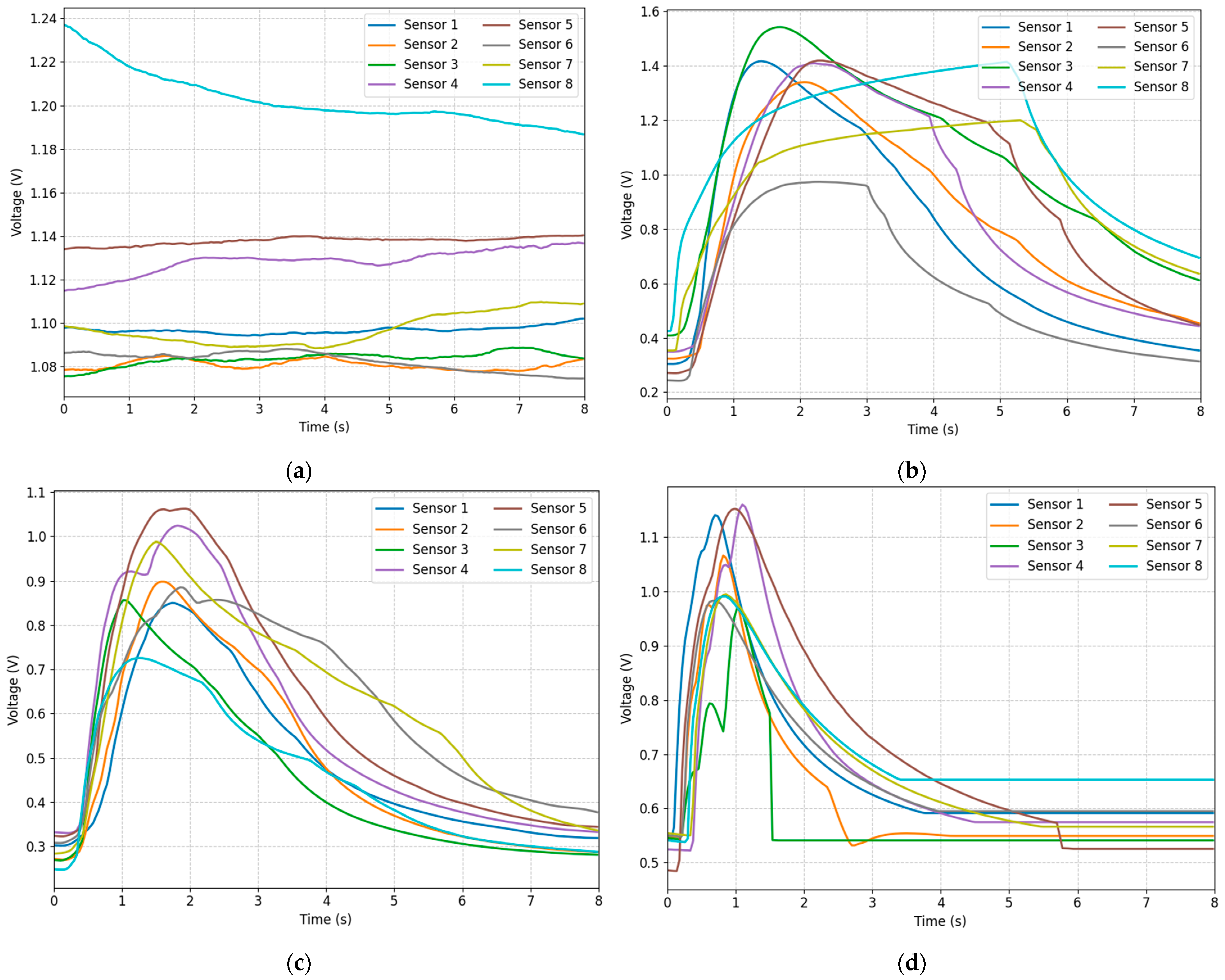
2.1. Meta-Training Set
2.2. Meta-Testing Set
2.3. Experimental Environment
2.4. Signal Preprocessing
- (1)
- Normalization: First, we normalized all sensor data to make them have the same scale. This eliminates the differences in response intensities between different sensors and makes the model more sensitive to the range of input data.
- (2)
- Channel Shuffling: During each training round, we randomly shuffle and rearrange the sensor channels for all samples within the batch. This aims to prevent the model from over-relying on a specific channel order, thereby enhancing its ability to calculate similarity under different channel orders. Essentially, this is a data augmentation technique that increases the number of training samples and enables the model to learn more generalizable feature representations.
3. Methodology
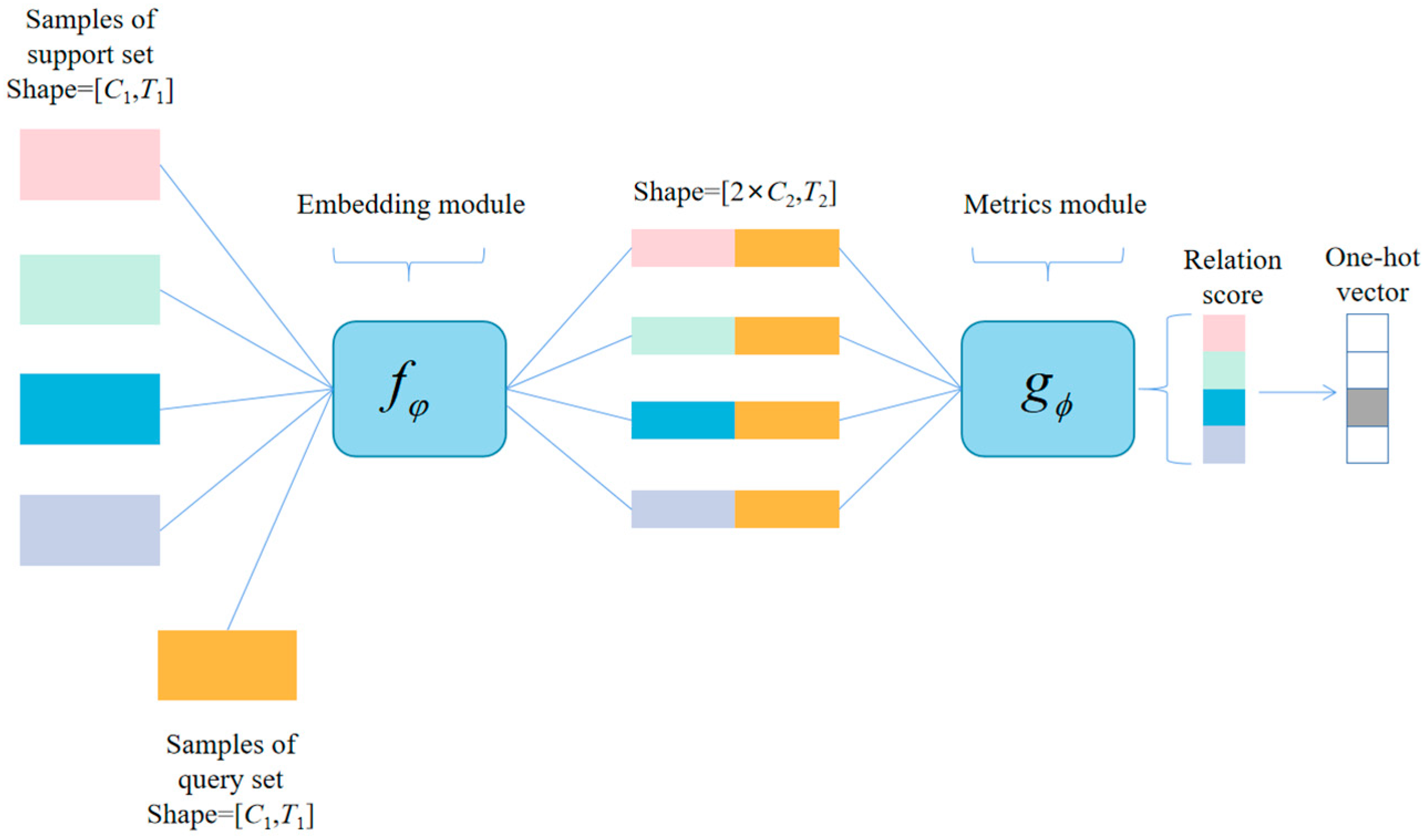
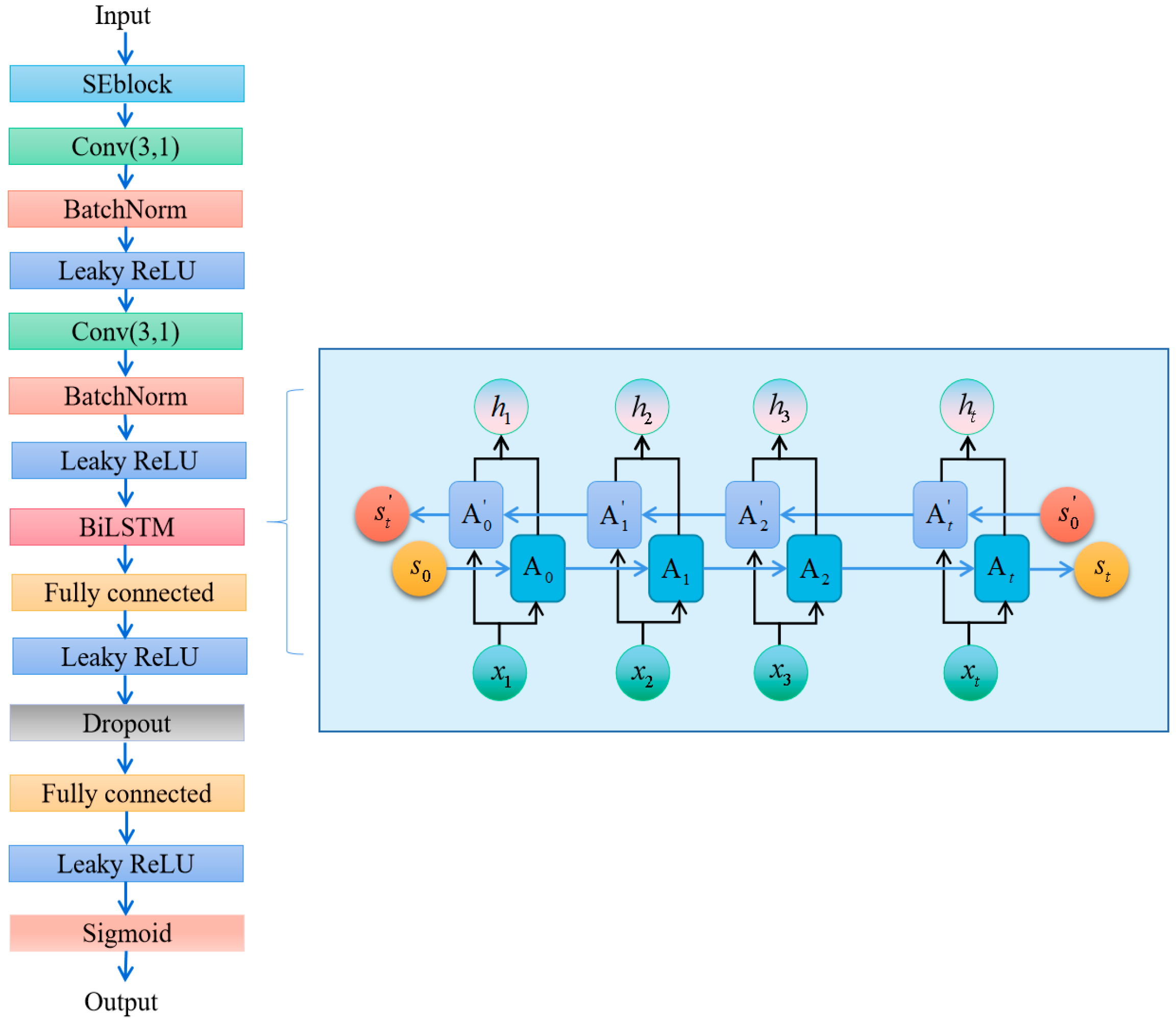
3.1. Training Method of SE-RelationNet
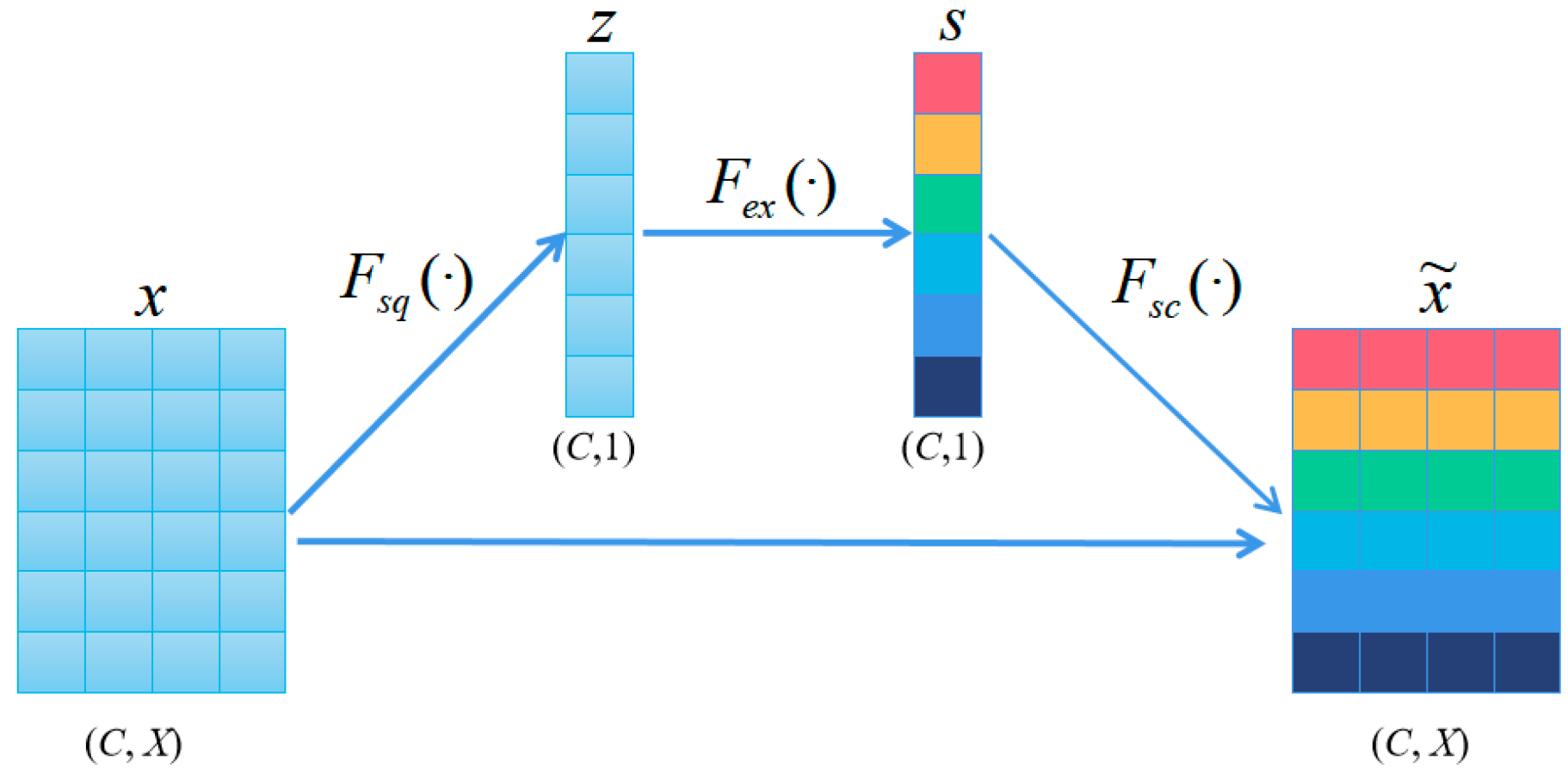
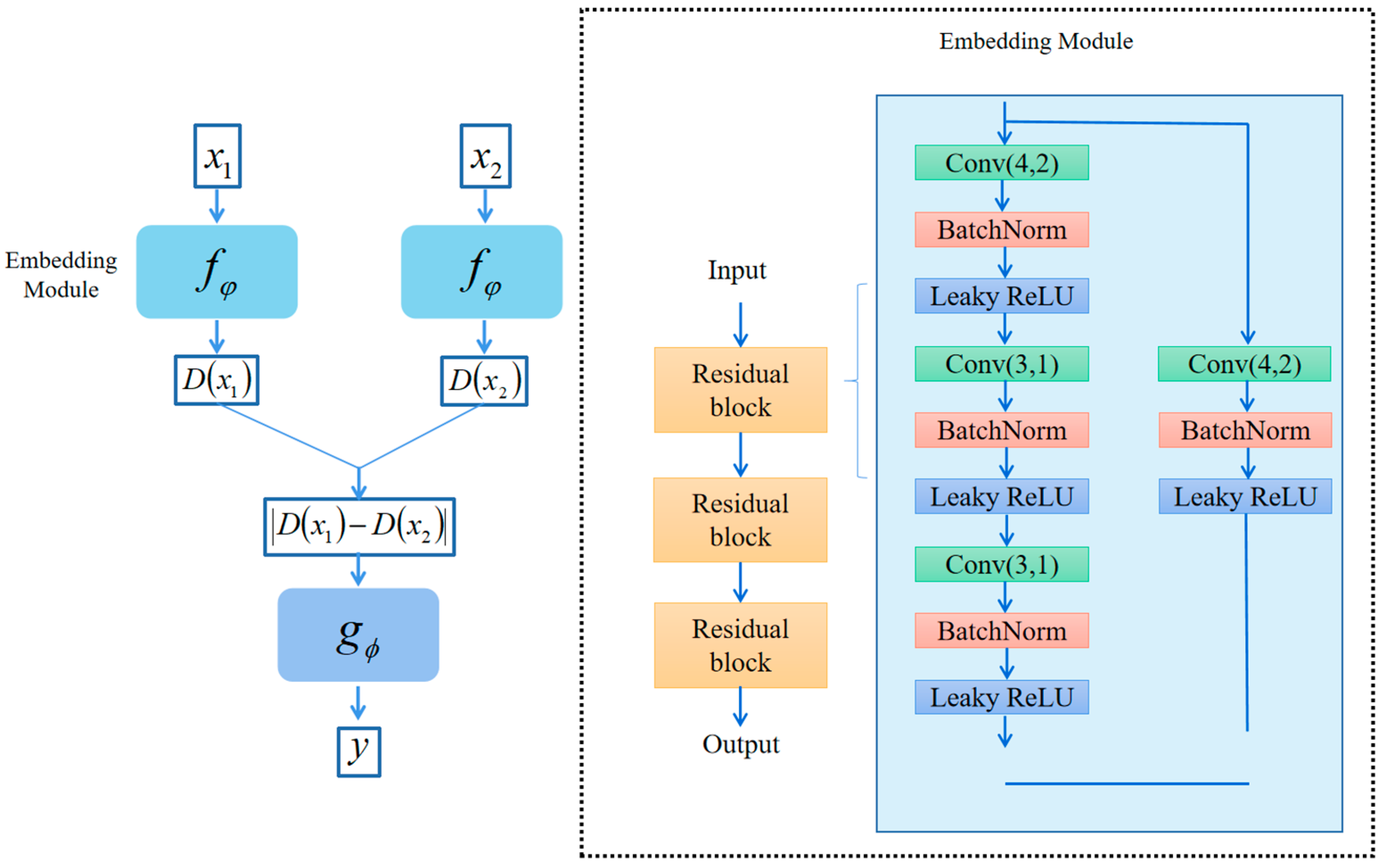
3.2. Embedding Module
- (1)
- Squeeze (Fsq). Aggregates the features of each channel by averaging pooling:
- (2)
- Extraction (Fex). The compressed vectors undergo two fully connected layers to produce channel weights. To improve computational efficiency, we set a reduction factor and halve the number of neurons in the first layer by while using ReLU as a nonlinear function. The second layer has the same number of neurons as the input and applies the sigmoid function to confine the weights between 0 and 1. These fully connected layers are parameterized by and .
- (3)
- Scale (Fsc). The importance score of each channel is obtained from the “Extraction“ stage, which we use to reweight the channels. This involves sequentially multiplying each channel with its corresponding weight to produce the calibrated attention channels.
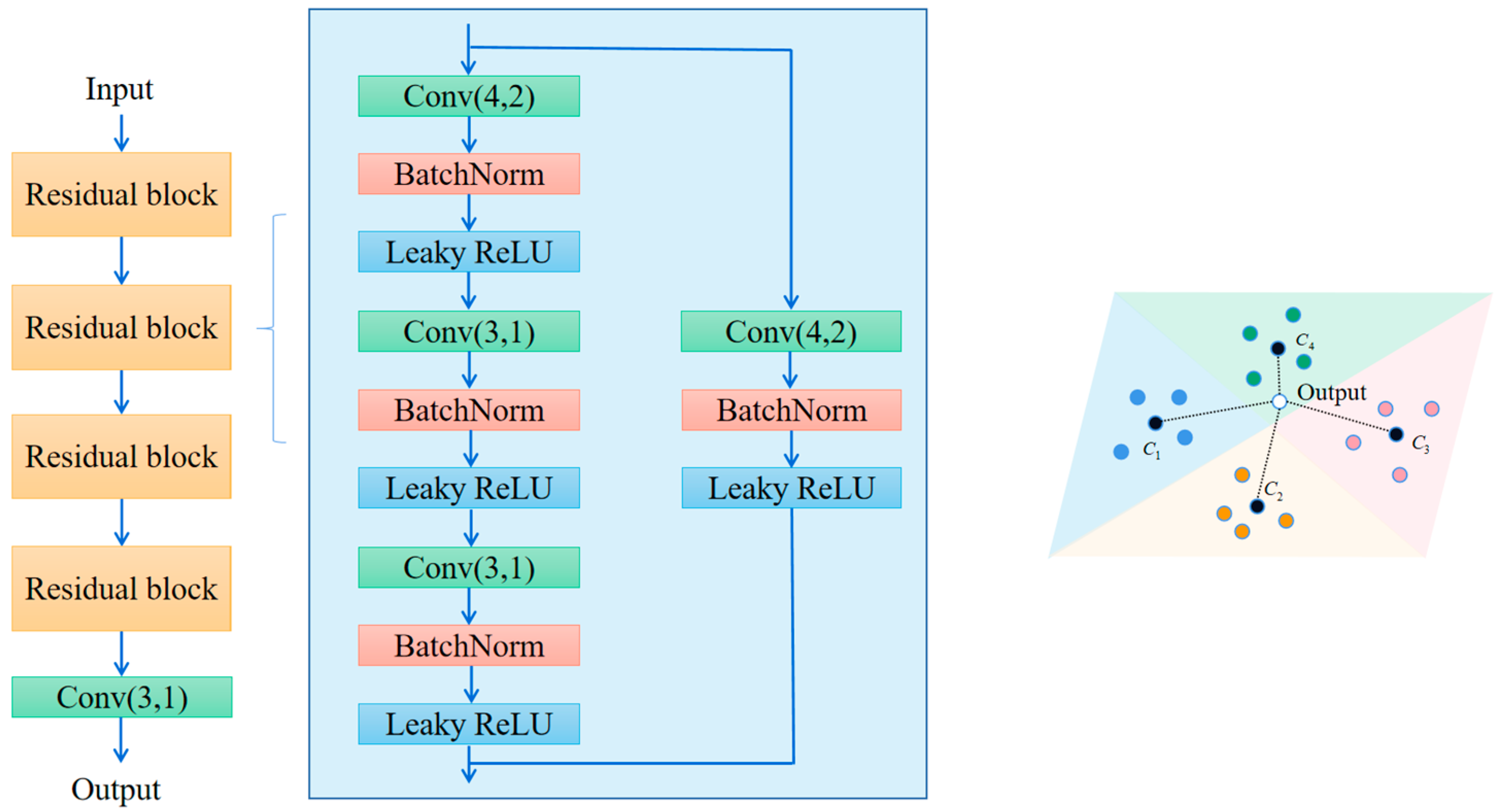
3.3. Metrics Module
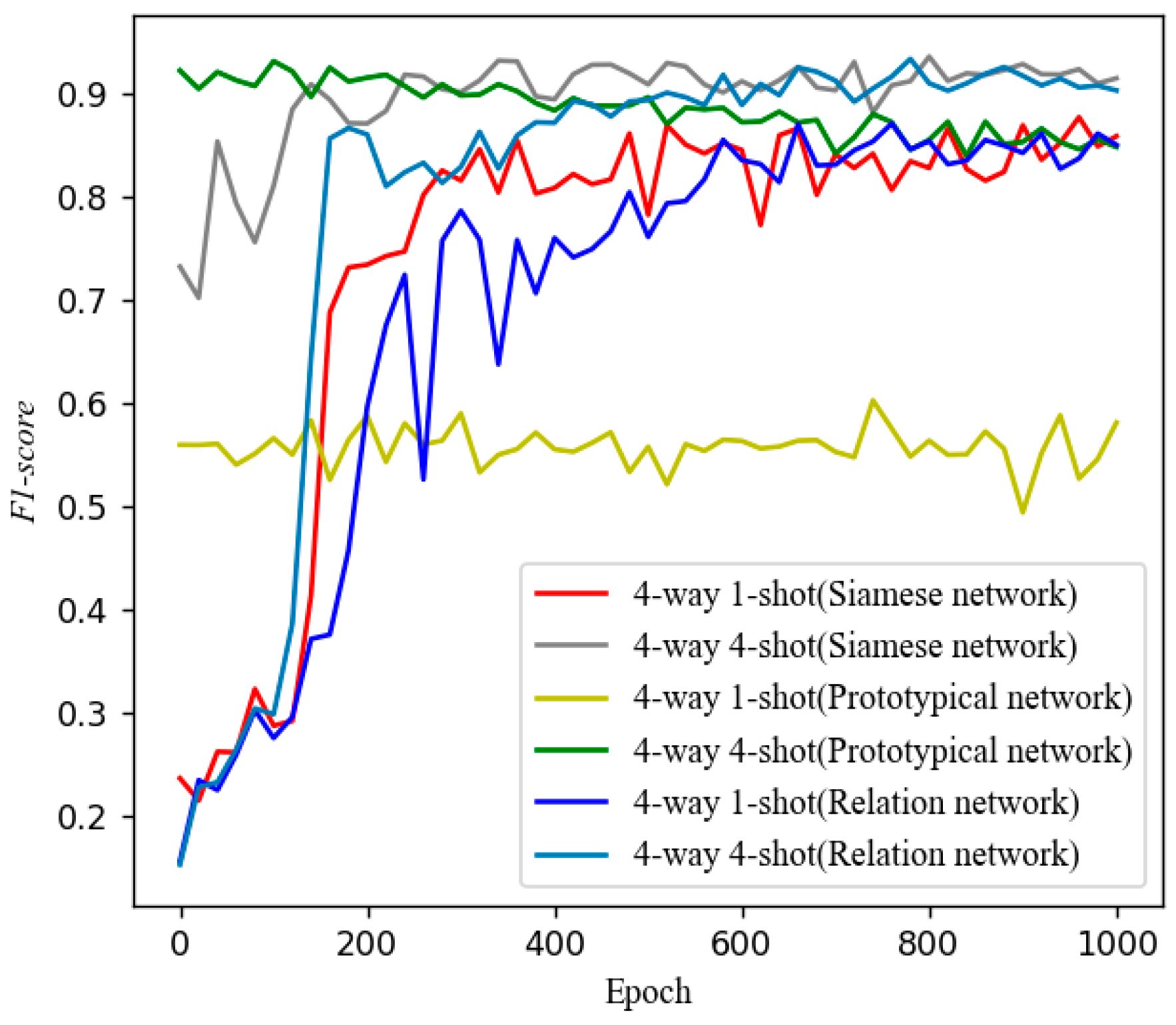
4. Experiments and Analysis
4.1. Parameter Optimization of the SE-RelationNet
4.2. Selection of Evaluation Indicators
- (1)
- K = 1 performance: The strong baseline accuracy (e.g., >0.85 mean_F1-score in 4-way tasks) indicates effective generalization, as a single sample suffices to capture core class characteristics. However, individual sample noise or outliers can degrade prototype fidelity.
- (2)
- K > 1 refinement: Increasing K averages out noise and incorporates diverse sample variations, enhancing prototype stability. This explains the gradual accuracy rise up to K = 4.
- (3)
- Asymptotic behavior beyond K = 4: Once K exceeds a threshold (~4 in our experiments), prototypes saturate in representational quality. Further samples yield diminishing returns, as the embedding space already encodes class-discriminative features efficiently.
5. Results and Discussion
5.1. Making Changes to the BiGRU Block
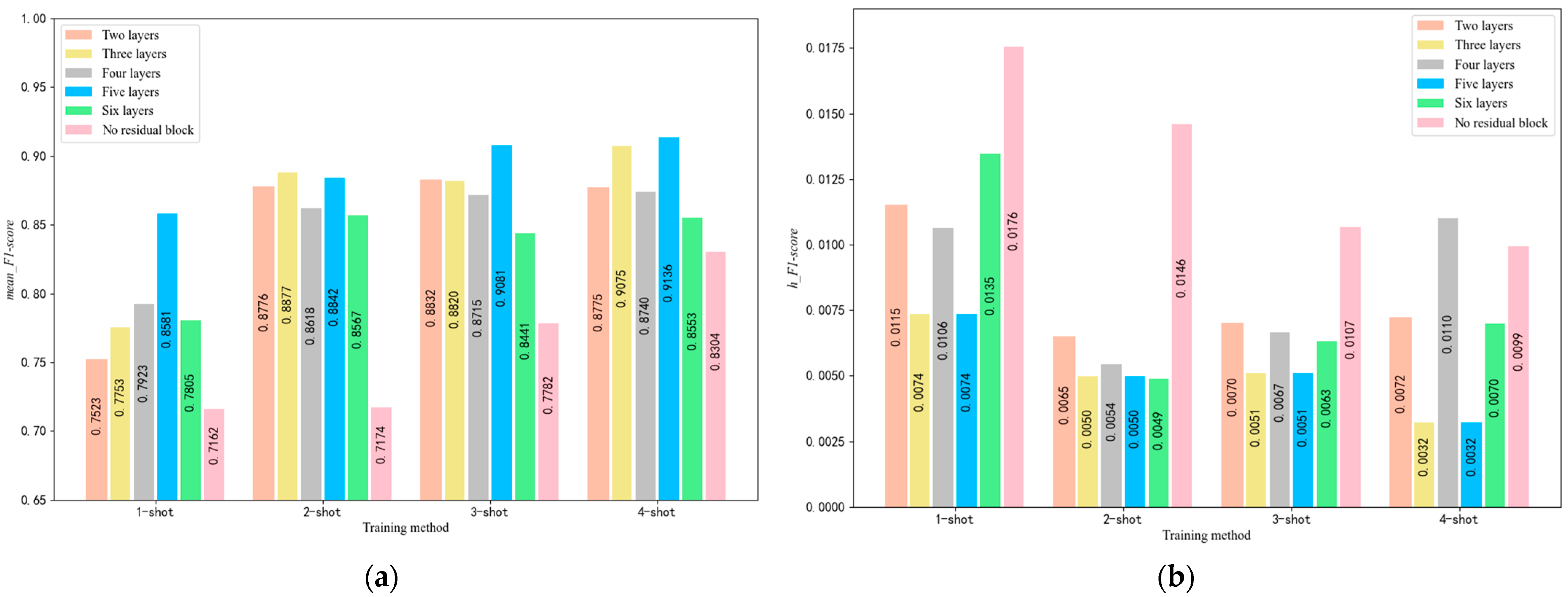
5.2. Selection of the Number of Residual Block Layers
5.3. Control Experiments with Other Models
6. Conclusions
- (1)
- Cross-device generalizability: While SE-RelationNet reduces sensor dependency (Section 2.1 and Section 2.2), performance fluctuations occur when meta-training/meta-testing sensor arrays differ significantly (h_accuracy ≤ 0.010 in Table 7).
- (2)
- Clinical-scale validation: Current validation used curated public datasets. Real-world clinical trials with diverse patient cohorts are needed to assess robustness against comorbidities like asthma or pneumonia.
- (1)
- Extending the model to multi-class COPD severity detection (mild/moderate/severe) using VOC profiles, leveraging the COPD-LUCSS risk correlation.
- (2)
- Integrating lung cancer biomarkers (e.g., aldehyde/ketone signatures) into sensor arrays for joint screening.
- (3)
- Addressing the above limitations through hybrid sensor-fusion algorithms and multi-center clinical trials.
- (1)
- Multi-class COPD subtype detection—Extend SE-RelationNet to classify COPD severity (mild/moderate/severe) using VOC profiles, leveraging the established COPD-LUCSS risk correlation.
- (2)
- Biomarker integration—Incorporate lung cancer-specific biomarkers (e.g., aldehyde/ketone signatures) into the sensor array, enabling simultaneous COPD/lung cancer screening.
- (3)
- Hybrid risk modeling—Develop algorithms combining COPD subtypes, biomarkers, and clinical factors to generate quantifiable risk scores.
- (4)
- Prospective validation—Conduct multi-center trials to validate stratification efficacy prior to clinical deployment.
- (5)
- This framework bridges the gap between our technology and actionable cancer-prevention strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmad, A.S.; Mayya, A.M. A new tool to predict lung cancer based on risk factors. Heliyon 2020, 2, e3402. [Google Scholar] [CrossRef]
- El-Khoury, V.; Schritz, A.; Kim, S.; Lesur, A.; Sertamo, K.; Bernardin, F.; Petritis, K.; Pirrotte, P.; Selinsky, C.; Whiteaker, J.R.; et al. Identification of a blood-based protein biomarker panel for lung cancer detection. Cancers 2020, 6, 1629. [Google Scholar] [CrossRef]
- Cainap, C.; Bălăcescu, O.; Cainap, S.S.; Pop, L. Next generation sequencing technology in lung cancer diagnosis. Biology 2021, 9, 864. [Google Scholar] [CrossRef]
- Binson, V.A.; Subramoniam, M.; Sunny, Y.; Mathew, L. Prediction of pulmonary diseases with electronic nose using SVM and XGBoost. IEEE Sens. J. 2021, 18, 20886–20895. [Google Scholar] [CrossRef]
- Rennard, S.I.; Martinez, F.J.; Rabe, K.F.; Sethi, S.; Pizzichini, E.; McIvor, A.; Siddiqui, S.; Anzueto, A.; Zhu, H. Effects of roflumilast in COPD patients receiving inhaled corticosteroid/long-acting β2-agonist fixed-dose combination: RE2SPOND rationale and study design. Int. J. Chronic Obstruct. Pulm. Dis. 2016, 11, 1921–1928. [Google Scholar] [CrossRef] [PubMed]
- Sekine, Y.; Katsura, H.; Koh, E.; Hiroshima, K.; Fujisawa, T. Early detection of COPD is important for lung cancer surveillance. Eur. Respir. J. 2012, 5, 1230–1240. [Google Scholar] [CrossRef]
- Mirza, S.; Clay, R.D.; Koslow, M.A.; Scanlon, P.D. COPD guidelines: A review of the 2018 GOLD report. Mayo Clin. Proc. 2018, 93, 1488–1502. [Google Scholar] [CrossRef]
- Wilson, D.O.; de Torres, J.P. Lung cancer screening: How do we make it better? Quant. Imaging Med. Surg. 2020, 10, 533–536. [Google Scholar] [CrossRef]
- Li, X.O.; Cheng, J.; Shen, Y.; Chen, J.; Wang, T.; Wen, F.; Chen, L. Metabolomic analysis of lung cancer patients with chronic obstructive pulmonary disease using gas chromatography-mass spectrometry. J. Pharm. Biomed. Anal. 2020, 180, 113524. [Google Scholar] [CrossRef]
- Bregy, L.; Nussbaumer-Ochsner, Y.; Martinez-Lozano Sinues, P.; García-Gómez, D.; Suter, Y.; Gaisl, T.; Stebler, N.; Gaugg, M.T.; Kohler, M.; Zenobi, R. Real-time mass spectrometric identification of metabolites characteristic of chronic obstructive pulmonary disease in exhaled breath. Clin. Mass Spectrom. 2018, 10, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Bodduluri, S.; Nakhmani, A.; Reinhardt, J.M.; Wilson, C.G.; McDonald, M.N.; Rudraraju, R.; Jaeger, B.C.; Bhakta, N.R.; Castaldi, P.J.; Sciurba, F.C.; et al. Deep neural network analyses of spirometry for structural phenotyping of chronic obstructive pulmonary disease. JCI Insight 2020, 5, e134123. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Oh, J.; Kim, Y.; Ban, H.; Kwon, Y.; Oh, I.; Kim, K.; Kim, Y.; Lim, S. Differences in classification of COPD group using COPD assessment test (CAT) or modified Medical Research Council (mMRC) dyspnea scores: A cross-sectional analysis. BMC Pulm. Med. 2013, 13, 35. [Google Scholar] [CrossRef]
- Tinkelman, D.; Price, D.; Nordyke, R.; Halbert, R. Misdiagnosis of COPD and asthma in primary care patients 40 years of age and over. J. Asthma 2009, 46, 75–80. [Google Scholar] [CrossRef]
- Akopov, A.; Papayan, G. Photodynamic theranostics of central lung cancer: Present state and future prospects. Photodiagn. Photodyn. Ther. 2021, 33, 102203. [Google Scholar] [CrossRef]
- Peng, J.; Mei, H.; Yang, R.; Meng, K.; Shi, L.; Zhao, J.; Zhang, B.; Xuan, F.; Wang, T.; Zhang, T. Olfactory diagnosis model for lung health evaluation based on pyramid pooling and SHAP-based dual encoders. ACS Sens. 2024, 9, 4934–4946. [Google Scholar] [CrossRef]
- Shooshtari, M.M.; Salehi, S. An electronic nose based on carbon nanotube-titanium dioxide hybrid nanostructures for detection and discrimination of volatile organic compounds. Sens. Actuators B Chem. 2022, 357, 131418. [Google Scholar] [CrossRef]
- Mota, I.; Teixeira-Santos, R.; Rufo, J.C. Detection and identification of fungal species by electronic nose technology: A systematic review. Fungal Biol. Rev. 2021, 38, 45–56. [Google Scholar] [CrossRef]
- Hidayat, S.N.; Julian, T.; Dharmawan, A.B.; Puspita, M.; Chandra, L.; Rohman, A.; Julia, M.; Rianjanu, A.; Nurputra, D.K.; Triyana, K.; et al. Hybrid learning method based on feature clustering and scoring for enhanced COVID-19 breath analysis by an electronic nose. Artif. Intell. Med. 2022, 127, 102323. [Google Scholar] [CrossRef]
- Le Maout, P.; Wojkiewicz, J.; Redon, N.; Lahuec, C.; Seguin, F.; Dupont, L.; Mikhaylov, S.; Noskov, Y.; Ogurtsov, N.; Pud, A. Polyaniline nanocomposites based sensor array for breath ammonia analysis: Portable e-nose approach to non-invasive diagnosis of chronic kidney disease. Sens. Actuators B Chem. 2018, 261, 616–626. [Google Scholar] [CrossRef]
- Ma, H.; Wang, T.; Li, B.; Cao, W.; Zeng, M.; Yang, J.; Su, Y.; Hu, N.; Zhou, Z.; Yang, Z. A low-cost and efficient electronic nose system for quantification of multiple indoor air contaminants utilizing HC and PLSR. Sens. Actuators B Chem. 2022, 366, 130768. [Google Scholar] [CrossRef]
- Burgués, J.; Esclapez, M.D.; Doñate, S.; Marco, S. RHINOS: A lightweight portable electronic nose for real-time odor quantification in wastewater treatment plants. iScience 2021, 24, 103371. [Google Scholar] [CrossRef]
- Andre, R.S.; Facure, M.H.M.; Mercante, L.A.; Correa, D.S. Electronic nose based on hybrid free-standing nanofibrous mats for meat spoilage monitoring. Sens. Actuators B Chem. 2022, 369, 131114. [Google Scholar] [CrossRef]
- Li, P.; Niu, Z.; Shao, K.; Wu, Z. Quantitative analysis of fish meal freshness using an electronic nose combined with chemometric methods. Measurement 2021, 171, 109484. [Google Scholar] [CrossRef]
- Kim, C.; Kim, S.; Lee, Y.; Nguyen, T.M.; Lee, J.; Moon, J.; Han, D.; Oh, J. A phage- and colorimetric sensor-based artificial nose model for banana ripening analysis. Sens. Actuators B Chem. 2022, 372, 131763. [Google Scholar] [CrossRef]
- Machungo, C.; Berna, A.Z.; McNevin, D.; Wang, R.; Trowell, S. Comparison of the performance of metal oxide and conducting polymer electronic noses for detection of aflatoxin using artificially contaminated maize. Sens. Actuators B Chem. 2022, 368, 131681. [Google Scholar] [CrossRef]
- Cao, H.; Jia, P.; Xu, D.; Jiang, Y.; Qiao, S. Feature extraction of citrus juice during storage for electronic nose based on cellular neural network. IEEE Sens. J. 2020, 20, 3803–3812. [Google Scholar] [CrossRef]
- Xu, Y.; Mei, H.; Bing, Y.; Zhang, F.; Sui, N.; Zhou, T.; Fan, X.; Wang, L.; Zhang, T. High selectivity MEMS C2H2 sensor for transformer fault characteristic gas detection. Adv. Sens. Eng. 2024, 4, e202400032. [Google Scholar] [CrossRef]
- Shooshtari, M.; Vollebregt, S.; Vaseghi, Y.; Rajati, M.; Pahlavan, S. The sensitivity enhancement of TiO2-based VOCs sensor decorated by gold at room temperature. Nanotechnology 2023, 34, 255501. [Google Scholar] [CrossRef]
- Mei, H.; Peng, J.; Wang, T.; Zhou, T.; Zhao, H.; Zhang, T.; Yang, Z. Overcoming the limits of cross-sensitivity: Pattern recognition methods for chemiresistive gas sensor array. Nano-Micro Lett. 2024, 16, 269. [Google Scholar] [CrossRef]
- Mahmodi, K.; Mostafaei, M.; Mirzaee-Ghaleh, E. Detection and classification of diesel-biodiesel blends by LDA, QDA and SVM approaches using an electronic nose. Fuel 2019, 239, 116114. [Google Scholar] [CrossRef]
- Binson, V.A.; Thomas, S.; Ragesh, G.K.; Kumar, A. Non-invasive diagnosis of COPD with E-nose using XGBoost algorithm. In Proceedings of the 2nd International Conference on Advances in Computing, Communication, Embedded and Secure Systems (ACCESS), Ernakulam, India, 20–22 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Jia, P.; Tian, F.; He, Q.; Fan, S.; Liu, J.; Yang, S.X. Feature extraction of wound infection data for electronic nose based on a novel weighted KPCA. Sens. Actuators B Chem. 2014, 202, 555–566. [Google Scholar] [CrossRef]
- Li, Q.; Gu, Y.; Wang, N. Application of random forest classifier by means of a QCM-based e-nose in the identification of Chinese liquor flavors. IEEE Sens. J. 2017, 17, 1788–1794. [Google Scholar] [CrossRef]
- Avian, C.; Mahali, M.I.; Putro, N.A.S.; Prakosa, S.W.; Leu, J. Fx-Net and PureNet: Convolutional neural network architecture for discrimination of chronic obstructive pulmonary disease from smokers and healthy subjects through electronic nose signals. Comput. Biol. Med. 2022, 147, 105913. [Google Scholar] [CrossRef]
- Bakiler, H.; Güney, S. Estimation of concentration values of different gases based on long short-term memory by using electronic nose. Biomed. Signal Process. Control 2021, 65, 102908. [Google Scholar] [CrossRef]
- Koch, G.R. Siamese neural networks for one-shot image recognition. arXiv 2015, arXiv:1506.07428. Available online: https://api.semanticscholar.org/CorpusID:13874643 (accessed on 31 July 2025).
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one-shot learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3630–3638. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4077–4087. [Google Scholar] [CrossRef]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.; Hospedales, T.M. Learning to compare: Relation network for few-shot learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; Volume 41, pp. 1–14. [Google Scholar] [CrossRef]
- Xu, H.; Li, W.; Cai, Z. Analysis on methods to effectively improve transfer learning performance. Theor. Comput. Sci. 2023, 934, 90–107. [Google Scholar] [CrossRef]
- Vergara, A.; Fonollosa, J.; Mahiques, J.; Trincavelli, M.; Rulkov, N.; Huerta, R. On the performance of gas sensor arrays in open sampling systems using inhibitory support vector machines. Sens. Actuators B Chem. 2013, 188, 462–477. [Google Scholar] [CrossRef]
- Durán Acevedo, C.M.; Cuastumal Vasquez, C.A.; Carrillo Gómez, J.K. Electronic nose dataset for COPD detection from smokers and healthy people through exhaled breath analysis. Data Brief 2021, 34, 106767. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Jie, S.; Albanie, S.; Sun, G.; Enhua, Y. Squeeze-and-excitation networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 201–213. [Google Scholar] [CrossRef]
- Cornegruta, S.; Bakewell, R.; Withey, S.; Montana, G. Modelling radiological language with bidirectional long short-term memory networks. arXiv 2016. [Google Scholar] [CrossRef]
- Jiao, Z.; Sun, S.; Ke, S. Chinese lexical analysis with deep bi-GRU-CRF network. In Proceedings of the International Conference on Computational Linguistics, Santa Fe, NM, USA, 17–23 August 2018; pp. 123–130. [Google Scholar] [CrossRef]
- Ni, S.; Jia, P.; Xu, Y.; Zeng, L.; Li, X.; Xu, M. Prediction of CO concentration in different conditions based on Gaussian-TCN. Sens. Actuators B Chem. 2023, 379, 133010. [Google Scholar] [CrossRef]




| Detection Method | Accuracy | Speed | Cost | Complexity | Personnel Requirement | Invasive? | Key Limitations |
|---|---|---|---|---|---|---|---|
| Gas Chromatography–Mass Spectrometry (GC-MS) [9,10] | High | Slow (hrs) | High | High | Specialized | No | Time-consuming, expensive equipment and maintenance, complex sample prep and analysis |
| Spirometry [11,12,13] | Moderate | Moderate | Low– Mod | Moderate | Trained | No | Effort-dependent, may miss early disease, requires patient cooperation |
| Sputum Cytometry | Variable | Moderate | Mod | Moderate | Trained | No | Sample variability, requires specialized staining/analysis |
| Chest Radiography (X-ray) [14] | Low– Mod | Fast | Low– Mod | Low | Trained (interpretation) | No | Low sensitivity for early COPD, limited specificity (other lung conditions look similar) |
| Fluoroscopic Bronchoscopy | High | Slow | High | High | Specialist | Yes | Invasive, requires sedation/anesthesia, risk of complications, expensive |
| Electronic Nose (E-nose) [15] | High (Emerging) | Fast (mins) | Lower (Potential) | Lower | Minimal Training | No | Requires algorithm development/validation, sensor drift/calibration needs |
| No. | Location | Type | Mean Contribution | Slope Contribution | Contribution Score | Sensitive Gas |
|---|---|---|---|---|---|---|
| 1 | <4,4> | TGS2600 | 0.5131 | 0.6426 | 0.5778 | Hydrogen, carbon, monoxide |
| 2 | <5,2> | TGS2612 | 0.9244 | 0.7229 | 0.8236 | Methane, propane, butane |
| 3 | <5,3> | TGS2610 | 0.5159 | 0.4822 | 0.4991 | Propane |
| 4 | <5,4> | TGS2600 | 0.8593 | 1.0441 | 0.9517 | Hydrogen, carbon, monoxide |
| 5 | <5,5> | TGS2602 | 0.4782 | 0.5130 | 0.5130 | Ammonia, H2S, volatile organic compounds (VOC) |
| 6 | <5,6> | TGS2602 | 0.5004 | 0.5228 | 0.5116 | Ammonia, H2S, VOC |
| 7 | <5,7> | TGS2620 | 0.4925 | 0.5665 | 0.5295 | Carbon, monoxide, combustible gases, VOC |
| 8 | <5,8> | TGS2620 | 0.5246 | 0.5920 | 0.5583 | Carbon, monoxide, combustible gases, VOC |
| Class | Molecular Formula | Concentration (ppm) | Number of Gas Samples |
|---|---|---|---|
| Acetaldehyde | 500 | 1800 | |
| Acetone | 2500 | 1800 | |
| Ammonia | 10,000 | 1800 | |
| Benzene | 200 | 1800 | |
| Butanol | 100 | 1500 | |
| Carbon monoxide | 4000 | 1571 | |
| Carbon monoxide | 1000 | 449 | |
| Ethylene | 500 | 1800 | |
| Methane | 1000 | 1800 | |
| Methanol | 200 | 1800 | |
| Toluene | 200 | 1800 |
| Class | The Number of Samples |
|---|---|
| COPD | 40 |
| Smokers | 8 |
| Control | 20 |
| Air | 10 |
| Parameter Names | Parameter Values |
|---|---|
| Optimizer | Adam |
| Loss function | Mseloss |
| Training epochs | 1001 |
| Testing epochs | 50 |
| Batch num per class during training | 20 |
| BiGRU’s hidden layers | 1 |
| Learning rate | 0.0001 |
| Seed | 512 |
| Dropout | 0.3 |
| ratio | 16 |
| Reference | |||
|---|---|---|---|
| Positive | Negative | ||
| Prediction | Positive | TP | FP |
| Negative | FN | TN | |
| mean_accuracy | h_accuracy | mean_F1-score | h_F1-score | |
|---|---|---|---|---|
| 4-way 1-shot | 0.858 | 0.010 | 0.852 | 0.011 |
| 4-way 2-shot | 0.896 | 0.005 | 0.890 | 0.006 |
| 4-way 3-shot | 0.922 | 0.008 | 0.919 | 0.008 |
| 4-way 4-shot | 0.933 | 0.007 | 0.931 | 0.008 |
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | |
|---|---|---|---|---|---|---|---|
| 4-way 1-shot | 0.852 | 0.845 | 0.842 | 0.816 | 0.823 | 0.808 | 0.819 |
| 4-way 2-shot | 0.890 | 0.869 | 0.874 | 0.893 | 0.902 | 0.855 | 0.880 |
| 4-way 3-shot | 0.919 | 0.904 | 0.919 | 0.919 | 0.915 | 0.878 | 0.893 |
| 4-way 4-shot | 0.931 | 0.915 | 0.915 | 0.925 | 0.926 | 0.882 | 0.905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Tian, Y.; Jia, P. A Few-Shot SE-Relation Net-Based Electronic Nose for Discriminating COPD. Sensors 2025, 25, 4780. https://doi.org/10.3390/s25154780
Xie Z, Tian Y, Jia P. A Few-Shot SE-Relation Net-Based Electronic Nose for Discriminating COPD. Sensors. 2025; 25(15):4780. https://doi.org/10.3390/s25154780
Chicago/Turabian StyleXie, Zhuoheng, Yao Tian, and Pengfei Jia. 2025. "A Few-Shot SE-Relation Net-Based Electronic Nose for Discriminating COPD" Sensors 25, no. 15: 4780. https://doi.org/10.3390/s25154780
APA StyleXie, Z., Tian, Y., & Jia, P. (2025). A Few-Shot SE-Relation Net-Based Electronic Nose for Discriminating COPD. Sensors, 25(15), 4780. https://doi.org/10.3390/s25154780








