Research on Damage Identification in Transmission Tower Structures Based on Cross-Correlation Function Amplitude Vector
Abstract
1. Introduction
2. Damage Identification Theory
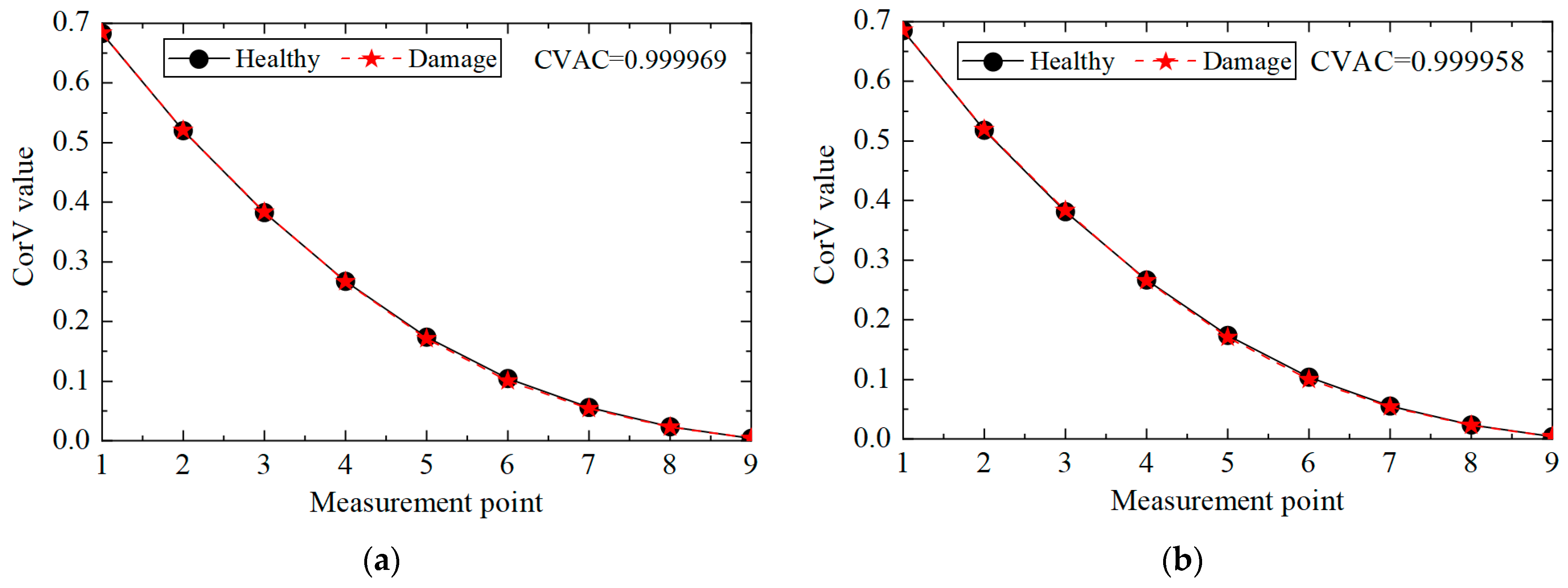
2.1. Cross-Correlation Function Amplitude Vector
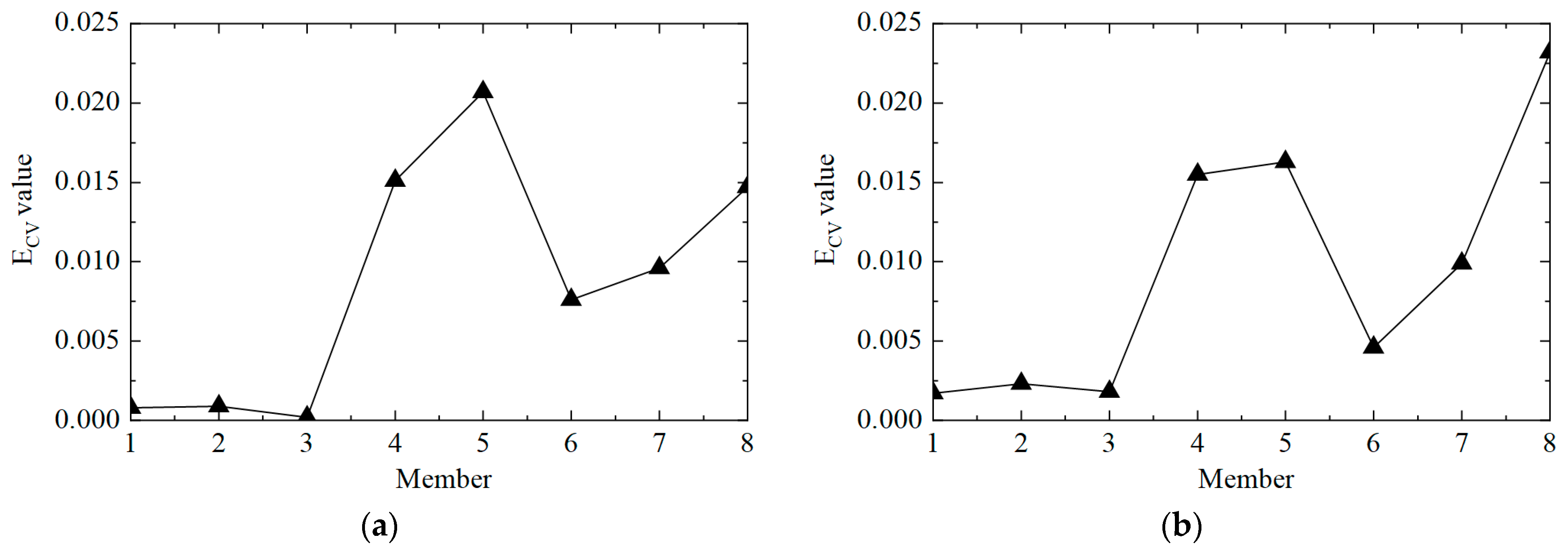
2.2. Damage Index
3. Numerical Simulation Verification
3.1. Finite Element Model
3.2. Damage Identification
4. Parametric Analysis
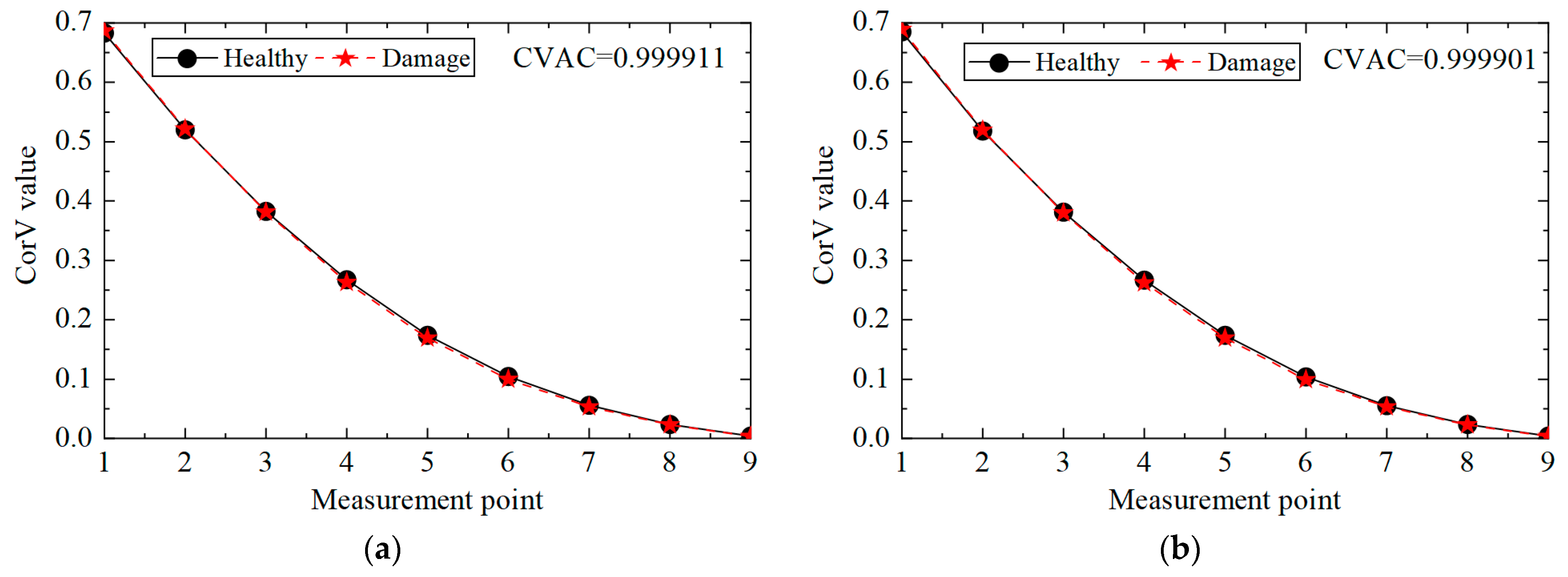
4.1. Anti-Noise Analysis
4.2. Response Type Analysis
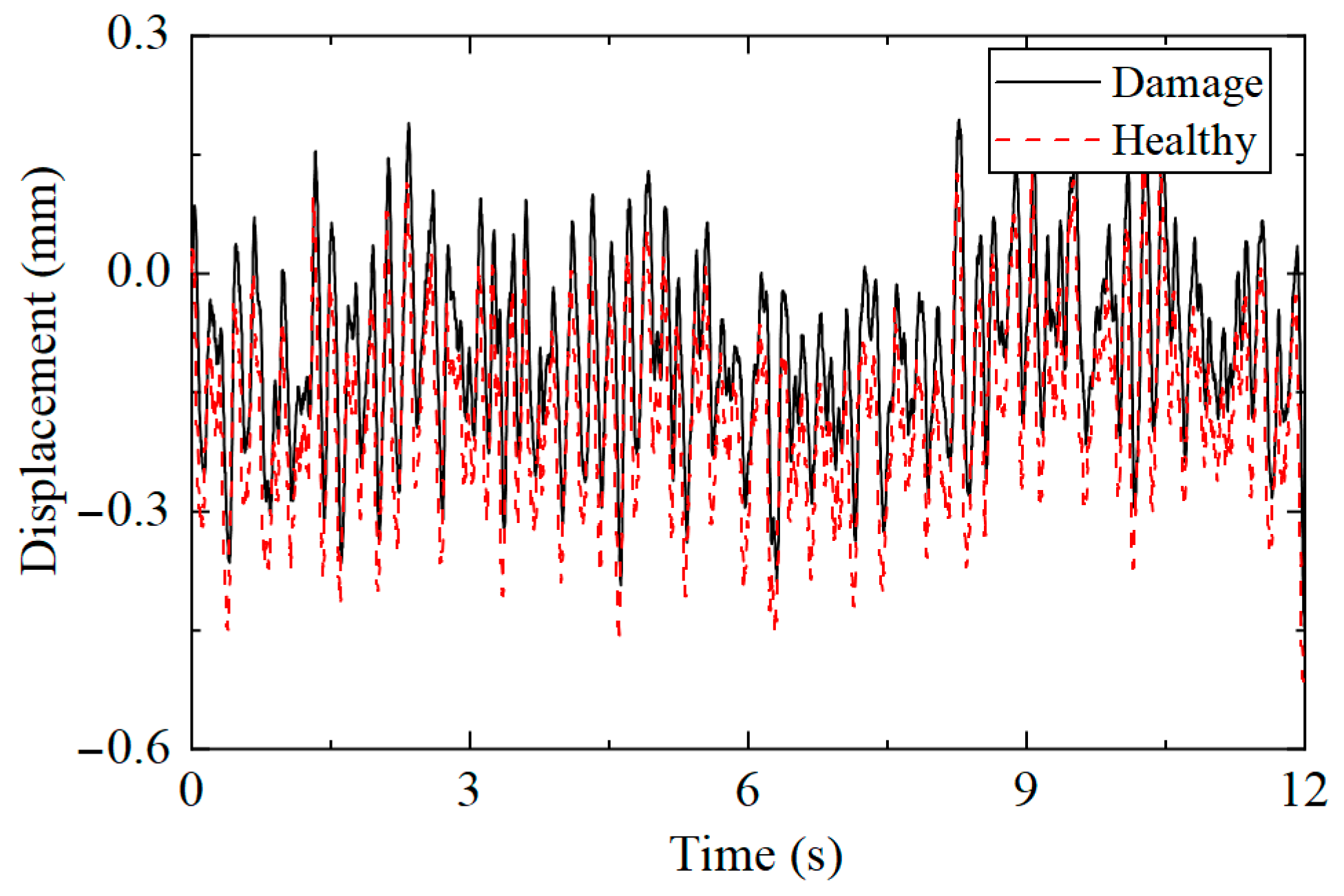
5. Model Test Verification
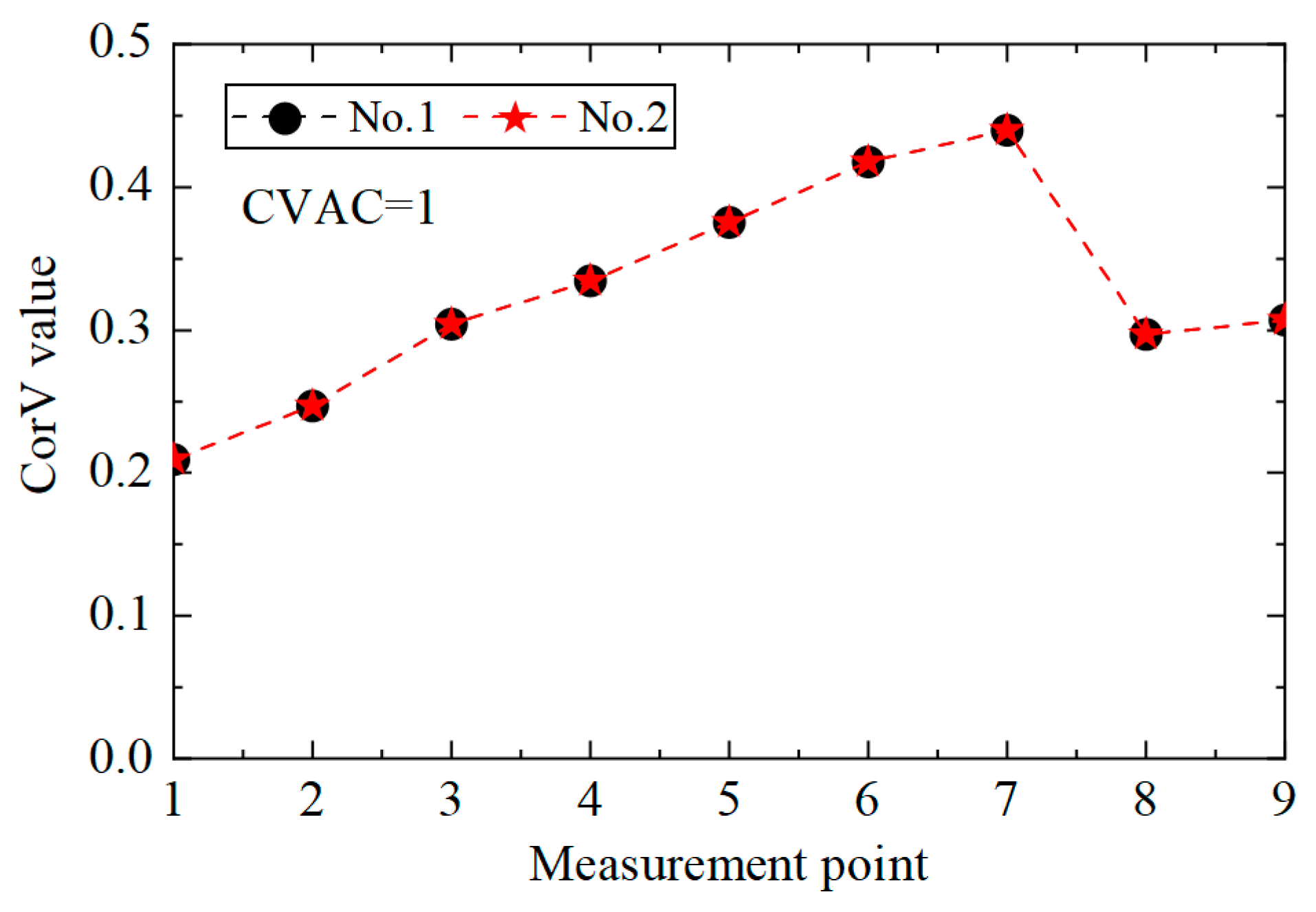
5.1. Scale Model
5.2. Analysis of Identification Results
6. Summary and Conclusions
- (1)
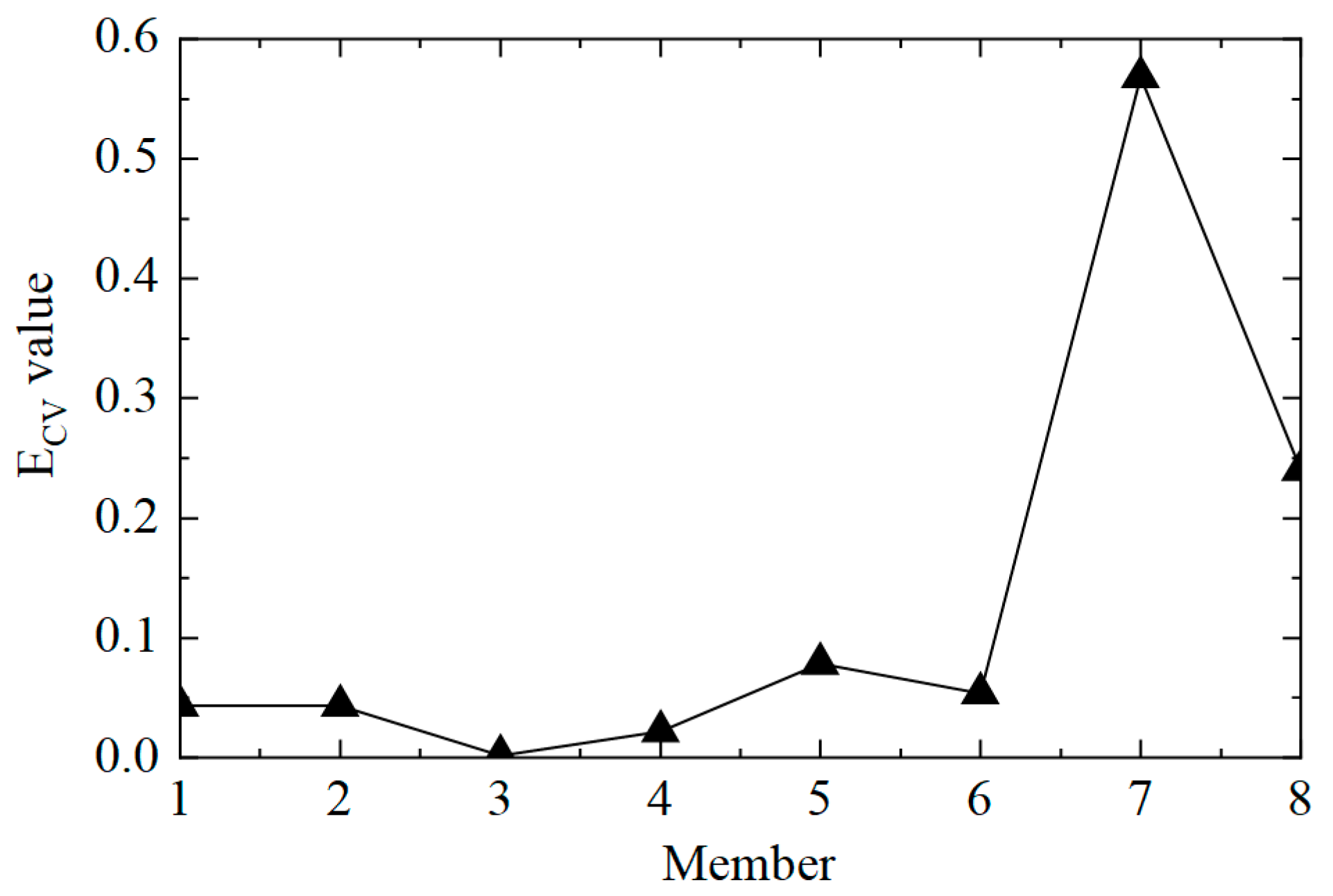
- When the CVAC value of the transmission tower is significantly less than one, it indicates that the structure is damaged. The damage element of the transmission tower structure can be located according to the mutation position in the first-order difference curve of ECV.
- (2)
- The proposed method is applicable to damage identification using different types of dynamic responses.
- (3)
- The proposed method can still identify the damage location under 10% noise interference.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- de Araújo, A.R.J.; Kurokawa, S.; Seixas, C.M.; Kordi, B. Optimization of tower-footing grounding impedance for guyed-V transmission towers. Electr. Power Syst. Res. 2019, 177, 105947. [Google Scholar] [CrossRef]
- Jiang, W.Q.; Wang, Z.Q.; McClure, G.; Wang, G.L.; Geng, J.D. Accurate modeling of joint effects in lattice transmission towers. Eng. Struct. 2011, 33, 1817–1827. [Google Scholar] [CrossRef]
- Mills, J.E.; Ma, X.; Zhuge, Y. Experimental study on multi-panel retrofitted steel transmission towers. J. Constr. Steel Res. 2012, 78, 58–67. [Google Scholar] [CrossRef]
- Rao, N.P.; Rokade, R.P.; Balagopal, R.; Palani, G.S. Segmental instability failures in transmission line towers. J. Constr. Steel Res. 2023, 211, 108195. [Google Scholar] [CrossRef]
- Chen, D.D.; Shen, Z.H.; Huo, L.S.; Narazaki, Y. Percussion-based quasi real-time void detection for concrete-filled steel tubular structures using dense learned features. Eng. Struct. 2023, 274, 115197. [Google Scholar] [CrossRef]
- Chen, D.D.; Zhang, N.N.; Huo, L.S.; Song, G.B. Full-range bolt preload monitoring with multi-resolution using the time shifts of the direct wave and coda waves. Struct. Health Monit.-Int. J. 2023, 22, 3871–3890. [Google Scholar] [CrossRef]
- Tan, X.; Poorghasem, S.; Huang, Y.; Feng, X.; Bao, Y. Monitoring of pipelines subjected to interactive bending and dent using distributed fiber optic sensors. Autom. Constr. 2024, 160, 105306. [Google Scholar] [CrossRef]
- Dias, C.F.; de Oliveira, J.R.; de Mendonça, L.D.; de Almeida, L.M.; de Lima, E.R.; Wanner, L. An IoT-Based System for Monitoring the Health of Guyed Towers in Overhead Power Lines. Sensors 2021, 21, 6173. [Google Scholar] [CrossRef]
- Fu, X.; Du, W.L.; Li, H.N.; Xie, W.P.; Xiao, K.; Lei, X. Gust Response Factor of a Transmission Tower Under Typhoon. Int. J. Struct. Stab. Dyn. 2021, 21, 2150001. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, X.; Ren, L.; Jia, Z.G. Modal parameters of a transmission tower considering the coupling effects between the tower and lines. Eng. Struct. 2020, 220, 110947. [Google Scholar] [CrossRef]
- Dorvash, S.; Pakzad, S.N.; LaCrosse, E.L. Statistics based localized damage detection using vibration response. Smart Struct. Syst. 2014, 14, 85–104. [Google Scholar] [CrossRef]
- Katunin, A. Damage Identification and Quantification in Beams Using Wigner-Ville Distribution. Sensors 2020, 20, 6638. [Google Scholar] [CrossRef]
- Kim, H.S.; Melhem, H. Damage detection of structures by wavelet analysis. Eng. Struct. 2004, 26, 347–362. [Google Scholar] [CrossRef]
- Dlugosz, J.; Dao, P.B.; Staszewski, W.J.; Uhl, T. Damage Detection in Glass Fibre Composites Using Cointegrated Hyperspectral Images. Sensors 2024, 24, 1980. [Google Scholar] [CrossRef]
- Roveri, N.; Severa, L.; Milana, S.; Tronci, E.M.; Culla, A.; Betti, R.; Carcaterra, A. ADACTA-Advanced component analysis technique for damage detection. Struct. Health Monit.-Int. J. 2025. [Google Scholar] [CrossRef]
- Wang, N.B.; Ren, W.X.; Huang, T.L. Baseline-free damage detection method for beam structures based on an actual influence line. Smart Struct. Syst. 2019, 24, 475–490. [Google Scholar]
- Wang, S.; Huseynov, F.; Casero, M.; Obrien, E.J.; Fidler, P.; McCrum, D.P. A novel bridge damage detection method based on the equivalent influence lines—Theoretical basis and field validation. Mech. Syst. Signal Proc. 2023, 204, 110738. [Google Scholar] [CrossRef]
- Cai, Q.L.; Chen, Z.W.; Zhu, S.Y.; Mo, L.Y. On damage detection of beam structures using multiple types of influence lines. Structures 2022, 42, 449–465. [Google Scholar] [CrossRef]
- Ono, R.; Ha, T.M.; Fukada, S. Analytical study on damage detection method using displacement influence lines of road bridge slab. J. Civ. Struct. Health Monit. 2019, 9, 565–577. [Google Scholar] [CrossRef]
- Chang, K.C.; Kim, C.W. Modal-parameter identification and vibration-based damage detection of a damaged steel truss bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Radzienski, M.; Krawczuk, M.; Palacz, M. Improvement of damage detection methods based on experimental modal parameters. Mech. Syst. Signal Proc. 2011, 25, 2169–2190. [Google Scholar] [CrossRef]
- Titurus, B.; Friswell, M.I. Damage detection using successive parameter subset selections and multiple modal residuals. Mech. Syst. Signal Proc. 2014, 45, 193–206. [Google Scholar] [CrossRef]
- Morales, F.A.O.; Cury, A.A. Analysis of thermal and damage effects over structural modal parameters. Struct. Eng. Mech. 2018, 65, 43–51. [Google Scholar]
- Zhang, F.L.; Gu, D.K.; Li, X.; Ye, X.W.; Peng, H.Y. Structural damage detection based on fundamental Bayesian two-stage model considering the modal parameters uncertainty. Struct. Health Monit.-Int. J. 2023, 22, 2305–2324. [Google Scholar] [CrossRef]
- Dewangan, P.; Parey, A.; Hammami, A.; Chaari, F.; Haddar, M. Damage detection in wind turbine gearbox using modal strain energy. Eng. Fail. Anal. 2020, 107, 104228. [Google Scholar] [CrossRef]
- Bel-Hadj, Y.; Weil, M.; Weijtjens, W.; Devriendt, C. Experimental validation of automated OMA and mode tracking for structural health monitoring of transmission towers. Struct. Health Monit. 2025, 24, 1272–1291. [Google Scholar] [CrossRef]
- Yin, T.; Lam, H.F.; Chow, H.M.; Zhu, H.P. Dynamic reduction-based structural damage detection of transmission tower utilizing ambient vibration data. Eng. Struct. 2009, 31, 2009–2019. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, N.F.; Lam, H.F.; Yang, J.H.; Lin, Z.S.; Zhu, H.P. Brace damage identification of a transmission tower via a sparse Bayesian learning method with variational inference and enhanced PSO algorithm. Structures 2025, 77, 109170. [Google Scholar] [CrossRef]
- Xu, Y.L.; Lin, J.F.; Zhan, S.; Wang, F.Y. Multistage damage detection of a transmission tower: Numerical investigation and experimental validation. Struct. Control Health Monit. 2019, 26, e2366. [Google Scholar] [CrossRef]
- Karami-Mohammadi, R.; Mirtaheri, M.; Salkhordeh, M.; Hariri-Ardebili, M.A. Vibration Anatomy and Damage Detection in Power Transmission Towers with Limited Sensors. Sensors 2020, 20, 1731. [Google Scholar] [CrossRef]
- Kouchaki, M.; Salkhordeh, M.; Mashayekhi, M.; Mirtaheri, M.; Amanollah, H. Damage detection in power transmission towers using machine learning algorithms. Structures 2023, 56, 104980. [Google Scholar] [CrossRef]
- Duvnjak, I.; Damjanovic, D.; Bartolac, M.; Skender, A. Mode Shape-Based Damage Detection Method (MSDI): Experimental Validation. Appl. Sci. 2021, 11, 4589. [Google Scholar] [CrossRef]

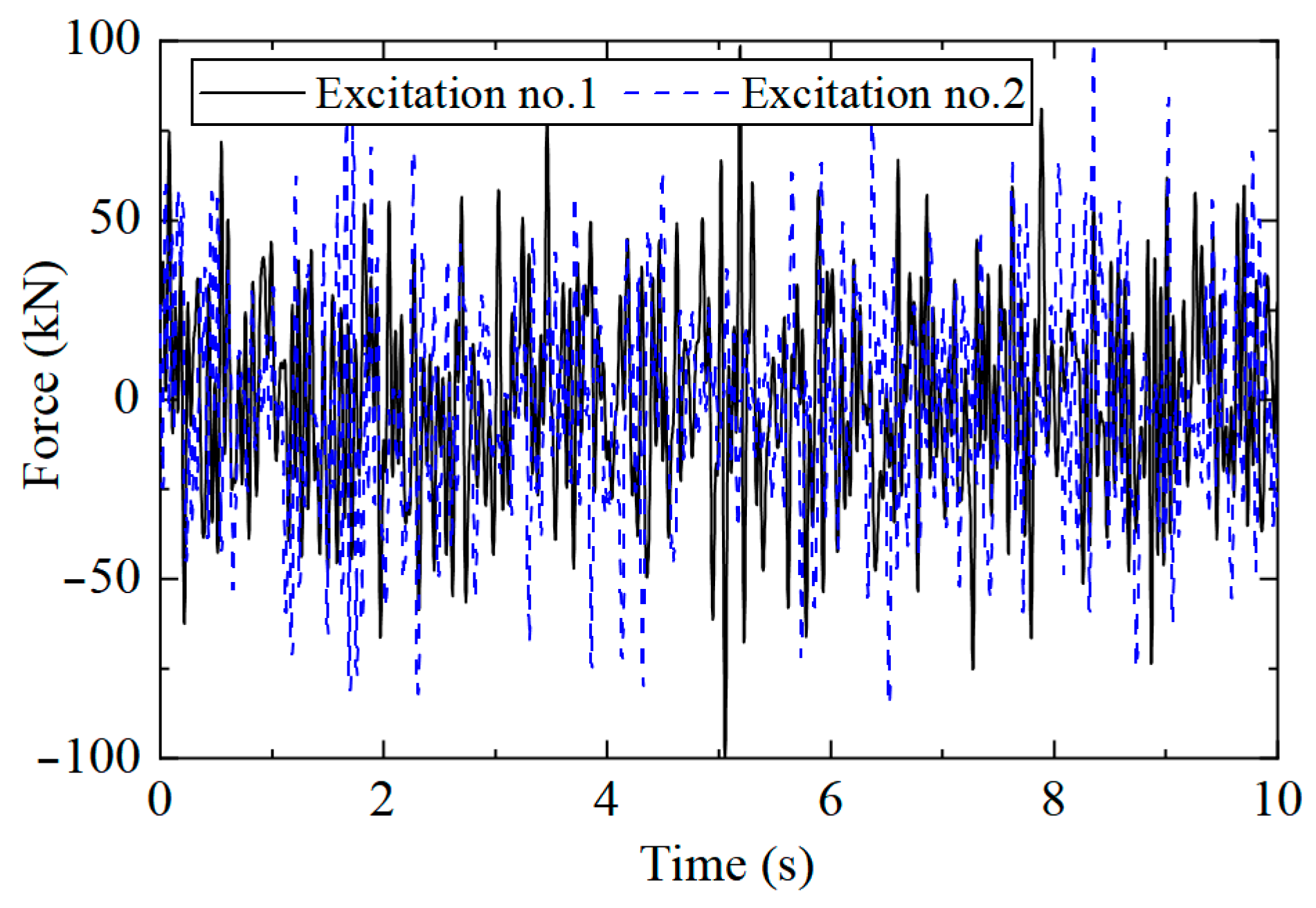
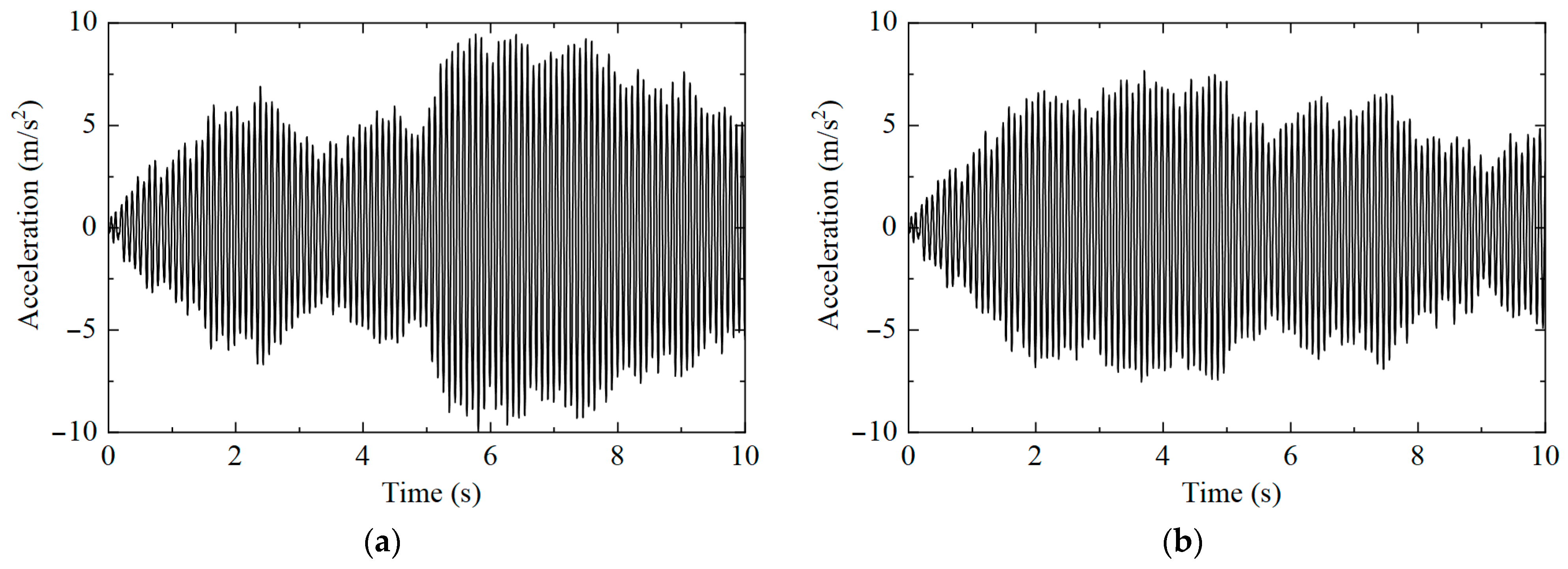

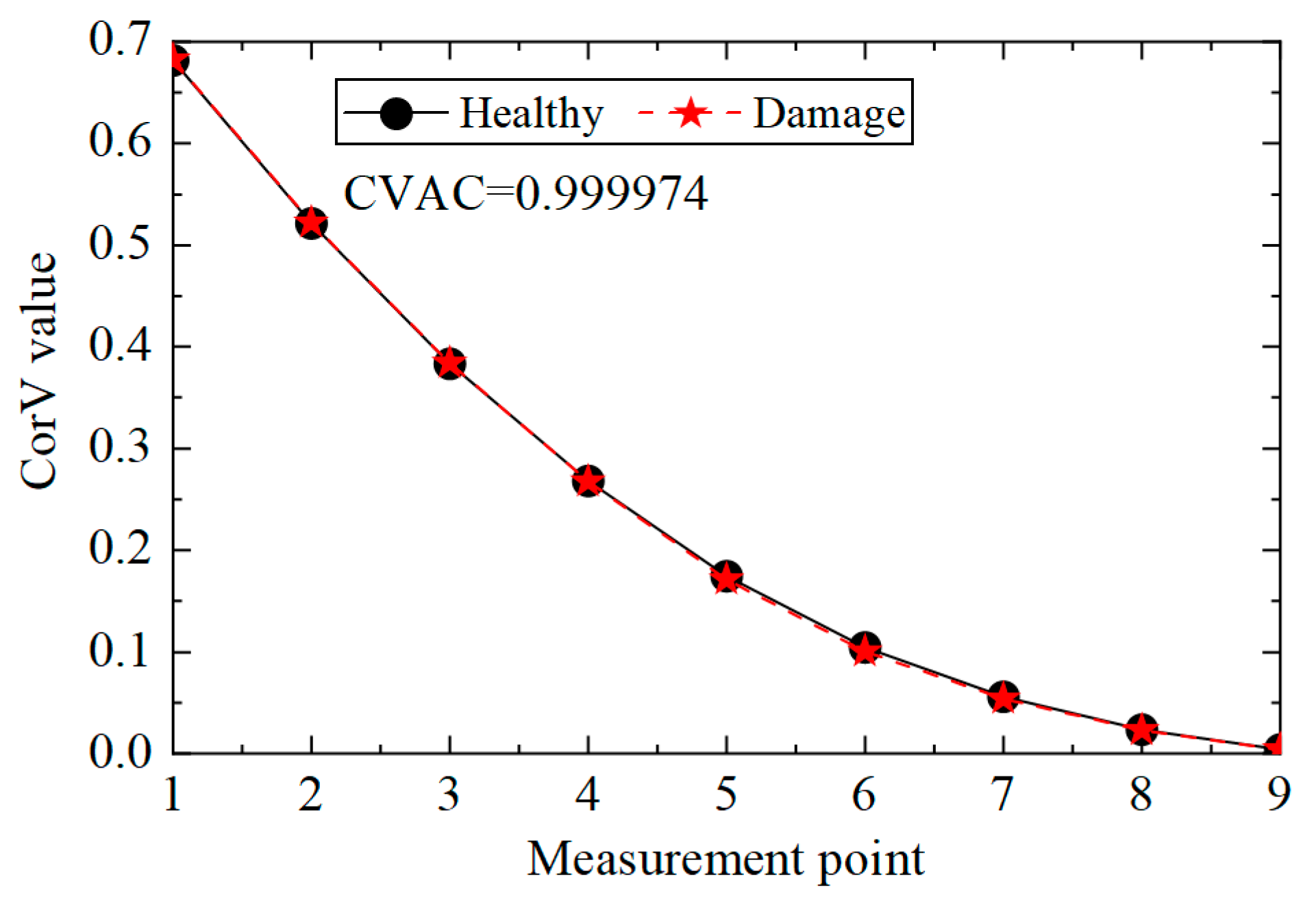
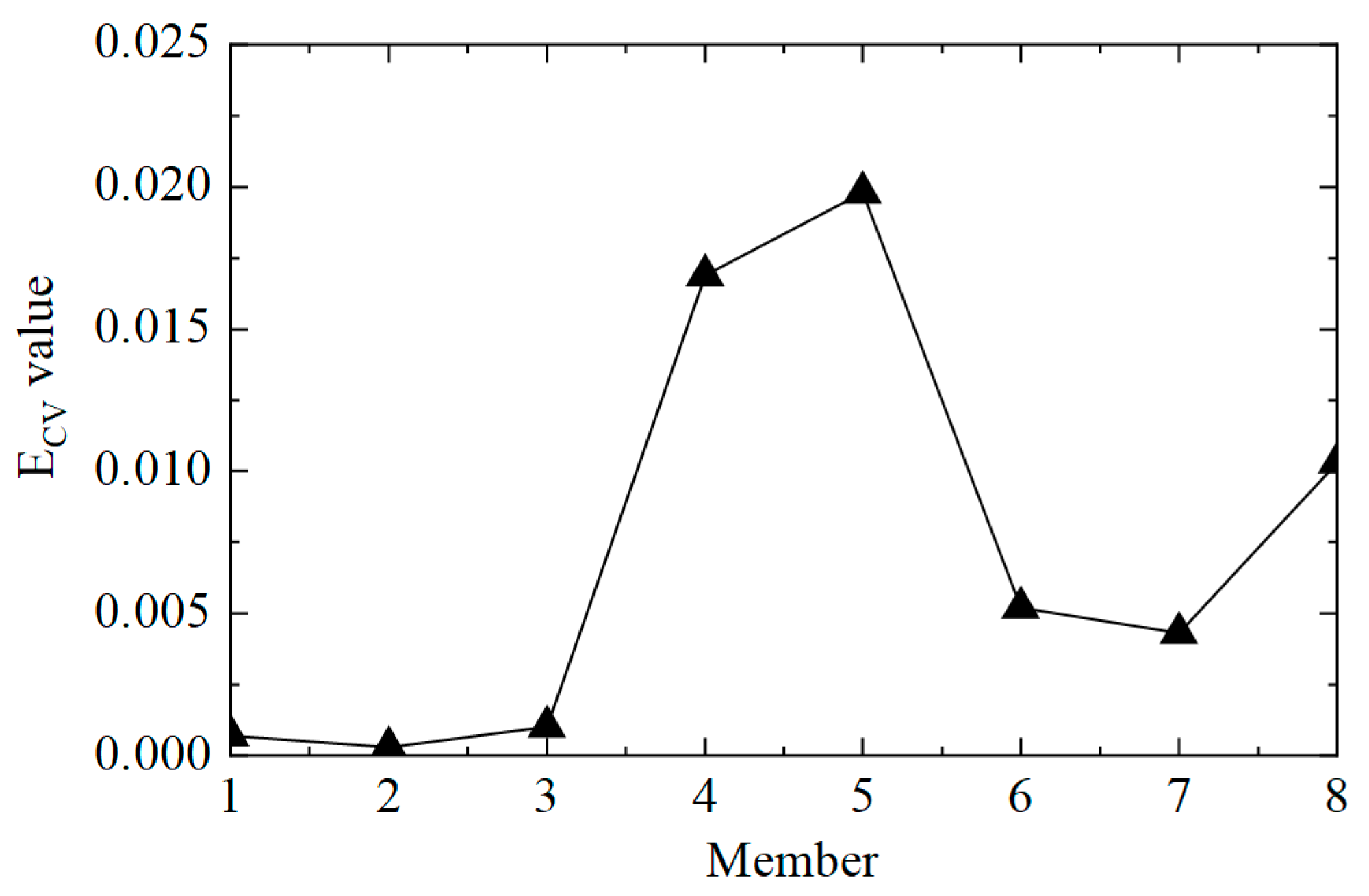
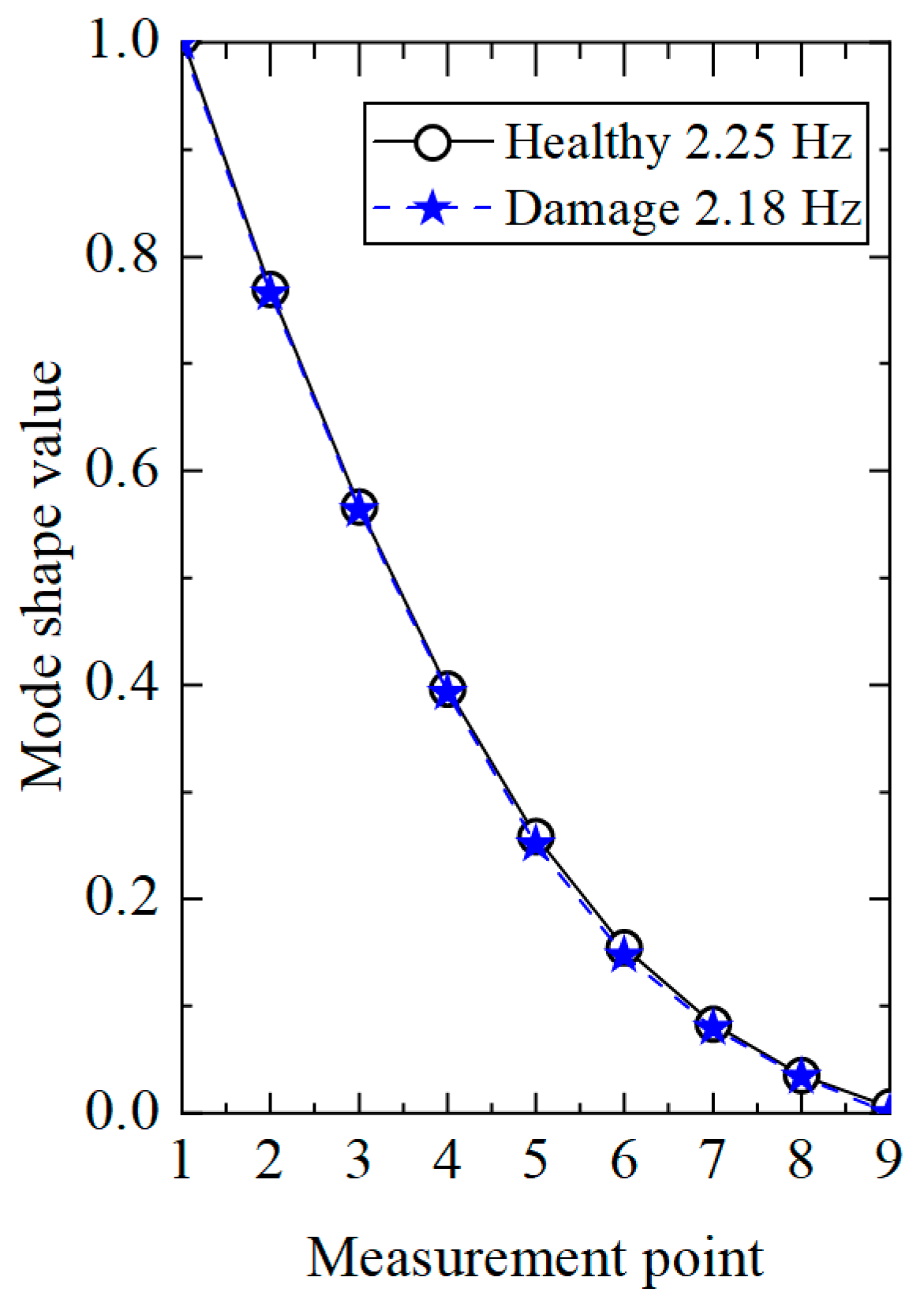
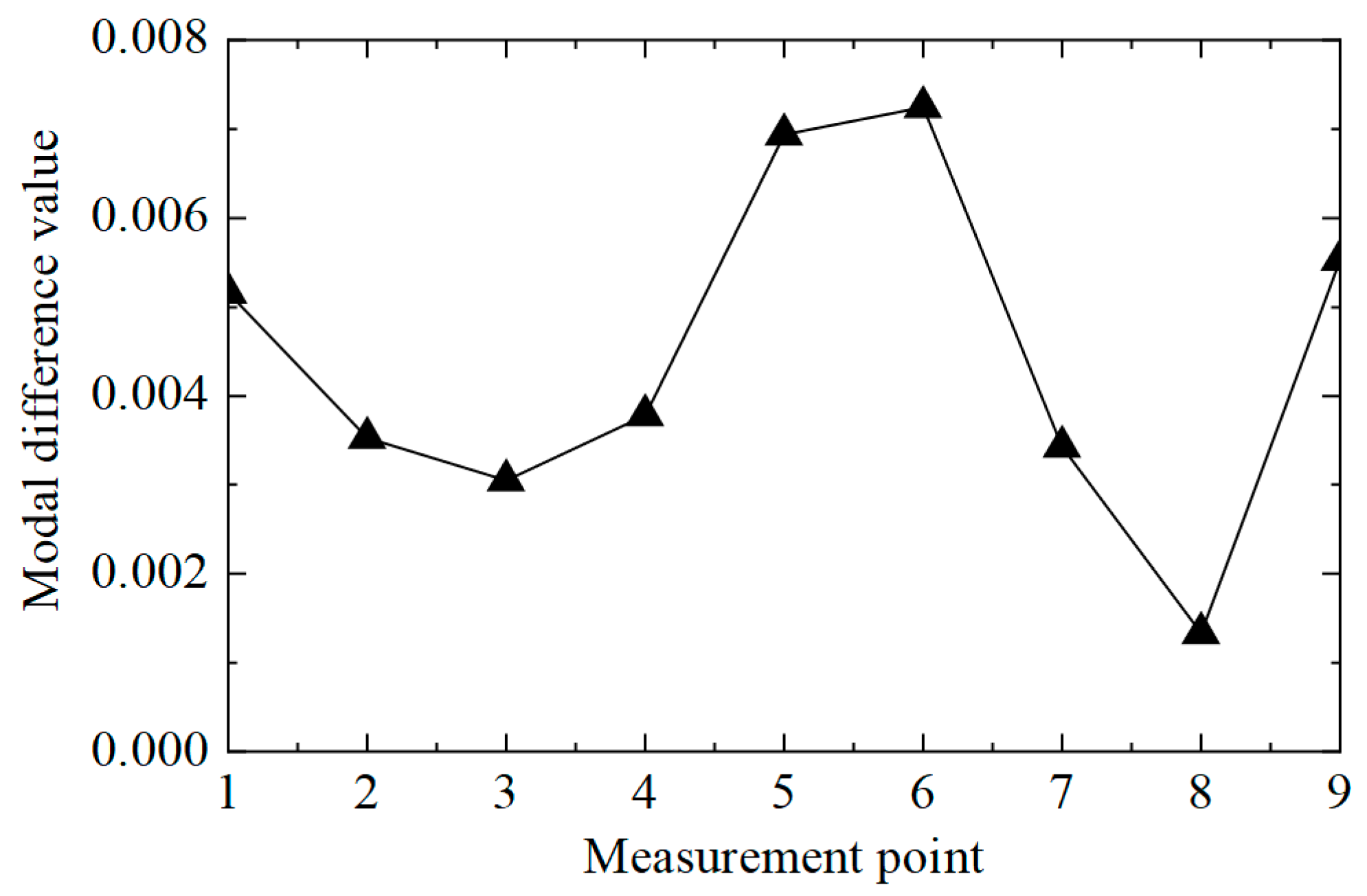
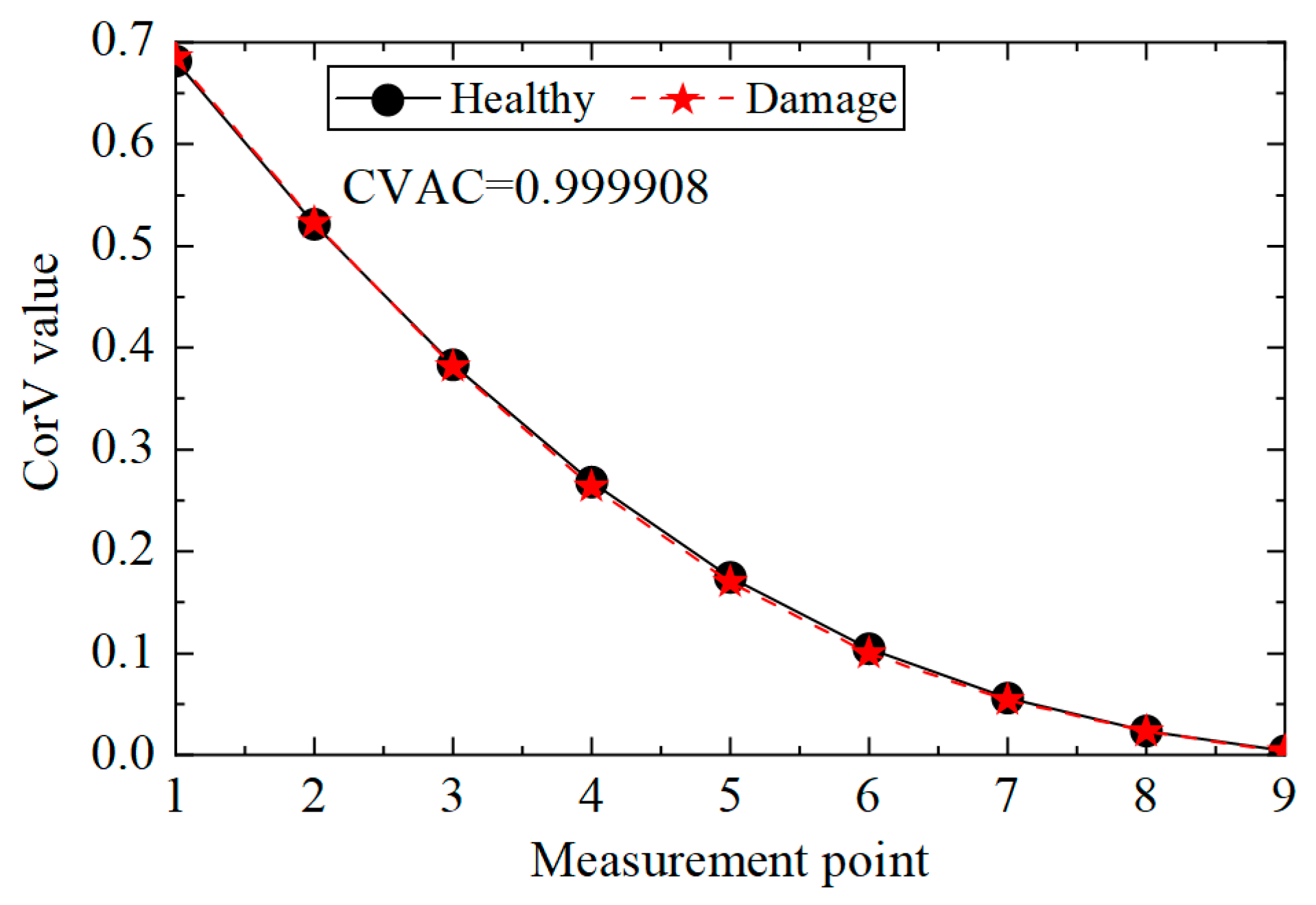

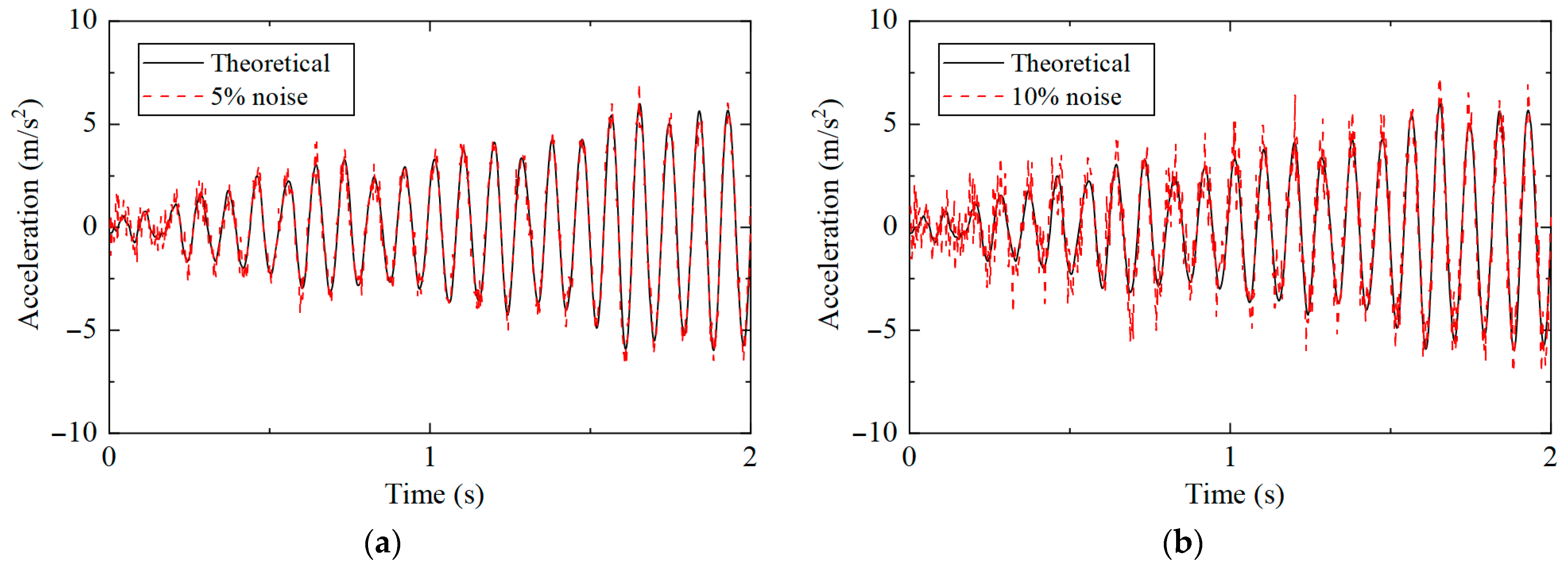

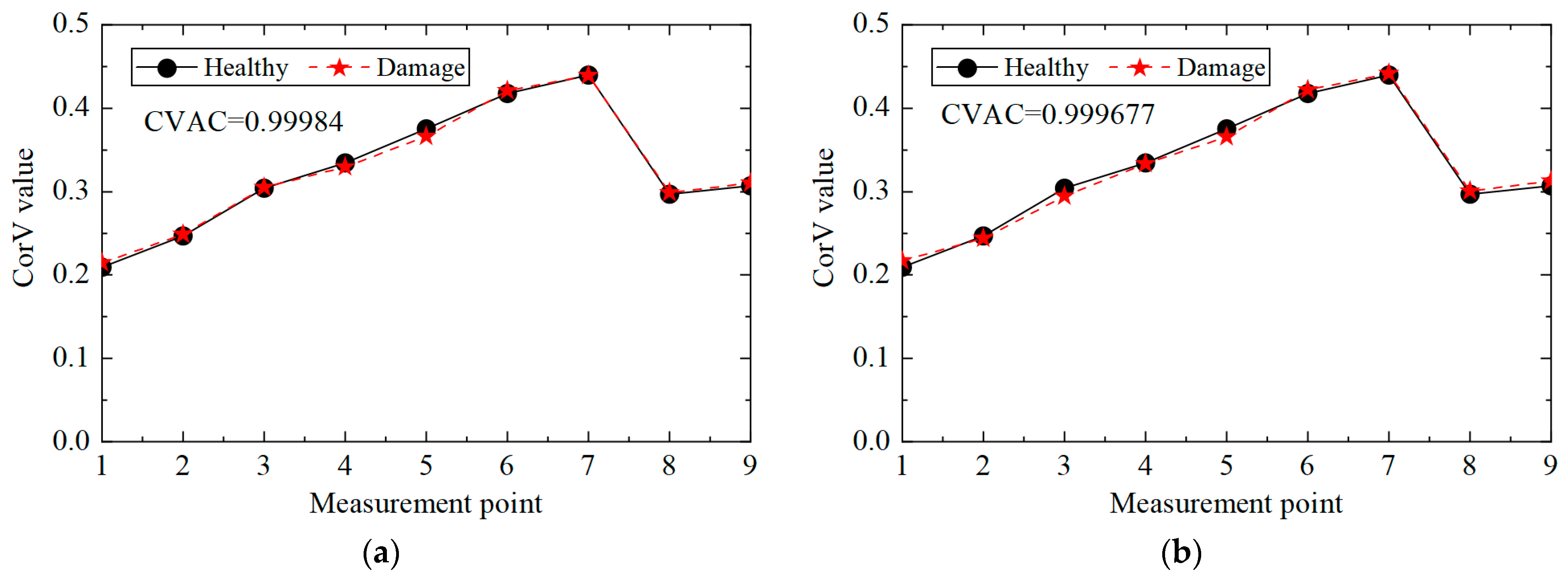


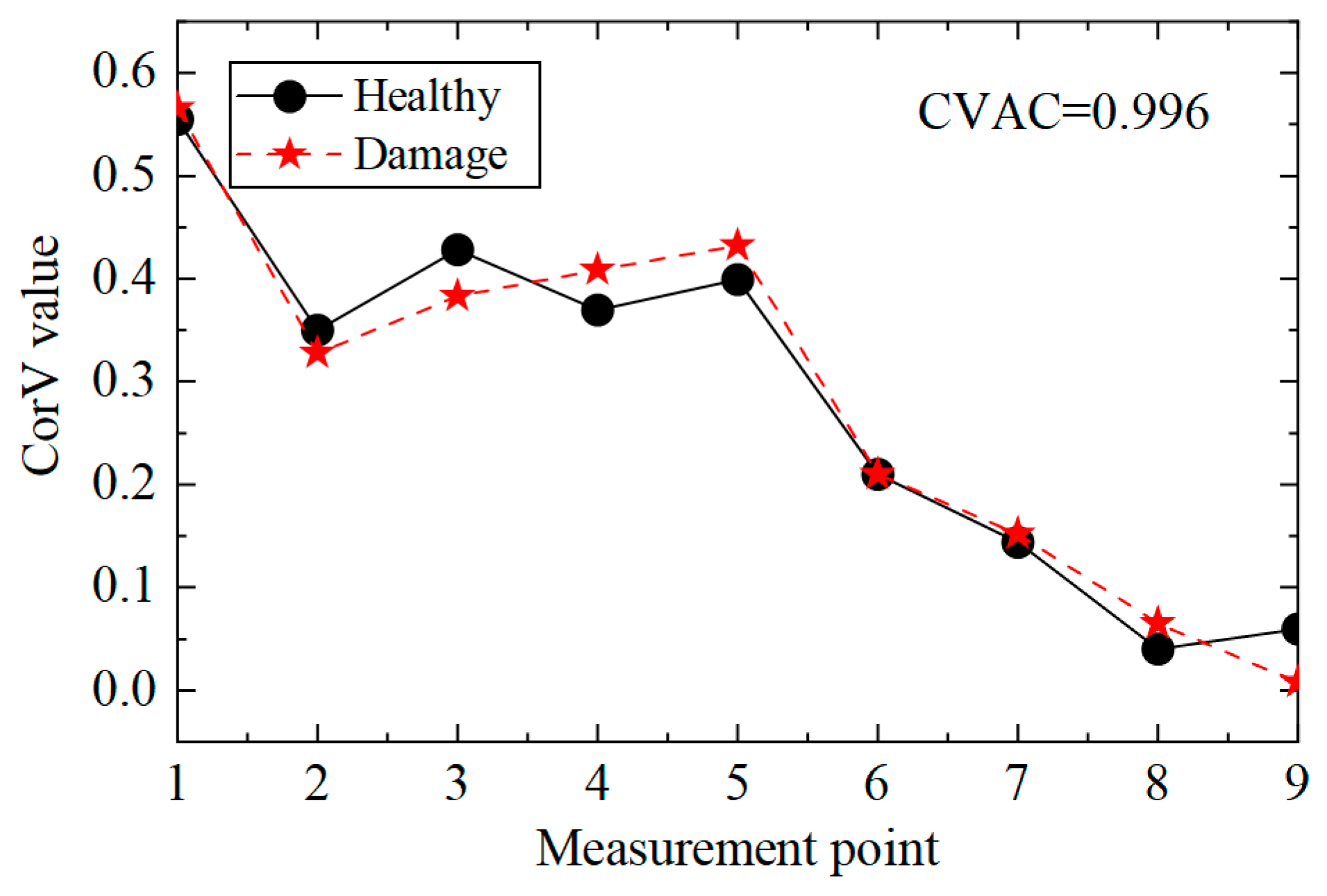
| Working Conditions | Structure Status |
|---|---|
| 1 | Healthy (two loads) |
| 2 | Element No. 5 damage (stiffness reduction of 50%, one excitation) |
| 3 | Damage to elements No. 3 and No. 5 (stiffness reduced by 50%, one excitation) |
| Measurement Point | Working Condition 1 | Working Condition 2 | Relative Change |
|---|---|---|---|
| 1 | 0.6816 | 0.6822 | 0.09% |
| 2 | 0.5212 | 0.5222 | 0.19% |
| 3 | 0.3834 | 0.3840 | 0.16% |
| 4 | 0.2679 | 0.2674 | 0.19% |
| 5 | 0.1745 | 0.1713 | 1.83% |
| 6 | 0.1044 | 0.1005 | 3.74% |
| 7 | 0.0557 | 0.0541 | 2.87% |
| 8 | 0.0235 | 0.0229 | 2.55% |
| 9 | 0.003744 | 0.003729 | 0.40% |
| Measurement Point | Working Condition 1 | Working Condition 3 | Relative Change |
|---|---|---|---|
| 1 | 0.6816 | 0.6852 | 0.53% |
| 2 | 0.5212 | 0.5229 | 0.34% |
| 3 | 0.3834 | 0.3814 | 0.53% |
| 4 | 0.2679 | 0.2636 | 1.60% |
| 5 | 0.1745 | 0.1695 | 2.88% |
| 6 | 0.1044 | 0.0997 | 4.49% |
| 7 | 0.0557 | 0.0536 | 3.76% |
| 8 | 0.0235 | 0.0227 | 3.11% |
| 9 | 0.003744 | 0.003649 | 2.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Fu, X.; Jiang, W.; Jin, H. Research on Damage Identification in Transmission Tower Structures Based on Cross-Correlation Function Amplitude Vector. Sensors 2025, 25, 4659. https://doi.org/10.3390/s25154659
Zhang Q, Fu X, Jiang W, Jin H. Research on Damage Identification in Transmission Tower Structures Based on Cross-Correlation Function Amplitude Vector. Sensors. 2025; 25(15):4659. https://doi.org/10.3390/s25154659
Chicago/Turabian StyleZhang, Qing, Xing Fu, Wenqiang Jiang, and Hengdong Jin. 2025. "Research on Damage Identification in Transmission Tower Structures Based on Cross-Correlation Function Amplitude Vector" Sensors 25, no. 15: 4659. https://doi.org/10.3390/s25154659
APA StyleZhang, Q., Fu, X., Jiang, W., & Jin, H. (2025). Research on Damage Identification in Transmission Tower Structures Based on Cross-Correlation Function Amplitude Vector. Sensors, 25(15), 4659. https://doi.org/10.3390/s25154659








