Development of Low-Cost Single-Chip Automotive 4D Millimeter-Wave Radar
Abstract
1. Introduction
- Cost Advantage: Millimeter-wave radar is more cost-effective than LiDAR, making it better suited for mass deployment in automotive and industrial applications.
- Environmental Adaptability: Unlike cameras, millimeter-wave radar operates independently of ambient light and maintains stable performance in complex weather conditions (e.g., fog, rain, snow).
- High Reliability: With robust anti-interference capability, millimeter-wave radar ensures consistent functionality even in electromagnetically noisy environments, such as urban areas with dense wireless signals.
- (1)
- Single-Chip Design: We propose a design scheme for a single-chip 4D millimeter-wave radar, realizing a low-cost and high-performance 4D radar system through a highly integrated hardware platform and an optimized sparse MIMO antenna array. We developed high-gain, low-sidelobe antenna arrays to enhance detection capability and anti-interference performance. This design breaks through the cost constraints of traditional multi-chip cascade solutions, offering the potential for large-scale commercial applications.
- (2)
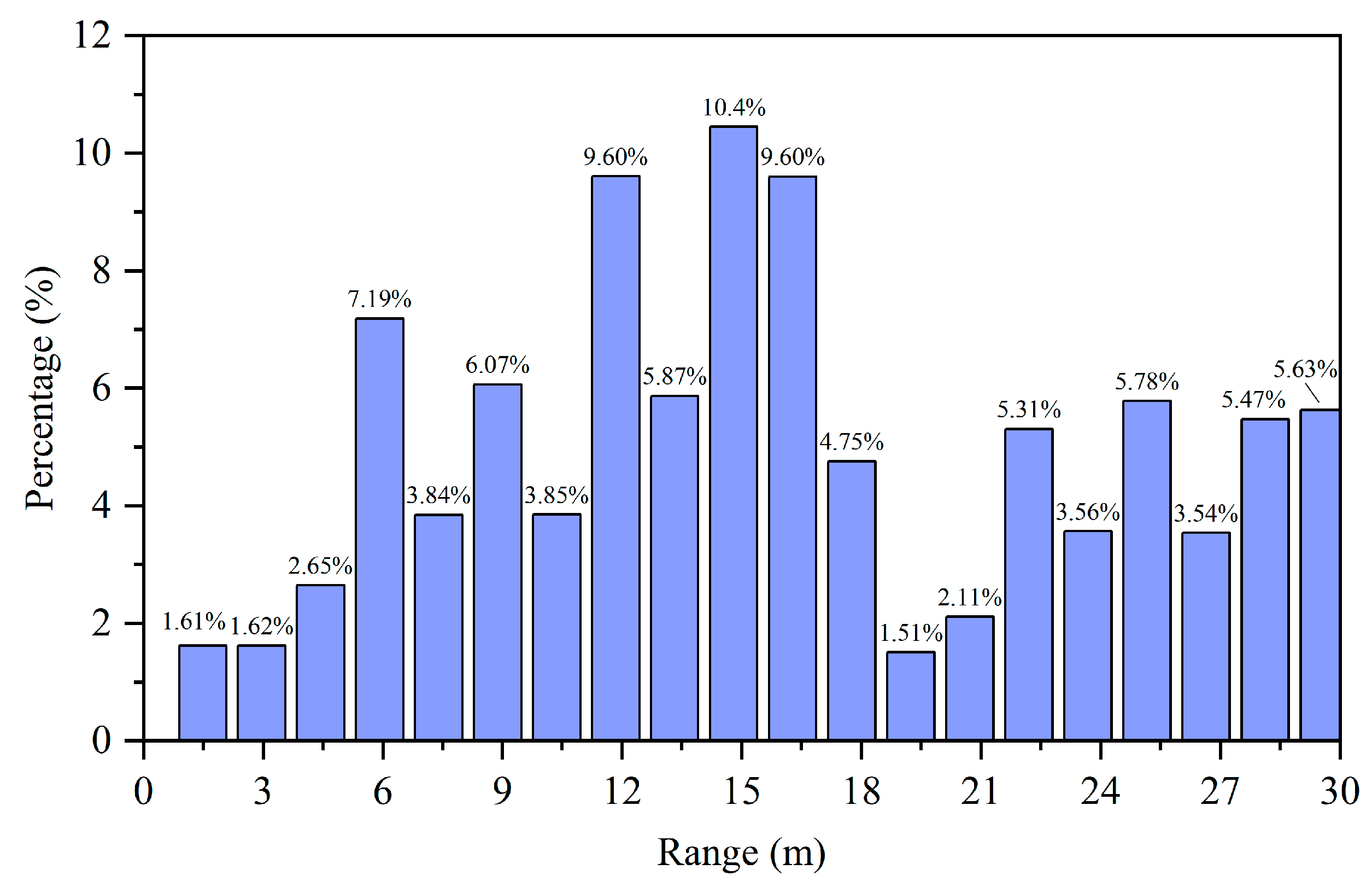
- Rain Clutter Identification: A rain clutter identification method based on the distribution characteristics of raindrops is proposed. By statistically analyzing the speed and distance distribution of raindrops, this method effectively distinguishes between raindrops and real targets, thereby reducing the interference of rain clutter on radar detection.
- (3)
- Noise Point Suppression: A noise-suppression method based on angular FFT peak-amplitude variance is proposed. By designing an effective strategy, this approach suppresses noise point interference while preserving true targets, thereby enhancing radar target-detection stability in complex environments.
2. Radar System Hardware Platform and Beam Design
- (1)
- RF and Signal Processing Circuit
- (2)
- Power Management Circuit
- (3)
- CAN Transceiver Circuit
- (4)
- Peripheral Storage Circuit
3. Signal Processing
3.1. FMCW Radar Signal Processing and Angle Accuracy
- Formation of the horizontal and elevation arrays;
- Derivation methodology for target azimuth and elevation angles.
3.2. Clutter Suppression
3.2.1. Mitigation and Avoidance of Rain Clutter Interference
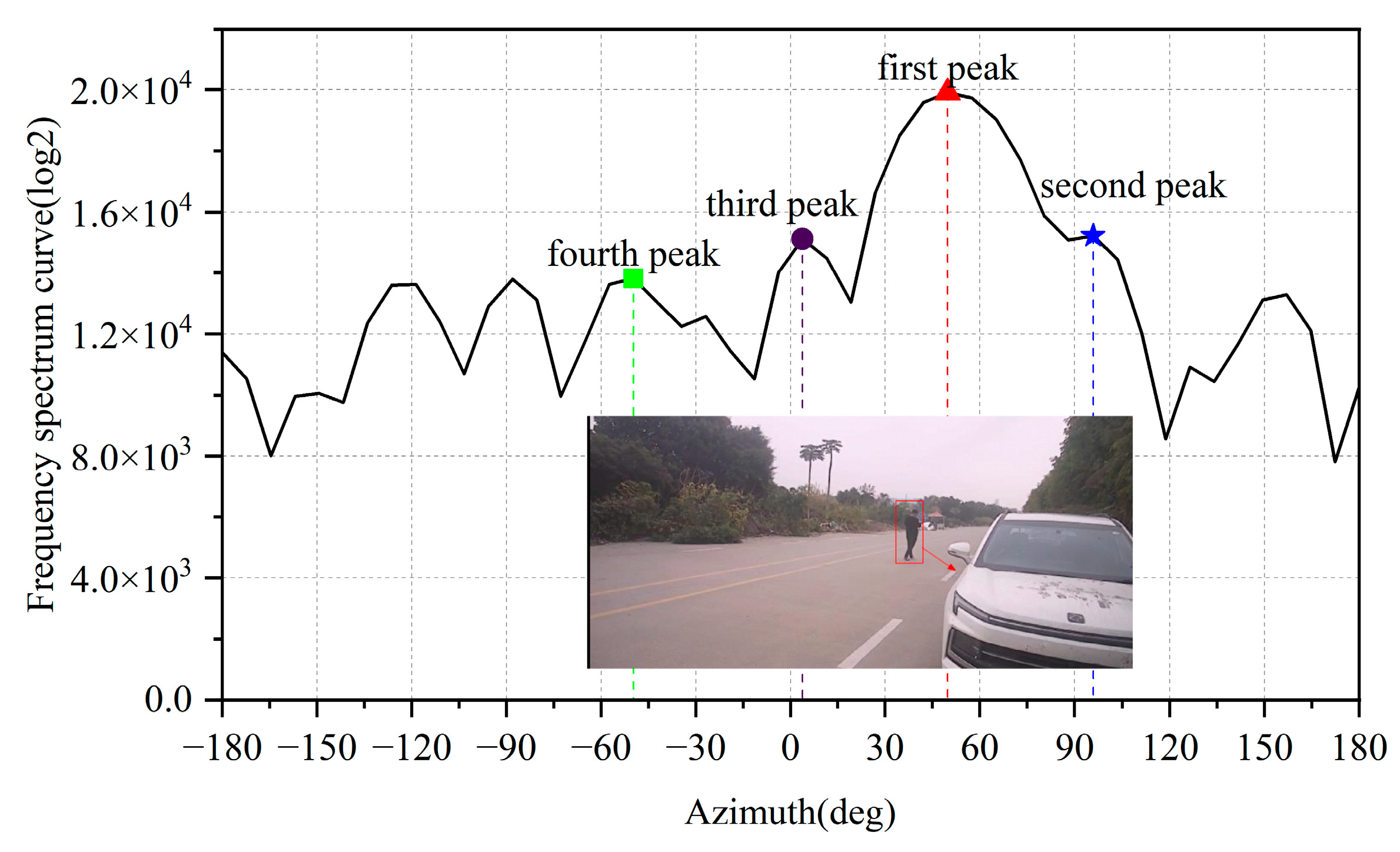
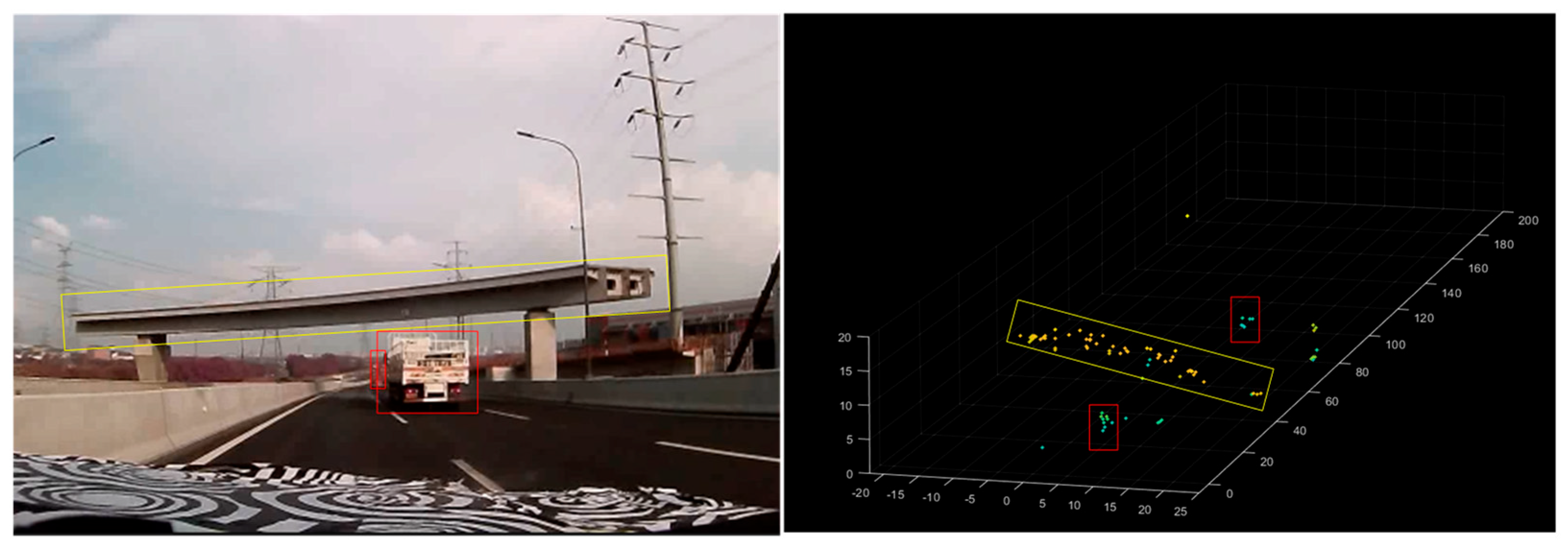
3.2.2. Noise Point Elimination Method in Complex Environments
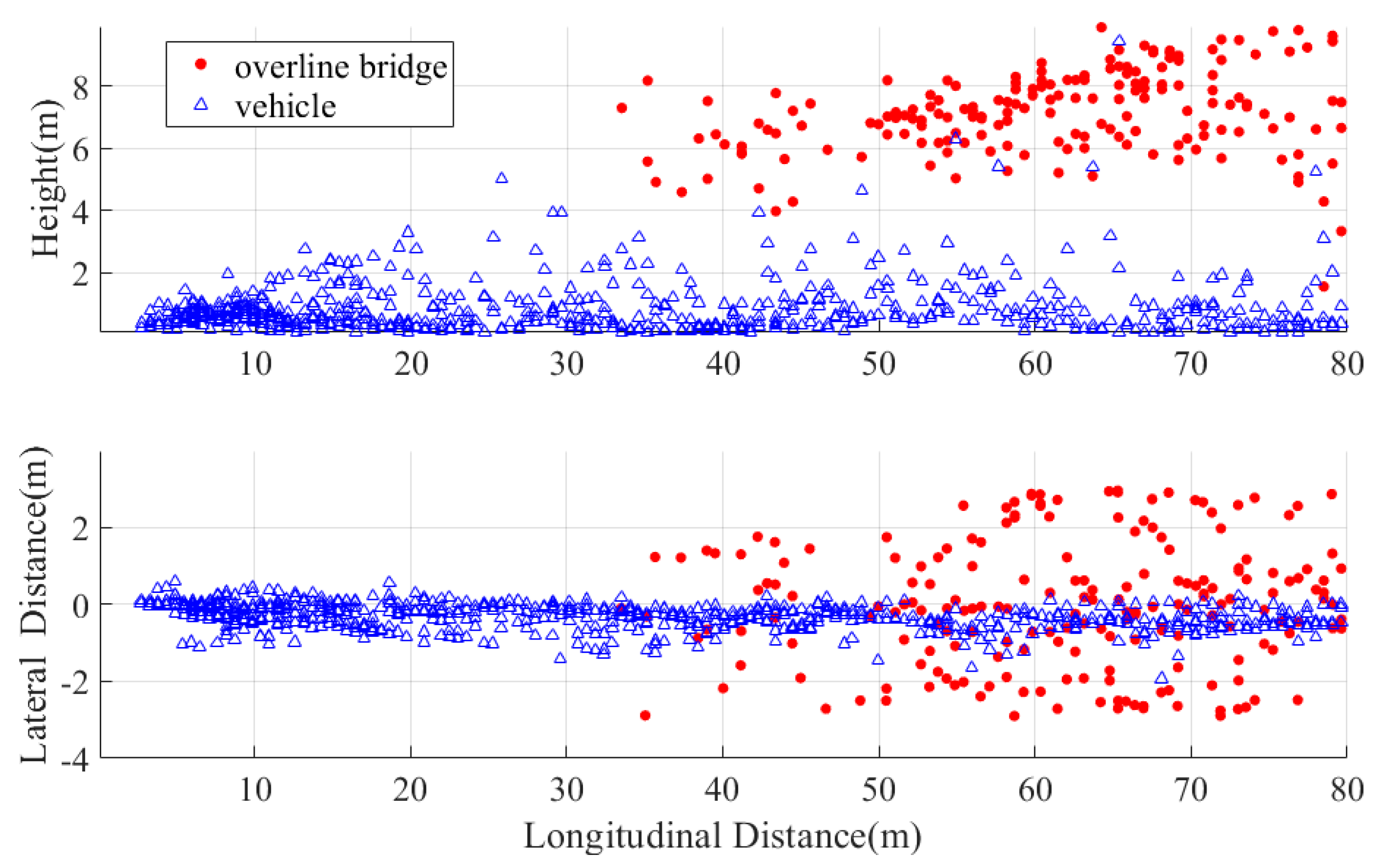
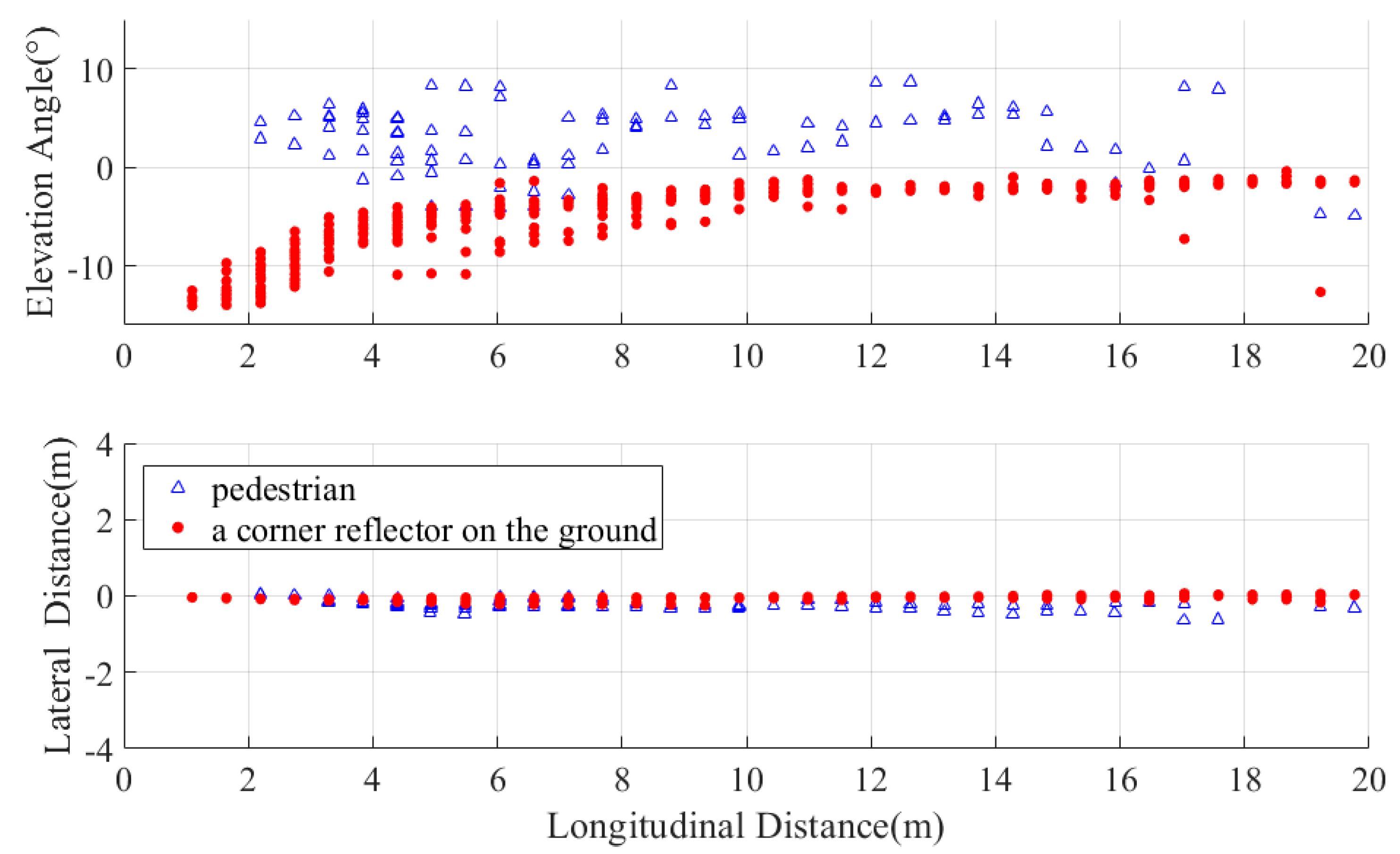
- Targets of interest: Electric two-wheelers and automobiles;
- Undesired interference sources: Ground clutter, multipath reflections, and vegetation-induced noise points.
- Identification rate of unwanted noise points;
- Misidentification probability of valid targets.
- Zone 1: Valid two-wheeler targets;
- Zone 2: Multipath reflections from roadside vegetation edges;
- Zone 3: Ground clutter-induced noise points.
- >70% ground clutter rejection rate;
- ~90% vehicle multipath detection accuracy;
- <5% false identification rate for legitimate targets.
4. Radar Performance Test
5. Discussion
- (1)
- Chip cascade technology, exemplified by the AWR2243 chip cascade scheme from Texas Instruments (TI), features a single chip equipped with three transmitters (TX) and four receivers (RX). By cascading four chips, a configuration of 12 TX and 16 RX is achieved, resulting in a total of 192 virtual channels.
- (2)
- A single-chip design enables the transmission and reception of multiple signals on a single chip. A notable example is Arbe’s chipset, which can be expanded to accommodate 48 transmitters (TX) and 48 receivers (RX), generating a total of 2304 virtual channels. In contrast, the radar-on-chip solution from the US company Uhnder utilizes a 12 TX/8 RX configuration, capable of forming 96 virtual channels.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hakobyan, G.; Yang, B. High-Performance Automotive Radar: A Review of Signal Processing Algorithms and Modulation Schemes. IEEE Signal Process. Mag. 2019, 36, 32–44. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Y.D. 4D Automotive Radar Sensing for Autonomous Vehicles: A Sparsity-Oriented Approach. IEEE J. Sel. Top. Signal Process. 2021, 15, 879–891. [Google Scholar] [CrossRef]
- Li, G.; Sit, Y.L.; Manchala, S.; Kettner, T.; Ossowska, A.; Krupinski, K.; Sturm, C.; Goerner, S.; Lübbert, U. Pioneer Study on Near-Range Sensing with 4D MIMO-FMCW Automotive Radars. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019. [Google Scholar]
- Abdullah, H.; Mabrouk, M.; Kabeel, A.E.; Hussein, A. High-Resolution and Large-Detection-Range Virtual Antenna Array for Automotive Radar Applications. Sensors 2021, 21, 1702. [Google Scholar] [CrossRef] [PubMed]
- Paek, D.H.; Kong, S.H.; Wijaya, K.T. K-radar: 4d radar object detection for autonomous driving in various weather conditions. Adv. Neural Inform. Process. Syst. 2022, 35, 3819–3829. [Google Scholar]
- Choi, M.; Yang, S.; Han, S.; Lee, M.; Choi, K.H.; Kim, K.S. MSC-RAD4R: ROS-Based Automotive Dataset With 4D Radar. IEEE Robot. Autom. Lett. 2024, 8, 3307005. [Google Scholar] [CrossRef]
- Kronauge, M.; Rohling, H. New chirp sequence radar waveform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2870–2877. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Yang, Q.; Fu, S. Signal Processing for TDM MIMO FMCW Millimeter-Wave Radar Sensors. IEEE Access 2021, 9, 167959–167971. [Google Scholar] [CrossRef]
- Stove, A.G. Modern FMCW radar-techniques and applications. In Proceedings of the First European Radar Conference, Amsterdam, The Netherlands, 14–15 October 2004. [Google Scholar]
- Lin, J.J.; Li, Y.P.; Hsu, W.C.; Lee, T.S. Design of an FMCW radar baseband signal processing system for automotive application. SpringerPlus 2016, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Roberts, I.P. Advancements in Millimeter-Wave Radar Technologies for Automotive Systems: A Signal Processing Perspective. Electronics 2025, 14, 1436. [Google Scholar] [CrossRef]
- Waldschmidt, C.; Hasch, J.; Menzel, W. Automotive Radar-From First Efforts to Future Systems. IEEE J. Microw. 2021, 1, 135–148. [Google Scholar] [CrossRef]
- Vasanelli, C.; Batra, R.; Di, Serio, A.; Boegelsack, F.; Waldschmidt, C. Assessment of a millimeter-wave antenna system for MIMO radar applications. IEEE Antennas Wirel. Propag. Lett. 2016, 16, 1261–1264. [Google Scholar] [CrossRef]
- Steinhauser, D.; Held, P.; Thöresz, B.; Brandmeier, T. Towards safe autonomous driving: Challenges of pedestrian detection in rain with automotive rada. In Proceedings of the 17th European Radar Conference (EuRAD 2020), Utrecht, The Netherlands, 13–15 January 2021. [Google Scholar]
- Jang, B.J.; Jung, I.T.; Chong, K.S.; Lim, S. Rainfall observation system using automotive radar sensor for ADAS based driving safety. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Li, H.; Bamminger, N.; Magosi, Z.F.; Feichtinger, C.; Zhao, Y.; Mihalj, T.; Orucevic, F.; Eichberger, A. The effect of rainfall and illumination on automotive sensors detection performance. Sustainability 2023, 15, 7260. [Google Scholar] [CrossRef]
- Ong, C.R.; Miura, H.; Koike, M. The terminal velocity of axisymmetric cloud drops and raindrops evaluated by the immersed boundary method. J. Atmos. Sci. 2021, 78, 1129–1146. [Google Scholar] [CrossRef]
- Montero-Martínez, G.; García-García, F. On the behaviour of raindrop fall speed due to wind. Q. J. R. Meteorol. Soc. 2016, 142, 2013–2020. [Google Scholar] [CrossRef]
- Tan, B.; Ma, Z.; Zhu, X.; Huang, L.; Bai, J. Tracking of multiple static and dynamic targets for 4D automotive millimeter-wave radar point cloud in urban environments. Remote Sens. 2023, 15, 2923. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, L.; Zhao, H.; López-Benítez, M.; Yu, L.; Yue, Y. Towards deep radar perception for autonomous driving: Datasets, methods, and challenges. Sensors 2022, 22, 4208. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, N.; Kraus, F.; Appenrodt, N.; Dickmann, J.; Sick, B. Object detection for automotive radar point clouds—A comparison. AI Perspect. Adv. 2021, 3, 6. [Google Scholar] [CrossRef]
- Alland, S.; Stark, W.; Ali, M.; Hegde, M. Interference in automotive radar systems: Characteristics, mitigation techniques, and current and future research. IEEE Signal Process. Mag. 2019, 36, 45–59. [Google Scholar] [CrossRef]
- Tavanti, E.; Rizik, A.; Fedeli, A.; Caviglia, D.D.; Randazzo, A. A short-range FMCW radar-based approach for multi-target human-vehicle detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]







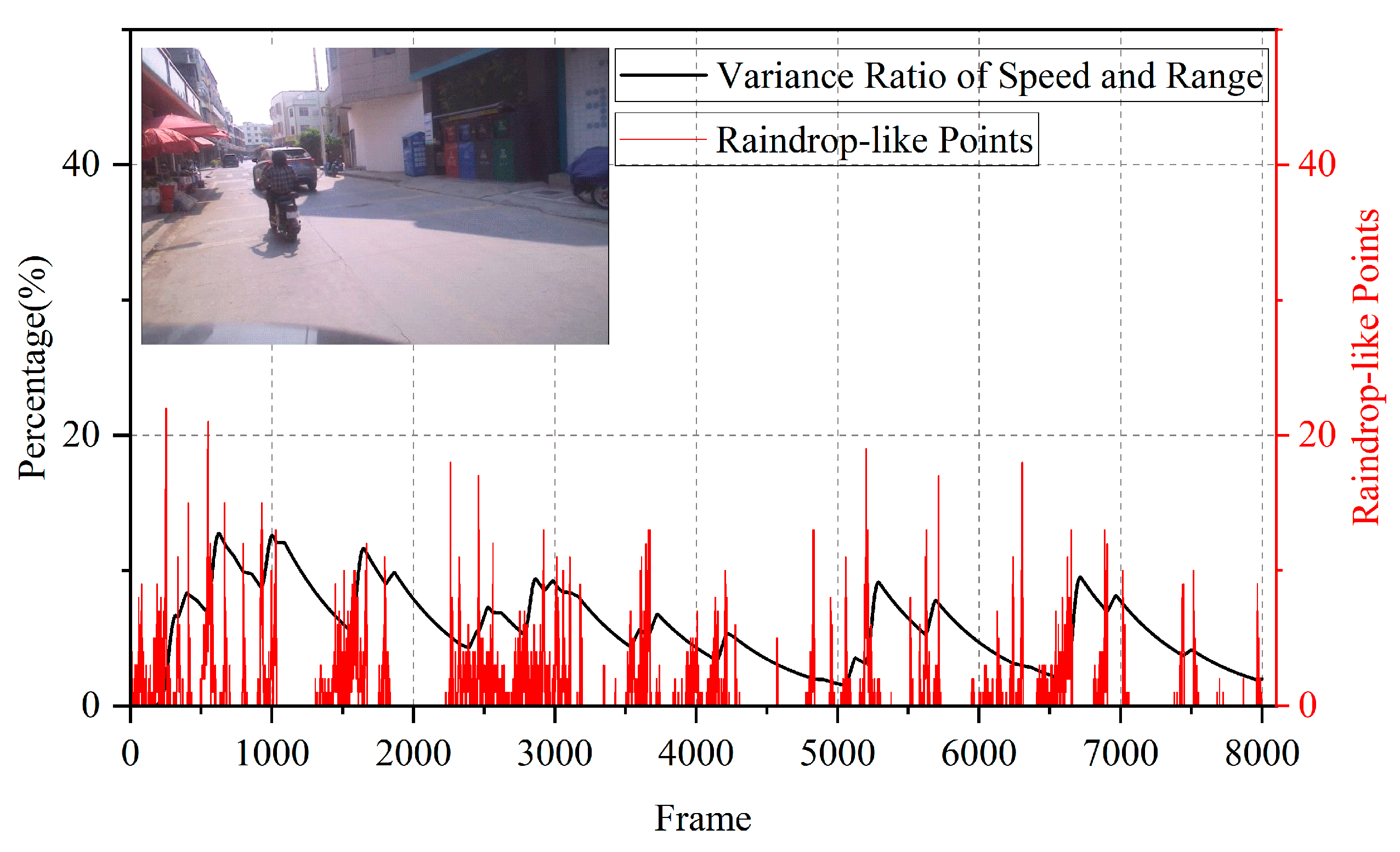





| Normal Point Clouds | Noise Point Clouds | ||
|---|---|---|---|
| Δp1-2 | 2548 | Δp1-2 | 521 |
| Δp1-3 | 2944 | Δp1-3 | 736 |
| Δp1-4 | 3560 | Δp1-4 | 832 |
| Target | Number of Tests | Total Points | Marked Points | Recognition Rate (%) | Average Recognition Rate (%) |
|---|---|---|---|---|---|
| Pedestrian | first | 164 | 3 | 1.83 | 3.65 |
| second | 204 | 13 | 6.37 | ||
| third | 182 | 5 | 2.75 | ||
| Car | first | 415 | 29 | 6.99 | 5.19 |
| second | 520 | 22 | 4.23 | ||
| third | 322 | 14 | 4.35 | ||
| Two-wheel cart | first | 322 | 10 | 3.11 | 3.66 |
| second | 432 | 21 | 4.86 | ||
| third | 332 | 10 | 3.01 |
| Target | Number of Tests | Total Points | Marked Points | Recognition Rate (%) | Average Recognition Rate (%) |
|---|---|---|---|---|---|
| Multipath points caused by cars | first | 62 | 56 | 90.32 | 87.60 |
| second | 56 | 48 | 85.71 | ||
| third | 68 | 59 | 86.76 | ||
| Ground clutter | first | 288 | 201 | 69.79 | 73.41 |
| second | 304 | 230 | 75.66 | ||
| third | 321 | 240 | 74.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Bai, J.; Shen, H.-L.; Huang, L.; Rao, B.; Wang, H. Development of Low-Cost Single-Chip Automotive 4D Millimeter-Wave Radar. Sensors 2025, 25, 4640. https://doi.org/10.3390/s25154640
Cai Y, Bai J, Shen H-L, Huang L, Rao B, Wang H. Development of Low-Cost Single-Chip Automotive 4D Millimeter-Wave Radar. Sensors. 2025; 25(15):4640. https://doi.org/10.3390/s25154640
Chicago/Turabian StyleCai, Yongjun, Jie Bai, Hui-Liang Shen, Libo Huang, Bing Rao, and Haiyang Wang. 2025. "Development of Low-Cost Single-Chip Automotive 4D Millimeter-Wave Radar" Sensors 25, no. 15: 4640. https://doi.org/10.3390/s25154640
APA StyleCai, Y., Bai, J., Shen, H.-L., Huang, L., Rao, B., & Wang, H. (2025). Development of Low-Cost Single-Chip Automotive 4D Millimeter-Wave Radar. Sensors, 25(15), 4640. https://doi.org/10.3390/s25154640







