Highly Accelerated Dual-Pose Medical Image Registration via Improved Differential Evolution
Abstract
1. Introduction
- (1)
- Dual-Pose Strategy for Dimensional Accuracy: To tackle the issue of significant errors in specific dimensions, we introduce a dual-pose strategy for medical image registration. Utilizing the prior DRR image from the frontal pose, which is derived from the single-posture image, we generate the DRR image for the lateral pose by amalgamating the transformation matrix employed for lateral pose conversion. This approach offers a novel perspective to validate the registration accuracy of the single-posture stance from a different viewpoint, effectively rectifying biases in specific dimensions.
- (2)
- Composite Similarity Measure for Fuzzy Image Challenges: To mitigate the interference from fuzzy images during registration, we design a composite similarity measure. This measure aims to precisely compute the composite similarity between the frontal–lateral posture DRR image and the X-ray image using contour-based similarity metrics, ensuring accurate registration.
- (3)
- Phased Differential Evolution (PDE) for Optimal Results: Addressing the propensity of the registration outcome to converge to local optima, we propose a Phased Differential Evolution (PDE) optimization algorithm. This iterative approach refines the objective function, continuously calculating the composite similarity between the frontal–lateral posture DRR image and the X-ray image to achieve optimal registration results.
- (4)
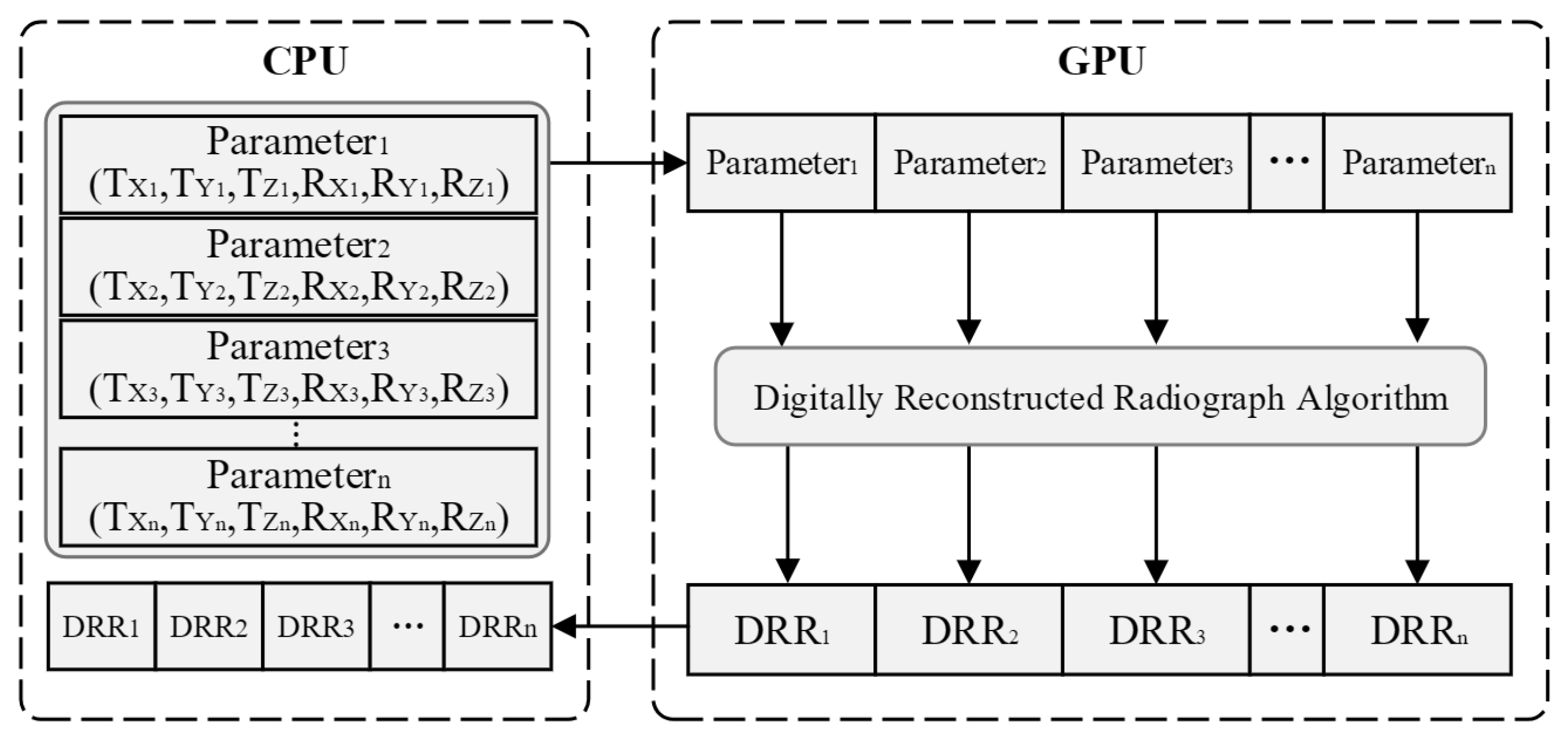
- Efficiency Enhancement via GPU-Accelerated Parallel Computation: To expedite the registration process, we employ multi-threaded parallel computation leveraging Graphics Processing Units (GPUs). This significantly boosts the efficiency of DRR image generation and minimizes data transmission overheads during the registration procedure.
2. Method
- (1)
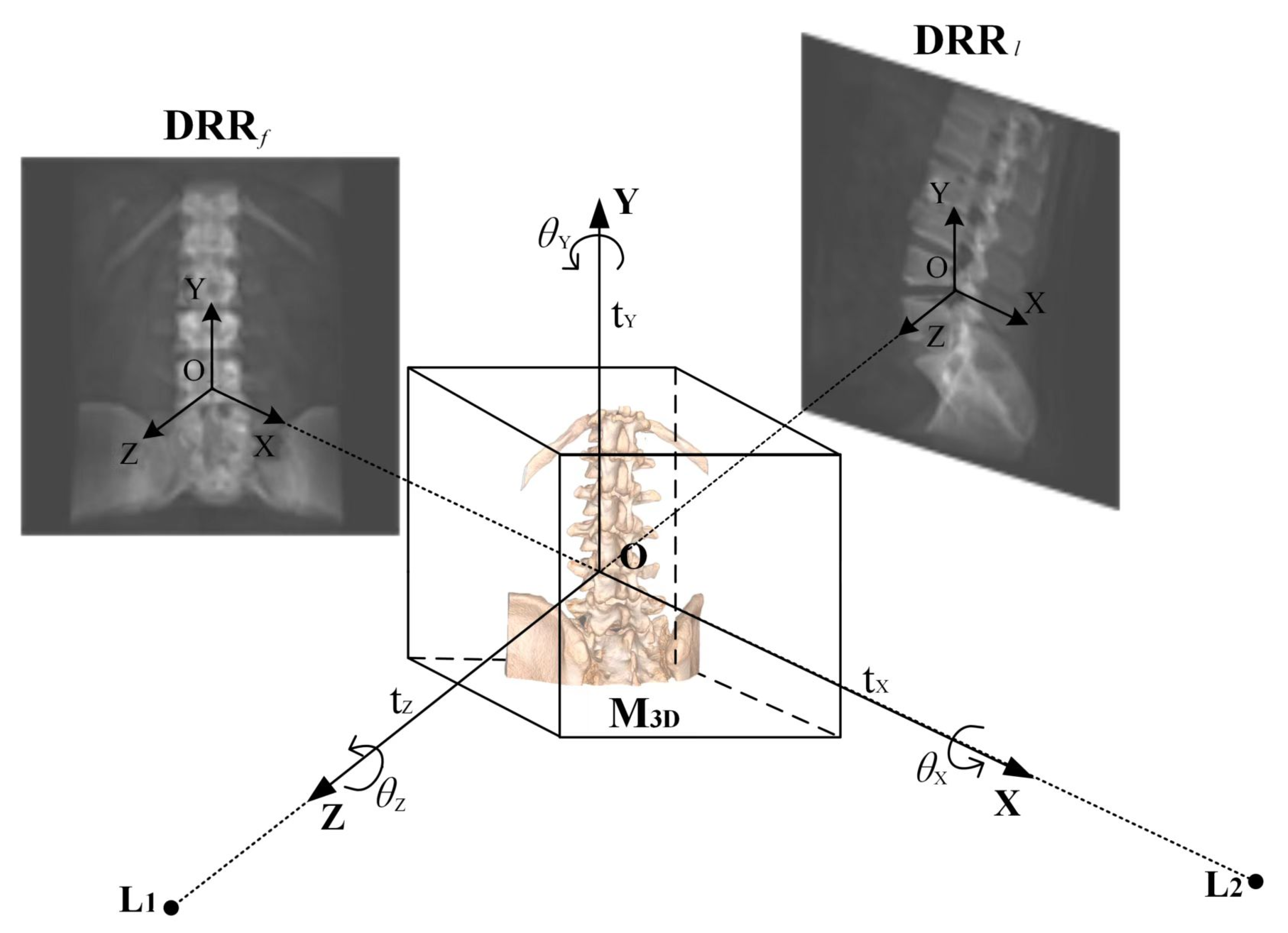
- Acquisition of Reference Image Data: In contrast to traditional single-posture registration algorithms, this step involves acquiring X-ray image information from two frontal–lateral positions.
- (2)
- Generation of Frontal and Lateral DRR Images: After identifying the six-degree-of-freedom parameters of the initial pose through manual registration, DRR images for frontal and lateral poses are obtained. Utilizing the transformation matrix (LateralMat) for lateral pose projection, GPU parallel processing accelerates the rendering process to generate the DRR images.
- (3)
- Similarity Measure Calculation: Contour information is extracted from both the reference image and the floating image. The composite similarity between the DRR image and the reference image under the dual-pose configuration is then calculated.
- (4)
- Optimization Algorithm for Parameter Tuning: An optimization algorithm is employed to find the optimal parameters by identifying the smallest or largest value of the objective function.
3. A Dual-Pose Medical Image Registration Algorithm Based on Improved Differential Evolution
3.1. Acquisition of DRR in the Frontal and Lateral Positions
3.2. Digitally Reconstructed Radiograph Imaging Based on GPU Parallel Acceleration
3.3. Similarity Measure
| Algorithm 1. Similarity measure based on contour points. |
| : Number of contour point pixels |
| : Coordinates of the contour points of the reference image |
| : Coordinates of the contour points in the image to be registered |
| 1: Preprocessing of images to remove noise |
| 2: Computing image contour images using the Canny operator |
| 3: Calculating similarity: |
| for = 1 : do: |
| if = |
| Calculate the number of contour points in the region counted in |
| Construct |
| Construct |
| End(for) |
| Similarity |
| Return: Similarity |
| End |
3.4. Composite Similarity
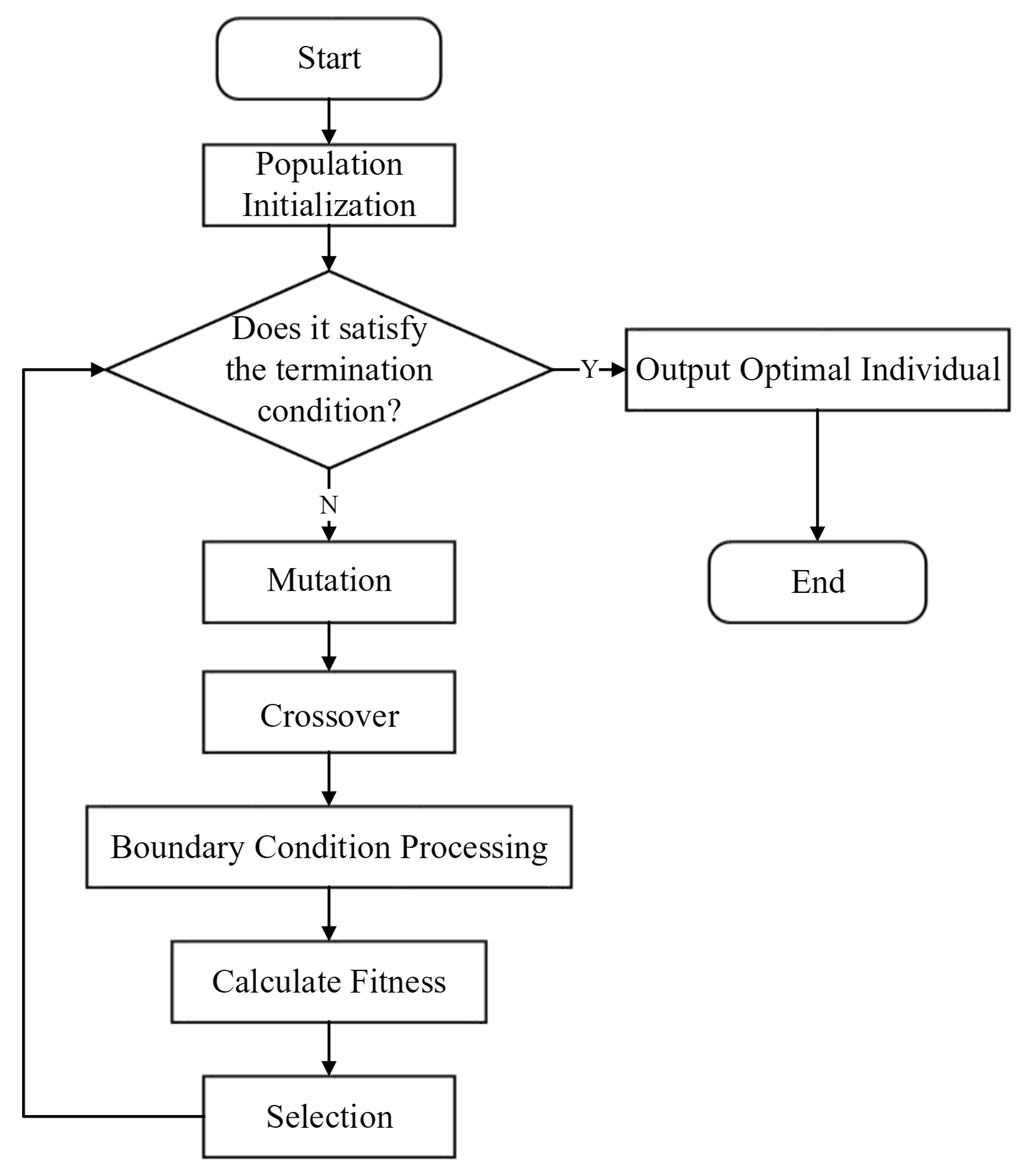
3.5. Intelligent Optimization Algorithm
3.5.1. Population Initialization
3.5.2. Mutation
3.5.3. Crossover
3.5.4. Selection
| Algorithm 2. Improved Differential Evolution. |
| : Population size |
| : Dimension of solution space |
| : Objective function (to be minimized) |
| : Search bounds |
| : Maximum number of generations |
| : Crossover probability |
| : Scaling factor (0.5 for first half, 0.8 for second half) |
| 1: Initialize population randomly within bounds |
| 2: Compute fitness values for all individuals |
| 3: Set initial optimal solution , |
| 4: Set generation counter |
| 5: While do: |
| Set if , else |
| for do: |
| Randomly select 5 distinct indices |
| Generate mutant vector: |
| Generate trial vector via crossover: |
| for do: |
| if or : |
| else: |
| Evaluate fitness |
| if , update and |
| End(for) |
| Update and if new minimum found |
| Increment generation counter |
| 6: Return and |
| End |
4. Experimental and Results
4.1. Dataset and Experimental Setup
4.2. Experiments with Intelligent Optimization Algorithms
4.3. Experiments on GPU Parallel Generation of DRR
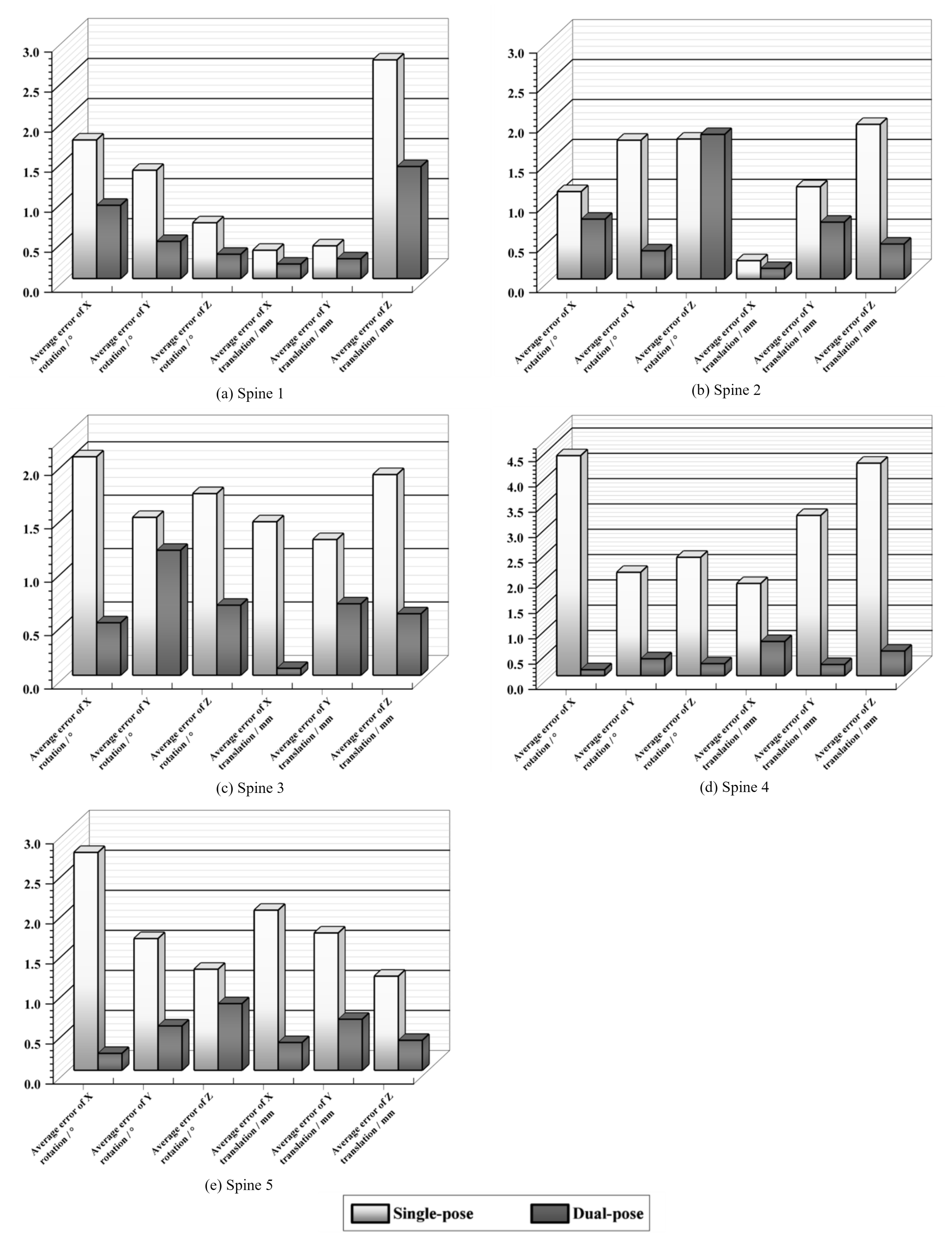
4.4. Dual-Pose Registration Experiments
4.5. Comparative Experiments of Registration Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ou, X.Y.; Chen, X.; Xu, X.N.; Xie, L.L.; Chen, X.F.; Hong, Z.Z.; Bai, H.; Liu, X.W.; Chen, Q.S.; Li, L.; et al. Recent Development in X-Ray Imaging Technology: Future and Challenges. Research 2021, 2021, 9892152. [Google Scholar] [CrossRef] [PubMed]
- Qin, C.X.; Cao, Z.G.; Fan, S.C.; Wu, Y.Q.; Sun, Y.; Politis, C.; Wang, C.L.; Chen, X.J. An oral and maxillofacial navigation system for implant placement with automatic identification of fiducial points. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Zhang, L.; Sun, Y.; Miao, S.; Chefd’Hotel, C. A Review of Recent Advances in Registration Techniques Applied to Minimally Invasive Therapy. IEEE Trans. Multimedia 2013, 15, 983–1000. [Google Scholar] [CrossRef]
- Naik, R.R.; Anitha, H.; Bhat, S.N.; Ampar, N.; Kundangar, R. Realistic C-arm to PCT registration for vertebral localization in spine surgery. Med. Biol. Eng. Comput. 2022, 60, 2271–2289. [Google Scholar] [CrossRef] [PubMed]
- Frysch, R.; Pfeiffer, T.; Rose, G. A novel approach to 2D/3D registration of X-ray images using Grangeat’s relation. Med. Image Anal. 2021, 67, 101815. [Google Scholar] [CrossRef] [PubMed]
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable Medical Image Registration: A Survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef] [PubMed]
- Gobbi, D.; Comeau, R.; Lee, B.; Peters, T. Integration of intra-operative 3D ultrasound with pre-operative MRI for neurosurgical guidance. In Proceedings of the 22nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (Cat. No. 00CH37143), Chicago, IL, USA, 23–28 July 2000; Volume 3, pp. 1738–1740. [Google Scholar] [CrossRef]
- Ban, Y.X.; Wang, Y.; Liu, S.; Yang, B.; Liu, M.Z.; Yin, L.R.; Zheng, W.F. 2D/3D Multimode Medical Image Alignment Based on Spatial Histograms. Appl. Sci. 2022, 12, 8261. [Google Scholar] [CrossRef]
- Regodic, M.; Bardosi, Z.; Freysinger, W. Automated fiducial marker detection and localization in volumetric computed tomography images: A three-step hybrid approach with deep learning. J. Med. Imaging 2021, 8, 025002. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.M.; Tannast, M.; Zheng, G.Y. Non-rigid free-form 2D-3D registration using a B-spline-based statistical deformation model. Pattern Recognit. 2017, 63, 689–699. [Google Scholar] [CrossRef]
- Kuppala, K.; Banda, S.; Barige, T.R. An overview of deep learning methods for image registration with focus on feature-based approaches. Int. J. Image Data Fusion 2020, 11, 113–135. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, H.; Ding, Y. Medical image registration algorithm research based on mutual information similarity measure. Proc. SPIE 2008, 6625, 51–59. [Google Scholar] [CrossRef]
- Tsai, T.Y.; Lu, T.W.; Chen, C.M.; Kuo, M.Y.; Hsu, H.C. A volumetric model-based 2D to 3D registration method for measuring kinematics of natural knees with single-plane fluoroscopy. Med. Phys. 2010, 37, 1273–1284. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Wang, Z.Q.; Liu, Y.; Ye, Z.Y. Generic and Automatic Markov Random Field-Based Registration for Multimodal Remote Sensing Image Using Grayscale and Gradient Information. Remote Sens. 2018, 10, 1228. [Google Scholar] [CrossRef]
- Damas, S.; Cordón, O.; Santamaría, J. Medical Image Registration Using Evolutionary Computation: An Experimental Survey. IEEE Comput. Intell. Mag. 2011, 6, 26–42. [Google Scholar] [CrossRef]
- Ma, G.X.; Ahmed, N.K.; Willke, T.L.; Yu, P.S. Deep graph similarity learning: A survey. Data Min. Knowl. Discov. 2021, 35, 688–725. [Google Scholar] [CrossRef]
- Li, M.D.; Chang, K.; Bearce, B.; Chang, C.Y.; Huang, A.J.; Campbell, J.; Brown, J.M.; Singh, P.; Hoebel, K.V.; Erdoğmuş, D.; et al. Siamese neural networks for continuous disease severity evaluation and change detection in medical imaging. NPJ Digit. Med. 2020, 3, 48. [Google Scholar] [CrossRef] [PubMed]
- Taigman, Y.; Ming, Y.; Ranzato, M.; Wolf, L. DeepFace: Closing the Gap to Human-Level Performance in Face Verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1701–1708. [Google Scholar] [CrossRef]
- McCauley, J.; Soleymani, S.; Williams, B.; Dando, J.; Nasrabadi, N.; Dawson, J. Identical Twins as a facial similarity benchmark for human facial recognition. In Proceedings of the 2021 International Conference of the Biometrics Special Interest Group (BIOSIG), Darmstadt, Germany, 15–17 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yunsheng, B.; Hao, D.; Yizhou, S.; Wei, W. Convolutional set matching for graph similarity. arXiv 2018. [Google Scholar] [CrossRef]
- Spoerk, J.; Gendrin, C.; Weber, C.; Figl, M.; Pawiro, S.A.; Furtado, H.; Fabri, D.; Bloch, C.; Bergmann, H.; Gröller, E.; et al. High-performance GPU-based rendering for real-time, rigid 2D/3D-image registration and motion prediction in radiation oncology. Z. Med. Phys. 2012, 22, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Banks, S.A.; Hodge, W.A. Accurate measurement of three-dimensional knee replacement kinematics using single-plane fluoroscopy. IEEE Trans. Biomed. Eng. 1996, 43, 638–649. [Google Scholar] [CrossRef] [PubMed]
- Akter, M.; Lambert, A.J.; Pickering, M.R.; Scarvell, J.M.; Smith, P.N. A 2D-3D image registration algorithm using log-polar transforms for knee kinematic analysis. In Proceedings of the 2012 International Conference on Digital Image Computing Techniques and Applications (DICTA), Fremantle, Australia, 3–5 December 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Shamshad, F.; Khan, S.; Zamir, S.W.; Khan, M.H.; Hayat, M.; Khan, F.S.; Fu, H.Z. Transformers in medical imaging: A survey. Med. Image Anal. 2023, 88, 102802. [Google Scholar] [CrossRef] [PubMed]
- Almeida, D.F.; Astudillo, P.; Vandermeulen, D. Three-dimensional image volumes from two-dimensional digitally reconstructed radiographs: A deep learning approach in lower limb CT scans. Med. Phys. 2021, 48, 2448–2457. [Google Scholar] [CrossRef] [PubMed]
- Fluck, O.; Vetter, C.; Wein, W.; Kamen, A.; Preim, B.; Westermann, R. A survey of medical image registration on graphics hardware. Comput. Methods Programs Biomed. 2011, 104, E45–E57. [Google Scholar] [CrossRef] [PubMed]
- Tahmasebi, N.; Boulanger, P.; Yun, J.Y.; Fallone, G.; Noga, M.; Punithakumar, K. Real-Time Lung Tumor Tracking Using a CUDA Enabled Nonrigid Registration Algorithm for MRI. IEEE J. Transl. Eng. Health Med. 2020, 8, 4300308. [Google Scholar] [CrossRef] [PubMed]
- Xi, C.; Li, Z.; Zheng, Y. Deep similarity learning for multimodal medical images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 248–252. [Google Scholar] [CrossRef]
- Chen, X.X.; Wang, X.M.; Zhang, K.; Fung, K.M.; Thai, T.C.; Moore, K.; Mannel, R.S.; Liu, H.; Zheng, B.; Qiu, Y.C. Recent advances and clinical applications of deep learning in medical image analysis. Med. Image Anal. 2022, 79, 102444. [Google Scholar] [CrossRef] [PubMed]
- Nikolic, M.; Tuba, E.; Tuba, M. Edge detection in medical ultrasound images using adjusted Canny edge detection algorithm. In Proceedings of the 2016 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.F.; Cai, X.; Zhao, H.M.; Song, Y.J.; Xu, J.J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Torres-Cerna, C.E.; Alanis, A.Y.; Poblete-Castro, I.; Bermejo-Jambrina, M.; Hernandez-Vargas, E.A. A comparative study of differential evolution algorithms for parameter fitting procedures. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 4662–4666. [Google Scholar] [CrossRef]
- Gao, S.C.; Yu, Y.; Wang, Y.R.; Wang, J.H.; Cheng, J.J.; Zhou, M.C. Chaotic Local Search-Based Differential Evolution Algorithms for Optimization. IEEE Trans. Syst. Man Cybern.-Syst. 2021, 51, 3954–3967. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Yazdani, D.; Branke, J.; Omidvar, M.N.; Li, X.; Li, C.; Mavrovouniotis, M.; Nguyen, T.T.; Yang, S.; Yao, X. IEEE CEC 2022 competition on dynamic optimization problems generated by generalized moving peaks benchmark. arXiv 2021, arXiv:2106.06174. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, B.; Zhang, Q.; Liang, J.; Suganthan, P.; Qu, B. Problem Definitions and Evaluation Criteria for CEC 2015 Special Session on Bound Constrained Single-Objective Computationally Expensive Numerical Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2014. [Google Scholar]


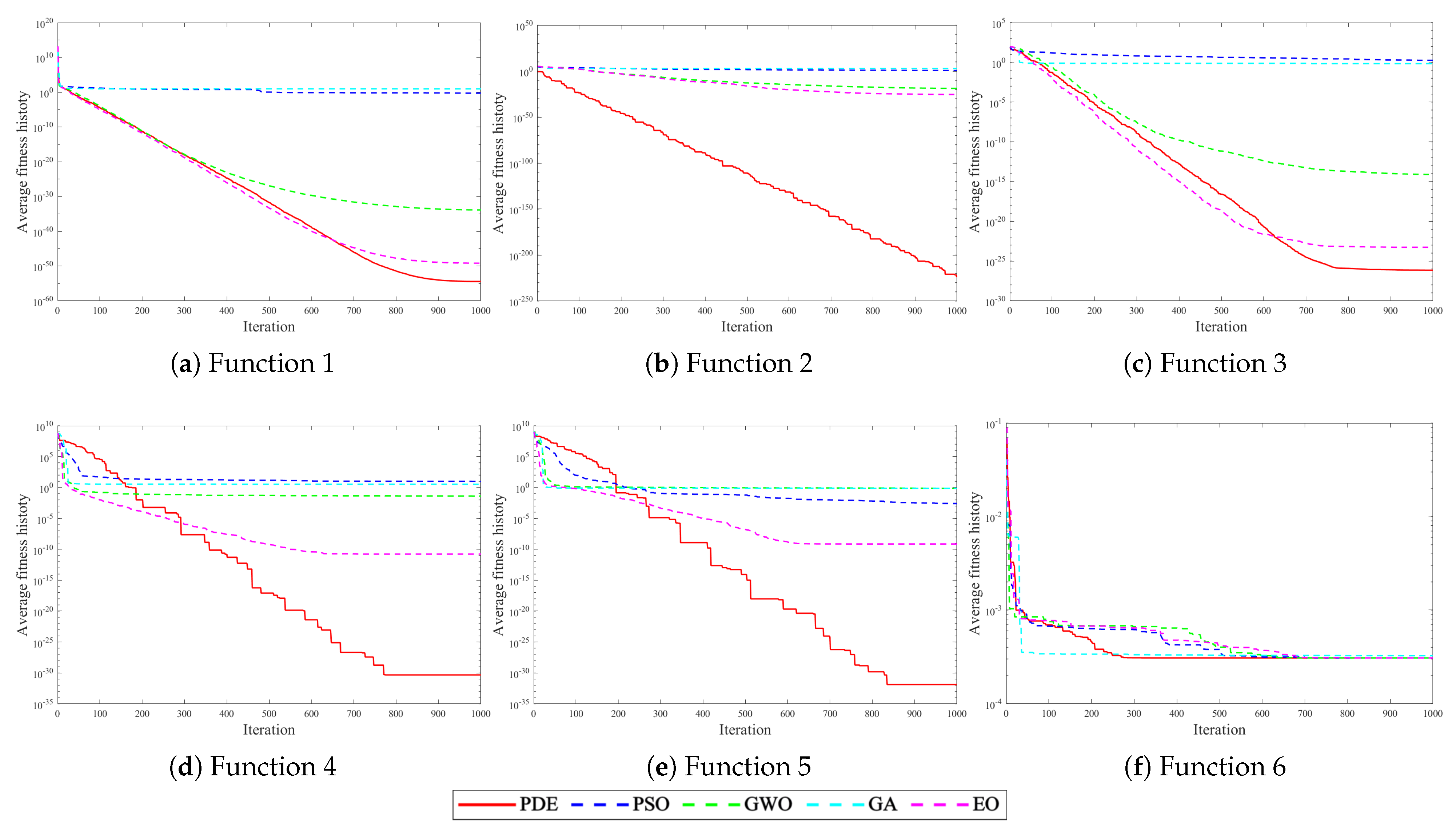
| Function | Search Scope | Theoretical Optimal Value |
|---|---|---|
| F1 = Schwefel 2.22 | [−10,10] | 0 |
| F2 = Schwefel 1.2 | [−100,100] | 0 |
| F3 = Schwefel 2.21 | [−100,100] | 0 |
| F4 = Generalized Penalized 1 | [−50,50] | 0 |
| F5 = Generalized Penalized 2 | [−50,50] | 0 |
| F6 = Kowalik | [−5,5] | 0.0003075 |
| Bone Type | Algorithm | Average Error of X Rotation / ° | Average Error of Y Rotation / ° | Average Error of Z Rotation / ° | Average Error of X Translation / mm | Average Error of Y Translation / mm | Average Error of Z Translation / mm | Average Registration Time / s |
|---|---|---|---|---|---|---|---|---|
| Spine 1 | PSO | 4.403 | 2.866 | 1.839 | 1.082 | 1.621 | 5.504 | 62.16 |
| EO | 2.252 | 1.768 | 1.417 | 0.437 | 3.553 | 5.508 | 62.65 | |
| PDE (ours) | 1.732 | 1.353 | 0.698 | 0.354 | 0.409 | 2.731 | 58.12 | |
| Spine 2 | PSO | 5.913 | 2.115 | 3.984 | 0.671 | 1.670 | 5.086 | 64.61 |
| EO | 3.784 | 2.039 | 2.564 | 0.489 | 1.487 | 3.047 | 65.93 | |
| PDE (ours) | 1.095 | 1.739 | 1.753 | 0.229 | 1.156 | 1.937 | 63.72 | |
| Spine 3 | PSO | 4.005 | 1.924 | 4.693 | 1.772 | 2.551 | 2.464 | 56.08 |
| EO | 2.133 | 3.102 | 1.257 | 2.040 | 4.054 | 4.851 | 57.24 | |
| PDE (ours) | 2.046 | 1.479 | 1.701 | 1.438 | 1.271 | 1.880 | 54.86 |
| Bone Type | Conventional Registration Time/ s | GPU Parallel Generation of DRR Registration Time/s | Speedup Ratio |
|---|---|---|---|
| Spine 1 | 58.12 | 31.00 | 1.8749 |
| Spine 2 | 63.72 | 35.87 | 1.7762 |
| Spine 3 | 54.86 | 30.19 | 1.8168 |
| Spine 4 | 46.78 | 26.82 | 1.7445 |
| Spine 5 | 64.42 | 38.29 | 1.6825 |
| Algorithm | Bone Type | Average Error of X Rotation / ° | Average Error of Y Rotation / ° | Average Error of Z Rotation / ° | Average Error of X Translation / mm | Average Error of Y Translation / mm | Average Error of Z Translation / mm | Average Registration Time / s |
|---|---|---|---|---|---|---|---|---|
| SSD | Lumbar 1 | 3.723 | 4.578 | 3.986 | 3.052 | 5.005 | 8.690 | 61.08 |
| Lumbar 2 | 3.690 | 2.468 | 2.726 | 2.267 | 16.194 | 8.639 | ||
| Lumbar 3 | 2.598 | 5.953 | 1.463 | 1.581 | 5.183 | 10.356 | ||
| Thoracic vertebra 1 | 13.035 | 8.614 | 3.915 | 8.009 | 1.223 | 8.464 | ||
| Thoracic vertebra 2 | 5.951 | 1.160 | 1.792 | 4.799 | 1.286 | 10.555 | ||
| Thoracic vertebra 3 | 5.142 | 1.712 | 3.950 | 5.484 | 8.544 | 15.533 | ||
| Thoracic vertebra 4 | 4.620 | 4.316 | 2.114 | 16.006 | 1.751 | 14.582 | ||
| Spine | 10.234 | 1.740 | 1.617 | 12.165 | 3.361 | 11.208 | ||
| Pelvis 1 | 11.077 | 5.547 | 2.511 | 3.837 | 2.663 | 6.221 | ||
| Pelvis 2 | 4.744 | 2.534 | 1.651 | 2.875 | 3.402 | 14.787 | ||
| Tibia | 4.550 | 9.989 | 9.410 | 10.999 | 4.369 | 5.166 | ||
| Calcaneus | 2.750 | 4.440 | 12.936 | 1.675 | 7.716 | 13.753 | ||
| NCC | Lumbar 1 | 3.258 | 1.683 | 0.737 | 2.212 | 7.603 | 4.182 | 61.80 |
| Lumbar 2 | 1.267 | 1.759 | 1.422 | 1.091 | 2.098 | 4.027 | ||
| Lumbar 3 | 3.898 | 1.172 | 0.560 | 2.163 | 7.645 | 5.649 | ||
| Thoracic vertebra 1 | 9.279 | 4.383 | 0.833 | 7.519 | 5.109 | 6.742 | ||
| Thoracic vertebra 2 | 6.402 | 4.854 | 4.558 | 2.816 | 6.941 | 4.325 | ||
| Thoracic vertebra 3 | 4.497 | 1.401 | 3.986 | 5.094 | 7.301 | 9.764 | ||
| Thoracic vertebra 4 | 9.643 | 1.157 | 1.281 | 9.412 | 0.184 | 7.363 | ||
| Spine | 7.598 | 0.115 | 1.024 | 8.685 | 9.761 | 11.525 | ||
| Pelvis 1 | 3.774 | 9.057 | 8.350 | 9.205 | 11.867 | 3.560 | ||
| Pelvis 2 | 8.481 | 4.837 | 6.500 | 8.868 | 3.868 | 4.276 | ||
| Tibia | 9.374 | 8.001 | 7.040 | 2.810 | 5.012 | 5.138 | ||
| Calcaneus | 0.207 | 6.988 | 2.897 | 2.899 | 1.881 | 15.986 | ||
| MI | Lumbar 1 | 5.976 | 2.148 | 2.408 | 1.310 | 7.922 | 5.484 | 59.41 |
| Lumbar 2 | 7.576 | 1.030 | 0.467 | 0.854 | 9.813 | 3.748 | ||
| Lumbar 3 | 4.917 | 4.354 | 0.276 | 3.746 | 6.800 | 3.947 | ||
| Thoracic vertebra 1 | 6.506 | 2.365 | 1.077 | 8.694 | 1.595 | 3.794 | ||
| Thoracic vertebra 2 | 1.422 | 0.936 | 3.358 | 3.156 | 2.775 | 6.203 | ||
| Thoracic vertebra 3 | 7.899 | 3.544 | 1.844 | 0.714 | 4.794 | 8.123 | ||
| Thoracic vertebra 4 | 6.546 | 2.873 | 6.148 | 0.469 | 2.295 | 5.637 | ||
| Spine | 5.510 | 0.364 | 3.185 | 8.540 | 4.761 | 2.559 | ||
| Pelvis 1 | 2.762 | 1.364 | 1.973 | 9.802 | 0.840 | 5.788 | ||
| Pelvis 2 | 3.879 | 3.054 | 1.795 | 5.028 | 1.882 | 7.962 | ||
| Tibia | 7.399 | 6.420 | 3.047 | 1.071 | 8.159 | 5.883 | ||
| Calcaneus | 5.769 | 6.759 | 4.747 | 1.359 | 4.488 | 7.308 | ||
| Siamese Network [17] | Lumbar 1 | 12.321 | 1.156 | 2.452 | 2.390 | 4.013 | 9.817 | 85.90 |
| Lumbar 2 | 10.792 | 3.091 | 0.907 | 3.632 | 6.290 | 8.256 | ||
| Lumbar 3 | 5.071 | 1.233 | 1.721 | 7.114 | 5.561 | 9.095 | ||
| Thoracic vertebra 1 | 4.698 | 4.640 | 1.096 | 6.680 | 3.713 | 14.319 | ||
| Thoracic vertebra 2 | 8.912 | 4.417 | 2.791 | 1.086 | 2.338 | 11.113 | ||
| Thoracic vertebra 3 | 2.169 | 1.273 | 3.541 | 1.478 | 6.854 | 12.723 | ||
| Thoracic vertebra 4 | 7.006 | 2.799 | 1.371 | 4.092 | 2.346 | 13.122 | ||
| Spine | 6.778 | 3.513 | 1.049 | 6.110 | 4.078 | 7.576 | ||
| Pelvis 1 | 10.407 | 3.111 | 5.189 | 4.311 | 5.125 | 6.297 | ||
| Pelvis 2 | 4.598 | 2.691 | 1.745 | 8.870 | 6.588 | 5.394 | ||
| Tibia | 7.967 | 9.225 | 3.046 | 0.104 | 10.223 | 11.749 | ||
| Calcaneus | 3.519 | 6.179 | 9.991 | 2.709 | 2.361 | 13.900 | ||
| FaceNet [19] | Lumbar 1 | 10.492 | 1.529 | 2.118 | 1.048 | 2.653 | 6.935 | 83.97 |
| Lumbar 2 | 12.086 | 2.478 | 1.754 | 1.487 | 8.517 | 14.821 | ||
| Lumbar 3 | 11.723 | 5.121 | 1.790 | 5.137 | 6.051 | 8.622 | ||
| Thoracic vertebra 1 | 6.208 | 2.650 | 1.207 | 3.987 | 7.017 | 11.059 | ||
| Thoracic vertebra 2 | 13.220 | 3.072 | 1.253 | 2.421 | 1.769 | 10.890 | ||
| Thoracic vertebra 3 | 9.350 | 2.131 | 6.797 | 0.339 | 10.311 | 12.198 | ||
| Thoracic vertebra 4 | 8.563 | 4.131 | 3.147 | 8.157 | 3.768 | 8.893 | ||
| Spine | 9.116 | 2.266 | 1.576 | 10.652 | 7.985 | 7.920 | ||
| Pelvis 1 | 4.897 | 3.762 | 8.898 | 9.023 | 9.158 | 9.114 | ||
| Pelvis 2 | 9.766 | 2.048 | 4.638 | 8.412 | 3.551 | 4.645 | ||
| Tibia | 4.457 | 6.847 | 11.349 | 1.032 | 8.848 | 15.491 | ||
| Calcaneus | 1.551 | 5.217 | 9.441 | 2.222 | 5.412 | 10.160 | ||
| Ours | Lumbar 1 | 0.916 | 0.465 | 0.304 | 0.182 | 0.248 | 1.400 | 61.38 |
| Lumbar 2 | 0.750 | 0.353 | 1.812 | 0.132 | 0.712 | 0.438 | ||
| Lumbar 3 | 0.492 | 1.171 | 0.657 | 0.065 | 0.670 | 0.577 | ||
| Thoracic vertebra 1 | 0.120 | 0.336 | 0.240 | 0.677 | 0.223 | 0.489 | ||
| Thoracic vertebra 2 | 0.212 | 0.555 | 0.834 | 0.348 | 0.639 | 0.375 | ||
| Thoracic vertebra 3 | 0.912 | 0.884 | 0.796 | 1.003 | 0.664 | 0.633 | ||
| Thoracic vertebra 4 | 0.986 | 0.425 | 0.765 | 1.036 | 1.674 | 0.401 | ||
| Spine | 0.727 | 0.271 | 0.414 | 0.277 | 0.730 | 0.837 | ||
| Pelvis 1 | 0.614 | 0.545 | 0.143 | 0.674 | 0.723 | 0.520 | ||
| Pelvis 2 | 0.914 | 0.832 | 0.416 | 0.266 | 0.215 | 0.297 | ||
| Tibia | 0.628 | 0.956 | 0.883 | 0.355 | 0.359 | 0.496 | ||
| Calcaneus | 0.294 | 0.158 | 0.904 | 0.331 | 0.753 | 0.217 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Xing, F.; Liu, W.; Liu, F. Highly Accelerated Dual-Pose Medical Image Registration via Improved Differential Evolution. Sensors 2025, 25, 4604. https://doi.org/10.3390/s25154604
Zhou D, Xing F, Liu W, Liu F. Highly Accelerated Dual-Pose Medical Image Registration via Improved Differential Evolution. Sensors. 2025; 25(15):4604. https://doi.org/10.3390/s25154604
Chicago/Turabian StyleZhou, Dibin, Fengyuan Xing, Wenhao Liu, and Fuchang Liu. 2025. "Highly Accelerated Dual-Pose Medical Image Registration via Improved Differential Evolution" Sensors 25, no. 15: 4604. https://doi.org/10.3390/s25154604
APA StyleZhou, D., Xing, F., Liu, W., & Liu, F. (2025). Highly Accelerated Dual-Pose Medical Image Registration via Improved Differential Evolution. Sensors, 25(15), 4604. https://doi.org/10.3390/s25154604






