Non-Invasive Blood Cortisol Estimation from Sweat Analysis by Kinetic Modeling of Cortisol Transport Dynamics
Abstract
1. Introduction
2. Methods
2.1. Clinical Trial Dataset
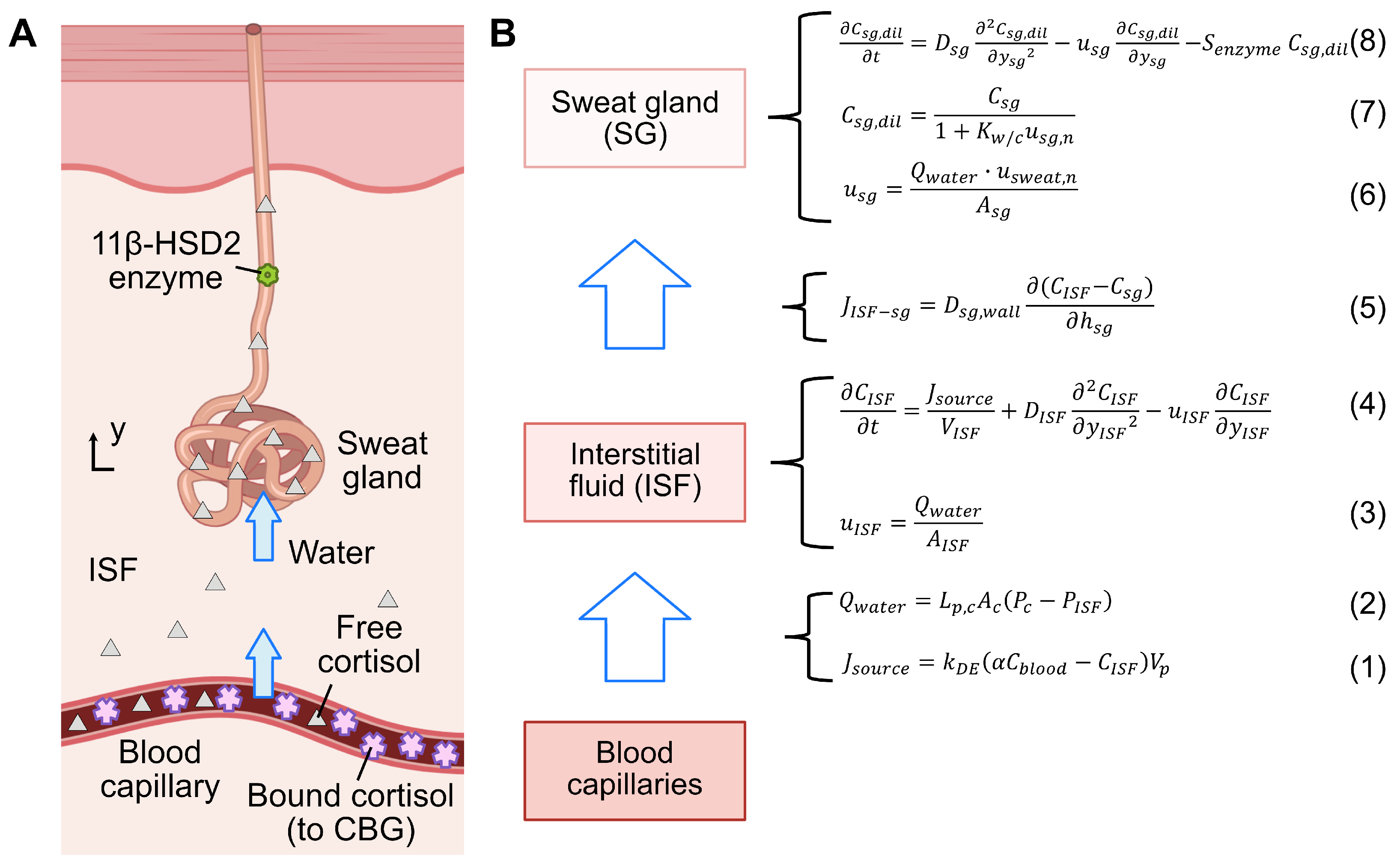
2.2. Cortisol Transport Model
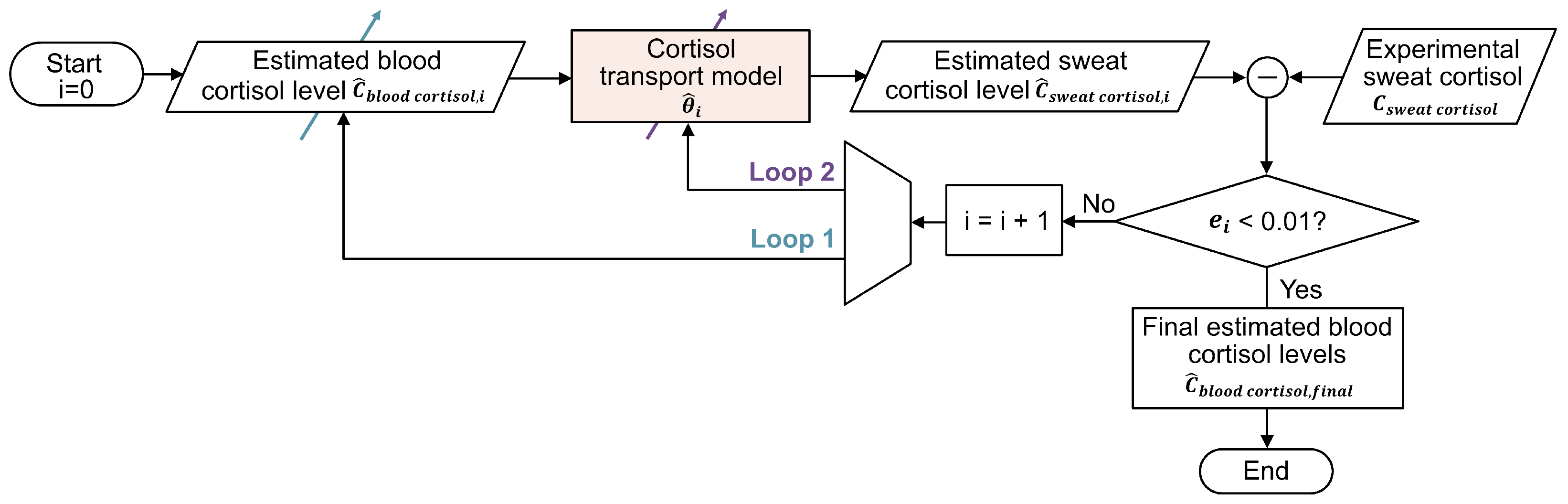
2.3. Strategies for Blood Cortisol Estimation
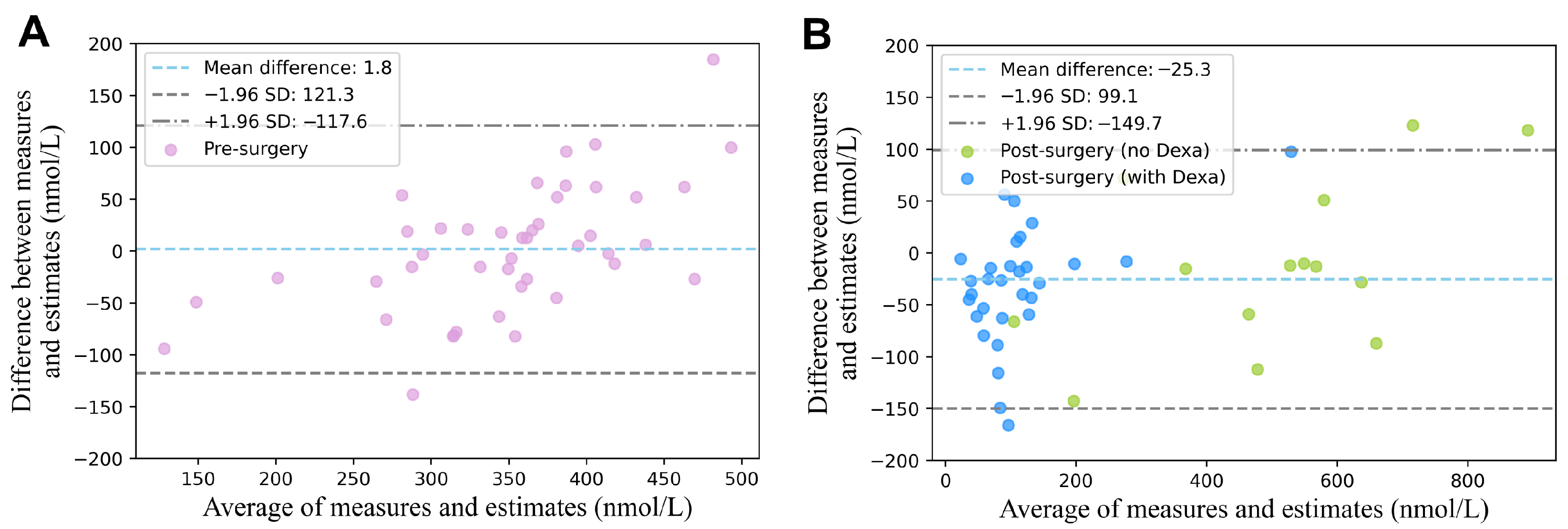
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nieman, L.K.; Biller, B.M.K.; Findling, J.W.; Newell-Price, J.; Savage, M.O.; Stewart, P.M.; Montori, V.M. The Diagnosis of Cushing’s Syndrome: An Endocrine Society Clinical Practice Guideline. J. Clin. Endocrinol. Metab. 2008, 93, 1526–1540. [Google Scholar] [CrossRef] [PubMed]
- Boscaro, M.; Arnaldi, G. Approach to the Patient with Possible Cushing’s Syndrome. J. Clin. Endocrinol. Metab. 2009, 94, 3121–3131. [Google Scholar] [CrossRef] [PubMed]
- Savas, M.; Mehta, S.; Agrawal, N.; van Rossum, E.F.; Feelders, R.A. Approach to the Patient: Diagnosis of Cushing Syndrome. J. Clin. Endocrinol. Metab. 2022, 107, 3162–3174. [Google Scholar] [CrossRef] [PubMed]
- Burton, C.; Cottrell, E.; Edwards, J. Addison’s disease: Identification and management in primary care. Br. J. Gen. Pract. 2015, 65, 488–490. [Google Scholar] [CrossRef] [PubMed]
- Chakera, A.J.; Vaidya, B. Addison Disease in Adults: Diagnosis and Management. Am. J. Med. 2010, 123, 409–413. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.L.; Wang, D.X.; Li, L.-H.; Shan, G.-J.; Li, J.; Yu, Q.-J.; Shi, C.-X. High serum cortisol level is associated with increased risk of delirium after coronary artery bypass graft surgery: A prospective cohort study. Crit. Care 2010, 14, R238. [Google Scholar] [CrossRef] [PubMed]
- Kazmierski, J.; Banys, A.; Latek, J.; Bourke, J.; Jaszewski, R. Cortisol levels and neuropsychiatric diagnosis as markers of postoperative delirium: A prospective cohort study. Crit. Care 2013, 17, R38. [Google Scholar] [CrossRef] [PubMed]
- Islam, R.; Islam, R.; Ahmed, I.; Al Moktadir, A.; Nahar, Z.; Islam, M.S.; Shahid, S.F.B.; Islam, S.N.; Islam, S.; Hasnat, A. Elevated serum levels of malondialdehyde and cortisol are associated with major depressive disorder: A case-control study. Sage Open Med. 2018, 6, 2050312118773953. [Google Scholar] [CrossRef] [PubMed]
- Upton, T.J.; Zavala, E.; Methlie, P.; Kämpe, O.; Tsagarakis, S.; Øksnes, M.; Bensing, S.; Vassiliadi, D.A.; Grytaas, M.A.; Botusan, I.R.; et al. High-resolution daily profiles of tissue adrenal steroids by portable automated collection. Sci. Transl. Med. 2023, 15, eadg8464. [Google Scholar] [CrossRef] [PubMed]
- Vignesh, V.; Castro-Dominguez, B.; James, T.D.; Gamble-Turner, J.M.; Lightman, S.; Reis, N.M. Advancements in Cortisol Detection: From Conventional Methods to Next-Generation Technologies for Enhanced Hormone Monitoring. ACS Sens. 2024, 9, 1666–1681. [Google Scholar] [CrossRef] [PubMed]
- Düztepeliler, S.; Gürol Arslan, G. The Effect of Vibration on Pain and Anxiety During Intravenous Blood Sampling in Adults. J. Educ. Res. Nurs. 2020, 17, 10–17. [Google Scholar] [CrossRef]
- Baker, L.B.; Wolfe, A.S. Physiological mechanisms determining eccrine sweat composition. Eur. J. Appl. Physiol. 2020, 120, 719–752. [Google Scholar] [CrossRef] [PubMed]
- Stetler, C.; Miller, G.E. Depression and Hypothalamic-Pituitary-Adrenal Activation: A Quantitative Summary of Four Decades of Research. Psychosom. Med. 2011, 73, 114–126. [Google Scholar] [CrossRef] [PubMed]
- Sonner, Z.; Wilder, E.; Heikenfeld, J.; Kasting, G.; Beyette, F.; Swaile, D.; Sherman, F.; Joyce, J.; Hagen, J.; Kelley-Loughnane, N.; et al. The microfluidics of the eccrine sweat gland, including biomarker partitioning, transport, and biosensing implications. Biomicrofluidics 2015, 9, 031301. [Google Scholar] [CrossRef] [PubMed]
- Moonen, E.J.M.; Verberne, W.; Pelssers, E.; Heikenfeld, J.; Toonder, J.M.J.D. Discretised microfluidics for noninvasive health monitoring using sweat sensing. Lab Chip 2024, 24, 5304–5317. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.K.; Chung, S.; Chang, A.-Y.; Wang, J.; Hall, D.A. A non-invasive wearable stress patch for real-time cortisol monitoring using a pseudoknot-assisted aptamer. Biosens. Bioelectron. 2023, 227, 115097. [Google Scholar] [CrossRef] [PubMed]
- Torrente-Rodríguez, R.M.; Tu, J.; Yang, Y.; Min, J.; Wang, M.; Song, Y.; Yu, Y.; Xu, C.; Ye, C.; IsHak, W.W.; et al. Investigation of Cortisol Dynamics in Human Sweat Using a Graphene-Based Wireless mHealth System. Matter 2020, 75, 921–937. [Google Scholar] [CrossRef] [PubMed]
- Adelaars, S. Non-Invasive Patient Monitoring: Towards Clinical Applications of Biomarkers in Sweat and Saliva. Ph.D. Dissertation, Eindhoven University of Technology, Eindhoven, The Netherlands, 2025; pp. 107–123. [Google Scholar]
- Yin, X.; Peri, E.; Pelssers, E.; Toonder, J.D.; Klous, L.; Daanen, H.; Mischi, M. A personalized model and optimization strategy for estimating blood glucose concentrations from sweat measurements. Comput. Methods Programs Biomed. 2025, 265, 108743. [Google Scholar] [CrossRef] [PubMed]
- Bae, Y.J.; Kratzsch, J. Corticosteroid-binding globulin: Modulating mechanisms of bioavailability of cortisol and its clinical implications. Best Pract. Res. Clin. Endocrinol. Metab. 2015, 29, 761–772. [Google Scholar] [CrossRef] [PubMed]
- Limor, R.; Tordjman, K.; Marcus, Y.; Greenman, Y.; Osher, E.; Sofer, Y.; Stern, N. Serum free cortisol as an ancillary tool in the interpretation of the low-dose 1-ug ACTH test: Measurement of serum free cortisol. Clin. Endocrinol. 2011, 75, 294–300. [Google Scholar] [CrossRef] [PubMed]
- Hirasawa, G.; Sasano, H.; Takahashi, K.I.; Fukushima, K.; Suzuki, T.; Hiwatashi, N.; Toyota, T.; Krozowski, Z.S.; Nagura, H. Colocalization of 11-Hydroxysteroid Dehydrogenase Type II and Mineralocorticoid Receptor in Human Epithelia. J. Clin. Endocrinol. Metab. 1997, 82, 3859–3863. [Google Scholar] [CrossRef] [PubMed]
- Raul, J.S.; Cirimele, V.; Ludes, B.; Kintz, P. Detection of physiological concentrations of cortisol and cortisone in human hair. Clin. Biochem. 2004, 37, 1105–1111. [Google Scholar] [CrossRef] [PubMed]
- Le Roux, C.W.; Chapman, G.A.; Kong, W.M.; Dhillo, W.S.; Jones, J.; Alaghband-Zadeh, J. Free Cortisol Index Is Better Than Serum Total Cortisol in Determining Hypothalamic-Pituitary-Adrenal Status in Patients Undergoing Surgery. J. Clin. Endocrinol. Metab. 2003, 88, 2045–2048. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Adelaars, S.; Peri, E.; Pelssers, E.; Toonder, J.D.; Bouwman, A.; Van de Kerkhof, D.; Mischi, M. A novel kinetic model estimating the urea concentration in plasma during non-invasive sweat-based monitoring in hemodialysis. Front. Physiol. 2025, 16, 1547117. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, R.; Nitsche, J.M.; Kasting, G.B. Dermal Clearance Model for Epidermal Bioavailability Calculations. Rev. Chem. Eng. 2012, 101, 2094–2108. [Google Scholar] [CrossRef] [PubMed]
- Himeno, Y.; Ikebuchi, M.o. Mechanisms underlying the volume regulation of interstitial fluid by capillaries: A simulation study. Integr. Med. Res. 2016, 5, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Kellen, M.R.; Bassingthwaighte, J.B. Transient transcapillary exchange of water driven by osmotic forces in the heart. Am. J.-Physiol.-Heart Circ. Physiol. 2003, 285, H1317–H1331. [Google Scholar] [CrossRef] [PubMed]
- Haggerty, A.; Nirmalan, M. Capillary dynamics, interstitial fluid and the lymphatic system. Anaesth. Intensive Care Med. 2019, 20, 182–189. [Google Scholar] [CrossRef]
- Gordic, M. Theoretical Modeling of Cortisol Sensor. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2008. [Google Scholar]
- Hibbs, R.G. The fine structure of human eccrine sweat glands. Am. J. Anat. 1958, 103, 201–217. [Google Scholar] [CrossRef] [PubMed]
- Nie, S.; Zhang, C.; Song, J. Thermal management of epidermal electronic devices/skin system considering insensible sweating. Sci. Rep. 2018, 8, 14121. [Google Scholar] [CrossRef] [PubMed]
- Zainol Abidin, A.; Rahim, R.; Arshad, M.K.M.; Nabilah, M.F.F.; Voon, C.H.; Tang, T.-H.; Citartan, M. Current and Potential Developments of Cortisol Aptasensing towards Point-of-Care Diagnostics (POTC). Sensors 2017, 17, 1180. [Google Scholar] [CrossRef] [PubMed]
- Vogeser, M.; Felbinger, T.W.; Kilger, E.; Röll, W.; Fraunberger, P.; Jacob, K. Corticosteroid-binding globulin and free cortisol in the early postoperative period after cardiac surgery. Clin. Biochem. 1999, 32, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Khoo, B.; Boshier, P.R.; Freethy, A.; Tharakan, G.; Saeed, S.; Hill, N.; Williams, E.L.; Moorthy, K.; Tolley, N.; Jiao, L.R.; et al. Redefining the stress cortisol response to surgery. Clin. Endocrinol. 2017, 87, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Prete, A.; Yan, Q.; Al-Tarrah, K.; Akturk, H.K.; Prokop, L.J.; Alahdab, F.; Foster, M.A.; Lord, J.M.; Karavitaki, N.; Wass, J.A.; et al. The cortisol stress response induced by surgery: A systematic review and meta-analysis. Clin. Endocrinol. 2018, 89, 554–567. [Google Scholar] [CrossRef] [PubMed]
- Christ-Crain, M.; Jutla, S.; Widmer, I.; Couppis, O.; KönIg, C.; Pargger, H.; Puder, J.; Edwards, R.; MülLer, B.; Grossman, A.B. Measurement of Serum Free Cortisol Shows Discordant Responsivity to Stress and Dynamic Evaluation. J. Clin. Endocrinol. Metab. 2007, 92, 1729–1735. [Google Scholar] [CrossRef] [PubMed]
- Coolens, J.L.; Van Baelen, H.; Heyns, W. Clinical use of unbound plasma cortisol as calculated from total cortisol and corticosteroid-binding globulin. J. Steroid Biochem. 1987, 26, 197–202. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Unit | Value | Ref. |
|---|---|---|---|
| Capillary hydrostatic pressure: | mmHg | 30 | [29] |
| Capillary hydraulic conductivity of water: | m s−1 mmHg−1 | [28] | |
| Clearance constant of steroids: | s−1 | [26] | |
| Diffusion coefficient of cortisol for sweat gland wall: | m2 s−1 | [30] | |
| Diffusion coefficient of cortisol in ISF: | m2 s−1 | [30] | |
| Diffusion coefficient of cortisol in sweat: | m2 s−1 | [30] | |
| Effective area of sweat gland: | m2 | [31] | |
| Effective surface area of capillary: | m2 | [27] | |
| Effective cross-sectional area of ISF: | m2 | [27] | |
| Effective volume of capillary: | m3 | [27] | |
| Effective volume of ISF: | m3 | [27] | |
| Interstitial hydrostatic pressure: | mmHg | −3 | [29] |
| Proportion of free cortisol: | - | 5% | [20] |
| Ratio of volumetric flow rate of water to cortisol: | - | 20 | [33] |
| Thickness of sweat gland wall: | m | [14] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Adelaars, S.; Peri, E.; Pelssers, E.; den Toonder, J.; Bouwman, A.; van de Kerkhof, D.; Mischi, M. Non-Invasive Blood Cortisol Estimation from Sweat Analysis by Kinetic Modeling of Cortisol Transport Dynamics. Sensors 2025, 25, 4551. https://doi.org/10.3390/s25154551
Yin X, Adelaars S, Peri E, Pelssers E, den Toonder J, Bouwman A, van de Kerkhof D, Mischi M. Non-Invasive Blood Cortisol Estimation from Sweat Analysis by Kinetic Modeling of Cortisol Transport Dynamics. Sensors. 2025; 25(15):4551. https://doi.org/10.3390/s25154551
Chicago/Turabian StyleYin, Xiaoyu, Sophie Adelaars, Elisabetta Peri, Eduard Pelssers, Jaap den Toonder, Arthur Bouwman, Daan van de Kerkhof, and Massimo Mischi. 2025. "Non-Invasive Blood Cortisol Estimation from Sweat Analysis by Kinetic Modeling of Cortisol Transport Dynamics" Sensors 25, no. 15: 4551. https://doi.org/10.3390/s25154551
APA StyleYin, X., Adelaars, S., Peri, E., Pelssers, E., den Toonder, J., Bouwman, A., van de Kerkhof, D., & Mischi, M. (2025). Non-Invasive Blood Cortisol Estimation from Sweat Analysis by Kinetic Modeling of Cortisol Transport Dynamics. Sensors, 25(15), 4551. https://doi.org/10.3390/s25154551









