Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys
Abstract
Highlights
- Paramagnetic USV offers a cost-effective solution for marine magnetic surveys by significantly reducing operational expenses compared to conventional research vessels.
- Paramagnetic hull effectively reduces magnetic noise and shortens the duration of viscous magnetization.
- Comparative analysis of the correction methods from various platforms highlights that employing a 9-component susceptibility tensor is the most robust.
- Validated relative accuracy but revealed consistent ~200 nT offset vs. towed scalar data.
Abstract
1. Introduction
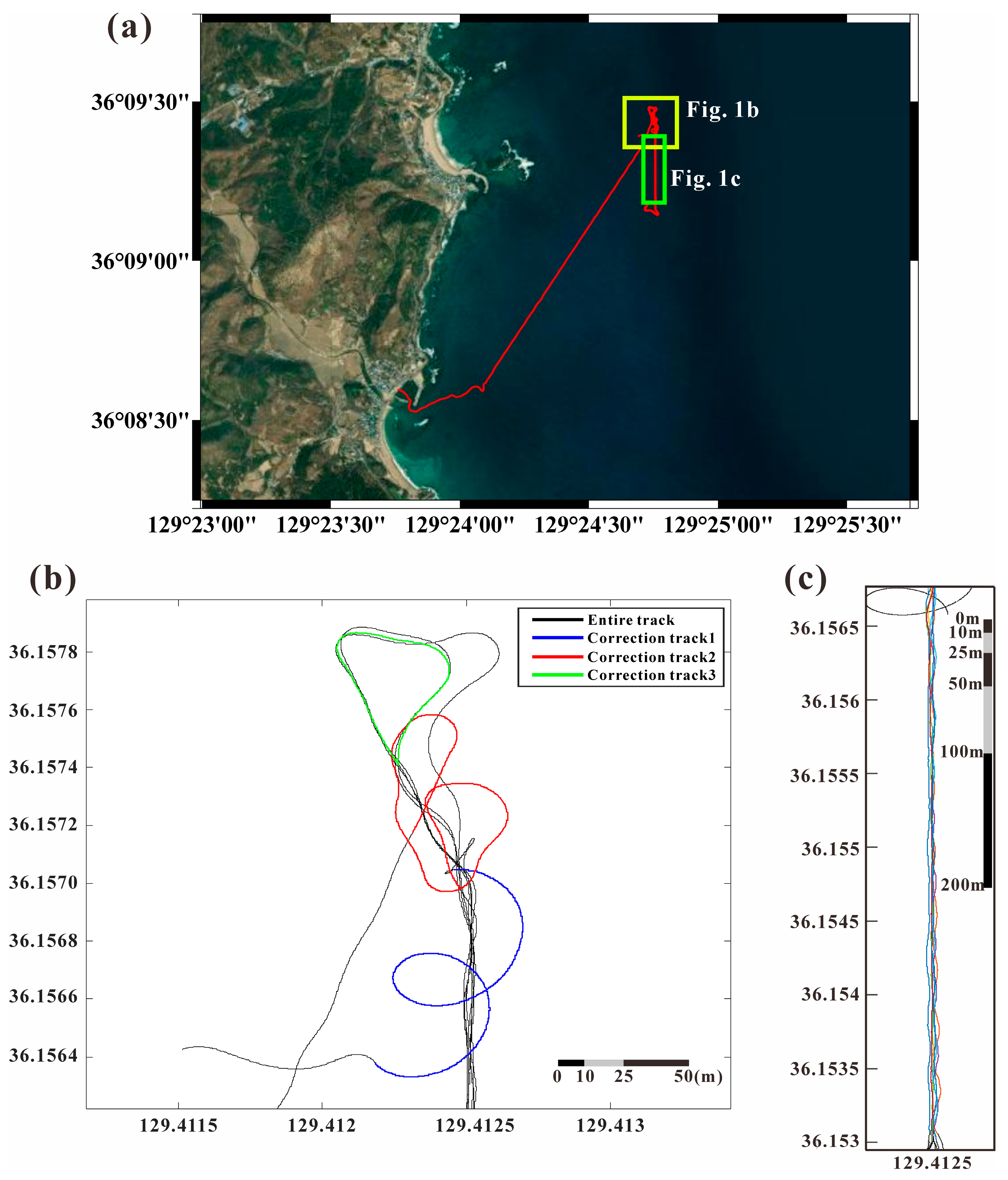
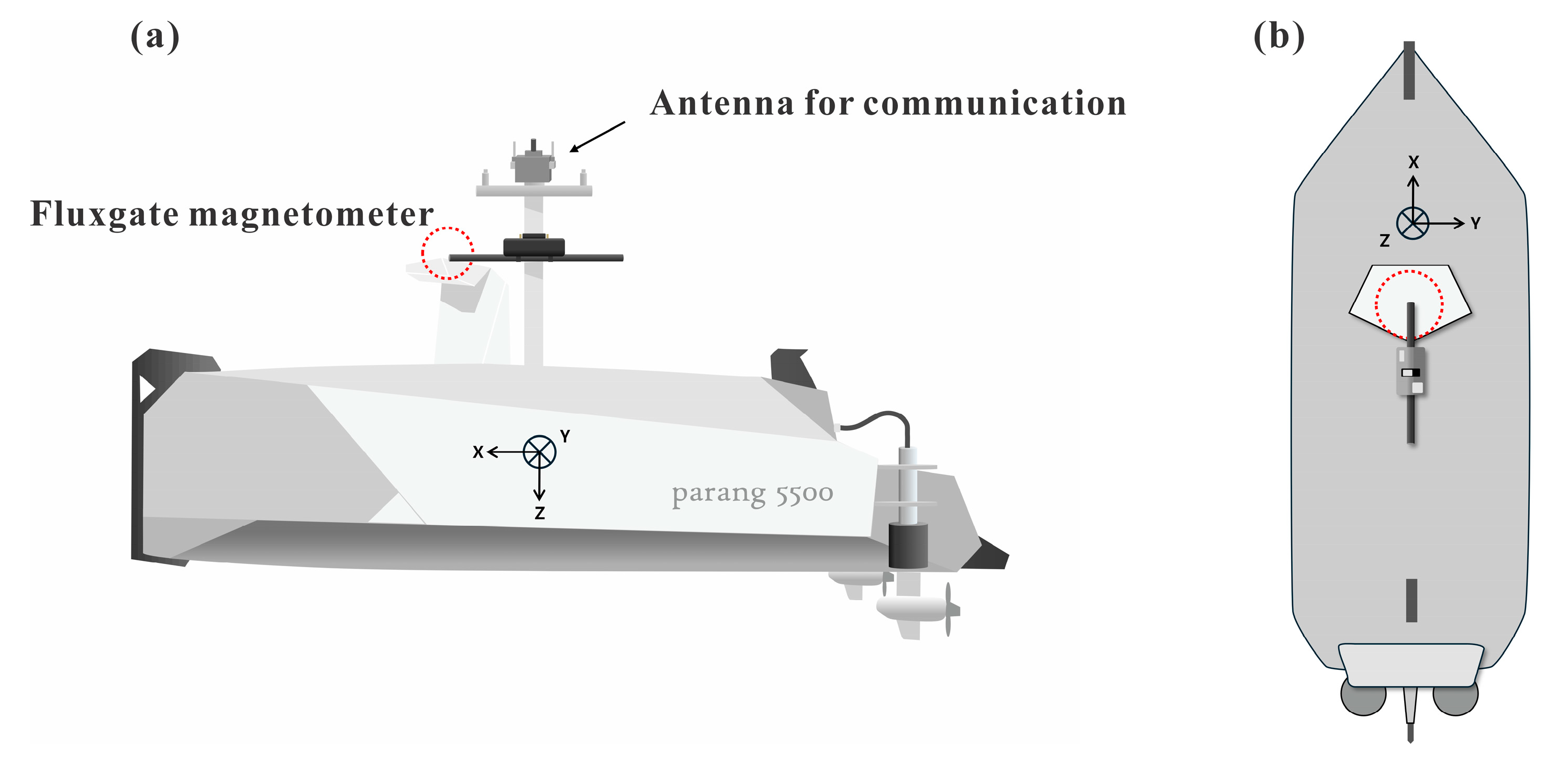
2. Methods
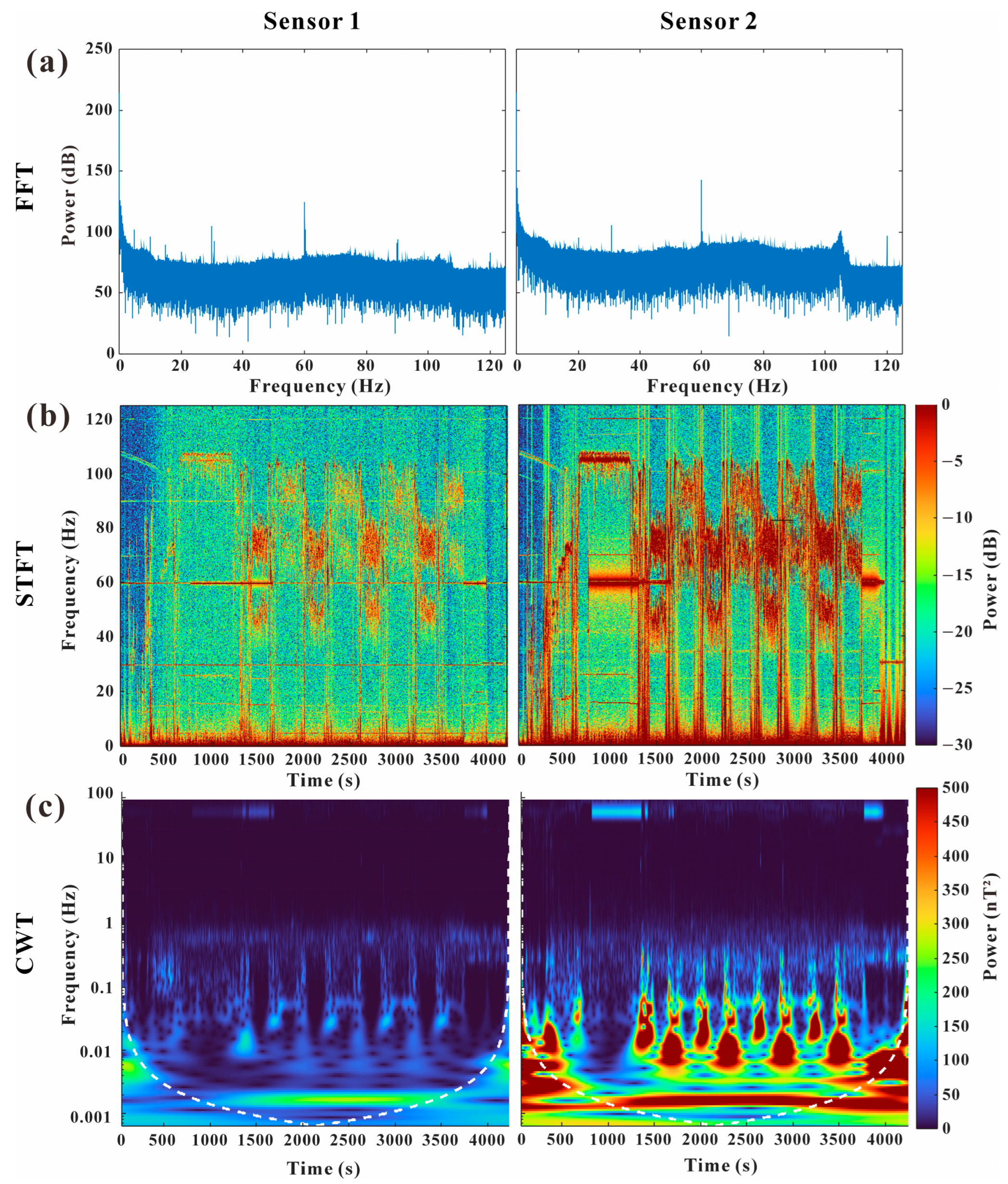
3. Characteristics of Magnetic Signal
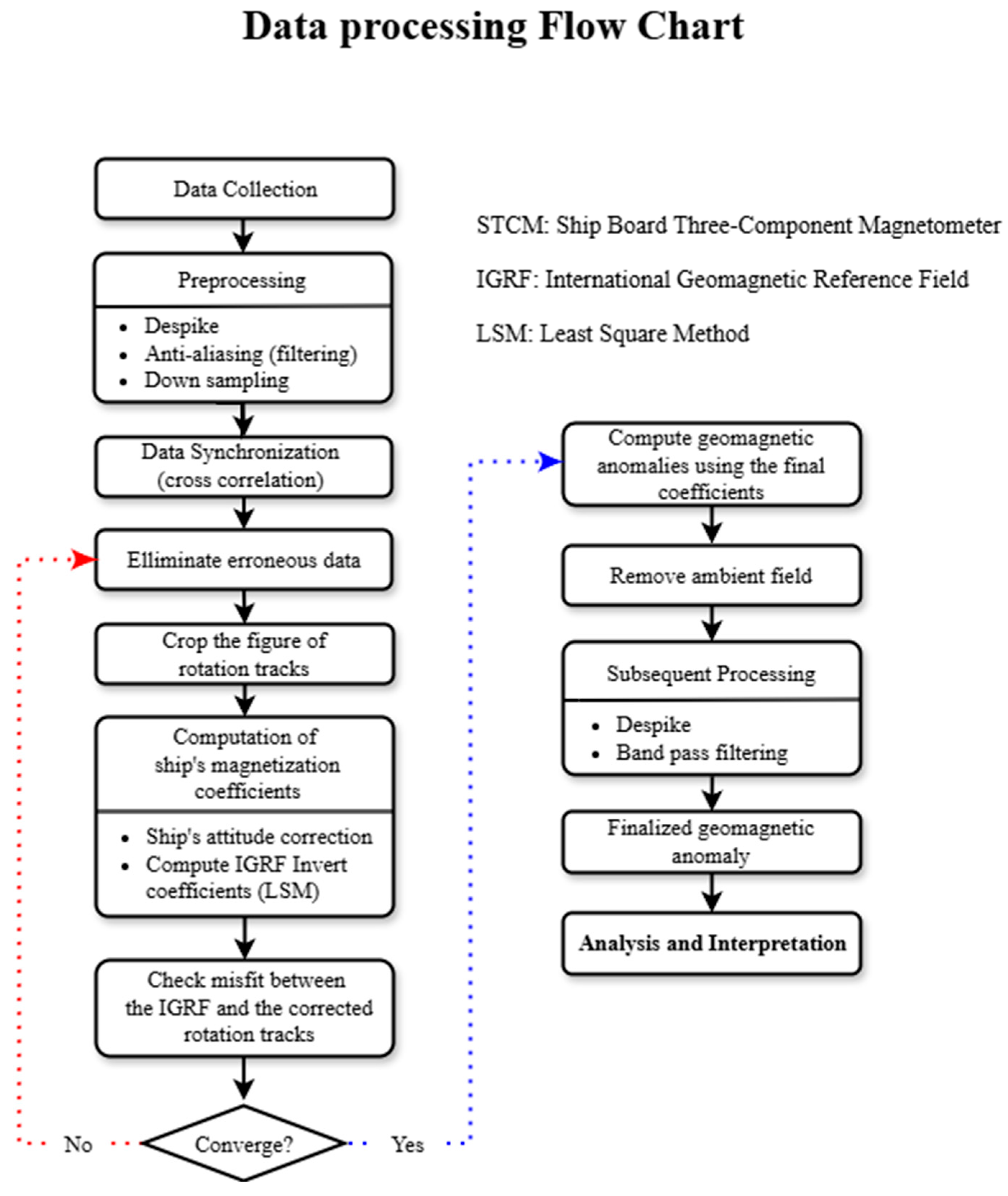
4. Data Processing
4.1. Preprocessing
4.2. Correction for the USV’s Attitude and Magnetization
4.3. Post Processing
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nabighian, M.N.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Peirce, J.W.; Ruder, M.E. The historical development of the magnetic method in exploration. Geophysics 2005, 70, 33ND–61ND. [Google Scholar] [CrossRef]
- Choe, H.; Dyment, J. Fading magnetic anomalies, thermal structure and earthquakes in the Japan trench. Geology 2020, 48, 278–282. [Google Scholar] [CrossRef]
- Choe, H.; Seama, N. A new correction method for ship’s viscous magnetization effect on shipboard three-component magnetic data using a total field magnetometer. Geophys. Geophys. Explor. 2024, 27, 119–128. [Google Scholar] [CrossRef]
- Oehler, J.-F.; Schifano, V.; Marquis, G.; Reiller, H.; Lucas, S.; Bougeault, C. Processing of unmanned underwater vehicle vector magnetometer data. Geophys. Prospect. 2024, 72, 2902–2918. [Google Scholar] [CrossRef]
- Engels, M.; Barckhausen, U.; Gee, J.S. A new towed marine vector magnetometer: Methods and results from a Central Pacific cruise. Geophys. J. Int. 2008, 172, 115–129. [Google Scholar] [CrossRef][Green Version]
- Sasaki, T.; Yamazaki, T.; Ishizuka, O. A revised spreading model of the West Philippine Basin. Earth Planets Space 2014, 66, 83. [Google Scholar] [CrossRef]
- Nogi, Y.; Kaminuma, K. Measurements of vector magnetic anomalies on board the icebreaker Shirase and the magnetization of the ship. Ann. Geophys. 1999, 42, 161–170. [Google Scholar] [CrossRef]
- König, M. Processing of Shipborne Magnetometer Data and Revision of the Timing and Geometry of the Mesozoic Break-Up of Gondwana; Berichte zur Polarforschung No. 525; Alfred Wegener Institute for Polar and Marine Research: Bremerhaven, Germany, 2006. [Google Scholar] [CrossRef]
- Choe, H.; Dyment, J.; So, B.-D. A crossover error correction algorithm for sea-surface marine magnetic data: Application to Northwest Pacific. J. Geol. Soc. Korea 2021, 57, 67–77. [Google Scholar] [CrossRef]
- Gavazzi, B.; Le Maire, P.; de Lépinay, J.M.; Calou, P.; Munschy, M. Fluxgate three-component magnetometers for cost-effective ground, UAV and airborne magnetic surveys for industrial and academic geoscience applications and comparison with current industrial standards through case studies. Geomech. Energy Environ. 2019, 20, 100117. [Google Scholar] [CrossRef]
- Le Maire, P.; Bertrand, L.; Munschy, M.; Diraison, M.; Géraud, Y. Aerial magnetic mapping with an unmanned aerial vehicle and a fluxgate magnetometer: A new method for rapid mapping and upscaling from the field to regional scale. Geophys. Prospect. 2020, 68, 2307–2319. [Google Scholar] [CrossRef]
- Gavazzi, B.; Reiller, H.; Munschy, M. An integrated approach for ground and drone-borne magnetic surveys and their interpretation in archaeological prospection. ArcheoSciences 2021, 451, 165–168. [Google Scholar] [CrossRef]
- Lipovský, P.; Draganová, K.; Novotňák, J.; Szőke, Z.; Fiľko, M. Indoor mapping of magnetic fields using uav equipped with fluxgate magnetometer. Sensors 2021, 21, 4191. [Google Scholar] [CrossRef] [PubMed]
- Lenz, J.E. A Review of Magnetic Sensors. Proc. IEEE 1990, 78, 973–989. [Google Scholar] [CrossRef]
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Khan, M.A.; Sun, J.; Li, B.; Przybysz, A.; Kosel, J. Magnetic sensors-A review and recent technologies. Eng. Res. Express 2021, 3, 022005. [Google Scholar] [CrossRef]
- Ripka, P. Review of fluxgate sensors. Sens. Actuators A Phys. 1992, 33, 129–141. [Google Scholar] [CrossRef]
- Nielsen, O.V.; Petersen, J.R.; Primdahl, F.; Brauer, P.; Hernando, B.; Fernandez, A.; Merayo, J.M.G.; Ripka, P. Development, construction and analysis of the ‘OErsted’ fluxgate magnetometer. Meas. Sci. Technol. 1995, 6, 1099. [Google Scholar] [CrossRef]
- Magnes, W.; Oberst, M.; Valavanoglou, A.; Hauer, H.; Hagen, C.; Jernej, I.; Neubauer, H.; Baumjohann, W.; Pierce, D.; Means, J.; et al. Highly integrated front-end electronics for spaceborne fluxgate sensors. Meas. Sci. Technol. 2008, 19, 115801. [Google Scholar] [CrossRef]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 26, 1292–1306. [Google Scholar] [CrossRef]
- Kurowski, M.; Thal, J.; Damerius, R.; Korte, H.; Jeinsch, T. Automated survey in very shallow water using an unmanned surface vehicle. IFAC-PapersOnLine 2019, 52, 146–151. [Google Scholar] [CrossRef]
- Roeser, H.A.; Steiner, C.; Schreckenberger, B.; Block, M. Structural development of the Jurassic Magnetic Quiet Zone off Morocco and identification of Middle Jurassic magnetic lineations. J. Geophys. Res. 2002, 107, 2207. [Google Scholar] [CrossRef]
- Key, K.; Constable, S. Inverted long-baseline acoustic navigation of deep-towed CSEM transmitters and receivers. Mar. Geophys. Res. 2021, 42, 6. [Google Scholar] [CrossRef]
- Isezaki, N. A new shipboard three-component magnetometer. Geophysics 1986, 51, 1992–1998. [Google Scholar] [CrossRef]
- Seama, N. Studies of Vector Geomagnetic Anomalies in the Oceans. J. Jpn. Soc. Mar. Surv. Technol. 1992, 4, 41–49. [Google Scholar] [CrossRef]
- Olsen, N.; Clausen, L.T.; Sabaka, T.J.; Brauer, P.; Merayo, J.M.G.; Jørgensen, J.L.; Léger, J.M.; Nielsen, O.V.; Primdahl, F.; Risbo, T. Calibration of the Ørsted vector magnetometer. Earth Planets Space 2003, 55, 11–18. [Google Scholar] [CrossRef]
- Esri. Satellite Imagery. 2024. Available online: https://www.esri.com (accessed on 28 August 2024).
- Korenaga, J. Comprehensive analysis of marine magnetic vector anomalies. J. Geophys. Res. Solid Earth 1995, 100, 365–378. [Google Scholar] [CrossRef]
- Nogi, Y.; Seama, N.; Isezaki, N. Preliminary report of three components of geomagnetic field measured on board the icebreaker SHIRASE during JARE-30, 1988–1989. Proc. NIPR Symp. Antarct. Geosci. 1990, 4, 191–200. [Google Scholar]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International geomagnetic reference field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Seama, N. Cruise Report of KR 05-17; JAMSTEC: Yokosuka-city, Japan, 2005. [Google Scholar] [CrossRef]
- Birsan, M.; Tan, R. The effect of roll and pitch motion on ship magnetic signature. J. Magn. 2016, 21, 503–508. [Google Scholar] [CrossRef]
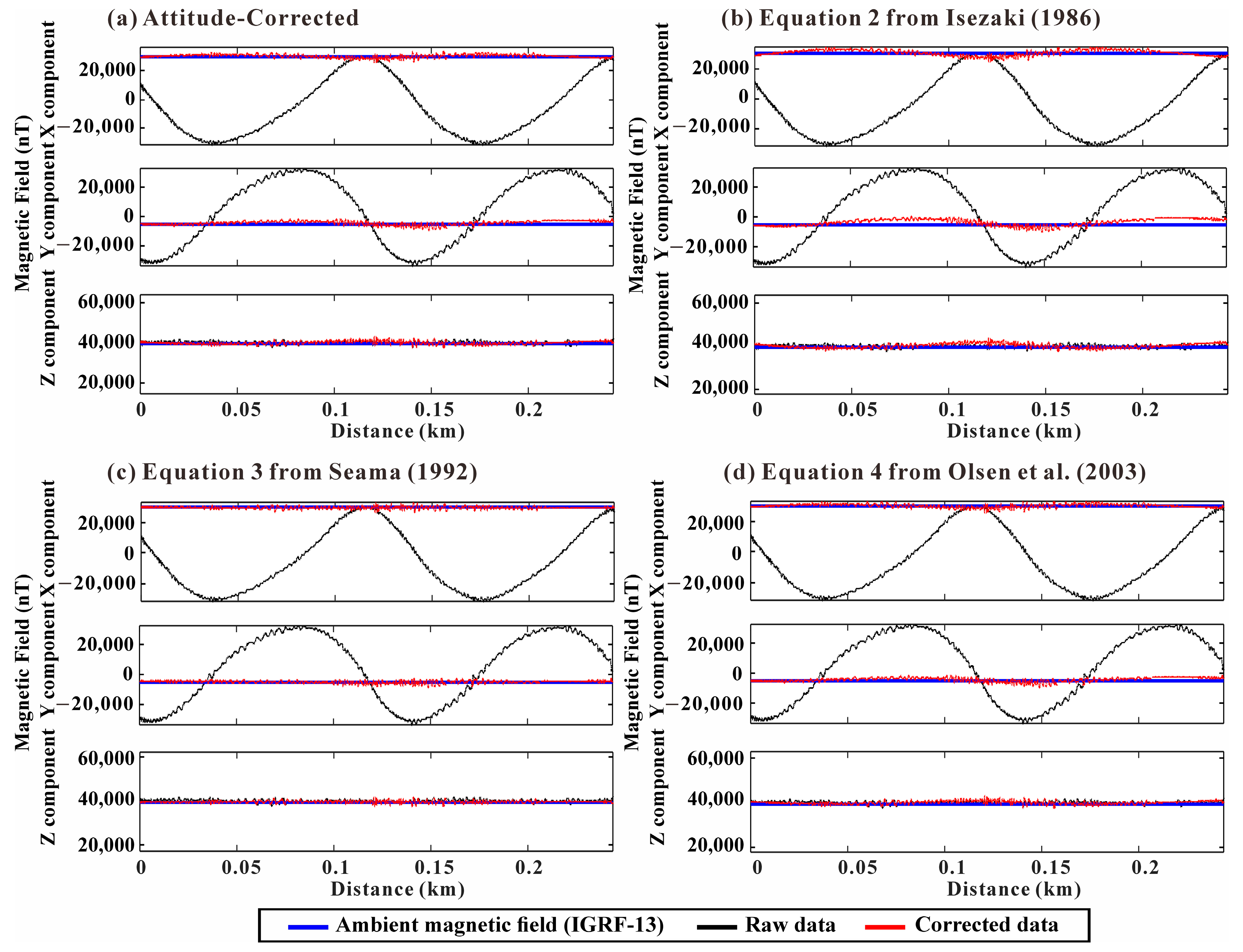


| Correction coefficients from Equation (2) |
| Correction coefficients from Equation (3) |
| Correction coefficients from Equation (4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.; Kim, M.; Park, Y.; Moon, G.; Choe, H. Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys. Sensors 2025, 25, 4511. https://doi.org/10.3390/s25144511
Choi S, Kim M, Park Y, Moon G, Choe H. Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys. Sensors. 2025; 25(14):4511. https://doi.org/10.3390/s25144511
Chicago/Turabian StyleChoi, Seonggyu, Mijeong Kim, Yosup Park, Gidon Moon, and Hanjin Choe. 2025. "Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys" Sensors 25, no. 14: 4511. https://doi.org/10.3390/s25144511
APA StyleChoi, S., Kim, M., Park, Y., Moon, G., & Choe, H. (2025). Magnetic Data Correction for Fluxgate Magnetometers on a Paramagnetic Unmanned Surface Vehicle: A Comparative Analysis in Marine Surveys. Sensors, 25(14), 4511. https://doi.org/10.3390/s25144511






