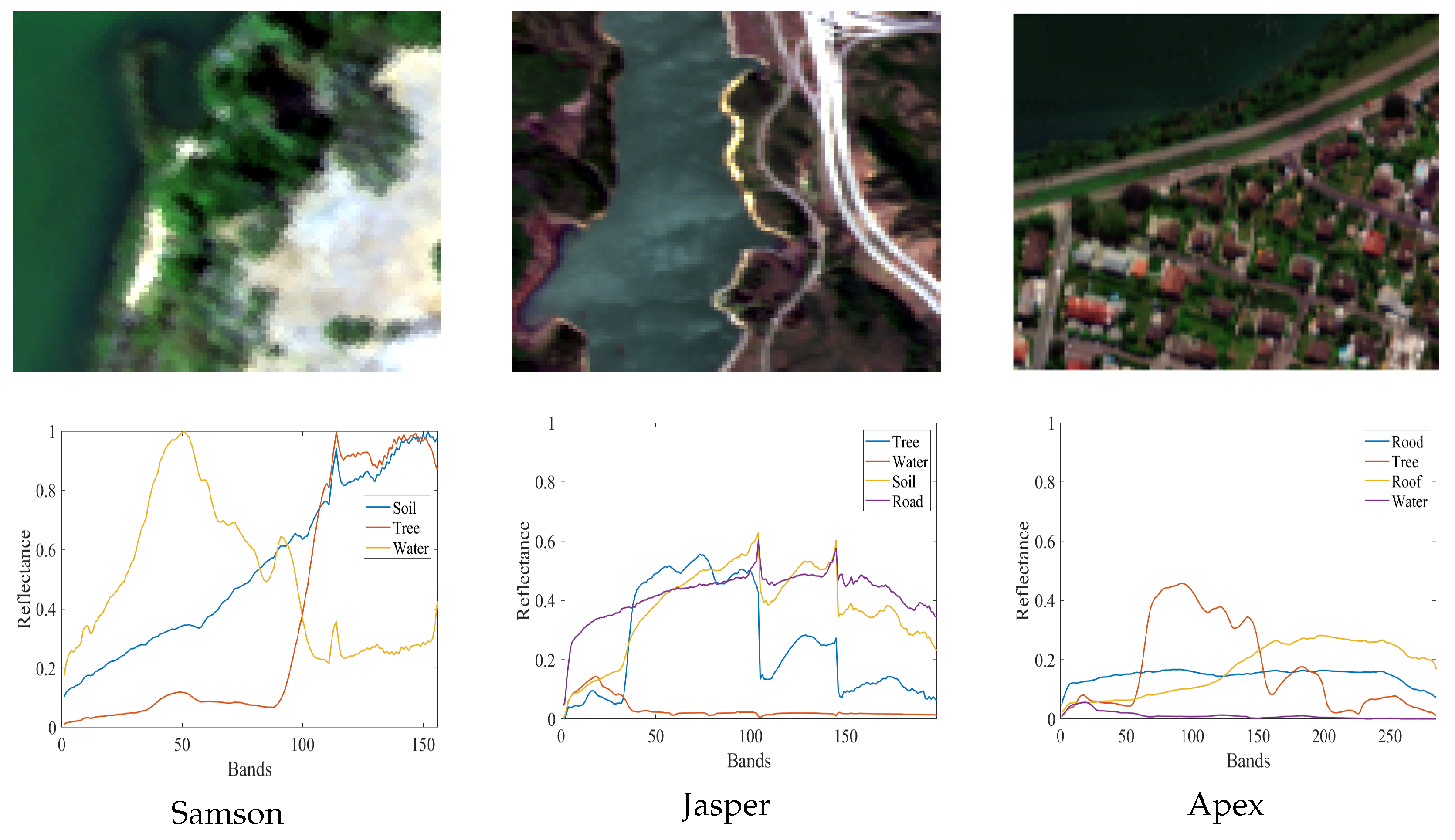
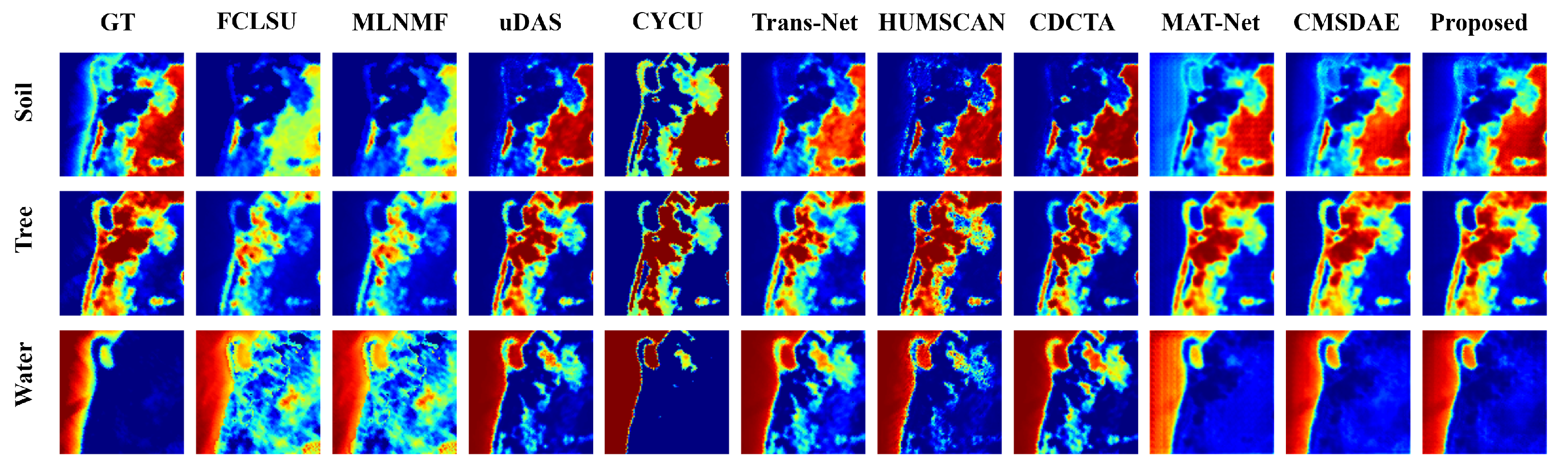
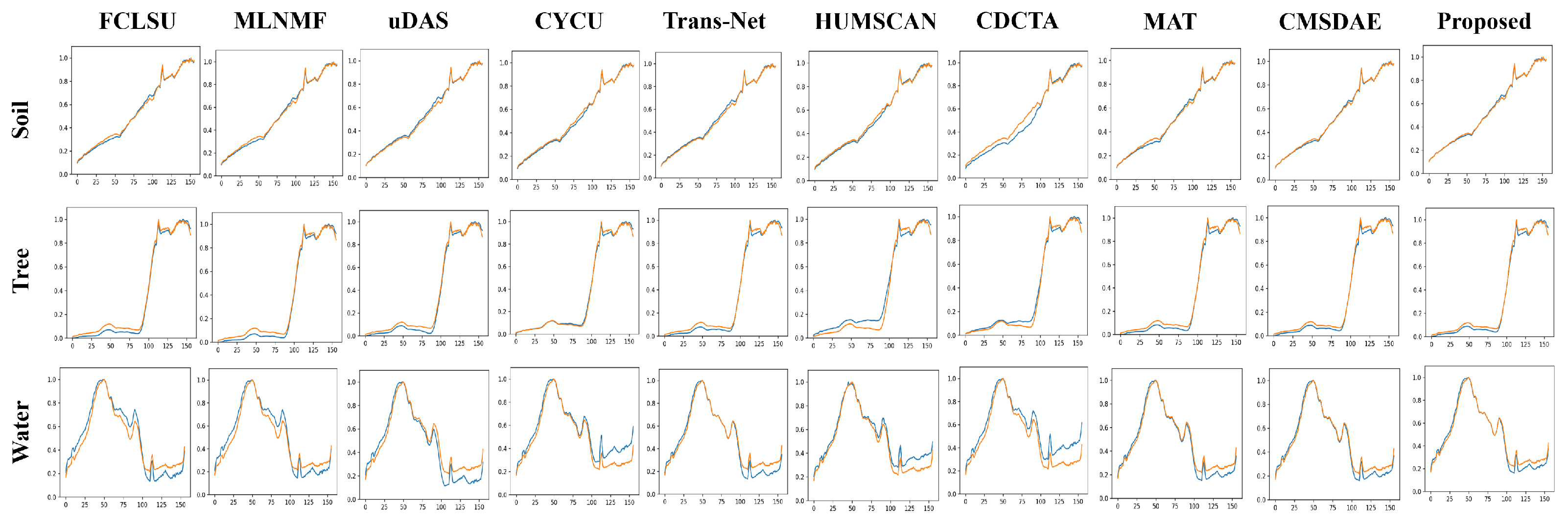
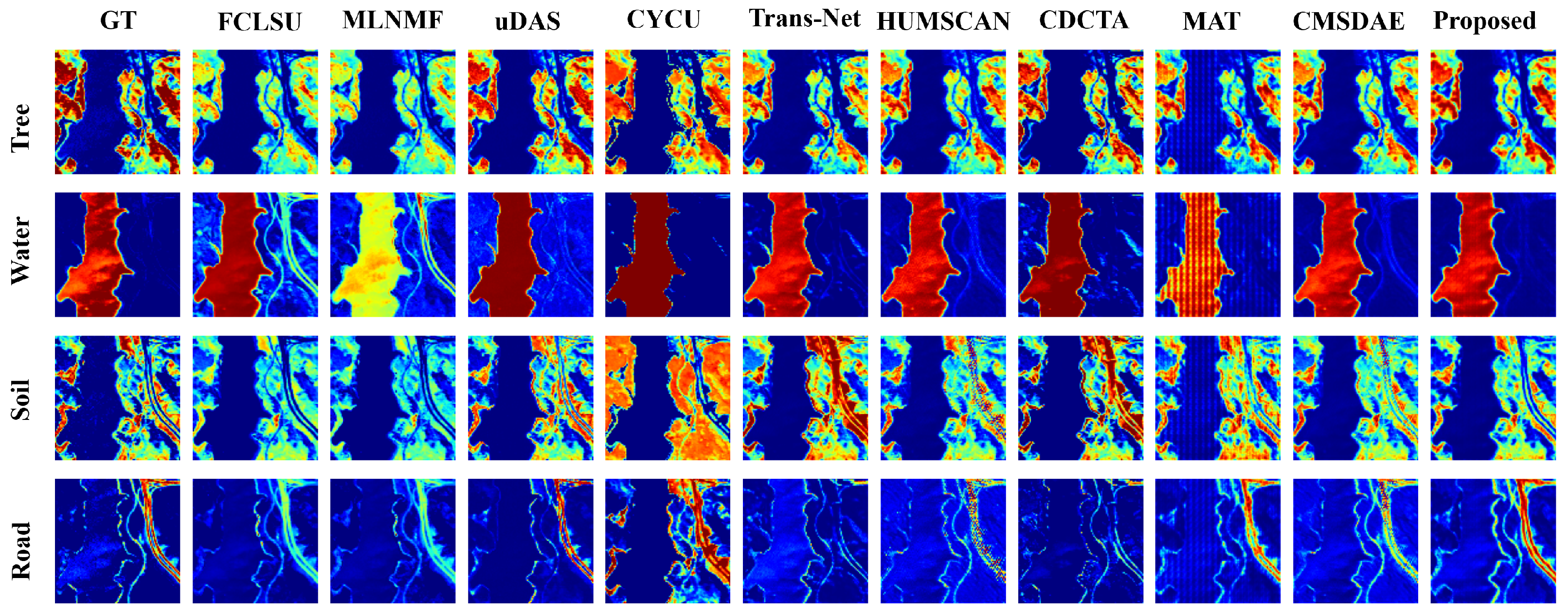
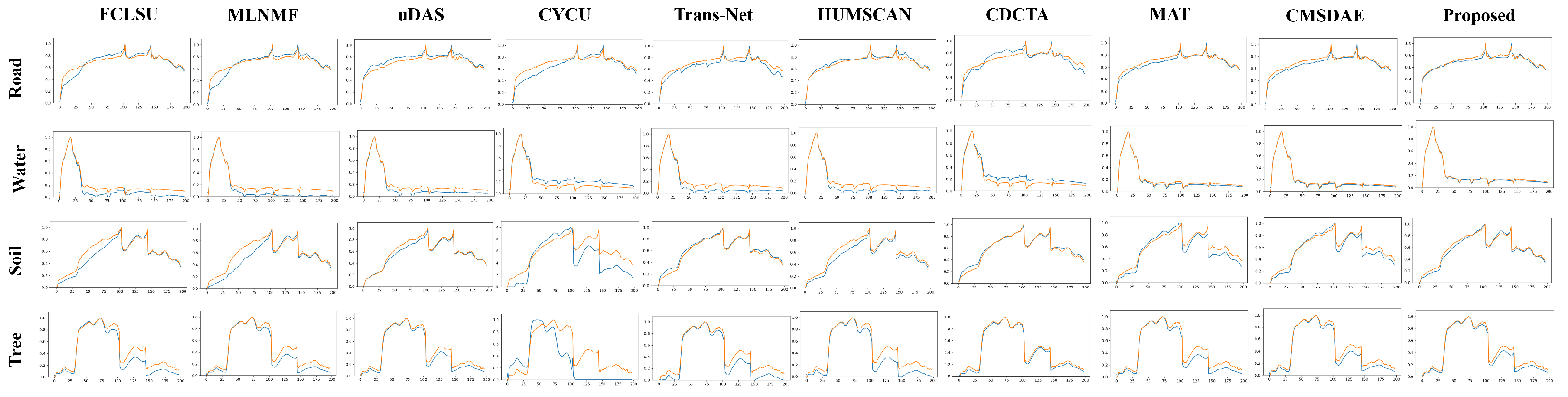
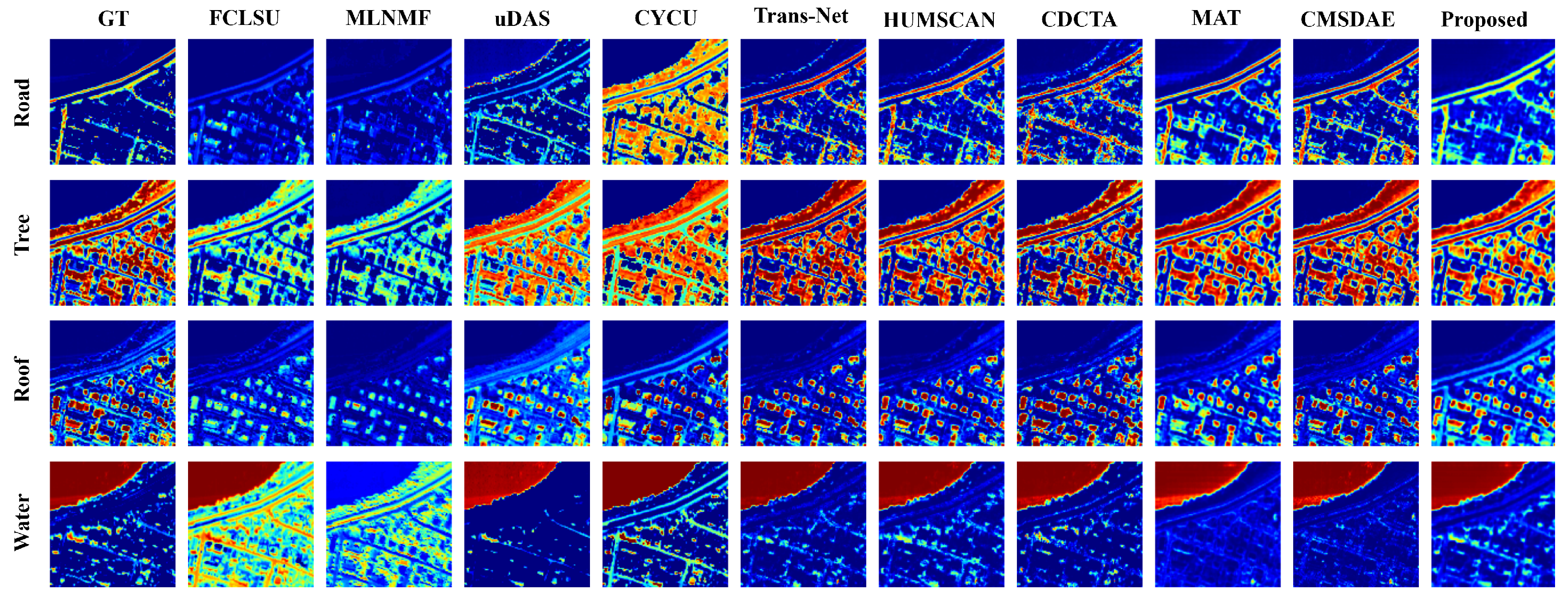
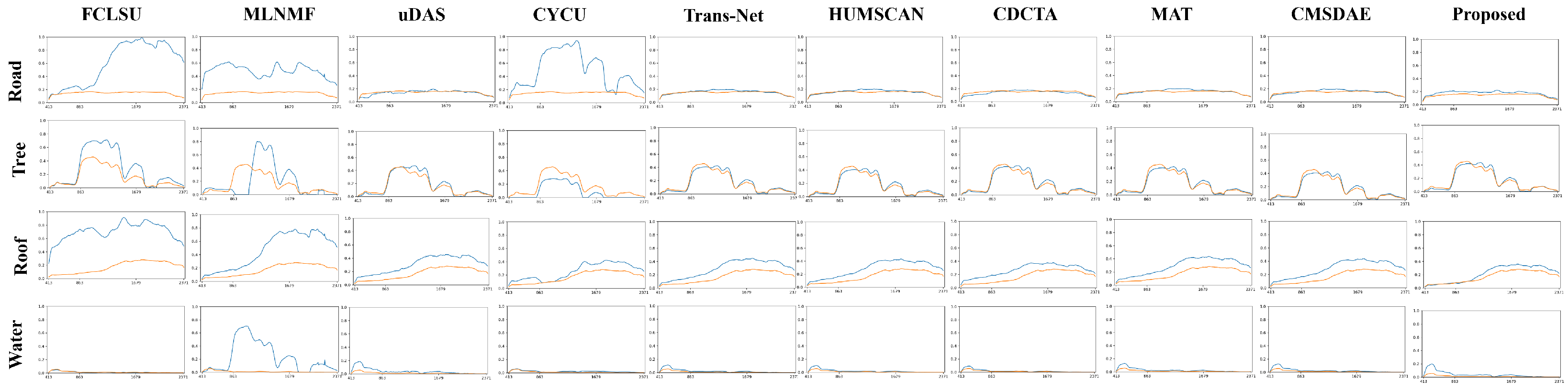
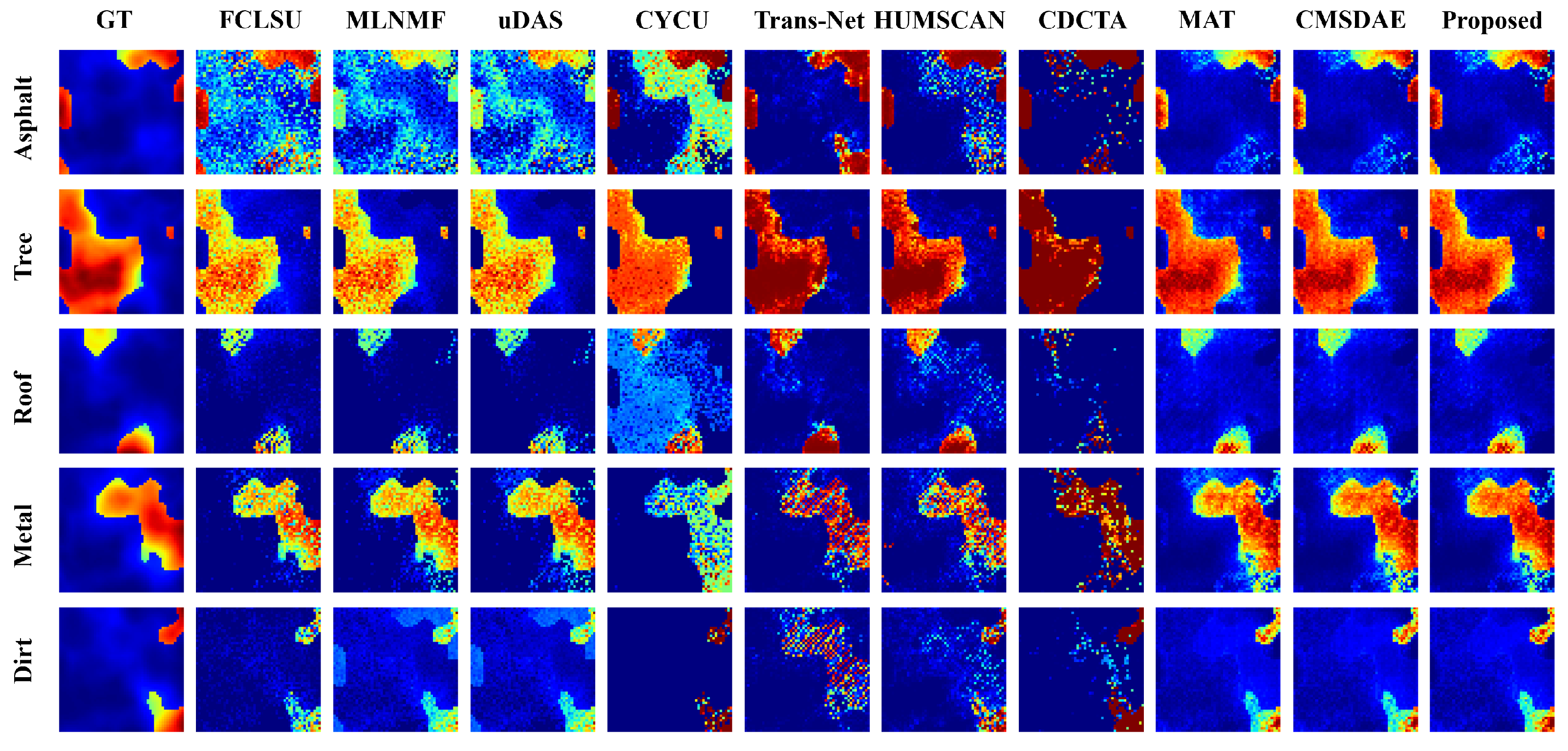
1. Introduction
Hyperspectral images (HSIs) are three-dimensional data cubes that contain both spatial and spectral information, typically consisting of tens to hundreds of spectral bands. These bands typically span a spectral range from the visible to the short-wave infrared regions, approximately from 400 to 2500 nm [
1]. Unlike traditional RGB images that are limited to three channels (red, green, and blue), HSIs provide detailed spectral signatures of materials along with their spatial distribution, making them widely applicable in diverse fields such as food safety [
2], environmental monitoring [
3], and mineral exploration [
4]. However, due to limitations in imaging technology, HSIs generally suffer from a low spatial resolution [
5], where each pixel often contains a mixture of spectral information from multiple materials—commonly referred to as mixed pixels [
6]. The presence of a large number of mixed pixels significantly degrades the performance of HSI-based applications. Therefore, it is essential to decompose these mixed pixels to retrieve the pure spectral components (known as endmembers) and their corresponding proportions within each pixel, a process known as hyperspectral unmixing (HU). The task of extracting the pure spectral signatures from mixed pixels is referred to as endmember extraction [
7], while estimating their proportion in each pixel is called abundance estimation [
8]. Under physically meaningful constraints, abundance values are typically required to satisfy two conditions: the Abundance Nonnegative Constraint (ANC) and the Abundance Sum-to-one Constraint (ASC) [
9,
10].
In HU tasks, the linear mixing model (LMM) [
11] has become the most widely adopted unmixing framework due to its clear physical interpretability and computational simplicity. Based on the LMM assumption, numerous unmixing approaches have been proposed to effectively estimate endmember spectra and their corresponding abundance distributions.
Traditional HU methods include geometric approaches, statistical models [
12], and sparse regression-based techniques [
13,
14]. Among geometric methods, vertex component analysis (VCA) [
15] and fully constrained least squares unmixing (FCLSU) [
16] are widely used. VCA projects the HSI onto directions orthogonal to the subspace formed by the selected endmembers and iteratively extracts potential endmember spectra. Under the assumption that pure pixels exist, this method can effectively identify pure material spectra in the scene, providing a basis for subsequent abundance estimation. FCLSU, on the other hand, performs least-squares regression to estimate abundances given known endmembers, while enforcing the non-negativity and sum-to-one constraints. However, in practical scenarios, pixels composed entirely of a single material are rarely observed, making the pure-pixel assumption often invalid and limiting the applicability of VCA. In addition, the performance of FCLSU heavily relies on the accuracy of the extracted endmembers. If the estimated endmembers deviate from the actual spectra, the resulting abundance maps may also suffer in accuracy, thereby degrading the overall unmixing performance. To address these limitations, a family of methods based on non-negative matrix factorization (NMF) has been proposed [
17,
18,
19,
20]. Unlike geometric approaches, NMF does not depend on the pure-pixel assumption. Instead, it decomposes the observed HSI into a product of two nonnegative matrices representing the endmember spectra and their abundances, respectively. This allows for a fully unsupervised estimation of both components, making NMF more robust in highly mixed scenes. Qian et al. [
21] introduced the
sparsity constraint into NMF for HU, referred to as
-NMF, which improves the unmixing accuracy by promoting sparsity in abundance estimation. Compared with the traditional
-norm, the
-norm induces stronger sparsity and is mathematically non-convex. Rajabi and Ghassemian [
22] proposed a multilayer extension called Multilayer NMF (MLNMF), which iteratively factorizes the observation matrix into multiple hierarchical layers to refine unmixing performance. Sparse regression-based methods assume that each pixel can be represented as a linear combination of a small subset of endmembers from a predefined spectral library. These methods aim to identify both the contributing endmembers and their corresponding proportions through sparse optimization. Bioucas-Dias and Figueiredo [
23] proposed Sparse Unmixing via Variable Splitting and Augmented Lagrangian (SUnSAL), which incorporates a
-norm regularization term to enforce sparsity. SUnSAL is particularly effective when a large spectral library is available and pure pixels are difficult to obtain.
Recently, deep learning (DL) networks have provided effective solutions for HU [
24,
25]. A typical DL-based unmixing framework adopts an autoencoder (AE) architecture, which consists of an encoder and a decoder. The encoder is responsible for extracting low-dimensional representations from the input HSI, which correspond to abundance estimations. The decoder reconstructs the original HSI using the estimated abundances and the learned endmember spectra [
26]. Based on the AE framework, the integration of different feature extraction modules and the design of tailored loss functions can further improve unmixing performance [
27,
28]. For instance, Qu and Qi [
29] proposed an untied denoising autoencoder with sparsity (uDAS), which introduces an
-norm constraint to enhance the accuracy of abundance estimation. This regularization helps reduce redundancy in the learned features and improves the robustness and precision of the encoder in estimating abundance maps. Su et al. [
30] introduced the Stacked Nonnegative Sparse Autoencoders (SNSAEs), which employ an end-to-end fully connected (FC) AE structure. Without explicitly incorporating spatial modeling, this approach leverages spectral feature learning to effectively estimate abundance representations under unsupervised conditions, achieving robust unmixing performance for HSIs.
Early AE-based unmixing methods primarily relied on FC layers to construct the encoder and decoder. During the processing of HSIs, each pixel (or spectral vector) is often treated as an independent sample, or the entire HSI is flattened into a long vector for spectral feature learning. However, these approaches typically ignore the spatial relationships between neighboring pixels. To more effectively leverage the valuable spatial information in HSIs, researchers have introduced convolutional neural networks (CNNs) into AE architectures to further improve HU performance. Palsson et al. [
31] proposed a CNN Autoencoder Unmixing (CNNAEU) framework, which integrates convolutional encoders and decoders to extract spatial features and reconstruct spectral information. This approach enables a more accurate abundance estimation by jointly learning spatial–spectral representations. Rasti et al. [
32] introduced an unsupervised HU method based on deep CNNs, termed Unmixing Deep Prior (UnDIP). By exploiting the structural prior embedded in the network itself, UnDIP models the relationships between endmembers and abundances without external supervision, thereby enhancing unmixing accuracy and robustness. Gao et al. [
33] proposed a Cycle-Consistency Unmixing Network (CyCU-Net), which cascades two autoencoders for HU and introduces cycle-consistency constraints through spectral and abundance reconstruction losses. This framework strengthens the representational capacity of both endmembers and abundances, improving both the accuracy and stability of unmixing. While CNN-based AE unmixing methods are capable of extracting local spatial features, such feature extraction is primarily dependent on the size of convolutional kernels, which inherently rely on limited receptive fields. This constraint hampers their ability to capture long-range spatial dependencies and global spectral relationships, leading to the loss of critical contextual features during unmixing. Moreover, due to the high dimensionality of HSIs, although some CNN-based methods enhance global modeling via encoder–decoder or residual structures, they still rely on stacked local operations, whereas the transformer captures long-range spatial–spectral dependencies more efficiently through self-attention.
Transformer architectures have rapidly gained attention in remote sensing image processing due to their superior ability to model long-range dependencies and capture global contextual features. In recent years, several studies have explored the application of transformers to HU and have achieved promising results [
34,
35,
36]. Ghosh et al. [
37] proposed the first hybrid HU model that combines transformer and CNN architectures. In this approach, the multi-head self-attention mechanism of the transformer is employed to complement the limited receptive field of the CNN, thereby enhancing the robustness and accuracy of the unmixing process. This work laid a foundation for subsequent transformer-based HU research. Recently, there has been increasing interest in integrating CNNs and transformers to further improve unmixing performance. Hu et al. [
34] introduced the Multiscale Convolution Attention Network (HUMSCAN), which consists of an endmember estimation sub-network and an abundance estimation sub-network. By leveraging multiscale convolutions to extract spatial features at different scales and attention mechanisms to enhance salient feature representations, HUMSCAN effectively improves HU performance. Yang et al. [
35] proposed the Cascaded Dual-Constrained Transformer Autoencoder (CDCTA), which constructs a progressive, cascaded structure by stacking multiple transformer encoder–decoder modules. This design enhances the model’s depth and expressive capacity for complex mixed pixels. Moreover, CDCTA incorporates two additional constraints—endmember separability and abundance sparsity—into the network to improve the accuracy of both endmember extraction and abundance estimation. Wang et al. [
38] proposed the Multiscale Aggregation Transformer Network (MAT-Net), which fully exploits CNN-extracted spectral and multiscale spatial features and then fuses them using a transformer encoder. MAT-Net features a dual-stream, multi-branch CNN encoder and an enhanced multiscale self-attention module that adaptively aggregates information across scales, achieving effective and accurate endmember extraction and abundance estimation. Gan et al. [
39] proposed a Channel Multi-Scale Dual-Stream Autoencoder (CMSDAE), which performs multiscale feature modeling along the channel dimension to effectively reduce redundancy in the spatial domain and enhance feature representation, thereby improving the accuracy of endmember extraction and abundance estimation. Hadi et al. [
40] introduced a Dual-branch Spectral–Spatial Feature Fusion Transformer (DSSFT), which integrates spectral and spatial information through two parallel branches. The spectral branch employs a self-attention mechanism to model complex spectral variations and enhance endmember identification, while the spatial branch adopts patch-level embedding to capture global spatial context, improving the discriminative ability for endmembers and abundances in heterogeneous regions. In addition, Xiang et al. [
41] proposed an Endmember-Oriented Transformer Network (EOT-Net), which combines endmember bundle modeling with directional subspace projection to extract endmember-specific features and incorporates a low-redundancy attention mechanism to enhance feature discrimination, effectively improving unmixing accuracy.
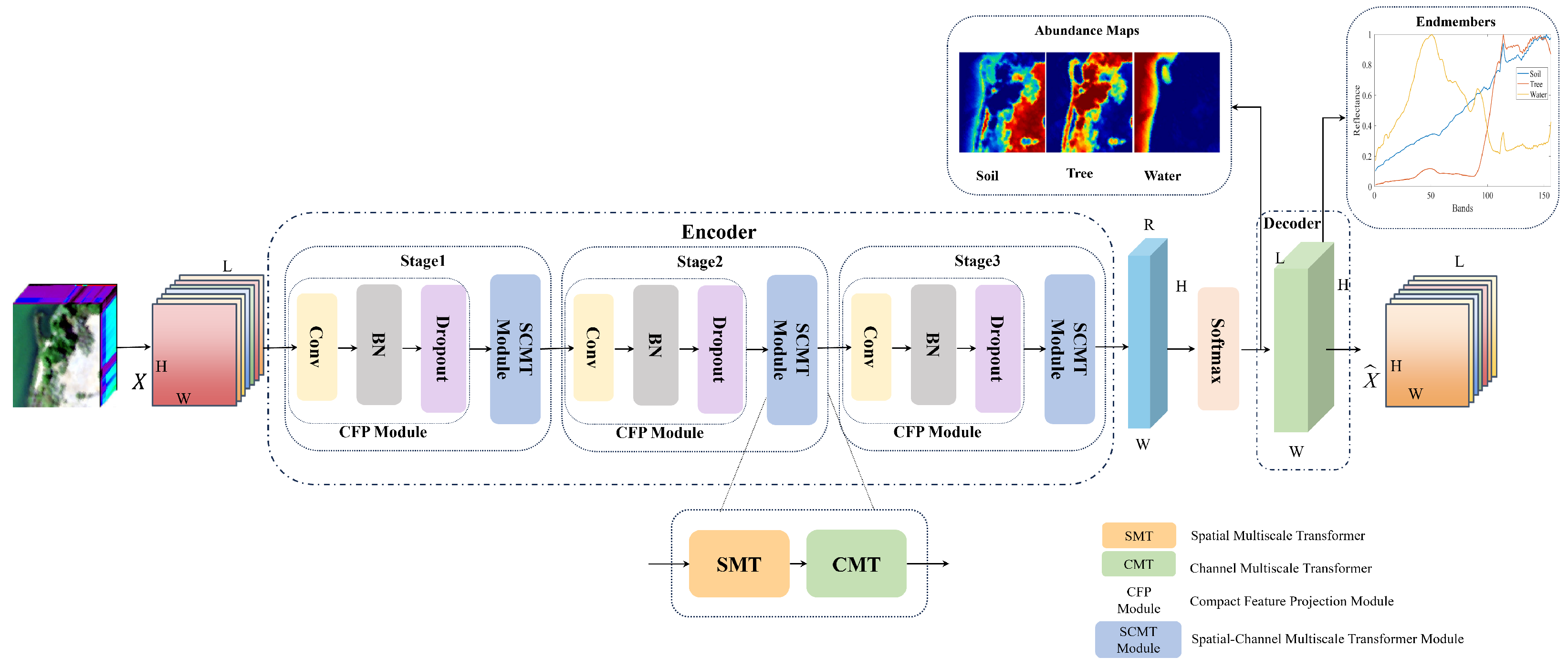
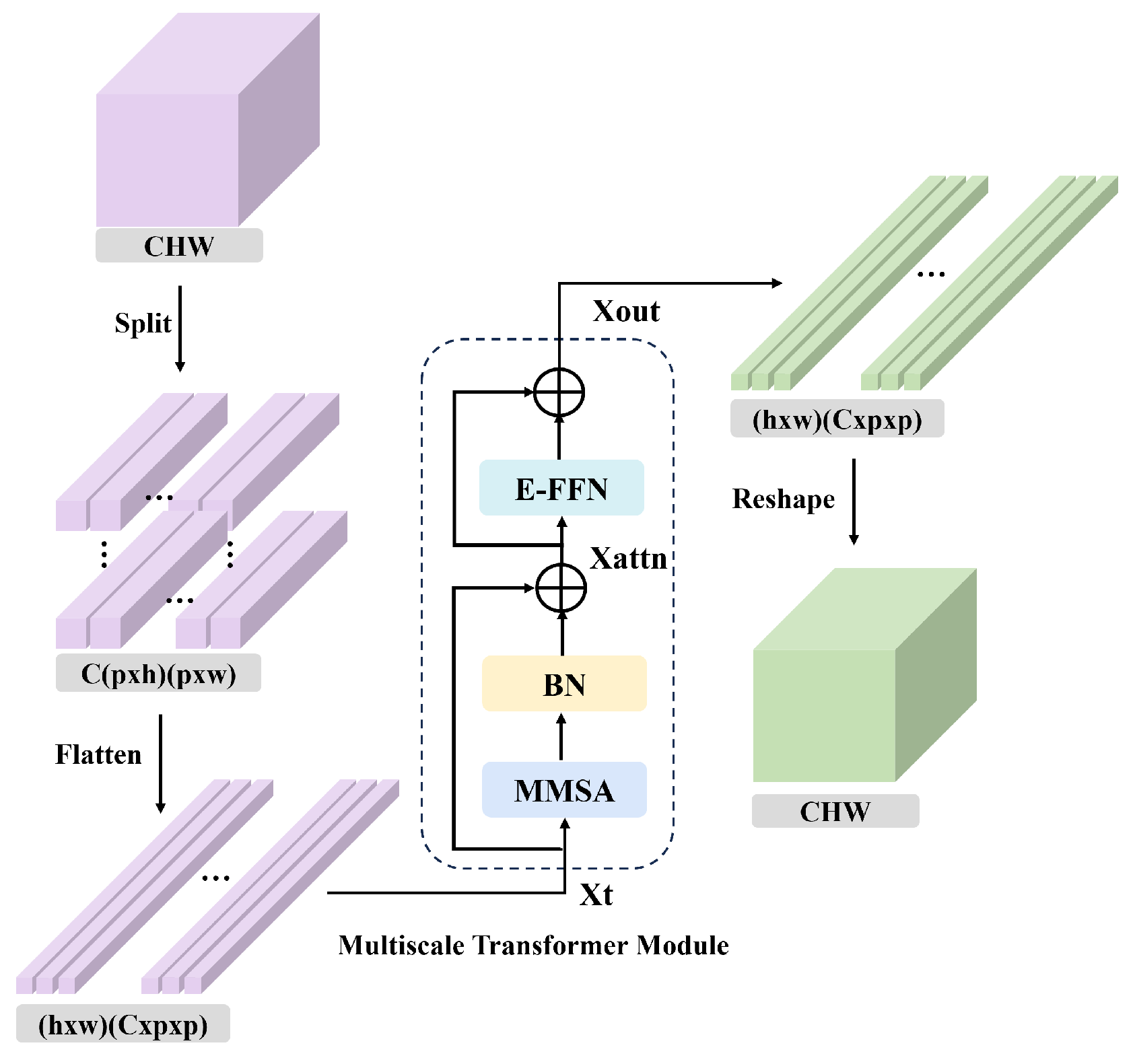
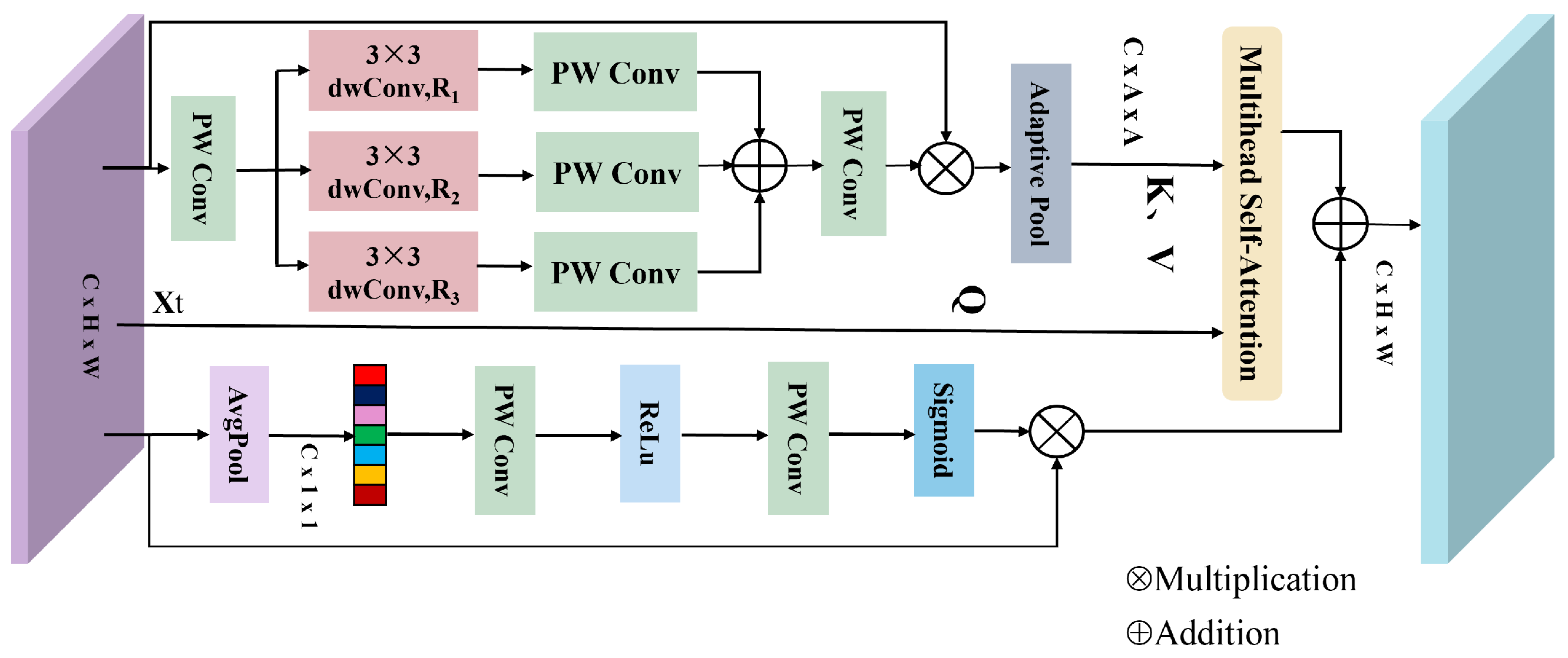
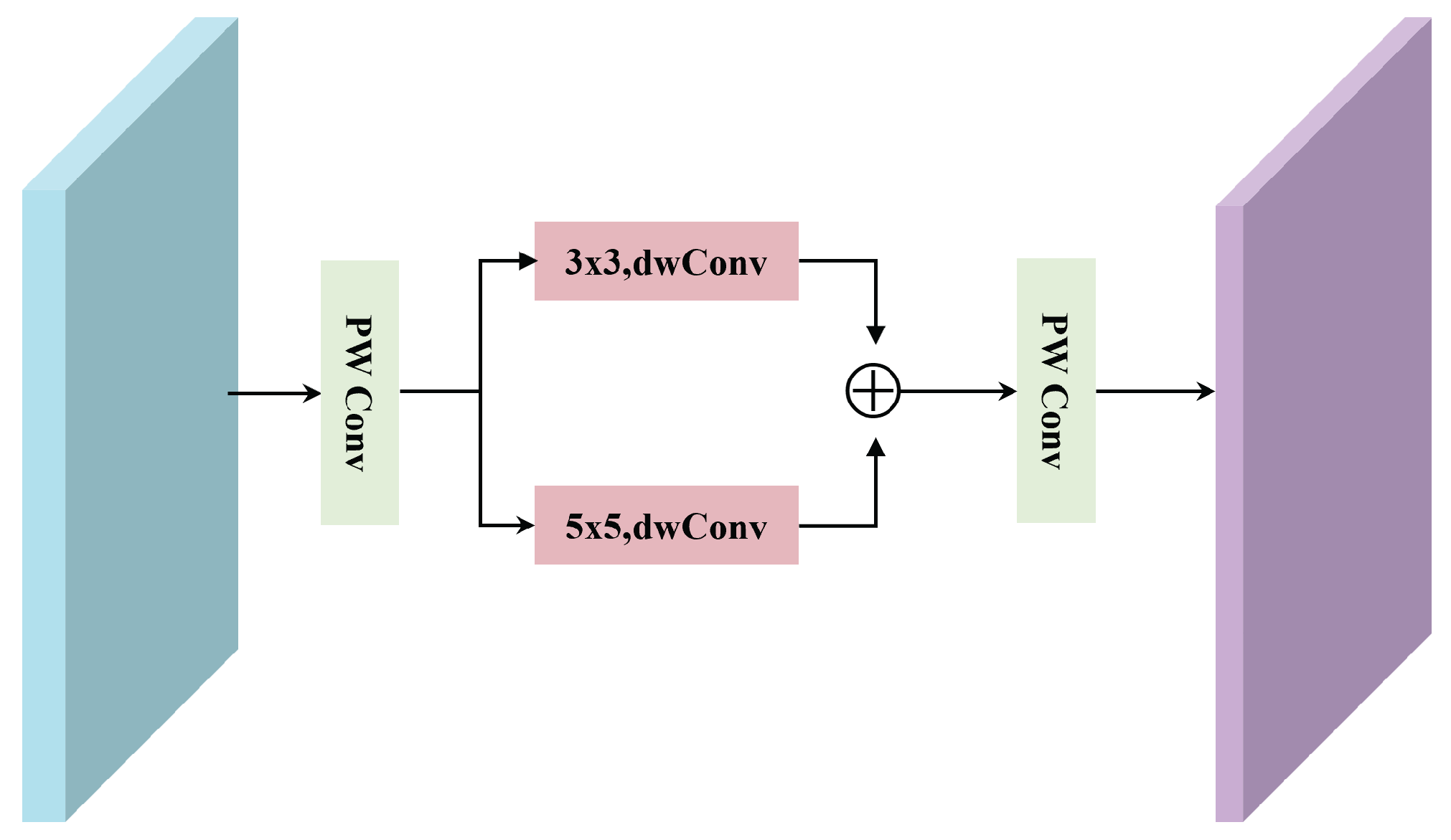
However, existing HU methods that combine CNNs and transformers often fail to fully exploit the channel-wise information of HSIs, and they lack dynamic interaction mechanisms for multiscale global contextual modeling. These limitations restrict the joint representation capability of spatial and spectral features in HSIs. To address this issue, we propose a Spatial-Channel Multiscale Transformer Network (SCMT-Net) for HU. Specifically, a spatial multiscale transformer (SMT) module is first introduced to learn spatial features of the HSI, followed by a channel multiscale transformer (CMT) module designed to capture long-range dependencies across spectral channels. The integration of these two modules enables global and dynamic modeling across spatial and spectral dimensions. Moreover, a multiscale multihead self-attention (MMSA) mechanism is incorporated into both the SMT and CMT modules to effectively extract rich spatial–spectral contextual information. Finally, an efficient feed-forward network (E-FFN) is employed to enhance inter-channel information flow and feature fusion, thereby further improving unmixing performance.
The main contributions of this article are summarized as follows:
1. We propose a novel unmixing network, SCMT-Net, which integrates a CFP module and a spatial-channel multiscale transformer module to enable the collaborative modeling of local details and a global context, achieving the dynamic learning of multiscale spatial and spectral relationships.
2. A CMT module is designed to deeply capture long-range dependencies across HSI spectral channels. By combining it with the SMT module, we construct the core SCMT module, which significantly enhances the modeling capacity of spatial-channel global relationships in complex scenarios.
3. A new MMSA module is introduced, embedding multiscale global contextual and channel information into the attention mechanism to capture rich spatial–spectral features. Additionally, an E-FFN is incorporated to further strengthen inter-channel information interaction, thereby improving overall unmixing performance.
The remainder of this article is organized as follows.
Section 2 introduces the background and related concepts of HU.
Section 3 presents the architecture and fundamental principles of the proposed SCMT-Net.
Section 4 discusses the experimental results on three real-world hyperspectral datasets and one synthetic dataset, including comparisons with several representative HU methods and ablation studies on SCMT-Net. Finally,
Section 5 concludes the article with a summary of key findings.
2. Background
In HSIs, due to the limited spatial resolution and the mixed distribution of surface materials, each pixel typically contains a mixture of multiple pure spectral components (endmembers). The most commonly used LMM assumes that the observed pixel spectrum can be represented as a weighted linear combination of several endmember spectra. Its mathematical expression is given by
The input HSI is denoted as , where H, W, and L represent the height, width, and number of spectral bands of the original HSI, respectively. The HSI can be mathematically reshaped into a matrix , where denotes the total number of pixels and L represents the number of spectral bands. It is important to note that this reshaping is used solely for notational purposes; in practice, the encoder retains the spatial structure before explicitly flattening the input for the transformer. The endmember matrix is denoted as , where R represents the number of endmembers present in the HSI. The corresponding abundance cube (i.e., the stack of R abundance maps) is represented as , which can be reshaped into a matrix ; represents the additive noise present in .
In addition, HU tasks typically require the following three physical constraints to be satisfied:
First, the endmember matrix must be non-negative, that is, ; second, the abundance matrix is subject to the ANC, i.e., ; finally, the ASC must also be satisfied: , where denotes an all-ones column vector of dimension n.
Although the LMM offers good physical interpretability and modeling simplicity, under non-ideal imaging conditions such as illumination variations, terrain undulations, material inhomogeneity, or multipath scattering, the actual mixing process often exhibits pixel-wise spectral variability. This leads to the inability of the LMM to accurately model such complex scenarios. To address this issue, researchers have proposed a generalized version of the LMM, which enhances the adaptability and representational capacity of the model while preserving its linear structure.
GLMM introduces scaling factors for endmembers at the pixel level, allowing endmember spectra to vary across different pixels, thereby enhancing the ability to model spectral variability in real-world scenarios. Its mathematical expression is as follows:
Specifically, denotes the observed spectrum of the nth pixel, denotes the endmember spectral matrix of that pixel, denotes the corresponding abundance vector, and denotes the additive noise. GLMM extends the standard LMM by introducing pixel-level endmember scaling factors, allowing endmembers to vary across different pixels, thereby enhancing the ability to represent spectral variability while preserving the linear mixing structure.
In this study, although SCMT-Net adopts the LMM as a physical foundation and constraint framework for task modeling, the network itself is essentially a nonlinear unmixing method. Its architecture integrates multiscale attention mechanisms, nonlinear activation functions, and multiscale depthwise separable convolution modules, enabling the end-to-end learning of complex nonlinear mappings from input hyperspectral images to abundance maps and endmember spectra. Therefore, SCMT-Net does not rely on the strict linear assumptions of LMM; instead, it builds upon this physical modeling basis to achieve a more expressive and flexible nonlinear modeling process. This design allows the model to maintain robust performance and generalization capability, even under complex mixing scenarios involving pixel-level endmember variability or nonlinear interactions.