Single-Sensor Impact Source Localization Method for Anisotropic Glass Fiber Composite Wind Turbine Blades
Abstract
1. Introduction
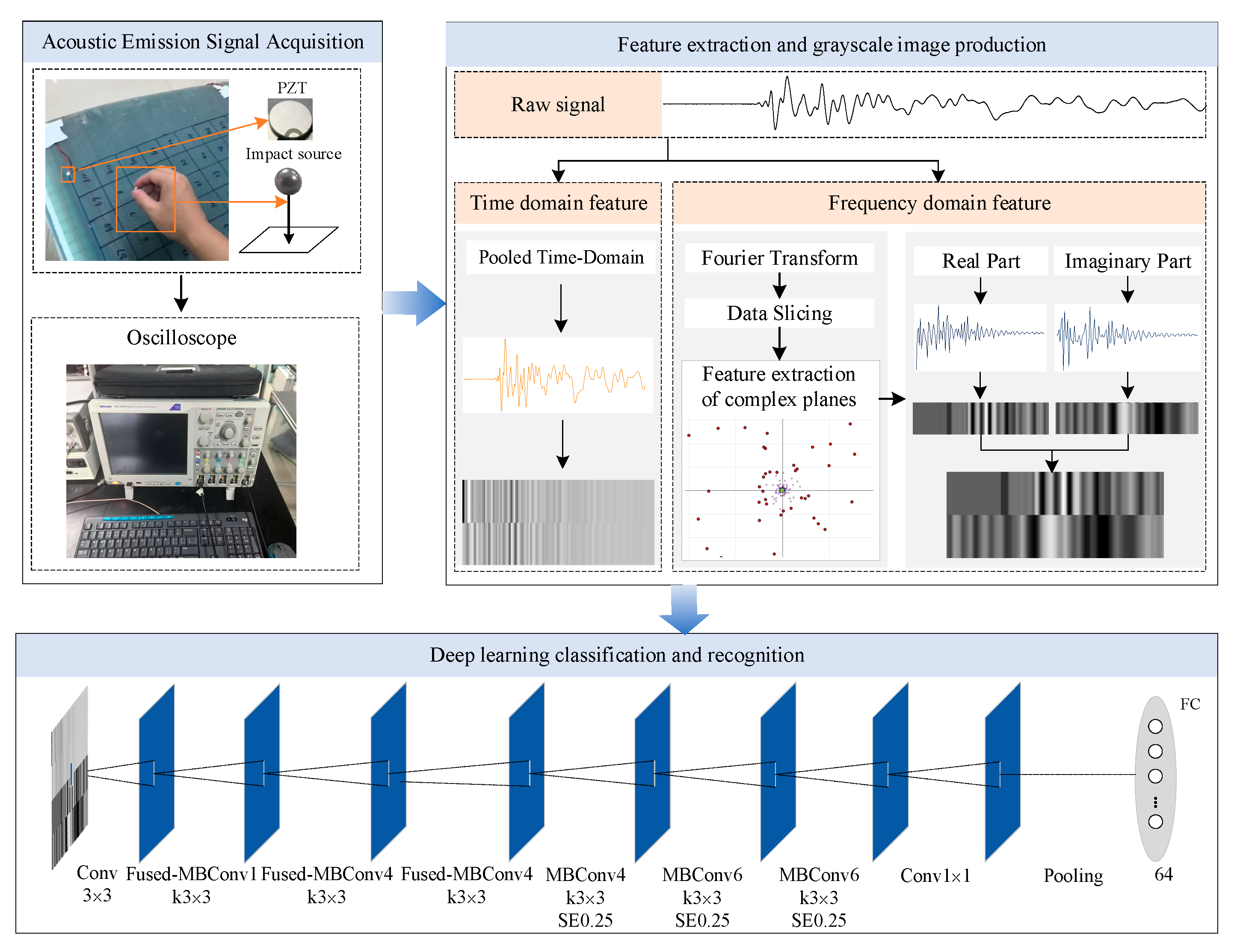
2. Methodology
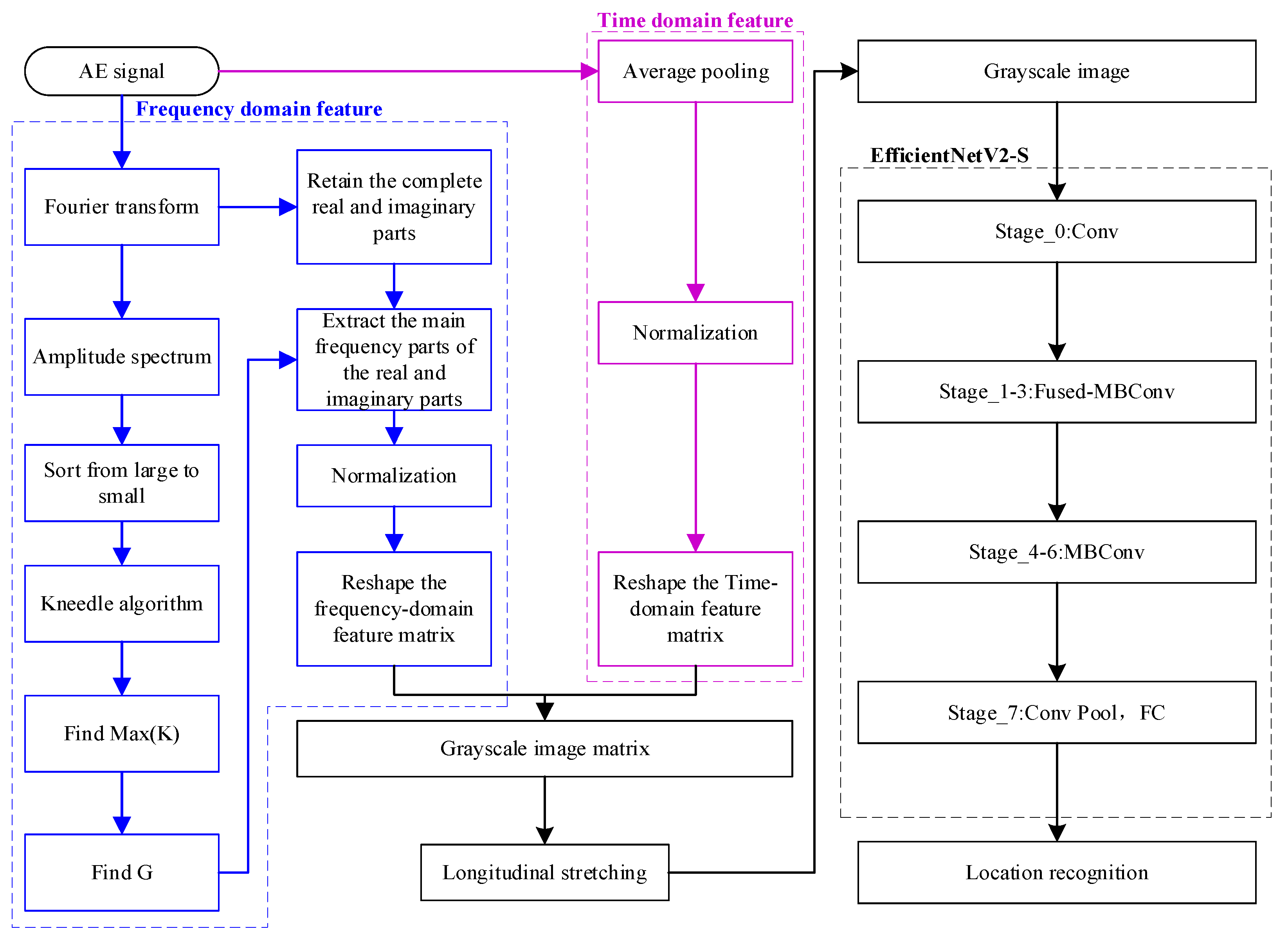
2.1. Feature Matrix Construction
2.1.1. Frequency-Domain Feature Selection
- (1)
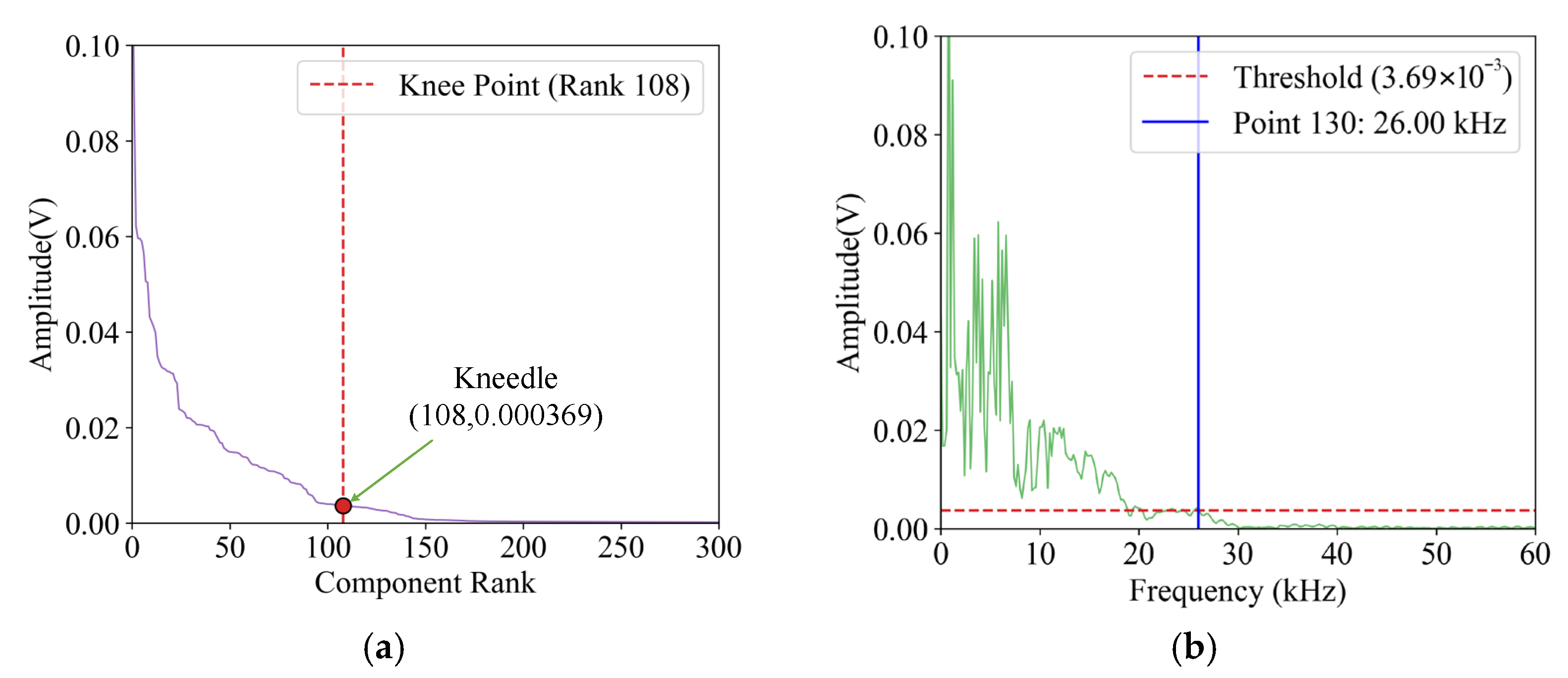
- F(ω) is rearranged in accordance with the amplitude value of each frequency from high to low, giving rise to the reordered spectrogram Fs.
- (2)
- Smoothing splines are employed to retain the waveform of the reordered spectrogram as
- (3)
- The points of the smooth curve are normalized as
- (4)
- The difference curve (i.e., Dd) between the smoothed curve Dsn and the line connecting its first and last points is calculated, i.e.,
- (5)
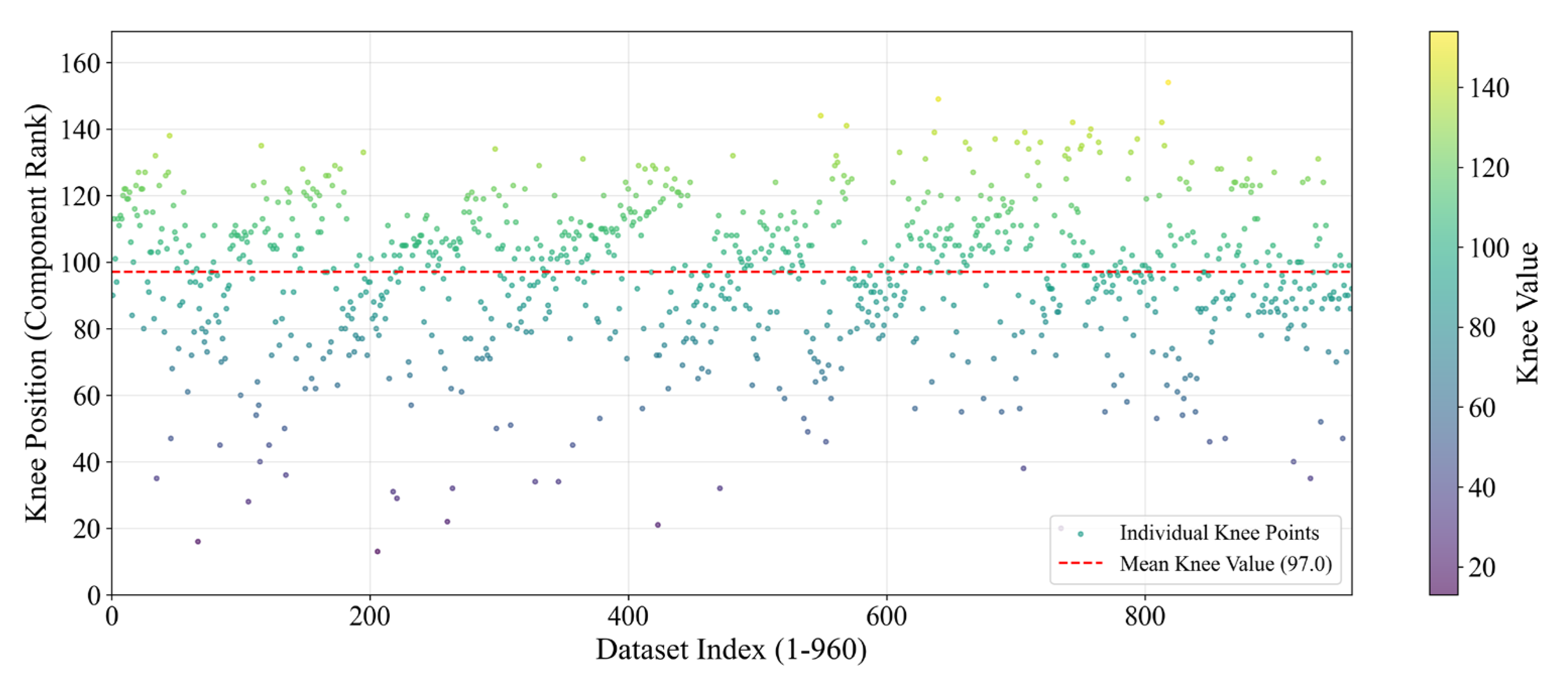
- Local maximum points are identified in the difference curve that correspond to candidate knee points where the original curve converges to a level;
- (6)
- The dynamic threshold is set upon the sensitivity parameter, designated S, which serves to ascertain whether the knee point has been attained;
- (7)
- In the event of a continuous decrease in the data until the next local maximum of the difference curve is reached and the data falls below the threshold of the current local maximum, the current local maximum point is recognized as the knee point, as illustrated in Equation (7). Conversely, if the difference increases, the threshold is reset to 0 and the next local maximum point is sought.
2.1.2. Time-Domain Feature Selection
2.1.3. Feature Matrix Construction and Grayscale Map Transformation
2.2. Impact Source Localization via EfficientNetV2-S
2.2.1. Deep Learning Model Selection
2.2.2. Impact Source Localization
- (1)
- Acoustic Emission Signal Acquisition: Capturing the shock-event-triggered wide-frequency-domain stress wave signals via a single PZT sensor;
- (2)
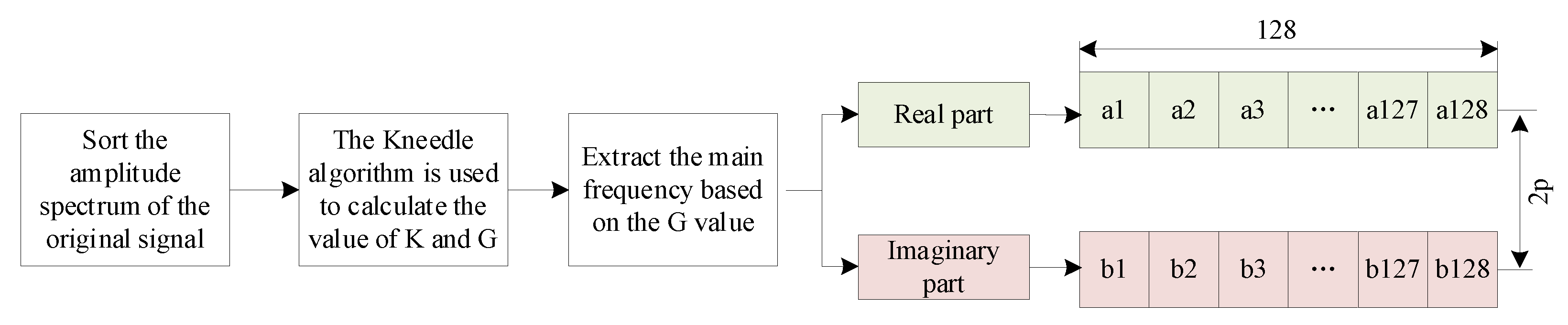
- Feature Extraction: Involving the use of Fourier transform to extract the real and imaginary components in frequency domain, and the compression of time-domain signals by average pooling to preserve their arrival delays and waveform features;
- (3)
- Grayscale Map Transformation: Involving the integration of frequency-domain and time-domain features into a two-dimensional matrix, and then that matrix is normalized and mapped to a 128 × 128 grayscale image;
- (4)
- Model Training and Classification: The grayscale map is to be entered into the EfficientNetV2-S model, with the resultant probability distribution of 64 regions being outputted through the Softmax layer. This completes the classification and identification of the location of the impact source.
3. Experiments
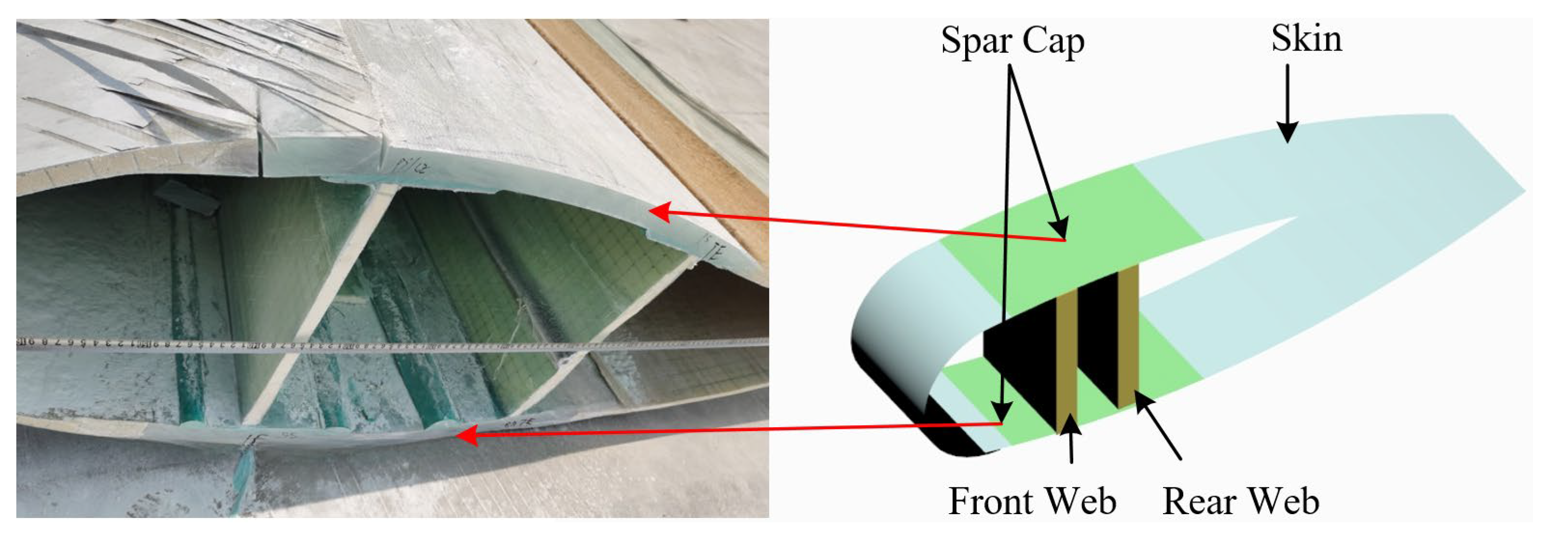
3.1. Experimental Setup
3.2. Experimental Data Processing
4. Results and Discussions
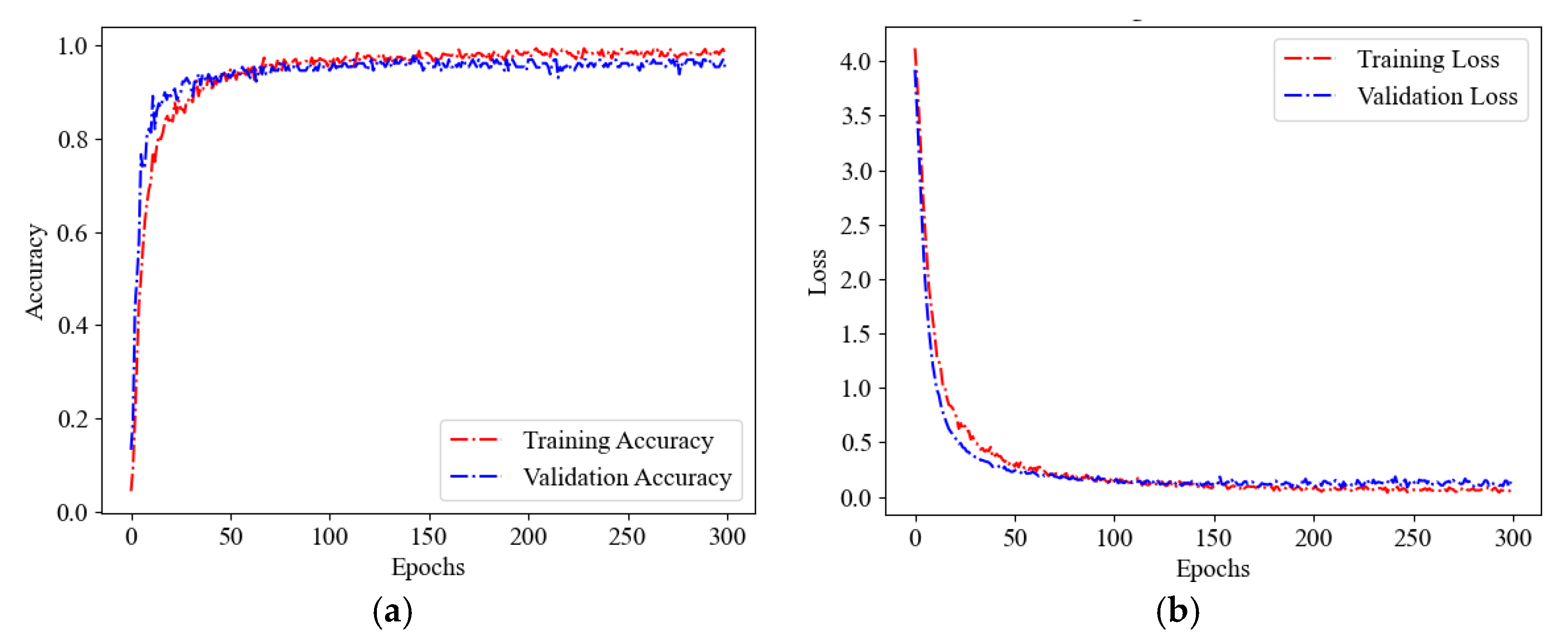
4.1. Impact Source Localization via the Proposed Method
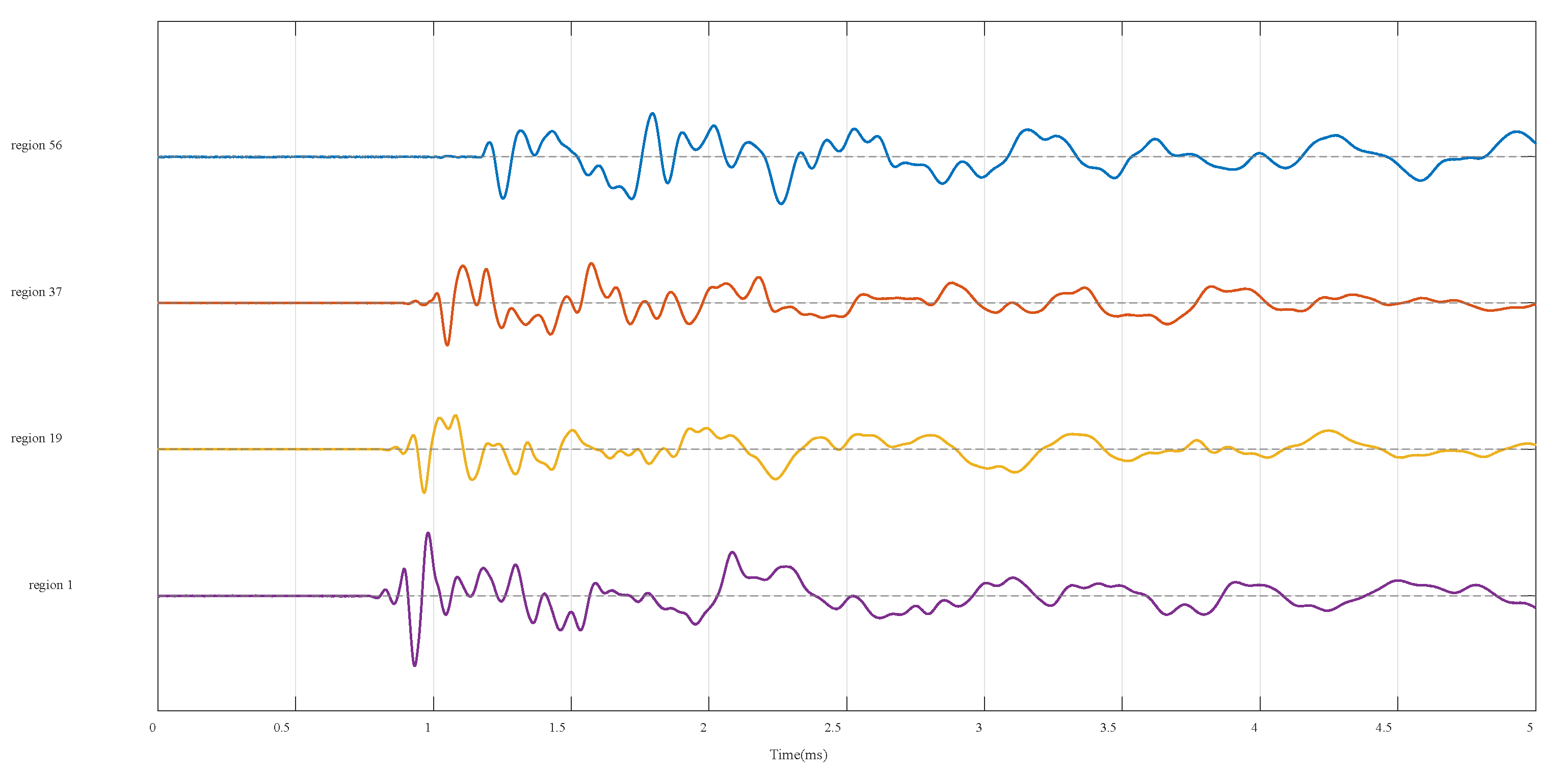
4.2. Error Analysis
5. Conclusions
- (1)
- If features in both frequency and time domains are exploited, a 96.9% localization accuracy is achieved, and there is only one sample in the test set that produces a localization error be larger than one grid, demonstrating the effectiveness and accuracy of the proposed method.
- (2)
- The method converts the impact source localization problem into a classification task. Its spatial localization accuracy depends on the granularity of region division—the finer the division, the smaller the localization error.
- (3)
- The method achieves precise localization of impact sources on wind turbine blade structures without requiring prior knowledge of wave velocity, imposes no restrictions on material properties, and utilizes only a single sensor. It may provide an economic yet efficient monitoring solution for wind turbine blades.
- (4)
- The current validation is limited to single impact events. Performance under simultaneous multi-impact events requires further investigation due to potential signal superposition effects. In addition, while the method imposes no material restrictions theoretically, its performance on other composite materials (e.g., carbon fiber blades) remains untested.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dimitrova, M.; Aminzadeh, A.; Meiabadi, M.S.; Sattarpanah, K.S.; Taheri, H.; Ibrahim, H. A survey on non-destructive smart inspection of wind turbine blades based on industry 4.0 strategy. Appl. Mech. 2022, 3, 1299–1326. [Google Scholar] [CrossRef]
- Cox, K.; Echtermeyer, A. Structural design and analysis of a 10 MW wind turbine blade. Energy Procedia 2012, 24, 194–201. [Google Scholar] [CrossRef]
- Chen, N.Z.; Zhao, Z.; Lin, L. A hybrid deep learning method for AE source localization for heterostructure of wind turbine blades. Mar. Struct. 2024, 94, 103562. [Google Scholar] [CrossRef]
- Wang, W.; Xue, Y.; He, C.; Zhao, Y. Review of the typical damage and damage-detection methods of large wind turbine blades. Energies 2022, 15, 5672. [Google Scholar] [CrossRef]
- Verma, A.S.; Vedvik, N.P.; Haselbach, P.U.; Gao, Z.; Jiang, Z. Comparison of numerical modelling techniques for impact investigation on a wind turbine blade. Compos. Struct. 2019, 209, 856–878. [Google Scholar] [CrossRef]
- Khazaee, M.; Derian, P.; Mouraud, A. A comprehensive study on Structural Health Monitoring (SHM) of wind turbine blades by instrumenting tower using machine learning methods. Renew. Energy 2022, 199, 1568–1579. [Google Scholar] [CrossRef]
- Li, H.; Peng, W.; Huang, C.G.; Guedes, S.C. Failure rate assessment for onshore and floating offshore wind turbines. J. Mar. Sci. Eng. 2022, 10, 1965. [Google Scholar] [CrossRef]
- Li, D.; Ho, S.; Song, G.; Ren, L.; Li, H. A review of damage detection methods for wind turbine blades. Smart Mater. Struct. 2015, 24, 033001. [Google Scholar] [CrossRef]
- Jayawickrema, U.M.N.; Herath, H.M.C.M.; Hettiarachchi, N.K.; Sooriyaarachchi, H.P.; Epaarachchi, J.A. Fibre-optic sensor and deep learning-based structural health monitoring systems for civil structures: A review. Measurement 2022, 199, 111543. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R.; Gómez, J. Post-processing algorithms for distributed optical fiber sensing in structural health monitoring applications. Struct. Health Monit. 2021, 20, 661–680. [Google Scholar] [CrossRef]
- Jiménez, A.A.; Muñoz, C.Q.G.; Márquez, F.P.G. Machine learning for wind turbine blades maintenance management. Energies 2018, 11, 13. [Google Scholar] [CrossRef]
- Andreades, C.; Fierro, G.P.M.; Meo, M. A nonlinear ultrasonic SHM method for impact damage localisation in composite panels using a sparse array of piezoelectric PZT transducers. Ultrasonics 2020, 108, 106181. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Luo, Z.; Zeng, L.; Lin, J. Detection and localization of corrosion using the combination information of multiple Lamb wave modes. Ultrasonics 2024, 138, 107246. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Yu, K.; Lu, S. Direction finding for transient acoustic source based on biased TDOA measurement. IEEE Trans. Instrum. Meas. 2016, 65, 2442–2453. [Google Scholar] [CrossRef]
- Li, X.; Deng, Z.D.; Rauchenstein, L.T.; Carlson, T.J. Contributed Review: Source-localization algorithms and applications using time of arrival and time difference of arrival measurements. Rev. Sci. Instrum. 2016, 87, 041502. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, K.; Luo, Z.; Zhang, J.; Bi, Y. Damage identification of wind turbine blades based on acoustic emission. Insight 2022, 64, 279–284. [Google Scholar] [CrossRef]
- Kouroussis, D.; Anastassopoulos, A.; Vionis, P.; Kolovos, V. Acoustic emission monitoring of a 12 m wind turbine FRP blade during static and fatigue loading. In Emerging Technologies in NDT; CRC Press: Boca Raton, FL, USA, 2022; pp. 59–66. [Google Scholar]
- Hay, D.R.; Cavaco, J.A.; Mustafa, V. Monitoring the civil infrastructure with acoustic emission: Bridge case studies. J. Acoust. Emiss. 2009, 27, 1–10. [Google Scholar]
- Shi, Q.; Zhang, J.; Jin, Y. Recent progress and development trends of acoustic emission detection technology for concrete structures. Water Conserv. Civ. Constr. 2023, 1, 406–412. [Google Scholar]
- So, H.C.; Hui, S.P. Constrained location algorithm using TDOA measurements. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E Ser. 2003, 86, 3291–3293. [Google Scholar]
- Zhou, J.; Cai, X.; Rui, Y.; Chen, L.; Wan, H. Acoustic emission source location considering refraction in layered media with cylindrical surface. Trans. Nonferrous Met. Soc. China 2020, 30, 789–799. [Google Scholar] [CrossRef]
- Ai, L.; Zhang, B.; Ziehl, P. A transfer learning approach for acoustic emission zonal localization on steel plate-like structure using numerical simulation and unsupervised domain adaptation. Mech. Syst. Signal Process. 2023, 192, 110216. [Google Scholar] [CrossRef]
- Lu, J.; Zheng, Y.; Zhang, H.; Cao, Y. Bayesian approach of elliptical loci and RAPID for damage localization in wind turbine blade. Smart Mater. Struct. 2024, 33, 045008. [Google Scholar] [CrossRef]
- Al-Jumaili, S.K.; Pearson, M.R.; Holford, K.M.; Eaton, M.J.; Pullin, R. Acoustic emission source location in complex structures using full automatic delta T mapping technique. Mech. Syst. Signal Process. 2016, 72, 513–524. [Google Scholar] [CrossRef]
- Bhandari, B.; Maung, P.T.; Prusty, G.B. Novel response surface technique for composite structure localization using variable acoustic emission velocity. Sensors 2024, 24, 3450. [Google Scholar] [CrossRef]
- Jones, M.R.; Rogers, T.J.; Worden, K.; Cross, E.J. A Bayesian methodology for localising acoustic emission sources in complex structures. Mech. Syst. Signal Process. 2022, 163, 108143. [Google Scholar] [CrossRef]
- Zhou, Z.; Rui, Y.; Cai, X.; Lu, J. Constrained total least squares method using TDOA measurements for jointly estimating acoustic emission source and wave velocity. Measurement 2021, 182, 109758. [Google Scholar] [CrossRef]
- Sikdar, S.; Mirgal, P.; Banerjee, S.; Ostachowicz, W. Damage-induced acoustic emission source monitoring in a honeycomb sandwich composite structure. Compos. B Eng. 2019, 158, 179–188. [Google Scholar] [CrossRef]
- Li, Y.; Cao, M.; Hoa, T.N.; Khatir, S.; Minh, H.L.; Thanh, S.; Thanh, C.D.; Wahab, M.A. Metamodel-assisted hybrid optimization strategy for model updating using vibration response data. Adv. Eng. Softw. 2023, 185, 103515. [Google Scholar] [CrossRef]
- Thanh, B.T.; Thanh, N.C.; Thang, L.X.; Hoa, T.N. Enhancing bridge damage assessment: Adaptive cell and deep learning approaches in time-series analysis. Constr. Build. Mater. 2024, 439, 137240. [Google Scholar] [CrossRef]
- Hoa, T.N.; Thanh, L.X.; Khatir, S.; Roeck, G.D.; Thanh, B.T.; Wahab, M.A. A promising approach using Fibonacci sequence-based optimization algorithms and advanced computing. Sci. Rep. 2023, 13, 3405. [Google Scholar] [CrossRef]
- Loutas, T.; Eleftheroglou, N.; Zarouchas, D. A data-driven probabilistic framework towards the in-situ prognostics of fatigue life of composites based on acoustic emission data. Compos. Struct. 2017, 161, 522–529. [Google Scholar] [CrossRef]
- Fu, T.; Zhang, Z.; Liu, Y.; Leng, J. Development of an artificial neural network for source localization using a fiber optic acoustic emission sensor array. Struct. Health Monit. 2015, 14, 168–177. [Google Scholar] [CrossRef]
- Guo, C.; Jiang, L.; Yang, F.; Yang, Z.; Zhang, X. Impact load identification and localization method on thin-walled cylinders using machine learning. Smart Mater. Struct. 2023, 32, 065018. [Google Scholar] [CrossRef]
- Satopaa, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a” kneedle” in a haystack: Detecting knee points in system behavior. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops (IEEE), Minneapolis, MN, USA, 20–24 June 2011; pp. 166–171. [Google Scholar]
- Liang, P.; Zhang, Y.; Yao, X.; Yu, G.; Han, Q.; Liu, J. Objective determination of initiation stress and damage stress in rock failure using acoustic emission and digital image correlation. Alex. Eng. J. 2025, 121, 156–166. [Google Scholar] [CrossRef]
- Gholamalinezhad, H.; Khosravi, H. Pooling methods in deep neural networks: A review. arXiv 2020, arXiv:2009.07485. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 2002, 86, 2278–2324. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the International Conference on Machine Learning (PMLR), Virtual, 18–24 July 2021; pp. 10096–10106. [Google Scholar]





| Stage | Operator | Stride | Channels | Layers | Kernel_Size |
|---|---|---|---|---|---|
| 0 | Conv | 2 | 24 | 1 | 3 |
| 1 | Fused-MBConv1 | 1 | 24 | 2 | 3 |
| 2 | Fused-MBConv4 | 2 | 48 | 4 | 3 |
| 3 | Fused-MBConv4 | 2 | 64 | 4 | 3 |
| 4 | MBConv4 | 2 | 128 | 6 | 3 |
| 5 | MBConv6 | 1 | 160 | 9 | 3 |
| 6 | MBConv6 | 2 | 256 | 15 | 3 |
| 7 | Conv&Pooling&FC | - | 1280 | 1 | 1 |
| Feature Combinations | Localization Accuracy | Statistics of Misclassified Cases | |
|---|---|---|---|
| Xerror ≤ 1 & Yerror ≤ 1 | Xerror > 1 or Yerror > 1 | ||
| Real part only | 68.8% | 16 | 24 |
| Imaginary part only | 75.8% | 11 | 20 |
| Real + Imaginary parts | 86.7% | 8 | 9 |
| Real + Imaginary parts + Time domain features | 96.9% | 3 | 1 |
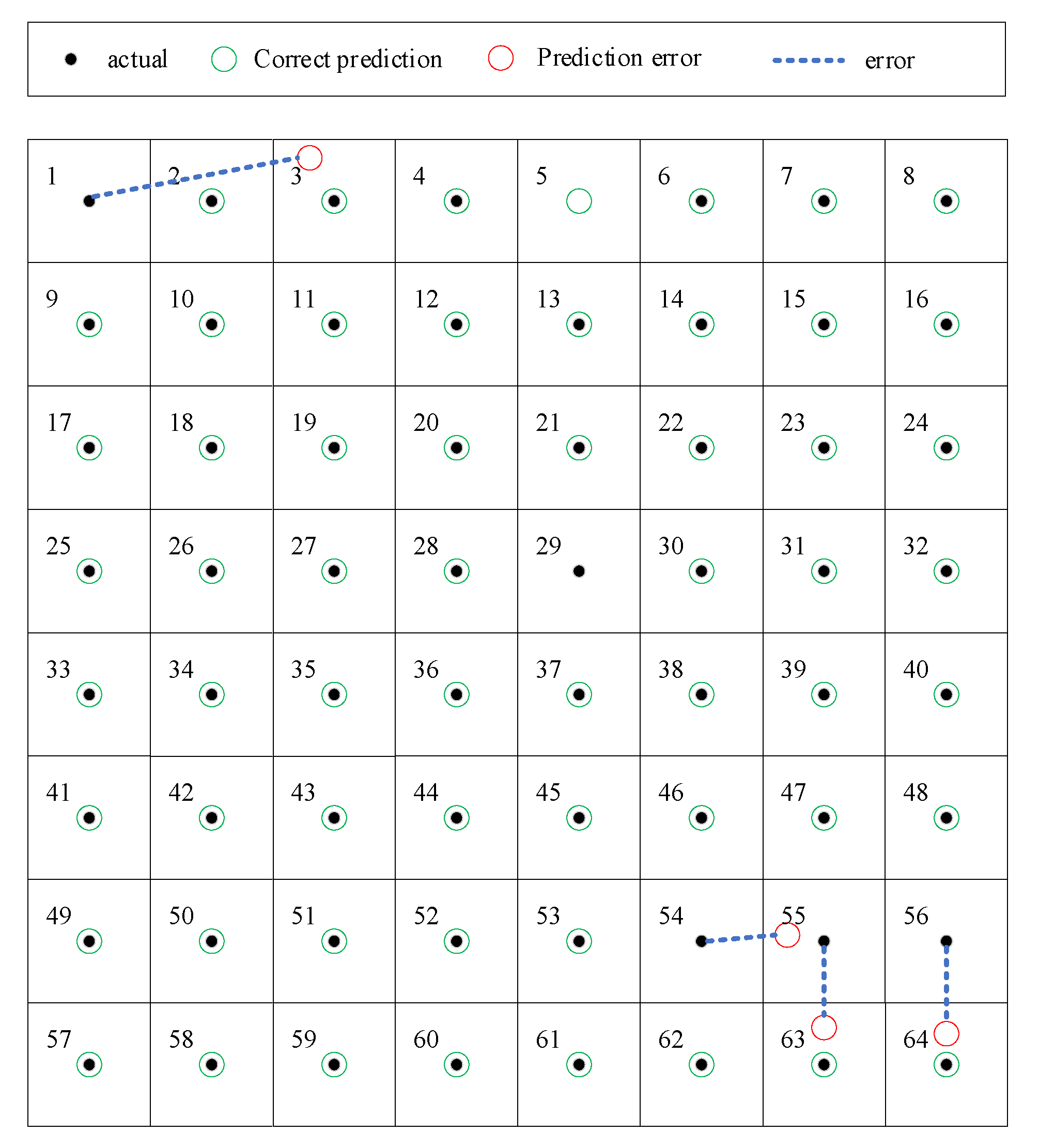
| Actual Region | Predicted Region | Xerror | Yerror |
|---|---|---|---|
| 1 | 3 | 2 | 0 |
| 54 | 55 | 1 | 0 |
| 55 | 63 | 0 | 1 |
| 56 | 64 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Lu, K.; Zeng, L. Single-Sensor Impact Source Localization Method for Anisotropic Glass Fiber Composite Wind Turbine Blades. Sensors 2025, 25, 4466. https://doi.org/10.3390/s25144466
Huang L, Lu K, Zeng L. Single-Sensor Impact Source Localization Method for Anisotropic Glass Fiber Composite Wind Turbine Blades. Sensors. 2025; 25(14):4466. https://doi.org/10.3390/s25144466
Chicago/Turabian StyleHuang, Liping, Kai Lu, and Liang Zeng. 2025. "Single-Sensor Impact Source Localization Method for Anisotropic Glass Fiber Composite Wind Turbine Blades" Sensors 25, no. 14: 4466. https://doi.org/10.3390/s25144466
APA StyleHuang, L., Lu, K., & Zeng, L. (2025). Single-Sensor Impact Source Localization Method for Anisotropic Glass Fiber Composite Wind Turbine Blades. Sensors, 25(14), 4466. https://doi.org/10.3390/s25144466







