Meta-Learning Task Relations for Ensemble-Based Temporal Domain Generalization in Sensor Data Forecasting
Abstract
1. Introduction
- We propose METDG, a novel ensemble-based meta-learning framework that segments sensor time series into semantically meaningful tasks and learns task-specific forecasting models via variational inference. A Transformer-based encoder is further leveraged to capture long-range inter-task relationships and generate relationship-aware model parameters.
- We design an adaptive ensemble inference mechanism that evaluates each query using all task-specific models, enabling the dynamic integration of temporal perspectives.
- We conduct extensive experiments on different real-world temporal forecasting tasks to show that our method outperforms state-of-the-art time series prediction methods and temporal domain generalization methods.
2. Related Work
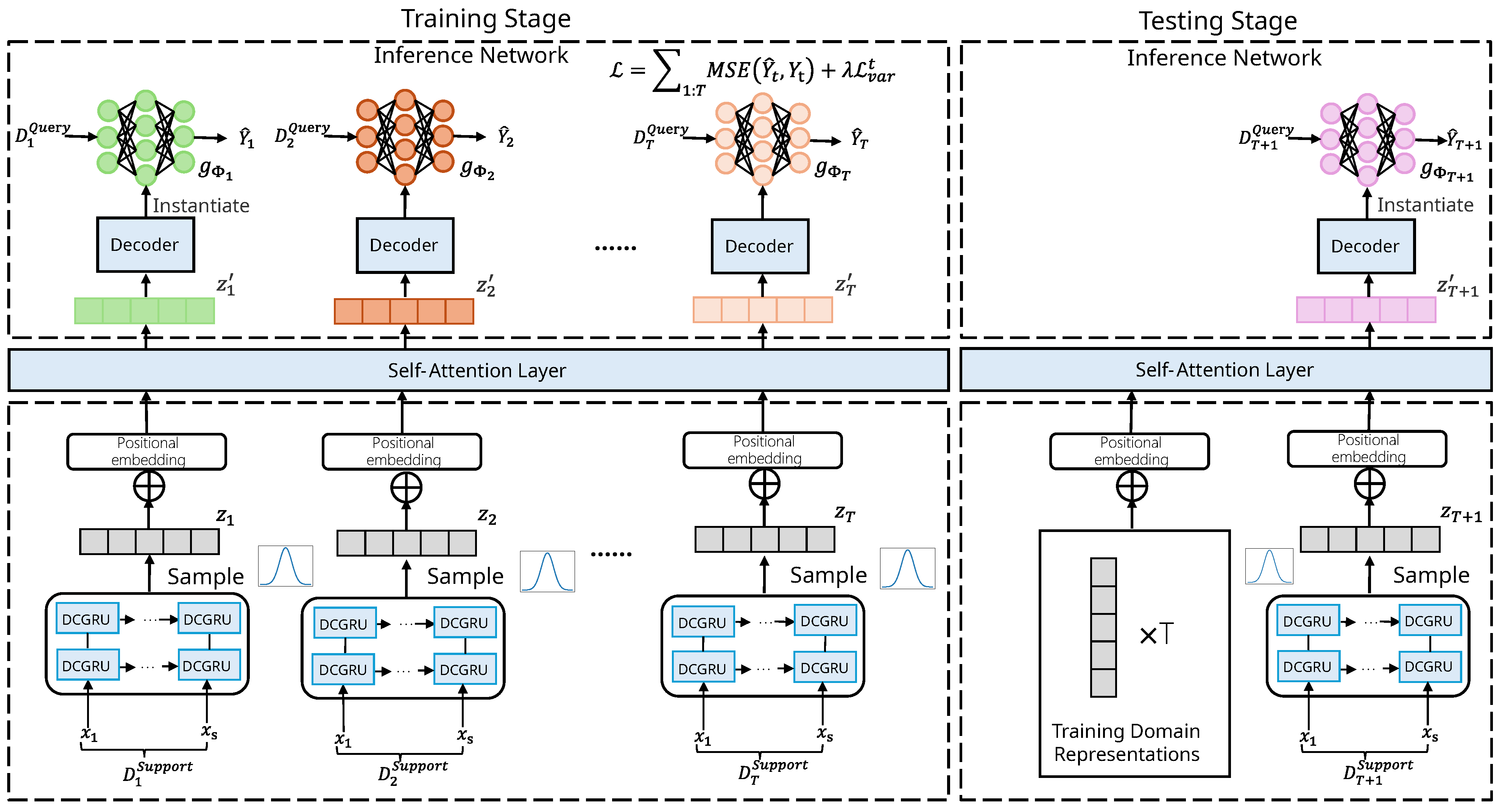
3. Methodology
3.1. Problem Formulation
3.2. Model Architecture
3.2.1. DCGRU-Based Encoder
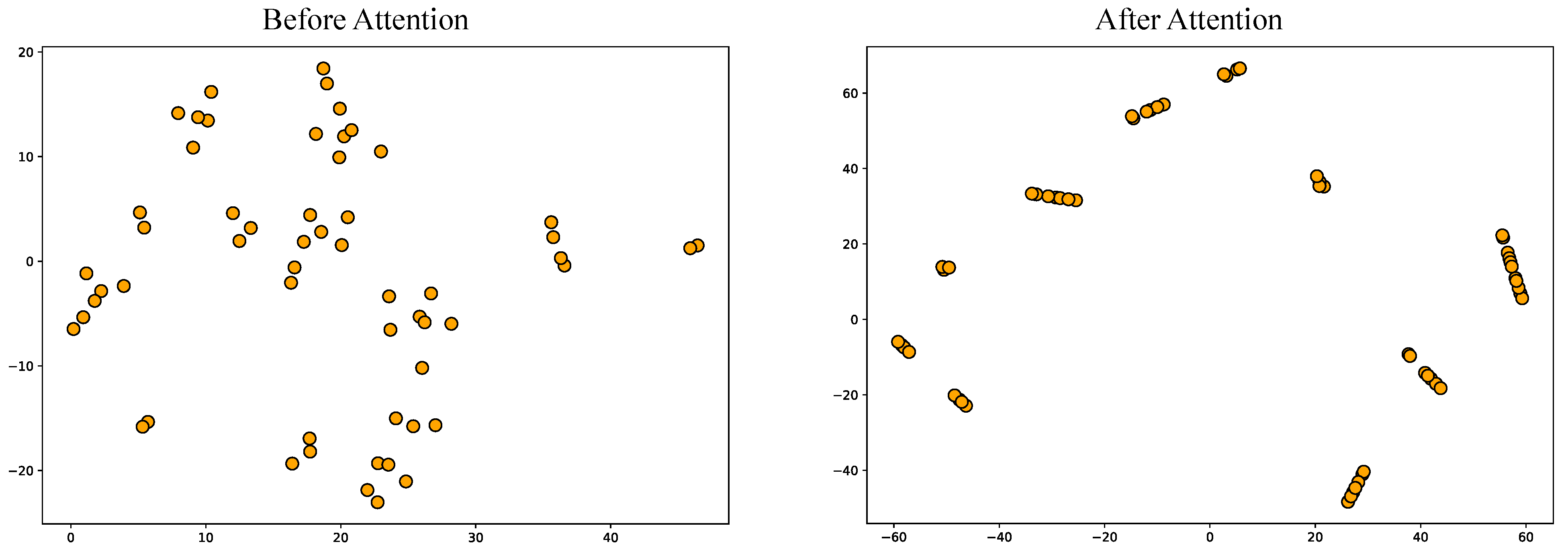
3.2.2. Domain Relation Modeling
3.2.3. Decoder and Inference Network
3.3. Model Training and Testing Process
| Algorithm 1 Training Procedure |
| Require: Training domain data ,…,, meta split ratio , learning rate , initialized |
| encoder |
| Initialize all learnable parameters |
| Split into and using split ratio |
| while not converge do |
| for in do |
| for to T do |
| Sample |
| Compute log likelihood using Equation (2) |
| end for |
| = |
| = |
| end for |
| Calculate supervised loss and Consistency loss with and |
| Update learnable parameters with learning rate |
| end while |
| Algorithm 2 Testing Procedure |
| Require: Training domain representation ,…,,Testing domain data , meta split |
| ratio |
| Split into and using split ratio |
| Sample |
| = |
| for each example in do |
| = |
| Calculate MSE loss with and Y |
| end for |
4. Theoretical Analysis
5. Experimental Evaluation
5.1. Datasets Descriptions
5.2. Baselines
5.3. Implementation Details
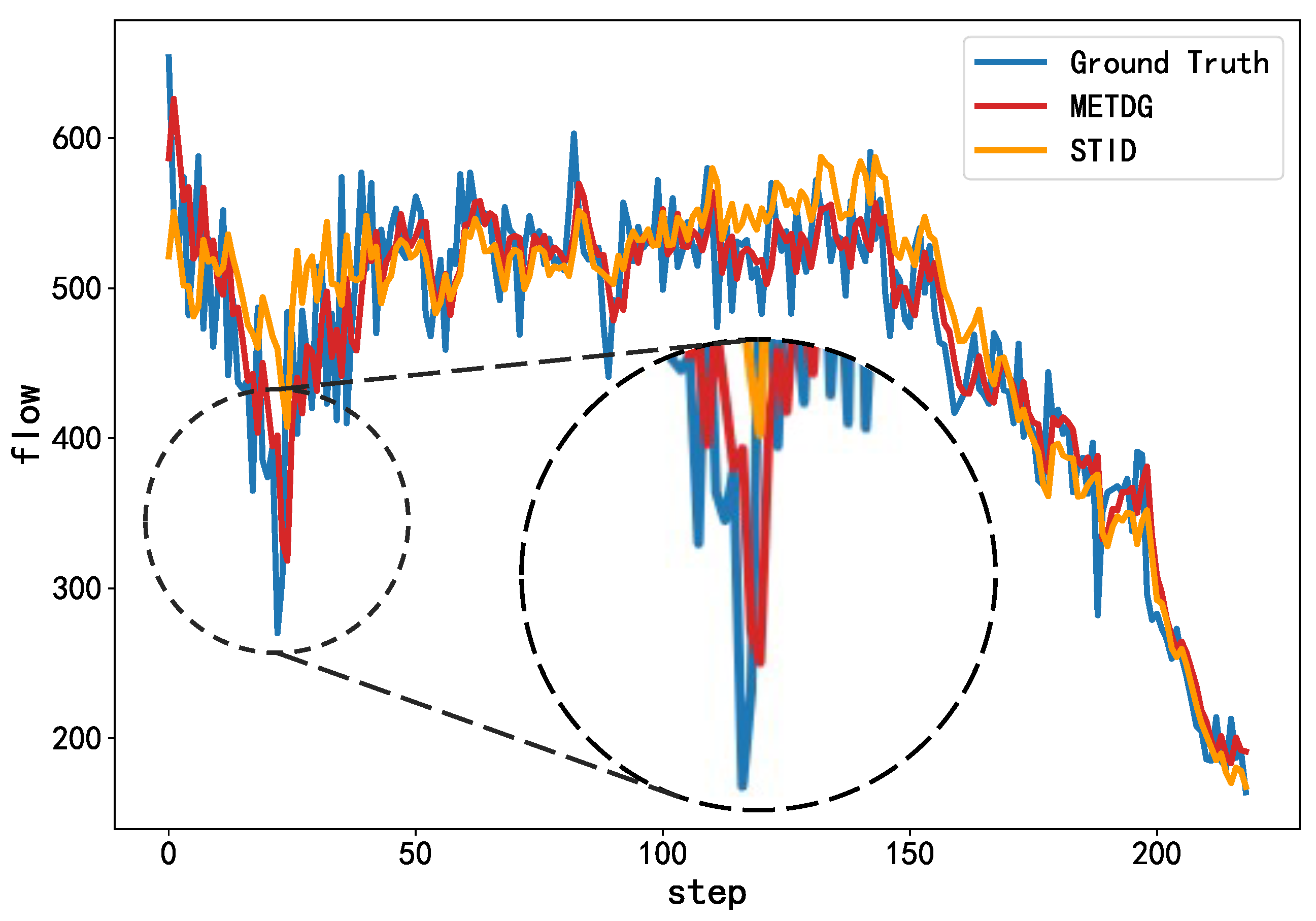
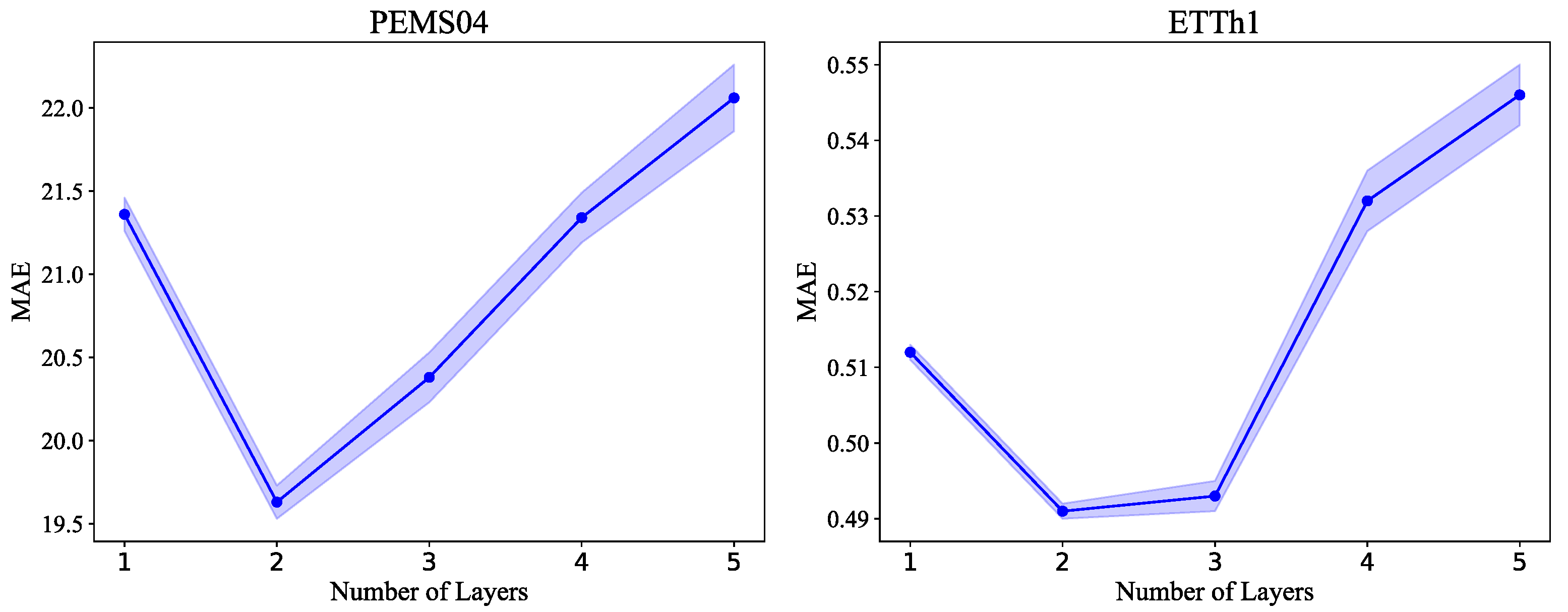
5.4. Results and Analysis
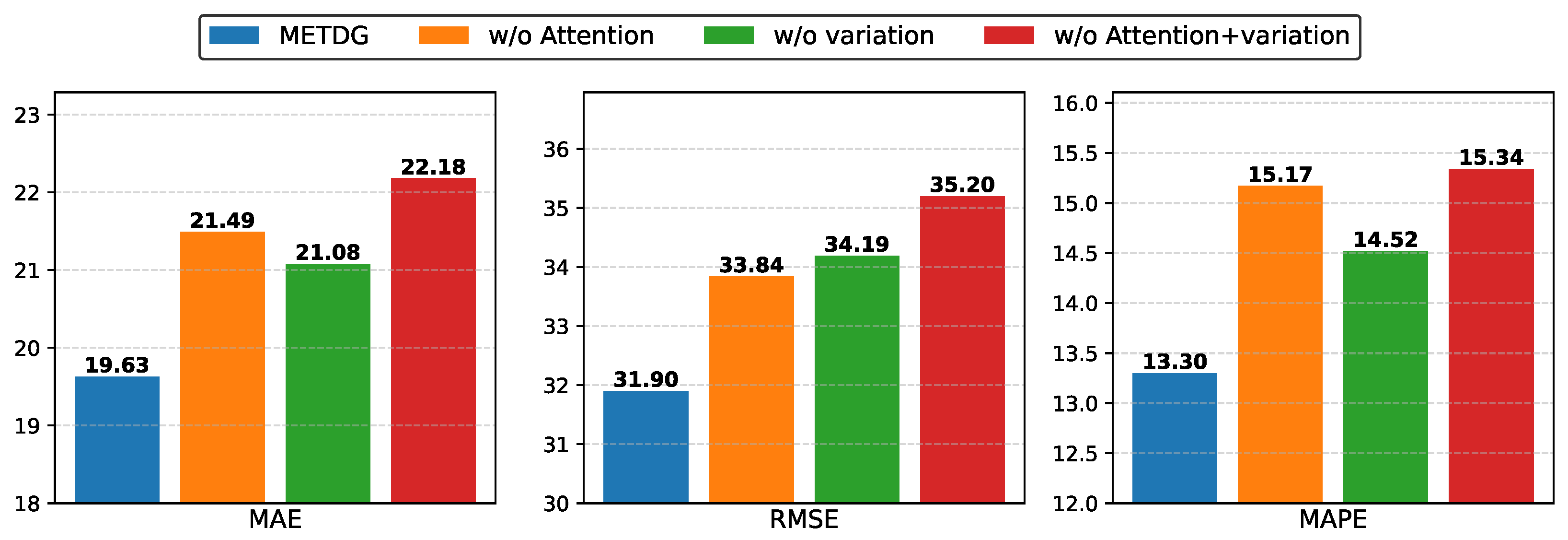
- w/o Attention: This variant excludes the self-attention mechanism. Domain features are first extracted using the DCGRU-based encoder, but the relationships between domains are not modeled with self-attention. Instead, the representation of each domain is directly used to generate the parameters of the corresponding inference network.
- w/o Variation: This variant omits variational inference. During training, the variational lower bound is not employed as a loss term to regularize the domain representation generation process.
- w/o Attention +V ariation: In this variant, both the self-attention mechanism and variational inference are removed. The inference network parameters are generated directly from domain representations, and the variational lower bound is excluded from the loss function.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Liu, M.; Zhu, T.; Ye, J.; Meng, Q.; Sun, L.; Du, B. Spatio-temporal autoencoder for traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5516–5526. [Google Scholar] [CrossRef]
- Cai, W.; Liang, Y.; Liu, X.; Feng, J.; Wu, Y. Msgnet: Learning multi-scale inter-series correlations for multivariate time series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2024; Volume 38, pp. 11141–11149. [Google Scholar]
- Du, Y.; Wang, J.; Feng, W.; Pan, S.; Qin, T.; Xu, R.; Wang, C. Adarnn: Adaptive learning and forecasting of time series. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, QLD, Australia, 1–5 November 2021; pp. 402–411. [Google Scholar]
- Bento, N.; Rebelo, J.; Carreiro, A.V.; Ravache, F.; Barandas, M. Exploring Regularization Methods for Domain Generalization in Accelerometer-Based Human Activity Recognition. Sensors 2023, 23, 6511. [Google Scholar] [CrossRef]
- Li, D.; Yang, Y.; Song, Y.Z.; Hospedales, T. Sequential learning for domain generalization. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 603–619. [Google Scholar]
- Nasery, A.; Thakur, S.; Piratla, V.; De, A.; Sarawagi, S. Training for the future: A simple gradient interpolation loss to generalize along time. Adv. Neural Inf. Process. Syst. 2021, 34, 19198–19209. [Google Scholar]
- Bai, G.; Ling, C.; Zhao, L. Temporal Domain Generalization with Drift-Aware Dynamic Neural Networks. In Proceedings of the The Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Li, W.; Yang, X.; Liu, W.; Xia, Y.; Bian, J. Ddg-da: Data distribution generation for predictable concept drift adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, Kragujevac, Serbia, 19–20 May 2022; Volume 36, pp. 4092–4100. [Google Scholar]
- Fan, W.; Wang, P.; Wang, D.; Wang, D.; Zhou, Y.; Fu, Y. Dish-ts: A general paradigm for alleviating distribution shift in time series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 7522–7529. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xu, Z.; Li, W.; Niu, L.; Xu, D. Exploiting low-rank structure from latent domains for domain generalization. In Proceedings of the Computer Vision—ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 628–643. [Google Scholar]
- Li, B.; Shen, Y.; Yang, J.; Wang, Y.; Ren, J.; Che, T.; Zhang, J.; Liu, Z. Sparse mixture-of-experts are domain generalizable learners. arXiv 2022, arXiv:2206.04046. [Google Scholar]
- Yao, H.; Yang, X.; Pan, X.; Liu, S.; Koh, P.W.; Finn, C. Leveraging domain relations for domain generalization. arXiv 2023, arXiv:2302.02609. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Makridakis, S.; Hibon, M. ARMA models and the Box–Jenkins methodology. J. Forecast. 1997, 16, 147–163. [Google Scholar] [CrossRef]
- de Bézenac, E.; Rangapuram, S.S.; Benidis, K.; Bohlke-Schneider, M.; Kurle, R.; Stella, L.; Hasson, H.; Gallinari, P.; Januschowski, T. Normalizing kalman filters for multivariate time series analysis. Adv. Neural Inf. Process. Syst. 2020, 33, 2995–3007. [Google Scholar]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationary transformers: Exploring the stationarity in time series forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 9881–9893. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar]
- Liu, Y.; Zhang, H.; Li, C.; Huang, X.; Wang, J.; Long, M. Timer: Generative Pre-trained Transformers Are Large Time Series Models. In Proceedings of the Forty-First International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR ’18), Vancouver, BC, Canada, 30 April 30–3 May 2018. [Google Scholar]
- He, H.; Queen, O.; Koker, T.; Cuevas, C.; Tsiligkaridis, T.; Zitnik, M. Domain adaptation for time series under feature and label shifts. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 12746–12774. [Google Scholar]
- Lu, W.; Wang, J.; Sun, X.; Chen, Y.; Ji, X.; Yang, Q.; Xie, X. Diversify: A general framework for time series out-of-distribution detection and generalization. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4534–4550. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhang, Y.; Shu, S.; Zheng, J. DEST-GNN: A double-explored spatio-temporal graph neural network for multi-site intra-hour PV power forecasting. Appl. Energy 2025, 378, 124744. [Google Scholar] [CrossRef]
- Fu, F.; Ai, W.; Yang, F.; Shou, Y.; Meng, T.; Li, K. SDR-GNN: Spectral Domain Reconstruction Graph Neural Network for incomplete multimodal learning in conversational emotion recognition. Knowl.-Based Syst. 2025, 309, 112825. [Google Scholar] [CrossRef]
- Hou, M.; Liu, Z.; Sa, G.; Wang, Y.; Sun, J.; Li, Z.; Tan, J. Parallel multi-scale dynamic graph neural network for multivariate time series forecasting. Pattern Recognit. 2025, 158, 111037. [Google Scholar] [CrossRef]
- Yanchenko, A.K.; Mukherjee, S. Stanza: A nonlinear state space model for probabilistic inference in non-stationary time series. arXiv 2020, arXiv:2006.06553. [Google Scholar]
- Gordon, J.; Bronskill, J.; Bauer, M.; Nowozin, S.; Turner, R. Meta-Learning Probabilistic Inference for Prediction. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Javed, K.; White, M. Meta-learning representations for continual learning. Adv. Neural Inf. Process. Syst. 2019, 32, 1818–1828. [Google Scholar]
- Yoon, J.; Kim, T.; Dia, O.; Kim, S.; Bengio, Y.; Ahn, S. Bayesian model-agnostic meta-learning. Adv. Neural Inf. Process. Syst. 2018, 31, 7343–7353. [Google Scholar]
- Cui, Y.; Xie, J.; Zheng, K. Historical inertia: A neglected but powerful baseline for long sequence time-series forecasting. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, QLD, Australia, 1–5 November 2021; pp. 2965–2969. [Google Scholar]
- Lu, Z.; Zhou, C.; Wu, J.; Jiang, H.; Cui, S. Integrating granger causality and vector auto-regression for traffic prediction of large-scale WLANs. KSII Trans. Internet Inf. Syst. 2016, 10, 136. [Google Scholar]
- Li, F.; Feng, J.; Yan, H.; Jin, G.; Yang, F.; Sun, F.; Jin, D.; Li, Y. Dynamic graph convolutional recurrent network for traffic prediction: Benchmark and solution. ACM Trans. Knowl. Discov. Data 2023, 17, 1–21. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, Z.; Wang, F.; Wei, W.; Xu, Y. Spatial-temporal identity: A simple yet effective baseline for multivariate time series forecasting. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 4454–4458. [Google Scholar]
- Liu, H.; Dong, Z.; Jiang, R.; Deng, J.; Deng, J.; Chen, Q.; Song, X. Spatio-temporal adaptive embedding makes vanilla transformer sota for traffic forecasting. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 4125–4129. [Google Scholar]
- Sun, L.; Dai, W.; Muhammad, G. Gating Memory Network Multi-Layer Perceptron for Traffic Forecasting in Internet-of-Vehicles systems. IEEE Internet Things J. 2024, 12, 4783–4793. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]



| PEMS04 | Horizon 3 | Horizon 6 | Horizon 12 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| HI | 42.33 | 61.64 | 29.90% | 42.35 | 61.66 | 29.92% | 42.37 | 61.67 | 29.92% |
| VAR | 21.94 | 34.30 | 16.42% | 23.72 | 36.58 | 18.02% | 26.76 | 40.28 | 20.94% |
| DCRNN | 18.53 | 29.44 | 12.76% | 19.79 | 31.3 | 13.57% | 21.73 | 33.98 | 15.12% |
| DGCRN | 17.98 | 29.08 | 12.20% | 18.99 | 30.9 | 12.86% | 20.44 | 33.23 | 13.87% |
| STID | 17.51 | 28.48 | 12.00% | 18.29 | 29.86 | 12.46% | 19.58 | 31.79 | 13.38% |
| DRAIN | 19.57 | 30.74 | 13.37% | 21.84 | 33.62 | 14.27% | 23.22 | 35.32 | 15.28% |
| STAEformer | 17.47 | 28.9 | 11.94% | 18.20 | 30.31 | 12.35% | 19.30 | 32.10 | 13.19% |
| GMMLP | 17.39 | 28.41 | 12.03% | 18.18 | 29.82 | 12.34% | 19.37 | 31.57 | 13.58% |
| Ours | 17.17 | 28.32 | 11.43% | 17.97 | 29.68 | 12.25% | 19.63 | 31.90 | 13.30% |
| PEMS07 | Horizon 3 | Horizon 6 | Horizon 12 | ||||||
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| HI | 49.02 | 71.16 | 22.73% | 49.03 | 71.18 | 22.75% | 49.06 | 71.20 | 22.79% |
| VAR | 32.02 | 48.83 | 18.30% | 35.18 | 52.91 | 20.54% | 38.37 | 56.82 | 22.04% |
| DCRNN | 19.75 | 31.74 | 8.31% | 21.6 | 35.12 | 9.00% | 24.76 | 40.75 | 10.39% |
| DGCRN | 18.43 | 30.97 | 8.76% | 20.43 | 34.12 | 8.69% | 21.44 | 37.93 | 9.91% |
| STID | 18.37 | 30.39 | 7.74% | 19.66 | 32.82 | 8.28% | 21.53 | 36.04 | 9.13% |
| DRAIN | 21.23 | 34.18 | 9.02% | 23.23 | 37.71 | 10.14% | 27.29 | 44.24 | 13.26% |
| STAEformer | 18.09 | 30.15 | 7.56% | 19.38 | 32.99 | 8.97% | 21.41 | 35.99 | 8.97% |
| GMMLP | 17.98 | 30.05 | 7.67% | 19.24 | 32.66 | 8.08% | 20.89 | 35.76 | 8.77% |
| Ours | 17.87 | 30.13 | 7.54% | 19.17 | 32.40 | 7.96% | 20.64 | 35.70 | 8.69% |
| PEMS08 | Horizon 3 | Horizon 6 | Horizon 12 | ||||||
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| HI | 34.55 | 50.41 | 21.60% | 34.57 | 50.43 | 21.63% | 34.59 | 50.44 | 21.68% |
| VAR | 19.52 | 29.73 | 12.54% | 22.25 | 30.30 | 14.23% | 26.17 | 38.97 | 17.32% |
| DCRNN | 15.64 | 25.48 | 10.04% | 17.88 | 27.63 | 11.38% | 22.51 | 34.21 | 14.17% |
| DGCRN | 13.89 | 22.07 | 9.19% | 14.92 | 23.99 | 9.85% | 16.73 | 26.88 | 10.84% |
| STID | 13.85 | 21.92 | 9.03% | 15.00 | 24.04 | 9.78% | 16.77 | 26.91 | 10.93% |
| DRAIN | 16.88 | 26.73 | 11.13% | 18.86 | 30.17 | 13.22% | 23.24 | 36.16 | 14.84% |
| STAEformer | 13.85 | 21.99 | 8.76% | 14.41 | 23.72 | 9.26% | 15.34 | 26.03 | 9.91% |
| GMMLP | 13.18 | 21.62 | 8.55% | 14.09 | 23.59 | 9.18% | 15.32 | 26.06 | 9.90% |
| Ours | 13.12 | 21.53 | 8.50% | 13.99 | 23.24 | 9.01% | 15.24 | 25.89 | 9.85% |
| Methods | Ours | HI | VAR | DRAIN | MSGNet | Timesnet | DLiner | FEDformer | Informer | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| Weather | 96 | 0.160 | 0.199 | 0.894 | 0.553 | 0.458 | 0.491 | 0.236 | 0.278 | 0.163 | 0.212 | 0.220 | 0.196 | 0.196 | 0.255 | 0.217 | 0.296 | 0.300 | 0.384 |
| 192 | 0.207 | 0.244 | 0.621 | 0.628 | 0.648 | 0.580 | 0.279 | 0.301 | 0.212 | 0.254 | 0.219 | 0.261 | 0.237 | 0.296 | 0.276 | 0.336 | 0.598 | 0.544 | |
| 336 | 0.275 | 0.294 | 0.736 | 0.753 | 0.797 | 0.659 | 0.329 | 0.365 | 0.272 | 0.299 | 0.280 | 0.306 | 0.283 | 0.355 | 0.339 | 0.380 | 0.578 | 0.523 | |
| 720 | 0.364 | 0.360 | 1.005 | 0.934 | 0.869 | 0.672 | 0.379 | 0.428 | 0.350 | 0.348 | 0.365 | 0.359 | 0.345 | 0.381 | 0.403 | 0.428 | 1.059 | 0.741 | |
| ETTh1 | 96 | 0.372 | 0.395 | 1.264 | 0.934 | 0.871 | 0.749 | 0.440 | 0.451 | 0.390 | 0.411 | 0.384 | 0.402 | 0.386 | 0.400 | 0.376 | 0.419 | 0.865 | 0.713 |
| 192 | 0.420 | 0.432 | 1.457 | 0.980 | 1.554 | 1.317 | 0.490 | 0.482 | 0.442 | 0.442 | 0.436 | 0.429 | 0.437 | 0.432 | 0.420 | 0.448 | 1.008 | 0.792 | |
| 336 | 0.454 | 0.457 | 2.025 | 1.138 | 1.420 | 1.128 | 0.520 | 0.496 | 0.480 | 0.468 | 0.491 | 0.469 | 0.481 | 0.459 | 0.459 | 0.465 | 1.107 | 0.809 | |
| 720 | 0.510 | 0.491 | 2.383 | 1.376 | 1.937 | 1.322 | 0.511 | 0.502 | 0.494 | 0.488 | 0.521 | 0.500 | 0.519 | 0.516 | 0.506 | 0.507 | 1.181 | 0.865 | |
| ETTh2 | 96 | 0.311 | 0.330 | 2.576 | 1.148 | 1.539 | 1.618 | 0.346 | 0.388 | 0.328 | 0.371 | 0.340 | 0.374 | 0.333 | 0.387 | 0.358 | 0.397 | 3.755 | 1.525 |
| 192 | 0.329 | 0.347 | 3.338 | 1.783 | 2.879 | 1.534 | 0.392 | 0.407 | 0.402 | 0.414 | 0.402 | 0.414 | 0.477 | 0.476 | 0.429 | 0.439 | 5.602 | 1.931 | |
| 336 | 0.350 | 0.390 | 2.936 | 1.780 | 3.452 | 1.693 | 0.421 | 0.434 | 0.435 | 0.443 | 0.452 | 0.452 | 0.594 | 0.541 | 0.496 | 0.487 | 4.721 | 1.835 | |
| 720 | 0.385 | 0.440 | 4.625 | 3.821 | 5.385 | 2.097 | 0.452 | 0.473 | 0.417 | 0.441 | 0.462 | 0.468 | 0.831 | 0.657 | 0.463 | 0.474 | 3.647 | 1.625 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, J.; Jin, B.; Wei, X. Meta-Learning Task Relations for Ensemble-Based Temporal Domain Generalization in Sensor Data Forecasting. Sensors 2025, 25, 4434. https://doi.org/10.3390/s25144434
Zhang L, Liu J, Jin B, Wei X. Meta-Learning Task Relations for Ensemble-Based Temporal Domain Generalization in Sensor Data Forecasting. Sensors. 2025; 25(14):4434. https://doi.org/10.3390/s25144434
Chicago/Turabian StyleZhang, Liang, Jiayi Liu, Bo Jin, and Xiaopeng Wei. 2025. "Meta-Learning Task Relations for Ensemble-Based Temporal Domain Generalization in Sensor Data Forecasting" Sensors 25, no. 14: 4434. https://doi.org/10.3390/s25144434
APA StyleZhang, L., Liu, J., Jin, B., & Wei, X. (2025). Meta-Learning Task Relations for Ensemble-Based Temporal Domain Generalization in Sensor Data Forecasting. Sensors, 25(14), 4434. https://doi.org/10.3390/s25144434





