Intelligent Joint Space Path Planning: Enhancing Motion Feasibility with Goal-Driven and Potential Field Strategies
Abstract
1. Introduction
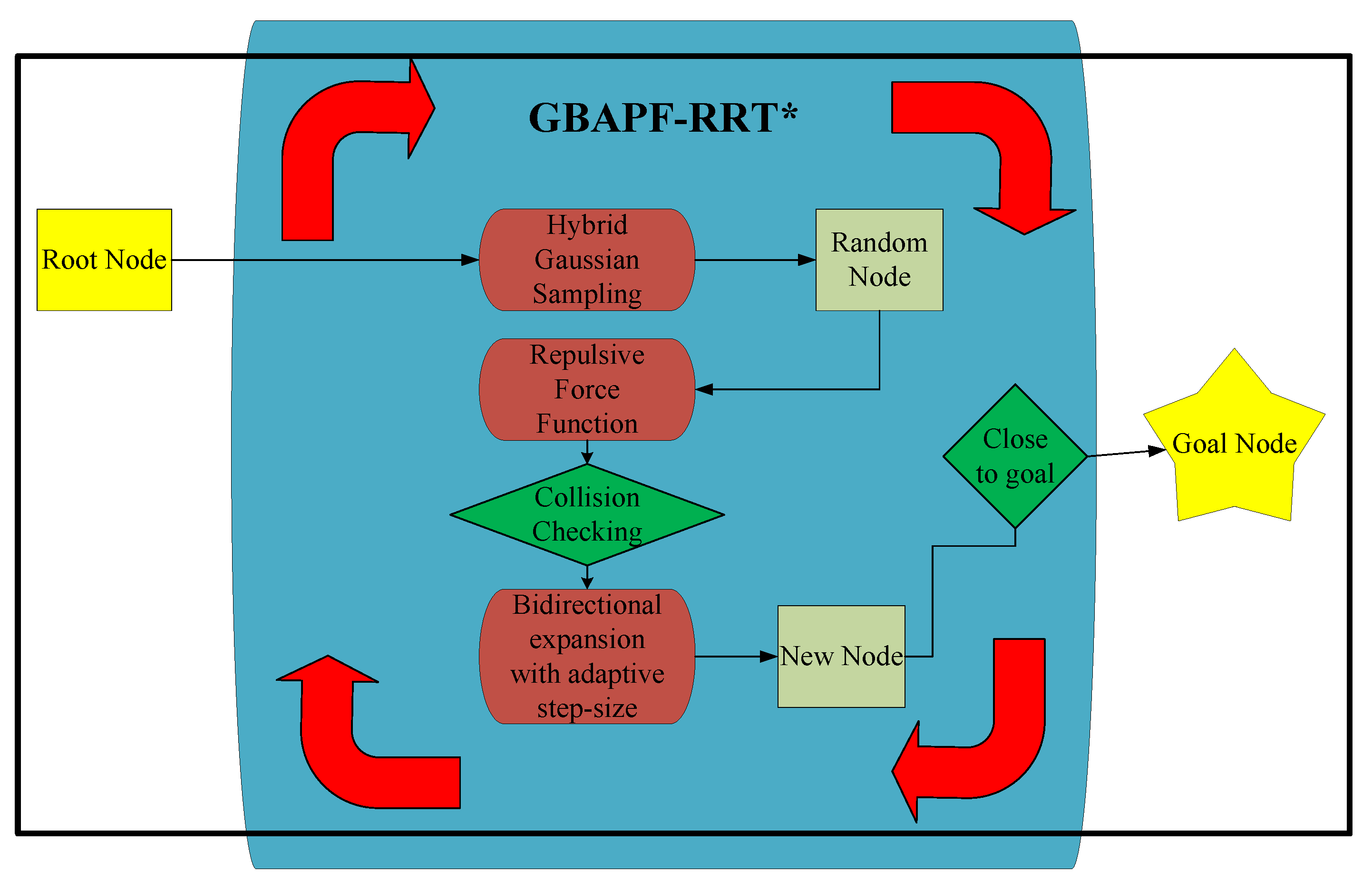
- Hybrid Gaussian Sampling Method—A hybrid Gaussian distribution is employed to optimize the sampling process, effectively guiding tree expansion toward the target point. This approach improves convergence speed, minimizes unnecessary sampling nodes, and enhances search efficiency. Compared to unguided RRT, this method significantly improves the efficiency of tree expansion and increases the likelihood of finding a feasible path within limited iterations.
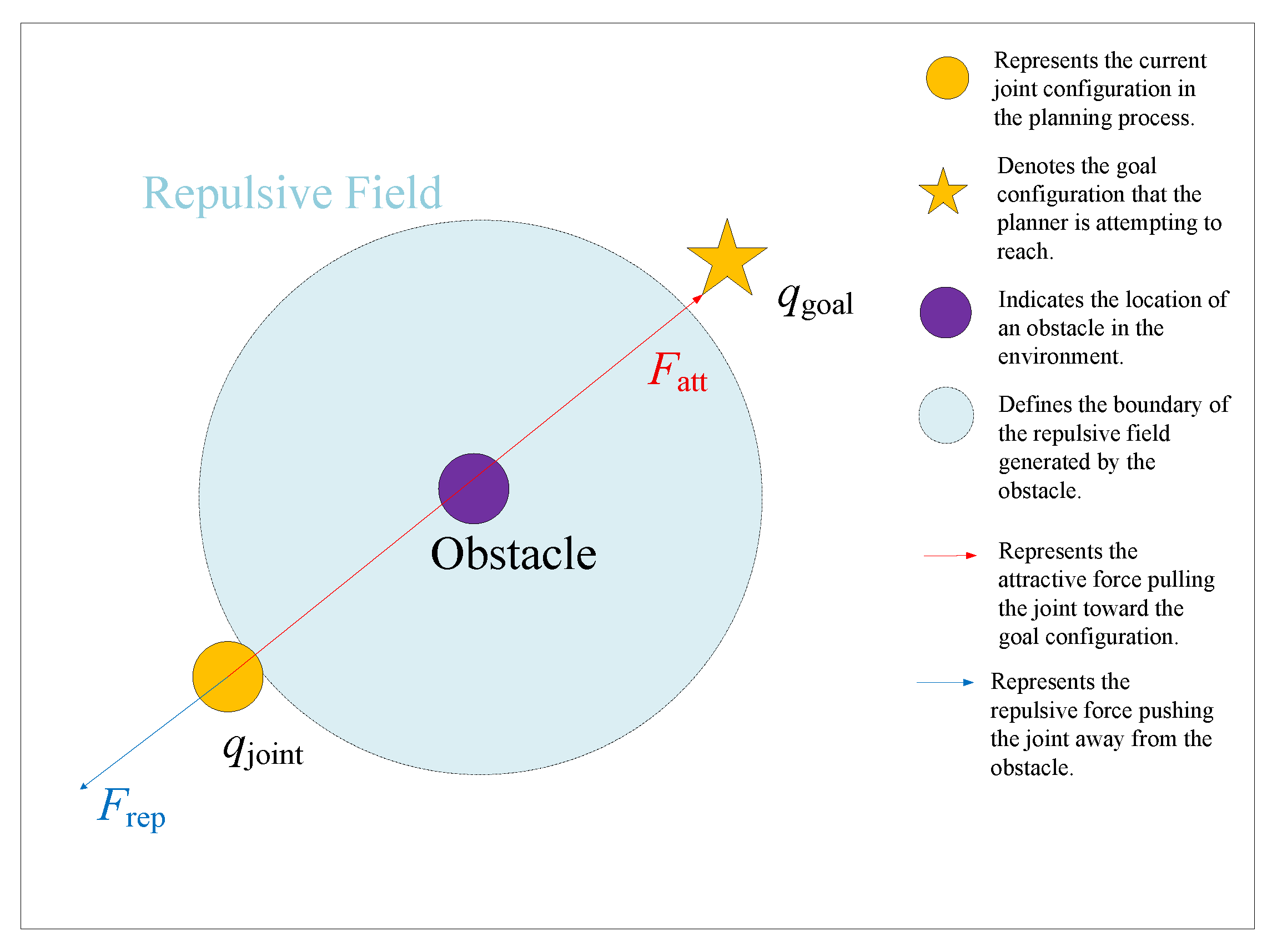
- Modified Repulsive Force Function—While the original APF method is not well-suited for path planning in high-dimensional space like joint space, an improved repulsive force function is integrated into the expansion process. This enhancement significantly improves obstacle avoidance performance in high-dimensional joint spaces, making it more effective for robotic manipulator path planning.
- Bidirectional expansion with adaptive step-size—A bidirectional tree expansion approach is adopted, allowing two trees to grow simultaneously and efficiently connect. Additionally, an adaptive step-size strategy mitigates local extreme issues, ensuring a more stable and flexible search process in complex environments. Compared to conventional single-tree expansion, this bidirectional strategy significantly accelerates the search process and improves pathfinding efficiency in high-dimensional spaces.
2. Related Work
2.1. Basic Algorithm
2.1.1. RRT
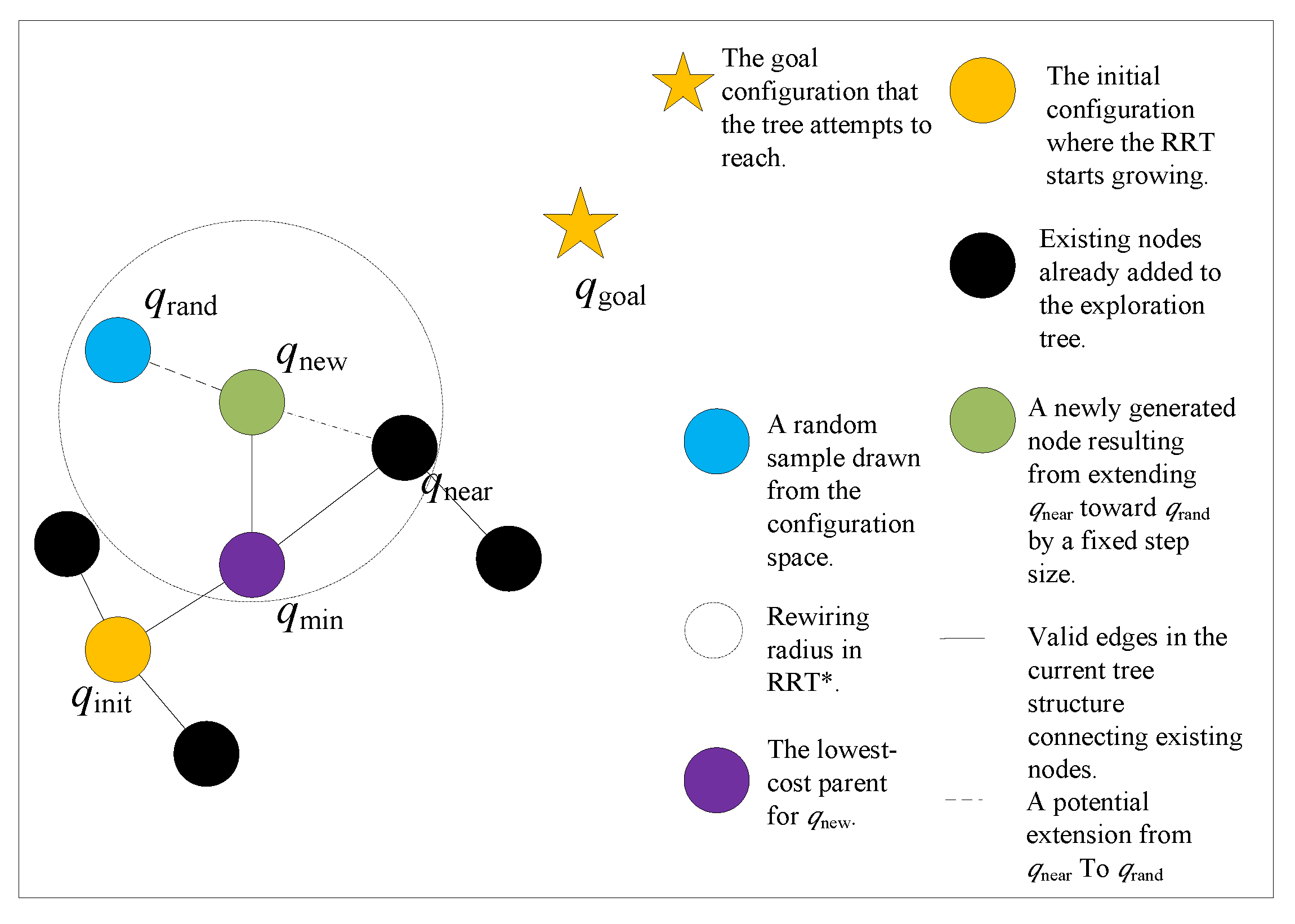
2.1.2. RRT Star
2.2. Improved Version
2.2.1. Dual-Tree Methods
2.2.2. Goal-Biased Methods
2.2.3. Modified APF Methods
3. Path-Planning Algorithm Design
3.1. Problem Formulation in Joint Space
3.2. Hybrid Gaussian Sampling Method
3.3. Modified Repulsive Force Function
3.4. Expansion Strategy
3.5. Collision Checking Strategy
| Algorithm 1 The proposed GBAPF-RRT* |
| Require: Start configuration , goal configuration , maximum iterations N, step size , threshold Ensure: A feasible path from to (if found)
|
4. Probabilistic Completeness
5. Simulation
5.1. Simulation Setup
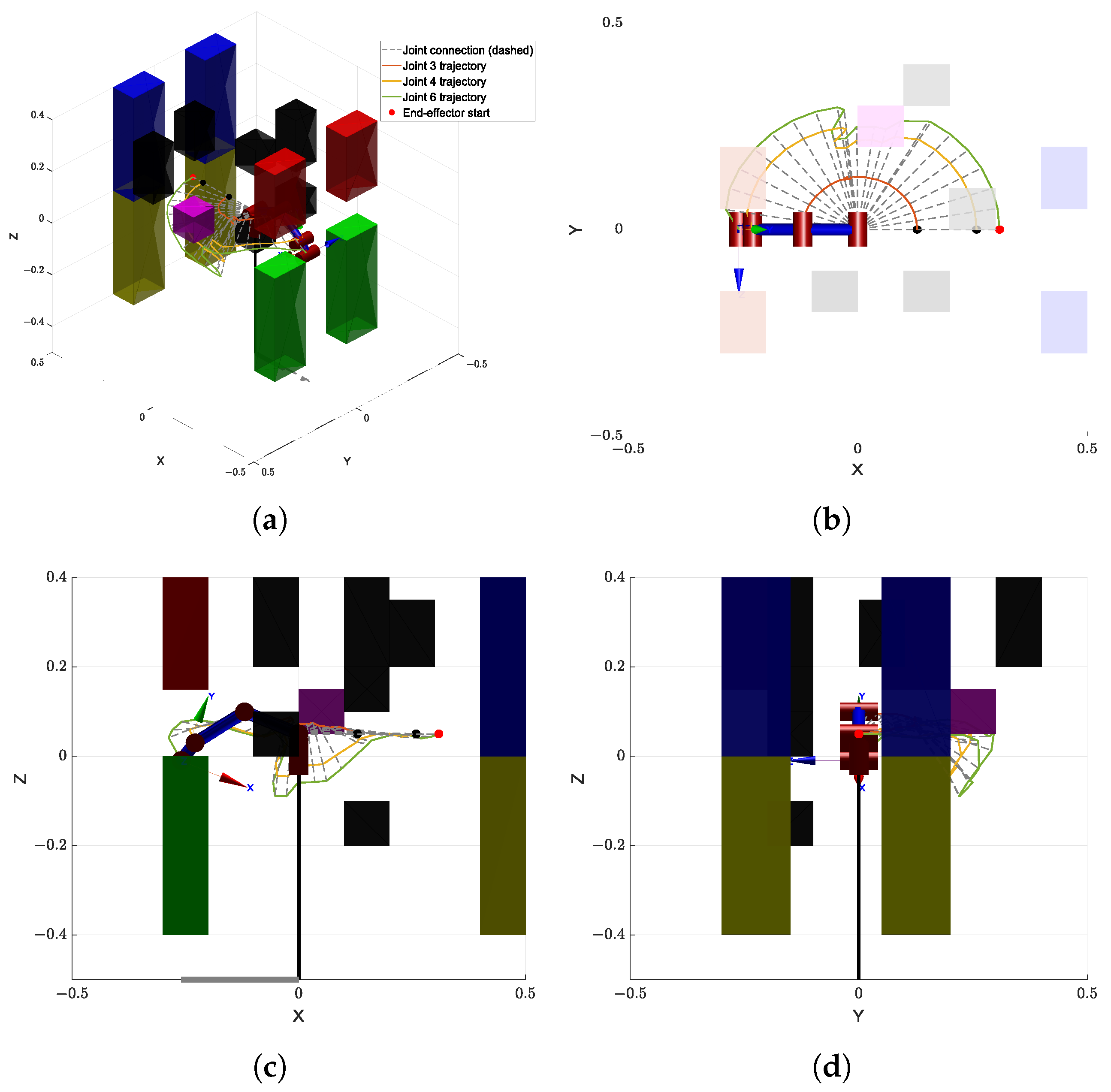
5.2. Simulation 1: Complex Obstacle Cluster Environment
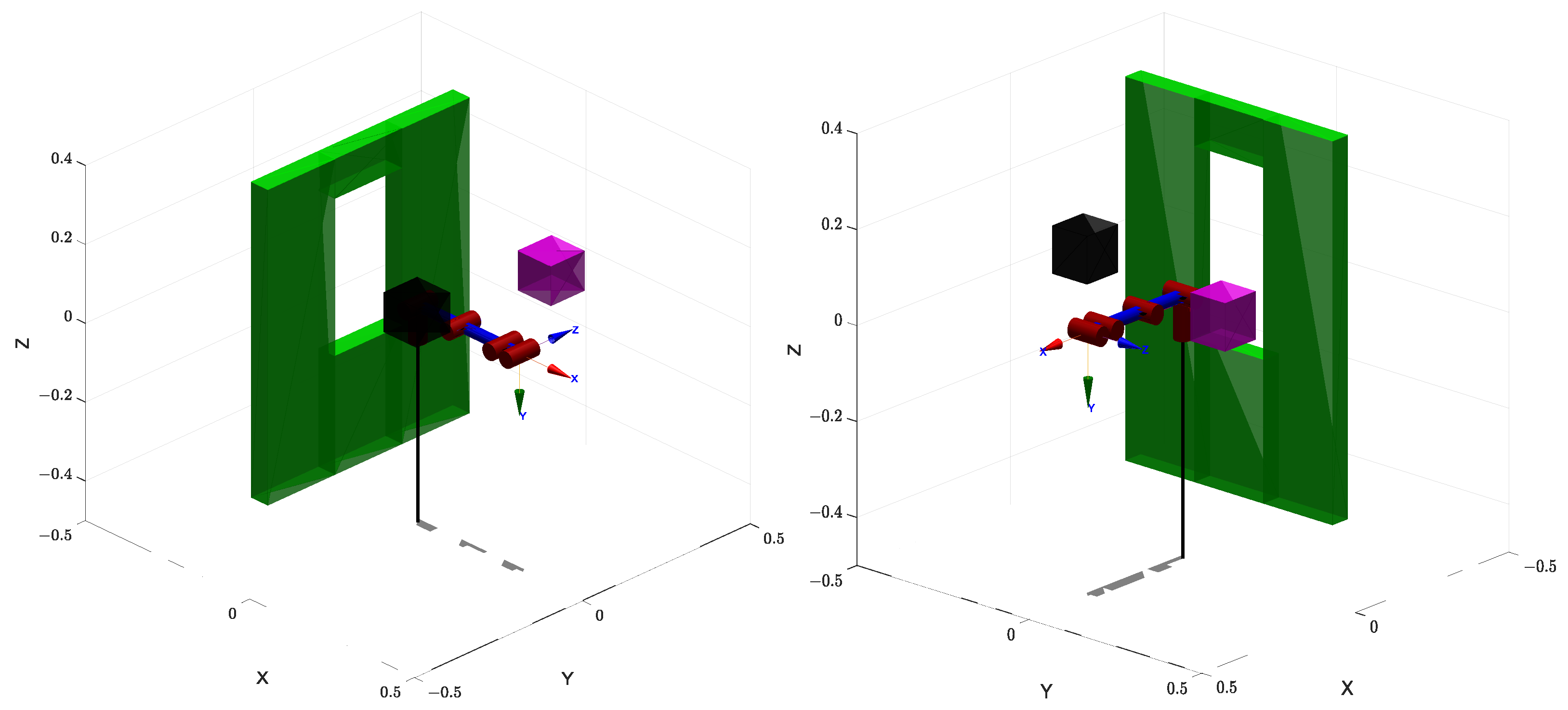
5.3. Simulation 2: Constrained Manipulation Through Structural Openings
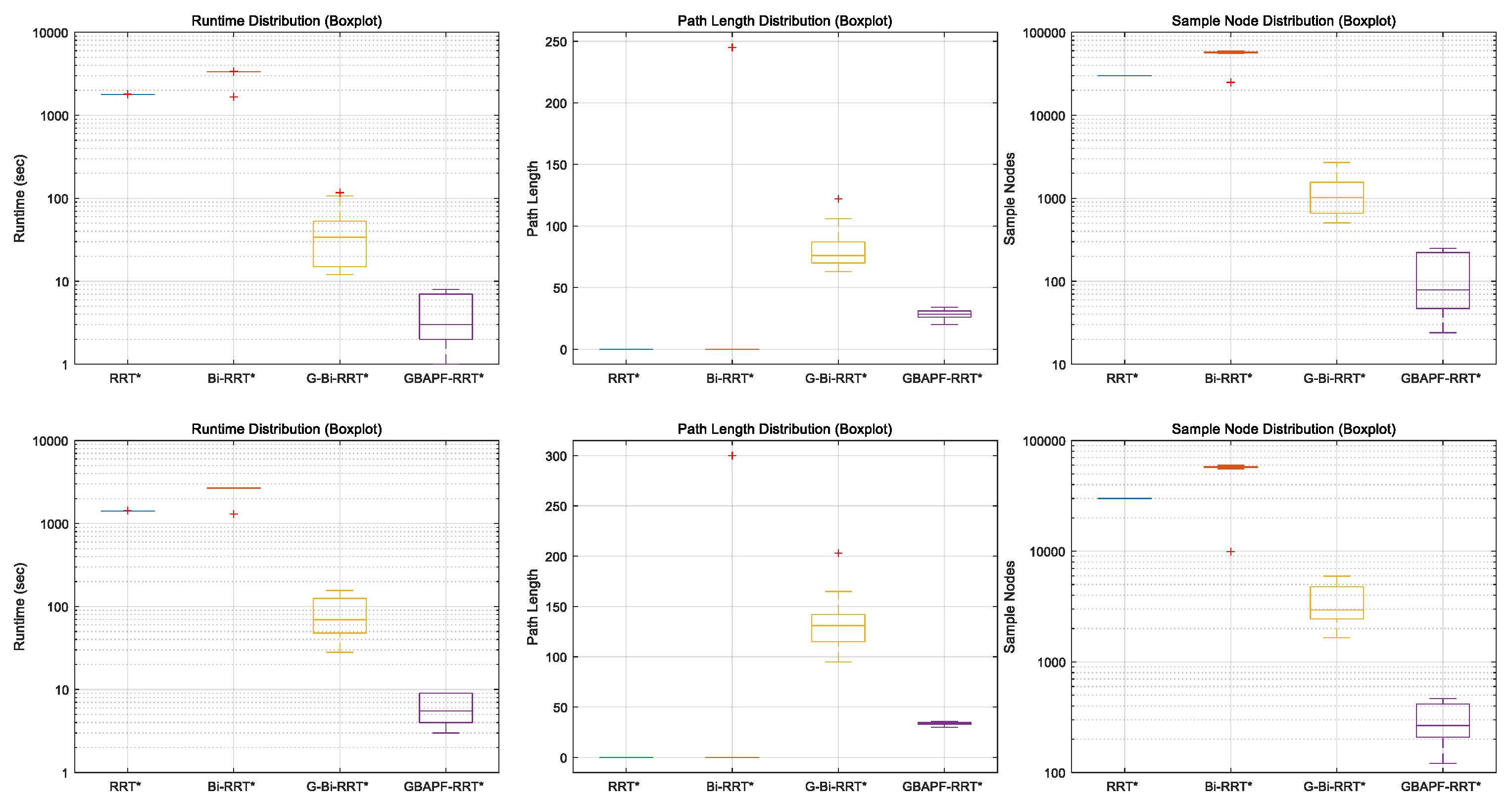
5.4. Results and Discussion
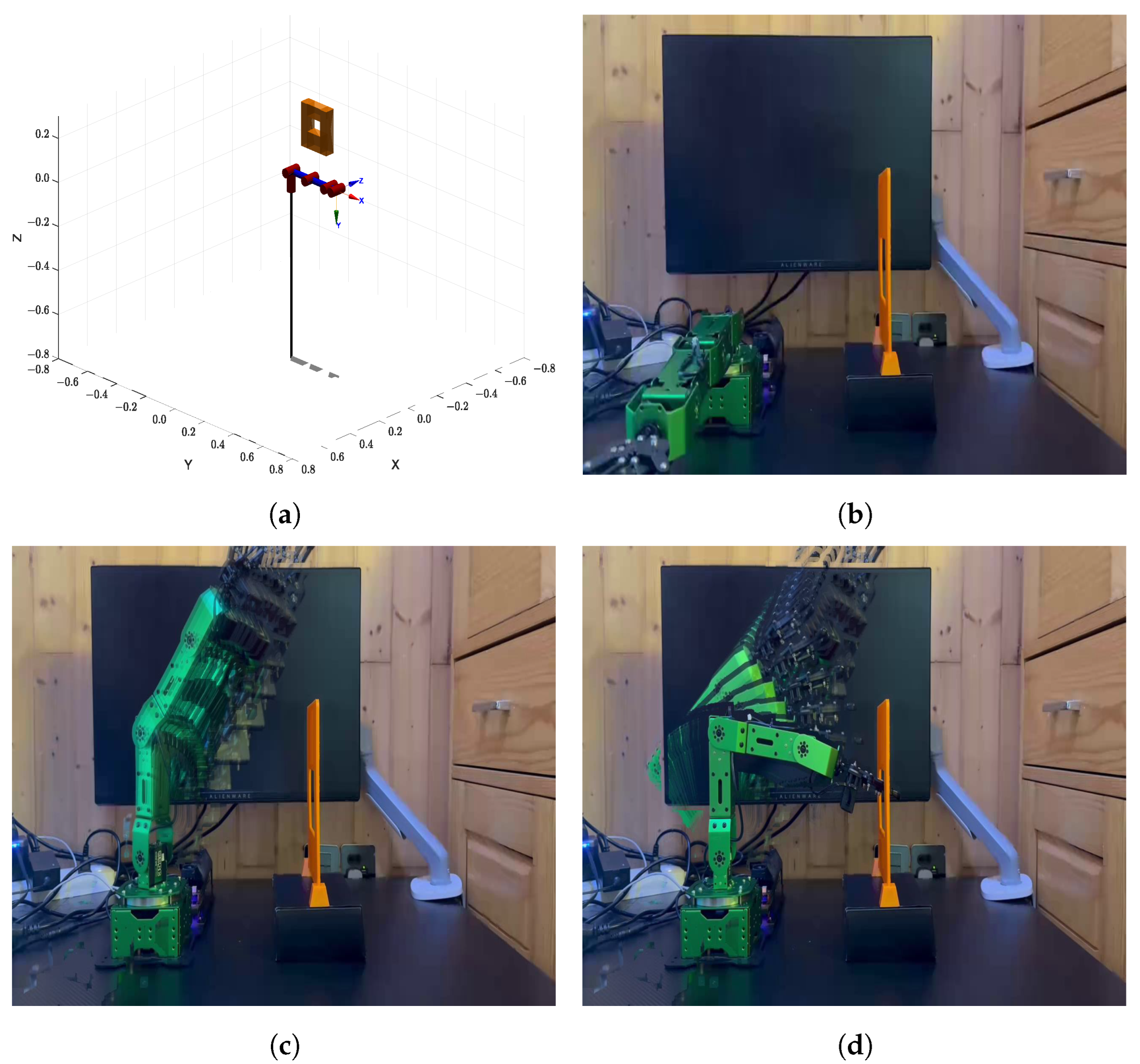
6. Real World Experiment
6.1. Experiment Setup
6.2. Real-World Experiment 1: Narrow Vertical Gap
6.3. Real-World Experiment 2: Rectangular Opening
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ranzani, T.; Cianchetti, M.; Gerboni, G.; Falco, I.D.; Menciassi, A. A soft modular manipulator for minimally invasive surgery: Design and characterization of a single module. IEEE Trans. Robot. 2016, 32, 187–200. [Google Scholar] [CrossRef]
- Zanchettin, A.M.; Ceriani, N.M.; Rocco, P.; Ding, H.; Matthias, B. Safety in human-robot collaborative manufacturing environments: Metrics and control. IEEE Trans. Autom. Sci. Eng. 2016, 13, 882–893. [Google Scholar] [CrossRef]
- Qiao, J.; Wu, H.; Yu, X. High-precision attitude tracking control of space manipulator system under multiple disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4274–4284. [Google Scholar] [CrossRef]
- Lin, Z.; Wu, K.; Shen, R.; Yu, X.; Huang, S. An efficient and accurate A-star algorithm for autonomous vehicle path planning. IEEE Trans. Veh. Technol. 2024, 73, 9003–9008. [Google Scholar] [CrossRef]
- Buzachis, A.; Celesti, A.; Galletta, A.; Wan, J.; Fazio, M. Evaluating an application aware distributed Dijkstra shortest path algorithm in hybrid cloud/edge environments. IEEE Trans. Sustain. Comput. 2022, 7, 289–298. [Google Scholar] [CrossRef]
- Prasad, N.L.; Ramkumar, B. 3-D Deployment and trajectory planning for relay based UAV assisted cooperative communication for emergency scenarios using Dijkstra’s algorithm. IEEE Trans. Veh. Technol. 2023, 72, 5049–5063. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Kavraki, L.E.; Kolountzakis, M.N.; Latombe, J.C. Analysis of probabilistic roadmaps for path planning. IEEE Trans. Robot. Autom. 1998, 14, 166–171. [Google Scholar] [CrossRef]
- Zhang, W.; Shan, L.; Chang, L.; Dai, Y. SVF-RRT*: A stream-based VF-RRT* for USVs path planning considering ocean currents. IEEE Robot. Autom. Lett. 2023, 8, 2413–2420. [Google Scholar] [CrossRef]
- Moon, C.b.; Chung, W. Kinodynamic planner dual-tree RRT (DT-RRT) for two-wheeled mobile robots using the rapidly exploring random tree. IEEE Trans. Ind. Electron. 2015, 62, 1080–1090. [Google Scholar] [CrossRef]
- Fan, J.; Chen, X.; Wang, Y.; Chen, X. UAV Trajectory planning in cluttered environments based on PF-RRT* algorithm with goal-biased strategy. Eng. Appl. Artif. Intell. 2022, 114, 105182. [Google Scholar] [CrossRef]
- Novosad, M.; Penicka, R.; Vonasek, V. CTopPRM: Clustering topological PRM for planning multiple distinct paths in 3D environments. IEEE Robot. Autom. Lett. 2023, 8, 7336–7343. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Ayaz, Y. Potential functions based sampling heuristic for optimal path planning. Auton. Robot. 2016, 40, 1079–1093. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, L.; Qi, J.; Hong, S. DBVS-APF-RRT*: A global path planning algorithm with ultra-high speed generation of initial paths and high optimal path quality. Expert Syst. Appl. 2024, 249, 123571. [Google Scholar] [CrossRef]
- Tran, B.; Xue, B.; Zhang, M. A new representation in PSO for discretization-Based feature selection. IEEE Trans. Cybern. 2018, 48, 1733–1746. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ezugwu, A.E.S.; Adewumi, A.O.; Frîncu, M.E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem. Expert Syst. Appl. 2017, 77, 189–210. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Zhang, J.; Yang, N.; Wang, P.; Tang, J.; Zhang, J.; Shi, L. APF-CPP: An artificial potential field based multi-robot online coverage path planning approach. IEEE Robot. Autom. Lett. 2024, 9, 9199–9206. [Google Scholar] [CrossRef]
- Yang, H.; He, Y.; Xu, Y.; Zhao, H. Collision avoidance for autonomous vehicles based on MPC with adaptive APF. IEEE Trans. Intell. Veh. 2024, 9, 1559–1570. [Google Scholar] [CrossRef]
- Ying, K.C.; Pourhejazy, P.; Cheng, C.Y.; Cai, Z.Y. Deep learning-based optimization for motion planning of dual-arm assembly robots. Comput. Ind. Eng. 2021, 160, 107603. [Google Scholar] [CrossRef]
- Gao, Q.; Yuan, Q.; Sun, Y.; Xu, L. Path planning algorithm of robot arm based on improved RRT* and BP neural network algorithm. J. King Saud Univ.—Comput. Inf. Sci. 2023, 35, 101650. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Cao, D.; Ma, L.; Li, K.; Jia, L.; Cui, Y. Coverage path planning for kiwifruit picking robots based on deep reinforcement learning. Comput. Electron. Agric. 2023, 205, 107593. [Google Scholar] [CrossRef]
- Srinivasu, P.N.; Bhoi, A.K.; Jhaveri, R.H.; Pandya, S.; Das, A.K. Probabilistic deep Q network for real-time path planning in censorious robotic procedures using force sensors. J. -Real-Time Image Process. 2021, 18, 1773–1785. [Google Scholar] [CrossRef]
- Francis, A.; Faust, A.; Chiang, H.T.L.; Hsu, J.; Kew, J.C.; Fiser, M.; Lee, T.W.E. Long-range indoor navigation with PRM-RL. IEEE Trans. Robot. 2020, 36, 1115–1134. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Z.; Sang, H.; Yu, S.; Yan, Y.; Er, M.J. Efficient exploration of mobile robot based on DL-RRT and AP-BO. IEEE Trans. Instrum. Meas. 2024, 73, 8505109. [Google Scholar] [CrossRef]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000; pp. 1–7. [Google Scholar]
- Ma, H.; Meng, F.; Ye, C.; Wang, J.; Meng, M.Q.H. Bi-Risk-RRT based efficient motion planning for autonomous ground vehicles. IEEE Trans. Intell. Veh. 2022, 7, 722–733. [Google Scholar] [CrossRef]
- Salzman, O.; Halperin, D. Asymptotically near-optimal RRT for fast, high-quality motion planning. IEEE Trans. Robot. 2016, 32, 473–483. [Google Scholar] [CrossRef]
- Arslan, O.; Berntorp, K.; Tsiotras, P. Sampling-based algorithms for optimal motion planning using closed-loop prediction. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4991–4996. [Google Scholar]






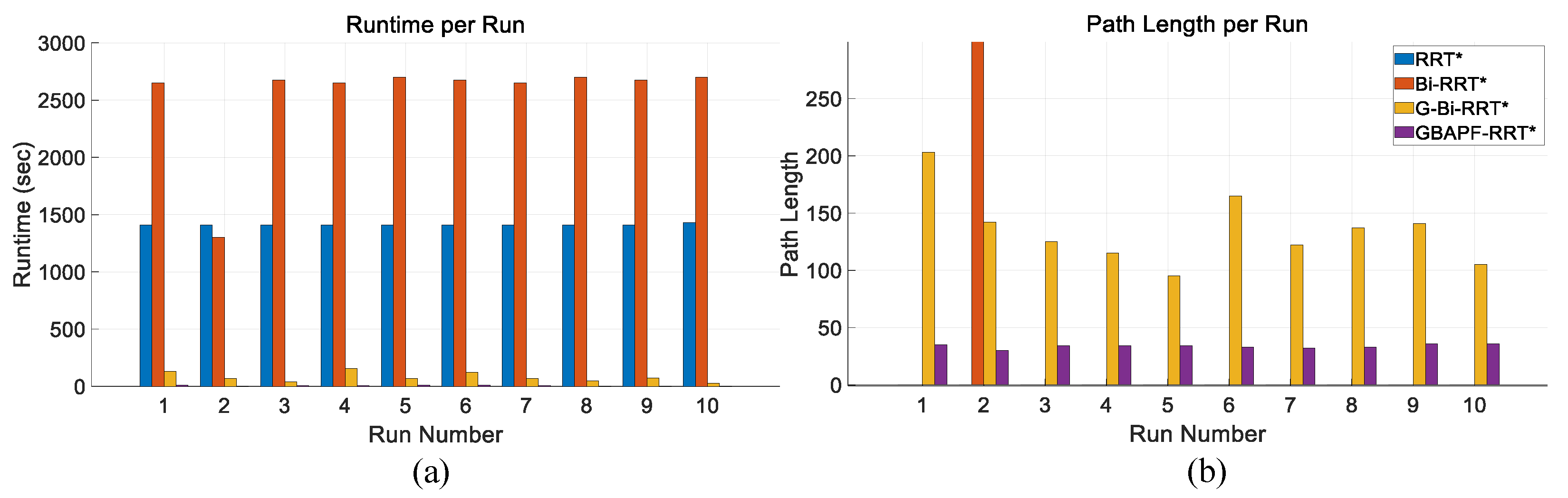


| Link i | [m] | [m] | [rad] | |
|---|---|---|---|---|
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 |
| Algorithm | (s) | (s) | (s) | ||||
|---|---|---|---|---|---|---|---|
| RRT* | 0 | 0 | 0 | 1780 | 1795 | 1788 | 0 |
| Bi-RRT* | 0 | 245 | 24 | 1670 | 3380 | 3184 | 1 |
| G-Bi-RRT* | 63 | 122 | 82 | 12 | 117 | 46 | 10 |
| GBAPF-RRT* | 20 | 34 | 28 | 1 | 8 | 4 | 10 |
| Algorithm | (s) | (s) | (s) | ||||
|---|---|---|---|---|---|---|---|
| RRT* | 0 | 0 | 0 | 1410 | 1430 | 1412 | 0 |
| Bi-RRT* | 0 | 300 | 30 | 1300 | 2700 | 2538 | 1 |
| G-Bi-RRT* | 95 | 203 | 135 | 28 | 156 | 81 | 10 |
| GBAPF-RRT* | 30 | 36 | 34 | 3 | 9 | 6 | 10 |
| Algorithm | (s) | (s) | (s) | ||||
|---|---|---|---|---|---|---|---|
| Single Tree | 24 | 32 | 28 | 12.13 | 25.10 | 17.66 | 5 |
| Dual-Tree | 26 | 30 | 27 | 2.01 | 4.40 | 3.18 | 5 |
| Algorithm | (s) | (s) | (s) | ||||
|---|---|---|---|---|---|---|---|
| Single Tree | 31 | 37 | 33 | 2.92 | 35.41 | 17.17 | 5 |
| Dual-Tree | 32 | 45 | 38 | 4.00 | 15.15 | 7.70 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, Y.; Liu, K.; Wen, C.-Y. Intelligent Joint Space Path Planning: Enhancing Motion Feasibility with Goal-Driven and Potential Field Strategies. Sensors 2025, 25, 4370. https://doi.org/10.3390/s25144370
Li Y, Yang Y, Liu K, Wen C-Y. Intelligent Joint Space Path Planning: Enhancing Motion Feasibility with Goal-Driven and Potential Field Strategies. Sensors. 2025; 25(14):4370. https://doi.org/10.3390/s25144370
Chicago/Turabian StyleLi, Yuzhou, Yefeng Yang, Kang Liu, and Chih-Yung Wen. 2025. "Intelligent Joint Space Path Planning: Enhancing Motion Feasibility with Goal-Driven and Potential Field Strategies" Sensors 25, no. 14: 4370. https://doi.org/10.3390/s25144370
APA StyleLi, Y., Yang, Y., Liu, K., & Wen, C.-Y. (2025). Intelligent Joint Space Path Planning: Enhancing Motion Feasibility with Goal-Driven and Potential Field Strategies. Sensors, 25(14), 4370. https://doi.org/10.3390/s25144370






