A UNet++-Based Approach for Delamination Imaging in CFRP Laminates Using Full Wavefield
Abstract
1. Introduction
- (1)
- UNet++ is employed to segment the energy distribution in 2D FDS, achieving end-to-end artifact free delamination imaging.
- (2)
- The model trained with multi-frequency FDS demonstrates accurate delamination imaging, even in scenarios with input frequency offsets, while also exhibiting good noise resistance.
- (3)
- The model trained on pure simulation dataset can be used to predict experimental samples with high accuracy. It provides a solution for quantitative detection of invisible delamination damage in CFRP.
2. Dataset Preparation
2.1. Material Properties of Specimen
2.2. Numerical Simulation
2.3. Frequency Domain Spectra Extraction
2.4. Flipping Augmentation
2.5. Dataset Labeling and Splitting
3. Delamination Imaging Model Construction, Training, and Evaluation Methods
3.1. Neural Network
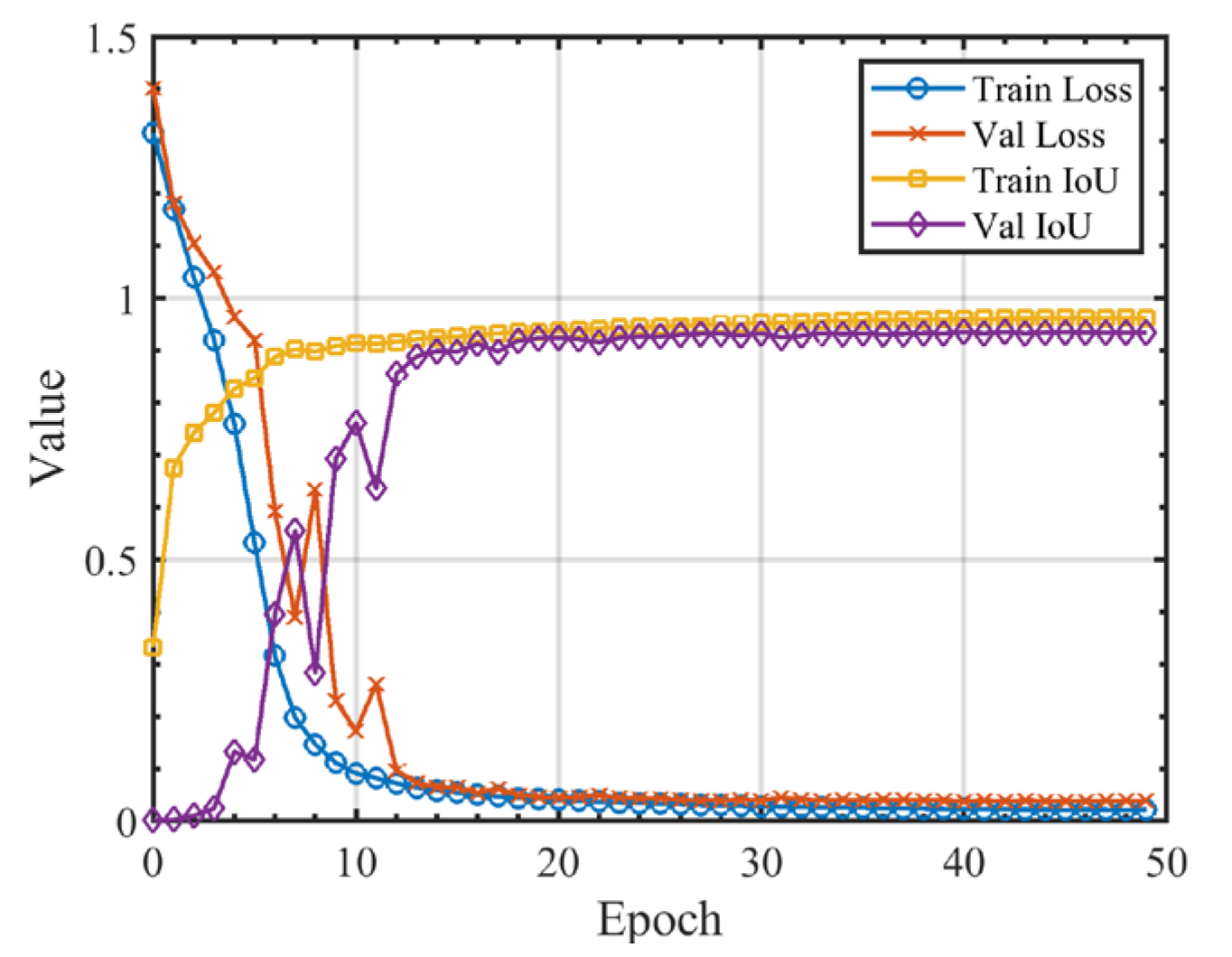
3.2. Training Strategy
3.3. Performance Evaluation Methods
- (1)
- Penalty for displacement: If there is a spatial offset in the predicted area, the IoU will decrease significantly, even if the size of the predicted area is correct.
- (2)
- Penalty for redundancy: If the prediction includes areas that do not correspond to the target (i.e., non-target areas), the IoU will decrease significantly, even if the target area is correctly covered.
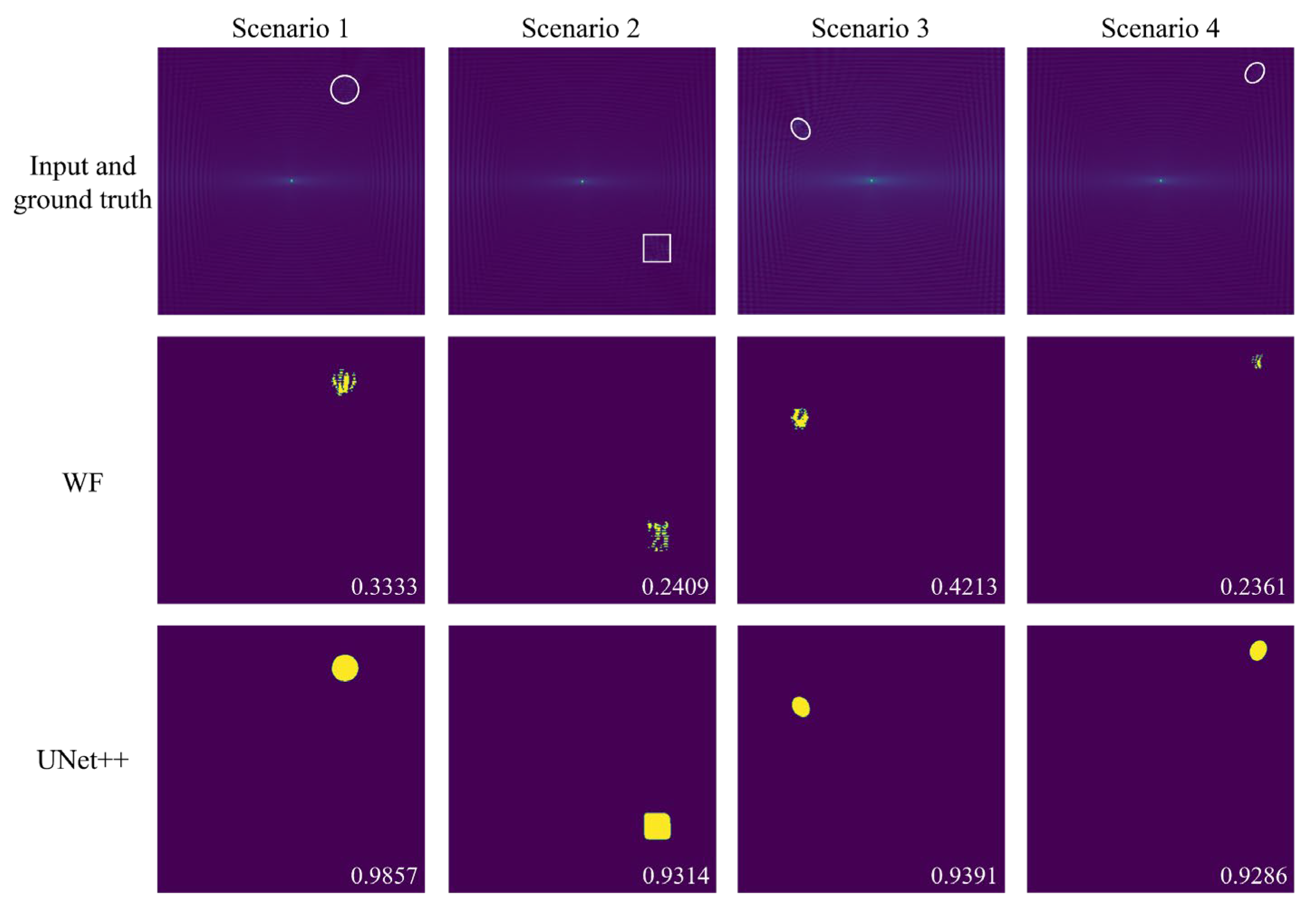
4. Results and Discussion
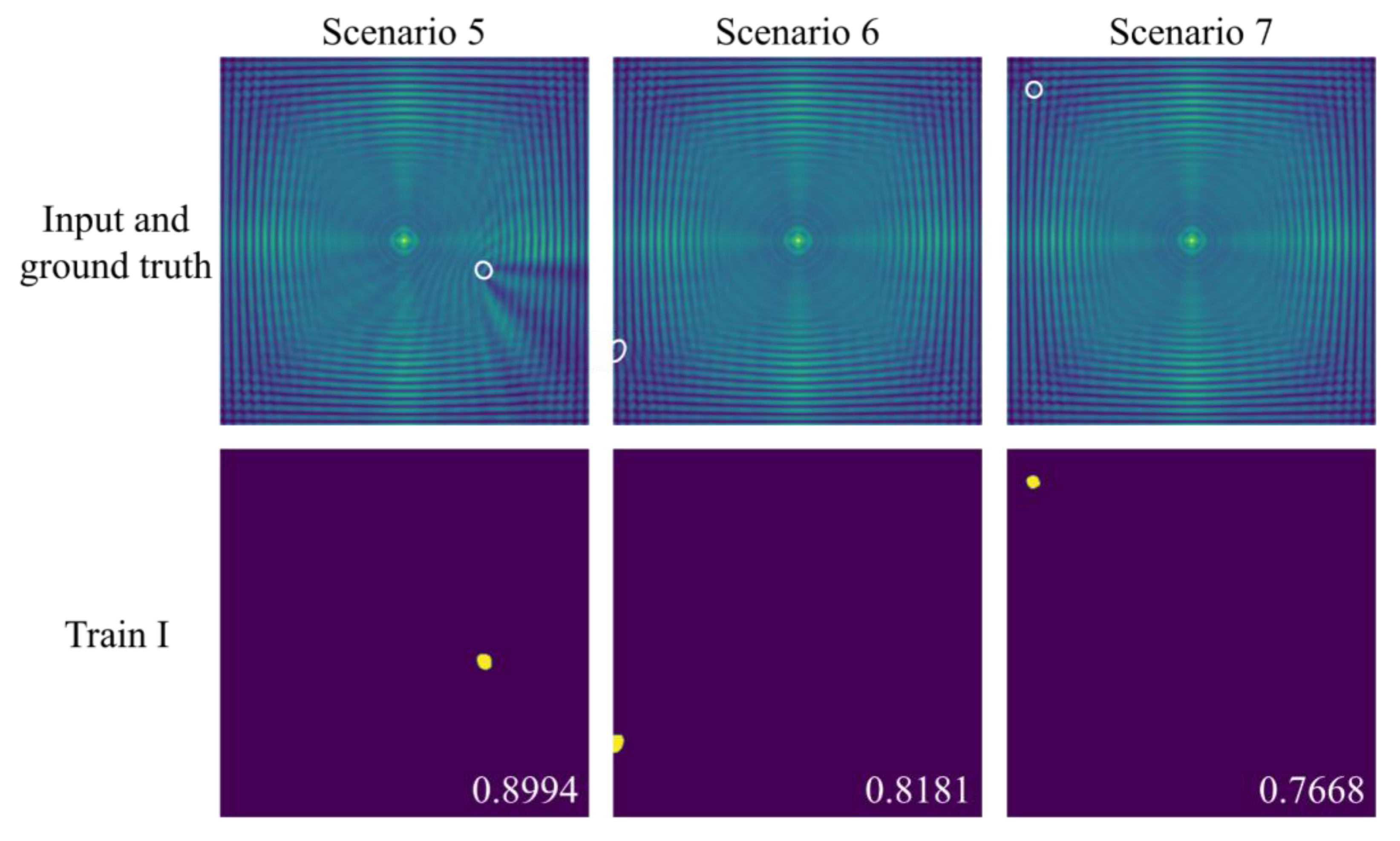
4.1. Generalization in the Simulation Test Set
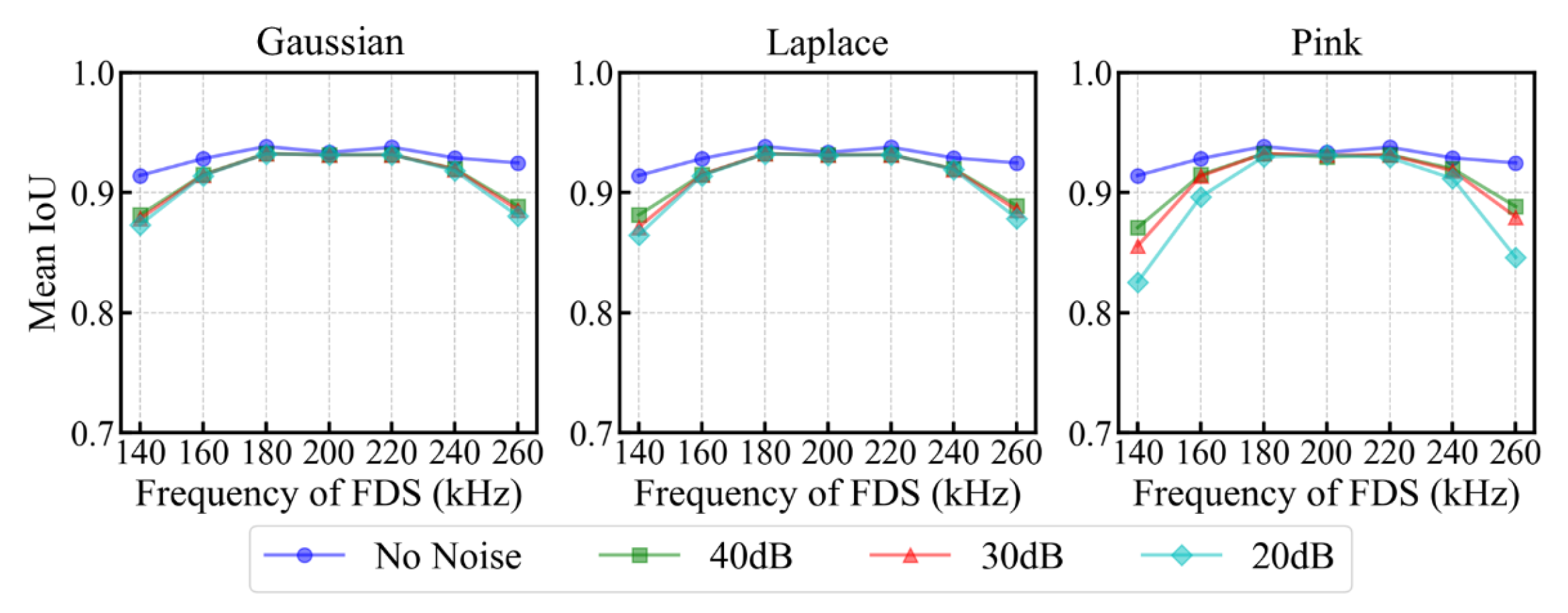
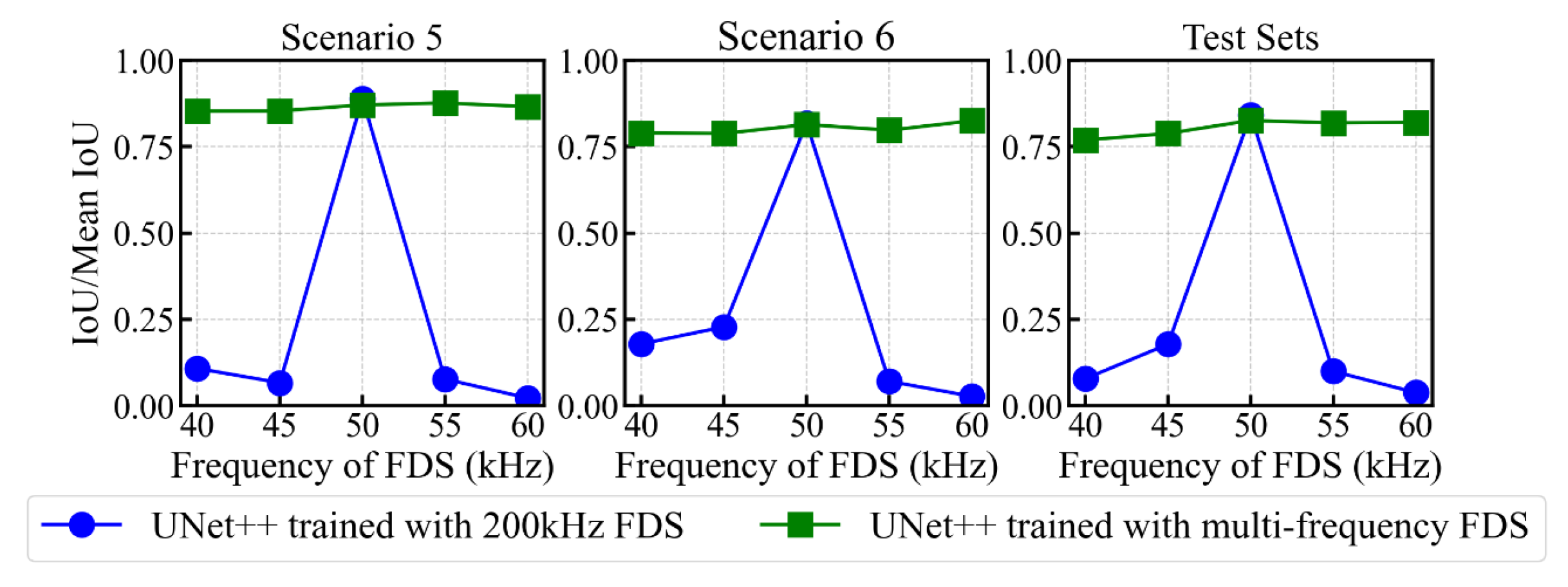
4.2. Generalization on Frequency Offset FDS
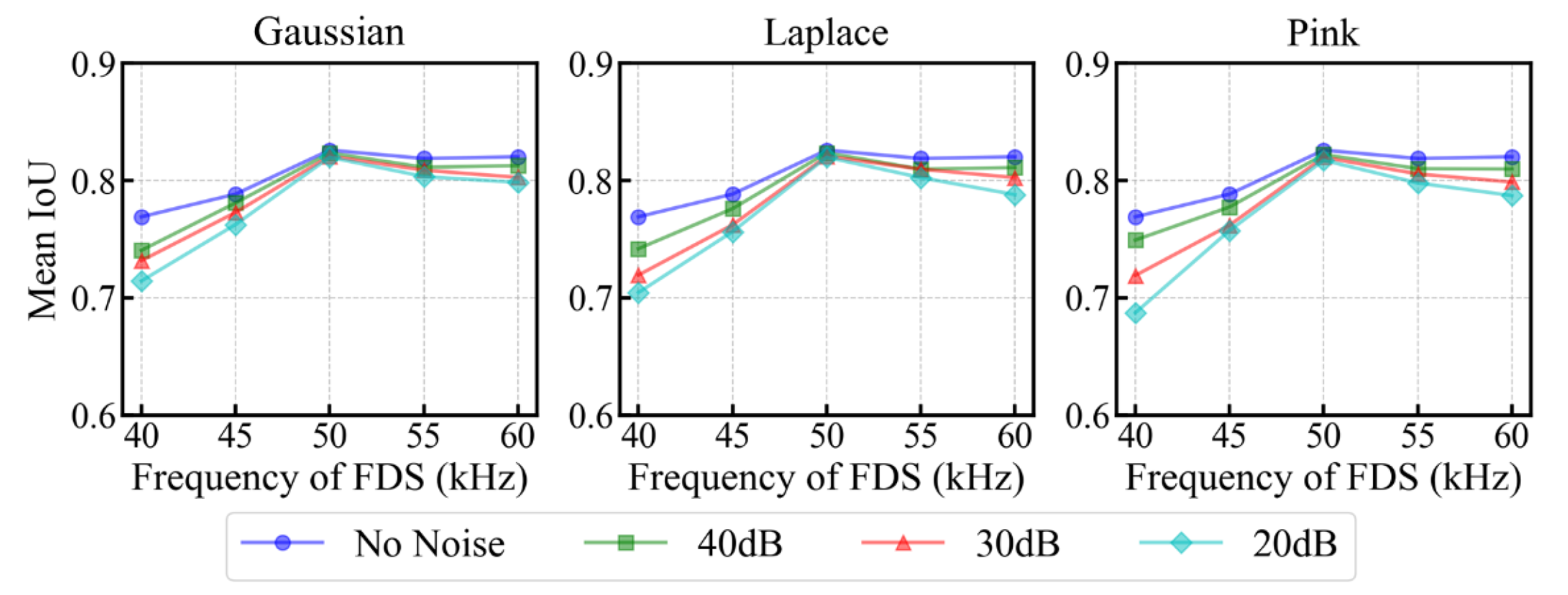
4.3. Robustness Under Noise Interference
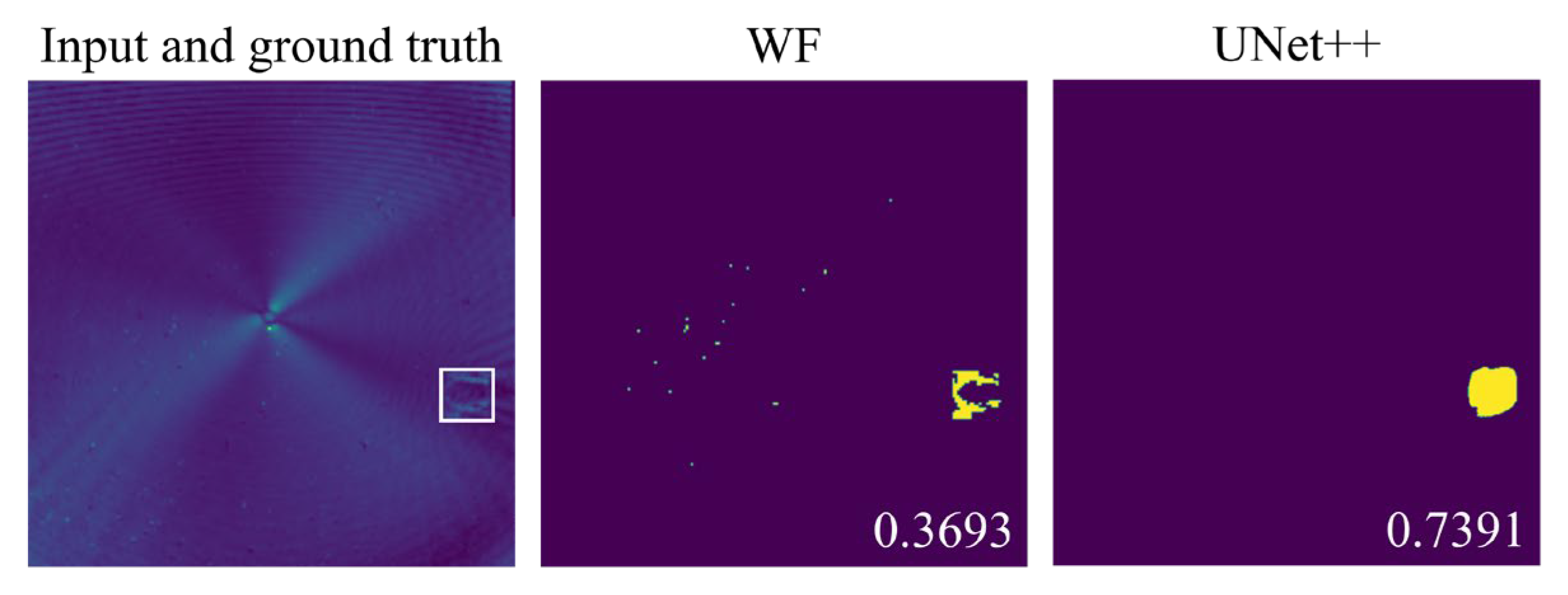
4.4. Experimental Test
4.5. Generalization on Another Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bafekrpour, E. Advanced Composite Materials: Properties and Applications; De Gruyter Open: Berlin, Germany, 2017; ISBN 3-11-057443-8. [Google Scholar]
- Toor, Z.S. Space applications of composite materials. J. Space Technol. 2018, 8, 65–70. [Google Scholar]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Chen, L.; Miao, L.; Xu, Q.; Yang, Q.; Zhu, W.; Ke, Y. Damage and failure mechanisms of CFRP due to manufacturing induced wrinkling defects. Compos. Struct. 2023, 326, 117624. [Google Scholar] [CrossRef]
- Banks-Sills, L. Interface Fracture and Delaminations in Composite Materials; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 3-319-60327-2. [Google Scholar]
- Fariñas, M.D.; Gómez Álvarez-Arenas, T.E.; Cuevas Aguado, E.; García Merino, M. Non-contact ultrasonic inspection of CFRP prepregs for aeronautical applications during lay-up fabrication. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 1590–1593. [Google Scholar]
- Chen, J.; Yu, Z.; Jin, H. Nondestructive testing and evaluation techniques of defects in fiber-reinforced polymer composites: A review. Front. Mater. 2022, 9, 986645. [Google Scholar] [CrossRef]
- Saito, O.; Sen, E.; Okabe, Y. 2D slowness visualization of ultrasonic wave propagation for delamination detection in CFRP laminates. NDT E Int. 2022, 131, 102696. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, B. In-Situ Defect Measurement Method for CFRP Plate Based on Air-Coupled Ultrasonic Lamb Wave. In Proceedings of the 2023 17th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 10–12 November 2023; pp. 1–5. [Google Scholar]
- Yang, Z.; Yang, H.; Tian, T.; Deng, D.; Hu, M.; Ma, J.; Gao, D.; Zhang, J.; Ma, S.; Yang, L. A review in guided-ultrasonic-wave-based structural health monitoring: From fundamental theory to machine learning techniques. Ultrasonics 2023, 133, 107014. [Google Scholar] [CrossRef]
- Xu, X.; Liu, C. Physics-guided deep learning for damage detection in CFRP composite structures. Compos. Struct. 2024, 331, 117889. [Google Scholar] [CrossRef]
- Nelon, C.; Myers, O.; Hall, A. The intersection of damage evaluation of fiber-reinforced composite materials with machine learning: A review. J. Compos. Mater. 2022, 56, 1417–1452. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, L.; Zhang, H.; Zhang, T.; Zhu, Q. Phased array ultrasonic inspection and automated identification of wrinkles in laminated composites. Compos. Struct. 2022, 300, 116170. [Google Scholar] [CrossRef]
- Cheng, X.; Ma, G.; Wu, Z.; Zu, H.; Hu, X. Automatic defect depth estimation for ultrasonic testing in carbon fiber reinforced composites using deep learning. NDT E Int. 2023, 135, 102804. [Google Scholar] [CrossRef]
- Feng, B.; Pasadas, D.J.; Ribeiro, A.L.; Ramos, H.G. Locating defects in anisotropic CFRP plates using ToF-based probability matrix and neural networks. IEEE Trans. Instrum. Meas. 2019, 68, 1252–1260. [Google Scholar] [CrossRef]
- Su, C.; Jiang, M.; Lv, S.; Lu, S.; Zhang, L.; Zhang, F.; Sui, Q. Improved Damage Localization and Quantification of CFRP Using Lamb Waves and Convolution Neural Network. IEEE Sens. J. 2019, 19, 5784–5791. [Google Scholar] [CrossRef]
- Rautela, M.; Gopalakrishnan, S. Ultrasonic guided wave based structural damage detection and localization using model assisted convolutional and recurrent neural networks. Expert Syst. Appl. 2021, 167, 114189. [Google Scholar] [CrossRef]
- Yang, J.; Su, Y.; He, Y.; Zhou, P.; Xu, L.; Su, Z. Machine learning-enabled resolution-lossless tomography for composite structures with a restricted sensing capability. Ultrasonics 2022, 125, 106801. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Lin, J.; Hua, J. Lamb wave-based damage assessment for composite laminates using a deep learning approach. Ultrasonics 2024, 141, 107333. [Google Scholar] [CrossRef]
- Ijjeh, A.A.; Ullah, S.; Kudela, P. Full wavefield processing by using FCN for delamination detection. Mech. Syst. Signal Process. 2021, 153, 107537. [Google Scholar] [CrossRef]
- Ijjeh, A.A.; Kudela, P. Deep learning based segmentation using full wavefield processing for delamination identification: A comparative study. Mech. Syst. Signal Process. 2022, 168, 108671. [Google Scholar] [CrossRef]
- Kudela, P.; Ijjeh, A. Synthetic dataset of a full wavefield representing the propagation of Lamb waves and their interactions with delaminations. Zenodo 2021. [Google Scholar] [CrossRef]
- Ahmad, Z.A.B.; Vivar-Perez, J.M.; Gabbert, U. Semi-analytical finite element method for modeling of lamb wave propagation. CEAS Aeronaut. J. 2013, 4, 21–33. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Zhou, J.; Zheng, Y.; Tang, J.; Li, J.; Yang, Z. FlipDA: Effective and Robust Data Augmentation for Few-Shot Learning. arXiv 2022. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: Redesigning Skip Connections to Exploit Multiscale Features in Image Segmentation. IEEE Trans. Med. Imaging 2020, 39, 1856–1867. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhang, Z. Improved Adam Optimizer for Deep Neural Networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar]
- Johnson, O.V.; Xinying, C.; Khaw, K.W.; Lee, M.H. ps-CALR: Periodic-Shift Cosine Annealing Learning Rate for Deep Neural Networks. IEEE Access 2023, 11, 139171–139186. [Google Scholar] [CrossRef]
- Ruby, U.; Yendapalli, V. Binary cross entropy with deep learning technique for Image classification. Int. J. Adv. Trends Comput. Sci. Eng. 2020, 9, 4. [Google Scholar] [CrossRef]
- Zhao, R.; Qian, B.; Zhang, X.; Li, Y.; Wei, R.; Liu, Y.; Pan, Y. Rethinking Dice Loss for Medical Image Segmentation. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–22 November 2020; pp. 851–860. [Google Scholar]
- Waoo, A.A.; Soni, B.K. Performance Analysis of Sigmoid and Relu Activation Functions in Deep Neural Network. In Intelligent Systems; Sheth, A., Sinhal, A., Shrivastava, A., Pandey, A.K., Eds.; Springer: Singapore, 2021; pp. 39–52. [Google Scholar]
- Zhang, H.; Sun, J.; Rui, X.; Liu, S. Delamination damage imaging method of CFRP composite laminate plates based on the sensitive guided wave mode. Compos. Struct. 2023, 306, 116571. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, C.; Yang, H.; Wang, L.; Kim, N.H.; Harley, J.B. Improving unsupervised long-term damage detection in an uncontrolled environment through noise-augmentation strategy. Mech. Syst. Signal Process. 2025, 224, 112076. [Google Scholar] [CrossRef]
- Ijjeh, A.; Ullah, S.; Radzienski, M.; Kudela, P. Deep learning super-resolution for the reconstruction of full wavefield of Lamb waves. Mech. Syst. Signal Process. 2023, 186, 109878. [Google Scholar] [CrossRef]








| ρ (kg/m3) | E1 (GPa) | E2 (GPa) | E3 (GPa) | G12 (GPa) | G13 (GPa) | G23 (GPa) | ν12 | ν13 | ν23 |
|---|---|---|---|---|---|---|---|---|---|
| 1600 | 172 | 11.6 | 11.6 | 7.8 | 7.8 | 3.9 | 0.36 | 0.36 | 0.55 |
| Composition | Train Set | Validation Set | Test Set | Total |
|---|---|---|---|---|
| Sample size | 1260 | 360 | 180 | 1800 |
| Method | IoU | |||
|---|---|---|---|---|
| Mean | Max | Min | SD | |
| WF | 0.4245 | 0.7400 | 0.1085 | ±0.1425 |
| UNet++ | 0.9449 | 0.9842 | 0.7595 | ±0.0292 |
| Frequency of FDS | 140 kHz | 160 kHz | 180 kHz | 200 kHz | 220 kHz | 240 kHz | 260 kHz | Total |
|---|---|---|---|---|---|---|---|---|
| Sample size | 178 | 179 | 184 | 186 | 170 | 178 | 185 | 1260 |
| Frequency of FDS | 40 kHz | 45 kHz | 50 kHz | 55 kHz | 60 kHz | Total |
|---|---|---|---|---|---|---|
| Sample size | 243 | 233 | 250 | 252 | 238 | 1216 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Yang, K.; Gou, Y.; Tang, Z.; Lv, F.; Zeng, Z.; Li, J.; Liu, Y. A UNet++-Based Approach for Delamination Imaging in CFRP Laminates Using Full Wavefield. Sensors 2025, 25, 4292. https://doi.org/10.3390/s25144292
Yan Y, Yang K, Gou Y, Tang Z, Lv F, Zeng Z, Li J, Liu Y. A UNet++-Based Approach for Delamination Imaging in CFRP Laminates Using Full Wavefield. Sensors. 2025; 25(14):4292. https://doi.org/10.3390/s25144292
Chicago/Turabian StyleYan, Yitian, Kang Yang, Yaxun Gou, Zhifeng Tang, Fuzai Lv, Zhoumo Zeng, Jian Li, and Yang Liu. 2025. "A UNet++-Based Approach for Delamination Imaging in CFRP Laminates Using Full Wavefield" Sensors 25, no. 14: 4292. https://doi.org/10.3390/s25144292
APA StyleYan, Y., Yang, K., Gou, Y., Tang, Z., Lv, F., Zeng, Z., Li, J., & Liu, Y. (2025). A UNet++-Based Approach for Delamination Imaging in CFRP Laminates Using Full Wavefield. Sensors, 25(14), 4292. https://doi.org/10.3390/s25144292






