Automatic PID Control Strategy via Energy Dissipation for Tapping Mode Atomic Force Microscopy
Abstract
1. Introduction
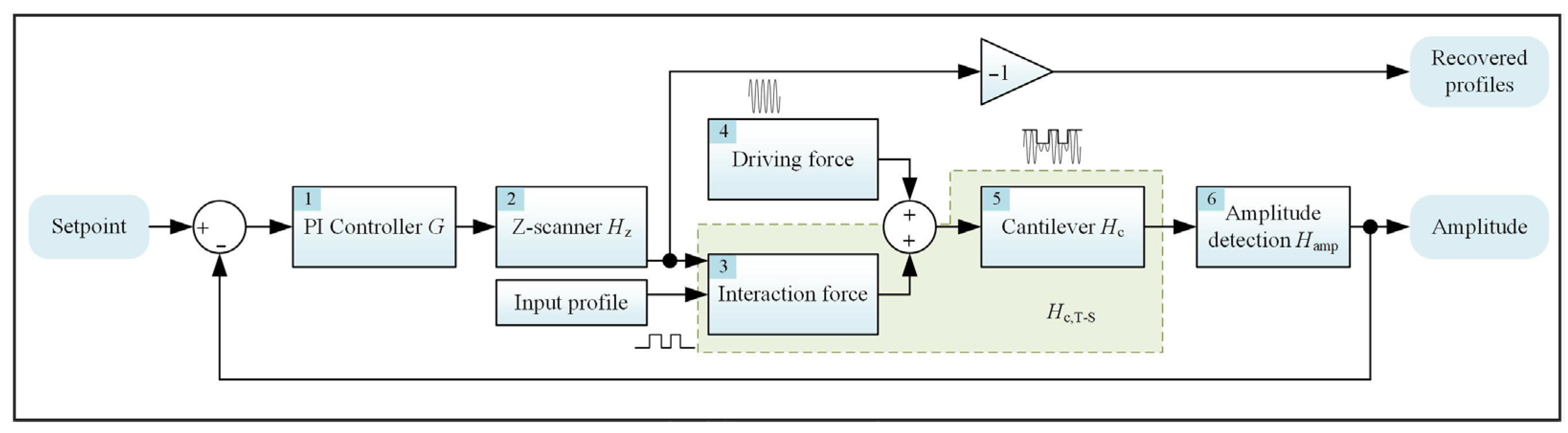
2. Methodology
2.1. Principle of TM-AFM
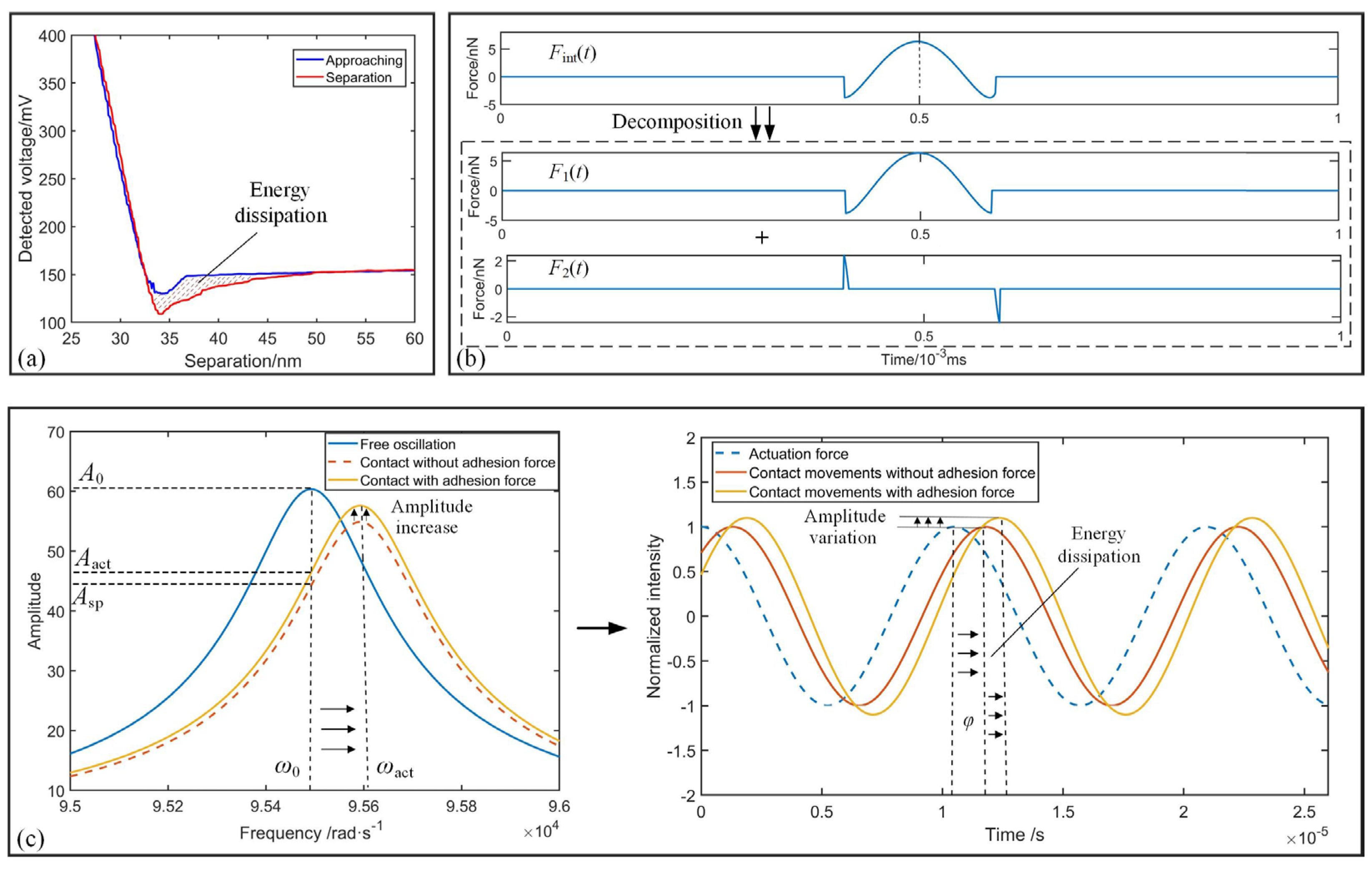
2.2. Phase Lag Modeling
2.3. System Stability Analysis
- (1)
- φ belongs to 0–90°
- (2)
- φ belongs to 90–180°
3. Simulations
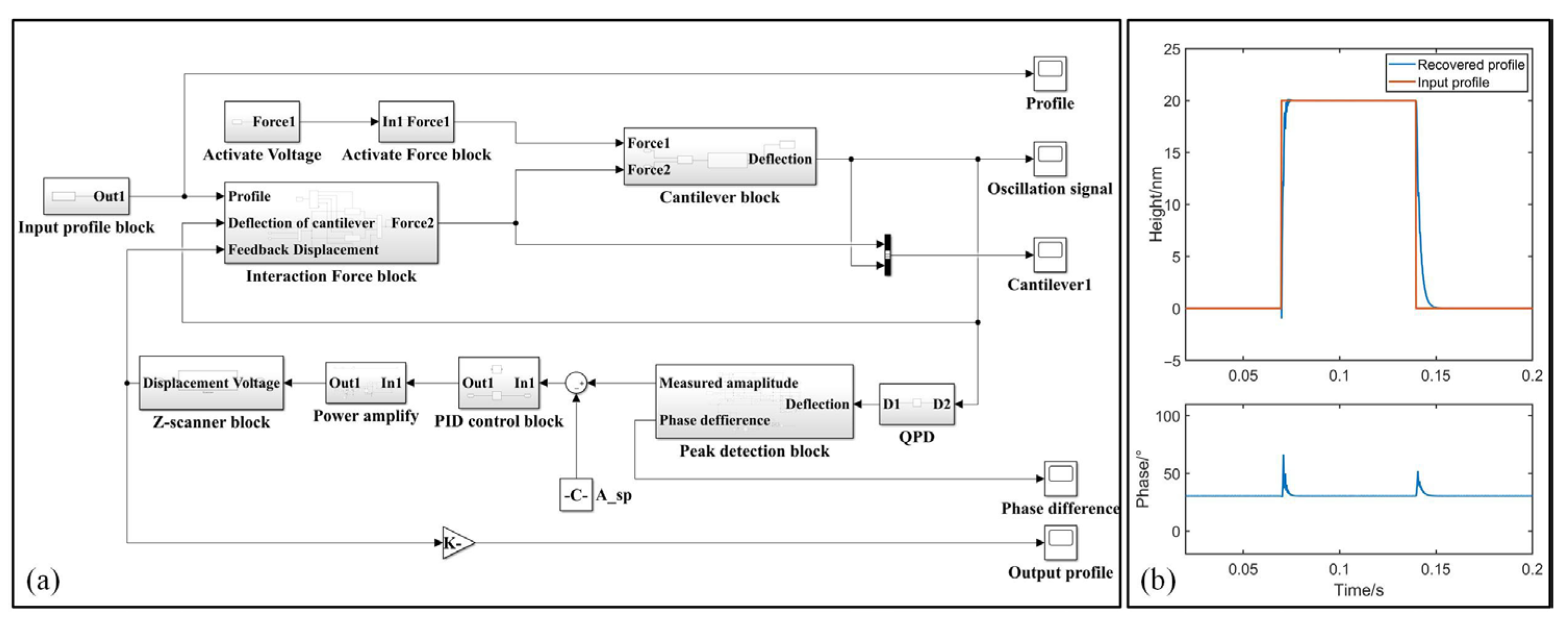
3.1. System Virtualization
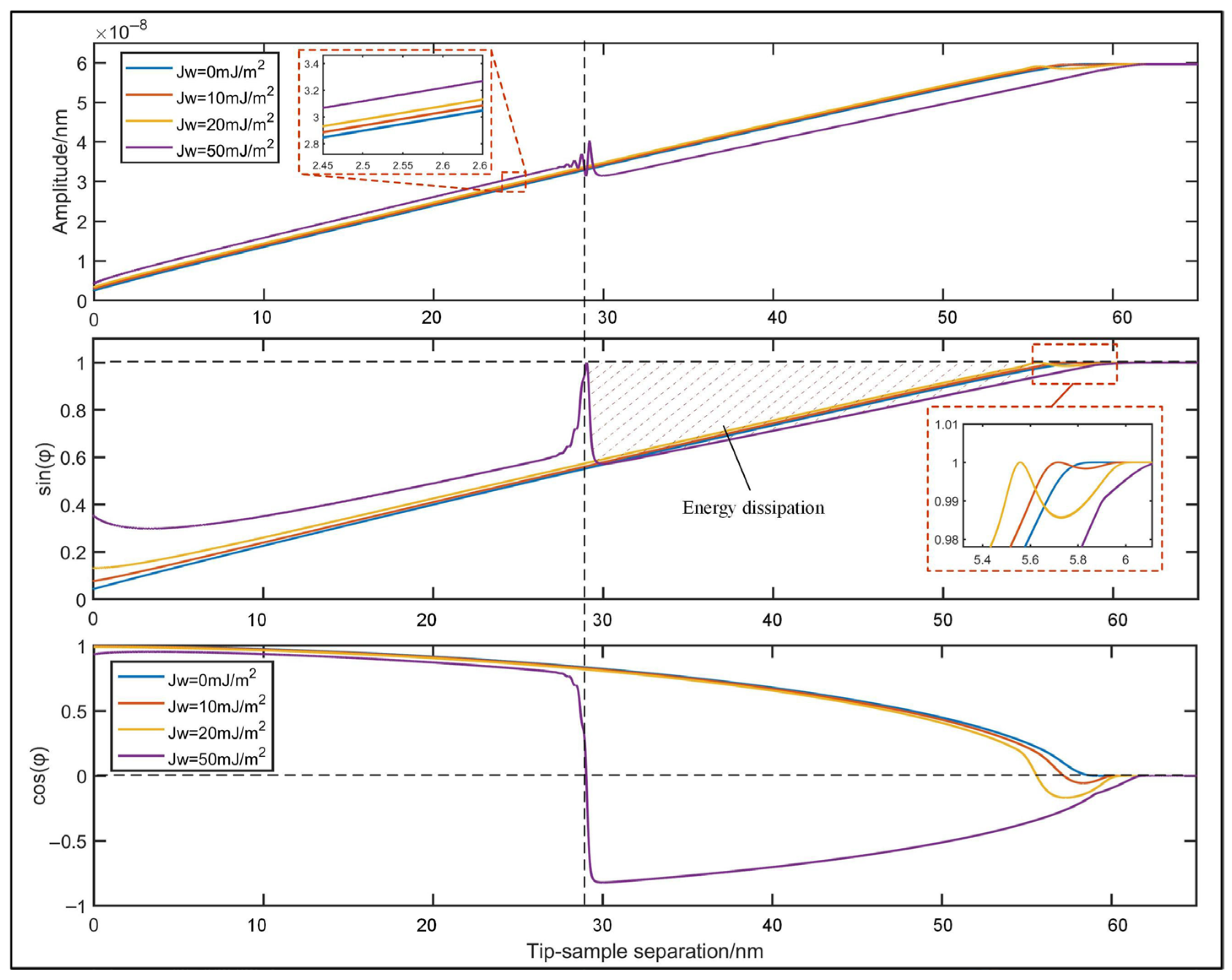
3.2. Phase Lag Analysis
4. Experiments
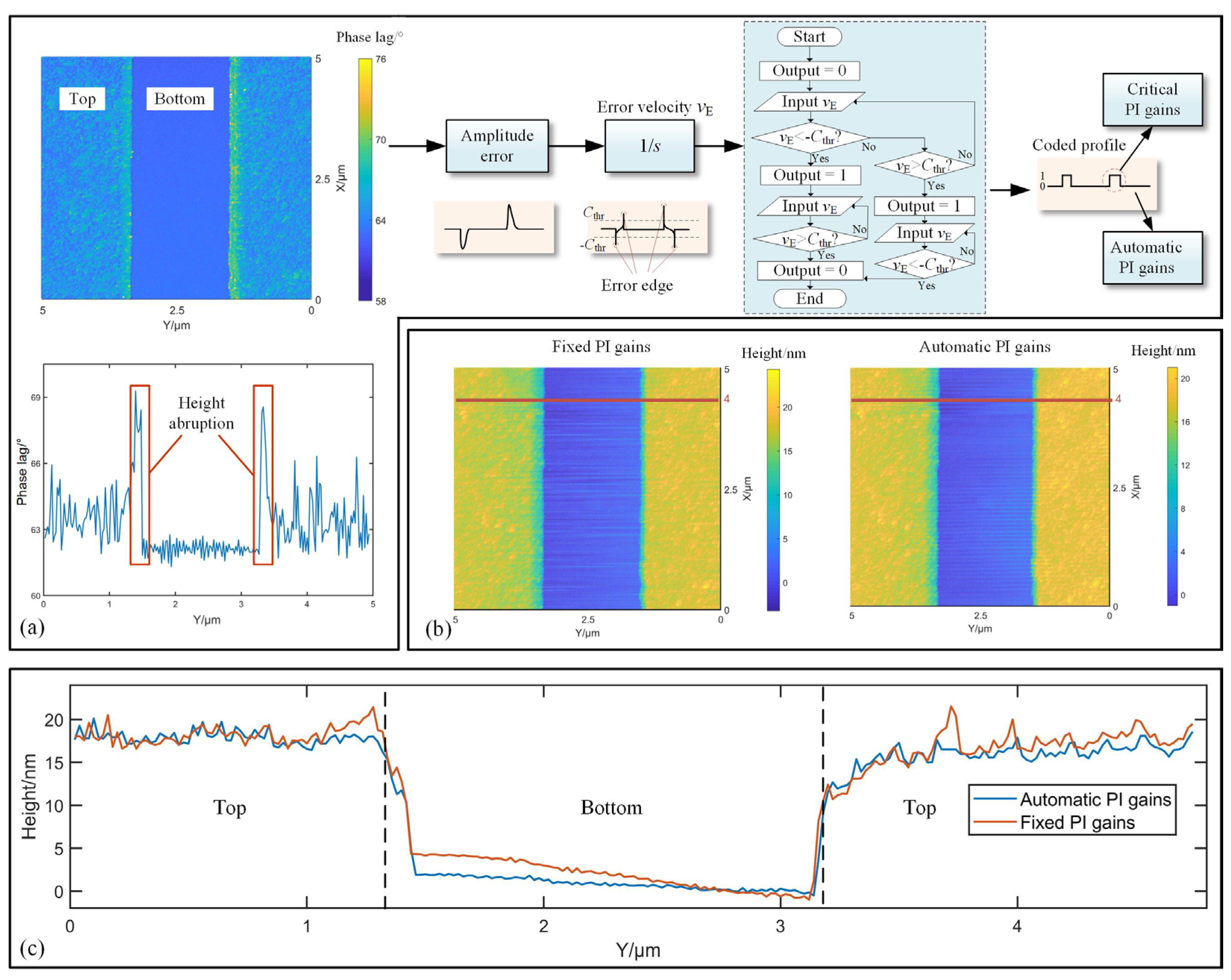
4.1. Standard Height Grid Measurement
4.2. Half-Coated Silicon Measurement
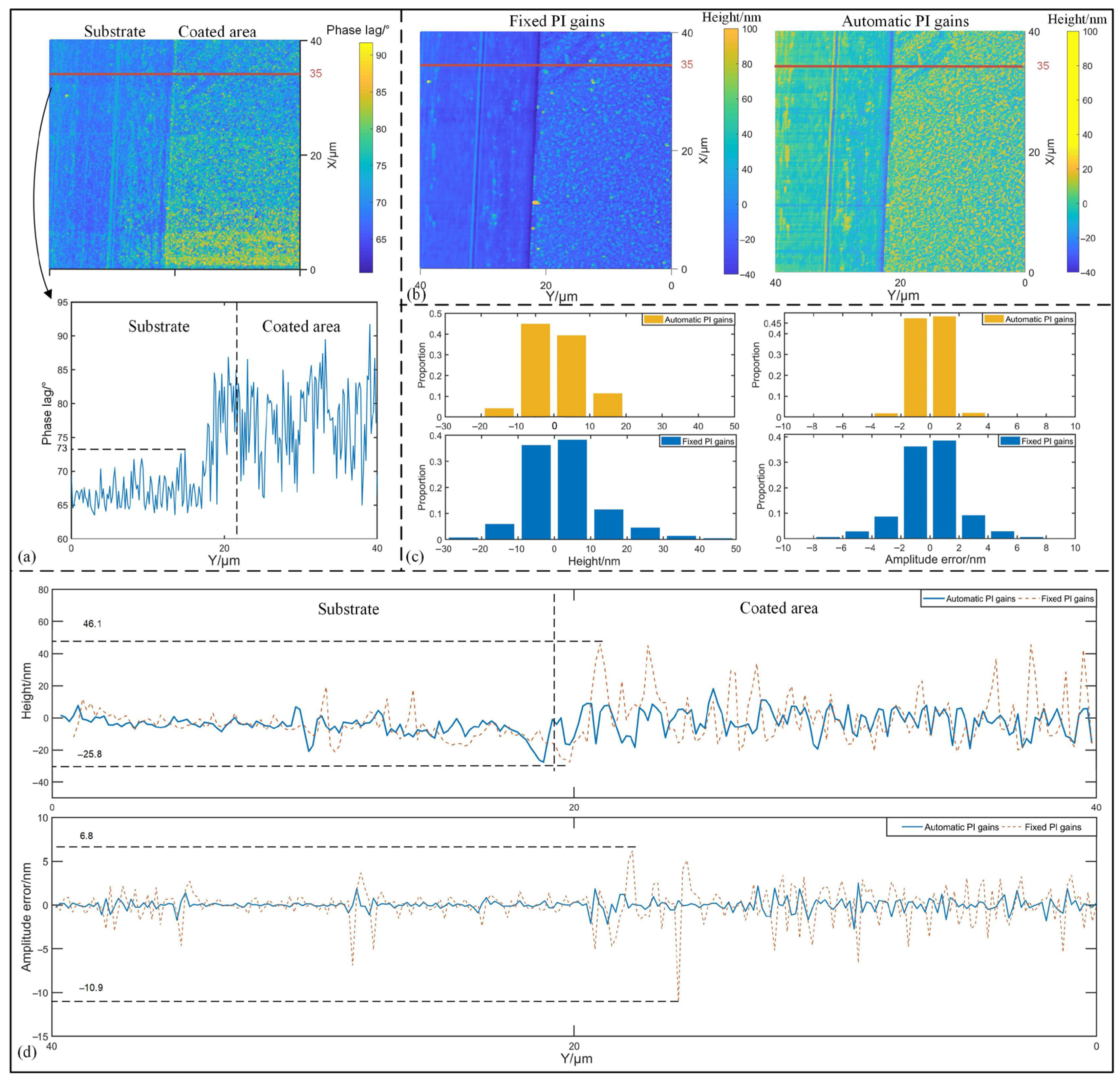
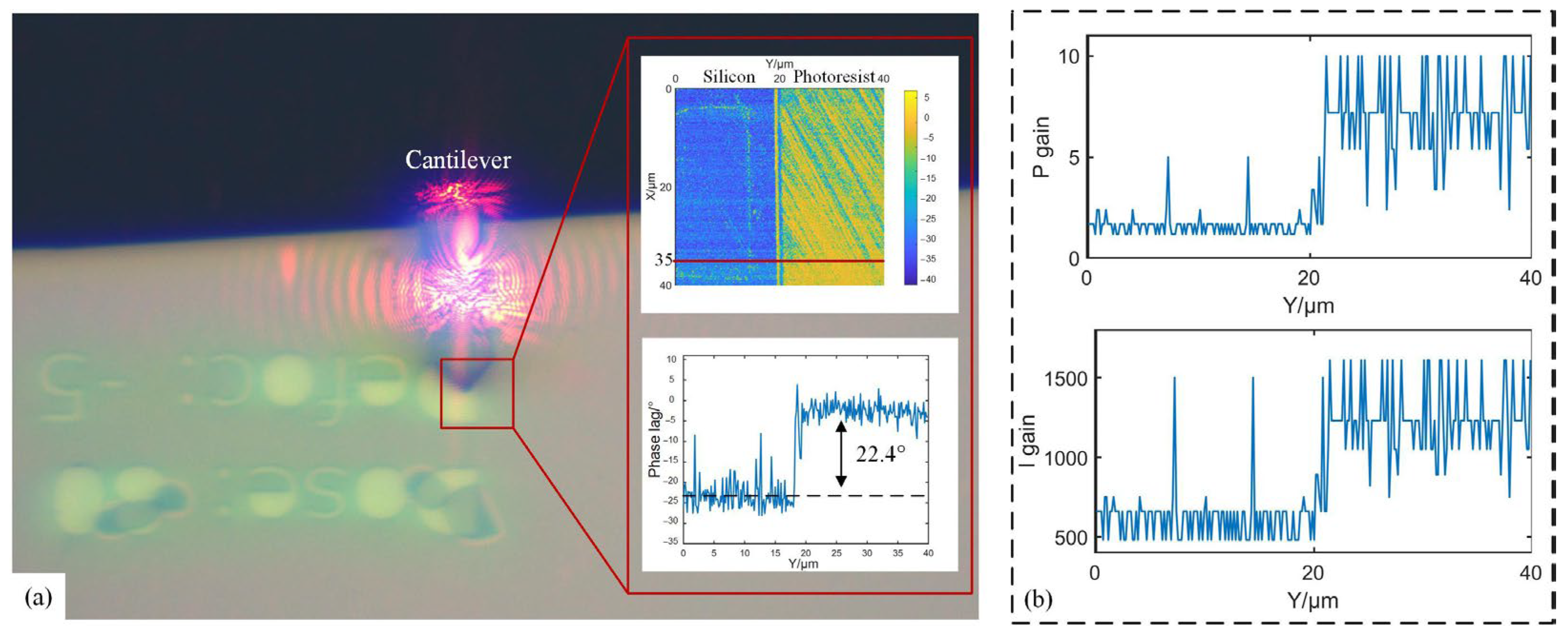
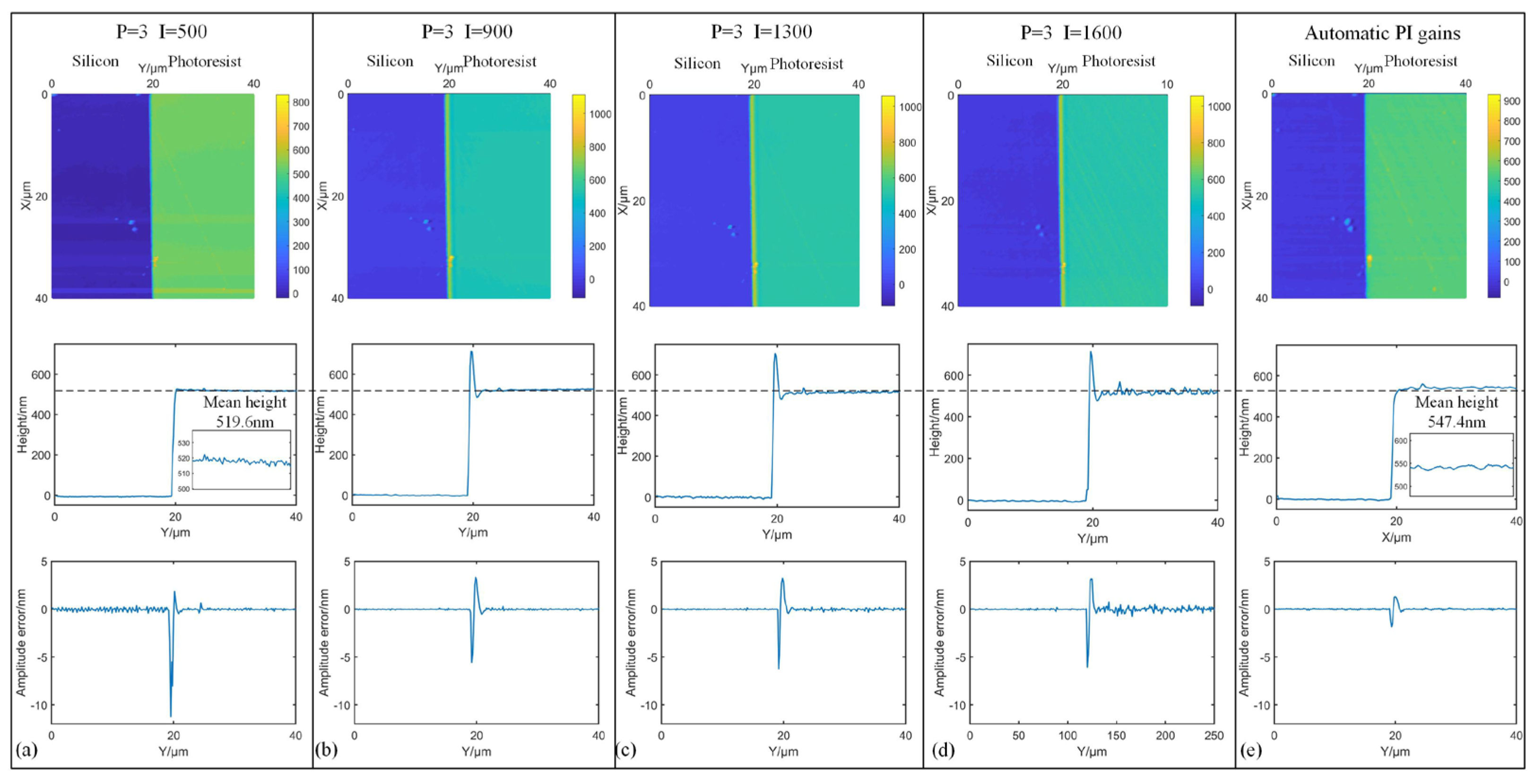
4.3. Silicon-Base Photoresist Substrate Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TM-AFM | Tapping Mode Atomic Force Microscopy |
| SPM | Scanning Probe Microscopy |
| STM | Scanning Tunneling Microscopy |
| SNOM | Scanning Near-Field Optical Microscopy |
| AFM | Atomic Force Microscopy |
| PID | Proportional Integral-Derivative |
| AI | Artificial Intelligence |
| RMS-DC | Root Mean Square to Direct Current |
| LIA | Lock-in Amplifier |
References
- Eigler, D.M.; Schweizer, E.K. Positioning Single Atoms with a Scanning Tunnelling Microscope. Nature 1990, 344, 524–526. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Binnig, G.; Rohrer, H. Scanning Tunneling Microscopy. Surf. Sci. 1982, 126, 236–244. [Google Scholar] [CrossRef]
- Betzig, E.; Trautman, J.K.; Harris, T.D.; Weiner, J.S.; Kostelak, R.L. Breaking the Diffraction Barrier: Optical Microscopy on a Nanometric Scale. Science 1991, 251, 1468–1470. [Google Scholar] [CrossRef] [PubMed]
- Martin, Y.; Williams, C.; Wickramasinghe, H. Atomic force microscope–force mapping and profiling on a sub 100-Å scale. J. Appl. Phys. 1987, 61, 4723–4729. [Google Scholar] [CrossRef]
- Zhong, Q.; Inniss, D.; Kjoller, K.; Elings, V. Fractured polymer/silica fiber surface studied by tapping mode atomic force microscopy. Sur. Sci. Lett. 1993, 290, 688–692. [Google Scholar]
- Andreas, K.; Sebastian, G.; Philipp, D.; Nicolas, H.; Markus, R.; Georg, P. An Integrated, Exchangeable Three-Electrode Electrochemical Setup for AFM-Based Scanning Electrochemical Microscopy. Sensors 2023, 23, 5228. [Google Scholar]
- Yang, P.C.; Chen, Y.; Vaez-Iravani, M. Attractive-Mode Atomic Force Microscopy with Optical Detection in an Orthogonal Cantilever/Sample Configuration. J. Appl. Phys. 1992, 71, 2499–2502. [Google Scholar] [CrossRef]
- Mertz, J.; Marti, O.; Mlynek, J. Regulation of a Microcantilever Response by Force Feedback. Appl. Phys. Lett. 1993, 62, 2344–2346. [Google Scholar] [CrossRef]
- Drake, B.; Weisenhorn, A.; Gould, S.; Albrecht, T.; Quate, C.; Cannell, D.; Hansma, H.; Hansma, P. Imaging Crystals, Polymers, and Processes in Water with the Atomic Force Microscope. Science 1989, 243, 1586–1589. [Google Scholar] [CrossRef]
- Matilde, G.; Bruno, T.; Faiza, A.S.; Massimo, V.; Michele, B. Adaptive Drive as a Control Strategy for Fast Scanning in Dynamic Mode Atomic Force Microscopy. Sensors 2025, 25, 860. [Google Scholar] [CrossRef] [PubMed]
- Paloczi, G.T.; Smith, B.L.; Hansma, P.K.; Walters, D.A.; Wendman, M.A. Rapid Imaging of Calcite Crystal Growth using Atomic Force Microscopy with Small Cantilevers. Appl. Phys. Lett. 1998, 73, 1658–1660. [Google Scholar] [CrossRef]
- Bar, G.; Brandsch, R.; Whangbo, M.-H. Effect of Viscoelastic Properties of Polymers on the Phase Shift in Tapping Mode Atomic Force Microscopy. Langmuir 1998, 14, 7343–7347. [Google Scholar] [CrossRef]
- Magonov, S.; Elings, V.; Whangbo, M. Phase imaging and stiffness in tapping-mode atomic force microscopy. Sur. Sci. 1997, 375, 385–391. [Google Scholar] [CrossRef]
- Vlassov, S.; Oras, S.; Antsov, M.; Sosnin, I.; Polyakov, B.; Shutka, A.; Yu Krauchanka, M.; Dorogin, L.M. Adhesion and Mechanical Properties of PDMS Based Materials Probed with AFM: A Review. Rev. Adv. Mater. Sci. 2018, 56, 62–78. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Cohen, G.H.; Coon, G.A. Theoretical Consideration of Retarded Control. Trans. ASME 1953, 75, 827–834. [Google Scholar] [CrossRef]
- Wu, H.; Su, W.; Liu, Z. PID Controllers: Design and Tuning Methods. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 808–813. [Google Scholar]
- Abramovitch, D.Y.; Hoen, S.; Workman, R. Semi-Automatic Tuning of PID Gains for Atomic Force Microscopes. Asian J. Control 2009, 11, 188–195. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Automatic Tuning of Simple Regulators with Specifications on Phase and Amplitude Margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef]
- Li, H.X.; Gatland, H.B. Conventional Fuzzy Control and Its Enhancement. IEEE Trans. Syst. Man Cybern. 1996, 26, 791–797. [Google Scholar]
- Sinthipsomboon, K.; Hunsacharoonro, I.; Khedari, J.; Pongaen, W.; Pratumsuwan, P. A Hybrid of Fuzzy and Fuzzy Self-Tuning PID Controller for Servo Electro-Hydraulic System. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 220–225. [Google Scholar]
- Liu, L.; Wu, S.; Wang, Y.Y.; Hu, X.D.; Hu, X.T. Adaptive Velocity-Dependent Proportional-Integral Controller for High Speed Atomic Force Microscopy. J. Microscop. 2019, 275, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Carlucho, I.; De Paula, M.; Villar, S.A.; Acosta, G. Incremental Q-Learning Strategy for Adaptive PID Control of Mobile Robots. Expert Syst. Appl. 2017, 80, 183–199. [Google Scholar] [CrossRef]
- Wang, X.; Cai, J.; Wang, R.; Shu, G.; Tian, H.; Wang, M. Deep Reinforcement Learning-PID based Supervisor Control Method for Indirect-Contact Heat Transfer Processes in Energy Systems. Eng. Appl. Artif. Intell. 2023, 117, 105551. [Google Scholar] [CrossRef]
- Saif, A.A.; Mohammed, A.A.; AlSunni, F.; Ferik, S.E. Active Vibration Control of a Cantilever Beam Structure Using Pure Deep Learning and PID with Deep Learning-Based Tuning. Appl. Sci. 2024, 14, 11520. [Google Scholar] [CrossRef]
- Sonnaillon, M.O.; Bonetto, F.J. A Low-Cost, High-Performance, Digital Signal Processor-Based Lock-In Amplifier Capable of Measuring Multiple Frequency Sweeps Simultaneously. Rev. Sci. Instrum. 2025, 76, 024703. [Google Scholar] [CrossRef]
- Levinson, N. The Wiener (Root Mean Square) Error Criterion in Filter Design and Prediction. J. Math. Phys. 1946, 25, 261–278. [Google Scholar] [CrossRef]
- Ando, T.; Uchihashi, T.; Kodera, N.; Yamamoto, D.; Miyagi, A.; Taniguchi, M.; Yamashita, H. High-speed AFM and nano-visualization of biomolecular processes. Pflugers Arch. Eur. J. Physiol. 2008, 456, 211–225. [Google Scholar] [CrossRef]
- Paulo, A.; García, R. Tip-Surface Forces, Amplitude, and Energy Dissipation in Amplitude-Modulation (Tapping Mode) Force Microscopy. Phys. Rev. B 2000, 64, 193411. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, S.S.; Liu, J.R.; Wu, S. A simulation model of atomic force microscope and its guidance for scanning surfaces with non-uniform mechanical properties. Nanotech. Precis. Eng. 2025, in press.




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 2.0 × 10−11 kg | cz | 2.1 × 10−5 |
| c | 2.8 × 10−8 | kz | 20 N/m |
| k | 26 N/m | Etip | 130 GPa |
| mz | 2 × 10−3 kg | Rtip | 10 nm |
| Interval of Phase Lag Variation | p Gain (Kp) | I Gain (Ki) |
|---|---|---|
| 0–4° | 10 | 1610 |
| 4–8° | 7.2 | 1230 |
| 8–12° | 5.4 | 1050 |
| 12–16° | 3.4 | 890 |
| 16–20° | 2.6 | 820 |
| 20–24° | 2.4 | 750 |
| 24–28° | 1.7 | 660 |
| 28–32° | 1.2 | 480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Xiao, S.-S.; Liu, J.-R.; Wu, S. Automatic PID Control Strategy via Energy Dissipation for Tapping Mode Atomic Force Microscopy. Sensors 2025, 25, 4277. https://doi.org/10.3390/s25144277
Zhao Y, Xiao S-S, Liu J-R, Wu S. Automatic PID Control Strategy via Energy Dissipation for Tapping Mode Atomic Force Microscopy. Sensors. 2025; 25(14):4277. https://doi.org/10.3390/s25144277
Chicago/Turabian StyleZhao, Yuan, Sha-Sha Xiao, Ji-Rui Liu, and Sen Wu. 2025. "Automatic PID Control Strategy via Energy Dissipation for Tapping Mode Atomic Force Microscopy" Sensors 25, no. 14: 4277. https://doi.org/10.3390/s25144277
APA StyleZhao, Y., Xiao, S.-S., Liu, J.-R., & Wu, S. (2025). Automatic PID Control Strategy via Energy Dissipation for Tapping Mode Atomic Force Microscopy. Sensors, 25(14), 4277. https://doi.org/10.3390/s25144277





