Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection
Abstract
1. Introduction
2. Related Works
3. Methodology
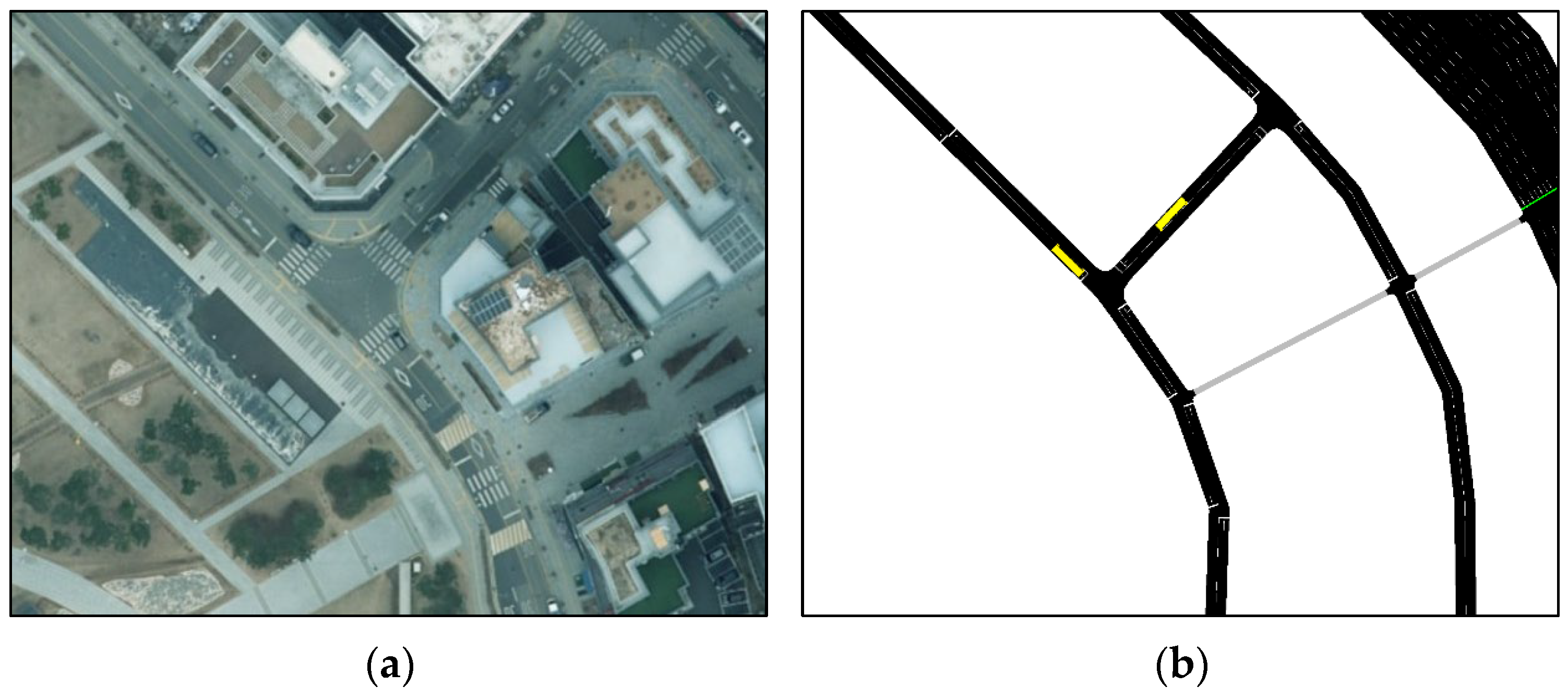
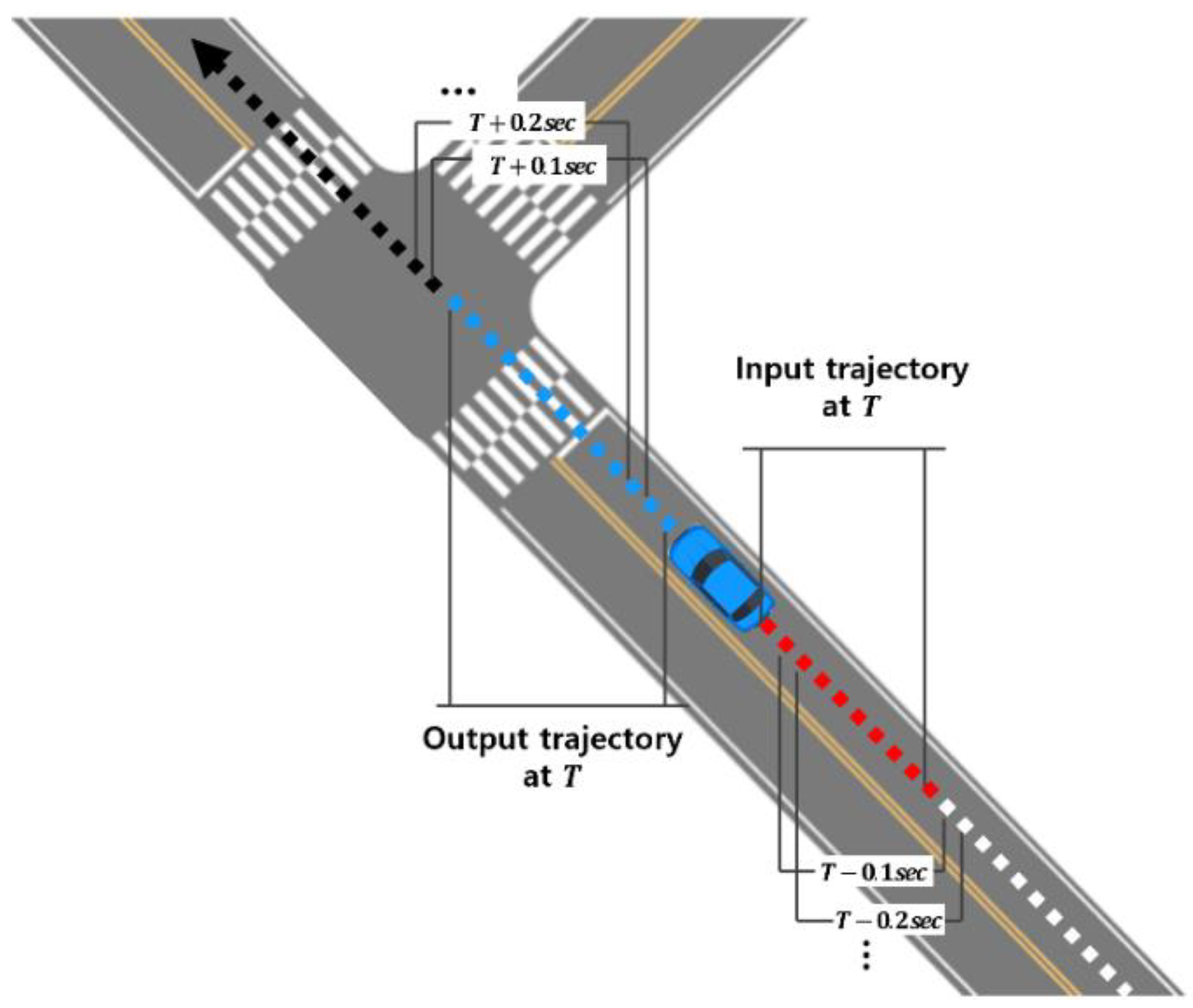
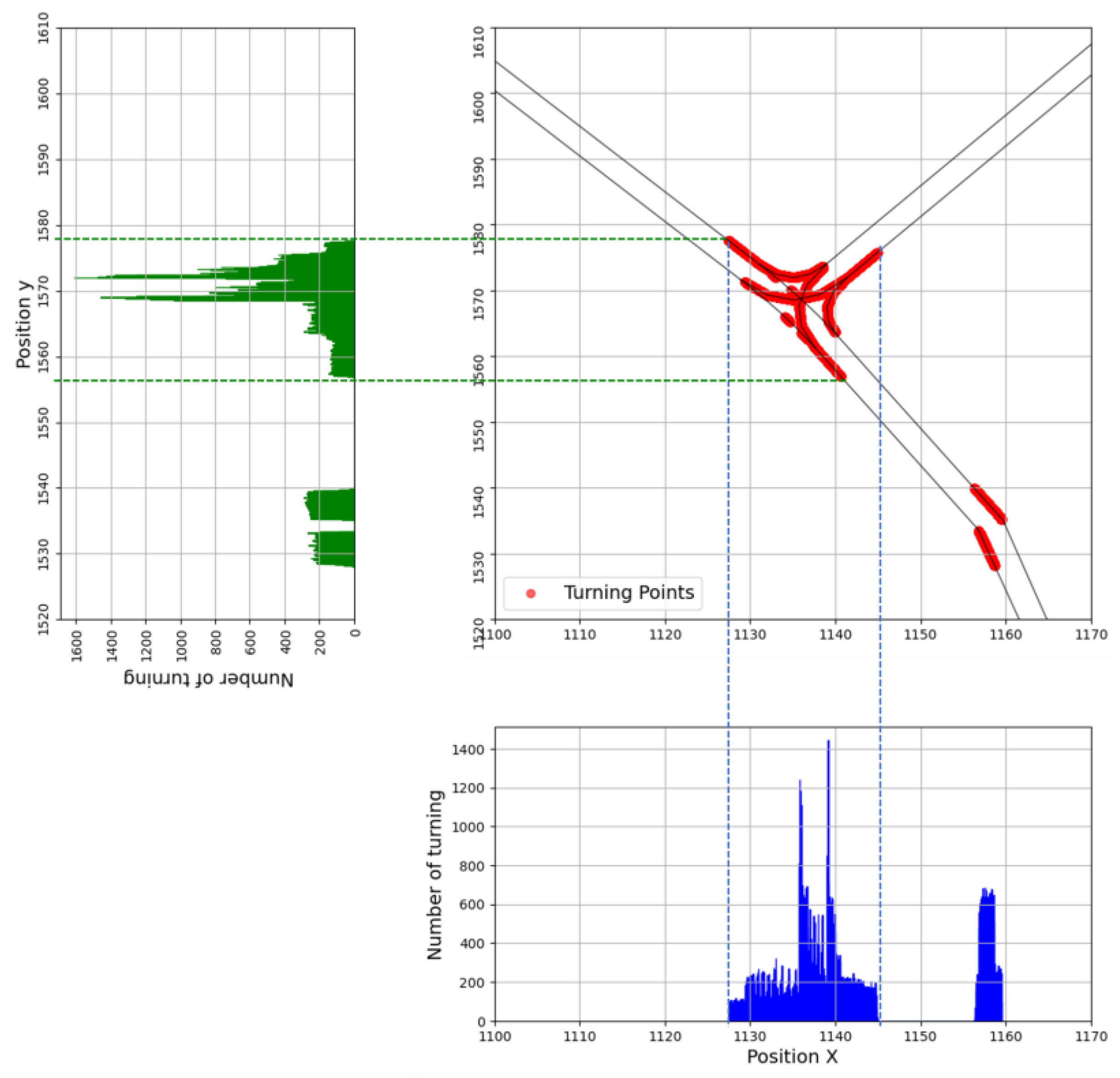
3.1. Trajectory Data Sampling
- Vehicle ID: ID to identify each vehicle in the dataset.
- Global time: The time at which each object’s location information was recorded. Recorded every simulation time step (0.1 s) [s].
- Departure time: The time of each vehicle’s appearance in the simulation [s].
- Arrival time: Simulation end-time for each vehicle [s].
- Position X, Position Y: The vehicle’s global coordinates (X, Y) in a simulation environment [m].
- Velocity: The vehicle’s speed [m/s].
- Acceleration: The vehicle’s acceleration [m/s2].
- Heading: The vehicle’s heading angle.
3.2. Preprocessing
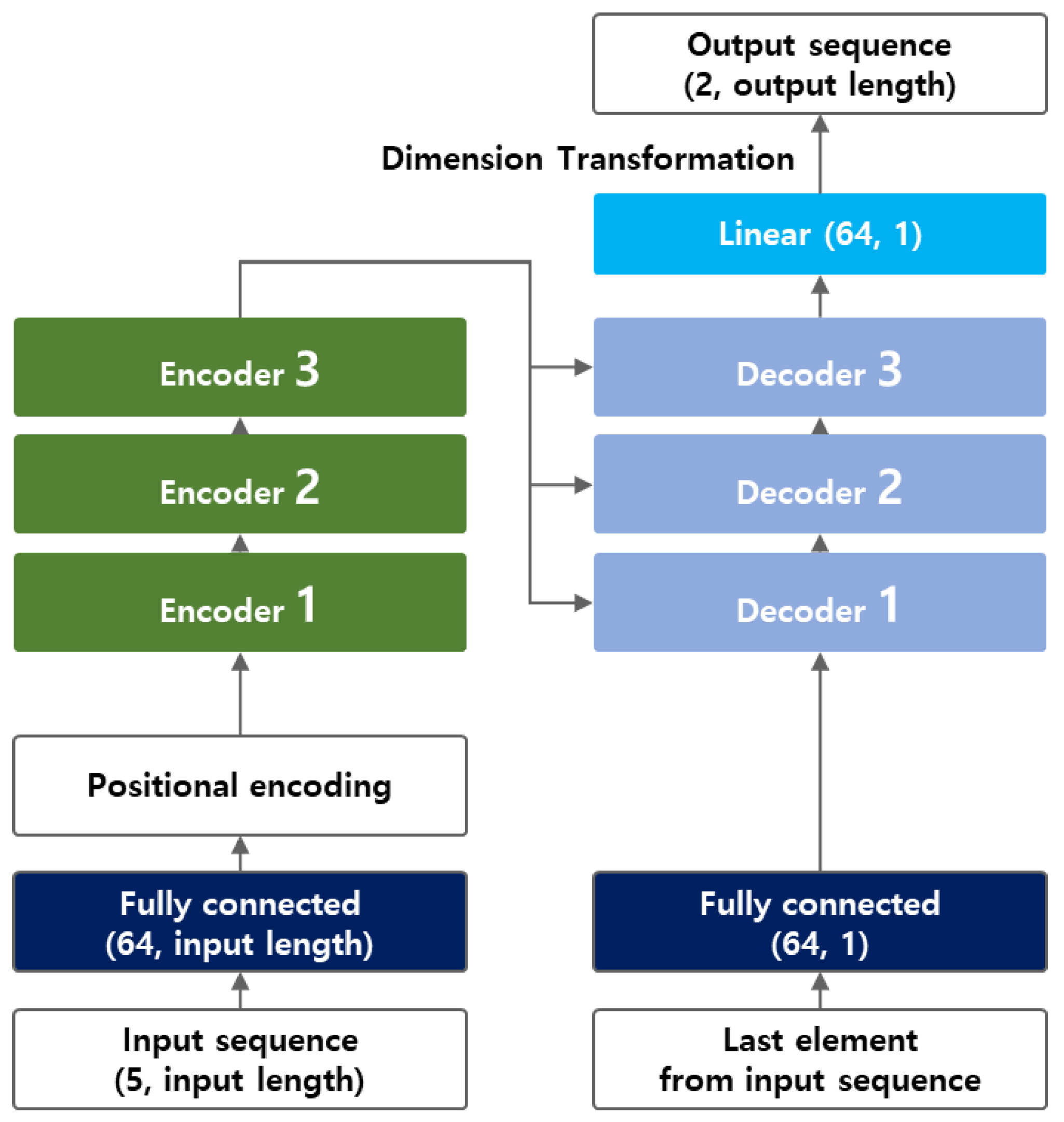
3.3. Transformer Model Structure
3.4. Loss Function
3.5. Performance Evaluation Methods
3.6. Training Environments and Methods
4. Trajectory-Prediction Model Design
4.1. Loss Function Selection
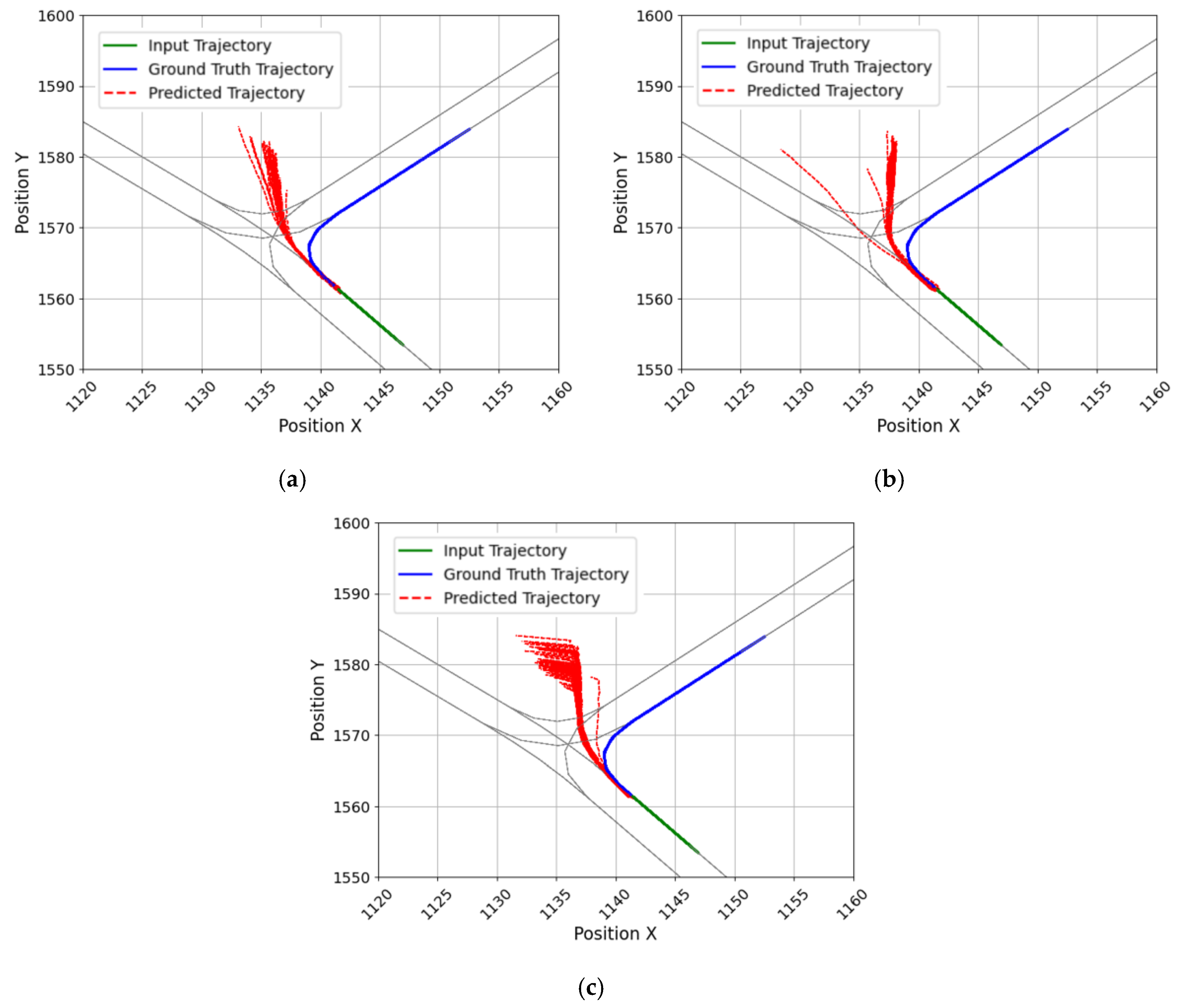
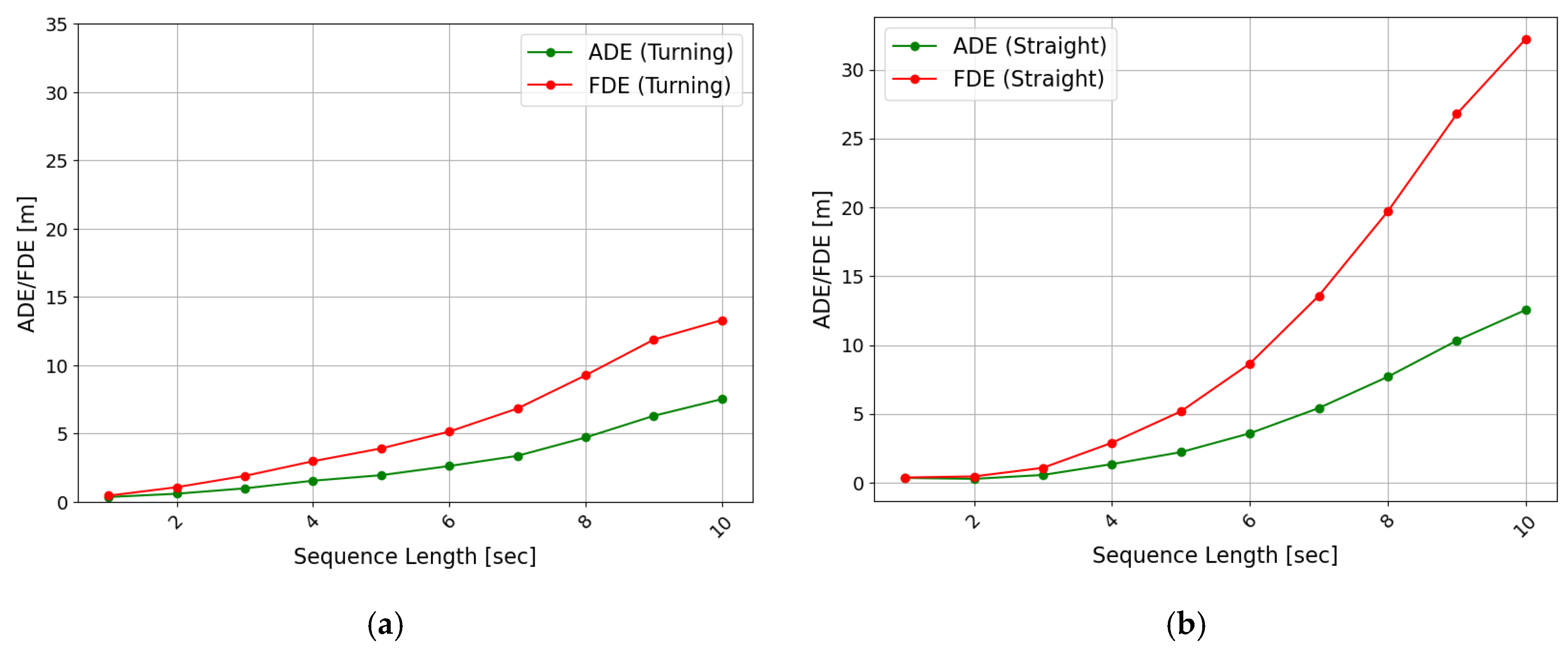
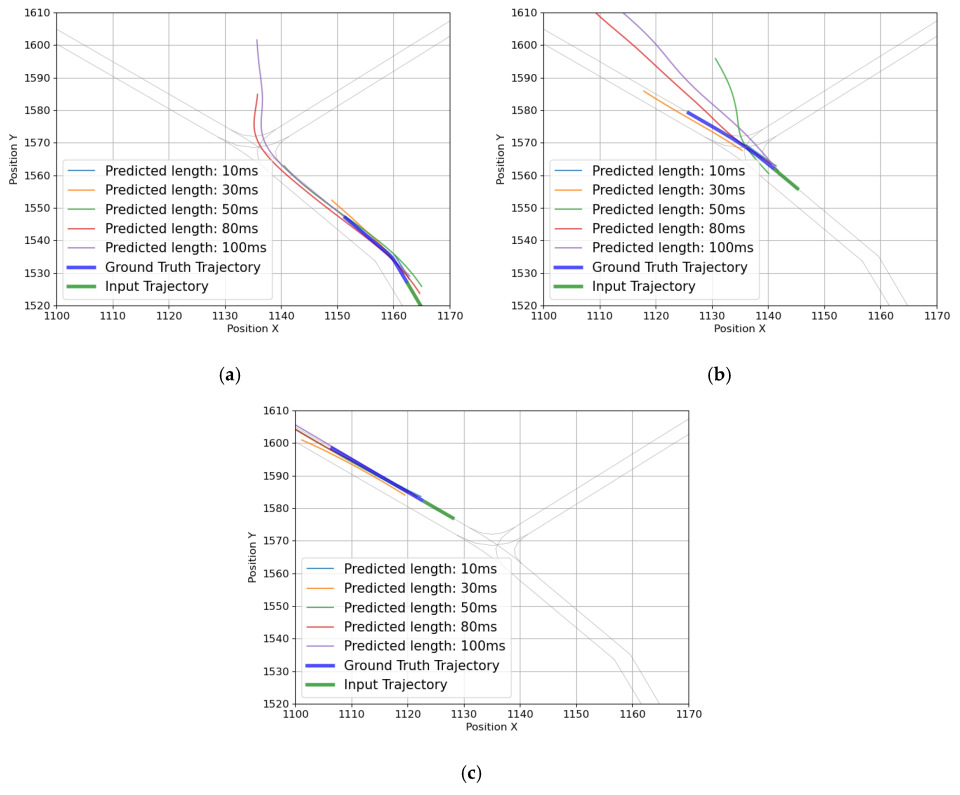
4.2. Evaluation Performance by Input and Output Lengths
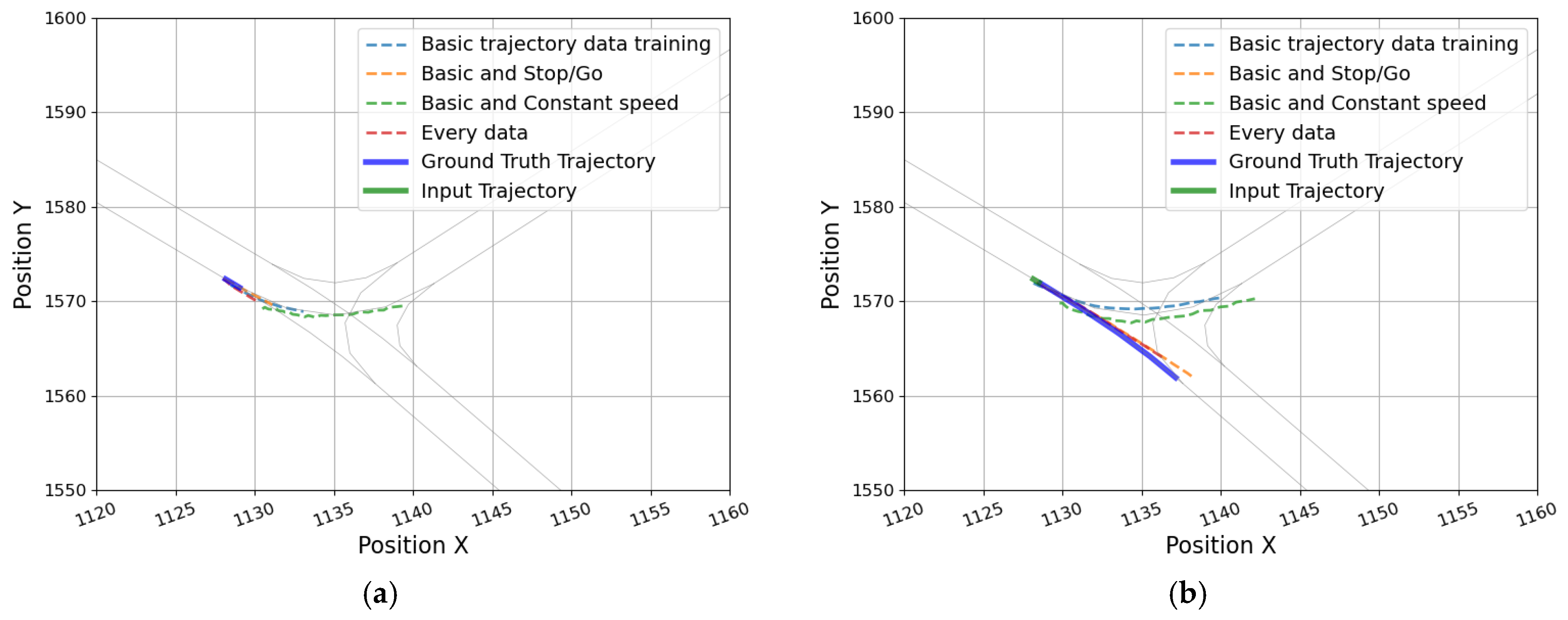
5. Model Evaluation and Improvement
5.1. Impacts of Deceleration and Acceleration
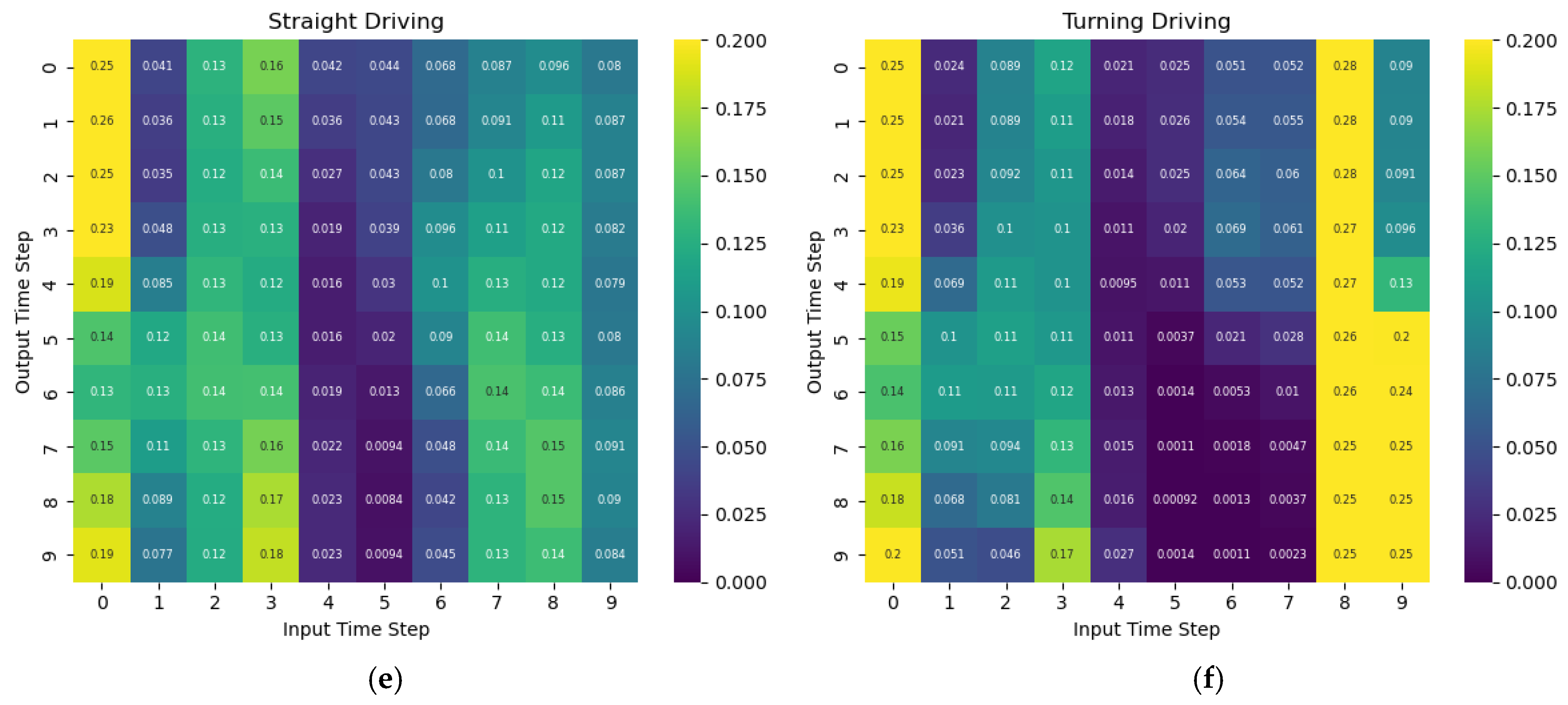
5.2. Impact of the Additional Feature Data
- X change, Y change: The variations in the current coordinate in the simulation environment, compared with the previous time step [m].
- Distance: The distance between the current and previous point coordinates in the simulation environment [m].
- Heading change: Variations in the current heading, compared with the previous time step heading.
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liao, C.; Shou, G.; Liu, Y.; Hu, Y.; Guo, Z. Intelligent traffic accident detection system based on mobile edge computing. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 2110–2115. [Google Scholar]
- Hasarinda, R.; Tharuminda, T.; Palitharathna, K.; Edirisinghe, S. Traffic Collision Avoidance with Vehicular Edge Computing. In Proceedings of the 2023 3rd International Conference on Advanced Research in Computing (ICARC), Belihuloya, Sri Lanka, 23–24 February 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 316–321. [Google Scholar]
- Zhang, X.; Sun, J.; Qi, X.; Sun, J. Simultaneous modeling of car-following and lane-changing behaviors using deep learning. Transp. Res. Part C Emerg. Technol. 2019, 104, 287–304. [Google Scholar] [CrossRef]
- Bi, H.; Fang, Z.; Mao, T.; Wang, Z.; Deng, Z. Joint prediction for kinematic trajectories in vehicle-pedestrian-mixed scenes. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 27 October–2 November 2019; pp. 10383–10392. [Google Scholar]
- Katariya, V.; Baharani, M.; Morris, N.; Shoghli, O.; Tabkhi, H. Deeptrack: Lightweight deep learning for vehicle trajectory prediction in highways. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18927–18936. [Google Scholar] [CrossRef]
- Mo, X.; Xing, Y.; Lv, C. Graph and recurrent neural network-based vehicle trajectory prediction for highway driving. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), New York, NY, USA, 19–22 September 2021; pp. 1934–1939. [Google Scholar]
- Deo, N.; Trivedi, M.M. Multi-modal trajectory prediction of surrounding vehicles with maneuver based lstms. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: New York, NY, USA, 2018; pp. 1179–1184. [Google Scholar]
- Nikhil, N.; Tran Morris, B. Convolutional neural network for trajectory prediction. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; IEEE: New York, NY, USA, 2016; pp. 961–971. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Amin, F.; Gharami, K.; Sen, B. TrajectoFormer: Transformer-based trajectory prediction of autonomous vehicles with spatio-temporal neighborhood considerations. Int. J. Comput. Intell. Syst. 2024, 17, 87. [Google Scholar] [CrossRef]
- Pazho, A.D.; Katariya, V.; Noghre, G.A.; Tabkhi, H. VT-Former: A transformer-based vehicle trajectory prediction approach for intelligent highway transportation systems. arXiv 2023, arXiv:2311.06623. [Google Scholar]
- Singh, D.; Srivastava, R. Multi-scale graph-transformer network for trajectory prediction of the autonomous vehicles. Intell. Serv. Robot. 2022, 15, 307–320. [Google Scholar] [CrossRef]
- Zhang, K.; Feng, X.; Wu, L.; He, Z. Trajectory prediction for autonomous driving using spatial-temporal graph attention transformer. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22343–22353. [Google Scholar] [CrossRef]
- Ngiam, J.; Caine, B.; Vasudevan, V.; Zhang, Z.; Chiang, H.T.L.; Ling, J.; Roelofs, R.; Bewley, A.; Liu, C.; Venugopal, A.; et al. Scene transformer: A unified architecture for predicting multiple agent trajectories. arXiv 2021, arXiv:2106.08417. [Google Scholar]
- Zhao, J.; Li, X.; Xue, Q.; Zhang, W. Spatial-channel transformer network for trajectory prediction on the traffic scenes. arXiv 2021, arXiv:2101.11472. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Agarwal, K.; Dheekollu, L.; Dhama, G.; Arora, A.; Asthana, S.; Bhowmik, T. Deep learning-based time series forecasting. Deep Learn. Appl. 2022, 3, 151–169. [Google Scholar]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16. Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 683–700. [Google Scholar]
- Zyner, A.; Worrall, S.; Nebot, E. A recurrent neural network solution for predicting driver intention at unsignalized intersections. IEEE Robot. Autom. Lett. 2018, 3, 1759–1764. [Google Scholar] [CrossRef]
- Zyner, A.; Worrall, S.; Nebot, E. Naturalistic driver intention and path prediction using recurrent neural networks. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1584–1594. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Deo, N.; Trivedi, M.M. Convolutional social pooling for vehicle trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 11–15 June 2018; pp. 1468–1476. [Google Scholar]
- O’shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014. NIPS’14. pp. 3104–3112. [Google Scholar]
- Wang, C.; Ma, L.; Li, R.; Durrani, T.S.; Zhang, H. Exploring trajectory prediction through machine learning methods. IEEE Access 2019, 7, 101441–101452. [Google Scholar] [CrossRef]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer Networks for Trajectory Forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 10335–10342. [Google Scholar]
- Yu, C.; Ma, X.; Ren, J.; Zhao, H.; Yi, S. Spatio-temporal graph transformer networks for pedestrian trajectory prediction. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 507–523. [Google Scholar]
- Chang, M.F.; Ramanan, D.; Hays, J.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; et al. Argoverse: 3D Tracking and Forecasting with Rich Maps. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- FHWA. Next Generation Simulation (NGSIM). 2007. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm (accessed on 24 April 2025).
- Houston, J.; Zuidhof, G.; Bergamini, L.; Ye, Y.; Chen, L.; Jain, A.; Omari, S.; Iglovikov, V.; Ondruska, P. One thousand and one hours: Self-driving motion prediction dataset. arXiv 2020, arXiv:2006.14480. [Google Scholar]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-document transformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Zhang, Z. Exploring round Dataset for Domain Generalization in Autonomous Vehicle Trajectory Prediction. Sensors 2024, 24, 7538. [Google Scholar] [CrossRef] [PubMed]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flotterod, Y.P.; Hilbrich, R.; Lucken, L.; Rummel, J.; Wagner, P.; Wiebner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2011; pp. 2575–2582. [Google Scholar]
- Krauß, S. Microscopic Modeling of Traffic Flow: Investigation of Collision Free Vehicle Dynamics; Deutsches Zentrum für Luft- und Raumfahrt e.V.: Köln, Germany, 1998. [Google Scholar]
- Wiedemann, R. Simulation des Strassenverkehrsflusses; UC Berkeley Transportation Library: Berkeley, CA, USA, 1974. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef] [PubMed]
- Girshick, R. Fast r-cnn. arXiv 2015, arXiv:1504.08083. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]




| Model Type | Advantages | Disadvantages | |
|---|---|---|---|
| RNN | - Simple structure - Sequential data training | - Gradient vanishing - Difficult to parallelize | [3,4,5,6] |
| LSTM/ GRU | - Improved long-term dependencies | - Increased computational cost than RNNs - Difficult to parallelize | [7,9,28] |
| Transformer | - Parallel sequence processing - Effectively captures long-term dependencies - Flexible to variable input length | - Complex structure | [11,12,13,14,15,16,17,18] |
| Trajectory Dataset | Driving Speed | Number of Vehicles | ||
|---|---|---|---|---|
| Basic | Stop-and-Go | Constant | ||
| Basic | 4571 | 447 | 0 | 5018 |
| Stop-and-go | 0 | 5225 | 0 | 5225 |
| Constant speed | 0 | 0 | 5265 | 5265 |
| Metric | MSE | Smooth L1 | Combined | |||
|---|---|---|---|---|---|---|
| ADE | FDE | ADE | FDE | ADE | FDE | |
| MSE | 0.667 | 1.671 | 1.084 | 2.059 | 0.63 | 1.24 |
| Smooth L1 | 0.615 | 1.506 | 0.979 | 1.891 | 0.576 | 1.095 |
| Combined | 0.635 | 1.483 | 0.995 | 2.017 | 0.597 | 1.027 |
| Inference time [ms] | 1.428 | 1.435 | 1.456 | |||
| Train Data | Test Data | Overall | Turning | Straight | |||
|---|---|---|---|---|---|---|---|
| ADE | FDE | ADE | FDE | ADE | FDE | ||
| Basic | Basic | 0.62 | 1.51 | 0.98 | 1.89 | 0.58 | 1.09 |
| Stop-and-go | 1.33 | 2.73 | 0.64 | 1.63 | 1.61 | 3.19 | |
| Constant speed | 0.98 | 2.44 | 1.40 | 3.55 | 0.72 | 1.75 | |
| Basic + Stop-and-go | Basic | 0.86 | 1.83 | 1.05 | 2.55 | 0.71 | 1.26 |
| Stop-and-go | 0.78 | 1.72 | 0.83 | 1.85 | 0.75 | 1.66 | |
| Constant speed | 1.13 | 2.59 | 1.52 | 3.75 | 0.88 | 1.87 | |
| Basic + Constant speed | Basic | 0.76 | 1.79 | 1.19 | 2.14 | 0.72 | 1.37 |
| Stop-and-go | 1.57 | 2.92 | 0.93 | 1.99 | 1.84 | 3.31 | |
| Constant speed | 1.01 | 2.37 | 1.33 | 3.36 | 0.80 | 1.75 | |
| Basic + Stop-and-go + Constant speed | Basic | 0.86 | 1.92 | 1.19 | 2.19 | 0.76 | 1.16 |
| Stop-and-go | 0.91 | 2.14 | 0.87 | 2.19 | 0.93 | 2.13 | |
| Constant speed | 1.16 | 2.59 | 1.46 | 3.62 | 0.97 | 1.94 | |
| Train/Test Feature | Overall | Turning | Straight | Inference Time [ms] | |||
|---|---|---|---|---|---|---|---|
| ADE | FDE | ADE | FDE | ADE | FDE | ||
| Position X, Position Y, speed, acceleration, heading | 0.62 | 1.51 | 0.98 | 1.89 | 0.58 | 1.10 | 1.435 |
| speed, acceleration, heading, X change, Y change, distance, heading change | 5.36 | 5.63 | 4.97 | 5.56 | 5.67 | 5.69 | 1.452 |
| Position X, Position Y, speed, acceleration, heading, X change, Y change, distance, heading change | 0.86 | 1.83 | 1.05 | 2.65 | 0.71 | 1.20 | 1.604 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.K. Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection. Sensors 2025, 25, 4256. https://doi.org/10.3390/s25144256
Lee JK. Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection. Sensors. 2025; 25(14):4256. https://doi.org/10.3390/s25144256
Chicago/Turabian StyleLee, Jae Kwan. 2025. "Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection" Sensors 25, no. 14: 4256. https://doi.org/10.3390/s25144256
APA StyleLee, J. K. (2025). Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection. Sensors, 25(14), 4256. https://doi.org/10.3390/s25144256







