A Study on Distributed Multi-Sensor Fusion for Nonlinear Systems Under Non-Overlapping Fields of View
Abstract
1. Introduction
- The design of a GM-JMNS-CPHD distributed fusion framework for non-overlapping FoV scenarios: A nonlinear system modeling approach is developed from both the state-space partitioning and algorithmic perspectives to address challenges in distributed multi-sensor tracking under non-overlapping fields of view (FoVs).
- The integration of an adaptive thresholding strategy in the SOS outlier handling module: A stochastic outlier selection (SOS) algorithm approximating the ideal solution is introduced to replace heuristic or manual threshold tuning, enhancing the robustness and adaptability of the filter in cluttered or uncertain environments.
- Robust target cardinality estimation through intensity function decomposition and multi-Bernoulli reconstruction: The posterior intensity is partitioned into regional sub-intensities, each associated with a subspace. Cardinality distributions are estimated within each region using multi-Bernoulli modeling, thereby improving the accuracy in scenarios with varying target densities and spatial distribution.
2. Research Background
2.1. Analysis of the Impact of Non-Overlapping Fields of View on Nonlinear Moving-Target Tracking
2.2. Impact of Non-Overlapping Fields of View on Distributed Fusion Results for Nonlinear Moving Targets
3. Distributed Fusion Algorithm Combining T-S-GM-JMNS-CPHD
3.1. GM-JMNS-CPHD Filter
3.2. SFM-TOPSIS-SOS Fusion
3.2.1. Splitting
- Boundary segmentation of different perspectives
- 2.
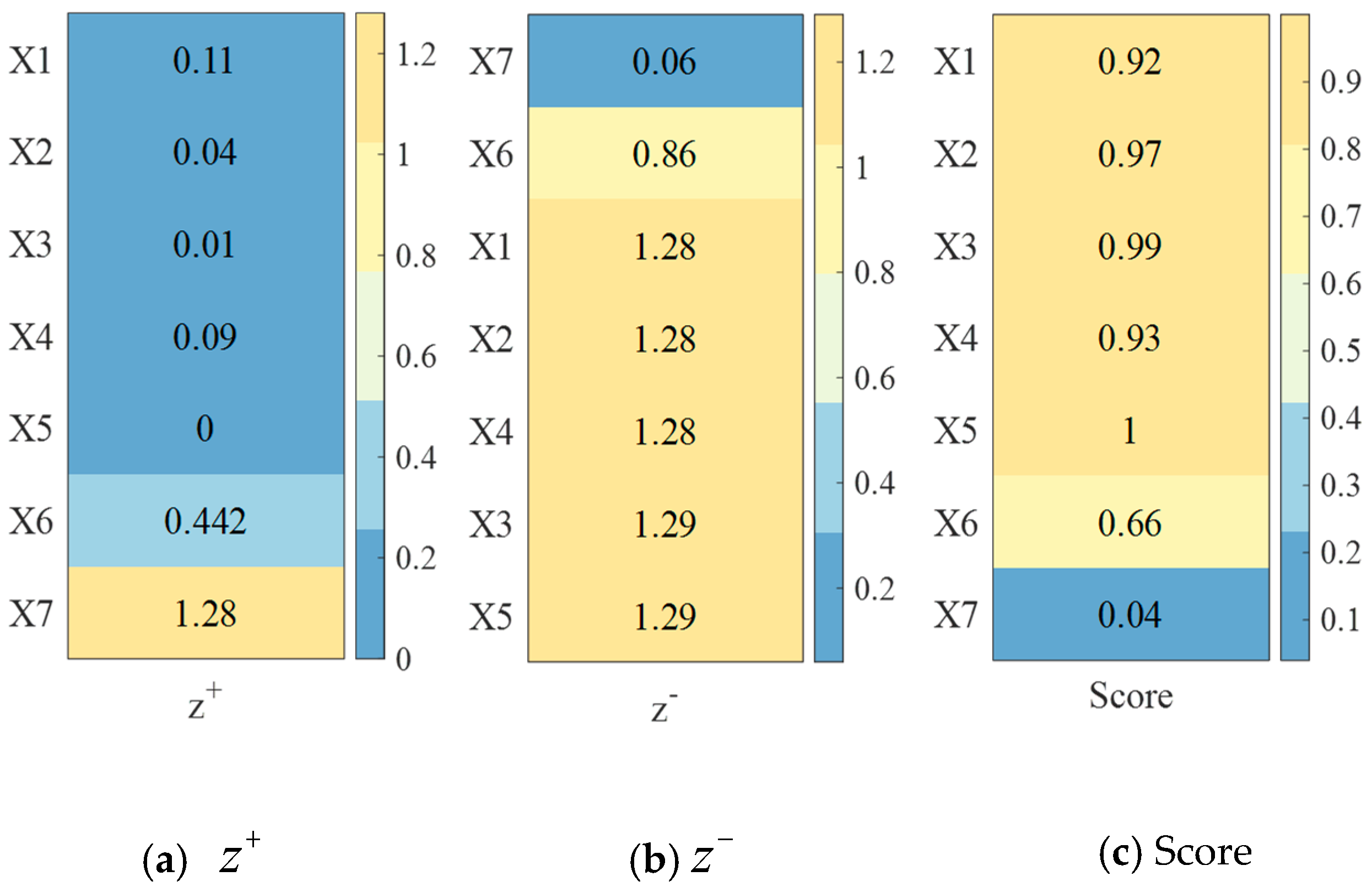
- The Technique for Order Preference by Similarity to Ideal Solution–Stochastic Outlier Selection (TOPSIS-SOS)
- ➀
- Data normalization
- ➁
- Data standardization
- ➂
- Calculation of optimal solution and worst solution
- ➃
- Calculation of relative proximity
- 3.
- TOPSIS-SOS clustering of GCs
3.2.2. Fusion
3.2.3. Merging
| Algorithm 1. Multi-sensor, multi-perspective T-S-GM-JMNS-CPHD fusion algorithm |
| Input: |
| , β, , , |
| Each sensor i operates as a GM-JMNS-CPHD filter |
| Execute T number of flooding communication iterations. |
| for do |
| for do |
| for do |
| Find the particles positioned in the area of |
| For and do |
| Calculate by Algorithm 1 |
| Calculate |
| end for |
| end for |
| Calculate by (17) |
| Calculate by (20) |
| end for |
| end for |
| Calculate GA/AA fusion strategy |
| Calculate cardinality distribution and fusion target state density after merging by (30) and (31) |
| Output: |
3.2.4. Algorithm Complexity Analysis
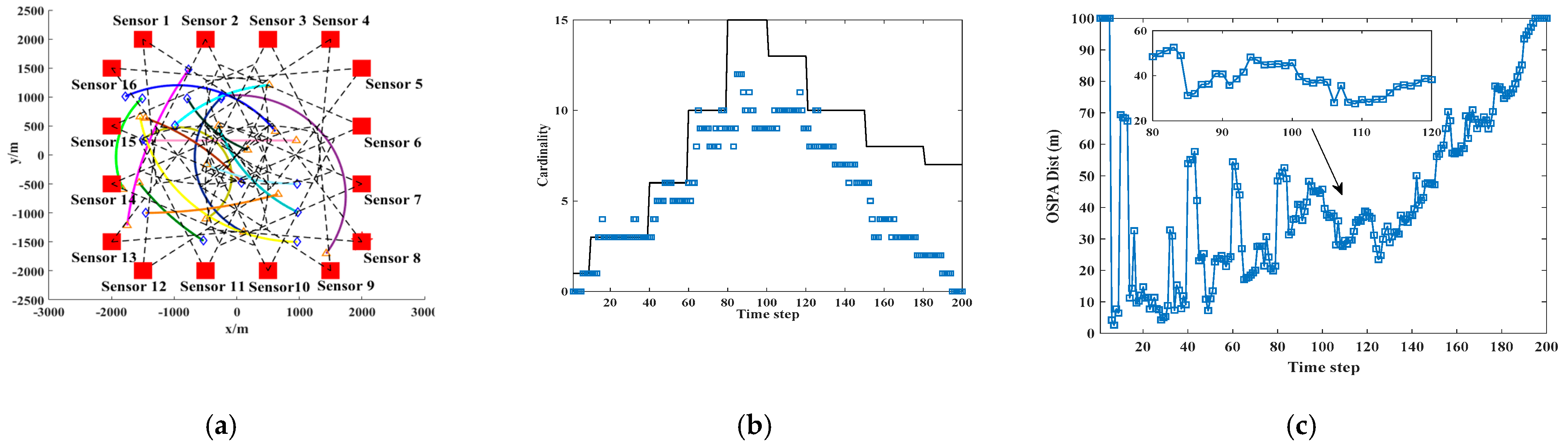
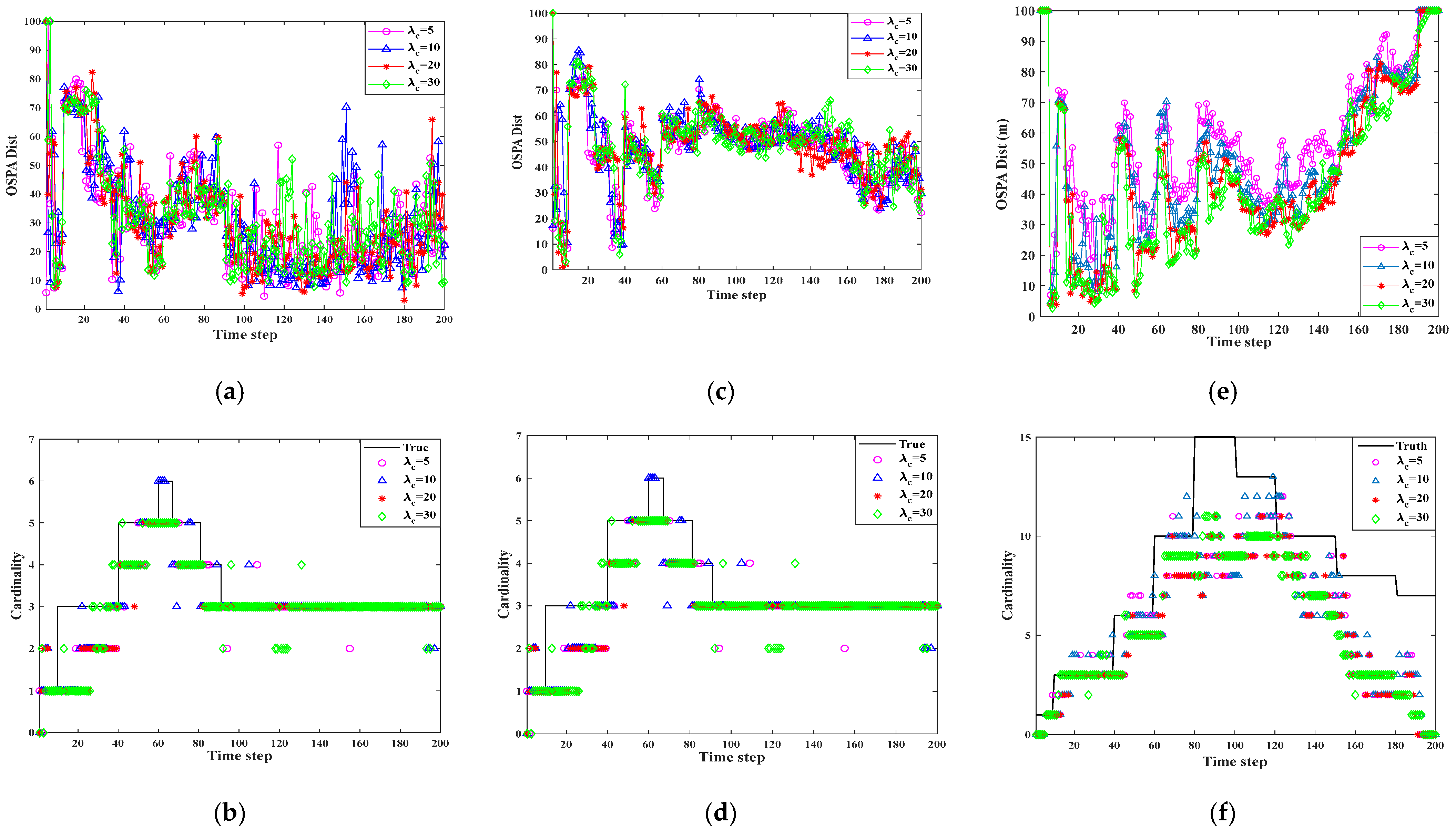
4. Simulation Result
4.1. Comparison of Algorithms Applied to Simulation in Multiple Scenarios
- In the three scenarios, the OSPA of multi-sensor multi-target tracking receives different object detection probabilities .
- There is a significant difference between the OSPA values produced for and .
- In the three scenarios, the OSPA of multi-sensor multi-target tracking will be more affected by different object detection probabilities, .
- There is a significant difference between the OSPA values produced for and .
- The T-S-GM-JMNS-CPHD algorithm is strongly influenced by , and that influence does not change significantly with increased numbers of motion trajectories of the detected motion targets and sensors.
4.2. Comparison of the Algorithm with Other Algorithm Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trinh, M.L.; Nguyen, D.T.; Dinh, L.Q.; Nguyen, M.D.; Setiadi, D.R.I.M.; Nguyen, M.T. Unmanned Aerial Vehicles (UAV) Networking Algorithms: Communication, Control, and AI-Based Approaches. Algorithms 2025, 18, 244. [Google Scholar] [CrossRef]
- Lei, X.; Hu, X.; Wang, G.; Luo, H. A Multi-UAV Deployment Method for Border Patrolling Based on Stackelberg Game. J. Syst. Eng. Electron. 2023, 34, 99–116. [Google Scholar] [CrossRef]
- Gargalakos, M. The Role of Unmanned Aerial Vehicles in Military Communications: Application Scenarios, Current Trends, and Beyond. J. Def. Model. Simul. 2024, 21, 313–321. [Google Scholar] [CrossRef]
- Dagan, O.; Cinquini, T.L.; Ahmed, N.R. Non-Linear Heterogeneous Bayesian Decentralized Data Fusion. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 9262–9268. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Bao, F.; Zhang, Z.; Zhang, G. An ensemble score filter for tracking high-dimensional nonlinear dynamical systems. Comput. Methods Appl. Mech. Eng. 2024, 432, 104123. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, G.; Song, S. Event-triggered distributed diffusion robust nonlinear filter for sensor networks. Signal Process. 2025, 226, 109662. [Google Scholar] [CrossRef]
- Cheng, C.; Tourneret, J.-Y.; Yıldırım, S. A variational Bayesian marginalized particle filter for jump Markov nonlinear systems with unknown measurement noise parameters. Signal Process. 2025, 233, 109954. [Google Scholar] [CrossRef]
- Wu, Y.; Qian, W. Adaptive memory-event-triggered-based double asynchronous fuzzy control for nonlinear semi-Markov jump systems. Fuzzy Sets Syst. 2025, 514, 109405. [Google Scholar] [CrossRef]
- Shen, H.; Wang, G.; Xia, J.; Park, J.H.; Xie, X.-P. Interval type-2 fuzzy H∞ filtering for nonlinear singularly perturbed jumping systems: A semi-Markov kernel method. Fuzzy Sets Syst. 2025, 505, 109264. [Google Scholar] [CrossRef]
- Takata, H.; Komatsu, K.; Narikiyo, K. A Nonlinear Filter of EKF Type Using Formal Linearization Method. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 1317–1321. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, Z.; Zhao, Y.B.; Dullerud, G.E. Event-triggered asynchronous filtering for networked fuzzy non-homogeneous Markov jump systems with dynamic quantization. Int. J. Adapt. Control Signal Process. 2023, 37, 811–835. [Google Scholar] [CrossRef]
- Oliveira, A.M.D.; Santos, S.R.B.; Costa, O.L.V. Mixed Reduced-Order Filtering for Discrete-Time Markov Jump Linear Systems With Partial Information on the Jump Parameter. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6353–6364. [Google Scholar] [CrossRef]
- Sun, Y.C.; Kim, D.; Hwang, I. Multiple-model Gaussian mixture probability hypothesis density filter based on jump Markov system with state-dependent probabilities. IET Radar Sonar Navig. 2022, 16, 1881–1894. [Google Scholar] [CrossRef]
- Tao, J. Event-Triggered Control for Markov Jump Systems Subject to Mismatched Modes and Strict Dissipativity. IEEE Trans. Cybern. 2023, 53, 1537–1546. [Google Scholar] [CrossRef]
- Yu, X.; Feng, X.A. Joint multi-Gaussian mixture model and its application to multi-model multi-bernoulli filter. Digit. Signal Process. 2024, 153, 104616. [Google Scholar]
- Wang, G.Q.; Li, N.; Zhang, Y.G. Distributed maximum correntropy linear and nonlinear filters for systems with non-Gaussian noises. Signal Process. 2021, 182, 1–12. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, J.; Wu, S.; Liu, C. A Poisson multi-Bernoulli mixture filter for tracking multiple resolvable group targets. Digit. Signal Process. 2024, 144, 104279. [Google Scholar] [CrossRef]
- Lan, L.; Wei, L.G. Zonotopic distributed fusion for 2-D nonlinear systems under binary encoding schemes: An outlier-resistant approach. Information Fusion 2025, 120, 103103. [Google Scholar] [CrossRef]
- Hu, Z.; Guo, T. Distributed resilient fusion filtering for multi-sensor nonlinear singular systems subject to colored measurement noises. J. Frankl. Inst. 2025, 4, 362. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, L.; Hu, J. Distributed nonlinear fusion filtering for multi-sensor networked systems with random varying parameter matrix and missing measurements. Neurocomputing 2024, 610, 128491. [Google Scholar] [CrossRef]
- Luo, R.; Hu, J.; Dong, H.L.; Lin, N. Fusion filtering for nonlinear rectangular descriptor systems with Markovian random delays via dynamic event-triggered feedback. Commun. Nonlinear Sci. Numer. Simul. 2025, 143, 108663. [Google Scholar] [CrossRef]
- Jin, Y.W.; Lu, X.Y.; Li, J. Multisensor multitarget distributed fusion for discrepant fields of view. Digit. Signal Process. 2024, 153, 104585. [Google Scholar] [CrossRef]
- Chen, F.; Nguyen, H.V.; Leong, A.S. Sabita Panicker, Robin Baker, Ranasinghe, D.C. Distributed multi-object tracking under limited field of view heterogeneous sensors with density clustering. Signal Process. 2025, 228, 109703. [Google Scholar] [CrossRef]
- Li, G.C.; Battistelli, G.; Yi, W.; Kong, L.J. Distributed multi-sensor multi-view fusion based on generalized covariance intersection. Signal Process. 2020, 166, 107246. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, J.; Shi, L.; Zhang, J. A GM-JMNS-CPHD Filter for Different-Fields-of-View Stochastic Outlier Selection for Nonlinear Motion Tracking. Sensors 2024, 24, 3176. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, G.; Zhang, L.; Wang, T. Stochastic Outlier Selection via GM-CPHD Fusion for Multitarget Tracking Using Sensors With Different Fields of View. IEEE Sens. J. 2024, 24, 9148–9161. [Google Scholar] [CrossRef]
- Vo, B.N.; Pasha, A.; Tuan, H.D. A Gaussian Mixture PHD Filter for Nonlinear Jump Markov Models. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3162–3167. [Google Scholar]
- Mahler, R. On multitarget jump-Markov filters. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 149–156. [Google Scholar]
- Da, K.; Li, T.; Zhu, Y.; Fu, Q. Gaussian Mixture Particle Jump-Markov-CPHD Fusion for Multitarget Tracking Using Sensors With Limited Views. IEEE Trans. Signal Inf. Process. Over Netw. 2020, 6, 605–616. [Google Scholar] [CrossRef]
- Kabiri, S.; Lotfollahzadeh, T.; Shayesteh, M.G.; Kalbkhani, H.; Solouk, V. Technique for order of preference by similarity to ideal solution based predictive handoff for heterogeneous networks. IET Commun. 2016, 13, 1682–1690. [Google Scholar] [CrossRef]
- He, L.; Mohammad, Y.; Cheng, G.H.; Peng, W. A reliable probabilistic risk-based decision-making method: Bayesian Technique for Order of Preference by Similarity to Ideal Solution (B-TOPSIS). Soft Comput. A Fusion Found. Methodol. Appl. 2022, 26, 12137–12153. [Google Scholar]
- Gaeta, A.; Loia, V.; Orciuoli, F. An explainable prediction method based on Fuzzy Rough Sets TOPSIS and hexagons of opposition: Applications to the analysis of Information Disorder. Inf. Sci. 2024, 659, 120050. [Google Scholar] [CrossRef]
- Fernández, N.; Bella, J.; Dorronsoro, J.R. Supervised outlier detection for classification and regression. Neurocomputing 2022, 486, 77–92. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 4, 1523–1543. [Google Scholar] [CrossRef]








| Target | Initial State | Appearing Frame | Disappearing Frame |
|---|---|---|---|
| 1 | [−250 − 5.8857. 20. 1000 + 11.4102. 3. − wturn/3] | 1 | truth.K + 1 |
| 2 | [−1500 − 7.3806. 11. 250 + 6.7993. 10. − wturn/2] | 10 | truth.K + 1 |
| 3 | [−1500. 43. 250. 0. 0] | 10 | 66 |
| 4 | [−250 + 7.3806. − 12. 1000 − 6.7993. − 12. wturn/3] | 40 | truth.K + 1 |
| 5 | [250. − 50. 750. 0. − wturn/4] | 40 | 80 |
| 6 | [1000. − 50. 1500. − 80. 0] | 60 | 90 |
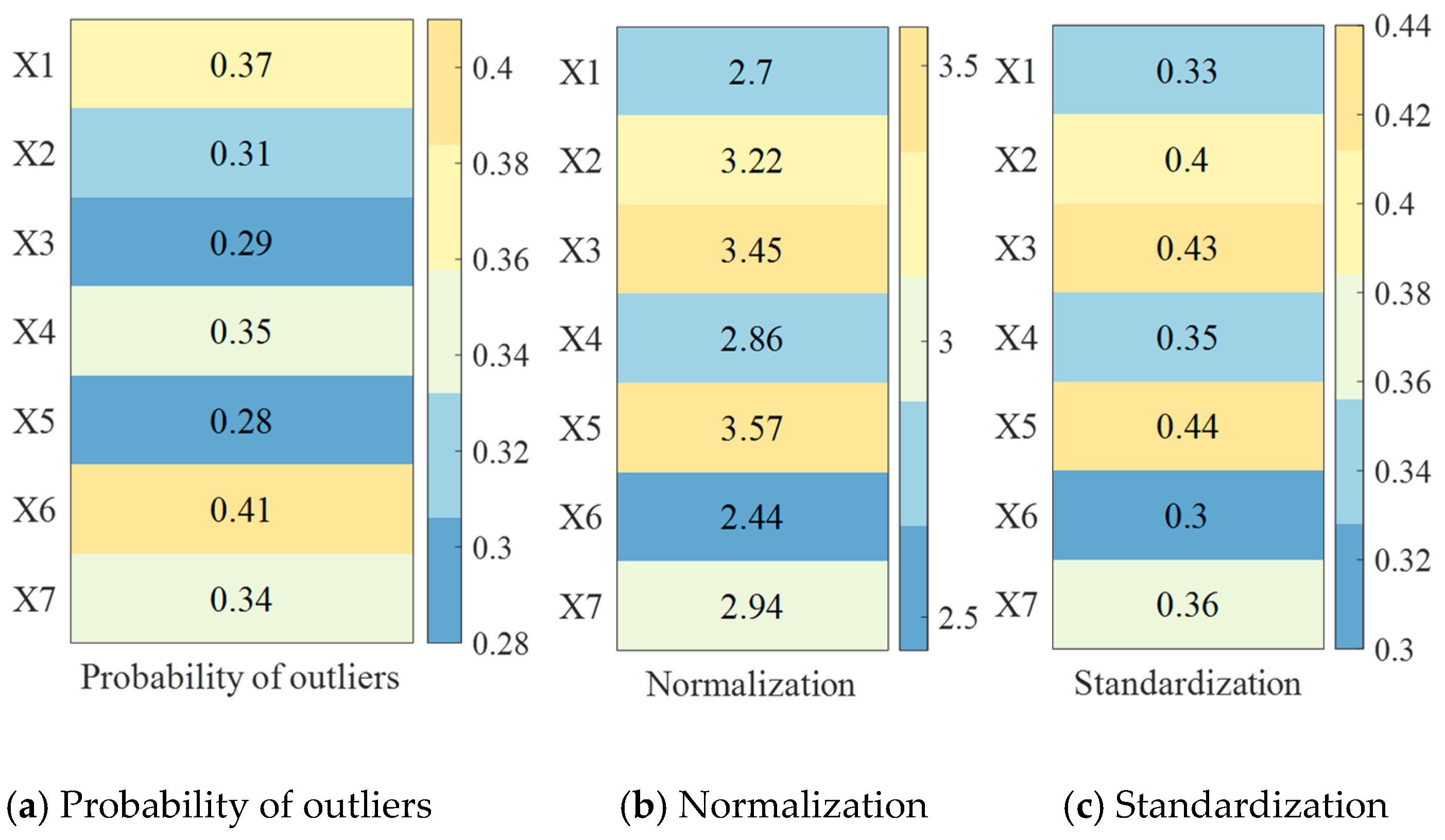
| Target | Outlier Probability | Number of Sensors Covered |
|---|---|---|
| X1 | 0.37 | 1 + 0.5 |
| X2 | 0.31 | 2 |
| X3 | 0.29 | 2 |
| X4 | 0.35 | 2 |
| X5 | 0.28 | 2 |
| X6 | 0.41 | 2 + 0.5 |
| X7 | 0.34 | 3 + 0.5 |
| Category | Parameter/Description | Category | Parameter/Description |
|---|---|---|---|
| Programming Environment | MATLAB R2023a | Birth Density Coordinates | (±800 m, ±800 m) |
| Monte Carlo Trials | 200 runs | Truncation Threshold | |
| Sensor Detection Probability | 0.9 | Merging Threshold | |
| Survival Probability | 0.99 | Max Gaussian Components | |
| Clutter Rate (Poisson Avg.) | 5 | Evaluation Metric | OSPA (c = 100, p = 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhou, Y.; Li, W.; Shi, L.; Zhao, J.; Wang, H. A Study on Distributed Multi-Sensor Fusion for Nonlinear Systems Under Non-Overlapping Fields of View. Sensors 2025, 25, 4241. https://doi.org/10.3390/s25134241
Wang L, Zhou Y, Li W, Shi L, Zhao J, Wang H. A Study on Distributed Multi-Sensor Fusion for Nonlinear Systems Under Non-Overlapping Fields of View. Sensors. 2025; 25(13):4241. https://doi.org/10.3390/s25134241
Chicago/Turabian StyleWang, Liu, Yang Zhou, Wenjia Li, Lijuan Shi, Jian Zhao, and Haiyan Wang. 2025. "A Study on Distributed Multi-Sensor Fusion for Nonlinear Systems Under Non-Overlapping Fields of View" Sensors 25, no. 13: 4241. https://doi.org/10.3390/s25134241
APA StyleWang, L., Zhou, Y., Li, W., Shi, L., Zhao, J., & Wang, H. (2025). A Study on Distributed Multi-Sensor Fusion for Nonlinear Systems Under Non-Overlapping Fields of View. Sensors, 25(13), 4241. https://doi.org/10.3390/s25134241






