Entropy, Irreversibility, and Time-Series Deep Learning of Kinematic and Kinetic Data for Gait Classification in Children with Cerebral Palsy, Idiopathic Toe Walking, and Hereditary Spastic Paraplegia
Abstract
1. Introduction
2. Methods
2.1. Participants
2.1.1. Movement Analysis Laboratory, CRC, Dublin
2.1.2. Laboratory of Human Movement, ONCE-UAM, Madrid
| Dublin | Madrid | ||||||||
| Control | ITW | CP | p-Value | Control | ITW | HSP | p-Value | ||
| (N = 96) | (N = 58) | (N = 300) | (N = 31) | (N = 23) | (N = 20) | ||||
| Sex (n) | |||||||||
| F | 48 (50%) | 14 (24.1%) | 126 (42%) | 0.006 | 12 (38.7%) | 9 (39.1%) | 7 (35%) | 0.954 | |
| M | 48 (50%) | 44 (75.9%) | 174 (58%) | 19 (61.3%) | 14 (60.9%) | 13 (65%) | |||
| Age (years) | |||||||||
| Median [Min, Max] | 9.00 [4.00, 16.0] | 9.09 [4.00, 15.0] | 9.65 [4.00, 16.0] | 0.331 | 9.00 [5.00, 16.0] | 9.00 [4.00, 12.0] | 6.50 [4.00, 16.0] | 0.23 | |
| Weight (kg) | |||||||||
| Median [Min, Max] | 31.3 [14.6, 94.7] | 35.3 [19.5, 76.7] | 31.9 [14.4, 103] | 0.574 | 28.6 [18.5, 75.3] | 37.0 [16.0, 55.5] | 27.1 [15.9, 64.0] | 0.651 | |
| Height (cm) | |||||||||
| Median [Min, Max] | 1.37 [1.05, 1.83] | 1.41 [1.12, 1.79] | 1.35 [1.02, 1.80] | 0.266 | 1.38 [1.00, 1.82] | 1.35 [1.08, 1.60] | 1.22 [1.05, 1.65] | 0.119 | |
| GMFCS | |||||||||
| I | 132 (44%) | 8 (40%) | |||||||
| II | 90 (30%) | 11 (55%) | |||||||
| III | 10 (3.3%) | 1 (5%) | |||||||
| Missing | 68 (22.7%) | ||||||||
| Normalised walking speed (s−1) | |||||||||
| Median [Min, Max] | 1.74 [1.16, 2.44] | 1.67 [1.07, 2.53] | 1.48 [0.642, 2.75] | 0.001 | 1.49 [1.15, 2.03] | 1.22 [0.933, 1.84] | 1.48 [0.671, 1.98] | 0.021 | |
| Cadence (steps/s) | |||||||||
| Median [Min, Max] | 2.18 [1.70, 2.95] | 2.10 [1.66, 2.96] | 2.10 [1.16, 3.32] | 0.004 | 1.92 [1.56, 2.73] | 1.94 [1.42, 2.47] | 2.06 [1.59, 2.57] | 0.388 | |
| Stance time (% gait cycle) | |||||||||
| Median [Min, Max] | 61.2 [57.8, 66.7] | 61.6 [57.5, 66.4] | 63.7 [56.8, 74.0] | 0.001 | 63.3 [60.2, 66.8] | 64.2 [61.7, 68.2] | 65.8 [62.7, 70.6] | 0.001 |
2.2. Gait Data Collection and Data Preprocessing
2.3. Statistical Physics Metrics
- Shannon’s entropy (SE): It is a fundamental entropy metric describing the uncertainty associated with the amplitude of the values in the time series. It is defined as , where represents the probability of observing the i-th symbol. In order to convert the original time series into a sequence of discrete symbols, values are transformed according to a number of identically sized bins given by the square root of the length of the time series. Values of E approaching zero indicate no uncertainty in the time series and thus that all values are the same; on the other hand, an entropy close to the maximum () suggests a uniform distribution of values.
- Permutation entropy (PE): It is Shannon’s entropy calculated over the distribution of ordinal patterns [41]. Given a time series, sub-windows of size D (also called the embedding dimension) are extracted; then, each sub-window is associated to a symbol representing the permutation that has to be performed in order to sort its values. Finally, Shannon’s entropy is calculated on the appearance frequency of the possible ordinal patterns; in mathematical terms, this is calculated as , where is the appearance probability of the ordinal pattern . Compared with the previous entropy, which is only sensitive to the distribution of individual values, permutation entropy is able to describe the causal relations between neighbouring values and has proven effective in describing multiple types of dynamical systems [42,43,44]. Due to the limited length of the time series available in this study and in order to obtain statistically significant distributions, D was here set to four [45].
- Weighted permutation entropy: It is the variation in the aforementioned permutation entropy, in which the contribution of each sub-window is weighted according to the variance of its values [46,47]. In mathematical terms, the previous probability is substituted by a weighted version ; the latter includes a weighting proportional to the amplitude of the signal, i.e., with . In other words, the contribution of each pattern includes both the frequency at which it appears, as well as how much its values deviate from the average. This ensures that the patterns of very small amplitude, e.g., only caused by noise, will have a smaller impact on the final metric. Its main advantage resides in the fact that it encodes information beyond the order structure of the time series.
- Irreversibility: It is a family of metrics describing the time-reversal invariance of a time series, i.e., the fact that a time series may be recognisable, in a statistical sense, from its time-reversal counterpart. To illustrate, a movie showing ice cubes melting in a glass is irreversible, as it is possible to detect whether it is played forward or backward. In the context of time-series analysis, irreversibility means that a given metric is different when calculated over the original series and over the backward version of the same. Irreversibility is usually associated with non-linear dynamics, (linear and non-linear) non-Gaussian dynamics, and the presence of memory [48,49,50]. When applied to gait, it implies that the dynamics is the result of its history and hence that some delayed control is in place. Several irreversibility metrics have been tested, specifically the BDS [51,52], Ramsey [53], and DFK [54] tests; the local Clustering Coefficient (lCC) [55]; the Ternary Coding method [56]; and an ensemble approach—for further information about them, the interested reader is referred to [57,58] and the references therein. Of these, the BDS test [51,52] was chosen, as it yielded consistently good results—see Figure A5.
2.4. Linear Mixed Effect Models
2.5. Classification and Validation
2.6. Deep Learning Classification
3. Results
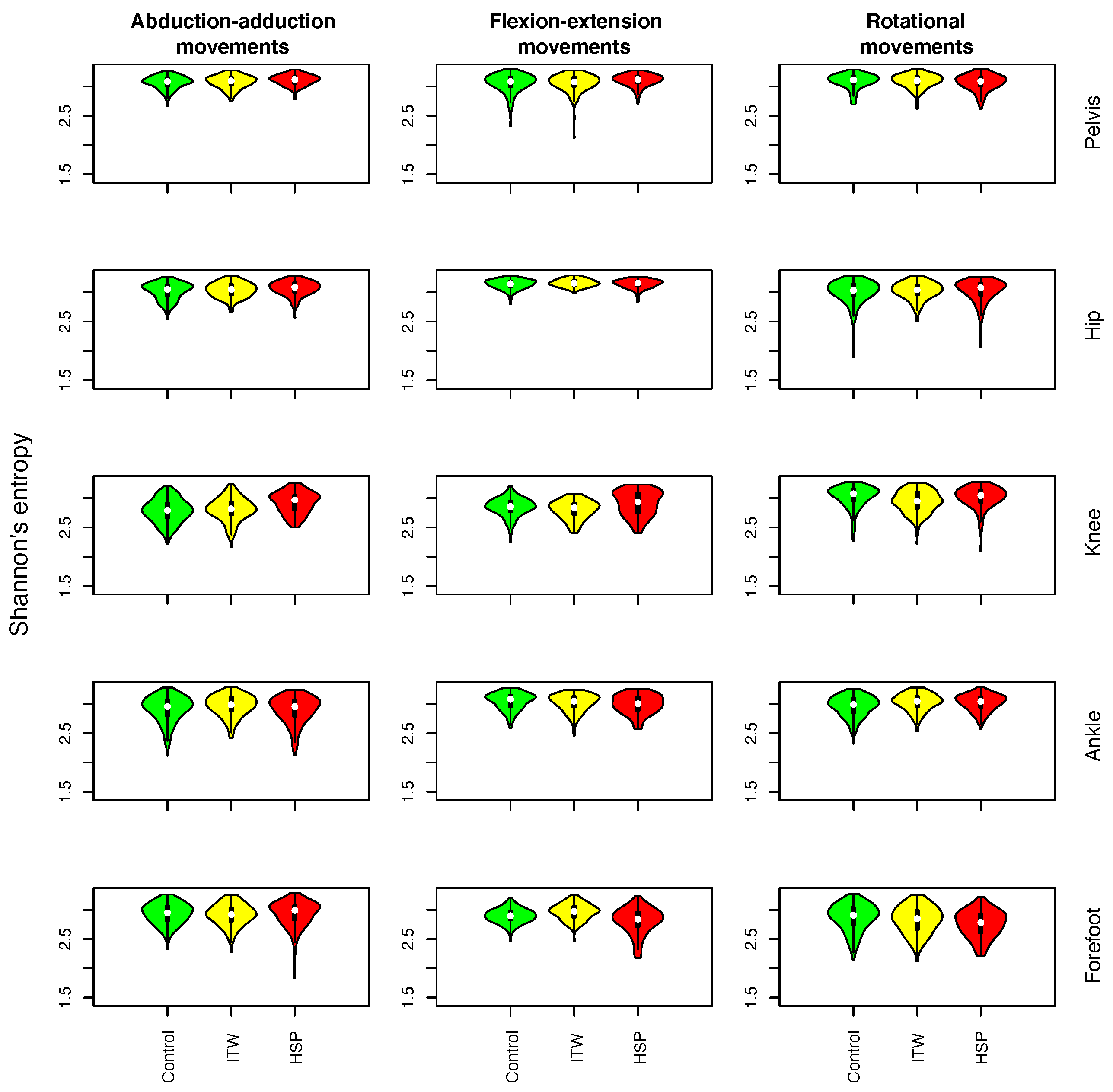
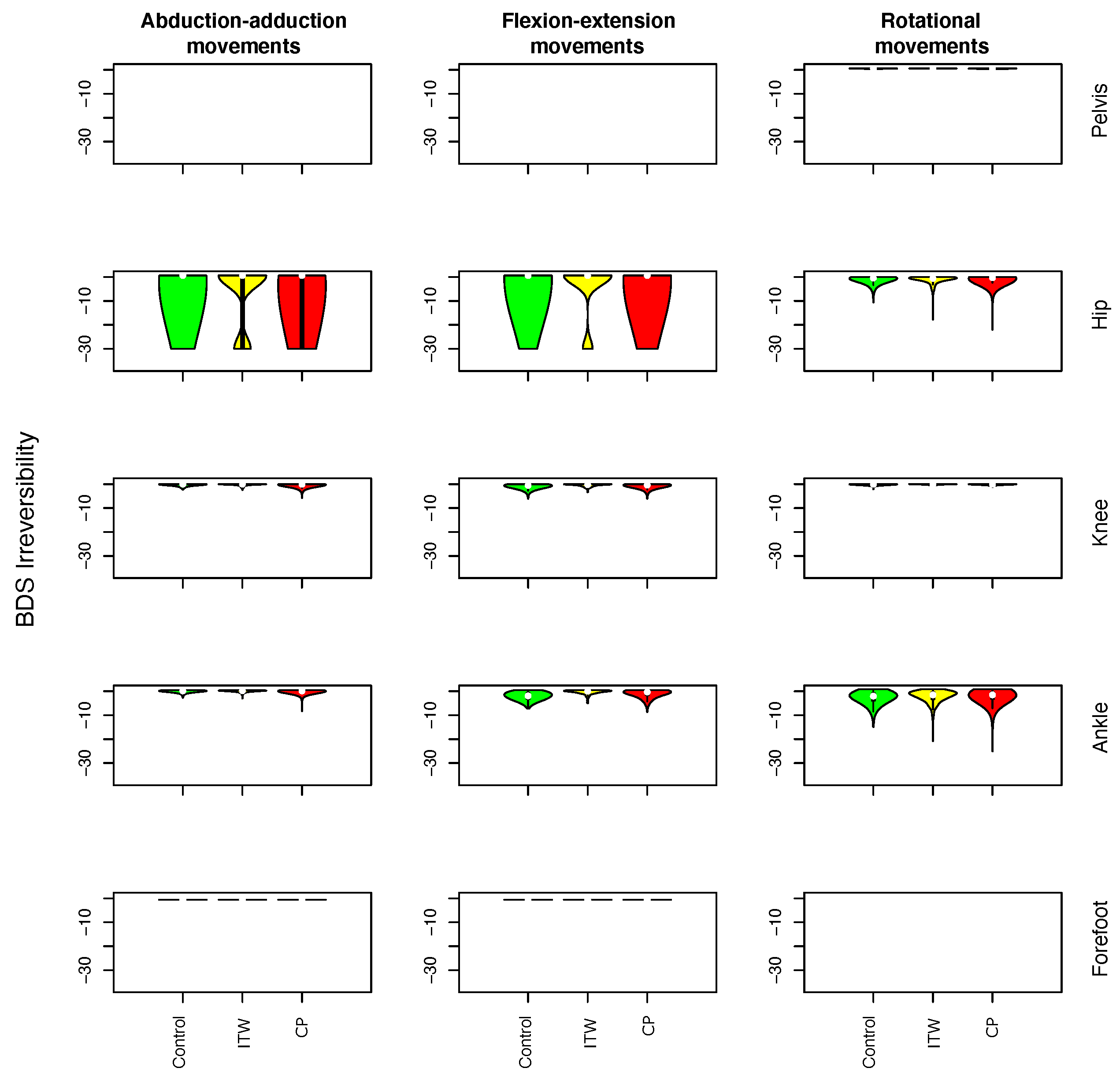
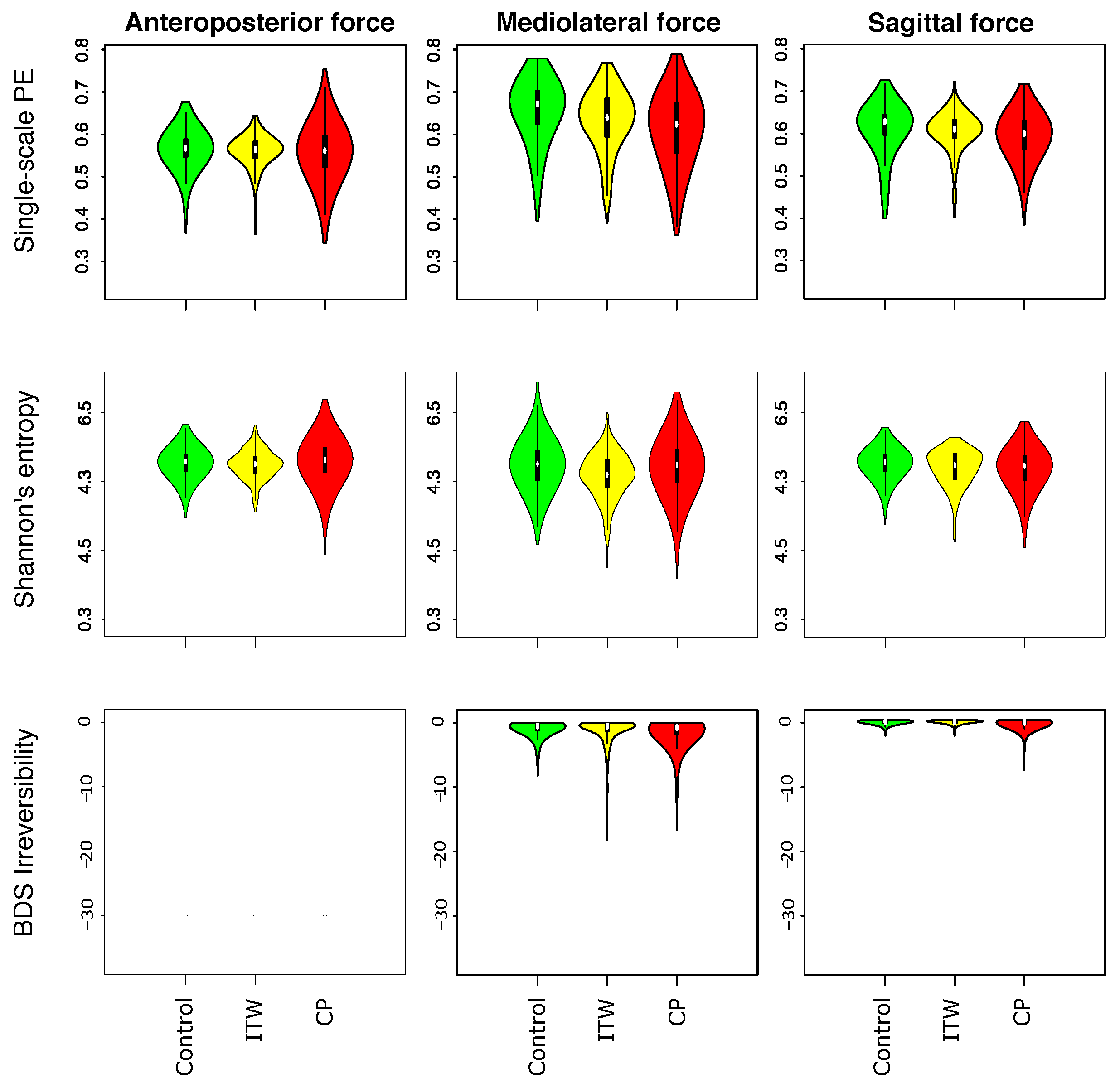
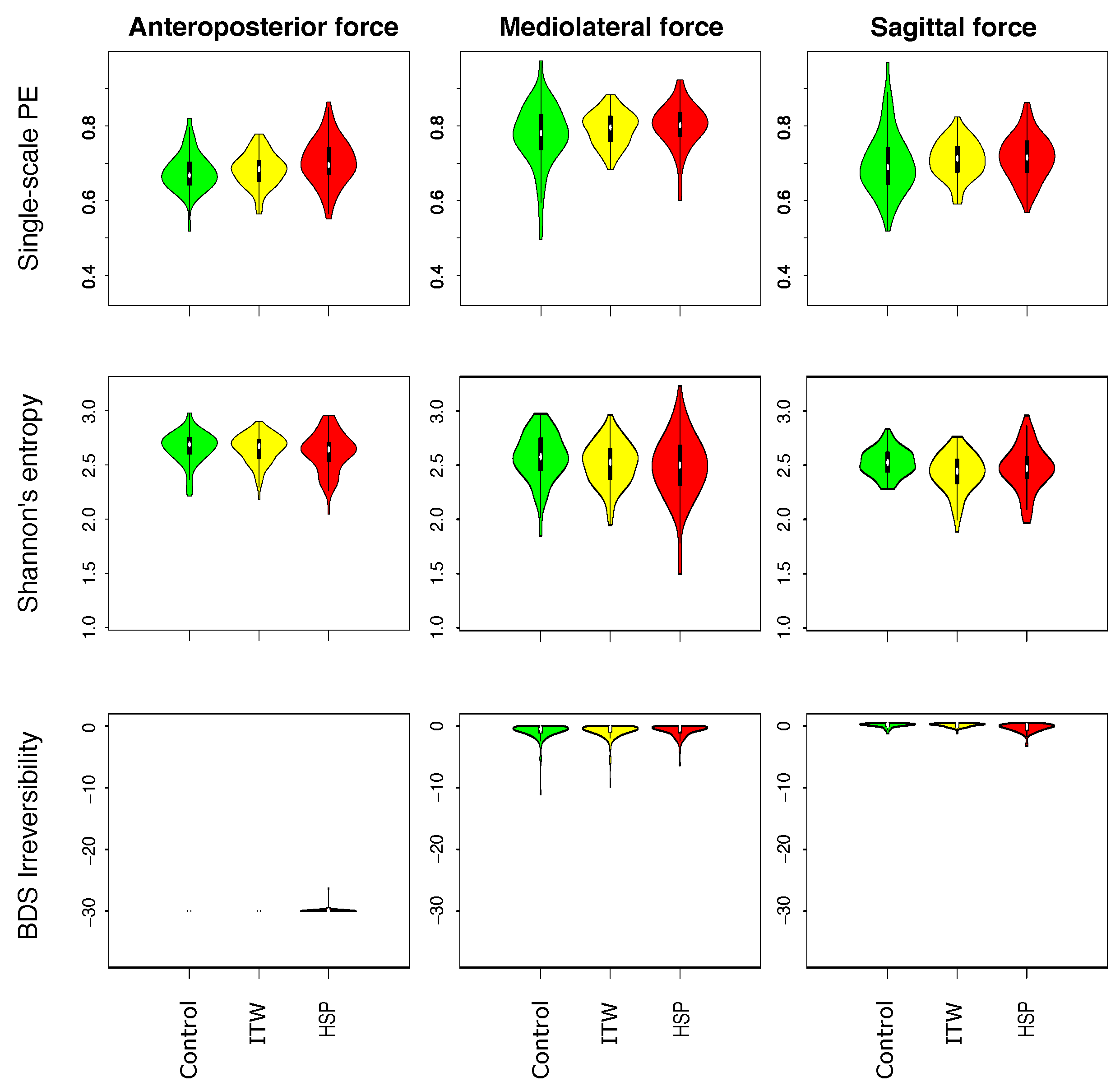
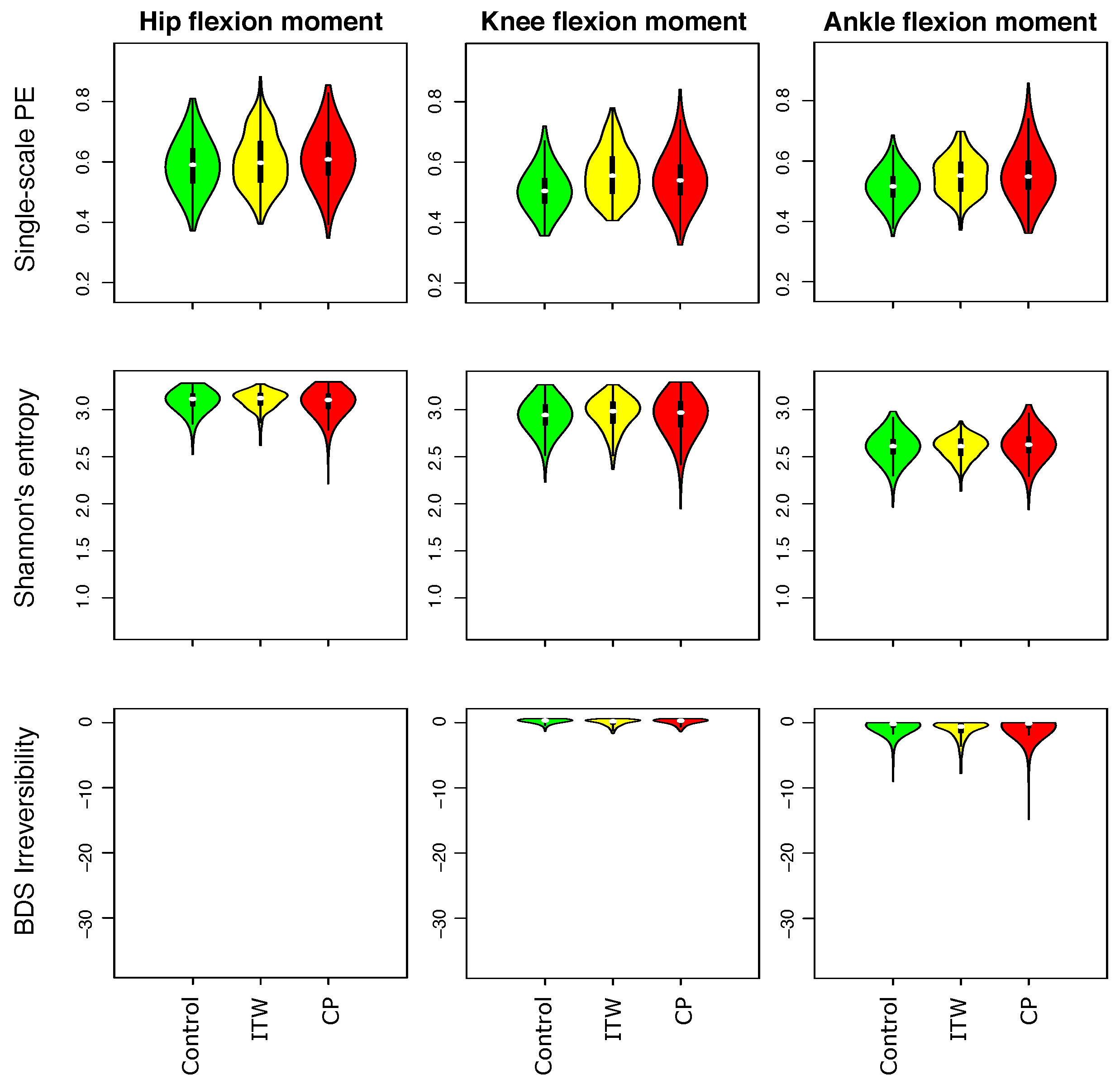
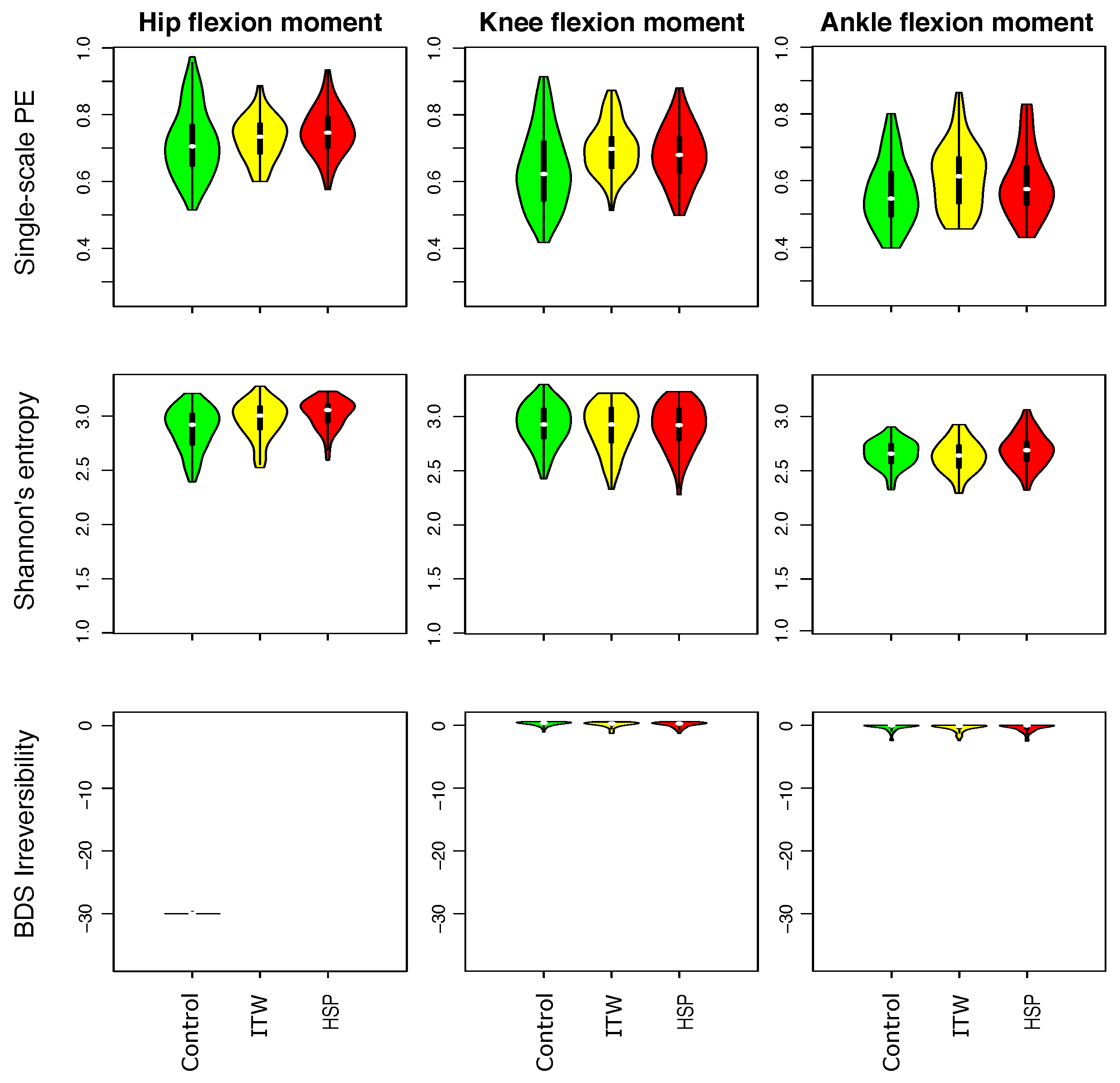
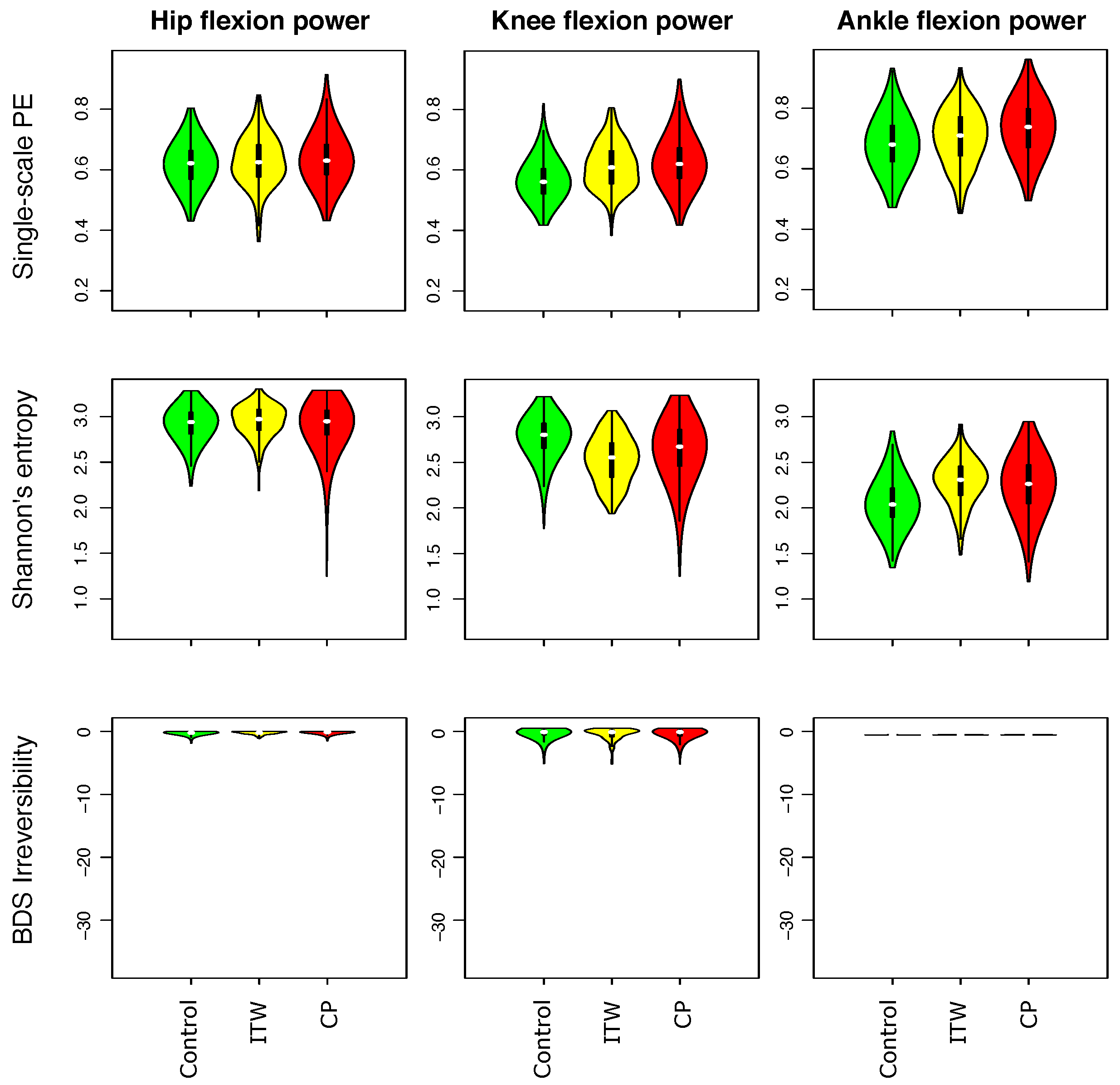
3.1. Description of Distribution of Statistical Physics Metrics Within and Between Groups of Gait Disorders
3.2. Comparison of Statistical Physics Metrics Between Groups of Gait Disorders
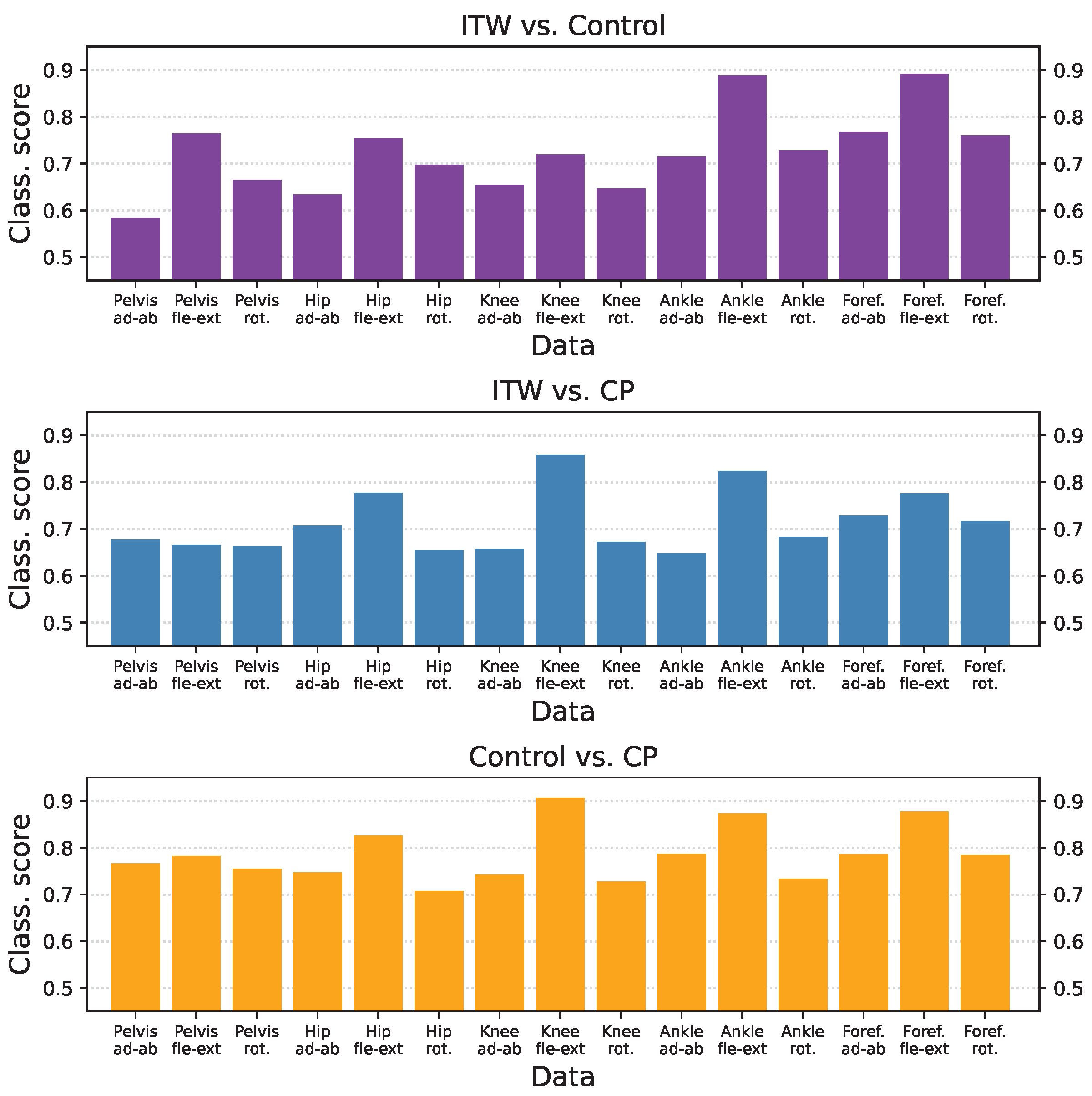
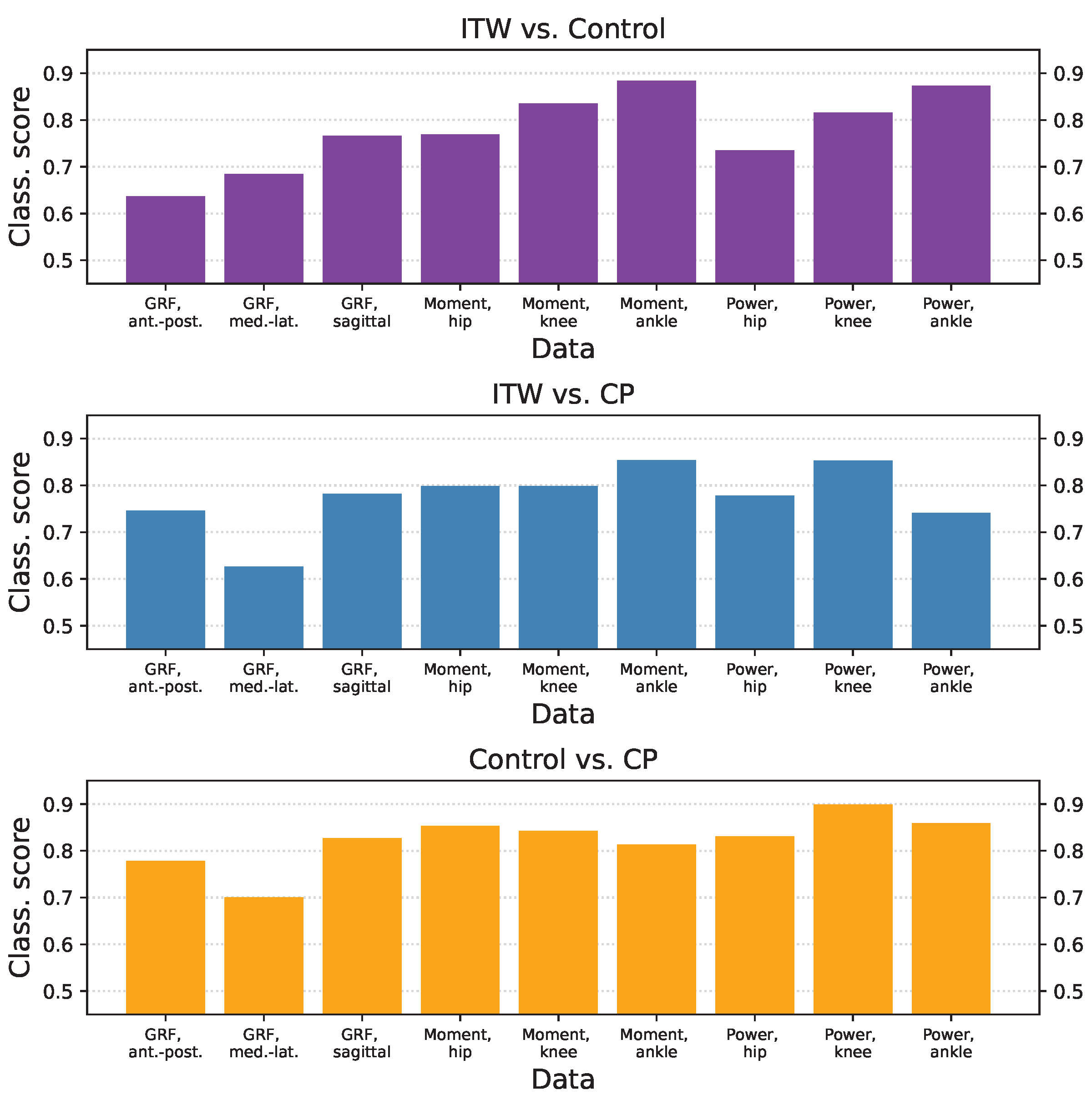
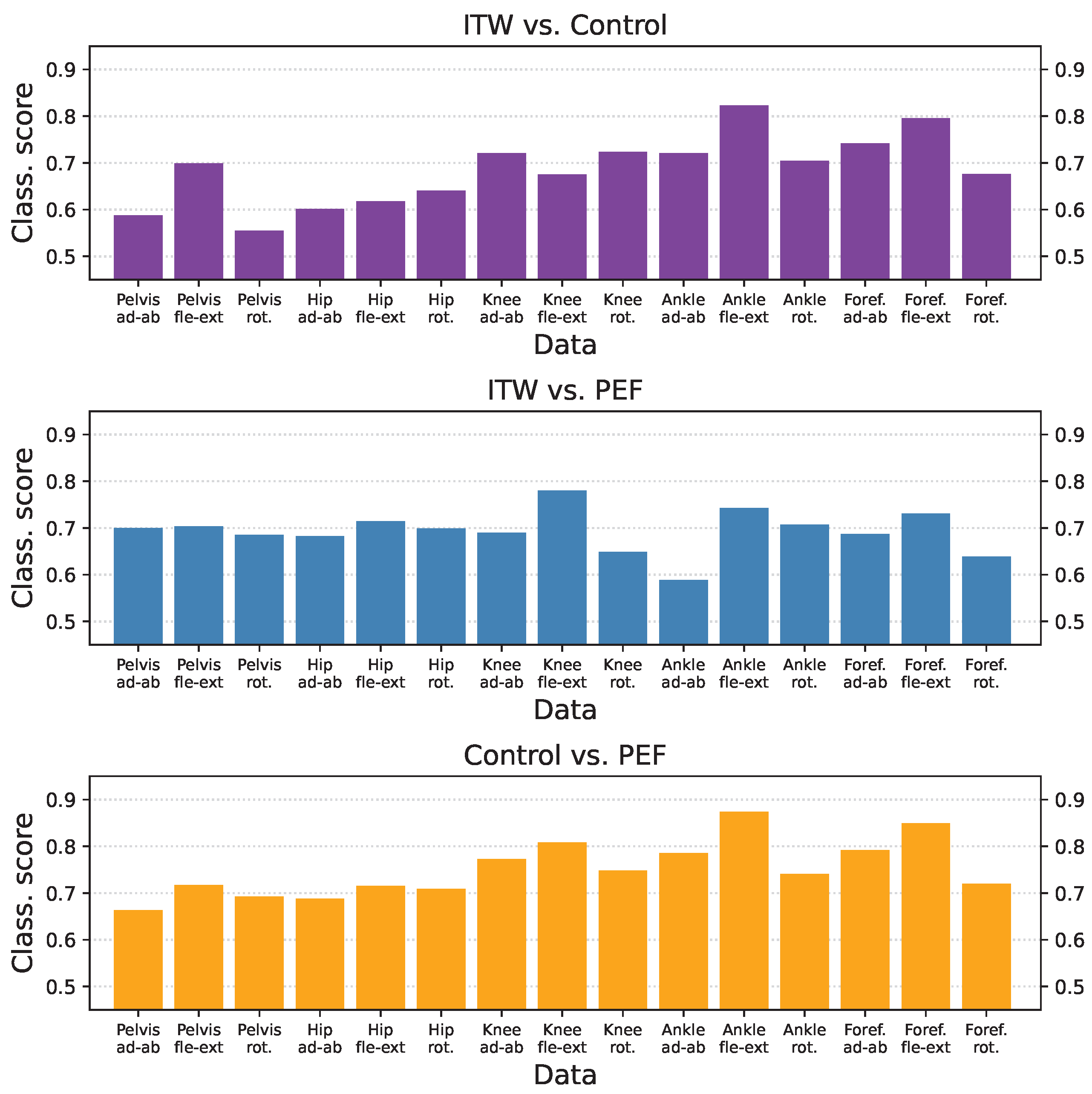
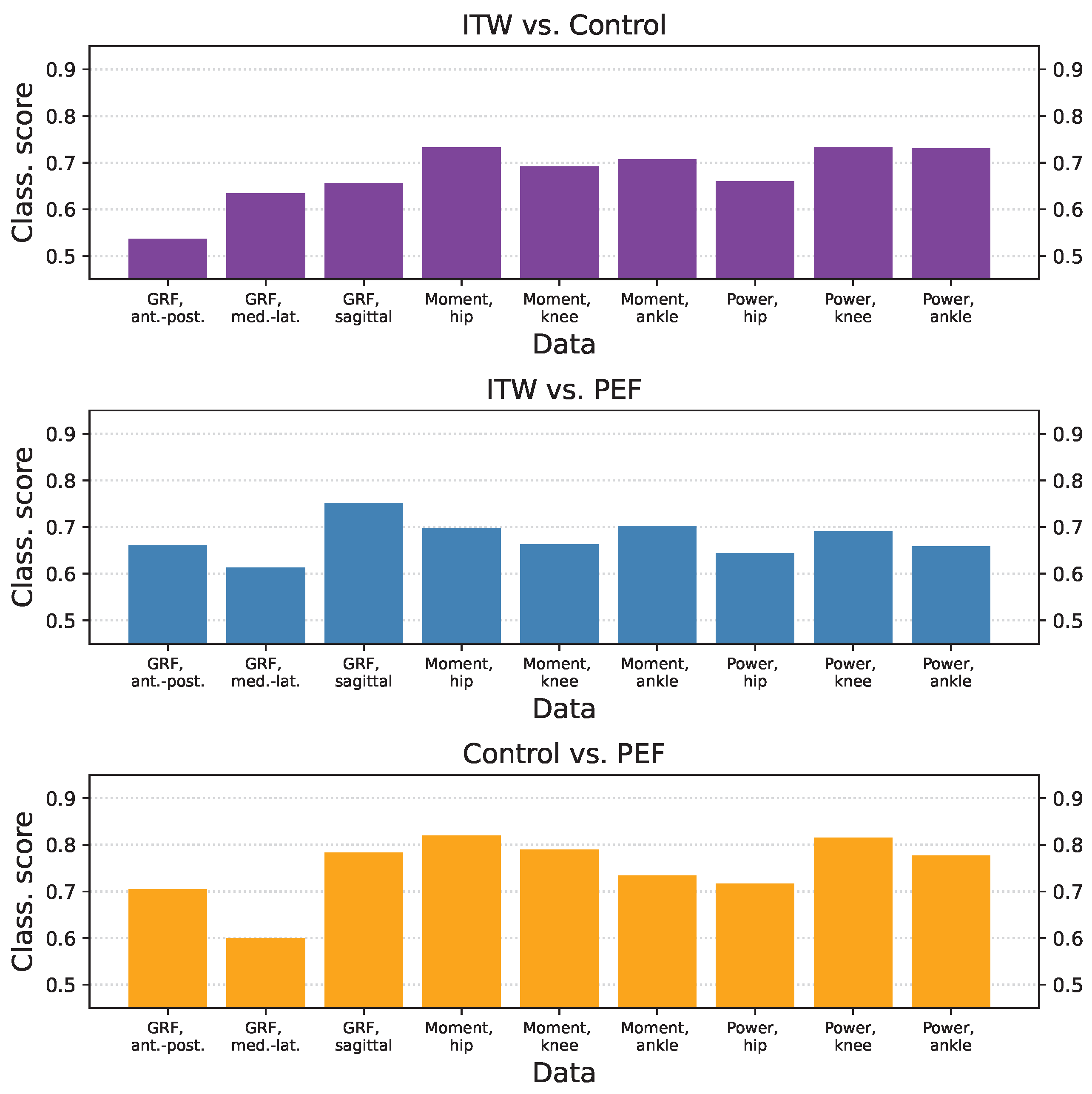
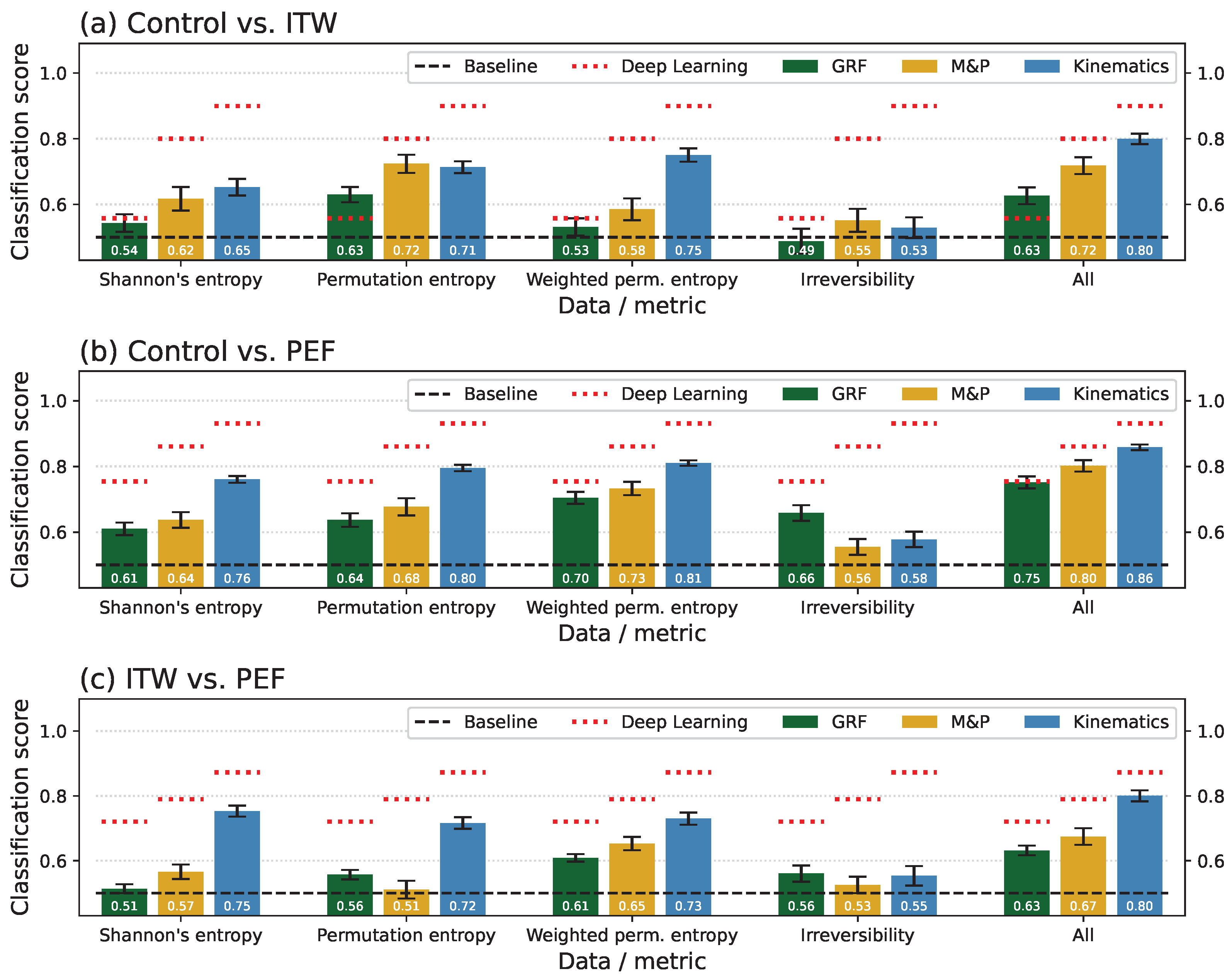
3.3. Classification Scores per Group and Time-Series Type
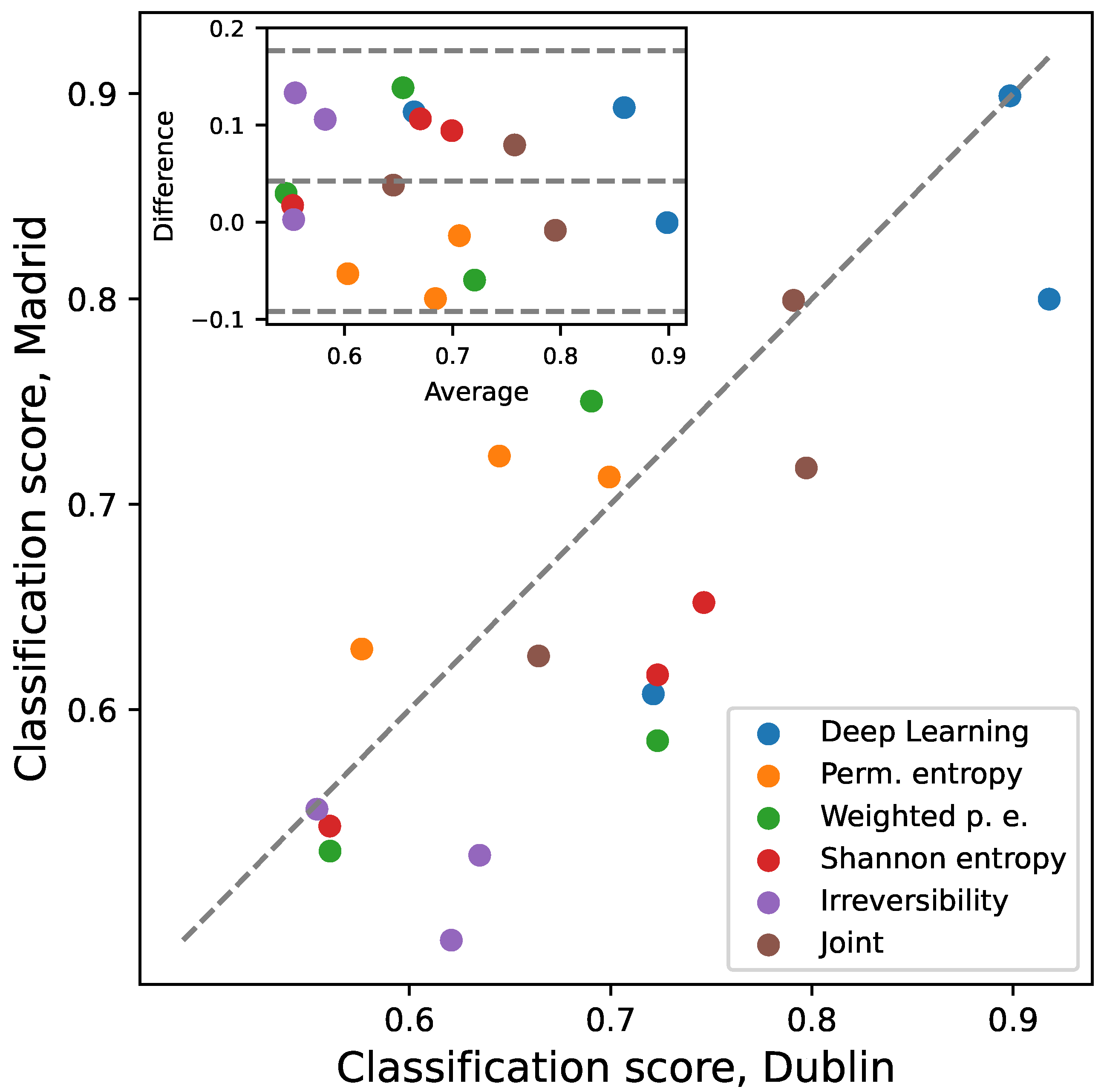
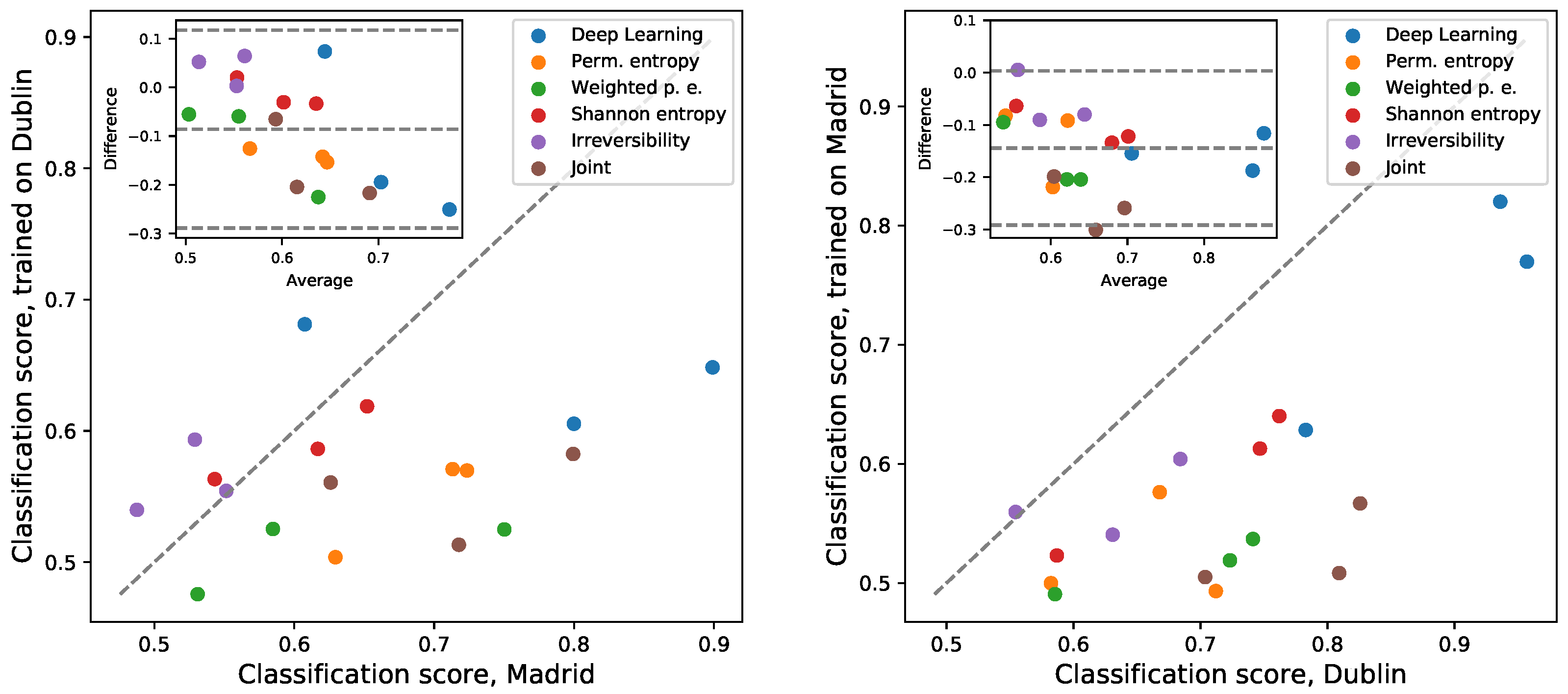
3.4. Inter-Laboratory Comparison
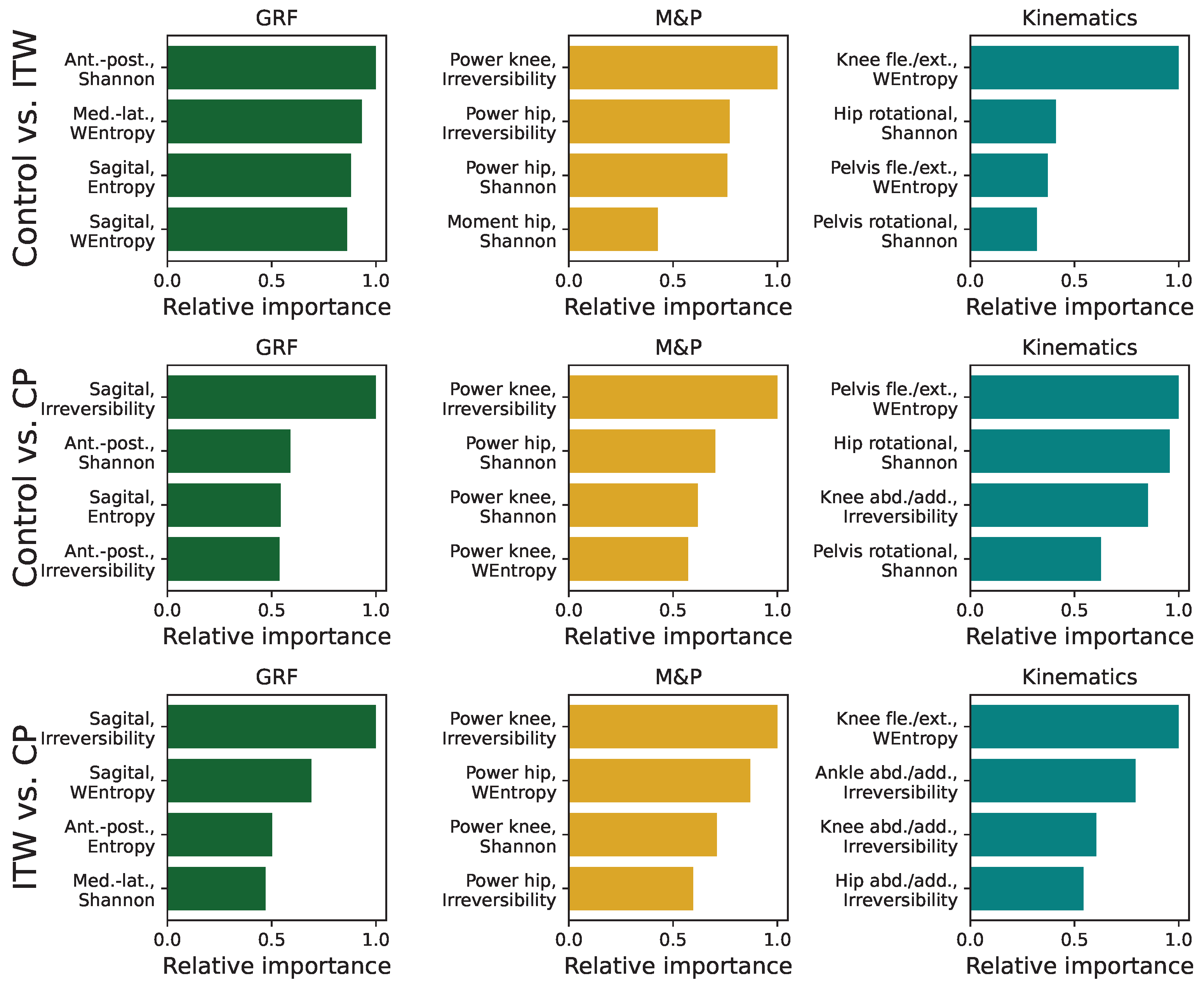
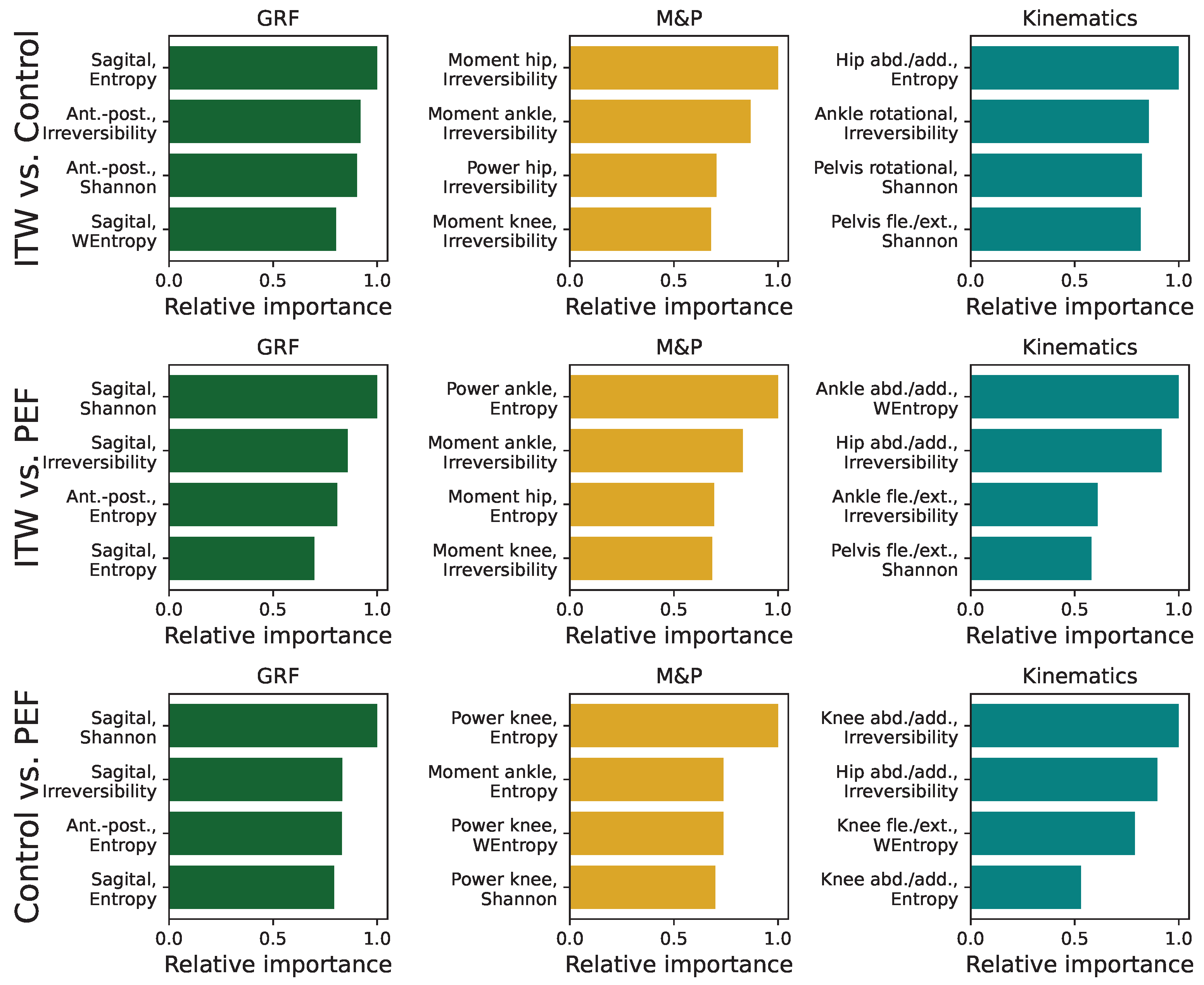
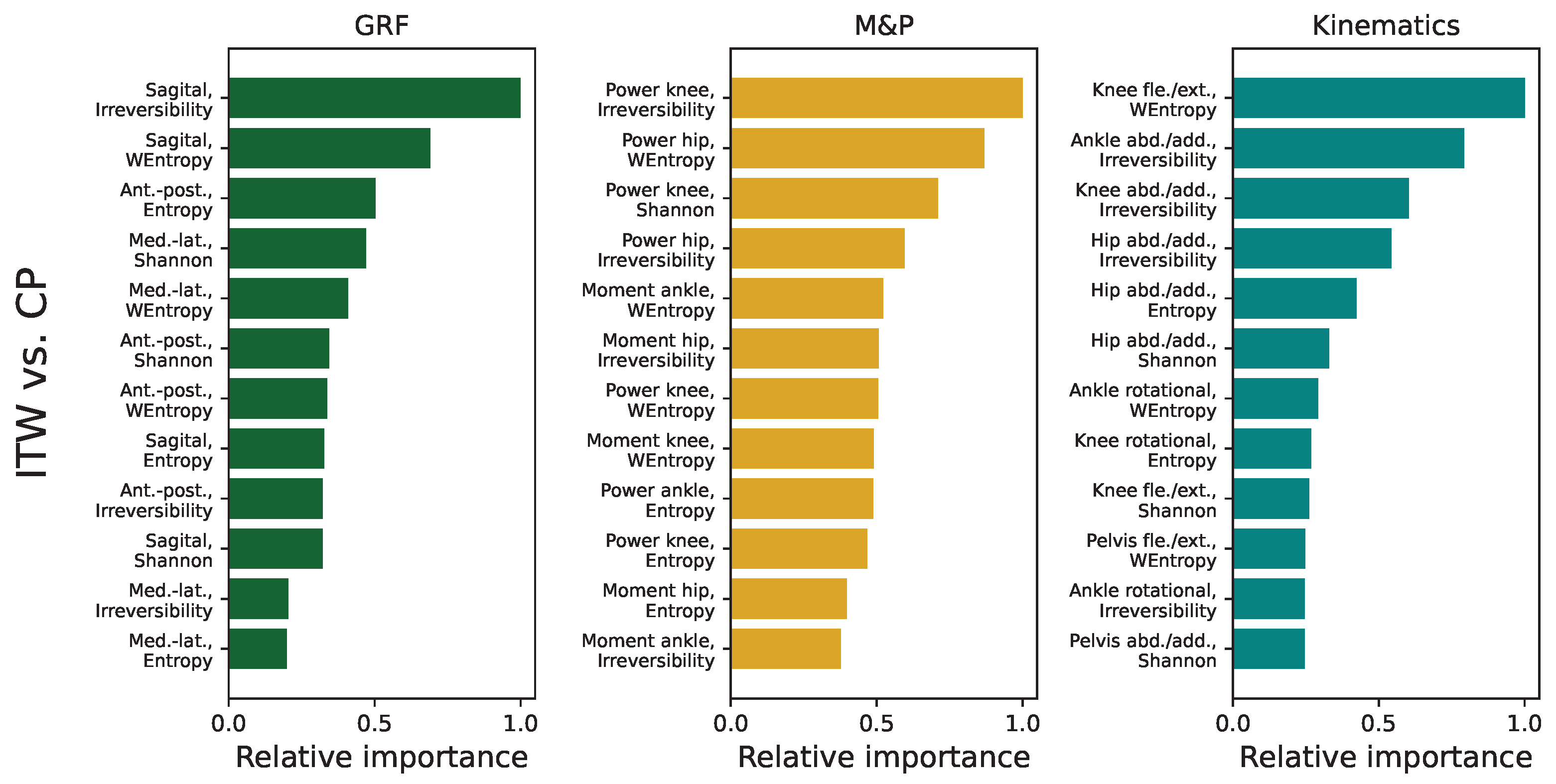
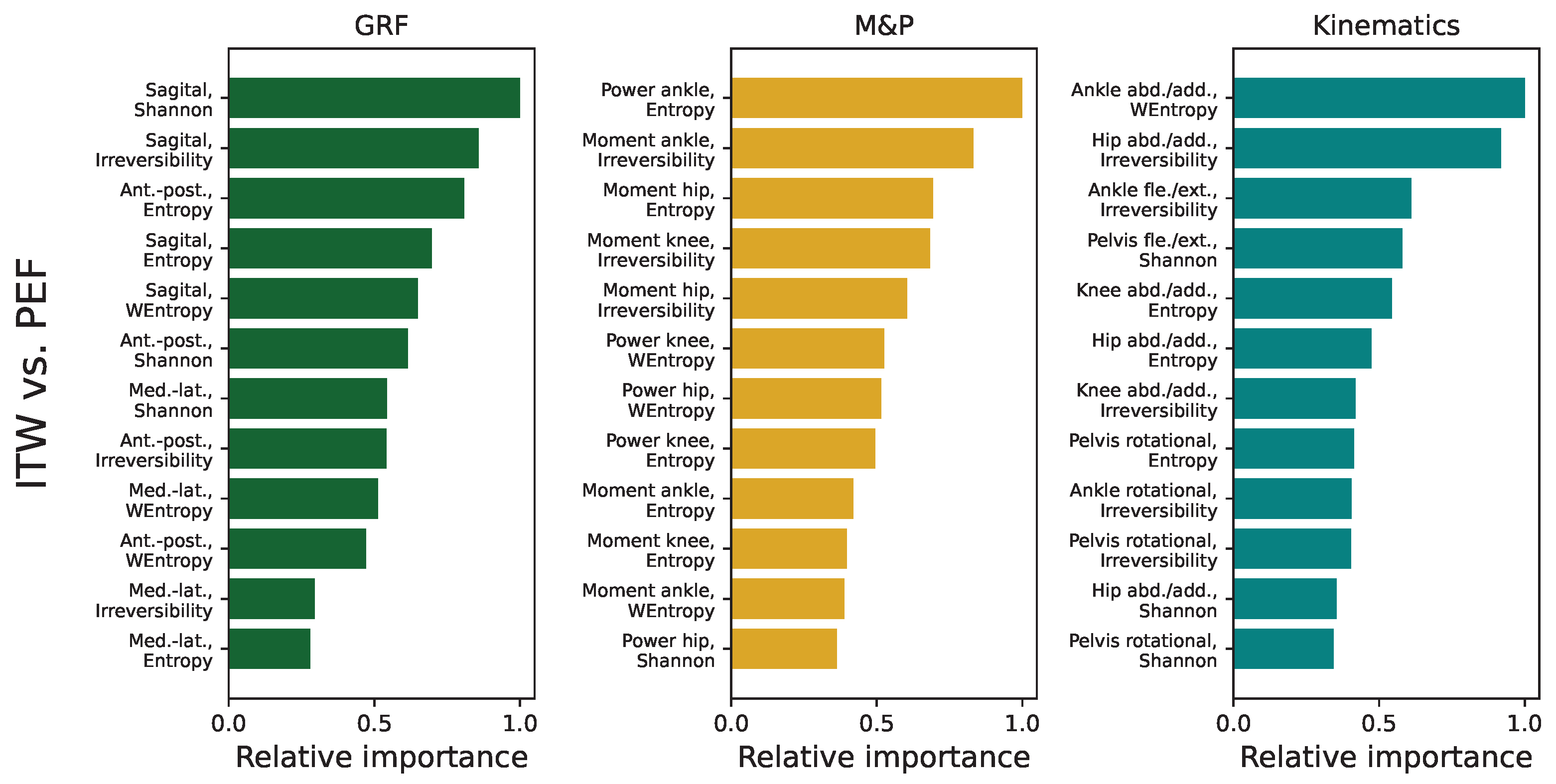
3.5. Analysis of Feature Importance in Statistical Physics Models
3.6. Classifications Based on Individual Time Series
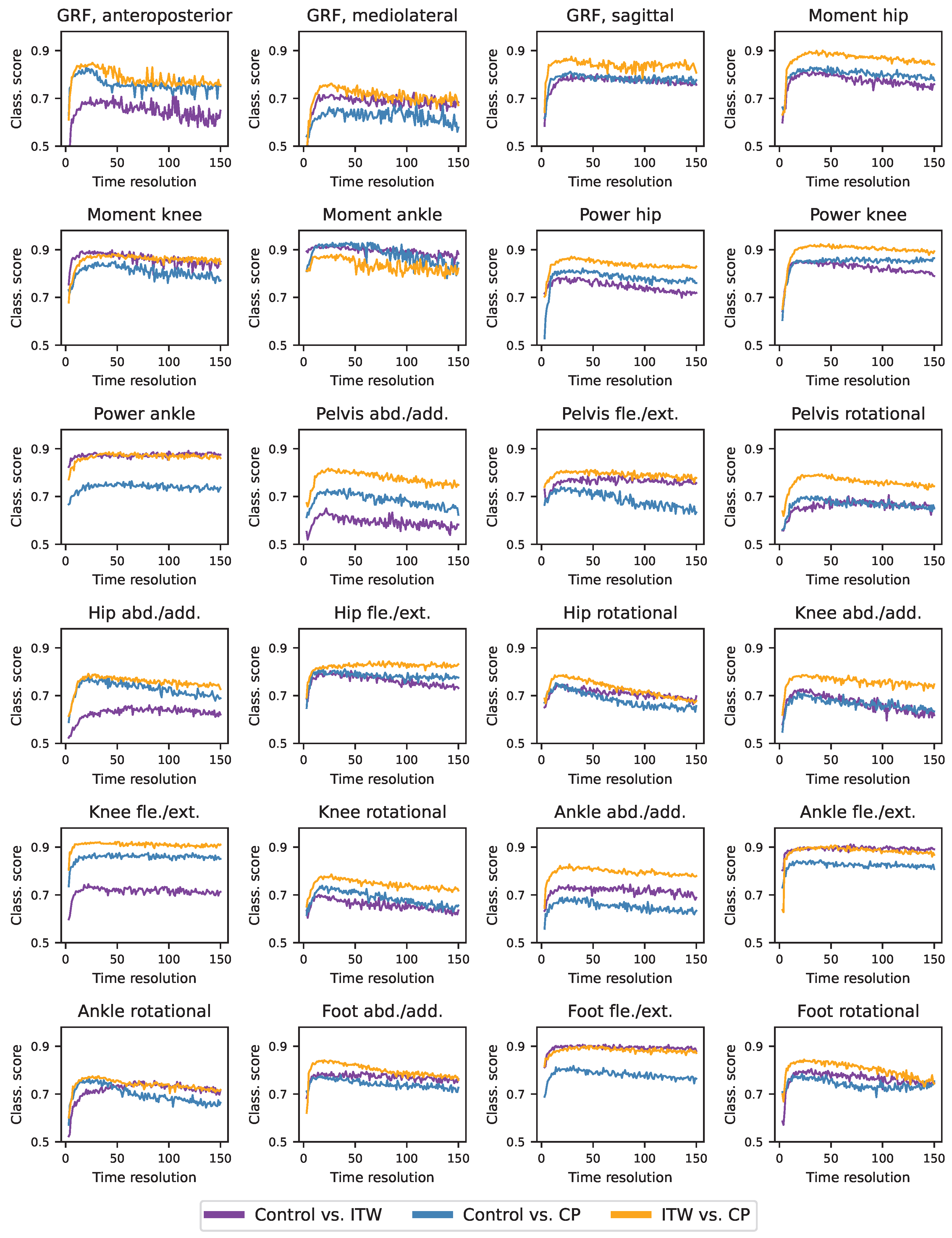
3.7. Optimal Resolution of Time Series
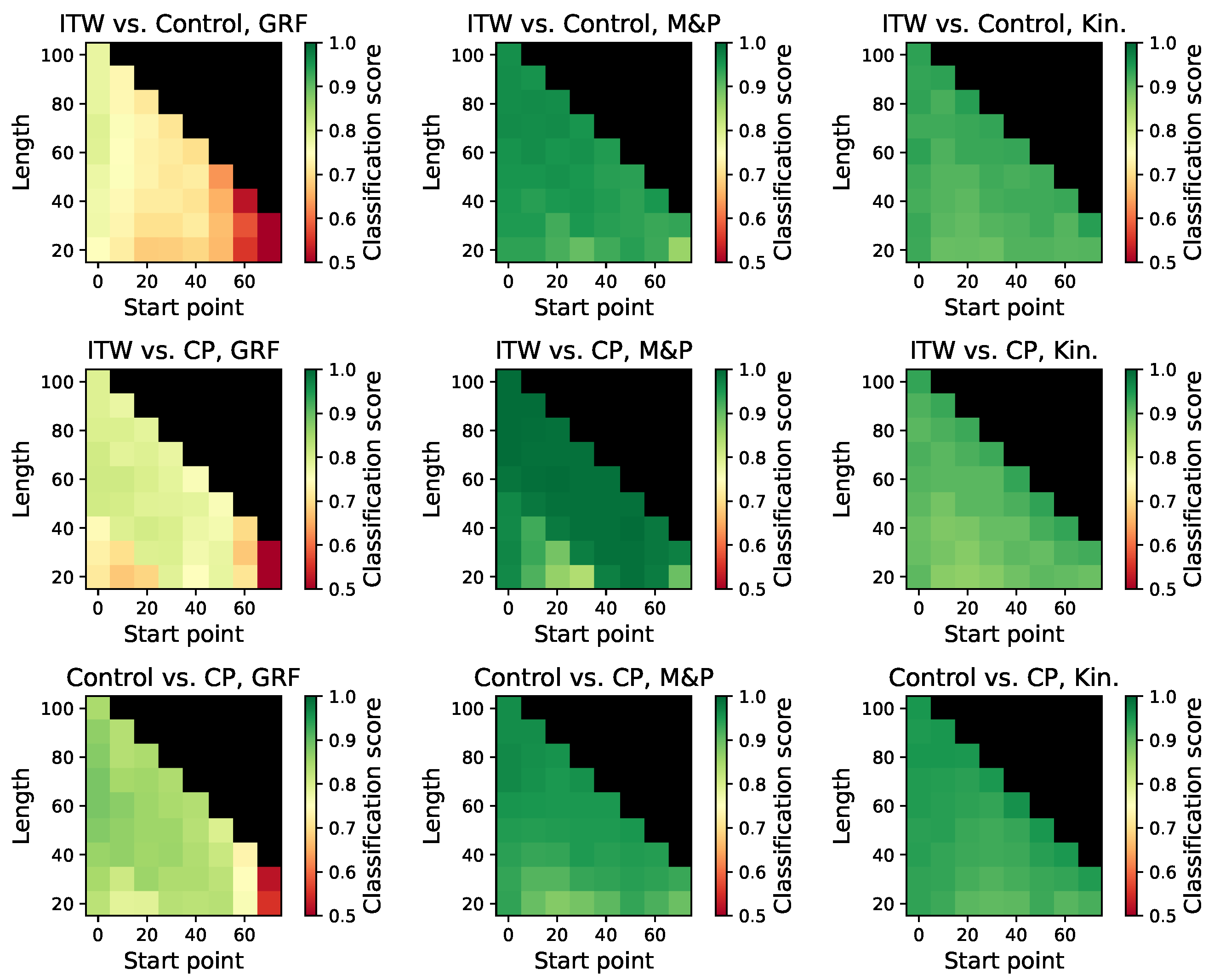
3.8. Analysis of Gait Sub-Windows
4. Discussion
4.1. Discussion from the Data Analysis Perspective
4.2. Insights into Motor Control Through Statistical Physic Metrics and Deep Learning
4.3. Considerations from a Medical Point of View
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


















References
- Perry, J.; Burnfield, J.M.; Gronley, J.K.; Mulroy, S.J. Toe walking: Muscular demands at the ankle and knee. Arch. Phys. Med. Rehabil. 2003, 84, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Engström, P.; Tedroff, K. Idiopathic Toe-Walking: Prevalence and Natural History from Birth to Ten Years of Age. J. Bone Joint Surg. Am. 2018, 100, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Schlough, K.; Andre, K.; Owen, M.; Adelstein, L.; Hartford, M.C.; Javier, B.; Kern, R. Differentiating Between Idiopathic Toe Walking and Cerebral Palsy: A Systematic Review. Pediatr. Phys. Ther. 2020, 32, 2–10. [Google Scholar] [CrossRef] [PubMed]
- Cappellini, G.; Sylos-Labini, F.; Avaltroni, P.; Dewolf, A.H.; Assenza, C.; Morelli, D.; Lacquaniti, F.; Ivanenko, Y. Comparison of the forward and sideways locomotor patterns in children with Cerebral Palsy. Sci. Rep. 2023, 13, 7286. [Google Scholar] [CrossRef]
- Fink, J.K. Hereditary spastic paraplegia. Curr. Neurol. Neurosci. Rep. 2006, 6, 65–76. [Google Scholar] [CrossRef]
- Pomarino, D.; Llamas, J.R.; Pomarino, A. Idiopathic Toe Walking: Tests and Family Predisposition. Foot Ankle Spec. 2016, 9, 301–306. [Google Scholar] [CrossRef]
- Novak, I.; Morgan, C.; Adde, L.; Blackman, J.; Boyd, R.N.; Brunstrom-Hernandez, J.; Cioni, G.; Damiano, D.; Darrah, J.; Eliasson, A.C.; et al. Early, Accurate Diagnosis and Early Intervention in Cerebral Palsy: Advances in Diagnosis and Treatment. JAMA Pediatr. 2017, 171, 897–907. [Google Scholar] [CrossRef]
- Suchowersky, O.; Ashtiani, S.; Au, P.Y.B.; McLeod, S.; Estiar, M.A.; Gan-Or, Z.; Rouleau, G.A. Hereditary spastic paraplegia initially diagnosed as cerebral palsy. Clin. Park. Relat. Disord. 2021, 5, 100114. [Google Scholar] [CrossRef]
- Whittle, M.W. Gait Analysis: An Introduction; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 2004, 556, 267–282. [Google Scholar] [CrossRef]
- Dominici, N.; Ivanenko, Y.P.; Cappellini, G.; d’Avella, A.; Mondì, V.; Cicchese, M.; Fabiano, A.; Silei, T.; Di Paolo, A.; Giannini, C.; et al. Locomotor primitives in newborn babies and their development. Science 2011, 334, 997–999. [Google Scholar] [CrossRef]
- Armand, S.; Watelain, E.; Mercier, M.; Lensel, G.; Lepoutre, F.X. Identification and classification of toe-walkers based on ankle kinematics, using a data-mining method. Gait Posture 2006, 23, 240–248. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, C.; De Vera, M.; Beauchamp, R.; Ward, V.; Black, A. Classification of idiopathic toe walking based on gait analysis: Development and application of the ITW severity classification. Gait Posture 2007, 26, 428–435. [Google Scholar] [CrossRef] [PubMed]
- Westberry, D.E.; Davids, J.R.; Davis, R.B.; de Morais Filho, M.C. Idiopathic Toe Walking: A Kinematic and Kinetic Profile. J. Pediatr. Orthop. 2008, 28, 352–358. [Google Scholar] [CrossRef] [PubMed]
- Habersack, A.; Fischerauer, S.F.; Kraus, T.; Holzer, H.P.; Svehlik, M. Kinematic and Kinetic Gait Parameters Can Distinguish between Idiopathic and Neurologic Toe-Walking. Int. J. Environ. Res. Public Health 2022, 19, 804. [Google Scholar] [CrossRef]
- Gage, J.R.; Schwartz, M.H.; Koop, S.E.; Novacheck, T.F. The Identification and Treatment of Gait Problems in Cerebral Palsy; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 180. [Google Scholar]
- Thomason, P.; Rodda, J.; Sangeux, M.; Selber, P.; Graham, K. Management of children with ambulatory cerebral palsy: An evidence-based review. Commentary by Hugh Williamson Gait Laboratory staff. J. Pediatr. Orthop. 2012, 32, S182–S186. [Google Scholar] [CrossRef]
- States, R.A.; Krzak, J.J.; Salem, Y.; Godwin, E.M.; Bodkin, A.W.; McMulkin, M.L. Instrumented gait analysis for management of gait disorders in children with cerebral palsy: A scoping review. Gait Posture 2021, 90, 1–8. [Google Scholar] [CrossRef]
- Graham, H.K.; Aoki, K.R.; Autti-Rämö, I.; Boyd, R.N.; Delgado, M.R.; Gaebler-Spira, D.J.; Gormley, M.E., Jr.; Guyer, B.M.; Heinen, F.; Holton, A.F.; et al. Recommendations for the use of botulinum toxin type A in the management of cerebral palsy. Gait Posture 2000, 11, 67–79. [Google Scholar] [CrossRef]
- Pulido-Valdeolivas, I.; Gómez-Andrés, D.; Martín-Gonzalo, J.A.; Rodríguez-Andonaegui, I.; López-López, J.; Pascual-Pascual, S.I.; Rausell, E. Gait phenotypes in paediatric hereditary spastic paraplegia revealed by dynamic time warping analysis and random forests. PLoS ONE 2018, 13, e0192345. [Google Scholar] [CrossRef]
- Buckley, C.; Alcock, L.; McArdle, R.; Rehman, R.Z.U.; Del Din, S.; Mazzà, C.; Yarnall, A.J.; Rochester, L. The role of movement analysis in diagnosing and monitoring neurodegenerative conditions: Insights from gait and postural control. Brain Sci. 2019, 9, 34. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of irregularity for psychiatric serial metrics. Bipolar Disord. 2006, 8, 430–440. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; James, C.J.; Hornero, R. Non-linear analysis of intracranial electroencephalogram recordings with approximate entropy and Lempel-Ziv complexity for epileptic seizure detection. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1953–1956. [Google Scholar]
- Averna, A.; Coelli, S.; Ferrara, R.; Cerutti, S.; Priori, A.; Bianchi, A.M. Entropy and fractal analysis of brain-related neurophysiological signals in Alzheimer’s and Parkinson’s disease. J. Neural Eng. 2023, 20, 051001. [Google Scholar] [CrossRef] [PubMed]
- Torres, B.D.L.C.; López, M.S.; Cachadiña, E.S.; Orellana, J.N. Entropy in the analysis of gait complexity: A state of the art. Br. J. Appl. Sci. Technol. 2013, 3, 1097. [Google Scholar] [CrossRef]
- McCamley, J.D.; Denton, W.; Arnold, A.; Raffalt, P.C.; Yentes, J.M. On the calculation of sample entropy using continuous and discrete human gait data. Entropy 2018, 20, 764. [Google Scholar] [CrossRef]
- Yentes, J.M.; Raffalt, P.C. Entropy analysis in gait research: Methodological considerations and recommendations. Ann. Biomed. Eng. 2021, 49, 979–990. [Google Scholar] [CrossRef]
- Bisi, M.C.; Stagni, R. Complexity of human gait pattern at different ages assessed using multiscale entropy: From development to decline. Gait Posture 2016, 47, 37–42. [Google Scholar] [CrossRef]
- Chakraborty, M.; Das, T.; Ghosh, D. Characterization of gait dynamics using fractal analysis for normal and Parkinson disease patients. In Proceedings of the 2015 IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 15–17 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 367–372. [Google Scholar]
- Orellana, J.N.; Sixto, A.S.; Torres, B.D.L.C.; Cachadiña, E.S.; Martín, P.F.; de la Rosa, F.B. Multiscale time irreversibility: Is it useful in the analysis of human gait? Biomed. Signal Process. Control 2018, 39, 431–434. [Google Scholar] [CrossRef]
- Martín-Gonzalo, J.A.; Pulido-Valdeolivas, I.; Wang, Y.; Wang, T.; Chiclana-Actis, G.; Algarra-Lucas, M.d.C.; Palmí-Cortés, I.; Fernandez Travieso, J.; Torrecillas-Narváez, M.D.; Miralles-Martinez, A.A.; et al. Permutation entropy and irreversibility in gait kinematic time series from patients with mild cognitive decline and early Alzheimer’s dementia. Entropy 2019, 21, 868. [Google Scholar] [CrossRef]
- Zanin, M.; Olivares, F.; Pulido-Valdeolivas, I.; Rausell, E.; Gomez-Andres, D. Gait analysis under the lens of statistical physics. Comput. Struct. Biotechnol. J. 2022, 20, 3257–3267. [Google Scholar] [CrossRef]
- Lempereur, M.; Guéret, G.; Houx, L.; Cacioppo, M.; Pons-Becmeur, C.; Rémy-Néris, O.; Rousseau, F.; Brochard, S. Can deep learning distinguish between children with idiopathic toe walking and spastic diplegia from their gait kinematics? Gait Posture 2021, 90, 136. [Google Scholar] [CrossRef]
- Chen, J.; Soangra, R.; Grant-Beuttler, M.; Nanehkaran, Y.A.; Wen, Y. Dense & Attention Convolutional Neural Networks for Toe Walking Recognition. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 2235–2245. [Google Scholar] [CrossRef] [PubMed]
- Slijepcevic, D.; Zeppelzauer, M.; Unglaube, F.; Kranzl, A.; Breiteneder, C.; Horsak, B. Explainable Machine Learning in Human Gait Analysis: A Study on Children With Cerebral Palsy. IEEE Access 2023, 11, 65906–65923. [Google Scholar] [CrossRef]
- Tao, W.; Zhang, X.; Chen, X.; Wu, D.; Zhou, P. Multi-scale complexity analysis of muscle coactivation during gait in children with cerebral palsy. Front. Hum. Neurosci. 2015, 9, 367. [Google Scholar] [CrossRef]
- Zanin, M.; Gómez-Andrés, D.; Pulido-Valdeolivas, I.; Martín-Gonzalo, J.A.; López-López, J.; Pascual-Pascual, S.I.; Rausell, E. Characterizing normal and pathological gait through permutation entropy. Entropy 2018, 20, 77. [Google Scholar] [CrossRef]
- Kadaba, M.P.; Ramakrishnan, H.; Wootten, M. Measurement of lower extremity kinematics during level walking. J. Orthop. Res. 1990, 8, 383–392. [Google Scholar] [CrossRef]
- Davis III, R.B.; Ounpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis data collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Amigó, J. Permutation Complexity in Dynamical Systems: Ordinal Patterns, Permutation Entropy and All That; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Leyva, I.; Martínez, J.H.; Masoller, C.; Rosso, O.A.; Zanin, M. 20 years of ordinal patterns: Perspectives and challenges. Europhys. Lett. 2022, 138, 31001. [Google Scholar] [CrossRef]
- Cuesta-Frau, D.; Murillo-Escobar, J.P.; Orrego, D.A.; Delgado-Trejos, E. Embedded dimension and time series length. Practical influence on permutation entropy and its applications. Entropy 2019, 21, 385. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Shang, P.; Wang, J.; Shi, W. Permutation and weighted-permutation entropy analysis for the complexity of nonlinear time series. Commun. Nonlinear Sci. Numer. Simul. 2016, 31, 60–68. [Google Scholar] [CrossRef]
- Weiss, G. Time-reversibility of linear stochastic processes. J. Appl. Probab. 1975, 12, 831–836. [Google Scholar] [CrossRef]
- Lawrance, A. Directionality and reversibility in time series. Int. Stat. Rev. Int. Stat. 1991, 59, 67–79. [Google Scholar] [CrossRef]
- Porporato, A.; Rigby, J.R.; Daly, E. Irreversibility and fluctuation theorem in stationary time series. Phys. Rev. Lett. 2007, 98, 094101. [Google Scholar] [CrossRef]
- Broock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Brock, W.A.; Brock, W.A.; Hsieh, D.A.; LeBaron, B.D. Nonlinear Dynamics, Chaos, and Instability: Statistical Theory and Economic Evidence; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Ramsey, J.B.; Rothman, P. Time irreversibility and business cycle asymmetry. J. Money Credit. Bank. 1996, 28, 1–21. [Google Scholar] [CrossRef]
- Daw, C.; Finney, C.; Kennel, M. Symbolic approach for measuring temporal “irreversibility”. Phys. Rev. E 2000, 62, 1912. [Google Scholar] [CrossRef]
- Donges, J.F.; Donner, R.V.; Kurths, J. Testing time series irreversibility using complex network methods. Europhys. Lett. 2013, 102, 10004. [Google Scholar] [CrossRef]
- Cammarota, C.; Rogora, E. Time reversal, symbolic series and irreversibility of human heartbeat. Chaos Solitons Fractals 2007, 32, 1649–1654. [Google Scholar] [CrossRef]
- Zanin, M.; Papo, D. Algorithmic approaches for assessing irreversibility in time series: Review and comparison. Entropy 2021, 23, 1474. [Google Scholar] [CrossRef]
- Zanin, M.; Papo, D. Algorithmic Approaches for Assessing Multiscale Irreversibility in Time Series: Review and Comparison. Entropy 2025, 27, 126. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1578–1585. [Google Scholar]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Zanin, M. Can deep learning distinguish chaos from noise? Numerical experiments and general considerations. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106708. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the OSDI’16, Savannah, GA, USA, 2–4 November 2016; Volume 16, pp. 265–283. [Google Scholar]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Wren, T.A.L.; Tucker, C.A.; Rethlefsen, S.A.; Gorton, G.E.; Õunpuu, S. Clinical efficacy of instrumented gait analysis: Systematic review 2020 update. Gait Posture 2020, 80, 274–279. [Google Scholar] [CrossRef]
- Burdack, J.; Horst, F.; Giesselbach, S.; Hassan, I.; Daffner, S.; Schöllhorn, W.I. Systematic comparison of the influence of different data preprocessing methods on the performance of gait classifications using machine learning. Front. Bioeng. Biotechnol. 2020, 8, 260. [Google Scholar] [CrossRef]
- Lempereur, M.; Rousseau, F.; Rémy-Néris, O.; Pons, C.; Houx, L.; Quellec, G.; Brochard, S. A new deep learning-based method for the detection of gait events in children with gait disorders: Proof-of-concept and concurrent validity. J. Biomech. 2020, 98, 109490. [Google Scholar] [CrossRef]
- Cui, C.; Bian, G.B.; Hou, Z.G.; Zhao, J.; Su, G.; Zhou, H.; Peng, L.; Wang, W. Simultaneous recognition and assessment of post-stroke hemiparetic gait by fusing kinematic, kinetic, and electrophysiological data. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 856–864. [Google Scholar] [CrossRef]
- Horst, F.; Lapuschkin, S.; Samek, W.; Müller, K.R.; Schöllhorn, W.I. Explaining the unique nature of individual gait patterns with deep learning. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Giarmatzis, G.; Zacharaki, E.I.; Moustakas, K. Real-time prediction of joint forces by motion capture and machine learning. Sensors 2020, 20, 6933. [Google Scholar] [CrossRef]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the differences of gait patterns between high and low-mileage runners with machine learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef]
- Zou, J.; Zhang, X.; Zhang, Y.; Li, J.; Jin, Z. Prediction on the medial knee contact force in patients with knee valgus using transfer learning approaches: Application to rehabilitation gaits. Comput. Biol. Med. 2022, 150, 106099. [Google Scholar] [CrossRef]
- Lehne, M.; Sass, J.; Essenwanger, A.; Schepers, J.; Thun, S. Why digital medicine depends on interoperability. npj Digit. Med. 2019, 2, 79. [Google Scholar] [CrossRef]
- Soda, P.; Carta, A.; Formica, D.; Guglielmelli, E. A low-cost video-based tool for clinical gait analysis. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3979–3982. [Google Scholar]
- Ugbolue, U.C.; Papi, E.; Kaliarntas, K.T.; Kerr, A.; Earl, L.; Pomeroy, V.M.; Rowe, P.J. The evaluation of an inexpensive, 2D, video based gait assessment system for clinical use. Gait Posture 2013, 38, 483–489. [Google Scholar] [CrossRef]
- Yang, C.; Ugbolue, U.C.; Kerr, A.; Stankovic, V.; Stankovic, L.; Carse, B.; Kaliarntas, K.T.; Rowe, P.J. Autonomous gait event detection with portable single-camera gait kinematics analysis system. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Żuk, M.; Pezowicz, C. Kinematic analysis of a six-degrees-of-freedom model based on ISB recommendation: A repeatability analysis and comparison with conventional gait model. Appl. Bionics Biomech. 2015, 2015, 503713. [Google Scholar] [CrossRef][Green Version]
- Nuñez-Lisboa, M.; Bastien, G.J.; Schepens, B.; Lacquaniti, F.; Ivanenko, Y.; Dewolf, A.H. Effect of age and speed on the step-to-step transition strategies in children. J. Biomech. 2023, 157, 111704. [Google Scholar] [CrossRef]
- Sutherland, D. The development of mature gait. Gait Posture 1997, 6, 163–170. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, Y. Application of supervised machine learning algorithms in the classification of sagittal gait patterns of cerebral palsy children with spastic diplegia. Comput. Biol. Med. 2019, 106, 33–39. [Google Scholar] [CrossRef] [PubMed]
- MacWilliams, B.A.; Carroll, K.L.; Stotts, A.K.; Kerr, L.M.; Schwartz, M.H. Discrimination between hereditary spastic paraplegia and cerebral palsy based on gait analysis data: A machine learning approach. Gait Posture 2022, 98, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Piccinini, L.; Cimolin, V.; D’Angelo, M.G.; Turconi, A.C.; Crivellini, M.; Galli, M. 3D gait analysis in patients with hereditary spastic paraparesis and spastic diplegia: A kinematic, kinetic and EMG comparison. Eur. J. Paediatr. Neurol. 2011, 15, 138–145. [Google Scholar] [CrossRef] [PubMed]
- Thevenon, A.; Gabrielli, F.; Lepvrier, J.; Faupin, A.; Allart, E.; Tiffreau, V.; Wieczorek, V. Collection of normative data for spatial and temporal gait parameters in a sample of French children aged between 6 and 12. Ann. Phys. Rehabil. Med. 2015, 58, 139–144. [Google Scholar] [CrossRef]
- Lopez-Lopez, J.; Pulido-Valdeolivas, I.; Martin-Gonzalo, J.A.; de Gorostegui, A.; Perez-Villena, A.; Abenza-Albidua, M.; Fernandez-Jimenez, J.; Gomez-Andres, D.; Rausell, E. Pain and Achilles tendon shortening in patients with idiopathic toe walking. Rev. Neurol. 2021, 73, 307–314. [Google Scholar]

| Metric | Statistical Physics Meaning | Gait Meaning |
|---|---|---|
| Shannon’s entropy | Uncertainty in the distribution of values | Degree of variability of a gait feature along the gait cycle |
| Permutation entropy | Uncertainty in the temporal sequence of values | Degree of temporal organisation of a gait feature along the gait cycle without considering the amplitude of changes |
| Weighted permutation entropy | Uncertainty in the temporal sequence and amplitude | Degree of temporal organisation of a gait feature along the gait cycle considering the amplitude of changes |
| Irreversibility | Non-linearities, memory | Degree of dependency of a gait feature on a previous value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Gorostegui, A.; Zanin, M.; Martín-Gonzalo, J.-A.; López-López, J.; Gómez-Andrés, D.; Kiernan, D.; Rausell, E. Entropy, Irreversibility, and Time-Series Deep Learning of Kinematic and Kinetic Data for Gait Classification in Children with Cerebral Palsy, Idiopathic Toe Walking, and Hereditary Spastic Paraplegia. Sensors 2025, 25, 4235. https://doi.org/10.3390/s25134235
de Gorostegui A, Zanin M, Martín-Gonzalo J-A, López-López J, Gómez-Andrés D, Kiernan D, Rausell E. Entropy, Irreversibility, and Time-Series Deep Learning of Kinematic and Kinetic Data for Gait Classification in Children with Cerebral Palsy, Idiopathic Toe Walking, and Hereditary Spastic Paraplegia. Sensors. 2025; 25(13):4235. https://doi.org/10.3390/s25134235
Chicago/Turabian Stylede Gorostegui, Alfonso, Massimiliano Zanin, Juan-Andrés Martín-Gonzalo, Javier López-López, David Gómez-Andrés, Damien Kiernan, and Estrella Rausell. 2025. "Entropy, Irreversibility, and Time-Series Deep Learning of Kinematic and Kinetic Data for Gait Classification in Children with Cerebral Palsy, Idiopathic Toe Walking, and Hereditary Spastic Paraplegia" Sensors 25, no. 13: 4235. https://doi.org/10.3390/s25134235
APA Stylede Gorostegui, A., Zanin, M., Martín-Gonzalo, J.-A., López-López, J., Gómez-Andrés, D., Kiernan, D., & Rausell, E. (2025). Entropy, Irreversibility, and Time-Series Deep Learning of Kinematic and Kinetic Data for Gait Classification in Children with Cerebral Palsy, Idiopathic Toe Walking, and Hereditary Spastic Paraplegia. Sensors, 25(13), 4235. https://doi.org/10.3390/s25134235







