Mobile Tunnel Lining Measurable Image Scanning Assisted by Collimated Lasers
Abstract
Highlights
- A novel mobile tunnel lining scanning method aided by collimated lasers is presented, significantly improving image-stitching accuracy.
- A complete measurement system was built, and a Laplace kernel, maximum correntropy criterion, camera-pose calibration algorithm was introduced to further enhance calibration precision.
- The proposed approach yields near-seamless stitched images of tunnel linings.
- Using the new calibration algorithm, when outliers increase from 0% to 25%, the Euler-angle error grows by about 44%, and the translation error by roughly 45%, outperforming comparable benchmark algorithms.
Abstract
1. Introduction
2. Background
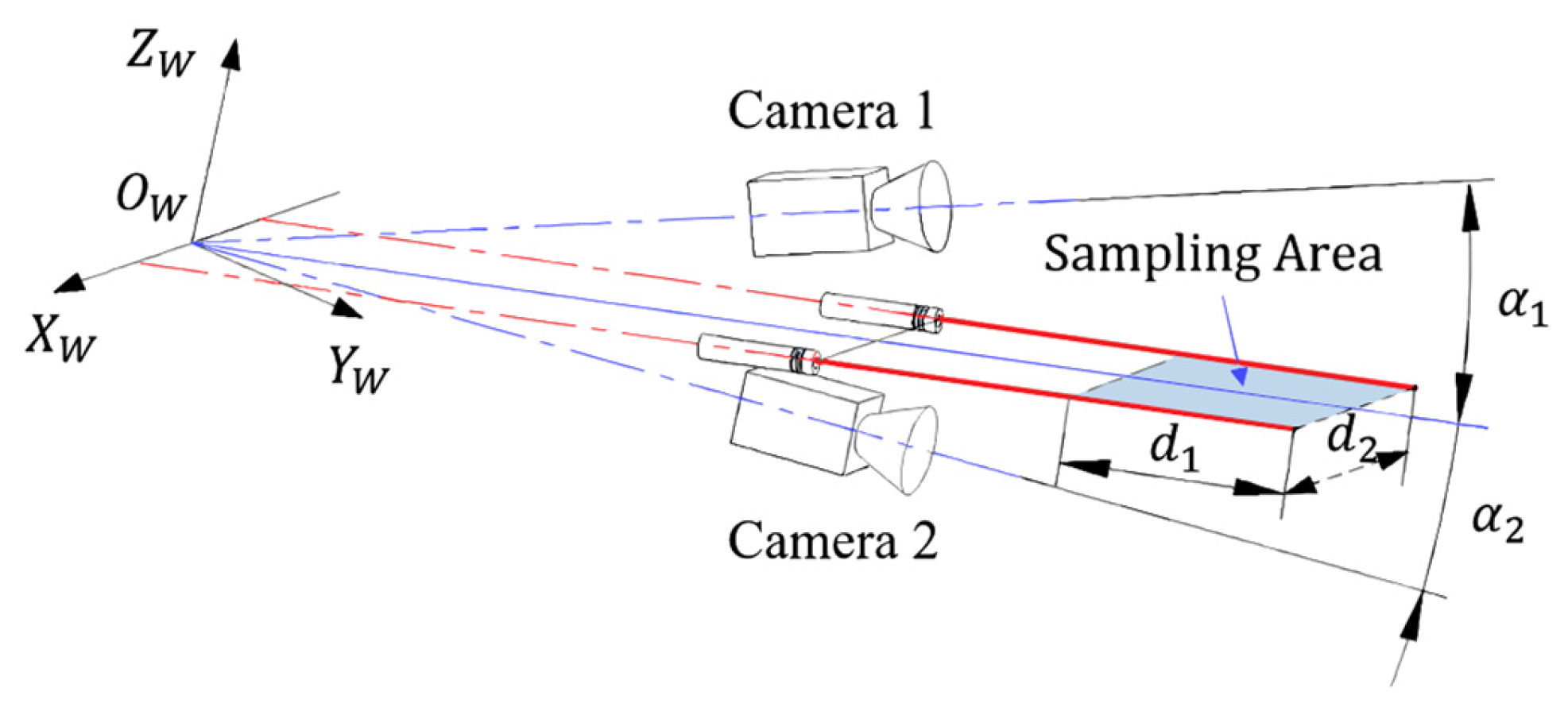
3. Schematic of the System
4. Methodology
4.1. RTL Scanning Schematic
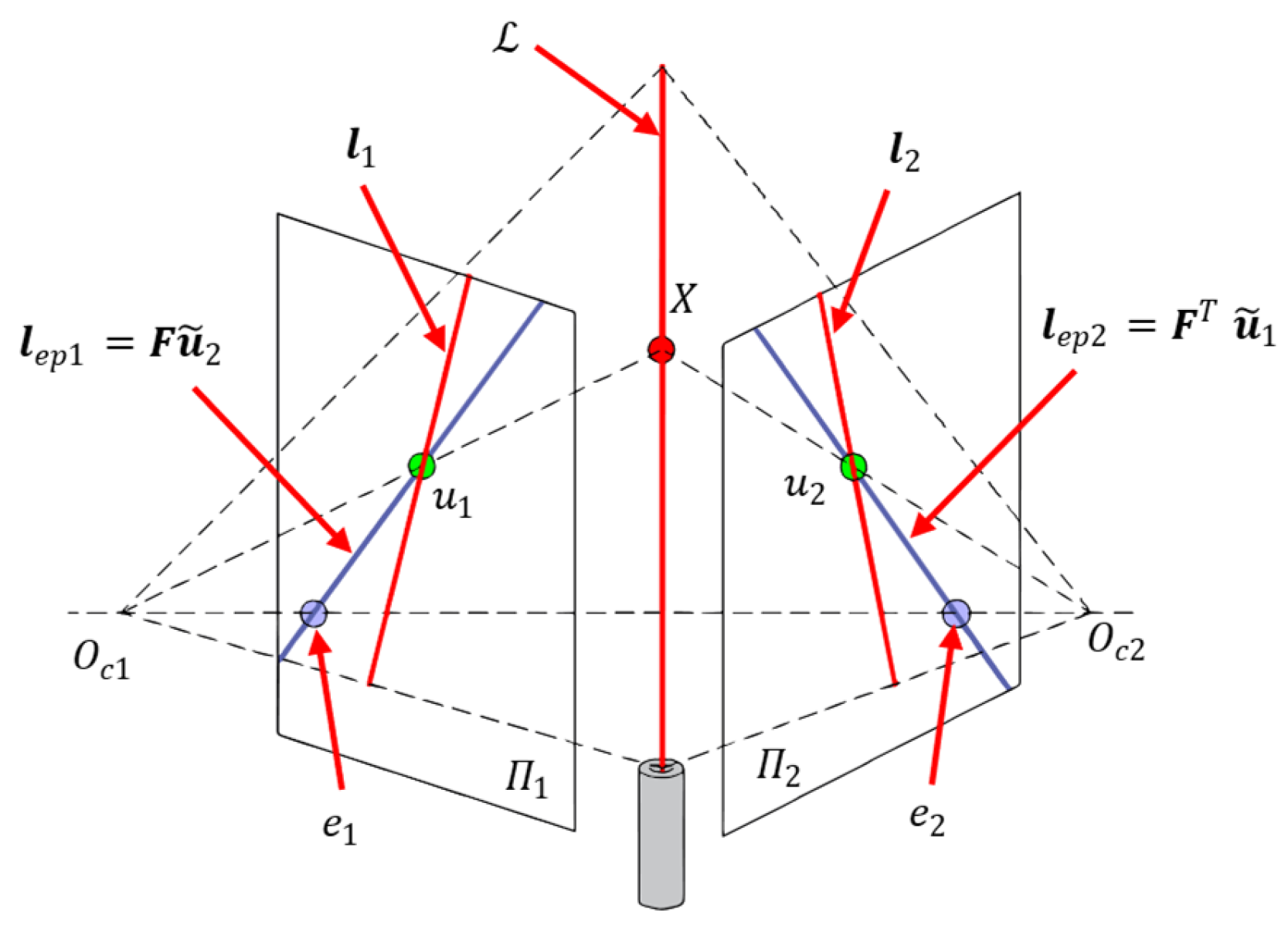
4.2. Reprojection and Stitching of Tunnel Lining Images
- (1)
- Equation (10) was used to project the border pixels of the image to determine the boundaries of the new image;
- (2)
- Equation (11) was used to calculate the backward interpolation mapping table of the new image, and interpolation is then performed to generate the new image.
- (1)
- The two-dimensional affine transformation parameters between two adjacent camera images are calculated based on the corresponding laser spots. Using these parameters, backward warping was applied to the benchmark camera images according to Equation (12). Obtain the overlapping region of the images, adjust the grayscale of the images, and finally perform pixel fusion within the overlapping region to generate the RTL profile images.
- (2)
- The overlapping region of the adjacent RTL profile images is roughly calculated based on the camera acquisition interval. Wavelet decomposition is then performed on the images in this region to separate the high- and low-frequency images. Next, Equation (13) is used to calculate the normalized cross-correlation (NCC) of the overlapping region between the two high-frequency images and to find its maximum position to achieve precise registration of adjacent profile images. Finally, the following pixel fusion was performed in the overlapping region to obtain a panoramic RTL image:
4.3. Fast Search for Laser Spot in Image
- (1)
- Search along the line to find , and then calculate for a coarse location of ;
- (2)
- In the vicinity of , methods such as grayscale centroid are used to estimate the precise value of .
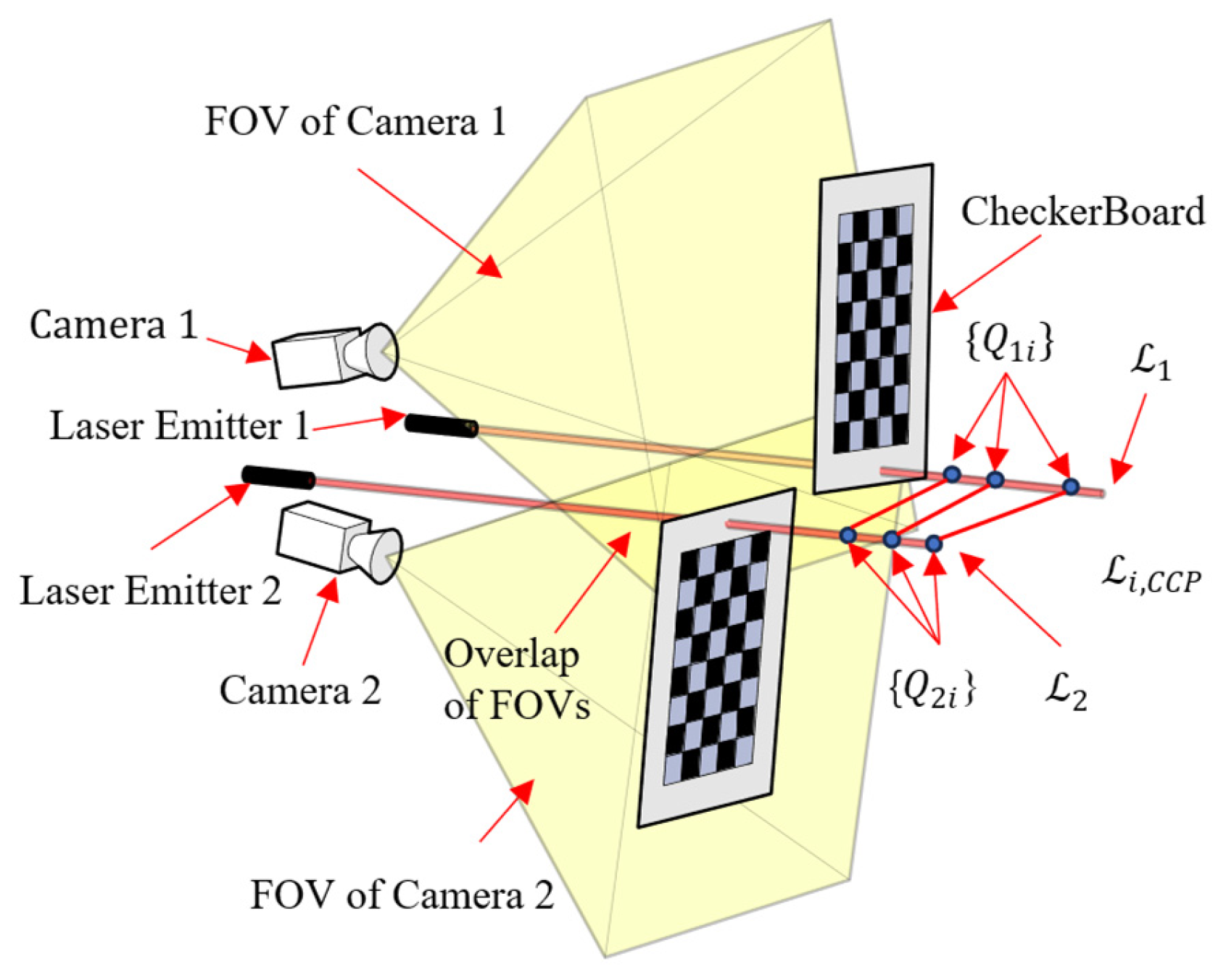
4.4. System Calibration
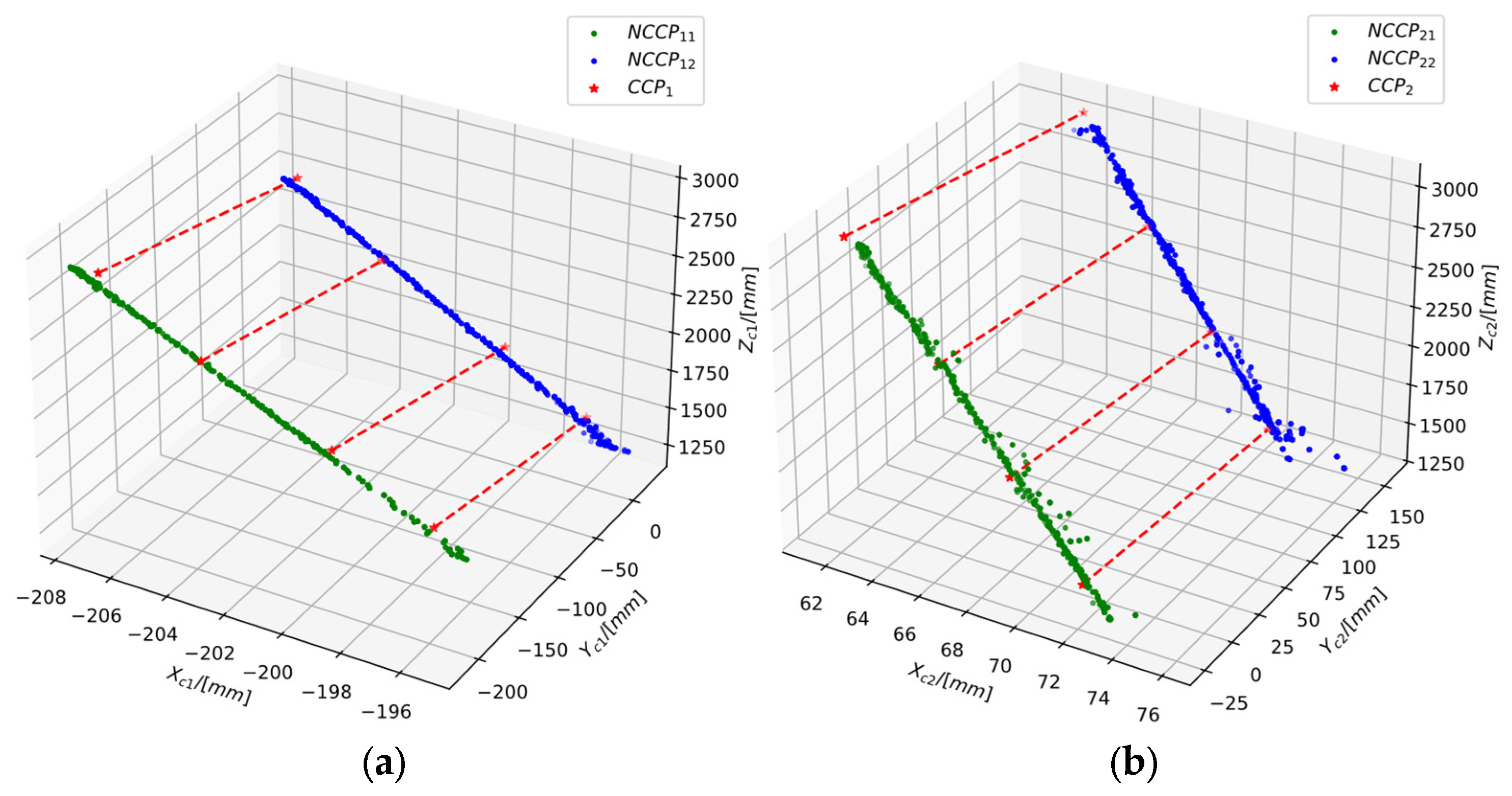
- (1)
- A checkerboard and the Perspective-n-Point (PNP) algorithm are used to independently sample the spatial points on the laser within the FOV of each camera, obtaining a non-corresponding control point (NCCP) coordinate set under the frames. Here, the subscript represents the index of the laser, represents the index of the coordinate in the set, and . Using these NCCP sets, the camera–laser triangulation unit can be calibrated based on Equations (7) and (8).
- (2)
- Using a flat plate, the corresponding control point (CCP) set is obtained under frames based on Equation (8).
- (1)
- According to Equation (5), a Plücker coordinate can be given by two three-dimensional points, thus three-dimensional points give Plücker coordinates. The NCCP coordinate set is used to obtain the NCCP–Plücker coordinate set for the -th laser beam, where is the index of the Plücker coordinate.
- (2)
- The CCP coordinate set is used to obtain the Plücker coordinates of several spatial lines that are not parallel to the lasers. These are called CCP–Plücker coordinates , where each coordinate in this set corresponds to a common line in the object space.
- (3)
- The and datasets are merged and input into the developed DQ-Laplacian maximum correntropy criterion (DLM) algorithm program to calculate the pose parameters of the two cameras.
4.5. DLM Algorithm
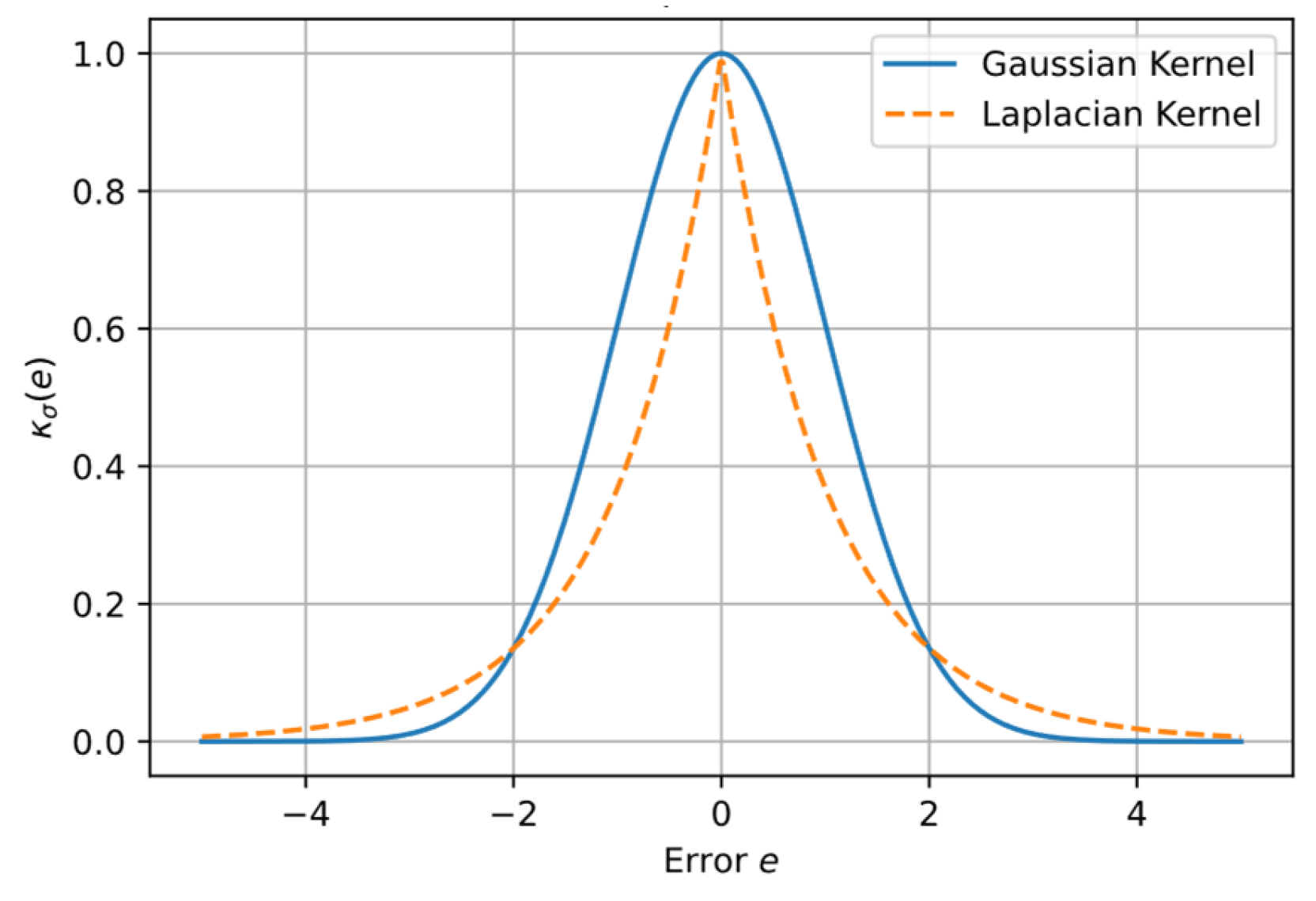
4.5.1. Introduction of Laplace–MMC
4.5.2. DLM Derivation
| Algorithm 1. DLM-MSR Algorithm |
| Input: |
| : A set of Plücker coordinates of at least 2 non-parallel lines in the -Frame; |
| : The corresponding set of Plücker coordinates in the -Frame; |
| : The maximum number of iterations for the solver; |
| The minimum update step size; |
| Process: |
| 0: Initialize , ; |
| for |
|
| end for |
| Return: and |
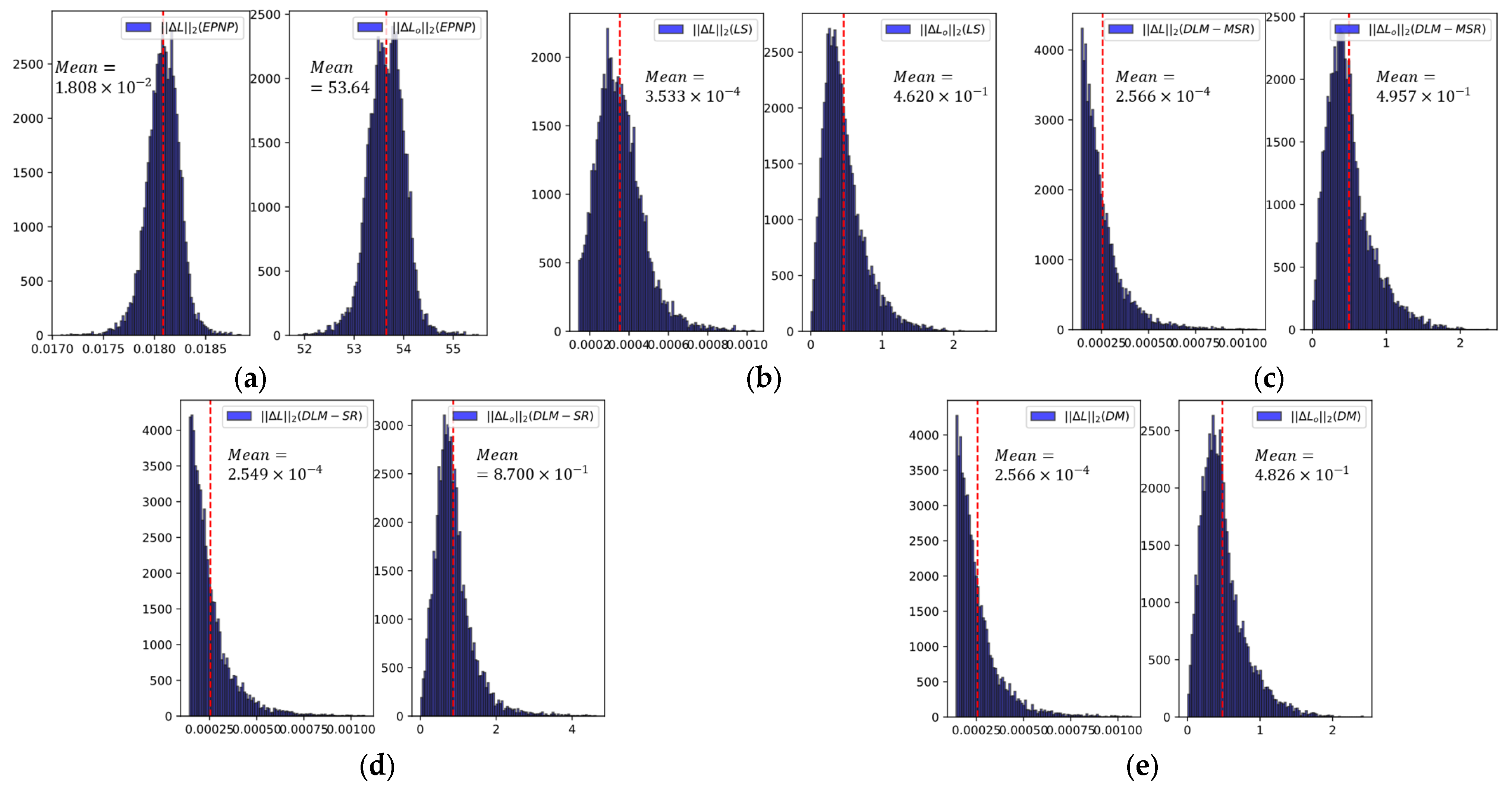
5. Experiment and Discussion
- (1)
- Section 5.1, Section 5.2 and Section 5.3 present a numerical simulation, an indoor test, and an outdoor field test that collectively evaluate the performance of the DLM algorithm. The simulation was implemented in Python 3.10, and the optimization problems in Equations (39) and (40) were solved with the CVXPY library (ver. 1.5.2).
- (2)
- In Section 5.4, the DLM algorithm was used to calibrate the RIC, and actual RTL images were collected to verify the feasibility of the proposed laser-assisted image stitching method. The experimental data were processed with custom Python scripts, OpenCV 4.9.0 was used for fundamental image operations, and the Pywt library (ver. 1.7.0) was employed for wavelet analysis.
5.1. DLM Simulation
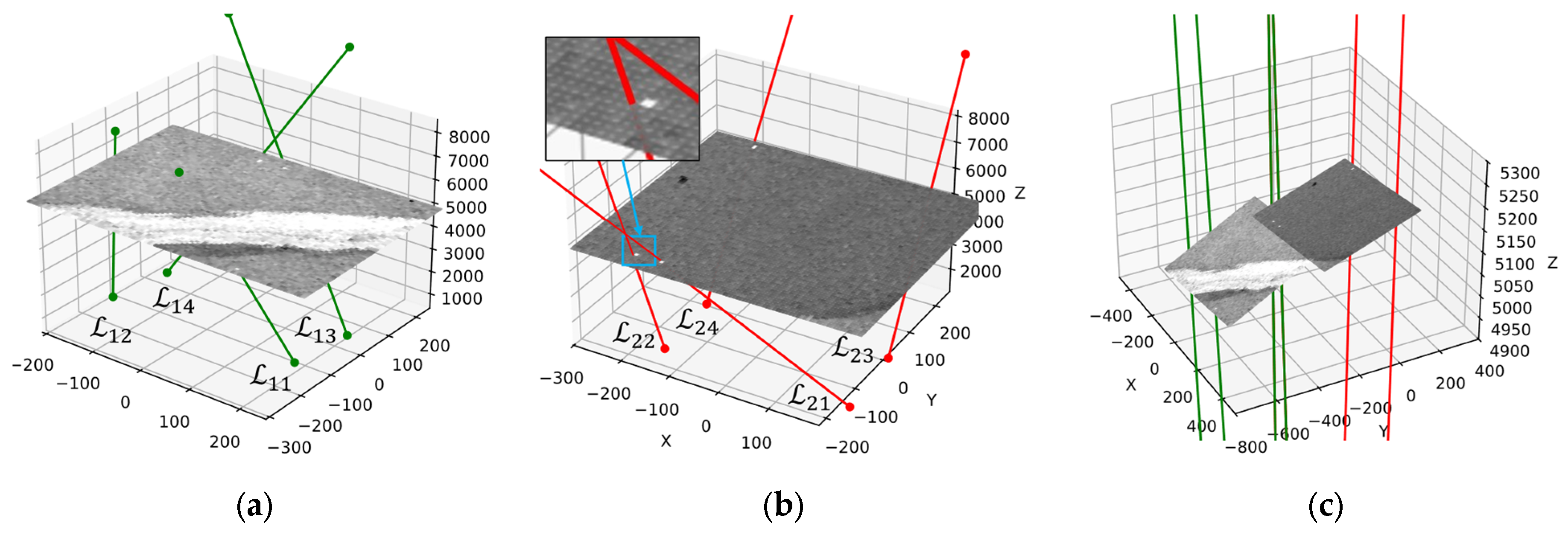
5.2. Indoor Experiment
- (1)
- A minimum point pair distance of 500 mm was used to eliminate Plücker coordinates generated by closely spaced point pairs in the NCCP–Plücker set;
- (2)
- A total of 500 Plücker coordinates were randomly selected from the filtered NCCP–Plücker set for calculation;
- (3)
- The chosen NCCP–Plücker coordinates with the CCP–Plücker coordinates were used to obtain the set used for pose estimation.
5.3. Outdoor Experiment
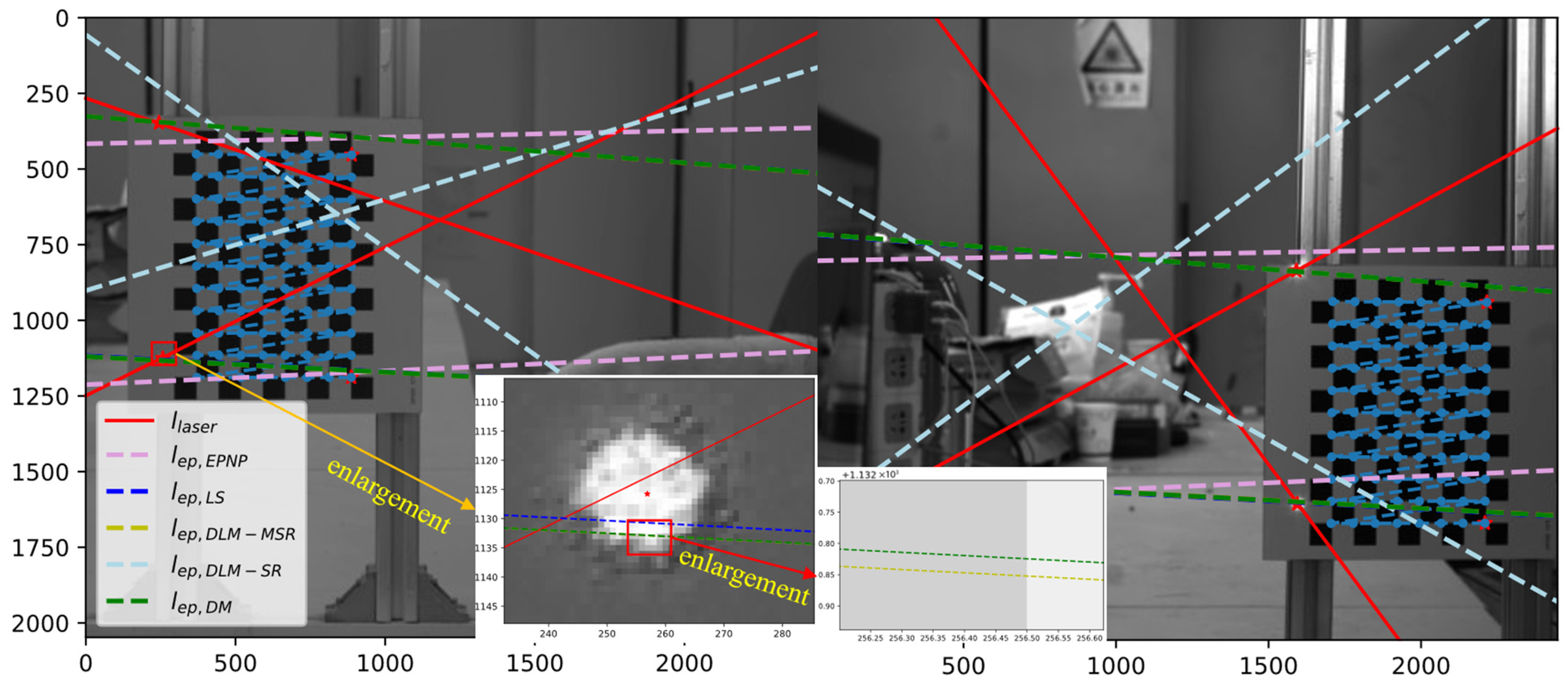
5.4. Image Stitching Experiment Based on Real RIC Data
5.4.1. Selected Cameras
5.4.2. RTL Image Mosaicking with Laser Aid
5.4.3. Comparison of RTL Image-Stitching Methods
6. Conclusions
- (1)
- This study assumes that the projection relationship between the camera images and tunnel lining is a planar projection, ignoring the curvature of the tunnel cross-section. Therefore, the laser array-assisted image stitching method proposed in this study is only applicable to tunnels with smooth cross-sectional profiles and may fail for tunnels with non-smooth cross-sectional profiles, such as immersed tube tunnels.
- (2)
- This study did not address the issue of image stitching when laser points are missing.
- (3)
- Because of the limitations of the current experimental conditions, this study did not analyze the pixel scale error in the stitched lining images, and the panoramic RTL image was not provided in this study.
- (4)
- Because insufficiently diverse set of real-world RTL images, quantitative stitching-error statistics are not yet available.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RTL | Road Tunnel Lining |
| RTL-D | RTL Deformation |
| RTL-ADs | RTL Appearance Defects |
| RTL-IDs | RTL Internal Defects |
| RIC | Road Tunnel Lining Inspection Car |
| FOVs | Fields of View |
| ASC | Area-scanning Camera |
| LSC | Line-scanning Camera |
| LSL | Line-scanning Laser |
| SVD | Singular Value Decomposition |
| NCC | Normalized Cross-correlation |
| PNP | Perspective-n-Point |
| NCCP | Non-corresponding Control Point |
| CCP | Corresponding Control Point |
| DQ | Dual Quaternions |
| MCC | Maximum Correntropy Criterion |
| DLM | DQ Laplace–MCC algorithm |
| RMS | Root Mean Square |
| MAE | Mean Absolute Error |
| MSR | Modified Silverman’s Rule |
| EEA | Estimation Error of Euler Angle |
| ET | Estimation Error of Translate |
| CT | Computation Time |
| ICE | Windows Image Composite Editor |
Appendix A
References
- Xu, G.; He, C.; Chen, Z.; Liu, C.; Wang, B.; Zou, Y. Mechanical behavior of secondary tunnel lining with longitudinal crack. Eng. Fail. Anal. 2020, 113, 104543. [Google Scholar] [CrossRef]
- Zhang, N.; Zhu, X.; Ren, Y. Analysis and Study on Crack Characteristics of Highway Tunnel Lining. Civ. Eng. J. 2019, 5, 1119–1123. [Google Scholar] [CrossRef]
- 2015-16896; National Tunnel Inspection Standards. Federal Highway Administration: Washington, DC, USA, 2015.
- FHWA-HIF-15-005; Tunnel Operations, Maintenance, Inspection, and Evaluation (TOMIE) Manual. Federal Highway Administration: Washington, DC, USA, 2015.
- Xiao, J.Z.; Dai, F.C.; Wei, Y.Q.; Min, H.; Xu, C.; Tu, X.B.; Wang, M.L. Cracking mechanism of secondary lining for a shallow and asymmetrically-loaded tunnel in loose deposits. Tunn. Undergr. Space Technol. 2014, 43, 232–240. [Google Scholar] [CrossRef]
- Tuchiya, Y.; Kurakawa, T.; Matsunaga, T.; Kudo, T. Research on the Long-Term Behaviour and Evaluation of Lining Concrete of the Seikan Tunnel. Soils Found. 2009, 49, 969–980. [Google Scholar] [CrossRef]
- Lei, M.; Peng, L.; Shi, C.; Wang, S. Experimental study on the damage mechanism of tunnel structure suffering from sulfate attack. Tunn. Undergr. Space Technol. 2013, 36, 5–13. [Google Scholar] [CrossRef]
- Kaise, S.; Maegawa, K.; Ito, T.; Yagi, H.; Shigeta, Y.; Maeda, K.; Shinji, M. Study of the image photographing of the tunnel lining as an alternative method to proximity visual inspection. In Tunnels and Underground Cities: Engineering and Innovation Meet Archaeology, Architecture and Art; CRC Press: Boca Raton, FL, USA, 2019; pp. 2325–2334. [Google Scholar]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional networks and transformers for intelligent road tunnel investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, L.; Zhang, J.; Yang, H. Real-time tunnel lining crack detection based on an improved You Only Look Once version X algorithm. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 181–195. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C.; Wu, W. Automatic tunnel lining crack detection via deep learning with generative adversarial network-based data augmentation. Undergr. Space 2023, 9, 140–154. [Google Scholar] [CrossRef]
- Pandey, A.; Pati, U.C. Image mosaicing: A deeper insight. Image Vis. Comput. 2019, 89, 236–257. [Google Scholar] [CrossRef]
- Ghosh, D.; Kaabouch, N. A survey on image mosaicing techniques. J. Vis. Commun. Image Represent. 2016, 34, 1–11. [Google Scholar] [CrossRef]
- Wang, Z.; He, L.; Li, T.; Tao, J.; Hu, C.; Wang, M. Tunnel Image Stitching Based on Geometry and Features; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; p. 012013. [Google Scholar]
- ZOYON. ZOYON-TFS. Available online: http://en.zoyon.com.cn/index.php/list/49.html (accessed on 25 June 2025).
- Du, M.; Fan, J.; Huang, Y.; Cao, M. Mosaicking of mountain tunnel images guided by laser rangefinder. Autom. Constr. 2021, 127, 103708. [Google Scholar] [CrossRef]
- Liao, J.; Yue, Y.; Zhang, D.; Tu, W.; Cao, R.; Zou, Q.; Li, Q. Automatic tunnel crack inspection using an efficient mobile imaging module and a lightweight CNN. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15190–15203. [Google Scholar] [CrossRef]
- Tian, L.; Li, Q.; He, L.; Zhang, D. Image-Range Stitching and Semantic-Based Crack Detection Methods for Tunnel Inspection Vehicles. Remote Sens. 2023, 15, 5158. [Google Scholar] [CrossRef]
- Tjgeo. Tjgeo Tunnel Inspection Vehicle TDV-H. Available online: https://www.cnssce.org/29/201901/2199.html (accessed on 25 June 2025).
- Liu, X.; Li, Y.; Xue, C.; Liu, B.; Duan, Y. Optimal modeling and parameter identification for visual system of the road tunnel detection vehicle. Chin. J. Sci. Instrum. 2018, 39, 152–160. [Google Scholar]
- Keisokukensa Co., Ltd. MIMM. Available online: https://www.keisokukensa.co.jp/english#ttl-navi05 (accessed on 25 June 2025).
- Tonox Co., Ltd. Tonox TC2. Available online: http://www.tonox.com/tunnel.html (accessed on 25 June 2025).
- Ricoh. Tunnel Monitoring System Visualizing the Condition of Tunnels in Order to Keep Such Social Infrastructure Safe. Available online: https://www.ricoh.com/technology/tech/087_tunnel_monitoring (accessed on 25 June 2025).
- NEXCO. Smart-EAGLE Type-T (Tunnel). Available online: https://www.w-e-shikoku.co.jp/product/product-429/ (accessed on 25 June 2025).
- NEXCO. Road L&L System. Available online: https://www.w-e-shikoku.co.jp/product/product-424/ (accessed on 25 June 2025).
- Takahiro Osaki, T.K. Tomohiko Masuda, Development of Run Type High-resolution Image Measurement System (Tunnel Tracer). Robot. Soc. Jpn. 2016, 34, 591–592. [Google Scholar] [CrossRef]
- Kim, I.; Lee, C. Development of video shooting system and technique enabling detection of micro cracks in the tunnel lining while driving. J. Korean Soc. Hazard Mitig. 2018, 18, 217–229. [Google Scholar] [CrossRef]
- Kim, C.N.; Kawamura, K.; Shiozaki, M.; Tarighat, A. An image-matching method based on the curvature of cost curve for producing tunnel lining panorama. J. JSCE 2018, 6, 78–90. [Google Scholar] [CrossRef]
- Nguyen, C.; Kawamura, K.; Shiozaki, M.; Tarighat, A. Development of an Automatic Crack Inspection System for Concrete Tunnel Lining Based on Computer Vision Technologies; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; p. 012015. [Google Scholar]
- Alpha-Product. FOCUSα-T for Tunnel. Available online: https://www.alpha-product.co.jp/focus (accessed on 25 June 2025).
- Zou, L.; Huang, Y.; Li, Y.; Chen, Y. Tunnel linings inspection using Bayesian-Optimized (BO) calibration of multiple Line-Scan Cameras (LSCs) and a Laser Range Finder (LRF). Tunn. Undergr. Space Technol. 2024, 147, 105653. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Q.; Zhai, J.; Yuan, D.; Zhang, W.; Xie, X.; Zhou, B.; Cai, J.; Lei, Y. Design of Fast Acquisition System and Analysis of Geometric Feature for Highway Tunnel Lining Cracks Based on Machine Vision. Appl. Sci. 2022, 12, 2516. [Google Scholar] [CrossRef]
- Pahwa, R.S.; Leong, W.K.; Foong, S.; Leman, K.; Do, M.N. Feature-less stitching of cylindrical tunnel. arXiv 2018, arXiv:1806.10278. [Google Scholar]
- Pahwa, R.S.; Chan, K.Y.; Bai, J.; Saputra, V.B.; Do, M.N.; Foong, S. Dense 3D reconstruction for visual tunnel inspection using unmanned aerial vehicle. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 7025–7032. [Google Scholar]
- Jiang, Y.; Zhang, X.; Taniguchi, T. Quantitative condition inspection and assessment of tunnel lining. Autom. Constr. 2019, 102, 258–269. [Google Scholar] [CrossRef]
- Toru Yasuda, H.Y. Yoshiyuki Shigeta, Tunnel Inspection System by using High-speed Mobile 3D Survey Vehicle: MIMM-R. J. Robot. Soc. Jpn. 2016, 34, 589–590. [Google Scholar] [CrossRef]
- Yasuda, T.; Yamamoto, H.; Enomoto, M.; Nitta, Y. Smart Tunnel Inspection and Assessment using Mobile Inspection Vehicle, Non-Contact Radar and AI. In Proceedings of the International Symposium on Automation and Robotics in Construction, Kitakyushu, Japan, 27–28 October 2020; (ISARC 2020). IAARC Publications: Oulu, Finland, 2020; pp. 1373–1379. [Google Scholar]
- Guo, H.; Mohanty, A.; Ding, Q.; Wang, T.T. Image mosaicking of a section of a tunnel lining and the detection of cracks through the frequency histogram of connected elements concept. In Proceedings of the 2012 International Workshop on Image Processing and Optical Engineering, Harbin, China, 9–10 January 2012; SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Lee, C.-H.; Chiu, Y.-C.; Wang, T.-T.; Huang, T.-H. Application and validation of simple image-mosaic technology for interpreting cracks on tunnel lining. Tunn. Undergr. Space Technol. 2013, 34, 61–72. [Google Scholar] [CrossRef]
- Tu, Y.; Song, Y.; Liu, F.; Zhou, Y.; Li, T.; Zhi, S.; Wang, Y. An Accurate and Stable Extrinsic Calibration for a Camera and a 1D Laser Range Finder. IEEE Sens. J. 2022, 22, 9832–9842. [Google Scholar] [CrossRef]
- Li, Y.; Ja, W.; Chen, P.; Wang, X.; Xu, M.; Xie, Z. Extrinsic calibration of non-overlapping multi-camera system with high precision using circular encoded point ruler. Opt. Lasers Eng. 2024, 174, 107927. [Google Scholar] [CrossRef]
- Van Crombrugge, I.; Penne, R.; Vanlanduit, S. Extrinsic camera calibration for non-overlapping cameras with Gray code projection. Opt. Lasers Eng. 2020, 134, 106305. [Google Scholar] [CrossRef]
- Yang, T.; Zhao, Q.; Zhou, Q.; Huang, D. Global Calibration of Multi-camera Measurement System from Non-overlapping Views. In Artificial Intelligence and Robotics; Springer: Cham, Switzerland, 2018; pp. 183–191. [Google Scholar]
- Yang, T.; Zhao, Q.; Wang, X.; Huang, D. Accurate calibration approach for non-overlapping multi-camera system. Opt. Laser Technol. 2019, 110, 78–86. [Google Scholar] [CrossRef]
- Liu, Z.; Li, F.; Zhang, G. An external parameter calibration method for multiple cameras based on laser rangefinder. Measurement 2014, 47, 954–962. [Google Scholar] [CrossRef]
- Farias, J.G.; De Pieri, E.D.; Martins, D. A Review on the Applications of Dual Quaternions. Machines 2024, 12, 402. [Google Scholar] [CrossRef]
- Rooney, J. A comparison of representations of general spatial screw displacement. Environ. Plan. B Plan. Des. 1978, 5, 45–88. [Google Scholar] [CrossRef]
- Pennestrì, E.; Stefanelli, R. Linear algebra and numerical algorithms using dual numbers. Multibody Syst. Dyn. 2007, 18, 323–344. [Google Scholar] [CrossRef]
- Dekel, A.; Harenstam-Nielsen, L.; Caccamo, S. Optimal least-squares solution to the hand-eye calibration problem. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 13598–13606. [Google Scholar]
- Yu, Q.; Xu, G.; Cheng, Y. An efficient and globally optimal method for camera pose estimation using line features. Mach. Vis. Appl. 2020, 31, 48. [Google Scholar] [CrossRef]
- Faugeras, O. Three-Dimensional Computer Vision, a Geometric Viewpoint; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Přibyl, I.B. Camera Pose Estimation from Lines Using Direct Linear Transformation. Ph.D. Thesis, Faculty of Information Technology, Brno University of Technology, Brno, Czech Republic, 2017. [Google Scholar]
- Hu, C.; Wang, G.; Ho, K.; Liang, J. Robust ellipse fitting with Laplacian kernel based maximum correntropy criterion. IEEE Trans. Image Process. 2021, 30, 3127–3141. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.-B. Dual Quaternions; Iowa State University: Ames, IA, USA, 2013. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An accurate O (n) solution to the PnP problem. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching using Invariant Features. Int. J. Comput. Vis. 2006, 74, 59–73. [Google Scholar] [CrossRef]

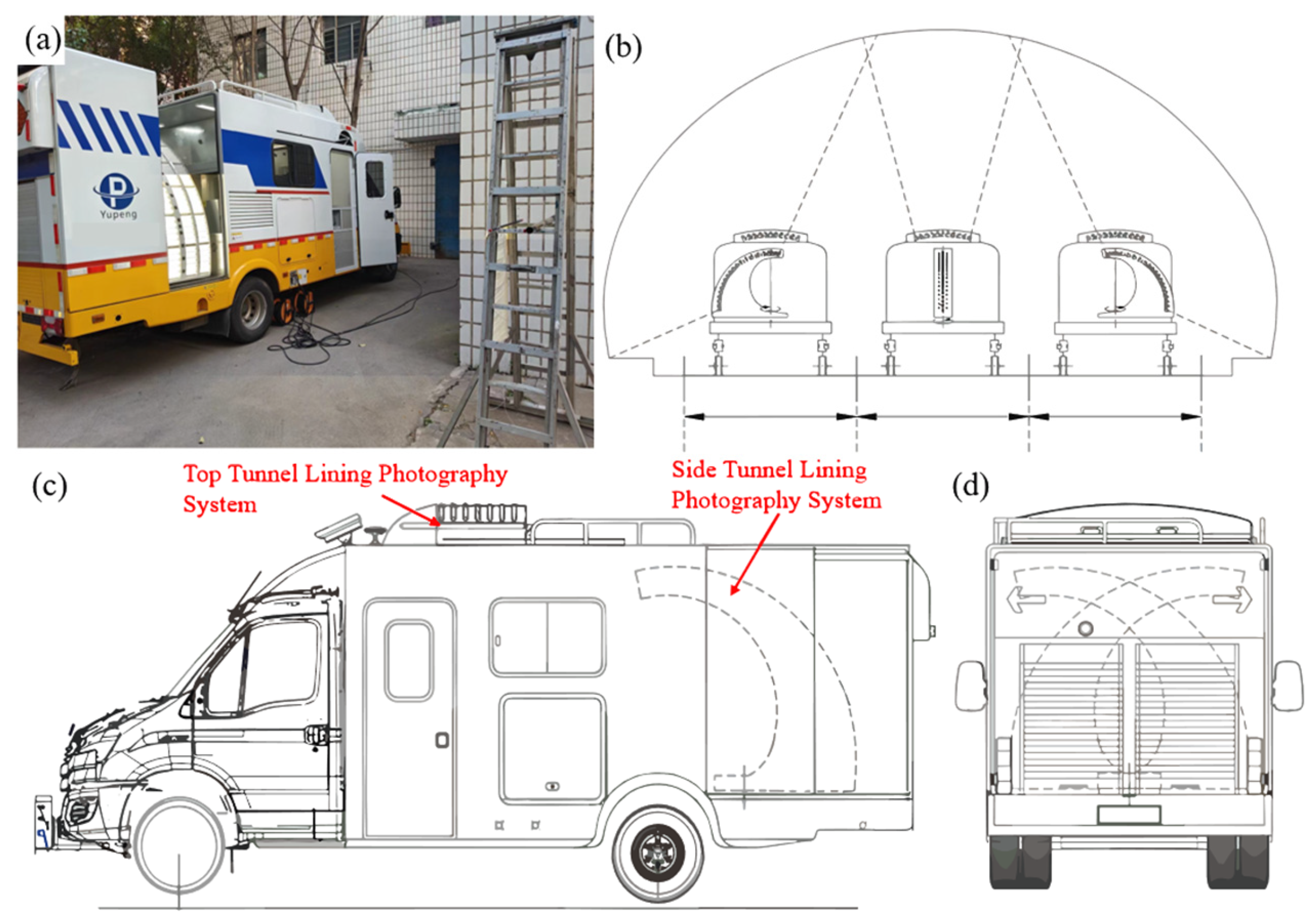
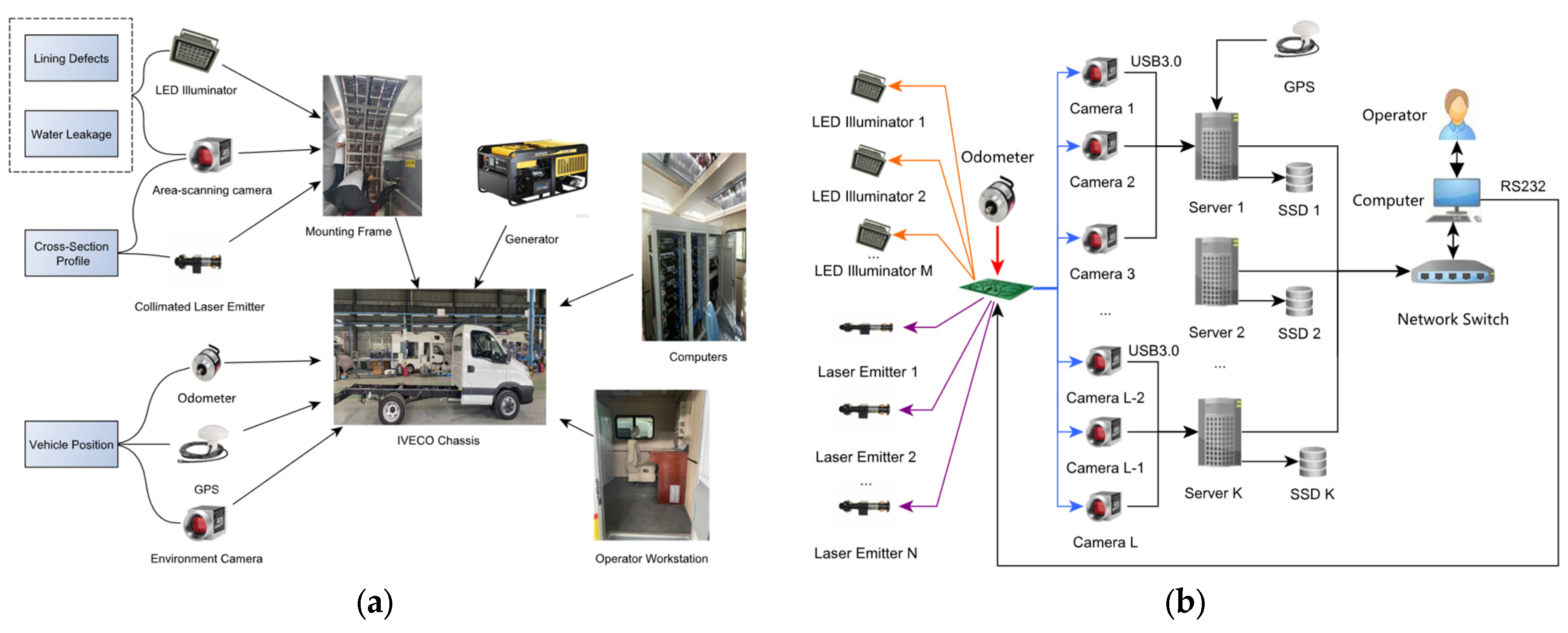










| RIC System | Camera Type | Illumination | Auxiliary Sensor | Manufacturer Location |
|---|---|---|---|---|
| ZOYON TFS [14,15,16,17,18] | ASC | LED | Lidar | China |
| tjgeo TDV-H [19] | ASC | LED | Lidar | China |
| TiDS [20] | LSC | LSL | Lidar | China |
| Keisokukensa Co., MIMM-R [21] | ASC | LED | Lidar | Japan |
| Tonox TC-2 [22] | LSC | LSL | \ | Japan |
| Ricoh TMS [23] | LSC | LSL | \ | Japan |
| NEXCO Smart-EAGLE [24,25] | LSC | LED | \ | Japan |
| Tunnel Tracer [26] | ASC | LED | \ | Japan |
| Kim’s [27] | ASC | LED | \ | South Korea |
| Nguyen’s [28,29] | ASC | LED | \ | Japan |
| Alpha-product FOCUSα-T [30] | ASC | LED | Collimated lasers | Japan |
| Zou’s [31] | LSC | LED | Lidar | China |
| Tongji University’s [32] | ASC | LED | Lidar | China |
| Component Type | Model | Key Parameters | Quantity | |
|---|---|---|---|---|
| Collimated laser | 520 nm collimated laser | Output power 70 mW | Top: 22 | Side: 44 |
| LED strobe module | In-house design | 18 × 18 W LED chips per module | Top: 120 | Side: 160 |
| Frequency divider | In-house design | FPGA: Altera EPF10K20TC144-4 | single | |
| Server computer | Advantech AIIS-3410U | Intel i7-6700 CPU, 8 GB RAM | Top: 3 | Side: 8 |
| Narrow-FOV camera | Basler acA2440-75 um/uc | 2440 × 2048 px, 3.45 µm pixel; lens focal length: f = 50 mm (side), f = 75 mm (top) | Top: 11 (Mono) | Side: 21 (Color) |
| Wide-FOV camera | Basler acA2440-75 uc | Same sensor as above; lens focal length: f = 8 mm | Top: 1 | Side: 3 |
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | ||
|---|---|---|---|---|---|---|---|
| DQ-LS | EEA | 0.0063 | 0.0063 | 0.0080 | 0.0093 | 0.0112 | 0.0125 |
| ET | 12.28 | 16.61 | 21.32 | 25.22 | 30.60 | 34.13 | |
| CT | 0.67 | 0.76 | 0.69 | 0.70 | 0.69 | 0.67 | |
| DLM-MSR | EEA | 0.0025 | 0.0026 | 0.0030 | 0.0031 | 0.0035 | 0.0036 |
| ET | 3.55 | 3.71 | 4.11 | 4.38 | 4.83 | 5.18 | |
| IC | 3.39 | 3.57 | 3.76 | 3.88 | 3.99 | 3.84 | |
| CT | 4.88 | 5.42 | 5.42 | 5.52 | 4.93 | 4.34 | |
| DLM-SR | EEA | 0.0029 | 0.0030 | 0.0031 | 0.0034 | 0.0038 | 0.0040 |
| ET | 3.99 | 4.2203 | 4.5065 | 4.7390 | 5.2032 | 5.6193 | |
| IC | 10.71 | 10.33 | 10.27 | 10.03 | 10.73 | 10.12 | |
| CT | 10.86 | 12.56 | 11.34 | 12.35 | 11.16 | 11.62 | |
| DM | EEA | 0.0025 | 0.0026 | 0.0030 | 0.0032 | 0.0035 | 0.0037 |
| ET | 3.56 | 3.74 | 4.18 | 4.51 | 4.97 | 5.30 | |
| CT | 2.12 | 2.34 | 2.11 | 2.18 | 2.03 | 2.03 |
| rad] | Displacement/[mm] | Mean CCP Reprojection Error/[mm] | Epipolar Constraint Error RMS/[pix] | |
|---|---|---|---|---|
| EPNP | [91.09, −1628.02, −7701.98 | [315.96, −7.48, 77.16] | 20.79 | 0.770 |
| DQ-LS | [54.38, −9.426, −6792.29] | [271.49, 19.70, 58.32] | 10.13 | 0.943 |
| DLM-MSR | [174.278, −69.579, −6781.41] | [271.24, 20.04, 62.71] | 10.24 | 0.944 |
| DLM-SR | [4515.932, −0.606, −6808.39] | [310.26, −63.43, −5777.59] | 5835.96 | 6.29 |
| DM | [222.435, −69.184, −6781.95] | [271.26, 20.13, 62.70] | 10.24 | 0.944 |
| Design Value | [0, 0, 0] | [280, 0, 0] |
| Algorithm | Euler Angles (Yaw, Pitch, Roll)/Degree | Translation/mm |
|---|---|---|
| DLM-MSR | (−2.309, 0.140, −3.514) (3.131, −0.272, −4.981) | (21.82, 120.50, 258.43) (−1.01, 117.72, −373.73) |
| DM | (−2.309, 0.143, −3.514) (3.131, −0.272, −4.981) | (21.82, 120.50, 258.43) (−1.01, 117.72, −373.73) |
| DQ-LS | (−2.486, 4.345, −3.530) (3.288, −4.677, −5.113) | (32.15, 121.58, 318.20) (15.97, 117.78, −410.87) |
| EPNP | (1.769, −11.624, 3.805) (−14.490, −22.829, 40.962) | (888.51, 96.96, −312.61) (1370.40, 1412.53, 1317.17) |
| Design value | (0, 0, −4.89) (0, 0, −4.95) |
| Algorithm | Laser Point Sets 1/4 Projection Error | Laser Point Sets 2/3 Projection Error | ||
|---|---|---|---|---|
| MAE/[mm] | RMS/[mm] | MAE/[mm] | RMS/[mm] | |
| DLM-MSR | (36.46, 19.85) | (36.50, 19.92) | (19.91, 8.03) | (19.92, 8.10) |
| DM | (37.36, 19.87) | (37.40, 19.94) | (20.98, 8.17) | (20.99, 8.18) |
| Intrinsic Parameters | Laser Plücker Coordinates | Camera Pose (Euler Angle and Translation) | |
|---|---|---|---|
| Camera 1 | |||
| Camera 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Ma, J.; Wang, J.; Song, H.; Xu, J. Mobile Tunnel Lining Measurable Image Scanning Assisted by Collimated Lasers. Sensors 2025, 25, 4177. https://doi.org/10.3390/s25134177
Wu X, Ma J, Wang J, Song H, Xu J. Mobile Tunnel Lining Measurable Image Scanning Assisted by Collimated Lasers. Sensors. 2025; 25(13):4177. https://doi.org/10.3390/s25134177
Chicago/Turabian StyleWu, Xueqin, Jian Ma, Jianfeng Wang, Hongxun Song, and Jiyang Xu. 2025. "Mobile Tunnel Lining Measurable Image Scanning Assisted by Collimated Lasers" Sensors 25, no. 13: 4177. https://doi.org/10.3390/s25134177
APA StyleWu, X., Ma, J., Wang, J., Song, H., & Xu, J. (2025). Mobile Tunnel Lining Measurable Image Scanning Assisted by Collimated Lasers. Sensors, 25(13), 4177. https://doi.org/10.3390/s25134177






