Design and Hysteresis Compensation of Novel Resistive Angle Sensor Based on Rotary Potentiometer
Abstract
1. Introduction
2. Methods
2.1. System Architecture
2.2. Principle of Operation
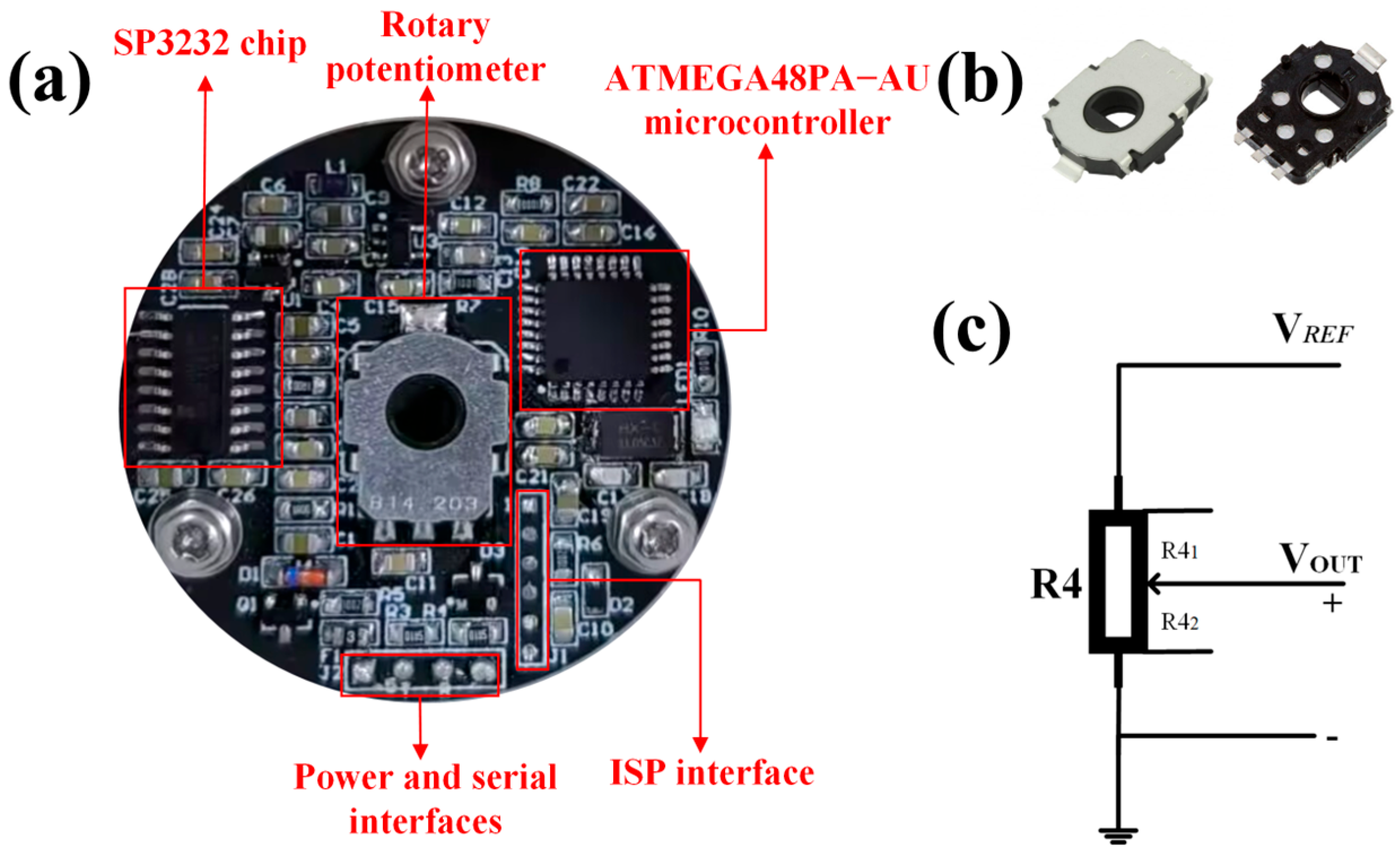
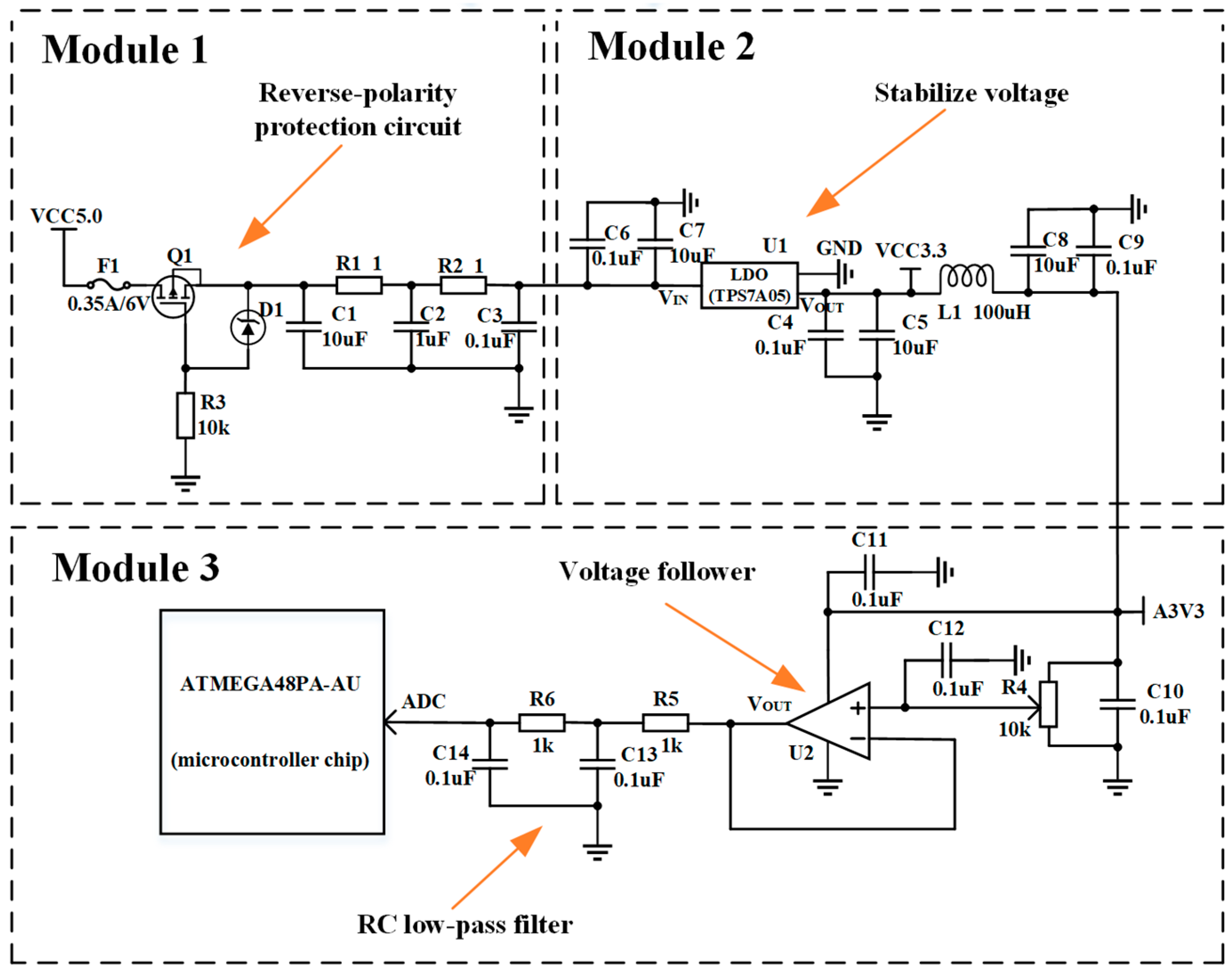
2.3. Microcontroller and Circuit
2.4. Mechanical Housing of Sensor
3. Experiments
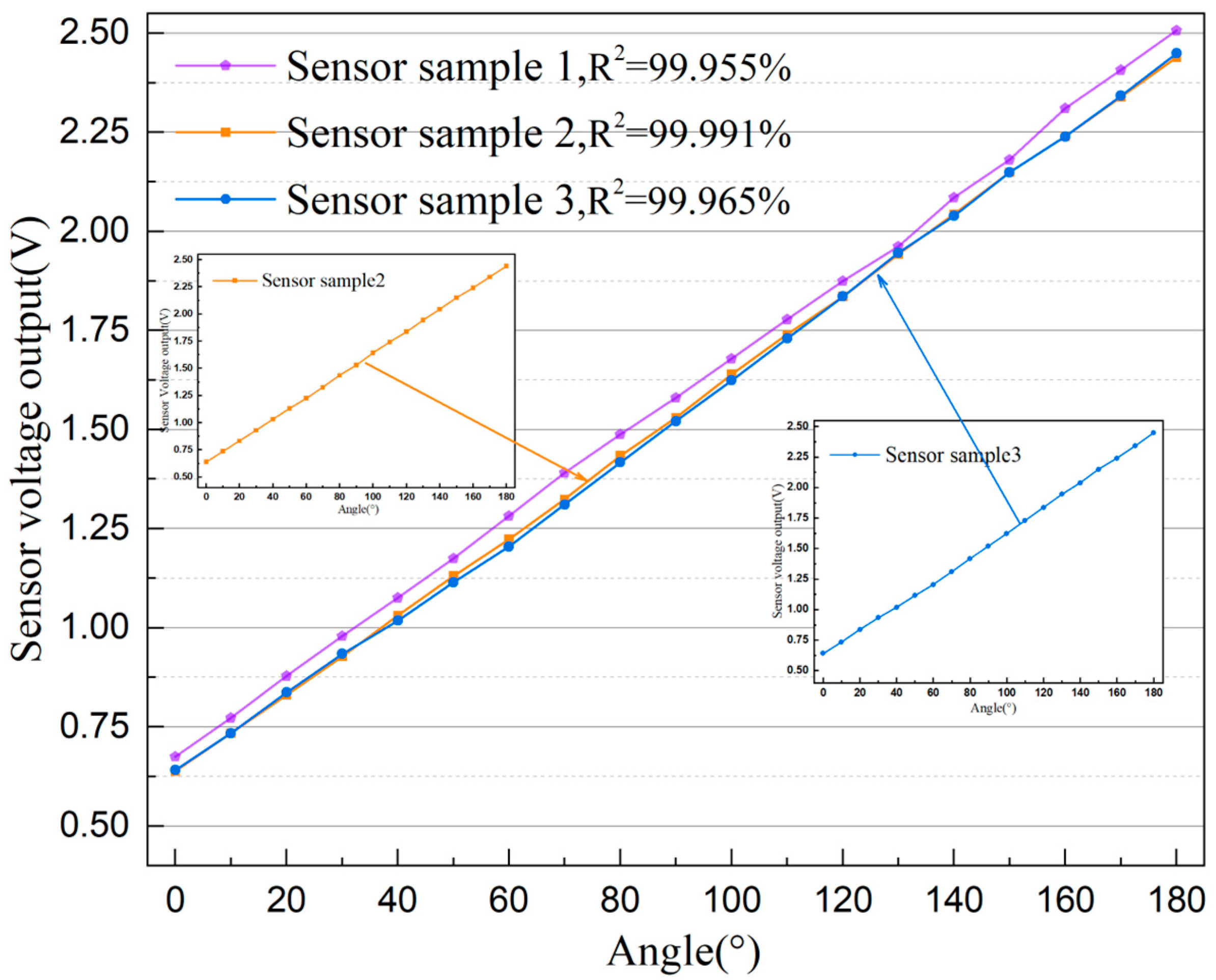
3.1. Consistency Testing
3.2. Linearity Testing
- Coefficient correlation:
- Coefficient correlation:
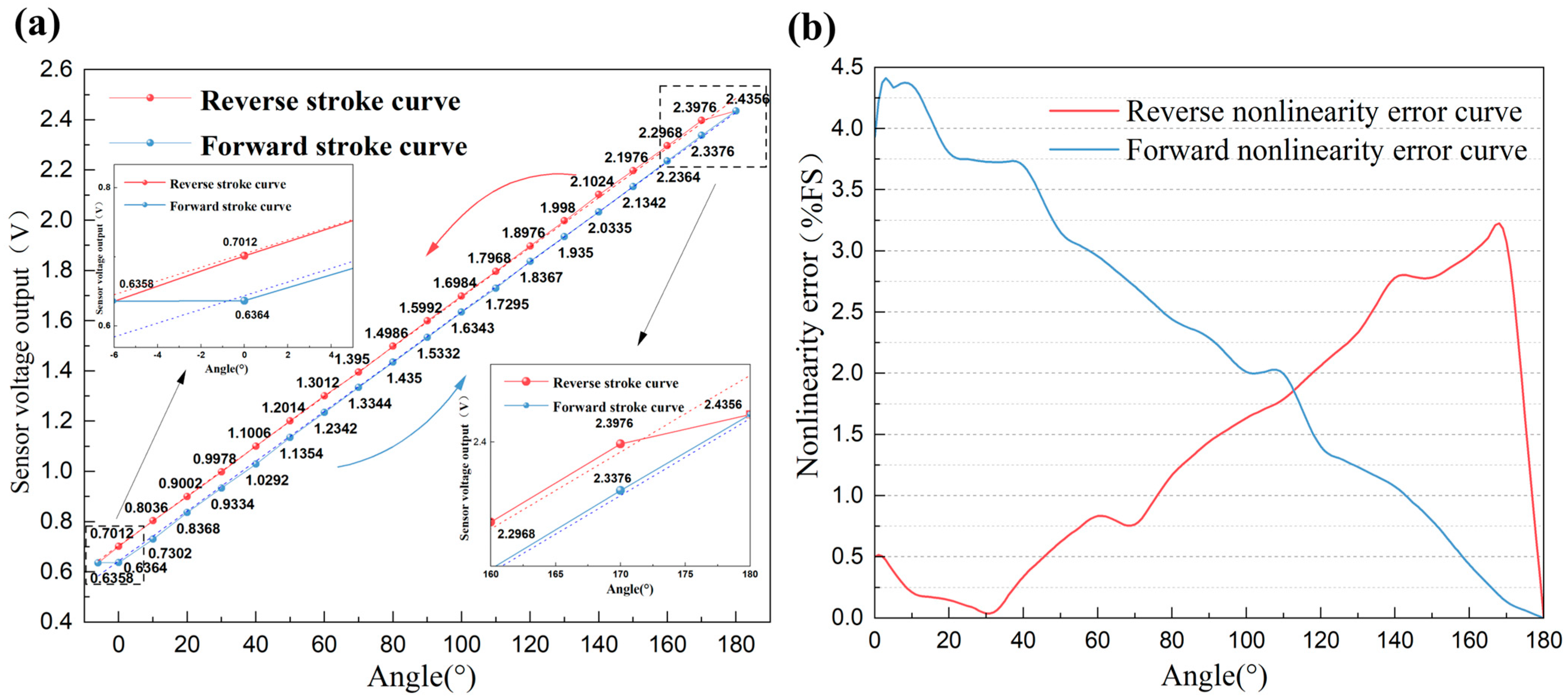
3.3. Hysteresis Testing
3.4. Temperature Drift and Humidity Tolerance Testing
3.5. Mechanical Vibration Testing
4. Hysteresis Compensation and Simulation Analysis
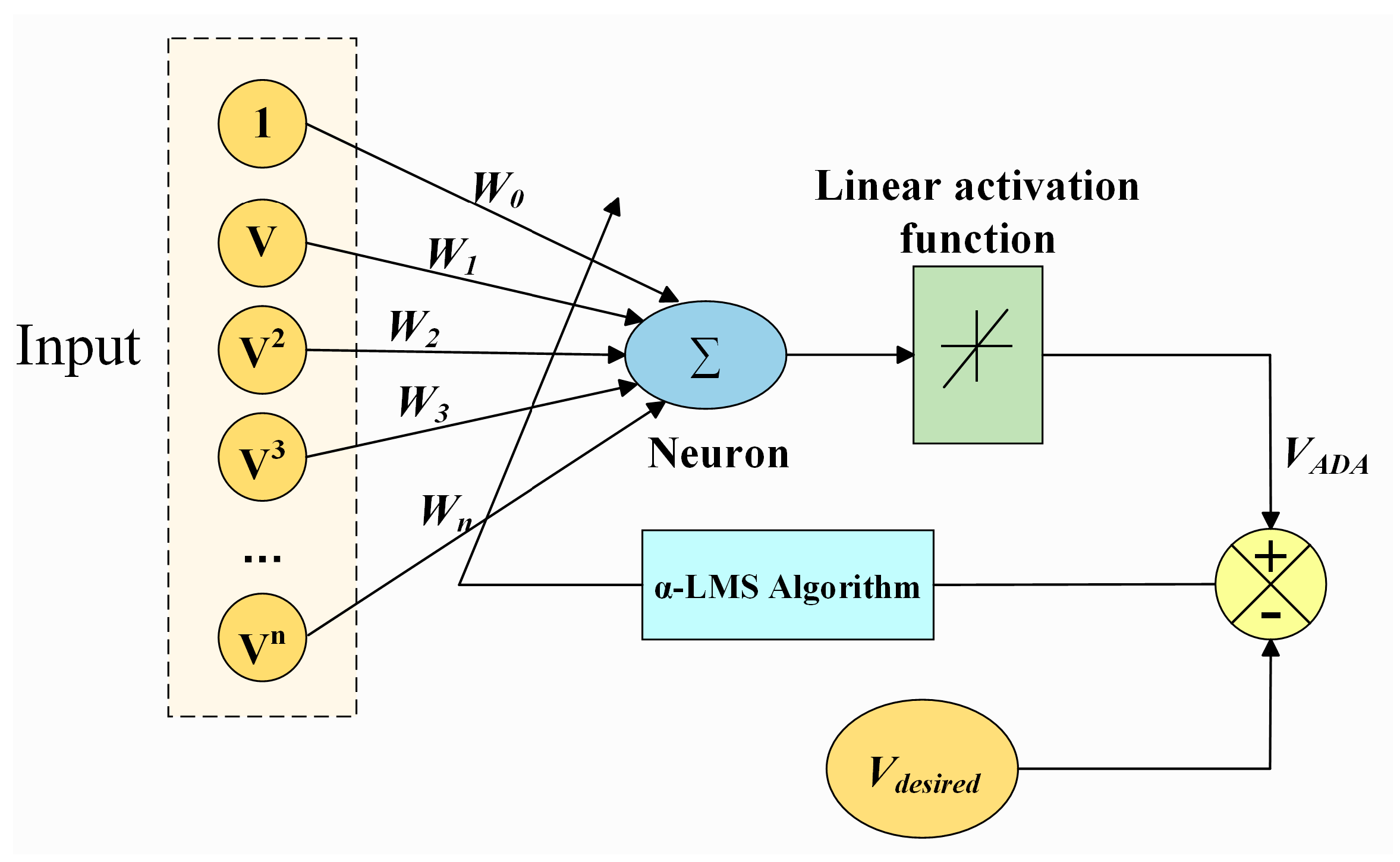
4.1. Adaptive Linear Neuron Model
4.2. α-LMS Algorithm
4.3. Simulation Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.A.; George, B.; Mukhopadhyay, S.C. Technologies and applications of angle sensors: A review. IEEE Sens. J. 2020, 21, 7195–7206. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Chen, X.; Tang, Q.; Zhang, T.; Wu, L. Absolute inductive angular displacement sensor for position detection of YRT turntable bearing. IEEE Trans. Ind. Electron. 2022, 69, 10644–10655. [Google Scholar] [CrossRef]
- Pu, H.; Wang, H.; Liu, X.; Yu, Z.; Peng, K. A high-precision absolute angular position sensor with Vernier capacitive arrays based on time grating. IEEE Sens. J. 2019, 19, 8626–8634. [Google Scholar] [CrossRef]
- Goto, D.; Sakaue, Y.; Kobayashi, T.; Kawamura, K.; Okada, S.; Shiozawa, N. Bending angle sensor based on double-layer capacitance suitable for human joint. IEEE Open J. Eng. Med. Biol. 2023, 4, 129–140. [Google Scholar] [CrossRef]
- Wu, L.; Su, R.; Tong, P.; Wu, Y. An inductive sensor for the angular displacement measurement of large and hollow rotary machinery. IEEE Sens. J. 2023, 23, 21709–21717. [Google Scholar] [CrossRef]
- Chen, X.; He, X.; Zhang, Y.; Gao, B. Angle Measurement Method Based on Cross-Orthogonal Hall Sensor. In Proceedings of the 2023 IEEE 16th International Conference on Electronic Measurement & Instruments (ICEMI), Harbin, China, 9–11 August 2023. [Google Scholar]
- Wang, S.; Ma, R.; Cao, F.; Luo, L.; Li, X. A review: High-precision angle measurement technologies. Sensors 2024, 24, 1755. [Google Scholar] [CrossRef] [PubMed]
- Leal-Junior, A.G.; Avellar, L.M.; Díaz, C.A.; Pontes, M.J.; Frizera, A. Polymer optical fiber sensor system for multi plane bending angle assessment. IEEE Sens. J. 2019, 20, 2518–2525. [Google Scholar] [CrossRef]
- Othman, A.; Hamzah, N.; Hussain, Z.; Baharudin, R.; Rosli, A.D.; Ani, A.I.C. Design and development of an adjustable angle sensor based on rotary potentiometer for measuring finger flexion. In Proceedings of the 2016 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 25–27 November 2016. [Google Scholar]
- De Fazio, R.; Mastronardi, V.M.; De Vittorio, M.; Visconti, P. Wearable sensors and smart devices to monitor rehabilitation parameters and sports performance: An overview. Sensors 2023, 23, 1856. [Google Scholar] [CrossRef]
- Duan, S.; Zhao, F.; Yang, H.; Hong, J.; Shi, Q.; Lei, W.; Wu, J. A pathway into metaverse: Gesture recognition enabled by wearable resistive sensors. Adv. Sens. Res. 2023, 2, 2200054. [Google Scholar] [CrossRef]
- Saggio, G.; Calado, A.; Errico, V.; Lin, B.-S.; Lee, I.-J. Dynamic measurement assessments of sensory gloves based on resistive flex sensors and inertial measurement units. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Tiboni, M.; Borboni, A.; Vérité, F.; Bregoli, C.; Amici, C. Sensors and actuation technologies in exoskeletons: A review. Sensors 2022, 22, 884. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xiao, A.; Zheng, T.; Xiao, H.; Huang, R. The relationship between sleeping position and sleep quality: A flexible sensor-based study. Sensors 2022, 22, 6220. [Google Scholar] [CrossRef] [PubMed]
- Sakthivel, M.; Tarafdar, U.; Anoop, C. A simple linear circuit for angle measurements using a non-contact potentiometer. In Proceedings of the 2022 IEEE Delhi Section Conference (DELCON), New Delhi, India, 11–13 February 2022. [Google Scholar]
- Sakthivel, M.; Tarafdar, U. Performance Analysis of a New Non-contact, Potentiometric Angle Sensor. In Proceedings of the 2022 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Toronto, ON, Canada, 1–4 June 2022. [Google Scholar]
- Hamid, Y.; Hutt, D.A.; Whalley, D.C.; Craddock, R. Relative Contributions of Packaging Elements to the Thermal Hysteresis of a MEMS Pressure Sensor. Sensors 2020, 20, 1727. [Google Scholar] [CrossRef] [PubMed]
- Lai, Z.-L.; Chen, Z.; Liu, X.-D.; Wu, Q.-H. A novel similarity-based hysteresis empirical model for piezoceramic actuators. Sens. Actuators A Phys. 2013, 197, 150–165. [Google Scholar] [CrossRef]
- Lien, J.; York, A.; Fang, T.; Buckner, G.D. Modeling piezoelectric actuators with hysteretic recurrent neural networks. Sens. Actuators A Phys. 2010, 163, 516–525. [Google Scholar] [CrossRef]
- Wang, X.; Ye, M. Hysteresis and nonlinearity compensation of relative humidity sensor using support vector machines. Sens. Actuators B Chem. 2008, 129, 274–284. [Google Scholar] [CrossRef]
- Hollingshead, R.; Henry-Etesse, L.; Tankere, E.; Kamper, D.; Tan, T. Characterization of hysteresis in resistive bend sensors. In Proceedings of the 2017 International Symposium on Wearable Robotics and Rehabilitation (WeRob), Houston, TX, USA, 5–8 November 2017. [Google Scholar]
- Islam, T.; Ghosh, S.; Saha, H. ANN-based signal conditioning and its hardware implementation of a nanostructured porous silicon relative humidity sensor. Sens. Actuators B Chem. 2006, 120, 130–141. [Google Scholar] [CrossRef]
- TIA-232-F; Interface Between Data Terminal Equipment and Data Circuit-Terminating Equipment Employing Serial Binary Data Interchange. Telecommunications Industry Association: Arlington, VA, USA, 1997.
- Sanca, A.S.; Rocha, J.C.; Eugenio, K.J.; Nascimento, L.B.; Alsina, P.J. Characterization of Resistive Flex Sensor Applied to Joint Angular Displacement Estimation. In 2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE); Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018. [Google Scholar]
- Bahari, M.; Davoodi, A.; Saneie, H.; Tootoonchian, F.; Nasiri-Gheidari, Z. A new variable reluctance PM-resolver. IEEE Sens. J. 2019, 20, 135–142. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, B. Design and realization of an optical rotary sensor. IEEE Sens. J. 2018, 18, 2675–2681. [Google Scholar] [CrossRef]
- Yu, Z.; Peng, K.; Liu, X.; Chen, Z.; Huang, Y. A high-precision absolute angular-displacement capacitive sensor using three-stage time-grating in conjunction with a remodulation scheme. IEEE Trans. Ind. Electron. 2018, 66, 7376–7385. [Google Scholar] [CrossRef]
- Wang, W.; Wang, R.; Chen, Z.; Sang, Z.; Lu, K.; Han, F.; Wang, J.; Ju, B. A new hysteresis modeling and optimization for piezoelectric actuators based on asymmetric Prandtl-Ishlinskii model. Sens. Actuators A Phys. 2020, 316, 112431. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Xie, X.; Li, M.; Li, L.; Mao, X. Development of MEMS composite sensor with temperature compensation for tire pressure monitoring system. J. Micromechanics Microengineering 2021, 31, 125015. [Google Scholar] [CrossRef]
- Wang, B.; Gu, X.; Ma, L.; Yan, S. Temperature error correction based on BP neural network in meteorological wireless sensor network. Int. J. Sens. Netw. 2017, 23, 265–278. [Google Scholar] [CrossRef]
- Li, B.; Sun, G.; Zhang, H.; Dong, L.; Kong, Y. Design of MEMS Pressure Sensor Anti-Interference System Based on Filtering and PID Compensation. Sensors 2024, 24, 5765. [Google Scholar] [CrossRef]
- IEC 60068-2-6; Environmental testing—Part 2–6: Tests—Test Fc: Vibration (sinusoidal). International Electrotechnical Commission: Geneva, Switzerland, 2018.
- Khan, S.A.; Shahani, D.; Agarwala, A. Sensor calibration and compensation using artificial neural network. ISA Trans. 2003, 42, 337–352. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Kumar, S.; Kamal, T.S. Fitting transducer characteristics to measured data using a virtual curve tracer. Sens. Actuators A Phys. 2004, 111, 145–153. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Pao, Y. Adaptive Pattern Recognition and Neural Networks; Addison-Wesley Longman Publishing Co., Inc: Boston, MA, USA, 1989. [Google Scholar]
- Kumar, A.A.; George, B. A noncontact angle sensor based on eddy current technique. IEEE Trans. Instrum. Meas. 2019, 69, 1275–1283. [Google Scholar] [CrossRef]






| Angle (°) | Test Temperature (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| −20 | −10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | |
| 30° | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 0.981 | 0.981 | 0.981 | 0.981 |
| 60° | 1.274 | 1.274 | 1.274 | 1.274 | 1.274 | 1.274 | 1.274 | 1.274 | 1.274 |
| 90° | 1.565 | 1.562 | 1.562 | 1.562 | 1.562 | 1.562 | 1.562 | 1.562 | 1.562 |
| 120° | 1.855 | 1.855 | 1.855 | 1.855 | 1.855 | 1.855 | 1.855 | 1.855 | 1.855 |
| 150° | 2.146 | 2.146 | 2.146 | 2.146 | 2.146 | 2.146 | 2.146 | 2.146 | 2.146 |
| Angle (°) | Pre-Compensation Forward Stroke Voltage (V) | Post-Compensation Forward Stroke Voltage (V) | Pre-Compensation Reverse Stroke Voltage (V) | Post-Compensation Reverse Stroke Voltage (V) |
|---|---|---|---|---|
| 0 | 0.6364 | 0.6922 | 0.7012 | 0.6936 |
| 20 | 0.8368 | 0.8875 | 0.9002 | 0.8873 |
| 40 | 1.0292 | 1.0747 | 1.1006 | 1.0822 |
| 60 | 1.2342 | 1.2739 | 1.3012 | 1.2769 |
| 80 | 1.4350 | 1.4688 | 1.4986 | 1.4686 |
| 100 | 1.6343 | 1.6620 | 1.6984 | 1.6622 |
| 120 | 1.8367 | 1.8577 | 1.8976 | 1.8549 |
| 140 | 2.0335 | 2.0482 | 2.1024 | 2.0529 |
| 160 | 2.2364 | 2.2441 | 2.2968 | 2.2405 |
| 180 | 2.4356 | 2.4418 | 2.4356 | 2.4223 |
| Parameters | Resistive Sensors | Inductive Sensors | Magnetoresistive Sensors | Optical Sensors | ||||
|---|---|---|---|---|---|---|---|---|
| This Work | WDD35D4 from MIRAN, CHN * | [37] | RI360P1 from TURCK, GER * | [6] | ADA4571 from ADI, USA * | [8] | E6CP-A from Omron, CHN * | |
| Range | 180° | 345° | 360° | 360° | 360° | 180° | 360° | 360° |
| Resolution | 0.31° | 0.07° | 0.08° | 0.09° | 0.1° | 0.5° | 0.02° | 8 bit |
| Output characteristics | Linear | Linear | Linear | Linear | Linear | Non-Linear | Linear | Non-Linear |
| Nonlinearity error of full scale | 0.18% | 0.3% | 0.25% | 0.3% | - | ±0.7° | 1.15% | ±1° |
| temperature drift (per °C) | 0.004° | 0.003° | - | ≤0.036° | - | ≤0.004° | - | - |
| Manufacturing complexity | Simple | Moderate | Simple | Moderate | Moderate | Complex | Complex | Complex |
| Sensitive to EMI | No | No | No | Yes | Yes | Yes | No | No |
| Cost | Low | Moderate | Low | Moderate | Moderate | Low | High | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Li, M.; Zhang, J.; Han, Z. Design and Hysteresis Compensation of Novel Resistive Angle Sensor Based on Rotary Potentiometer. Sensors 2025, 25, 4077. https://doi.org/10.3390/s25134077
Liu R, Li M, Zhang J, Han Z. Design and Hysteresis Compensation of Novel Resistive Angle Sensor Based on Rotary Potentiometer. Sensors. 2025; 25(13):4077. https://doi.org/10.3390/s25134077
Chicago/Turabian StyleLiu, Ruiqi, Min Li, Jiahong Zhang, and Zhengguo Han. 2025. "Design and Hysteresis Compensation of Novel Resistive Angle Sensor Based on Rotary Potentiometer" Sensors 25, no. 13: 4077. https://doi.org/10.3390/s25134077
APA StyleLiu, R., Li, M., Zhang, J., & Han, Z. (2025). Design and Hysteresis Compensation of Novel Resistive Angle Sensor Based on Rotary Potentiometer. Sensors, 25(13), 4077. https://doi.org/10.3390/s25134077





