Parameter Identification and Transition Process Online Calibration Method of Pulsed Eddy Current Receiving Coil Based on Underdamped Dynamic Response Characteristics
Abstract
1. Introduction
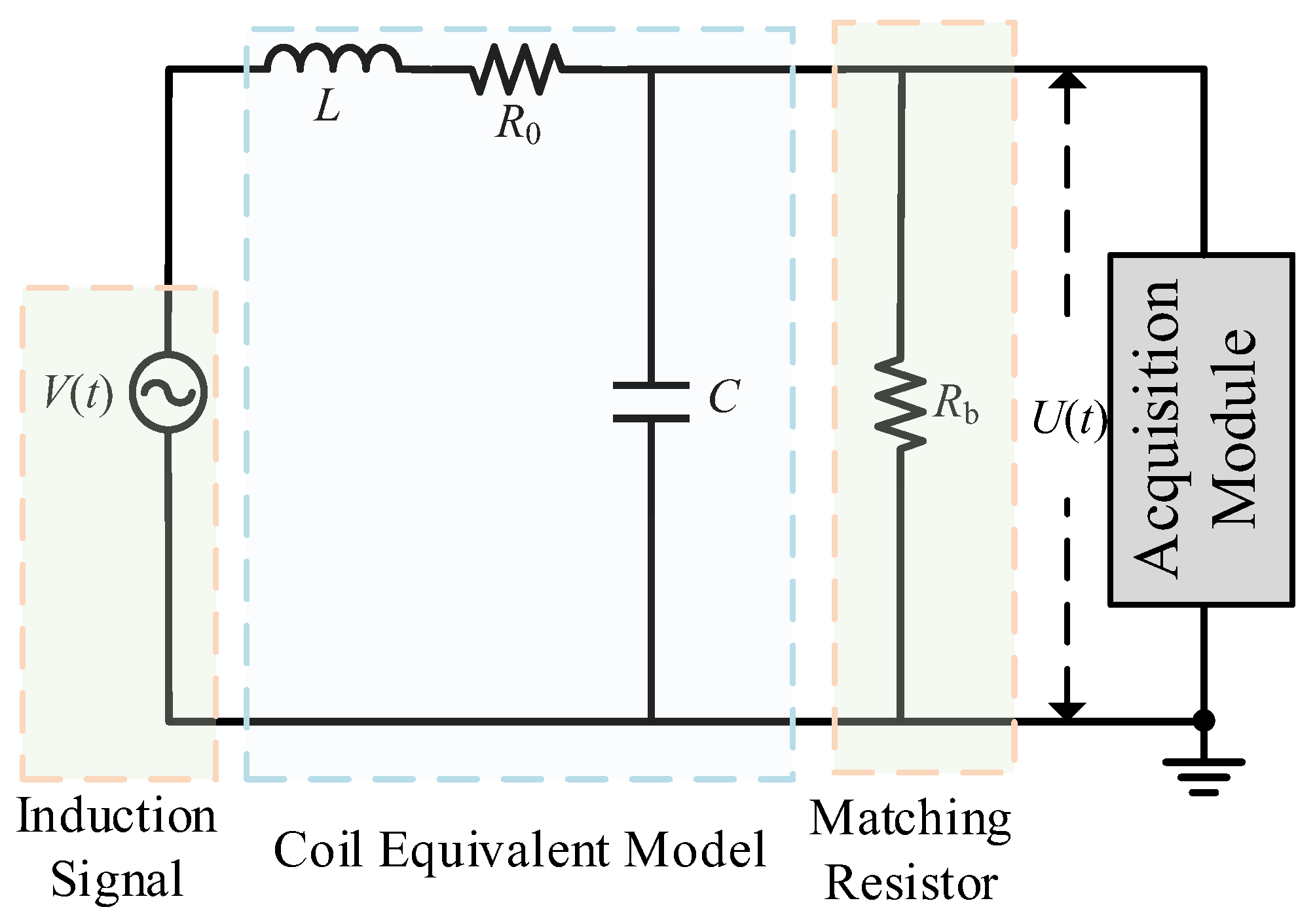
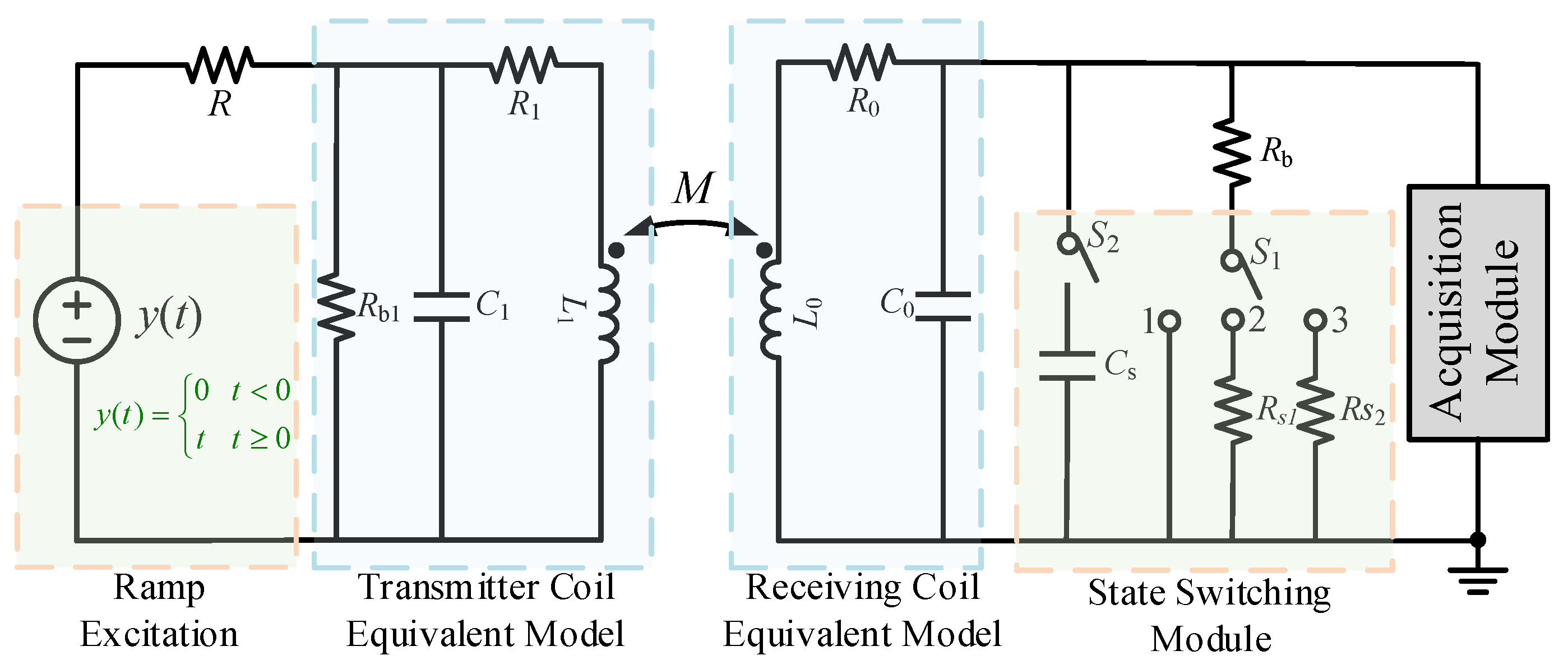
2. Dynamic Response Analysis of Receiving Coil System
3. Receiving Coil Parameter Identification Method
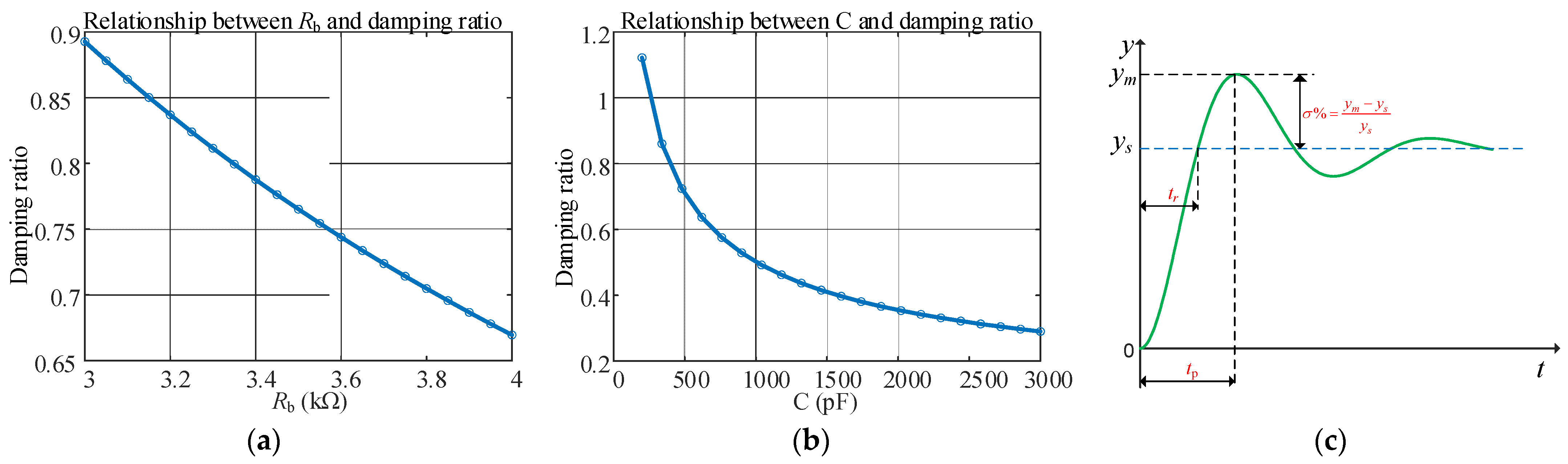
3.1. Characteristic Analysis of Underdamped Oscillation
3.2. Extraction and Calculation of Receiving Coil Characteristic Parameters
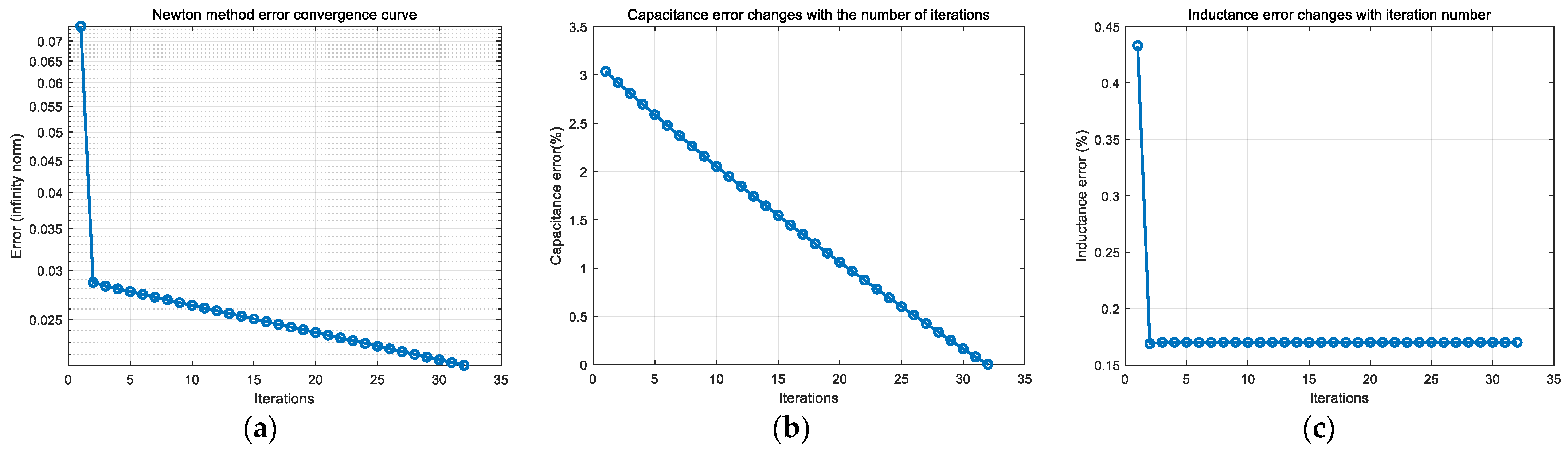
3.3. Nonlinear Identification of System Parameters Based on Newton’s Method
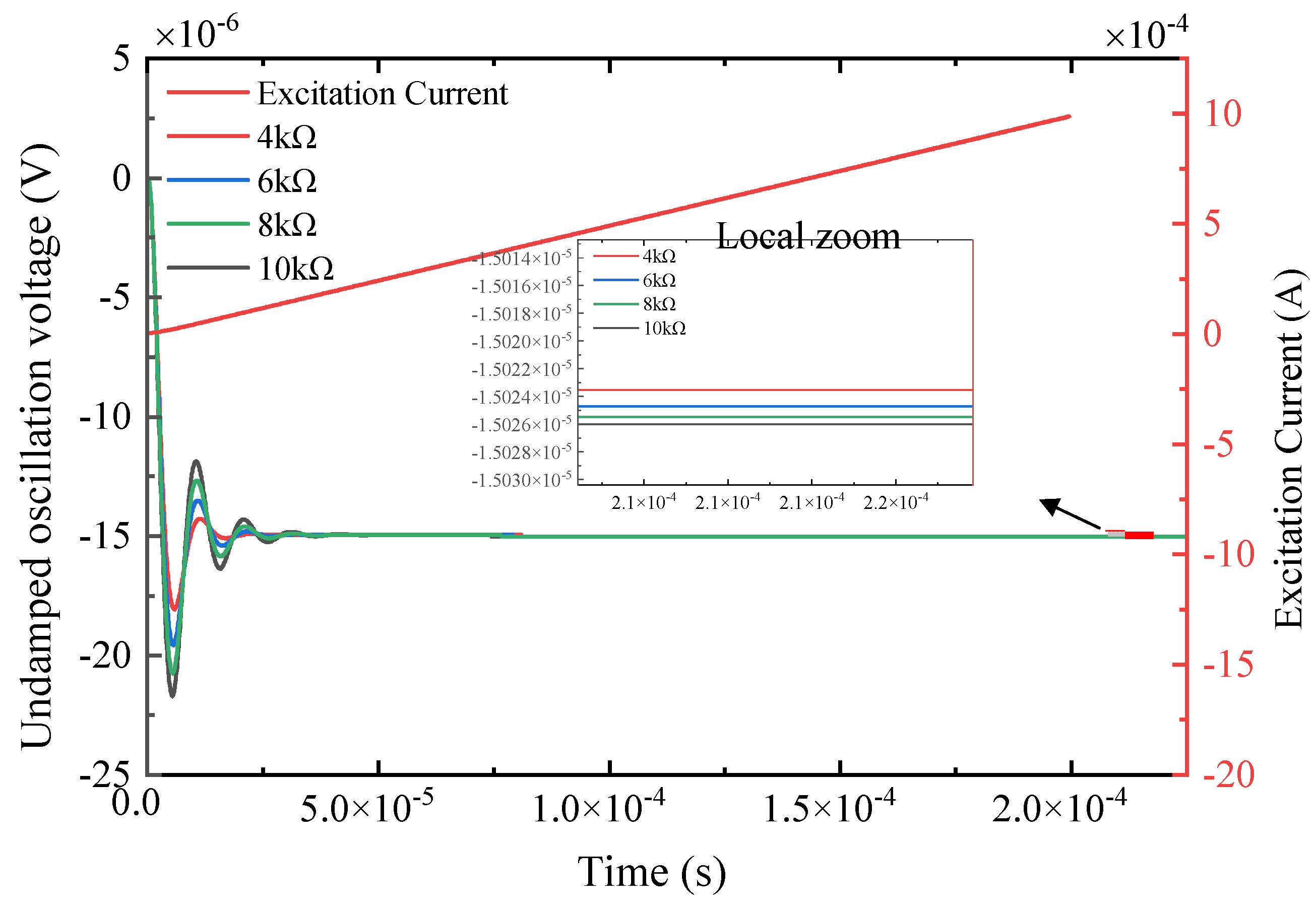
4. Experimental Results
5. Conclusions
- (1)
- The methods of increasing matching resistance and parallel capacitance to change the system state are compared. From the perspective of feature extraction and calculation accuracy of response signal characteristic parameters, the parallel capacitance method is proved to be better.
- (2)
- On the basis of obtaining the accuracy characteristic parameters, the Newton method is used. After parameter identification, the absolute error of the inductance of the receiving coil can be reduced to 0.023%, and the absolute error of the capacitance can be reduced to 0.004956%.
- (3)
- Under experimental conditions, the inductance identification error of the receiving coil can reach 0.17%, and the minimum error of the capacitance parameter can reach 0.038%. The parameter identification method proposed in this paper can efficiently, accurately, and conveniently identify and calibrate the system parameters of the receiving coil online, which is conducive to improving the signal inversion progress and detection accuracy in the pulsed eddy current detection process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, J.; Su, B.; Malekian, R.; Xing, X. Detection of Water-Filled Mining Goaf Using Mining Transient Electromagnetic Method. IEEE Trans. Ind. Inform. 2020, 16, 2977–2984. [Google Scholar] [CrossRef]
- Huang, P.; Pu, H.; Ding, Y.; Li, Z.; Yin, W.; Xu, L.; Xie, Y. A Sensitivity Enhancement PEC Method for Bottom Flaws and Corrosions Detection. Measurement 2022, 202, 111910. [Google Scholar] [CrossRef]
- Leung, C.M.; Wu, K.; Liu, M.; Yang, J. Advancing Eddy Current Detection Probes with Magnetoelectric Composite Materials: Enhancing Crack Detection in Conductive Materials. J. Magn. Magn. Mater. 2024, 592, 171816. [Google Scholar] [CrossRef]
- Silva, M.I.; Malitckii, E.; Santos, T.G.; Vilaca, P. Review of Conventional and Advanced Non-Destructive Testing Techniques for Detection and Characterization of Small-Scale Defects. Prog. Mater. Sci. 2023, 138, 101155. [Google Scholar] [CrossRef]
- Li, X.; Tian, G.; Li, K.; Wang, H.; Zhang, Q. Differential ECT Probe Design and Investigation for Detection of Rolling Contact Fatigue Cracks with Different Orientations. IEEE Sens. J. 2022, 22, 11615–11625. [Google Scholar] [CrossRef]
- Shkatov, P.N. Innovative Surface Eddy Current Probe for Non-Destructive Testing. In Proceedings of the 2023 7th International Conference on Information, Control, and Communication Technologies (ICCT), Astrakhan, Russia, 2–6 October 2023; pp. 1–3. [Google Scholar]
- Machado, M.A. Eddy Currents Probe Design for NDT Applications: A Review. Sensors 2024, 24, 5819. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Jiang, Y.; Yuan, M. Design and Study of Pulsed Eddy Current Sensor for Detecting Surface Defects in Small-Diameter Bars. Sensors 2024, 24, 8063. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Fu, Z.; Wang, Y.; Tai, H.; Qin, S.; Liao, X. A Time-Domain Feedback Calibration Method for Air-Coil Magnetic Sensor. Measurement 2019, 135, 61–70. [Google Scholar] [CrossRef]
- Ye, C.; Laureti, S.; Malekmohammadi, H.; Wang, Y.; Ricci, M. Swept-Frequency Eddy Current Excitation for TMR Array Sensor and Pulse-Compression: Feasibility Study and Quantitative Comparison of Time and Frequency Domains Processing. Measurement 2022, 187, 110249. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, X.; Liu, L.; Fu, N.; Fu, Z. Research on Small-Loop Transient Electromagnetic Method Forward and Nonlinear Optimization Inversion Method. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Fu, Z.; Wang, Y.; Tai, H.-M.; Chen, W. On-Site Calibration of Air-Coil Sensor for Transient Electromagnetic Exploration. Geophys. Prospect. 2019, 67, 1595–1610. [Google Scholar] [CrossRef]
- Zhao, P.; Li, L.; Gao, J.; Ma, Y. Method of Standard Field for LF Magnetic Field Meter Calibration. Measurement 2017, 104, 223–232. [Google Scholar] [CrossRef]
- Coillot, C.; Nativel, E.; Zanca, M.; Goze-Bac, C. The Magnetic Field Homogeneity of Coils by Means of the Space Harmonics Suppression of the Current Density Distribution. J. Sens. Sens. Syst. 2016, 5, 401–408. [Google Scholar] [CrossRef][Green Version]
- Zhang, S.; Liu, Z.; Chen, S. Calibration study of the damping characteristics of transient electromagnetic sensors. Geophys. J. 2014, 57, 662–670. [Google Scholar]
- He, Y.; Xue, G.; Chen, W.; Tian, Z. Three-Dimensional Inversion of Semi-Airborne Transient Electromagnetic Data Based on a Particle Swarm Optimization-Gradient Descent Algorithm. Appl. Sci. 2022, 12, 3042. [Google Scholar] [CrossRef]
- Xu, Z.; Fu, Z.; Fu, N. Firefly Algorithm for Transient Electromagnetic Inversion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]

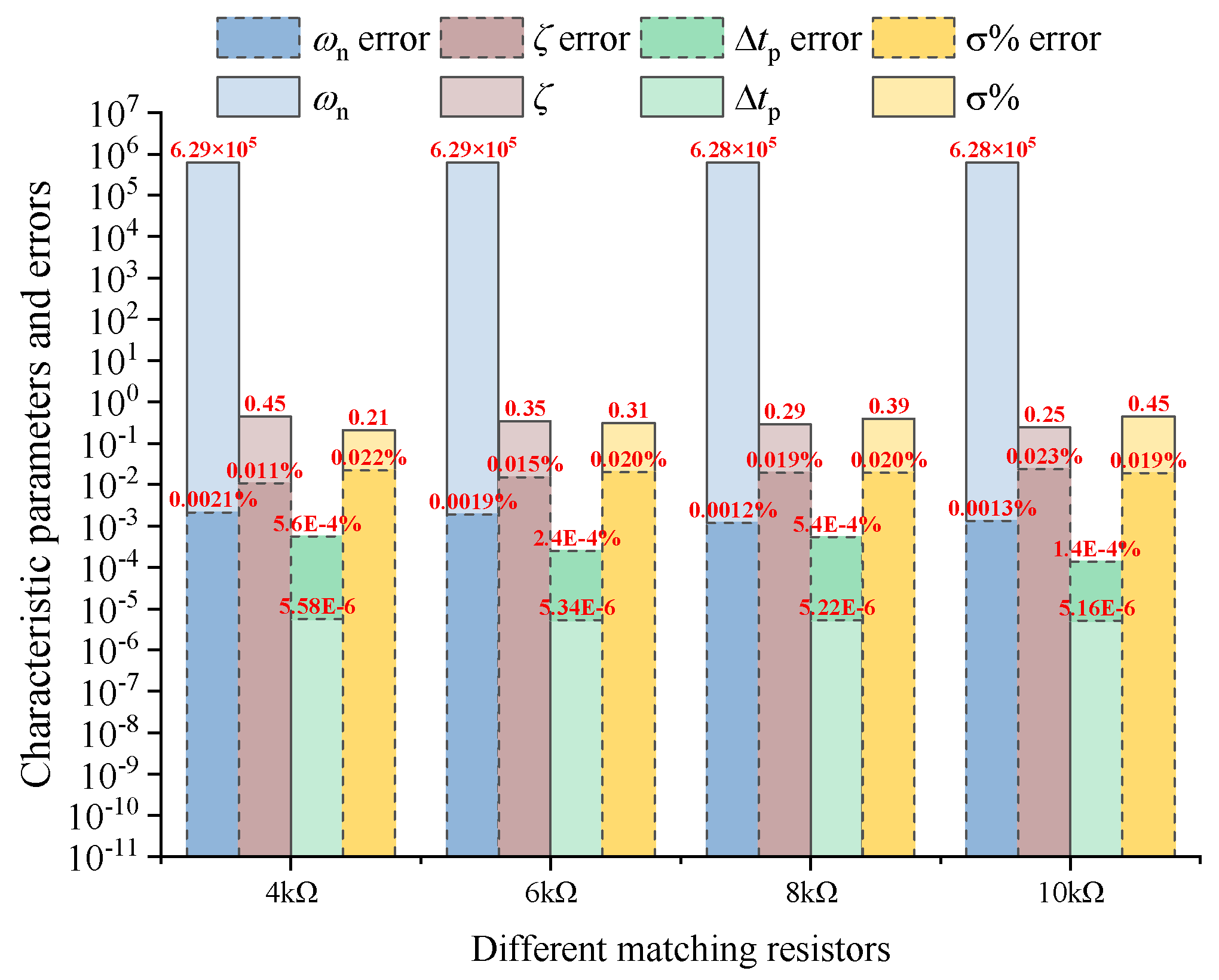

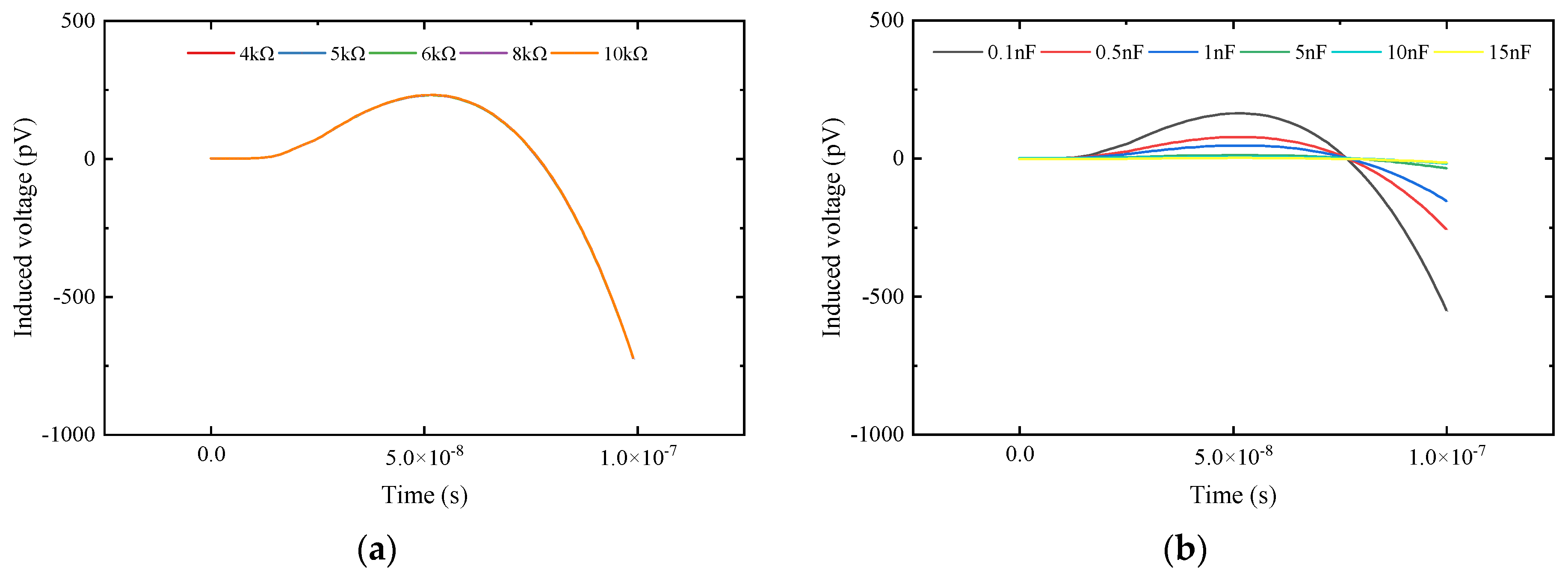


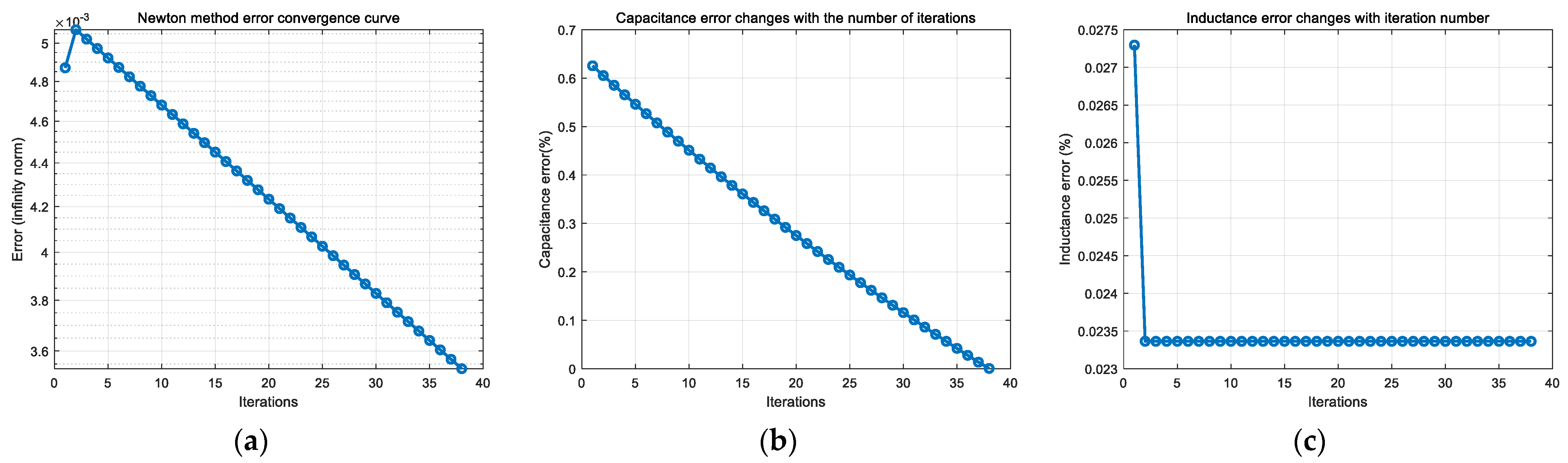


| Resistance (Ω) | 1 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|
| R0 (Ω) | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 | 2.6 |
| Receiving Coil Parameters | L (mH) | C (pF) | R (Ω) |
|---|---|---|---|
| Initial value | 10 | 250 | 2.6 |
| Real value | 10.09 | 251.6225 | 2.6 |
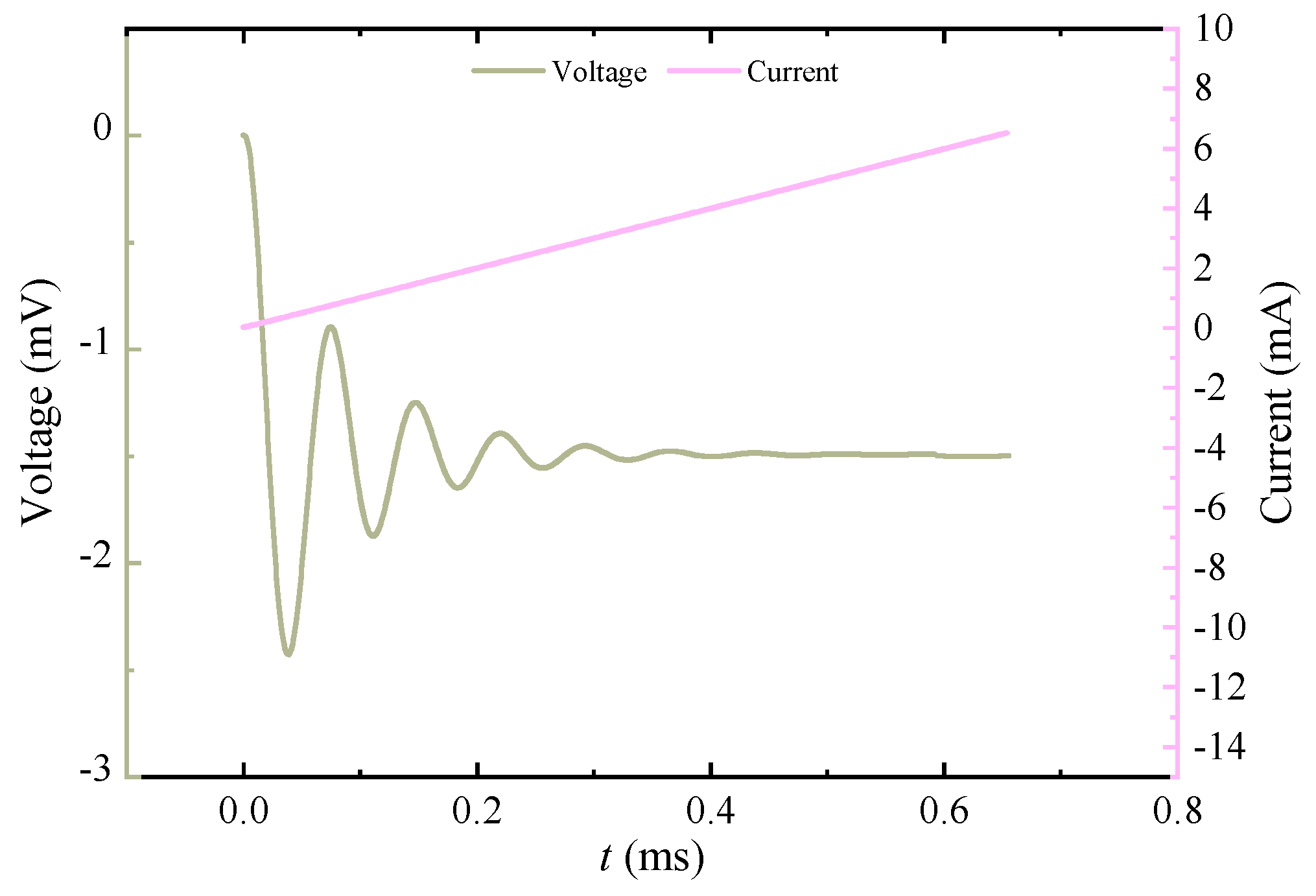
| Characteristic Parameters | Specific Values |
|---|---|
| Peak | 2.4631 mV |
| Adjacent peak time | 0.0364 ms |
| Steady-state value | 1.5017 mV |
| Overshoot | 64.03% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Wang, J.; Huang, X.; Zuo, Y.; Liu, Y.; Tian, X.; Pei, F.; Liu, K.; Chen, F.; Wang, X.; et al. Parameter Identification and Transition Process Online Calibration Method of Pulsed Eddy Current Receiving Coil Based on Underdamped Dynamic Response Characteristics. Sensors 2025, 25, 4049. https://doi.org/10.3390/s25134049
Zeng Z, Wang J, Huang X, Zuo Y, Liu Y, Tian X, Pei F, Liu K, Chen F, Wang X, et al. Parameter Identification and Transition Process Online Calibration Method of Pulsed Eddy Current Receiving Coil Based on Underdamped Dynamic Response Characteristics. Sensors. 2025; 25(13):4049. https://doi.org/10.3390/s25134049
Chicago/Turabian StyleZeng, Zhiwu, Jie Wang, Xiaoju Huang, Yun Zuo, Yuan Liu, Xu Tian, Feng Pei, Kui Liu, Fu Chen, Xiaotian Wang, and et al. 2025. "Parameter Identification and Transition Process Online Calibration Method of Pulsed Eddy Current Receiving Coil Based on Underdamped Dynamic Response Characteristics" Sensors 25, no. 13: 4049. https://doi.org/10.3390/s25134049
APA StyleZeng, Z., Wang, J., Huang, X., Zuo, Y., Liu, Y., Tian, X., Pei, F., Liu, K., Chen, F., Wang, X., & Wang, J. (2025). Parameter Identification and Transition Process Online Calibration Method of Pulsed Eddy Current Receiving Coil Based on Underdamped Dynamic Response Characteristics. Sensors, 25(13), 4049. https://doi.org/10.3390/s25134049







